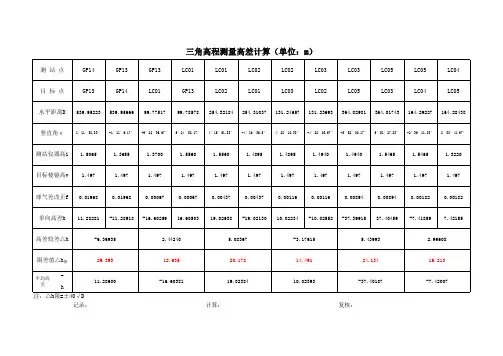
三角高程测记录表
- 格式:doc
- 大小:79.50 KB
- 文档页数:3


测距导线三角高程计算表改正数
(原创实用版)
目录
1.测距导线三角高程计算表的概念
2.测距导线三角高程计算表的改正数
3.测距导线三角高程计算表改正数的应用
4.测距导线三角高程计算表改正数的重要性
正文
测距导线三角高程计算表是一种用于测量地面高程的工具,主要通过测量水平距离和竖直角度来计算地面的高程。
在测量过程中,由于各种因素的影响,测量结果往往会存在误差,因此需要对测量结果进行修正。
这个修正的过程就是通过测距导线三角高程计算表的改正数来完成的。
测距导线三角高程计算表的改正数是指在测量过程中,对水平距离和竖直角度的测量值进行修正的数值。
这个数值的大小取决于测量过程中各种因素对测量结果的影响程度,例如大气折射、地球曲率、测量仪器的精度等。
测距导线三角高程计算表改正数的应用主要体现在对测量结果的修
正上。
通过将改正数应用到测量结果中,可以得到更加准确的地面高程。
这对于地形测绘、工程建设等领域具有重要的意义,因为这些领域需要对地面高程进行精确的测量和控制。
测距导线三角高程计算表改正数的重要性不言而喻。
只有通过准确的改正数,才能保证测量结果的准确性,从而保证工程建设的顺利进行。
第1页共1页。


§5.9 三角高程测量三角高程测量的基本思想是根据由测站向照准点所观测的垂直角(或天顶距)和它们之间的水平距离,计算测站点与照准点之间的高差。
这种方法简便灵活,受地形条件的限制较少,故适用于测定三角点的高程.三角点的高程主要是作为各种比例尺测图的高程控制的一部分.一般都是在一定密度的水准网控制下,用三角高程测量的方法测定三角点的高程.5.9.1 三角高程测量的基本公式1。
基本公式关于三角高程测量的基本原理和计算高差的基本公式,在测量学中已有过讨论,但公式的推导是以水平面作为依据的。
在控制测量中,由于距离较长,所以必须以椭球面为依据来推导三角高程测量的基本公式.如图5-35所示.设0s 为B A 、两点间的实测水平距离。
仪器置于A 点,仪器高度为1i 。
B 为照准点,砚标高度为2v ,R 为参考椭球面上B A ''的曲率半径.AF PE 、分别为过P 点和A 点的水准面。
PC 是PE 在P 点的切线,PN 为光程曲线。
当位于P 点的望远镜指向与PN 相切的PM 方向时,由于大气折光的影响,由N 点出射的光线正好落在望远镜的横丝上。
这就是说,仪器置于A 点测得M P 、间的垂直角为2,1a .由图5-35可明显地看出,B A 、 两地面点间的高差为NB MN EF CE MC BF h --++==2,1 (5-54) 式中,EF 为仪器高NB i ;1为照准点的觇标高度2v ;而CE 和MN 分别为地球曲率和折光影响.由2021s R CE = 2021s R MN '= 式中R '为光程曲线PN 在N 点的曲率半径.设,K R R ='则 20202.21S R K S R R R MN ='=K 称为大气垂直折光系数。
图5-35由于B A 、两点之间的水平距离0s 与曲率半径R 之比值很小(当km s 100=时,0s 所对的圆心角仅5'多一点),故可认为PC 近似垂直于OM ,即认为 90≈PCM ,这样PCM ∆可视为直角三角形。

测距导线三角高程计算表改正数
测距导线三角高程计算表是测绘工程中常用的一种测量工具,它主要用于计算地面上两点之间的高差。
然而,由于测量过程中可能存在的误差,使得计算结果并不完全准确,这时候就需要对测距导线三角高程计算表进行改正,而这个改正数就是我们要讨论的内容。
首先,我们需要明确改正数的定义。
改正数,顾名思义,就是对原有数据进行修正的数值。
在测距导线三角高程计算中,改正数主要用于修正由于测量误差导致的高程计算结果偏差。
改正数的计算方法主要依赖于测量误差的具体情况。
一般来说,如果误差是随机分布的,那么我们可以采用概率统计的方法来计算改正数;如果误差具有规律性,那么我们可以通过具体分析误差来源,采用相应的修正方法来计算改正数。
在实际应用中,改正数的使用可以大大提高测距导线三角高程计算的精度。
具体来说,首先需要根据实际情况,对测距导线三角高程计算表进行修正,然后使用修正后的计算表进行高程计算,这样可以有效提高计算结果的精度。
然而,测距导线三角高程计算表的改正数并不是一成不变的,随着测量条件的变化,改正数也需要进行相应的调整。
因此,如何优化改正数的计算,以适应不同的测量条件,是当前测绘工程中一个重要的研究课题。
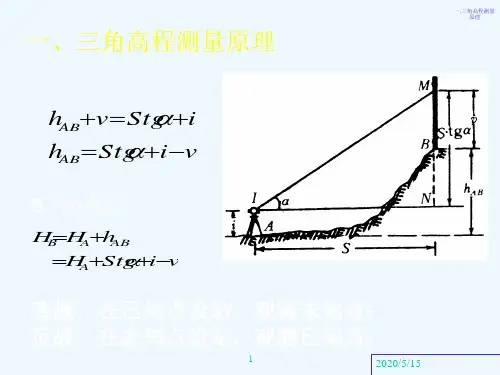

§4-6 三角高程测量一、三角高程测量原理及公式在山区或地形起伏较大的地区测定地面点高程时,采用水准测量进行高程测量一般难以进行,故实际工作中常采用三角高程测量的方法施测。
传统的经纬仪三角高程测量的原理如图4-12所示,设A点高程及AB两点间的距离已知,求B点高程。
方法是,先在A点架设经纬仪,量取仪器高i;在B点竖立觇标(标杆),并量取觇标高L,用经纬仪横丝瞄准其顶端,测定竖直角δ,则AB两点间的高差计算公式为:故(4-11)式中为A、B两点间的水平距离。
图4-12 三角高程测量原理当A、B两点距离大于300m时,应考虑地球曲率和大气折光对高差的影响,所加的改正数简称为两差改正:设c为地球曲率改正,R为地球半径,则c的近似计算公式为:设g为大气折光改正,则g的近似计算公式为:因此两差改正为:,恒为正值。
采用光电三角高程测量方式,要比传统的三角高程测量精度高,因此目前生产中的三角高程测量多采用光电法。
采用光电测距仪测定两点的斜距S,则B点的高程计算公式为:(4-12)为了消除一些外界误差对三角高程测量的影响,通常在两点间进行对向观测,即测定hAB和hBA,最后取其平均值,由于hAB和hBA反号,因此可以抵销。
实际工作中,光电三角高程测量视距长度不应超过1km,垂直角不得超过15°。
理论分析和实验结果都已证实,在地面坡度不超过8度,距离在以内,采取一定的措施,电磁波测距三角高程可以替代三、四等水准测量。
当已知地面两点间的水平距离或采用光电三角高程测量方法时,垂直角的观测精度是影响三角高程测量的精度主要因素。
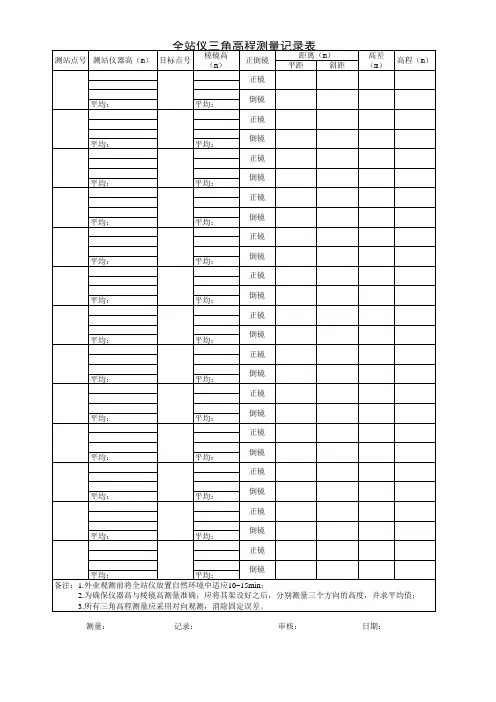
二、光电三角高程测量方法光电三角高程测量需要依据规范要求进行,如《公路勘测规范》中光电三角高程测量具体要求见表4-6。
表4-6 光电三角高程测量技术要求等级仪器测距边测回数垂直角测回数指标差较差(〞)垂直角较差(〞)对向观测高差较差(mm)附合或闭合路线闭合差(mm)三丝法中丝法四等往返各1—3五等112注:表4-6中为光电测距边长度。