三角高程测量的计算实例

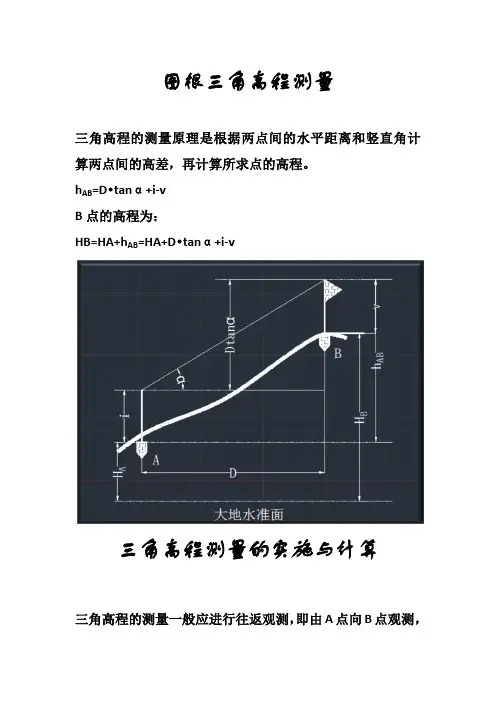
图根三角高程测量
三角高程的测量原理是根据两点间的水平距离和竖直角计算两点间的高差，再计算所求点的高程。

h AB=D•tanα+i-v
B点的高程为：
HB=HA+h AB=HA+D•tanα+i-v
三角高程测量的实施与计算
三角高程的测量一般应进行往返观测，即由A点向B点观测，
再由B点向A点观测，这样的观测称为对向观测。

对向观测可以消除地球曲率和大气折光的影响
观测时，安置经纬仪于测站上，首先量取仪器高i和标志高V，读书至0.4CM，量取两次结果之差不超过1CM，取其平均值至1CM，然后用经纬仪观测竖直角，完成了往测后，再进行反测。

计算时，先计算两点之间的往返高差，符合要求取其平均值，作为两点间的高差。

当用三角高程测量方法测定平面控制点的高程时，要求组成闭合或符合三角高程路线，在闭合差符合要求时，按闭合和符合路线计算各控制点的高程。

三角高程实例这是三角高程的测量数据和简图，A和B是已知高程点，2、3和4是待测的高程点。

原始测量数据如下图"三角高程原始数据表"所示：测站点距离（米）垂直角(°′″)仪器高(米)站标高（米）高程（米）A1474.44401.04401.3096.062021424.71703.25211.301.3431749.3220-0.38081.351.3541950.4120-2.45371.451.50B1.5295.9716三角高程原始数据表三角高程路线图（模拟）上图中r为垂直角在平差易中输入以上数据，如下图"三角高程数据输入"所示：三角高程数据输入在测站信息区中输入A、B、2、3和4号测站点，其中A、B为已知高程点，其属性为01，其高程如"三角高程原始数据表"；2、3、4点为待测高程点，其属性为00，其它信息为空。

因为没有平面坐标数据，故在平差易软件中也没有网图显示。

此控制网为三角高程，选择三角高程格式。

如下图"选择格式"所示：选择格式注意：在"计算方案"中要选择"三角高程"，而不是"一般水准"。

在观测信息区中输入每一个测站的三角高程观测数据测段A点至2号点的观测数据输入如下图"A－>2观测数据"所示：A－>2观测数据测段2点至3号点的观测数据输入如下图"2－>3观测数据"所示：A－>2观测数据测段3点至4号点的观测数据输入如下图"3－>4观测数据"所示：A－>2观测数据测段4点至B点的观测数据输入如下图"4－>B观测数据"所示：4－>B观测数据以上数据输入完后，点击"文件\另存为"，将输入的数据保存为平差易格式文件（格式内容详见附录A）为：[STATION]A,01,,,96.062000,1.30B,01,,,95.97160,2,00,,,,1.303,00,,,,1.354,00,,,,1.45[OBSER]A,2,,1474.444000,27.842040,,1.044000,1.3402,3,,1424.717000,85.289093,,3.252100,1.3503,4,,1749.322000,-19.353448,,-0.380800,1.5004,B,,1950.412000,-93.760085,,-2.452700,1.520。

三角高程测量的计算公式如图6.27所示，已知A点的高程H A，要测定B点的高程 H B，可安置经纬仪于A点，量取仪器高i A；在B点竖立标杆，量取其高度称为觇 B 标高v B；用经纬仪中丝瞄准其顶端，测定竖直角α。

如果已知AB两点间的水平距离D （如全站仪可直接测量平距），则AB两点间的高差计算式为：如果当场用电磁波测距仪测定两点间的斜距D′，则AB两点间的高差计算式为：以上两式中，α为仰角时tanα或sinα为正，俯角时为负。

求得高差h AB以后，按下式计算B 点的高程：以上三角高程测量公式(6.27)、(6.28)中，设大地水准面和通过A、B点的水平面为相互平行的平面，在较近的距离(例如200米)内可以认为是这样的。

但事实上高程的起算面——大地水准面是一曲面，在第一章1.4中已介绍了水准面曲率对高差测量的影响，因此由三角高程测量公式(6.27)、(6.28)计算的高差应进行地球曲率影响的改正，称为球差改正f1，如图6.28(见课本）所示。

按(1.4)式：式中:R为地球平均曲率半径，一般取R=6371km。

另外，由于视线受大气垂直折光影响而成为一条向上凸的曲线，使视线的切线方向向上抬高，测得竖直角偏大，如图6.28所示。

因此还应进行大气折光影响的改正，称为气差改正f2，f2恒为负值。

图6.23 三角高程测量图6.24 地球曲率及大气折光影响设大气垂直折光使视线形成曲率大约为地球表面曲率K倍的圆曲线(K称为大气垂直折光系数)，因此仿照(6.30)式，气差改正计算公式为：球差改正和气差改正合在一起称为球气差改正f，则f应为：大气垂直折光系数K随气温、气压、日照、时间、地面情况和视线高度等因素而改变，一般取其平均值，令K=0.14。

在表6.16中列出水平距离D=100m-200m的球气差改正值f，由于f1>f2，故f恒为正值。

考虑球气差改正时，三角高程测量的高差计算公式为：或由于折光系数的不定性，使球气差改正中的气差改正具有较大的误差。

中点单觇法三角高程测量的误差及精度分析摘要：本文主要探讨了中点单觇法三角高程测量中可能出现的误差及其精度分析。

首先，介绍了中点单觇法三角高程测量的基本原理和方法，然后分析了误差来源及其影响因素，最后对精度进行了分析，并给出了精度计算公式和实例。

关键词：中点单觇法；三角高程测量；误差分析；精度分析正文：一、中点单觇法三角高程测量基本原理和方法中点单觇法是三角高程测量中常用的一种方法。

其基本原理是在一定水平距离上设置两个观测点（称为A点和B点），并以两个观测点及目标物（称为C点）形成的三角形为基础，通过测量三角形三个内角，计算出目标物的高程。

中点单觇法的测量方法如下：1. 在距离目标物一定距离的A、B两点上分别设置测距仪。

2. A、B两个测距仪同时测量目标物到各自测距仪的距离。

3. A、B两个测距仪同时记录目标物与A、B两点的连线在水平方向上的夹角。

4. 利用三角函数和测量数据计算出目标物的高程。

二、误差来源及其影响因素中点单觇法三角高程测量中可能存在的误差主要包括观测误差、仪器误差、环境误差和计算误差等。

其中观测误差是指由于人为或自然因素造成的误差；仪器误差是指由于仪器本身的精度、灵敏度等因素引起的误差；环境误差是指由于气象、地形、天气等环境因素引起的误差；计算误差是指由于计算方法和步骤引起的误差。

影响中点单觇法三角高程测量精度的因素主要包括：1. 测量设备的精度和灵敏度2. 测量人员的水平和经验3. 环境因素的影响4. 测量方法选择的科学性和合理性三、精度分析及计算公式为了提高中点单觇法三角高程测量的精度，需要针对误差来源和影响因素进行分析，并采取相应的措施加以消减。

一般情况下，中点单觇法的精度可以通过以下公式进行计算：（式中，K为系数，a为目标物与A点的距离，b为目标物与B点的距离，α、β、γ分别为A、B、C三角形三个内角）具体的精度计算实例如下：假设A、B两点距离为100米，目标物离A、B两点的距离分别为70米和50米，并且测量误差为±1毫米，则根据上述公式计算得到中点单觇法的测量精度为：K=0.00179α=54.44°β=35.56°γ=90.00°a=70mb=50m∆H=2.0303×10^-4m四、结论中点单觇法三角高程测量是一种简单、直观、可靠的高程测量方法，但其精度受到多种因素的影响。

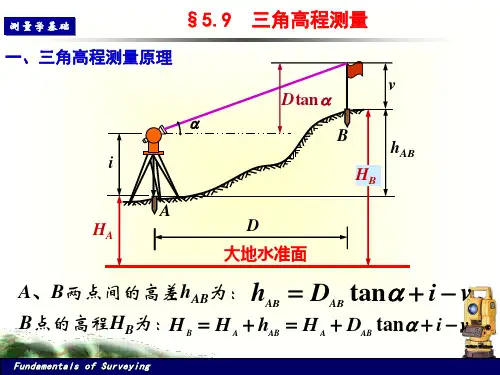
§4-6三角高程测量一、三角高程测量原理及公式在山区或地形起伏较大的地区测定地面点高程时，采用水准测量进行高程测量一般难以进行，故实际工作中常采用三角高程测量的方法施测。

传统的经纬仪三角高程测量的原理如图 4 —12所示，设A点高程及AB两点间的距离已知，求B点高程。

方法是，先在A点架设经纬仪，量取仪器高i;在B点竖立觇标(标杆)，并量取觇标高L,用经纬仪横丝瞄准其顶端，测定竖直角3,则AB两点间的高差计算公式为：h 血=+ i - L故 _ 』_ 也'二—(4-11 )式中匸为A、B两点间的水平距离。

图4-12三角高程测量原理当A、B两点距离大于300m时，应考虑地球曲率和大气折光对高差的影响，所加的改正数简称为两差改正：亡= -----设c为地球曲率改正，R为地球半径，则c的近似计算公式为：y=-0.014——设g为大气折光改正，则g的近似计算公式为：二」因此两差改正-为：-「，「恒为正值。

采用光电三角高程测量方式，要比传统的三角高程测量精度高，因此目前生产中的三角高程采用光电测距仪测定两点的斜距S，贝y B点的高程计算公式为：测量多采用光电法。

i 丄"’-■' （）4-12为了消除一些外界误差对三角高程测量的影响，通常在两点间进行对向观测，即测定hAB和hBA，最后取其平均值，由于hAB和hBA反号，因此-可以抵销。

实际工作中，光电三角高程测量视距长度不应超过1km，垂直角不得超过15°。

理论分析和实验结果都已证实，在地面坡度不超过8度，距离在1.5km 以内，采取一定的措施，电磁波测距三角高程可以替代三、四等水准测量。

当已知地面两点间的水平距离或采用光电三角高程测量方法时，垂直角的观测精度是影响三角高程测量的精度主要因素。

二、光电三角高程测量方法光电三角高程测量需要依据规范要求进行，如《公路勘测规范》中光电三角高程测量具体要求见表4-6。

表4-6光电三角高程测量技术要求注：表4-6中匸为光电测距边长度。

全站仪水平‎测量及计算‎公式因为用全站‎仪（附加棱镜）、经纬仪（附加塔尺）测量高程，是根据两点‎间的距离和‎竖直角，应用三角公‎式计算两点‎的高差，用全站仪测‎定高程的方‎法通常称为‎三角高程测‎量（或称测距高‎程）。

用全站仪测‎量高程的特‎点是，精度比用水‎准仪测量低‎，但是这种方‎法简便、灵活，受地形的限‎制小。

因此通常用‎于山区的高‎程测量和地‎形测量。

三角高程测‎量，一般应在一‎定密度的水‎准测量控制‎之下。

通常三角高‎程测量是高‎程控制测量‎的一种补充‎手段，其精度应同‎同等级的水‎准测量相同‎。

当我们采用‎全站仪（光电测距仪‎）进行高程测‎量放样时，如图2-2所示，由于全站仪‎的视线不都‎在一个水平‎面上，而全站仪所‎读读数由正‎负之分，在进行高程‎测量放样计‎算时，我们输入的‎数据必须以‎全站仪所读‎读数实际输‎入，设后视点B‎M的高程为‎H0，在同一测站‎下（全站仪的仪‎器高恒等），放样点的实‎测高程的计‎算公式（以下为棱镜‎高度保持不‎变的放样点‎高程推导公‎式）如下：视线高程H‎视线 = H0－h0 + v放样点高程‎H n = H视线－hn－v =（H0－h0 + v）+ hn－v= H0－h0 + hn当棱镜高度‎改变时，设棱镜改变‎后的高度相‎对与后视时‎的高度改变‎值为w（改变后的高‎度减去棱镜‎初始高度），则放样点的‎的实测高程‎为：Hn = H0－h0 + hn－w。

为避免误差‎因距离的传‎递，各等级的三‎角高程测量‎必须限制一‎次传递高程‎的距离。

三角高程测‎量路线的总‎长原则上可‎参考同等级‎的水准路线‎的长度，路线尽可能‎组成闭合多‎边形，以便对高差‎闭合差进行‎校核。

除以上介绍‎的基本方法‎外，采用全站仪‎测量高程中‎，视线高程有‎两种计算方‎法：一、若已知置站‎点地面高程‎，则视线高程‎为“置站点地面‎高程与全站‎仪仪器高之‎和”。

二、若已知后视‎点地面高程‎，则视线高程‎为“后视点地面‎高程减去后‎视高差读数‎加上棱镜高‎度”。

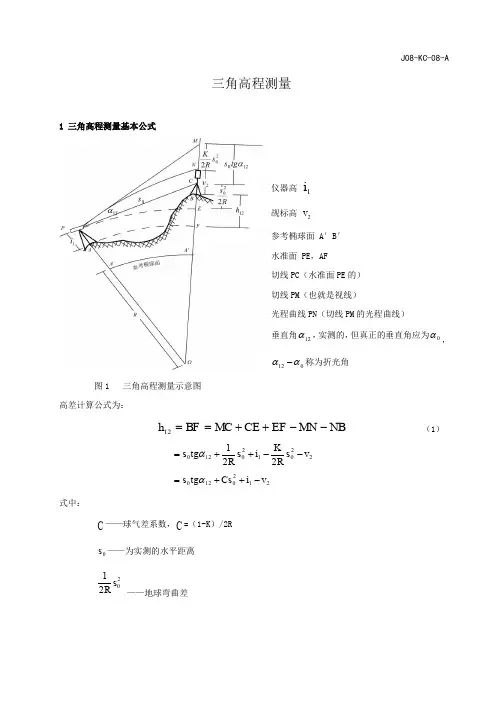
J08-KC-08-A三角高程测量1 三角高程测量基本公式仪器高 1i觇标高 2v 参考椭球面 A ′B ′ 水准面 PE ，AF切线PC （水准面PE 的） 切线PM （也就是视线）光程曲线PN （切线PM 的光程曲线） 垂直角12α，实测的，但真正的垂直角应为0α，012αα-称为折光角图1 三角高程测量示意图高差计算公式为：NB MN EF CE MC BF h --++==12 （1）220120120221v s RK i s R tg s --++=α 2120120v i Cs tg s -++=α式中：C ——球气差系数，C =（1-K ）/2R0s ——为实测的水平距离221s R ——地球弯曲差22s R K ——大气垂直折光差，K 为折光系数，一般在0.1～0.16之间，可用实验方法测定。

2 三角高程导线测量基本要求（1） 三、四等及等外高程导线测量，每公里高差中数的偶然中误差∆M 和全中误差wM 应符合表1的规定。

表 1 mm（2） 高程导线天顶距测量，一测回观测值中误差Z M 应符合以下规定。

三等 "3.1≤Z M 四等 "5.1≤Z M（3） 各等级高程导线的路线长度应符合表2的规定。

表 2 km（4） 高程导线的环线、附合路线闭合差和检查已测测段高差之差，不得超过表3的规定。

表 3 mm（5） 高程导线的视线长度和视线倾角应符合表4的规定。

J08-KC-08-A4 m表表5 m表 6 （°）3 三角高程导线测量流程3.1 路线设计与埋石（1）高程导线的路线设计应根据任务书的要求，收集测区及附近的地形图、交通图、水准点、气象等方面的资料，设计最佳方案，编写技术设计。

（2）测站和置觇点宜选择在高出周围地面的地形特征点上，尽量提高视线的高度。

视线高度和地面障碍物的距离不小于1.5m。

（3）视线和置觇点应尽量避免通过有强烈背景光和强磁场的地方，以及有吸热、散热变化大的区域，视线离较宽的水面和高压输电线的距离应大于2m。

三角高程测量是一种常用的测量方法，它可以用来测量地面上点的准确高程。

在这篇文章中，我们将着重介绍三角高程测量中的往返观测计算公式。

一、三角高程测量原理三角高程测量是利用三角形的相似性原理，通过已知两点的高程和这两点到待测点的水平距离，来计算待测点的高程。

三角高程测量的基本原理如下：1. 在地面上选择一个已知高程的点A，以及要测量高程的点P。

2. 通过测量仪器测量点A和点P之间的水平距离d和两点的高程差h。

3. 通过三角函数计算出点P的高程。

二、三角高程测量的往返观测在实际测量中，为了提高精度，常常采用往返观测的方法进行测量。

往返观测的原理是利用观测仪器来回测量两点之间的距离和高程差，然后取平均值作为最终结果，以减小由于观测仪器误差、大气温度、大气压力等因素造成的误差。

三、三角高程测量往返观测计算公式往返观测的三角高程测量计算公式如下：1. 求点P的高程差首先需要计算出点P的高程差，使用以下公式：\[ \Delta h = h_1 - h_2 \]其中，\(h_1\) 为第一次测量的高程，\(h_2\) 为第二次测量的高程。

2. 求两次测量的平均距离将两次测量的距离\(d_1\)和\(d_2\)求均值，得到平均距离：\[ \bar{d} = \frac{d_1 + d_2}{2} \]3. 计算点P的高程利用三角函数计算出点P的高程：\[ H = h_2 + \frac{\Delta h \times \bar{d}}{d_2} \]其中，\(H\)为最终计算出的点P的高程。

四、注意事项在进行三角高程测量的往返观测时，需要注意以下几点：1. 观测仪器的选择和校准非常重要，需要保证其精度和稳定性。

2. 大气温度和大气压力对测量结果有较大影响，需要进行相应的修正。

3. 观测时需要注意周围环境的影响，避免受到建筑物、树木、地形等因素干扰。

4. 测量终点的选取应当避免大坡度地形，以减小误差。

通过以上介绍，我们了解了三角高程测量中的往返观测计算公式及其应用注意事项。