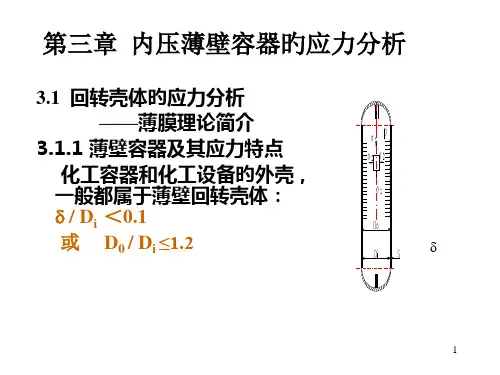
内压薄壁容器的应力
- 格式:ppt
- 大小:5.19 MB
- 文档页数:86





实验一薄壁容器内压应力测定实验一、实验目的通过实验测量薄壁容器内部的压应力,并对实验数据进行分析,掌握薄壁容器内部压应力的测量方法和技巧,加深对应力的理解和认识。
二、实验原理薄壁容器内部压应力的产生主要是因为容器内有压力。
薄壁容器内的压力是由容器内部的气体或液体所施加的作用力引起的。
在静止平衡的状态下,容器内部所受的压力与容器所产生的内部应力相等,即:σ = P × r / t其中,σ 为容器内部应力,P 为容器内部压力,r 为容器半径,t 为容器壁厚度。
通过测量容器壁的变形量可以求得内部应力的大小,具体方法可以使用:应变覆盖片法、电阻应变桥法、光栅应变传感器法、激光干涉法等,本次实验使用应变覆盖片法进行测量。
应变覆盖片法的原理是:在测量表面粘贴不同类型和数量的弹性薄膜传感器(应变覆盖片),并使用电缆将数字信号传递到计算机系统中,计算机通过解读信号来实现应变的测量。
三、实验器材和仪器实验器材:薄壁容器、虎钳、吸盘、加热器等。
仪器:应变覆盖片(包括型号为RSTR-1/120-LY8W的3片应变覆盖片、型号为KY-2000A 的数字化应变测量仪),加热器、计算机等。
四、实验步骤1、使用虎钳将薄壁容器夹住,并使用吸盘尽量固定在实验台上。
2、在薄壁容器上粘贴3片应变覆盖片,在不影响测量的前提下均匀地分布在容器上表面,并将每个应变覆盖片的信号通过电缆与计算机相连。
3、使用加热器和安装在容器上的温度传感器使容器内部的温度达到设定温度,保持一段时间,以使容器内部压力稳定。
4、在容器达到稳态后,记录容器内部压力P。
5、使用计算机记录每个应变覆盖片的信号,并根据不同的应变传感器标定曲线,计算出应变。
6、根据容器的几何尺寸和应变值,计算容器内部的应力大小σ,并与容器内部压力P 进行对比。
7、记录实验数据,撤除应变覆盖片和传感器。
五、实验注意事项1、粘贴应变覆盖片时要注意不能捏住或将温度传感器弄松或损坏。
如果损坏应变覆盖片或传感器,需要更换后重新进行测量。

精品行业资料,仅供参考,需要可下载并修改后使用!《化工设备机械基础》习题解答第三章 内压薄壁容器的应力分析一、名词解释 A 组:⒈薄壁容器:容器的壁厚与其最大截面圆的内径之比小于0.1的容器。
⒉回转壳体:壳体的中间面是直线或平面曲线绕其同平面内的固定轴线旋转360°而成的壳体。
⒊经线:若通过回转轴作一纵截面与壳体曲面相交所得的交线。
⒋薄膜理论:薄膜应力是只有拉压正应力没有弯曲正应力的一种两向应力状态,也称为无力矩理论。
⒌第一曲率半径:中间面上任一点M 处经线的曲率半径。
⒍小位移假设:壳体受力以后,各点位移都远小于壁厚。
⒎区域平衡方程式:计算回转壳体在任意纬线上径向应力的公式。
⒏边缘应力:内压圆筒壁上的弯曲应力及连接边缘区的变形与应力。
⒐边缘应力的自限性:当边缘处的局部材料发生屈服进入塑性变形阶段时,弹性约束开始缓解,原来不同的薄膜变形便趋于协调,边缘应力就自动限制。
二、判断题(对者画√,错着画╳) A 组:1. 下列直立薄壁容器,受均匀气体内压力作用,哪些能用薄膜理论求解壁内应力?哪些不能?(1) 横截面为正六角形的柱壳。
(×) (2) 横截面为圆的轴对称柱壳。
(√) (3) 横截面为椭圆的柱壳。
(×) (4) 横截面为圆的椭球壳。
(√) (5) 横截面为半圆的柱壳。
(×) (6) 横截面为圆的锥形壳。
(√)2. 在承受内压的圆筒形容器上开椭圆孔,应使椭圆的长轴与筒体轴线平行。
(×)3. 薄壁回转壳体中任一点,只要该点的两个曲率半径R R =,则该点的两向应力σσθ=m。
(√) 4. 因为内压薄壁圆筒的两向应力与壁厚成反比,当材质与介质压力一定时,则壁厚大的容器,壁内的应力总是小于壁厚小的容器。
(×)5. 按无力矩理论求得的应力称为薄膜应力,薄膜应力是沿壁厚均匀分布的。
(√) B 组:1. 卧式圆筒形容器,其内介质压力,只充满液体,因为圆筒内液体静载荷不是沿轴线对称分布的,所以不能用薄膜理论应力公式求解。

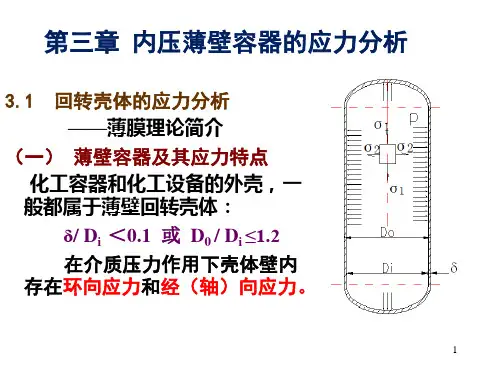


化工设备机械基础第三章习题解答(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第三章 内压薄壁容器的应力分析一、 名词解释A 组:⒈薄壁容器:容器的壁厚与其最大截面圆的内径之比小于的容器。
⒉回转壳体:壳体的中间面是直线或平面曲线绕其同平面内的固定轴线旋转360°而成的壳体。
⒊经线:若通过回转轴作一纵截面与壳体曲面相交所得的交线。
⒋薄膜理论:薄膜应力是只有拉压正应力没有弯曲正应力的一种两向应力状态,也称为无力矩理论。
⒌第一曲率半径:中间面上任一点M 处经线的曲率半径。
⒍小位移假设:壳体受力以后,各点位移都远小于壁厚。
⒎区域平衡方程式:计算回转壳体在任意纬线上径向应力的公式。
⒏边缘应力:内压圆筒壁上的弯曲应力及连接边缘区的变形与应力。
⒐边缘应力的自限性:当边缘处的局部材料发生屈服进入塑性变形阶段时,弹性约束开始缓解,原来不同的薄膜变形便趋于协调,边缘应力就自动限制。
二、 判断题(对者画√,错着画╳)A 组:1. 下列直立薄壁容器,受均匀气体内压力作用,哪些能用薄膜理论求解壁内应力哪些不能(1)横截面为正六角形的柱壳。
(×) (2)横截面为圆的轴对称柱壳。
(√) (3)横截面为椭圆的柱壳。
(×) (4)横截面为圆的椭球壳。
(√) (5)横截面为半圆的柱壳。
(×) (6)横截面为圆的锥形壳。
(√) 2.在承受内压的圆筒形容器上开椭圆孔,应使椭圆的长轴与筒体轴线平行。
(×) 3.薄壁回转壳体中任一点,只要该点的两个曲率半径R R 21=,则该点的两向应力σσθ=m 。
(√) 4.因为内压薄壁圆筒的两向应力与壁厚成反比,当材质与介质压力一定时,则壁厚大的容器,壁内的应力总是小于壁厚小的容器。
(×) 5.按无力矩理论求得的应力称为薄膜应力,薄膜应力是沿壁厚均匀分布的。
(√) B 组:1.卧式圆筒形容器,其内介质压力,只充满液体,因为圆筒内液体静载荷不是沿轴线对称分布的,所以不能用薄膜理论应力公式求解。
《化工设备机械基础》习题解答第三章 内压薄壁容器的应力分析一、名词解释A 组:⒈薄壁容器:容器的壁厚与其最大截面圆的内径之比小于0.1的容器。
⒉回转壳体:壳体的中间面是直线或平面曲线绕其同平面内的固定轴线旋转360°而成的壳体。
⒊经线:若通过回转轴作一纵截面与壳体曲面相交所得的交线。
⒋薄膜理论:薄膜应力是只有拉压正应力没有弯曲正应力的一种两向应力状态,也称为无力矩理论。
⒌第一曲率半径:中间面上任一点M 处经线的曲率半径。
⒍小位移假设:壳体受力以后,各点位移都远小于壁厚。
⒎区域平衡方程式:计算回转壳体在任意纬线上径向应力的公式。
⒏边缘应力:内压圆筒壁上的弯曲应力及连接边缘区的变形与应力。
⒐边缘应力的自限性:当边缘处的局部材料发生屈服进入塑性变形阶段时,弹性约束开始缓解,原来不同的薄膜变形便趋于协调,边缘应力就自动限制。
二、判断题(对者画√,错着画╳)A 组:1. 下列直立薄壁容器,受均匀气体内压力作用,哪些能用薄膜理论求解壁内应力?哪些不能?(1) 横截面为正六角形的柱壳。
(×)(2) 横截面为圆的轴对称柱壳。
(√)(3) 横截面为椭圆的柱壳。
(×)(4) 横截面为圆的椭球壳。
(√)(5) 横截面为半圆的柱壳。
(×)(6) 横截面为圆的锥形壳。
(√)2. 在承受内压的圆筒形容器上开椭圆孔,应使椭圆的长轴与筒体轴线平行。
(×)3. 薄壁回转壳体中任一点,只要该点的两个曲率半径R R 21=,则该点的两向应力σσθ=m。
(√)4. 因为内压薄壁圆筒的两向应力与壁厚成反比,当材质与介质压力一定时,则壁厚大的容器,壁内的应力总是小于壁厚小的容器。
(×)5. 按无力矩理论求得的应力称为薄膜应力,薄膜应力是沿壁厚均匀分布的。
(√)B 组:1. 卧式圆筒形容器,其内介质压力,只充满液体,因为圆筒内液体静载荷不是沿轴线对称分布的,所以不能用薄膜理论应力公式求解。