第五章 内压薄壁容器的应力分析

内压薄壁容器的应力测定一、实验目的1.了解电阻应变片的结构，作用及工作原理。

2.初步掌握常温下电阻应变片的粘帖技术，并对被测容器做好粘帖应变片、接线、防潮、检查等准备工作。

3.测定薄壁容器在内压作用时，圆筒及封头上的应力分布。

4.比较实测应力和理论计算应力，分析它们产生误差的原因。

5.掌握“应变电测法”测定容器应力的基本原理和测试技术。

二、实验原理由中低压容器设计的薄壳理论可知，薄壳回转容器在受压时，在离开与封头连接处的器壁厚度上将产生径向的和环向（切向）主薄膜应力σφ,σθ 及其相应的主薄膜应变εφ ,εθ,当它们超过材料的曲服强度时，就导至容器破坏或大面积屈服。

一方面，圆筒与封头连接的边缘地区，由于几何形状的不连续而成的附加弯曲应力，此应力与薄膜应力叠加会产生比薄膜应力高很多的综合应力 , 这种应力具有局部性，一离开边缘就快速衰减。

边缘应力对疲劳失效和脆性破坏有重大影响，其大小与容器的形式，制造质量及操作条件有关，而工程实际中，不少结构和零部件，由于形状比较复杂，理论上作应力分析相当困难，这时就要采用实测应力分析法，此外在一些重要的结构中，在进行理论分析的同时，还需要进行模型后实际结构的应力测量，以验正理论分析的可靠性和计算的精确度，因此实验应力分析在压力容器的应力分析与强度设计中占有重要的地位。

实测应力的方法很多，但目前应用的主要有两种，即光弹法和电测法，其中电测法应用的最多。

我们这个实验就是用电测法测容器中的应力。

一般容器器壁中的应力不能直接观察到，但变形无论多麽微小，总是可以测量的，由于变形和内力有一定的关系，只要知道这钟关系，就可以通过测量变形来达到测量应力的目的，由于薄膜容器的应力是两向应力，所以测出径向应变和环向应变，就可以根据广义虎克定律求相应应力：2 2σφ =E（εφ+μεθ）/（1－μ）（ a）σθ =E（εθ+μεφ）/（1－μ）（b）6式中： E—材料的弹性模量，碳钢为 0.21 × 10 Mpaεφ—实测的径向应变值，1×106Mpaεθ—实测的环向应变值，1×106Mpaσφ —径向应力σθ —环向应力图 1-1 惠斯顿电桥那么应变是怎样测得的呢？下面来介绍如何用电阻应变仪来进行应变测量。

内压薄壁容器应力实验报告本报告旨在介绍内压薄壁应力实验的目的、背景以及其意义和重要性。

内压薄壁是一种常见的工程结构，广泛应用于各行各业。

在使用过程中，受到内部介质的压力作用，会产生一定的应力分布。

了解和研究内部应力状态对于设计和使用具有重要意义。

该实验旨在通过在内压薄壁上施加不同的压力载荷，测量和分析的应力分布情况。

通过实验结果，我们可以了解在不同压力下的应力状态，从而更好地理解的强度和稳定性。

本实验的意义和重要性有以下几点：设计优化：通过了解在不同压力下的应力分布情况，可以更准确地确定的材料和结构设计。

这有助于提高的强度和性能，减少可能的失效风险。

安全性评估：了解的应力分布情况可以帮助评估的安全性能。

在某些特殊工况下，例如高压或长期使用等，内部应力可能超过材料的强度极限，从而导致破裂或泄漏。

通过实验研究，可以提供重要的数据和参考，帮助工程师评估的安全性。

质量控制：实验结果可以用于质量控制和验证的生产工艺。

通过测量内部应力，可以判断的加工和装配工艺是否符合设计要求，从而确保的质量和性能。

因此，通过内压薄壁应力实验的研究和分析，可以进一步提高的设计和使用效能，提升的安全性能，并且对于相关工程领域的发展也具有重要的指导意义。

内压薄壁压力测试仪器其他相关实验材料和设备（如果有）本节详细描述进行内压薄壁应力实验的步骤和操作方法。

实验器材和材料准备：准备一台内压实验机和薄壁样品。

确保实验机的压力计和温度计正常工作。

样品准备：安装样品在内压实验机中，确保样品固定且没有松动。

检查样品是否有任何损坏或异物。

实验参数设置：设置实验机的内部压力和温度，需要提前根据实验目的进行设定。

确保内部压力和温度的稳定性和准确性。

开始实验：启动内压实验机，使内部压力逐渐增加到设定值。

记录实验过程中的压力和温度变化。

实验数据收集：在实验过程中，定期记录实验机内部压力和表面的应力。

确保数据记录的准确性和完整性。

实验结果分析：根据实验数据，计算在不同条件下的应力变化。

实验五 内压薄壁容器应力测定实验一、实验目的1．把握电阻应变测量原理；2．学习电阻应变仪的利用方式，学习电阻应变片的贴片和接线技术； 3．了解封头在内压作用下的应力散布规律。

二、实验原理 1. 应力计算：薄壁压力容器要紧由封头和圆筒体两个部份组成，由于各部份曲率不同，在它们的连接处曲率发生突变。

受压后，在连接处会生产边缘力系——边缘力矩和边缘剪力。

使得折边区及其双侧必然距离内的圆筒体和封头中的应力散布比较复杂，某些位置会显现较高的局部应力。

利用电阻应变测量方式可对封头和与封头相连接的部份圆筒体的应力散布进行测量。

应力测定顶用电阻应变仪来测定封头各点的应变值，依照广义虎克定律换算成相应的应力值。

由于封头受力后是处于二向应力状态，在弹性范围内用广义虎克定律表示如下：经向应力：()21211μεεμσ+-=E(1-1) 环向应力：()12221μεεμσ+-=E(1-2) 式中：E —材料的弹性模量μ—材料的波桑比 ε1—经向应变 ε2—环向应变。

椭圆封头上各点的应力理论计算公式如下：经向应力：()[]bb a x a s p r 2122242--=σ （1-3）环向应力：()[]()⎥⎦⎤⎢⎣⎡-----=2224421222422b a x a a bba x a s p θσ （1-4） 2．电阻应变仪的大体原理：电阻应变仪将应变片电阻的微小转变，用电桥转换成电压电流的转变。

其进程为：()→∆∆→→放大器或电桥应变片I V RdR ε将()指示或纪录检流计或纪录仪放大或→∆∆I V将电阻应变片用胶水粘贴在封头外壁面上，应变片将随封头的拉伸或紧缩一路变形，应变片的变形会引发应变片电阻值的转变，二者之间存在如下关系：ε⋅=∆=∆K LlK R R (1-5) 式中：ΔR/R —电阻应变片的电阻转变率ΔL/L —电阻应变片的变形率 K —电阻应变片的灵敏系数； ε—封头的应变。

3. BZ2205C 型静态电阻应变仪 1) 电阻应变仪的组成：(1) 构件变形的感受和转换部份——电阻应变片； (2) 被转换量的传递和放大部份； (3)记录及读数部份。

薄壁容器内压应力测定实验装置说明书天津大学化工基础实验中心2012.03一.实验目的1. 测定薄壁容器承受内压作用时，筒体及封头（平板封头、锥形封头、球形封头、椭圆封头）上的应力分布。

2. 比较实测应力与理论计算应力，分析它们产生差异的原因。

3. 了解“应变电测法”测定容器应力的基本原理和掌握实验操作技能。

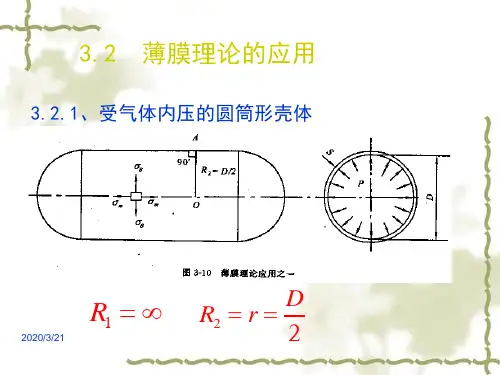
二.实验原理由中低容器设计的薄壳理论分析可知，薄壁回转容器在承受内压作用时，圆筒壁上任一点将产生两个方向的应力，经向应力m 和环向应力。

在实际工程中，不少结构由于形状与受力较复杂，进行理论分析时，困难较大；或是对于一些重要结构在进行理论分析的同时，还需对模型或实际结构进行应力测定，以验证理论分析的可靠性和设计的精确性；所以，实验应力分析在压力容器的应力分析和强度设计中有十分重要的作用。

现在实验应力分析方法已有十几种，而应用较广泛的有电测法和光弹法，其中前者在压力容器应力分析中广泛采用。

可用于测量实物与模型的表面应变，具有很高的灵敏度和精度；由于它在测量时输出的是电信号，因此易于实现测量数字化和自动化，并可进行无线电遥测；既可用于静态应力测量，也可用于动态应力测量，而且高温、高压、高速旋转等特殊条件下可进行测量。

电测法是通过测定受压容器在指定部位的应变状态，然后根椐弹性理论的虎克定律可得：⎪⎪⎭⎪⎪⎬⎫-=-=E E E Em mm σμσεσμσεθθθ (1)⎪⎪⎭⎪⎪⎬⎫+-=+-=)(1)(122m m m E E μεεμσμεεμσθθθ (2) 通过“应变电测法”测定容器中某结构部位的应变，然后根椐以上应力和应变的关系，就可确定这些部位的应力。

而应变m ε、θε的测量是通过粘贴在结构上的电阻应变片来实现的；电阻应变片与结构一起发生变形，并把变形转变成电阻的变化，再通过电阻应变仪直接可测得应变值m ε、θε，然后根椐(2)式可算出容器上测量位置的应力值，利用电阻应仪和预调平衡箱可同时测出容器上多个部位的应力，从而可以了解容器受压时的应力分布情况。

内压薄壁容器的应力测定实验一、实验目的1．了解薄壁容器在内压作用下，筒体、锥形封头、半球封头、椭圆封头的应力分布情况：验证薄壁容器筒体应力计算的理论公式；2．熟悉和掌握电阻应变片粘贴技术的方法和步骤；3．掌握用应变数据采集仪器测量应变的原理和操作方法。

二、实验原理1．理论计算（1）根据薄壁壳体的无力矩理论可以求得受内压的薄壁容器筒体部分的应力值：经向应力（轴向应力）： tt D p i 4)(+=φσ环向应力（周向应力）： tt D p i 2)(+=θσ式中：p —容器所受内压力（MPa ）； D i —容器内直径（mm ）； t —容器壁厚（mm ）；σΦ，σθ—经向应力，环向应力。

（2）锥形封头应力（相关尺寸参数如图α=30º）：αασφcos 22tan t pr t px ==αασθcos tan 2t pr t px t pR ===锥形壳体上经向应力、周向应力与x 呈线性关系，离锥顶越远，应力越大。

（3）球形封头应力tt D p i 4)(+==θφσσ （4）椭圆封头上各点的应力（相关尺寸见右图a/b=3）()()1242224422222a x a b pa a t ba x ab θσ⎡⎤⎡⎤--⎣⎦⎢⎥=---⎢⎥⎣⎦在壳体顶点处2212(0,),,2a pa x y b R R b btθϕσσ======; 在壳体赤道上(,0)x a y ==,1b R a=,2R a =,22,(1)22pa pa a t t b ϕθσσ==-； 2． 实验测定：（1）应力测定的基本原理：薄壁容器受内压后，器壁上各点均处于两向受力状态，当其变形在弹性范围以内，容器壁各点的应力符合虎克定律，即：)(12t x x Eμεεμσ+-=()1242222pR 22a x a b p t t bϕσ⎡⎤--⎣⎦==)(12x t t Eμεεμσ+-=故只要测得容器壁的经向应变和环向应变，即可根据虎克定律求得σx 和σt 。