小学奥数举一反三第15周数数图形
- 格式:docx
- 大小:100.88 KB
- 文档页数:3

第十五周图形问题专题简析:解答有关“图形面积”问题时,应注意以下几点:1,细心观察,把握图形特点,合理地进行切拼,从而使问题得以顺利地解决;2,从整体上观察图形特征,掌握图形本质,结合必要的分析推理和计算,使隐蔽的数量关系明朗化。
例1:人民路小学操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方米?分析与解答:用操场现在的面积减去操场原来的面积,就得到增加的面积。
操场现在的面积是(90+10)×(45+5)=5000平方米,操场原来的面积是90×45=4050平方米。
所以,现在的面积比原来增加5000-4050=950平方米。
练习一1,有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米?2,一块长方形铁板,长18分米,宽13分米。
如果长和宽各减少2分米,面积比原来减少多少平方分米?3,一块长方形地,长是80米,宽是45米。
如果把宽增加5米,要使面积不变,长应减少多少米?例2:一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?分析与解答:由“宽不变,长增加6米,面积增加54平方米”可知,它的宽为54÷6=9米;由“长不变,宽减少3米,面积减少36平方米”可知,它的长为36÷3=12米。
所以,这个长方形原来的面积是12×9=108平方米。
练习二1,一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2,一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
这个长方形原来的面积是多少平方米?3,一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米。


目录第1周平均数 (1)第2周等差数列 (3)第3周长方形、正方形的周长 (5)第4周长方形、正方形的面积 (8)第5周分类数图形 (11)第6周尾数和余数 (14)第7周一般应用题(一) (16)第8周一般应用题(二) (18)第9周一般应用题(三) (20)第10周数阵 (22)期中测试(一) (25)第11周周期问题 (27)第12周盈亏问题 (30)第13周长方体和正方体(一) (32)第14周长方体和正方体(二) (34)第15周长方体和正方体(三) (36)第16周倍数问题(一) (38)第17周倍数问题(二) (40)第18周组合图形的面积(一) (42)第19周组合图形的面积(二) (45)第20周数字趣味题 (48)期末测试(一) (50)第21周假设法解题 (52)第22周作图法解题 (54)第23周分解质因数(一) (56)第24周分解质因数(二) (58)第25周最大公约数 (60)第26周最小公倍数(一) (62)第27周最小公倍数(二) (64)第28周行程问题 (66)第29周行程问题(二) (68)第30周行程问题(三) (70)期中测试(二) (72)第31周行程问题(四) (74)第32周算式谜 (76)第33周包含与排除 (78)第34周转换问题 (80)第35周估值问题 (82)第36周火车行程问题 (84)第37周简单列举 (86)第38周最大最小问题 (88)第39周推理问题 (90)期末测试(二) (92)第1周平均数基础卷1.期中考试过后,李玲同学语文、数学的平均成绩为91分,语文、英语的平均成绩为88分,数学、英语的成绩为93分,李玲三门功课各得多少分?2.奶糖和水果糖混合起来,成为什锦糖,平均每千克售价9.13元,已知奶糖有35千克,每千克10.3元,水果糖每千克8.5元,那么有多少千克水果糖?3.7位同学进行跳绳比赛,平均每人跳148下。
由于记录失误,李强的成绩被错记成121下,因此他们的平均成绩变成145下,问:李强实际上跳了多少下?4.几位裁判员为一位体操运动员评分,去掉一个最高分后,平均成绩为8.82分。


数
数
图 形
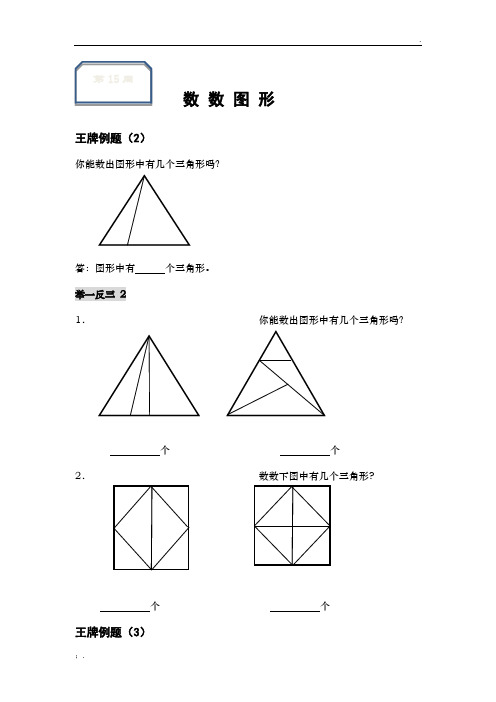
王牌例题(2)
你能数出图形中有几个三角形吗?
答:图形中有
个三角形。
举一反三 2
1.
你能数出图形中有几个三角形吗?
个
个 2.
数数下图中有几个三角形?
个
个 王牌例题(3)
第15周
数一数,下面的图形中有几个正方形?
答:图形中有个正方形。
举一反三3
1. 数一数,图中有多少个正方形?
个个2. 数一数,图中共有多少个正方形?
图中共有个正方形。
王牌例题(4)
数一数,下面共有多少个长方形?
答:下面共有个长方形。
举一反三4
1. 数一数,下面每个图形里各有几个长方形?
个个2. 数数下图中有几个长方形?
个个王牌例题(5)
数一数,图中共有多少个圆?
答:共有个圆形。
举一反三5
1. 数一数,图中共有多少个正方形?
共有个正方形。
2. 数一数,图中共有多少个三角形?
答:共有个三角形。
第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
如何灵活运用平均数的数量关系解答一些稍复杂的问题呢?下面的数量关系必须牢记:平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1 有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析与解答:(1)1箱苹果+1箱梨+1箱橘子=42×3=136(个);(2)1箱桃+1箱梨+1箱橘子=36×3=108(个)(3)1箱苹果+1箱桃=37×2=72(个)由(1)(2)两个等式可知:1箱苹果比1箱桃多126-108=18(个),再根据等式(3)就可以算出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
1箱苹果和1箱桃共有多少个:37×2=74(个)1箱苹果比1箱桃多多少个:42×3-36=18(个)1箱苹果有多少个:28+18=46(个)练习一1,一次考试,甲、乙、丙三人平均分91分,乙、丙、丁三人平均分89分,甲、丁二人平均分95分。
问:甲、丁各得多少分?2,甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?3,甲、乙、丙三个小组的同学去植树,甲、乙两组平均每组植树18棵,甲、丙两组平均每组植树17棵,乙、丙两组平均每组植树19棵。
三个小组各植树多少棵?例2 一次数学测验,全班平均分是91.2分,已知女生有21人,平均每人92分;男生平均每人90.5分。
求这个班男生有多少人?分析:女生每人比全班平均分高92-91.2=0.8(分),而男生每人比全班平均分低91.2-90.5=0.7(分)。
全体女生高出全班平均分0.8×21=16.8(分),应补给每个男生0.7分,16.8里包含有24个0.7,即全班有24个男生。
四年级奥数举一反三第十五周图形问题专题简析;解答有关“图形面积”问题时’应注意以下几点;1’细心观察’把握图形特点’合理地进行切拼’从而使问题得以顺利地解决;2’从整体上观察图形特征’掌握图形本质’结合必要的分析推理和计算’使隐蔽的数量关系明朗化。
例1;人民路小学操场长90米’宽45米。
改造后’长增加10米’宽增加5米。
现在操场面积比原来增加了多少平方米?分析与解答;用操场现在的面积减去操场原来的面积’就得到增加的面积。
操场现在的面积是[90+10]×[45+5]=5000平方米’操场原来的面积是90×45=4050平方米。
所以’现在的面积比原来增加5000-4050=950平方米。
练习一1’有一块长方形的木板’长22分米’宽8分米。
如果长和宽分别减少10分米、3分米’面积比原来减少多少平方分米?2’一块长方形铁板’长18分米’宽13分米。
如果长和宽各减少2分米’面积比原来减少多少平方分米?3’一块长方形地’长是80米’宽是45米。
如果把宽增加5米’要使面积不变’长应减少多少米?例2;一个长方形’如果宽不变’长增加6米’那么它的面积增加54平方米;如果长不变’宽减少3米’那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?分析与解答;由“宽不变’长增加6米’面积增加54平方米”可知’它的宽为54÷6=9米;由“长不变’宽减少3米’面积减少36平方米”可知’它的长为36÷3=12米。
所以’这个长方形原来的面积是12×9=108平方米。
练习二1’一个长方形’如果宽不变’长减少3米’那么它的面积减少24平方米;如果长不变’宽增加4米’那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2’一个长方形’如果宽不变’长增加5米’那么它的面积增加30平方米;如果长不变’宽增加3米’那么它的面积增加48平方米。
这个长方形原来的面积是多少平方米?3’一个长方形’如果它的长减少3米’或它的宽减少2米’那么它的面积都减少36平方米。
第15讲植树问题【专题简析】植树的学问真不少,这里面有许多有趣的问题,做这类题目要多动脑筋,弄清题意,理解树的棵数与间隔数的关系,掌握植树的解题方法,问题就迎刃而解了。
植树的问题,应该注意如果起点和终点都植树,树的棵数比间隔数多1,如果起点和终点不植树,树的棵数比间隔数少1,在解答这类应用题时,应该看清楚题目要求,然后根据棵数与间隔数的关系,结合已知条件,就能找到解决问题的方法了。
【例题1】一条路长72米,在路的一边每隔8米栽1棵松树,从头到尾一共可以栽多少棵松树?思路导航:每隔8米栽一棵树,72里面有9个8,这个9其实就是把72米平均分成了9个间隔,因为从头到尾都要栽树,所以树的棵数比间隔数多1,即9+1=10(棵),也就是棵数比间隔数多1.解:72÷8+1=10(棵)答:一共可以栽10棵松树.练习11.学校门前的一条路长42米,在路的一边从头到尾栽树,每7米栽一棵,一共能栽多少棵?2.教室前面到教室后面长8米,从头到尾每隔2米摆一盆花,一共摆了多少盆花?3.学校门前的一条路长56米,为迎接国庆节,在路的一边从头到尾都插上彩旗,每7米插一面,一共要插多少面彩旗?【例题2】同学们在一条公路的两边从头到尾每隔6米栽一棵树,共栽了22棵,这条公路长多少米?思路导航:在路的两旁栽树,共栽了22棵,那么每边栽了22÷2=11棵,由此可知,就是把这条路的每边分成了11-1=10(段),又因为每段是6米,10×6=60米,这就是这条公路的长了解:22÷2=11(棵)11-1=10(段)6×10=60(米)答:这条公路长60米。
练习21.少先队员在路的两旁每隔5米栽一棵树,起点和终点都栽了,一共栽了72棵树,这条路长多少米?2.绿化小组在学校的过道两边摆放月季花,每隔2米摆一盆,起点和终点都摆了,一共摆了24盆,这条过道长多少米?3.两根同样长的绳子上,每隔2米挂一个灯笼,起点和终点都挂,共挂了12个,每根绳子长多少米?【例题3】两栋楼之间每隔2米种一棵树,共种了5棵树,这两栋楼之间相距多少米?思路导航:种5棵树,两栋楼之间应有6个间隔。
第十五周图形问题专题简析:解答有关“图形面积”问题时,应注意以下几点:1,细心观察,把握图形特点,合理地进行切拼,从而使问题得以顺利地解决;2,从整体上观察图形特征,掌握图形本质,结合必要的分析推理和计算,使隐蔽的数量关系明朗化。
例1:人民路小学操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方米?分析与解答:用操场现在的面积减去操场原来的面积,就得到增加的面积。
操场现在的面积是(90+10)×(45+5)=5000平方米,操场原来的面积是90×45=4050平方米。
所以,现在的面积比原来增加5000-4050=950平方米。
练习一1,有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米?2,一块长方形铁板,长18分米,宽13分米。
如果长和宽各减少2分米,面积比原来减少多少平方分米?3,一块长方形地,长是80米,宽是45米。
如果把宽增加5米,要使面积不变,长应减少多少米?例2:一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?分析与解答:由“宽不变,长增加6米,面积增加54平方米”可知,它的宽为54÷6=9米;由“长不变,宽减少3米,面积减少36平方米”可知,它的长为36÷3=12米。
所以,这个长方形原来的面积是12×9=108平方米。
练习二1,一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2,一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
这个长方形原来的面积是多少平方米?3,一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米。
你能数出图形中有几个三角形吗?
答:图形中有个三角形。
1.你能数出图形中有几个三角形吗?
个个2.数数下图中有几个三角形?
个个王牌例题(3)
数一数,下面的图形中有几个正方形?
答:图形中有个正方形。
1. 数一数,图中有多少个正方形?
个个2. 数一数,图中共有多少个正方形?
图中共有个正方形。
王牌例题(4)
数一数,下面共有多少个长方形?
答:下面共有个长方形。
1. 数一数,下面每个图形里各有几个长方形?
个个2. 数数下图中有几个长方形?
个个王牌例题(5)
数一数,图中共有多少个圆?
答:共有个圆形。
1. 数一数,图中共有多少个正方形?
共有个正方形。
2. 数一数,图中共有多少个三角形?
答:共有个三角形。