当前位置：文档之家 › 复数与拉氏变换

复数与拉氏变换

  • 格式：ppt
  • 大小：621.00 KB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

拉氏变换的物理意义

拉氏变换的物理意义

拉氏变换的物理意义
拉氏变换是将时间函数f(t)变换为复变函数F(s)，或作相反变换。

时域(t)变量t是实数，复频域F(s)变量s是复数。

变量s又称“复频率”。

拉氏变换建立了时域与复频域(s域）之间的联系。

s=jw，当中的j是复数单位，所以使用的是复频域。

通俗的解释方法是，因为系统中有电感X=jwL、电容X=1/jwC，物理意义是，系统H(s)对不同的频率分量有不同的衰减，即这种衰减是发生在频域的，所以为了与时域区别，引入复数的运算。

但是在复频域计算的形式仍然满足欧姆定理、KCL、KVL、叠加法
Laplace变换是工程数学里的重要变换，主要是实现微分积分电路的代数运算，建议参看《积分变换》这书.在一阶和高阶电路中，有一些问题在频域中分析比在时域中分析要方便的多，而拉氏变换就是一个很好的分析工具。

它将时域中的信号输入，变换成S域中的信频输入，再由S域的输出，转换成时频的输出，很简洁明了，又可以分析出信号的多种变化.工程数学或者积分变换都可以解决你所提的问题.好吧
在一阶和高阶电路中，有一些问题在频域中分析比在时域中分析要方便的多，而拉氏变换就是一个很好的分析工具。

它将时域中的信号输入，变换成S域中的信频输入，再由S域的输出，转换成时频的输出，很简洁明了，又可以分析出信号的多种变化。

工程数学或者积分变换都可以解决你所提的问题。

第讲拉氏变换及传递函数

第讲拉氏变换及传递函数

例15： 待定系数法
F (s)
1 的逆变换 s(s 1)2
解：
ab
c
F (s)
s

s 1
(s 1)2
则 a ( s 1 ) 2 bs ( s 1 ) cs 1
对应项系数相等得
a 1, b 1, c 1

F
(s)

1 s

1 s 1

(s
1 1)2
f ( t ) 1 e t te t
29.01.2020
留数法
传递函F数 (s)B(s)/ A(s)B(s)/(sp1)(sp2)(spi)
c1 c2 ci
(sp1) (sp1)
(spi)
式中 pi(i 1,2,,n)是D(s)0的根 ,ci是常数
e at
s in t
cos t
F (s)
1
1s 1 s2 1 s3 1 (sa)
(s2 2)
s (s2 2)
29.01.2020
5 拉氏变换的几个重要定理
（1）线性性质 L a f 1 ( b tf 2 ( ) t a F ) 1 ( s b F 2 ( )s
（2）微分定理 L ft s F s f0
ci [M D((ss))(spi)]spi
（1）实根切为单根
例16：
F(s)
1
(s 1)(s 2)(s 3)
29.01.2020
c1 c2 c3 s 1 s 2 s 3
c1

[ (s

1)( s
1
2 )(
s

3)
(s

第二章 拉氏变换

第二章 拉氏变换
m
m 1
1、F(S)无重极点(n个不等根)时，F(s)可表示为
bm s bm 1s b1s b0 F ( s) an ( s p1 )( s p2 ) ( s pn )
m
m 1
Kn K1 K2 s p1 s p2 s pn
(a为实数)
L[e ] e e dt e 0 0
at at st


( s a )t
dt
1 sa
5、正弦函数
0 f (t ) sin t
其拉氏变换
t <0
t ≥0

(为实数)
L[sin t ] sin t e dt 0 2 2 s
在控制工程中,使用拉氏变换的主要目的: 用它来研究系统动态特性.
因为描述系统动态特性的传递函数和频 率特性都是建立在拉氏变换的基础之上 的。
第二节
一、拉氏变换定义
拉普拉斯变换
对时间函数f(t)，t≥0，f(t)的拉普拉斯变换L[f(t)] （简称拉氏变换）或F(s)定义为
0 一个函数可以进行拉氏变换的充要条件是： 原函数 象函数
第二章 拉普拉斯变换的数学方法
1 复数与复变函数 2 拉普拉斯变换及反变换
2.1 复数和复变函数
一、复数的概念
为了解方程的需要，人们引入了一个新数i, 称为虚数单位，并规定：
教材上：j
(1) i 1;
2
(2) i 可与实数进行四则运算.
复 数
形如 s j 的数称为复数.
实部 记作：Re(s)=σ
复数可以表示成
s σ jω r (cos i sin )

补充：拉氏变换

补充：拉氏变换

4、位移性质（也称复位移性质） ：L e 证明： L e ） 。 念 ．
− at
− at
f (= t ) F ( s + a) ；
f (= t )
∫
∞
0
= e − at f (t )e − st dt
∫
∞
0
t f (t )e − ( s + a )= dt F ( s + a ) （变量替换的概 ．．．．．．
4.指数函数 e
− at
∞ ∞ 1 − ( s + a )t ∞ 1 − at − at − st − ( s + a )t L − e |0 = ∫0 e e dt = ∫0 e dt = e = s+a s+a 5.正弦函数 sin ω t
ω s +ω2 6.余弦函数 cos ω t
0 0 − st
∞
∞
（分部积分法）
= e f (t ) + s ∫ f (t )e dt = sF ( s ) − f (0) = 一般地： L d f (t ) / dt s F ( s) − s
n n n n −1
f (0) − s n − 2 f (1) (0) − − f ( n −1) (0)
解：将 F ( s ) 展开为部分分式得
−1
1 jω t − jω t (e − e ) ，可得 2j
L [sin ω t ] = =
解法二：
sin ω te − st dt ∫=
0
∞
∫
∞
0
1 ∞ − ( s − jω )t 1 ∞ e jω t − e − jω t − st e dt e dt − ∫ e − ( s + jω )t dt = ∫ 2j 2j 0 2j 0

拉氏变换

拉氏变换
∞
F(s) = L[ f (t)] = ∫ eate−stdt
0−
1 −(s−a)t e =− s −a 0−
∞
1 = s −a
§13. 2 拉普拉斯变换的基本性质
一、线性性质
是两个任意的时间函数， 设f1(t)和f2(t)是两个任意的时间函数，它们的 和 是两个任意的时间函数 象函数分别为F 象函数分别为 1(s) 和F2(s) ，A1和A2是两个任意实 常数， 常数， L[A1f1(t)+ A2f2(t)] = A1L [f1(t) ] + A2L[f2(t)] = A1 F1(s) + A 2F2(s)
lim f (t ) = f (+∞) = limsF (s)
t →+∞ s →0
常用函数的拉氏变换(1) 常用函数的拉氏变换 原函数f(t) 原函数 Aδ(t) A ε(t) Ae-at 1-e-at sin(ωt) e-atsin(ωt) 象函数F(s) 象函数
A A/s
ω s2 + ω 2 ω (s +a)2 +ω2
O
ε (t)
t
2. 延迟单位阶跃函数
0 (t ≤ t ) ε (t − t ) = 1 (t ≥ t )
00 0+
ε (t)
O t0 t
延迟单位阶跃函数可以起始任意函数 f(t) f(t)ε(t− t0) ε
O
t0
t
O
t 0 (t ≤ t0- ) f (t )ε (t − t0 ) = f (t ) (t ≥ t0+ )

− st
称为收敛因子。 称为收敛因子。 收敛因子
的函数， 的函数。 积分的结果不再是 t 的函数，而是复变量 s的函数。 的函数 所以拉氏变换是把一个时间域的函数f(t)变换到 所以拉氏变换是把一个时间域的函数 变换到 s 域内的 复变函数F(s)。 复变函数 。

拉氏变换

拉氏变换

( II. 当 A(s) = (s − p1 )L s − pn ) = 0 有重根时
重根， (设 p1为m重根，其余为单根)
Cm Cm-1 Cm+1 Cn C1 F(s)= + + L+ + + L+ m m-1 (s-p1 ) (s-p1 ) s-p1 s-pm+1 s-pn
Cm = lim (s − p1 )m.F(s) s→p1 Cm C m- 1 C 1 d f(t) = L−1[ + + L+ 1 lim (s − p1 )m.F(s) (s-p1 )m (s-p1 )m- 1 s-p1 Cm- 1 = s→p 1! 1 ds C m +1 Cn L ] + + L+ s-pm +1 s-pn 1 d( j) lim j (s − p1 )m.F(s) Cm m −1 Cm-1 m − 2 Cm-j = s→p =[ t + t + ... + C2t + C1 ].e p1t j! 1 ds (m − 1 )! (m − 2 )! L n ( m−1) 1 d + ∑ C i e pi t C m lim i = m +1 1 = (m-1 )! s→p1 dsm−1 (s − p1 ) .F(s)
模 （3）复数的共轭 （4）解析
F ( s ) = Fx − jF y
若F(s)在 s 点的各阶导数都存在，则F(s)在 s 点解析。 在 点的各阶导数都存在， 在 点解析。
2 拉氏变换的定义 设f(t)为时间t的函数，并且当t<0时，f(t)=0，以下无穷积分存 在

拉氏变换

拉氏变换
确定。可对应于平面上的点 (x, y)，这样表示复数的
平面称为复平面或 z 平面。其中 x 轴称为实轴，y
轴称为虚轴。
y
Z（a，b）
z=a+bi uuur OZ (a,b)
O
x
复数的表示
• 代数形式： z x iy
• 三角形式： z r(cos i sin ) r | z | Arg z
例1
求 : f (t) sin( t)的象函数
解
F(s)
sin(t )

1

2
j
(e j t

e j t
)

1 2j

S
1
j

S
1
j


S2 2
注：欧拉公式 re jt r[cos(t) sin(t)]
2）. 微分性质
➢ 斜坡信号（Ramp Function）
r(t)

R

t

u(t)

Rt 0
r（t）
t0 t0
u(t)-----单位阶跃函数
Rt t g（）=R

时间 t
斜坡信号为匀速信号，适于测试匀速系统。
➢抛物线信号（Parabolic Function）
r
(t
)

0.5R

t
2

u(t
)

0.5R 0
t
s0
f (0 ) lim f (t) lim SF (S)
t0
s
证：
df (t) dt

sF (s)

(整理)拉氏变换讲稿

(整理)拉氏变换讲稿

第2+章 拉普拉斯变换的数学方法拉普拉斯变换简称拉氏变换，是分析研究线性动态系统的有力数学工具。

通过拉氏变换将时域的微分方程变换为复数域的代数方程，这不仅运算方便，使系统的分析大为简化，而且在经典控制论范畴，直接在频域中研究系统的动态特性，对系统进行分析、综合和校正，具有很广泛的实际意义。

2-1 复数和复变函数1.复数的概念复数，ωσj s +=其中σ、ω均为实数，分别称为S 的实部和虚部，记做Re()s σ=，)Im(s =ωj =虚部分别相等，一个复数为零，它的实部和虚部均必须为零。

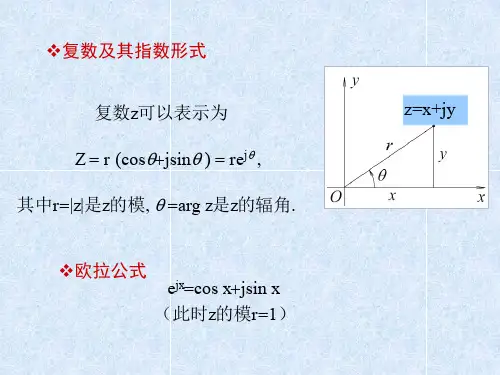
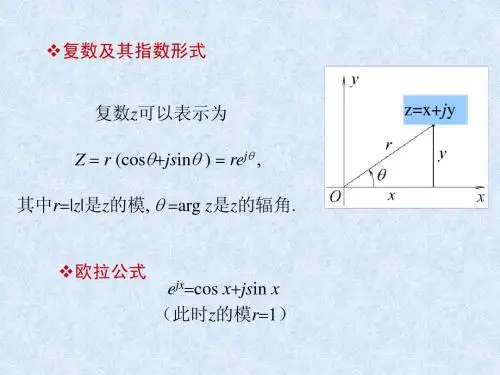
2.复数的表示方法：表达复数的直角坐标系平面称为复平面或S 平面。

（1）点表示法（2）向量表示法复数S 用从原点指向点（ωσ,）的向量来表示。

向量的长度称为复数S 的模或绝对值。

22ωσ+==r s向量与σ轴（横轴）的夹角θ称为复数的幅角，即σωθarctan =。

（3）三角表示法：由上图可看出：cos r σθ=⋅，θωsin ⋅=r 因此复数的三角表示法为：(cos sin )s r j θθ=+（4）指数表示法：利用欧拉公式：cos sin j e j θθθ=+，复数S 也可用指数表示为：j s r e θ=⋅3.复变函数、极点与零点的概念以复数ωσj s +=为自变量，按某一确定法则构成的函数G(s)称为复变函数，G(s)可写成：()G s u jv =+，在线性控制系统中，通常遇到的复变函数G(s)是S 的一个给定值，G(s)就唯一被确定。

若有复变函数 1212()()()()()()()m n k s z s z s z G s s s p s p s p ---=---当12,m s z z z =时，()0G s =,称12,z z ，·，m Z 为G(s)的零点； 当120,,n s p p p =时，()G s =∞，称120,,p p ，·，m P 为G(s)的极点。

2-2 拉氏变换与拉氏反变换的定义一、拉氏变换设有时间函数()f t ，0t ≥，则()f t 的拉氏变换记做[]()L f t 或()F s ，并定义为：[]0()()()st L f t F s f t e dt ∞-==⋅⎰ 式（2—1） 式中s 为复数，称()f t 为原函数，()F s 为象函数。

复数与拉氏变换.

复数与拉氏变换.

= ex(cos y+jsin y).
复数项级数
欧拉公式
设有复数项级数∑(un+ivn), 其中un, vn(n=1, 2, 3, )为实 常数或实函数.
如果实部所成的级数∑un收敛于和u, 并且虚部所成的级 数∑vn收敛于和v, 就说复数项级数收敛且和为u+iv.
绝对收敛
如果级∑(un+ivn)的各项的模所构成的级数∑|un+ivn|收敛, 则称级数∑(un+ivn)绝对收敛.
2!
n!
复变量指数函数
ez =1+ z + 1 z2 + + 1 zn + .
Байду номын сангаас
2!
n!
欧拉公式
当x=0时, z=iy , 于是
eiy =1+iy + 1 (iy)2 + + 1 (iy)n +
2!
n!
=1+iy - 1 y2 -i 1 y3 + 1 y4 +i 1 y5 - 2! 3! 4! 5!
Newton to one based on calculus, known as physical mechanics.
Laplace also systematized and elaborated probability theory in "Essai Philosophique sur les Probabilités" (Philosophical Essay on Probability, 1814). He was the first to publish the value of the Gaussian integral, . He studied the Laplace transform, although Heaviside developed the techniques fully. He proposed that the solar system had formed from a rotating solar nebula with rings breaking off and forming the planets. He discussed this theory in Exposition de système du monde (1796). He pointed out that sound travels adiabatically, accounting for Newton's too small value. Laplace formulated the mathematical theory of interparticulate forces which could be applied to mechanical, thermal, and optical phenomena. This theory was replaced in the 1820s, but its emphasis on a unified physical view was important.

拉氏变换复数位移定理 -回复

拉氏变换复数位移定理 -回复

拉氏变换复数位移定理-回复拉氏变换是一种重要的数学工具，广泛应用于信号处理、控制系统分析、电路分析等领域。

在拉氏变换中，有一个重要的定理被称为拉氏变换复数位移定理。

拉氏变换复数位移定理是指函数在复平面上的位移对其拉氏变换的影响。

具体而言，如果一个函数在时域上进行了复数位移，那么在频域上，其拉氏变换会发生相应的复数尺度的压缩或拉伸。

要理解拉氏变换复数位移定理，我们首先需要了解拉氏变换的基本概念。

拉氏变换是指将一个在时域上的函数转换为在频域上的函数。

拉氏变换的数学表达式为：F(s) = L[f(t)] = ∫[0,∞] f(t)e^(-st) dt其中，F(s)表示拉氏变换后的函数，f(t)表示原始函数，s为复数变量。

通过对原始函数进行积分，利用指数衰减的特性，将函数从时域转换到频域。

现在，我们来讨论拉氏变换复数位移定理。

拉氏变换复数位移定理是指，对于一个函数f(t)，如果它在时域上发生了复数位移t0，那么在频域上，其拉氏变换会发生尺度的压缩或拉伸，具体的变换关系可以通过如下公式描述：L[f(t - t0)] = e^(-st0)F(s)这里，L[f(t - t0)]表示对函数f(t)进行复数位移t0后的拉氏变换；F(s)表示函数f(t)的拉氏变换；e^(-st0)表示复数位移t0产生的衰减因子。

应用拉氏变换复数位移定理可以得到以下结论：1. 对于函数f(t - t0)的拉氏变换，在频域上会出现以e^(-st0)为因子的尺度压缩或拉伸。

如果t0大于零，那么函数在时域上发生了右移，对应的，在频域上会发生左压缩，即频率增大。

反之，如果t0小于零，函数在时域上发生了左移，对应的，在频域上会发生右拉伸，即频率减小。

2. 拉氏变换复数位移定理适用于时域上存在函数位移的情况，不仅限于实数位移，还包括复数位移。

复数位移可以看作实数位移在复平面上的推广，具有更广泛的适用性。

3. 拉氏变换复数位移定理与拉氏变换的线性性质结合起来，可以方便地分析和求解各种复杂的信号和系统。

复数与拉氏变换

复数与拉氏变换
σ + j∞
L [ F ( s )] = f (t ) =
1
1 2π
j∞ ….and we can transform it back too!
∫ F ( s )e jσ
ts
ds
The Laplace Transform
Transform Pairs: f(t)
te t e
at
F(s)
1
(s + a )2
The Laplace Transform
Building transform pairs:
∞ ∞e
L[e u(t )] = ∫ e e dt = ∫ e
0
at
L(e
at
at
st
( s + a ) t
dt
0
1 e ∞ L[e u( t )] = |0 = (s + a) s+a
A transform pair
把y换成x得 eix=cos x+jsin x, 这就是欧拉公式.
Appendix Lesson - Laplace Transforms
French physicist and mathematician who put the final capstone on mathematical astronomy by summarizing and extending the work of his predecessors in his five volume Mécanique Céleste (Celestial Mechanics) (1799-1825). This work was important because it translated the geometrical study of mechanics used by Newton to one based on calculus, known as physical mechanics. Laplace also systematized and elaborated probability theory in "Essai Philosophique sur les Probabilités" (Philosophical Essay on Probability, 1814). He was the first to publish the value of the Gaussian integral, . He studied the Laplace transform, although Heaviside developed the techniques fully. He proposed that the solar system had formed from a rotating solar nebula with rings breaking off and forming the planets. He discussed this theory in Exposition de système du monde (1796). He pointed out that sound travels adiabatically, accounting for Newton's too small value. Laplace formulated the mathematical theory of interparticulate forces which could be applied to mechanical, thermal, and optical phenomena. This theory was replaced in the 1820s, but its emphasis on a unified physical view was important. With Lavoisier, whose caloric theory he subscribed to, he determined specific heats for many substances using a calorimeter of his own design. Laplace borrowed the potential concept from Lagrange, but brought it to new heights. He invented gravitational potential and showed it obeyed Laplace's equation in empty space. Laplace believed the universe to be completely deterministic.

第2章 拉氏变换

第2章 拉氏变换


2.1.2 欧拉公式

把平面上的点（x,y）与复数 z=x+iy对应，就建立了平面上 全部的点和全体复数间的一一对应关系。
实轴：x轴 虚轴：y轴 复平面：z平面 模：向量OZ的长度

幅角：向量OZ与正实 轴的夹角

欧拉公式
ei cos i sin 复数的三角表达式：
复数的指数表达式： z
L[ f (t )] e F ( s)
st
2.5.9 复频域的位移定理

如果L[f (t)]=F (s)，则对于任意常数a，有如下结果：
L[e
at
f (t )] F ( s a)
2.6 拉氏反变换 2.6.1 拉氏反变换的定义

从象函数 F(s) 求原函数 f(t) 的运算，称为拉氏反变换，也称 拉氏逆变换，记为 L-1[F(s)]。


F ( j) f (t )e jt dt



1 f (t ) 2



F ( j )e jt d
2.3 常用函数的拉氏变换 2.3.1 指数函数的拉氏变换

指数函数是自动控制系统中常见的函数之一，f(t)=eat 的拉氏 变换为：
L[e ]
at

0
1 ( s a ) t e e dt e sa
at st

0
1 sa
2.3.2 阶跃函数的拉氏变换

阶跃函数，相当于一个恒定的信号突然加在系统上，其数学 表达式为：
0 (t 0) f (t ) r (t ) A (t 0)

A=1时称为单位阶跃函数。

拉氏变换1

拉氏变换1

4、指数表示法
e jθ = cosθ + j sinθ
r1 =| s1 |=
σ
2 1
+
ω12
θ1
=
arctan
ω1 σ1
σ
s = r ⋅ e jθ
三、复变函数、极点、零点
复变函数：以s为自变量构成的函数 G(s)
G(s) = u + jv
G(s) = K (s − z1)(s − z2 ) ⋅⋅⋅ (s − zn ) (s − p1)(s − p2 ) ⋅⋅⋅ (s − pn )
氏 变
sin ωt
ω s2 +ω2
换
cos ωt
s
s2 +ω2
e − at
1 s+a
MATLAB中的拉普拉斯变换与反变换
¾ 例：求f (t) = e-at的拉氏变换
>> syms a t; >> f=exp(-a*t); >> laplace(f) ans = 1/(s+a)
>> laplace(2*t) ans = 2/s^2
f (t) = t 3e−3t + e−t cos 2t + e−3t sin 4t
(t ≥ 0)
F(s) = 6 + s +1 +
4
(s + 3)4 (s + 1)2 + 22 (s + 3)2 + 42
4、相似定理
L
⎡⎣
f
(
at
)⎤⎦
=
1 a
F
⎛ ⎜⎝
s a
⎞ ⎟⎠
a=constant>0

拉氏变换复数位移定理 -回复

拉氏变换复数位移定理 -回复

拉氏变换复数位移定理-回复拉氏变换复数位移定理（Complex Shifting Theorem in Laplace Transform）是拉氏变换中的一个重要定理，它描述了在拉氏域中对原函数进行位移操作后其拉氏变换的相应关系。

本文将以拉氏变换复数位移定理为主题，深入介绍该定理的数学原理、应用场景以及具体的推导过程。

【引言】在探讨拉氏变换复数位移定理之前，我们先来回顾一下拉氏变换的基本概念。

拉氏变换是一种重要的数学工具，用于将一个函数从时域转换到复频域。

通过拉氏变换，我们可以将时域中的微分方程或积分方程转化为复频域中的代数方程，从而更便于求解。

【数学原理】1. 拉氏变换的定义设函数f(t)在区间[0, ∞)上可积，并满足某些充分条件，那么它的拉氏变换F(s)定义为：F(s) = L{f(t)} = ∫[0, ∞) f(t)e^(-st)dt其中，s为复变量。

2. 拉氏变换复数位移定理的表述设函数f(t)在区间[0, ∞)上可积，并满足拉氏变换的充分条件。

对任意复数a≥0，有如下关系成立：L{e^(at)f(t)} = F(s-a)其中，F(s)为f(t)的拉氏变换。

【应用场景】拉氏变换复数位移定理在信号与系统、电路分析、控制理论等领域具有广泛的应用。

下面以几个典型的应用场景为例，展示该定理的实际运用。

1. 系统响应计算在信号与系统分析中，我们经常需要计算线性时不变系统的响应。

通过使用拉氏变换复数位移定理，我们可以将输入信号的变换函数移动到系统函数的位置，从而直接得到系统的输出函数。

2. 瞬态响应分析在电路分析中，我们常常需要研究电路的瞬态响应，即在电路中加入一个初始条件或一个瞬时激励信号后，电路的暂态行为。

利用拉氏变换复数位移定理，我们可以很方便地将初始条件或瞬时激励信号的影响考虑在内，从而得到电路的瞬态响应。

3. 跨越频率边界当我们需要跨越频率边界进行信号处理时，拉氏变换复数位移定理也发挥了重要作用。

拉氏变换

拉氏变换

3
象函数F(s) 存在的条件：
0
f ( t )e
st
dt
e st 为收敛因子
3.信号典型函数 拉氏变换的计算
指数函数
三角函数 单位脉冲函数 单位阶跃函数 单位速度函数
单位加速度函数
幂函数
阶跃信号（Step Function）
R t 0 r (t ) R u (t ) 0 t 0
s t 0
f ( ) lim f ( t ) lim SF ( S )
t s 0
证：利用导数性质
lim 0 s 0
d f ( t )e st dt lim[ SF ( S ) f (0 )] s 0 dt
0
d st f ( t ) lim e dt f ( t ) s0 dt 0 f ( ) f ( 0 ) lim SF ( S ) f ( 0 )
反变换
0 积分下限从0 开始，称为0 拉氏变换 。 0 + 开始，称为0+ 拉氏变换 。 积分下限从 0 0
今后讨论的拉氏变换均为 0 拉氏变换,计及t=0时f(t) 包含的冲击。
F (S ) 简写 f (t )
注
1


f (t ) 1 F (S )
例2 解
求 : f (t ) δ( t )的象函数
du (t ) (t ) dt
1 [u (t )] s
δ(t )
推广：
1 d [ u (t )] S 1 dt S
d 2 f (t ) ' [ ] s[sF (s) f (0 )] f (0 ) 2 dt

拉普拉斯定理

拉普拉斯定理

复习拉普拉斯变换的有关内容1 复数有关概念 （1）复数、复函数 复数 ωσj s += 复函数 ()y x jF F s F += 例：()ωσj 22s s F ++=+= （2）复函数模、相角()()xy 2y 2x F F arctgs F F F s F =∠+= （3）复数的共轭 ()y x jF F s F -=（4）解析：若F(s)在s 点的各阶导数都存在，称F(s)在s 点解析。

2 拉氏变换定义：()()[]()dt e t f t f L s F st0-∞⋅==⎰⎩⎨⎧：像：原F(s))(t f 3 几种常见函数的拉氏变换⑴ 单位阶跃：()⎩⎨⎧≥<=0t 10t 0t 1()[][]()s110s 1e s1dt e 1t 1L 0stst =--=-=⋅=∞-∞-⎰ ⑵ 指数函数：⎩⎨⎧≥<=0t e 0t 0)t (f at()[]as 1)10(a s 1eas 1 dte dt e e )]t (f [L 0t)a s (0t a s st 0at -=---=--==⋅=∞--∞---∞⎰⎰⑶ 正弦函数：⎩⎨⎧≥<=0t t sin 0 t 0)t (f ω （欧拉公式j e e t tj t j 2sin ωωω--=）[][][]22220t )j s (0t )j s (0)t j s ()tj -(s -st 0t j tj 0st s s 2j 2j 1 j s 1j s 12j 1 e j s 1e j s 12j 1 dt e e 2j 1 dt e e e 2j 1 dte t sin )t (f L ωωωωωωωωωωωωωωω+=+⋅=⎥⎦⎤⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡+----=-=⋅-=⋅=∞+-∞--∞+--∞-∞-⎰⎰⎰4 拉氏变换的几个重要定理（1）线性性质： [])s (bF )s (aF )t (bf )t (af L 2121+=+ （2）微分定理： ()[]()()0f s F s t f L -⋅='()()()()()()()()stst 0-ststst 0f t e dt e df t e f t f t de0-f 0s f t e dt sF s f 0 ∞∞--∞∞-∞-'=⋅=⎡⎤=-⎣⎦=+⎡⎤⎣⎦=-=⎰⎰⎰⎰证明：左右()()()()()()()()()n n-2n 1n n-1n-2 L f t s F s s f 0s f 0sf 0f 0-⎡⎤'=-----⎣⎦进一步： 零初始条件下有：()()[]()s F s t f L n n ⋅=例：求[]t cos L ω 解：[]2222s ss s 1t n si L 1t cos ωωωωωωω+=+⋅⋅='=（3）积分定理：()[]()()()0f s1s F s1dt t f L 1-+⋅=⎰ （证略） 零初始条件下有：()[]()s F s1dt t f L ⋅=⎰ 进一步有：()()()()()()()()0f s 10f s 10f s 1s F s1dt t f L n 21n 1n n nn ----++++=⎥⎥⎦⎤⎢⎢⎣⎡⎰⎰⎰【重积分的表示n f f n )0()0()(-】● 例：求L[t]=? 解：()dt t 1t ⎰=[]()[]2t s 1ts1s 1s 1dt t 1L t L =+⋅==∴=⎰ ● 例：求⎥⎦⎤⎢⎣⎡2t L 2解：⎰=tdt 2t 2[]30t 222s12t s 1s 1s 1tdt L 2t L =⋅+⋅==⎥⎦⎤⎢⎣⎡∴=⎰ （4）位移定理实位移定理：()[]()s F e-t f L s⋅=-ττ ● 例：()()s F 0 t 01 t 0 10t 0t f 求⎪⎩⎪⎨⎧><<<=解：)1t (1)t (1)t (f --= ()()s s e 1s1e s1s1s F ---=⋅-=∴（5）复位移定理：()[]()a -s F t f e L at =⋅（证略） ● 例：求[]ate L:解[]()[]as 1e t 1L e L atat-=⋅= ● 例：[]()223s s 223t -53s 3s 5s s cos5t e L +++=+=⋅+→● 例：⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---)15t (5cos e L )35t (cos e L 2t2t ππ ()()222s 152s s 22s 15-52s 2s e 5s s e +++⋅=⎭⎬⎫⎩⎨⎧+=+-+→ππ （6）终值定理（极限确实存在时）()()()s F s lim f t f lim 0s t ⋅=∞=→∞→证明：由微分定理()()()0f s sF dt e t f st 0-='-∞⎰取极限：()()()0f s sF lim dt e t f lim 0s st 0s -='→-∞→⎰()[]()()()()()()0f s sF lim 0f f t f dt 1t f dt limet f 0s 000s st-==-∞==⋅⋅'='=→∞∞→-∞⎰⎰右左∴有：()() s sF lim f 0s →=∞证毕 ● 例：()()()b s a s s 1s F ++=求()f ∞解：()()()ab1b s a s s 1s lim f 0s =++=∞→● 例：()0s s limt sin f 220s t =+≠=∞→∞→ωωω拉氏变换附加作业 一． 已知f(t),求F(s)=?()1-t T111T1).f(t)1-eF s 11s s s s T T ==-=⎛⎫++ ⎪⎝⎭()22221s 0.122).f (t)0.03(1cos2t) F(s)0.03s s 2s s 2⎡⎤=-=-=⎢⎥++⎣⎦ s 15222250.866s 2.53).f (t)sin(5t ) F(s)e 3s 5s 5ππ+=+==++()0.4t 222s 0.4s 0.44).f (t)e cos12t F(s)s 0.8s 144.16s 0.412-++===++++[]05).f (t)t 11t t ⎡⎤=⋅--⎣⎦()()0t s0211t s e F s s --+=()()()223s 2s 86).F(s) f ? f(0)? f()1, f(0)0s s 2s 2s 4++=∞==∞==+++已知求 二．已知F(s),求f(t)=?()222s 5s 11).F(s) f(t)1cost-5sint s s 1-+==++()4t 24t s2).F(s) f(t)cos(t 14)s 8s 17 e cost 4sint --==+++=-t 10t321119t 3).F(s) f(t)e e s 21s 120s 1008181--+==-+++()2-2t t23s 2s 84).F(s) f(t)1-2e e s s 2(24)s s -++==+⋅+++ ()()t 3t 2s 221315).F(s) f(t)(t )e e 32412s s 1s 3--+==-++++5. 拉氏反变换 (1) 反变换公式：⎰∞+∞-=j j stds e ).s (F j 21)t (f σσπ (2) 查表法——分解部分分式(留数法，待定系数法，试凑法)f(t),)a s (s 1)s (F 1.求例+=⎥⎦⎤⎢⎣⎡+-=++=a s 1s 1a 1)a s (s s -a)(s a 1)s (.F 解 []at e 1a1)t (f --=∴ 微分方程一般形式：r b r b r b r b C C a C a C m 1-m )1-m (1)m (01-n )1-n (1)n (+'+++=+'+++ )0(:L 设初条件为[][]R(s)b s b s b s b )s (C a s a s a s a sm 1-m 1m 1m 0n 1-n 2-n 21-n 1n++++=+++++-)s (A )s (R ).s (B a s a s a s a s )R(s)b s b s b s (b C(s)n1-n 2-n 21-n 1n m 1-m 1m 1m 0=+++++++++=∴- )p s ()p s )(p s ()s (R ).s (B n 21---=∑=-=-++-+-+-=n1i ii n n 332211 p s cp s c p s c p s c p s c )s (C 特征根:p i∑==++++=∴n1i t p i tp n tp 3tp 2tp 1i n 321e c ec ec ec ec )t (f 模态:e t p i)s (F 的一般表达式为：[]r b r b r b r b C C a C a C m 1-m )1-m (1)m (01-n )1-n (1)n (+'+++=+'+++ 来自：（I ）)m n (a s a s a s a s b s b s b s b )s (A )s (B )s (F n1-n 2-n 21-n 1n m 1-m 1m 1m 0>+++++++++==- 其中分母多项式可以分解因式为：)p s ()p s )(p s ()s (A n 21---= (II))s (A p i 为的根(特征根)，分两种情形讨论：⑴：0)s (A =无重根时：(依代数定理可以把)s (F 表示为：)∑=-=-++-+-+-=n1i ii n n 332211p s cp s c p s c p s c p s c )s (F∑==++++=∴n1i t p i tp n tp 3tp 2tp 1i n 321e c ec ec ec ec )t (f即：若i c 可以定出来，则可得解：而i c 计算公式： )s (F ).p s (lim c i p s i i-=→(Ⅲ)ip s 'i )s (A )s (B c ==(Ⅲ′)(说明(Ⅲ)的原理，推导(Ⅲ′) ) ● 例2：34s s 2s )s (F 2+++= 求?)t (f = 解：3s c1s c 3)1)(s (s 2s )s (F 21+++=+++=2131213)1)(s (s 2s )1s (lim c 1s III1=+-+-=++++=-→2113233)1)(s (s 2s )3s (lim c 3s III2=+-+-=++++=-→3s 211s 21)s (F +++=∴ 3t t e 21e 21)t (f --+=∴ ● 例3：34s s 55s s )s (F 22++++= ，求?)t (f =解：不是真分式，必须先分解：(可以用长除法)3)1)(s (s 2s 134s s 2s 3)4s (s )s (F 22++++=++++++= 3t t e 21e 21)t ()t (f --++=∴δ● 例4：j1s c j -1s c j)1j)(s -1(s 3s 22s s 3s )s (F 212++++=++++=+++=解法一：2j j2j)1j)(s -1(s 3s )j -1s (lim c j1s 1+=+++++=+-→ 2jj-2j)1j)(s -1(s 3s )j 1s (lim c j-1s 2-=++++++=-→ j)t1(t )j 1(e2jj -2e 2j j 2)t (f --+--+=∴ []jt-jt t e )j 2(e )j 2(e 2j 1--+=- （t e e t j e e jt jt jt jt cos 2,sin 2=+=--- ） [])2sint cost (e j 4sint 2cost e 2j1t t+=+=-- 1)1s (21)1s (1s 1)1s (21s 1)1s (3s )s (F 2222++++++=++++=+++=t t e .2sint e .cost )t (f --+=∴虚位移定理解法二：)( sint .2e cost .e )t (f 11)(s 1211)(s 1s 11)(s 21s 11)(s 3s )s (F t t 22222222复位移定理--+=++++++=++++=+++=⑵：0)s (A =有重根时：设1p 为m 阶重根，n 1m s ,s +为单根 .则)s (F 可表示为：nn1m 1m 111-m 11-m m 1m p -s c p -s c p -s c )p -(s c )p -(s c )s (F ++++++=++ 其中单根n 1m c ,c +的计算仍由(1)中公式(Ⅲ) (Ⅲ′)来计算. 重根项系数的计算公式：(说明原理)[][][]⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧-=-=-=-=→→→→)s (F .)p s (ds d lim 1)!-(m 1c )s (F .)p s (ds d lim j!1c (IV) )s (F .)p s (ds d lim c )s (F .)p s (lim c m 1p s 1-m 1)-(m 1m1p s j (j)j -m m 1p s 1-m m 1p s m 1111[]V)( e c e .c t c t )!2m (c t )!1m (c p -s c p -s c p -s c )p -(s c )p -(s c L )s (F L )t (f t p n1m i i t p 122m 1-m 1m m n n 1m 1m 111-m 11-m m 1m 11i 1∑+=--++--+⎥⎦⎤⎢⎣⎡+++-+-=⎥⎦⎤⎢⎣⎡++++++==∴ ●例5 3)(s 1)s(s 2s )s (F 2+++= 求?)t (f =解：3s c s c 1s c 1)(s c )s (F 43122++++++=21)31)(1(213)(s 1)s(s 2s 1)(s lim c 221s IV2-=+--+-=++++=-→ 43)3(])3)[(2()3(lim 3)(s 1)s(s 2s 1)(s ds d limc 221221s IV1-=++++-+=⎥⎦⎤⎢⎣⎡++++=-→-→s s s s s s s s 323)(s 1)s(s 2s s.lim c 20s 3=+++=→1213)(s 1)s(s 2s 3).(s lim c 2-3s 4=++++=→ 3s 1.121s 1.321s 1.431)(s 1.21)s (F 2++++-+-=∴3t t t e 12132e 43te 21)t (f ---++--=∴。

拉氏变换

拉氏变换
x y
其中： 其中： F (s ) =
Fx+Fy
2 2
∠F (s ) = arctan
Fy F x
G (s ) = s
例如：
2 2
其中 : s = σ + jω = r∠ϕ
2
s = r ∠ 2ϕ
jGy
S平面 2
0
G(s)平面
4
σ
0
G
x
一、拉氏变换定义： 对于函数 x (t ) ，满足下列条件
s 2 + 2s + 3 3 其中： 3 = α (s + 1)3 (s + 1) = 2 s = −1 d 2 α 2 = ds s + 2s + 3 s =−1 = 2s + 2 s=−1 = 0
s 2 + 2s + 3 −1 [F (s )] = L−1 求:L 3 (s + 1)
2 −1 X (s ) = + s+1 s+ 2
s+3 c2 = × (s + 2 ) = −1 (s + 1)(s + 2 ) s = −2
x(t ) = 2e − e
−t
(
−2 t
)
2、含有共扼复极点情况：
例2 − 5 s+1 L 3 s + s2 + s
− st
dt
[t ]−1 复变量 量纲
二、简单函数的拉氏变换
1. 单位阶跃函数 1(t )
0 t < 0 1(t ) ∆ 1 t > 0
L[1(t )] = ∫ 1(t ) e

拉氏变换 (3)

拉氏变换 (3)

拉氏变换1. 简介拉氏变换（Laplace Transform）是一种用于解决常微分方程（ODE）的数学工具。

它将一个随时间变化的函数转换为一个复数域中的函数，使得常微分方程可以转化为代数方程来求解。

通过拉氏变换，我们可以将时域中的问题转化到频域中，从而简化问题的分析和求解。

拉氏变换的应用非常广泛，在控制系统、通信系统、信号处理等领域中起着重要的作用。

通过拉氏变换，我们可以分析系统的稳定性、阻尼特性、频率响应等性能指标。

2. 定义与性质拉氏变换是对一个函数f(t)的积分变换。

给定一个函数f(t)和复数s，拉氏变换可以用如下公式来表示：L{f(t)} = F(s) = ∫[0,∞] e^(-st) f(t) dt其中，e是自然常数，s是复变量。

拉氏变换有许多重要的性质。

以下是一些常见的性质：•线性性质：即拉氏变换满足线性运算。

对于任意常数a和b，以及函数f(t)和g(t)，有 L{a f(t) + b g(t)} = a F(s) + b G(s)。

•积分性质：对于函数f(t)的导数，有L{f’(t)} = sF(s) - f(0)，其中f(0)为f(t)在t=0时的初始值。

类似地，对于f(t)的n阶导数，有 L{f^(n)(t)} = s^n F(s) - s^(n-1) f(0) -s^(n-2) f’(0) - … - f^(n-1)(0)。

•初值定理：初值定理指出，当s趋于无穷大时，拉氏变换是函数f(t)的初始值的一阶逼近。

即lim(s→∞) sF(s) = f(0)。

•终值定理：终值定理指出，当s趋于零时，拉氏变换是函数f(t)的稳态值的一阶逼近。

即lim(s→0) sF(s) =lim(t→∞) f(t)。

3. 拉氏变换的应用3.1. 控制系统在控制系统中，拉氏变换被广泛应用于系统的稳定性分析、阻尼特性分析等。

通过将系统的微分方程转化为拉氏域的代数方程，可以求解系统的传递函数，从而分析系统的频率响应和稳定性。

实信号的拉氏变换其复数零点 极点必共轭成对出现 是什么意思

实信号的拉氏变换其复数零点 极点必共轭成对出现 是什么意思

实信号的拉氏变换其复数零点极点必共轭成对出现是什
么意思
标题“实信号的拉氏变换其复数零点极点必共轭成对出现”，指的是信号处理中的重要概念实信号的拉氏变换。

拉氏变换（Laplace transform）是一种非常常用的时域信号分析技巧，在科学技术的各个领域都有广泛的应用。

它是一种将时域函数转换为频域函数的一种方法。

拉氏变换的定义：当实信号的拉氏变换被计算时，它的复数零点和极点必定是成对出现的。

复数零点是拉氏变换中渐近函数的零点，极点是拉氏变换中渐近函数的极大点。

零点和极点成对出现，这是因为它们是时域函数中的本征频率对应的点，在频域中，一对零点和极点对应于一个本征频率。

在实际应用中，拉氏变换可以用来测量一个函数在不同频率上的特点，并且可以用来确定函数在其他域中的行为。

在信号处理中，拉氏变换可以帮助我们理解和提取信号的特征，如中心频率、频谱、峰值和噪声水平等。

拉氏变换同样可以用来计算系统的输入和输出，以及衡量系统的稳定性和抗扰性能。

此外，拉氏变换还可以用来处理常微分方程，因此它在工程技术中也是极为重要的。

拉氏变换可以用来实现滤波效果，并且可以用于维护振荡系统的稳定性，从而确保系统的正常运作。

总之，拉氏变换是信号处理中一个十分重要的数学技术，它的实信号的拉氏变换其复数零点极点必共轭成对出现，意味着信号处理中
有一对特定频率，它们的零点和极点是成对出现的，并可以用来确定函数在其他域中的行为，从而在工程技术中发挥重要作用。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
复数及其指数形式
复数z可以表示为
Z = r (cosqjsinq ) = rejq 其中r=|z|是z的模 q =arg z是z的辐角
z=x+jy
欧拉公式
ejx=cos xjsin x （此时z的模r=1）
三角函数与复变量指数函数之间的联系 因为 所以 ejx+ejx=2cos x exejx=2jsin x ejx =cos xj sin x ejx=cos xj sin x
dn f n n 1 n2 n 1 s F s s f 0 s f 0 f 0 n dt



5
dt
4 y = 2,
y (0) = 1
Solution:
First, take L of both sides
Rearrange, Take L-1,
dt
Application: Linear Differential Equations

we can solve differential equations (including initial conditions) using Laplace transforms Example: (D2 + 5D + 6) y(t) = (D + 1) f(t)
复变量指数函数
e z =1 z 1 z 2 1 z n 2! n! 欧拉公式
当x=0时 z=iy 于是
eiy =1 iy 1 (iy)2 1 (iy)n 2! n! =1 iy 1 y 2 i 1 y3 1 y 4 i 1 y5 2! 3! 4! 5! = (1 1 y 2 1 y 4 ) i( y 1 y3 1 y5 ) 2! 4! 3! 5! =cos yjsin y
Given the hard problem!
Convert it into the subsidiary equation (Simple Problem!)
Transform the subsidiary equation’s solution to obtain the solution of the given problem
因此
1 1 jx jx = = cos x (e e ) , sin x (ejx ejx ) 2 2j 复变量指数函数的性质 ez1 z2 = ez1 ez2 特殊地 有
exjy = exej y = ex(cos yjsin y)
复数项级数
欧拉公式
设有复数项级数∑(univn) 其中un vn(n=1 2 3 )为实 常数或实函数 如果实部所成的级数∑un收敛于和u 并且虚部所成的级 数∑vn收敛于和v 就说复数项级数收敛且和为uiv 绝对收敛 如果级∑(univn)的各项的模所构成的级数∑|univn|收敛 则称级数∑(univn)绝对收敛
把y换成x得 eix=cos xjsin x 这就是欧拉公式
Appendix Lesson - Laplace Transforms
French physicist and mathematician who put the final capstone on mathematical astronomy by summarizing and extending the work of his predecessors in his five volume Mécanique Céleste (Celestial Mechanics) (1799-1825). This work was important because it translated the geometrical study of mechanics used by Newton to one based on calculus, known as physical mechanics. Laplace also systematized and elaborated probability theory in "Essai Philosophique sur les Probabilités" (Philosophical Essay on Probability, 1814). He was the first to publish the value of the Gaussian integral, . He studied the Laplace transform, although Heaviside developed the techniques fully. He proposed that the solar system had formed from a rotating solar nebula with rings breaking off and forming the planets. He discussed this theory in Exposition de système du monde (1796). He pointed out that sound travels adiabatically, accounting for Newton's too small value. Laplace formulated the mathematical theory of interparticulate forces which could be applied to mechanical, thermal, and optical phenomena. This theory was replaced in the 1820s, but its emphasis on a unified physical view was important.
Solve the subsidiary equation (Purely algebraic!)
Application: Linear Differential Equations

Using differentiation in solve differential equations (including initial conditions) using Laplace transforms dy Example:
The Laplace Transform of a function, f(t), is defined as;
L[ f (t )] = F ( s) = f (t )e dt
st 0

What is the Inverse Laplace Transform?
Let F(s) be a Laplace transform of a function f(t). We can get f(t) by inverse Laplace Transform , via: The Inverse Laplace Transform is defined by
From Table :
2 5 sY s 1 4Y s = s 1 5s 2 y t = L s 5 s 4 y(t ) = 0.5 0.5e 0.8t

Using differentiation in time property dn f n n 1 n2 n 1 0 s F s s f 0 s f 0 f n
Laplace, Pierre (1749-1827)
With Lavoisier, whose caloric theory he subscribed to, he determined specific heats for many substances using a calorimeter of his own design. Laplace borrowed the potential concept from Lagrange, but brought it to new heights. He invented gravitational potential and showed it obeyed Laplace's equation in empty space. Laplace believed the universe to be completely deterministic.
An important point :
f (t ) F ( s )
The above is a statement that f(t) and F(s) are transform pairs. What this means is that for each f(t) there is a unique F(s) and for each F(s) there is a unique f(t). If we can remember the Pair relationships between approximately 10 of the Laplace transform pairs we can go a long way.
L [ F ( s )] = f (t ) =
1
1 2
too! j ….and we can transform it back
F ( s )e j
j
ts
ds
Why the transform?
A method to solve differential equations and corresponding initial and boundary value problems, particularly useful when driving forces are discontinuous, impulsive, or a complicated periodic/aperiodic function.