水力学 动量方程

恒定总流的动量方程利用前面介绍的连续性方程和能量方程，已经能够解决许多实际水力学问题，但对于某些较复杂的水流运动问题，尤其是涉及到计算水流与固体边界间的相互作用力问题，如水流作用于闸门的动水总压力，以及水流经过弯管时，对管壁产生的作用力等计算问题，用连续性方程和能量方程则无法求解，而必须建立动量方程来解决这些问题。

动量方程实际上就是物理学中的动量定理在水力学中的具体体现，它反映了水流运动时动量变化与作用力间的相互关系，其特点是可避开计算急变流范围内水头损失这一复杂的问题，使急变流中的水流与边界面之间的相互作用力问题较方便地得以解决。

一、动量方程式的推导及适用条件（一）动量方程式的推导由物理学可知，物体的质量m 与速度υ的乘积称为物体的动量。

动量是矢量，其方向与流速方向相同。

物体在外力作用下，速度会发生改变，同时动量也随之变化。

动量定理可表述为：运动物体单位时间内动量的变化等于物体所受外力的合力。

现将动量定理用于恒定流中，推导恒定流的动量方程。

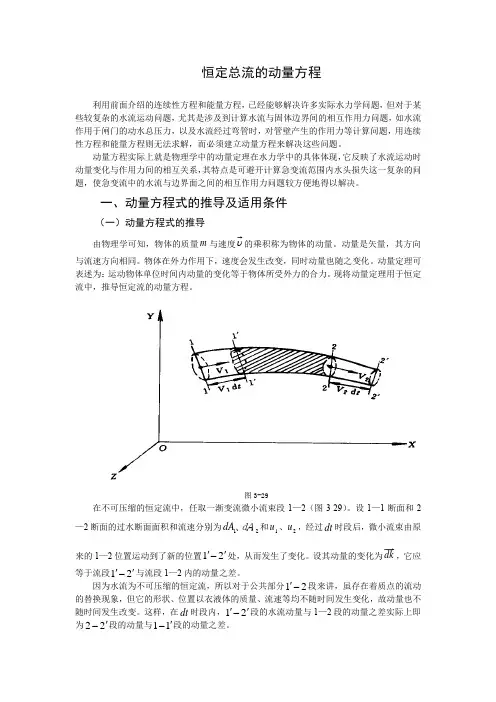
图3-29在不可压缩的恒定流中，任取一渐变流微小流束段1—2（图3-29）。

设1—1断面和2—2断面的过水断面面积和流速分别为21、dA dA 和1u 、2u ，经过dt 时段后，微小流束由原来的1—2位置运动到了新的位置21'-'处，从而发生了变化。

设其动量的变化为dk ，它应等于流段21'-'与流段1—2内的动量之差。

因为水流为不可压缩的恒定流，所以对于公共部分21-'段来讲，虽存在着质点的流动的替换现象，但它的形状、位置以衣液体的质量、流速等均不随时间发生变化，故动量也不随时间发生改变。

这样，在dt 时段内，21'-'段的水流动量与1—2段的动量之差实际上即为22'-段的动量与11'-段的动量之差。

在dt 时段内，通过11'-段的水体质量为11dtdA u ρ，通过22'-段的水体质量为22dtdA u ρ，对于不可压缩液体，根据连续性方程，可知dQdt dtdA u dtdA u ρρρ==2211，则微小流束段的动量变化为)(12u u dQdt k d -=ρ设总流两个过水断面的面积分别为21A A 与，将上述微小流束的动量变化k d 沿相应的总流过水断面进行积分，即可得到总流在dt 时段内动量的变化量为)()()(121112221212a dA u u dA u u dt u dQdt u dQdt u u dQdt k d A A QQ Q ⎰⎰⎰∑⎰⎰-=-=-=ρρρρ 由于实际液体过水断面上的流速分布均匀，且不易求得，故考虑用断面平均流速υ来代替断面上不均匀分布的流速u ，以便计算总流的动量。

流体的连续性方程和动量方程流体力学是研究流体运动和流体力学性质的学科。

在流体力学中，连续性方程和动量方程是两个重要的基本方程。

本文将详细介绍流体的连续性方程和动量方程的定义和应用。

一、流体的连续性方程连续性方程描述了流体的质量守恒原理，表达了流体在空间和时间上的连续性。

连续性方程的数学表达形式为：∂ρ/∂t + ∇·(ρv) = 0其中，ρ是流体的密度，t是时间，v是流体的速度矢量，∇·(ρv)表示速度矢量的散度。

该方程表示，流体的密度在一个闭合曲面上的变化率等于通过该曲面的质量流量。

连续性方程是基于质量守恒原理推导得出的。

它表明，在稳定流动条件下，流体在通道中的截面积变化时，速度会发生相应的变化，以保持质量的守恒。

根据连续性方程，我们可以推导出管道中的速度分布。

在管道的收缩段，速度增加，截面积减小，密度保持不变，从而保证质量守恒。

这也是为什么水管收缩后出水流速增加的原因。

二、流体的动量方程动量方程描述了流体运动的力学性质，表达了流体在空间和时间上的动量守恒。

动量方程的数学表达形式为：ρ(dv/dt) = -∇p + μ∇^2v + F其中，ρ是流体的密度，t是时间，v是流体的速度矢量，p是压强，μ是流体的粘度，∇p表示压强的梯度，∇^2v表示速度的拉普拉斯算子，F是外力的合力。

动量方程由牛顿第二定律推导而来。

它表示，在流体中，流体质点的动量变化等于合外力对质点的作用力。

动量方程用于描述流体在受力作用下的运动状态，通过求解动量方程，可以得到流体的速度分布。

根据动量方程，我们可以推导出流体中的压力分布。

在水管中，如果水流速度增大，则根据动量方程中的负梯度项，压力会降低。

这是因为速度增大会导致动能的增加，压力会减少以保持动量守恒。

综上所述，流体的连续性方程和动量方程是流体力学中的两个基本方程。

连续性方程描述了质量守恒原理，动量方程描述了动量守恒原理。

通过求解这两个方程，我们可以获得流体在空间和时间上的运动状态和力学性质。

2.1.恒定流：如果在流场中任何空间点上所有的运动要素都不随时间而改变。

非恒定流：如果在流场中任何空间点上有任何一个运动要素是随时间而变化。

均匀流：水流的流线为相互平行的直线。

非均匀流：水流的流线不是相互平行的直线。

渐变流：水流的流线虽然不是相互平行的直线，但几乎近于平行的直线。

急变流：水流的流线之间夹角很大或者流线的曲率半径很小。

按运动要素是否彼此平行的直线分为均匀流和非均匀流，而非均匀流按流线的不平行和弯曲程度又分为渐变流和急变流。

渐变流重要性质为：过水断面上近似服从静压分布：Z+P/y=C2.2.此时的A₁υ₁=A₂υ₂符合连续方程。

两个断面无支流，且上游水位恒定，则下游通过的流量一定，则流量保持平衡，满足该公式。

2.3能量方程：Ζ₁＋Ρ₁/ρg＋α₁（μ₁）²/2g=Ζ₂＋Ρ₂/ρg＋α₂（μ₂）²/2g＋hw’。

Ζ₁：位置水头；Ρ₁/ρg：压强水头；（μ₁）²/2g：流速水头；Ζ₂：单位位能；Ρ₂/ρg：单位压能；（μ₂）²/2g：单位动能；hw’：水头损失。

能量意义：在总流中任意选取两个过水断面，该两断面上液流所具有的总水头若为H₁和H₂，则：H₁=H₂+hw。

2.4这些说法都不对。

对于理想液体来说，在无支流进去的情况下，其各断面的流量总和是相等的，根据能量方程：Ζ₁＋Ρ₁/ρg＋α₁（μ₁）²/2g=Ζ₂＋Ρ₂/ρg＋α₂（μ₂）²/2g＋hw’，及连续方程：A₁υ₁=A₂υ₂。

可以看出：只要其流量不改变，能量的总和就不会变。

则水是由流速大地方向流速小的地方流这种说法就是错误的。

总流的动量方程：ΣF=ρQ（Β₂υ₂-Β₁υ₁），也说明了这一点。

2.5总水头线：把各断面H=Ζ＋Ρ/ρg＋α（μ）²/2g描出的点子连接起来得到的线就是总水头线；测压管水头线：把各断面的（Ζ＋Ρ/ρg）值的点子连接起来得到的线就是测压管水头线。

流体力学中的动量方程动量方程是流体力学中描述流体运动的基本方程之一。

它描述了流体在运动过程中动量的变化，通过掌握动量方程，可以深入理解和分析流体的运动特性。

一、动量的定义与表达式根据牛顿第二定律，一个物体的动量等于其质量与速度的乘积。

对于流体来说，动量可以用密度、速度和体积来表达。

根据这个定义，流体的动量可以表示为：M = ρ * V其中，M为动量，ρ为流体的密度，V为流体的速度。

二、流体的动量守恒流体的动量守恒是指在一个封闭系统中，动量的总量在时刻保持不变。

这可以通过动量方程来表示。

对于流体的动量守恒方程，有两个基本形式：1.欧拉动量方程欧拉动量方程适用于描述非粘性流体的动量守恒。

其表达式为：∂(ρV)/∂t + ∇(ρV*V) = -∇P + ρg其中，ρ为流体的密度，V为流体的速度，t为时间，P为压力，g 为重力加速度。

2.纳维-斯托克斯动量方程纳维-斯托克斯动量方程适用于描述粘性流体的动量守恒。

其表达式为：∂(ρV)/∂t + ∇(ρV*V) = -∇P + μ∇²V + ρg其中，ρ为流体的密度，V为流体的速度，t为时间，P为压力，μ为流体的动力黏度，g为重力加速度。

三、动量方程的应用动量方程在流体力学的研究中有广泛的应用。

它可以用来解释和预测流体的运动特性，如流体的速度分布、流体中的压力和力的作用等。

1.速度分布根据动量方程，可以推导出流体在不同速度条件下的速度分布规律。

通过研究流体的速度分布，可以了解到流体的流动状态，从而更好地控制和管理流体运动。

2.压力分布动量方程中的压力项描述了流体中压力的变化规律。

通过分析动量方程中的压力项，可以获得流体的压力分布情况。

这对于设计和优化流体系统具有重要意义。

3.流体之间的相互作用在实际应用中，流体通常与其他物体或流体相互作用。

通过动量方程，可以分析流体与其他物体的相互作用力，并进行力学计算和设计。

四、总结动量方程是流体力学中重要的基本方程之一，通过它可以深入研究和理解流体的运动特性。

水力学基本方程
水力学的基本方程分为质量守恒方程、动量守恒方程和能量守恒方程。

1. 质量守恒方程
质量守恒方程描述了在水流运动过程中,单位时间内通过某一截面的水量与该截面上下游的水量之差之间的关系。

其表示式为:
\frac{\partial Q}{\partial t} + \frac{\partial}{\partial x}(Qv) = 0
其中,Q为单位时间内通过截面的水量,v为水流速度,x为沿水流方向的坐标,\frac{\partial}{\partial x}为对x的偏导数。

2. 动量守恒方程
动量守恒方程揭示了水流运动中的动量转移与保存规律,其表示式为:
\frac{\partial}{\partial t}(Qv) + \frac{\partial}{\partial x}(Qv^2 + \frac{1}{2}gh^2) = f_L Qv
其中,g为重力加速度,h为水深,f_L为流动阻力系数。

3. 能量守恒方程
能量守恒方程描述了水流运动中的能量转移与保存规律,其表示式为:
\frac{\partial}{\partial t}(Qh) + \frac{\partial}{\partial x}(Qhv + \frac{1}{2}gh^2v) = f_L Qvh + Q\dot{E}
其中,\dot{E}为单位时间内对水流作用的外力功率。

水力学三大方程指的是连续性方程、动量方程和能量方程。

这三大方程是描述流体力学过程的基本方程，也是水力学研究和应用的基础。

连续性方程
连续性方程也称为质量守恒方程，它表述了流体在运动过程中质量守恒的基本原理。

连续性方程的数学表达式为：
∂ρ/∂t + ∇·(ρu) = 0
其中，ρ表示流体密度，t表示时间，u表示流体的速度，∇表示偏微分算符。

这个方程的物理含义是：任何一段流体管道中的质量流量都相等，即在单位时间内通过截面积相同的两个截面的流体质量相等。

动量方程
动量方程是描述流体运动动力学过程的方程，它表述了流体的动量守恒原理。

动量方程的数学表达式为：
ρ(∂u/∂t + u·∇u) = -∇p + ∇·τ+ ρg
其中，p表示流体的压力，τ表示流体的应力张量，g表示重力加速度。

这个方程的物理含义是：流体的动量随时间和空间的变化而改变，动量的变化量等于受到的力的作用量。

能量方程
能量方程描述了流体运动过程中能量守恒的基本原理。

能量方程的数学表达式为：
ρCv(∂T/∂t + u·∇T) = -p∇·u + ∇·(k∇T) + Q
其中，T表示流体的温度，Cv表示比热容，k表示导热系数，Q表示单位时间单位体积内的热源项。

这个方程的物理含义是：流体在运动过程中受到的压力和内能的变化，以及受到的热量和能量的变化，都会影响流体的温度和温度的变化。

水文动量平衡水文动量平衡是水文学中的一个重要概念，用于描述水体运动中的动量变化情况。

在水文学中，动量平衡是指水体在运动过程中受到的各种力的平衡状态，这些力包括惯性力、摩擦力、重力等。

了解水文动量平衡可以帮助我们更好地理解水体的运动规律和水文现象。

在水文学中，动量平衡可以用动量方程来描述。

动量方程是基于牛顿第二定律建立的，它描述了水体运动中动量的变化与受到的力之间的关系。

动量方程可以表示为：∂(ρu)/∂t + ∇·(ρu⃗u⃗) = -∇p + ∇·τ⃗+ ρg其中，ρ是水的密度，u是流速矢量，t是时间，p是压力，τ是应力张量，g是重力加速度。

动量方程的第一项表示动量的变化率，第二项表示对流项，第三项是压力梯度力，第四项是摩擦力，最后一项是重力的作用。

在水文学中，动量平衡是研究水体在河流、湖泊、海洋等环境中的运动规律和水文现象的重要基础。

通过动量平衡的分析，可以预测水流的速度、方向，水体的运动轨迹，水流的动力学特性等。

动量平衡的研究对于水资源的合理利用和水环境的保护具有重要意义。

动量平衡的研究也是水文学中的一个重要研究方向，研究者通过实验、模拟和观测等手段，探讨水体运动中的动量平衡机制，深入研究水文现象的成因和演变规律，为水文学的发展和水资源管理的实践提供科学依据。

总的来说，水文动量平衡是水文学中的一个重要概念，它描述了水体运动中的动量变化情况，是研究水文现象和水资源管理的重要基础。

通过对动量平衡的研究，可以更好地理解水体的运动规律，预测水文现象的发生，促进水资源的可持续利用和水环境的保护。

水文动量平衡的研究是水文学领域的一个重要方向，对于水文学的发展和水资源管理的实践具有重要的意义。

水力学动量方程说起水力学动量方程，这听起来挺高深莫测的，但咱们不妨把它想象成一场水世界的冒险游戏，咱们都是勇敢的水手，驾驶着小船在河流里闯荡。

想象一下，你站在船头，手里握着舵，眼前的水流忽急忽缓，仿佛是大自然给你出的谜题。

这时候，你就得用上水力学动量方程这个“秘籍”了。

别害怕，这秘籍其实不难懂，咱们一步步来拆解它。

首先，咱们得明白，水是有“脾气”的，它喜欢流动，而且流动的时候还带着一股子劲儿，这就是动量。

动量就像是水流的“肌肉”，越强壮的水流，动量就越大。

而水力学动量方程，就是用来描述这股子“肌肉”怎么在水里发挥作用的。

咱们的小船在水上漂，就像是水里的一个小石头，会搅动周围的水流。

小船往前冲的时候，它会带着前面的水流一起往前冲，这时候，水流就有了向前的动量。

但是，小船的尾部呢，就像是被拉开了一个口子，水流会从这里流走，这时候，水流就有了向后的动量。

这时候，水力学动量方程就登场了。

它说：“嘿，小船兄弟，你得注意啦！你往前冲的时候，别光顾着自己爽，还得看看周围的水流兄弟们。

你带着他们一起往前冲，那他们就帮你顶着前面的阻力；但是，你尾部的水流兄弟们流走了，他们就会产生一个向后的力量，试图把你拉回去。

”这个方程还告诉我们，水流的速度越快，它的动量就越大，产生的力量也就越强。

所以，咱们在划船的时候，就得掌握好速度，别一股脑儿地往前冲，得让水流的力量帮咱们一把。

当然啦，水力学动量方程不只是用在划船这么简单。

在造桥、修堤、挖河这些大工程里，它也发挥着巨大的作用。

工程师们就像是我们这些勇敢的水手，他们得用方程来算出水流的力量有多大，然后再决定怎么设计工程才能扛得住这股力量。

所以说啊，水力学动量方程就像是水世界的“交通规则”，它告诉我们水流是怎么运动的，也告诉我们怎么和水流打交道。

下次你再看到水流湍急的河流时，不妨想想这个方程，说不定你就能更好地理解大自然的奥秘了呢！。

通常所说的水力学三大方程为
通常所说的水力学三大方程为：连续方程、能量方程和动量方程。

扩展资料：
水力学是研究以水为代表的液体的宏观机械运动规律，及其在工程技术中的应用。

水力学包括水静力学和水动力学。

水力学作为学科而诞生始于水静力学。

公元前400余年，中国墨翟在《墨经》中，已有了浮力与排液体积之间关系的设想。

公元前250年，阿基米德在《论浮体》中，阐明了浮体和潜体的有效重力计算方法。

1586年德国数学家斯蒂文提出水静力学方程。

十七世纪中叶，法国帕斯卡提出液压等值传递的帕斯卡原理。

至此水静力学已初具雏形。