1-4动量方程与气体状态方程

理想气体定律理想气体状态方程的推导理想气体定律（理想气体状态方程）是描述理想气体性质的基本方程。

它通过研究气体的压强、体积和温度之间的关系，为研究气体的物理性质提供了重要的理论基础。

本文将对理想气体定律的推导进行详细介绍。

一、理想气体定律的基本假设理想气体定律是建立在以下基本假设的基础上：1. 气体由大量粒子组成，粒子之间没有相互作用力。

2. 气体粒子之间的碰撞是完全弹性的，即在碰撞过程中能量和动量的守恒得到保持。

3. 气体粒子的体积可以忽略不计，只考虑气体系统的总体积。

基于以上假设，我们可以推导出理想气体定律。

二、理想气体状态方程的推导设想我们有n个理想气体分子，体积为V，气体的压强为P，温度为T。

根据理想气体的性质，我们可以得到以下关系式：1. 压强与分子碰撞次数的关系根据动理论，气体分子的压强与其碰撞次数有关。

假设每个分子在单位时间内与容器壁面碰撞的次数为Z，容器的壁面数目为S，则分子与外界壁面碰撞总次数为nSZ。

而单位时间内，分子碰撞容器壁面的平均力为F，则气体的压强可以表示为P = F/S。

根据动力学理论，分子碰撞力的大小与温度有关，可以表示为F = mɑv^2，其中m表示分子的质量，ɑ表示碰撞时分子速度的改变量，v表示分子的速度。

将F代入压强的表达式中可得：P = (mɑv^2)/S。

2. 碰撞次数与分子速度的关系假设单位时间内，每个分子的碰撞次数为Z，由于气体分子速度的分布是随机的，因此我们假设所有分子的速度相等于v，则单位时间内与壁面碰撞的总数为nSZ。

而分子速度的大小与温度有关，可以表示为v = √(3kT/m)，其中k为玻尔兹曼常数。

将v代入碰撞次数的表达式中可得：nSZ = Z/(mɑ(3kT/m))。

将以上两个关系式合并，消去多余的变量，即可得到理想气体定律的推导式：P = (Z/3V)mv^2由于温度T与分子平均动能Ek的关系式为Ek = (1/2)mv^2，对于单原子分子气体而言，离子运动模式为自由度为3，则平均能量为(1/2)kT。

具有理想气体状态方程的流动控制方程全文共四篇示例，供读者参考第一篇示例：理想气体状态方程是描述理想气体在不同温度、压力、体积条件下的物理规律的方程。

流动控制方程则是描述气体在流动过程中随时间和空间的变化规律的方程。

将这两个方程结合起来，可以得到具有理想气体状态方程的流动控制方程，这对研究流体力学、气体动力学以及空气动力学等领域具有重要意义。

让我们回顾一下理想气体状态方程的公式：\[PV = nRT\]P表示气体的压力，V表示气体的体积，n表示气体的摩尔数，R 表示气体常数，T表示气体的绝对温度。

这个方程描述了理想气体在不同条件下的物理状态，是流体力学研究中最基本的公式之一。

下面，我们将理想气体状态方程和流动控制方程结合起来，推导出具有理想气体状态方程的流动控制方程。

我们首先引入质量守恒方程和动量守恒方程，然后利用理想气体状态方程进行简化处理，最终得到描述理想气体流动的控制方程。

质量守恒方程描述了流体的质量在单位时间内通过单位面积的变化率，可以用以下方程表示：\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho\mathbf{v}) = 0\]ρ表示流体的密度，t表示时间，v表示流体的速度矢量。

这个方程描述了流体的质量在时间和空间上的变化规律。

具有理想气体状态方程的流动控制方程是描述理想气体在流动过程中运动状态的方程。

这些方程在研究气体动力学、空气动力学、航空航天工程等领域起着重要作用，为科学家和工程师提供了研究和设计的基础。

希望通过深入研究和应用这些方程，我们可以更好地理解和控制气体的流动行为，为人类的科学技术发展做出贡献。

第二篇示例：理想气体状态方程是热力学中的一个基础方程，描述了理想气体的状态和性质。

根据这个方程，我们可以推导出流体力学中的流动控制方程，用于描述流体在流动过程中的变化和性质。

流动控制方程在工程领域有着广泛的应用，例如在飞机设计、液体输送、空气动力学等方面都扮演着至关重要的角色。

理想气体与气体状态方程的推导理想气体指的是在常温常压下服从理想气体状态方程的气体。

理想气体状态方程描述了理想气体的物理性质与状态，它是气体物理学中的基本方程之一。

1. 理想气体的假设理想气体的状态方程的推导基于以下假设：（1）气体分子之间相互作用力可以忽略不计；（2）气体分子的体积可以忽略不计。

2. 推导过程假设一个理想气体的体积为 V，温度为 T，压强为 P，气体的物质量为 m，分子数为 N。

根据状态方程推导的基本原理，可以得到以下推导过程：步骤一：分子动理论根据分子动理论，气体分子的平均动能与温度成正比，即：1/2 m v^2 = k_B T其中，m 为气体分子的质量，v 为分子的速率，k_B 为玻尔兹曼常数。

步骤二：气体分子的动量公式根据气体分子动量的定义，可以得到：p = m v其中，p 为气体分子的动量。

步骤三：气体分子的动能公式将步骤一和步骤二的结果结合，可以得到气体分子的动能公式：1/2 p^2/m = k_B T步骤四：单位体积的分子数假设单位体积内的分子数为 n，总分子数 N 可以表示为：N = n V步骤五：单位体积的分子动能将步骤三的结果乘以单位体积内的分子数 n，可以得到单位体积的分子动能：1/2 n p^2/m = n k_B T步骤六：单位体积的动能密度单位体积的动能密度可以表示为单位体积的分子动能除以单位体积：E = 1/2 n p^2/m V = n k_B T步骤七：单位体积的动能密度与内能的关系内能 U 是单位体积的动能密度乘以体积 V：U = n k_B T V步骤八：理想气体状态方程的推导根据理想气体状态方程的定义，内能与温度成正比，压强与温度成正比，体积与温度成反比，可以得到：U ∝ TP ∝ TV ∝ 1/T将步骤七的结果代入上述关系式，可以得到理想气体状态方程：P V = n k_B T3. 总结理想气体与气体状态方程的推导基于理想气体的假设，通过分子动理论和动量公式的推导，最终得到了理想气体状态方程 P V = n k_B T。

第四章 气体动理论一、基本要求1．理解平衡态的概念。

2．了解气体分子热运动图像和理想气体分子的微观模型，能从宏观和统计意义上理解压强、温度、内能等概念。

3．初步掌握气体动理论的研究方法，了解系统的宏观性质是微观运动的统计表现。

4．理解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义，理解气体分子运动的最概然速率、平均速率、方均根速率的意义，了解玻尔兹曼能量分布律。

5．理解能量按自由度均分定理及内能的概念，会用能量均分定理计算理想气体的内能。

6．了解气体分子平均碰撞频率及平均自由程的意义及其简单的计算。

二、基本内容1. 平衡态在不受外界影响的条件下，一个系统的宏观性质不随时间改变的状态。

2. 理想气体状态方程在平衡态下，理想气体各参量之间满足关系式pV vRT =或 n k T p =式中v 为气体摩尔数，R 为摩尔气体常量 118.31R J mol K --=⋅⋅，k 为玻尔兹曼常量 2311.3810k J K --=⨯⋅3. 理想气体压强的微观公式21233t p nm n ε==v4. 温度及其微观统计意义温度是决定一个系统能否与其它系统处于热平衡的宏观性质，在微观统计上32t kT ε=5. 能量均分定理在平衡态下，分子热运动的每个自由度的平均动能都相等，且等于2kT 。

以i 表示分子热运动的总自由度，则一个分子的总平均动能为2t i kT ε=6. 速率分布函数()dNf Nd =v v麦克斯韦速率分布函数232/22()4()2m kT m f e kTππ-=v v v7. 三种速率最概然速率p =≈v 平均速率==≈v 方均根速率==≈8. 玻尔兹曼分布律平衡态下某状态区间（粒子能量为ε）的粒子数正比于kT e /ε-。

重力场中粒子数密度按高度的分布（温度均匀）：kT m gh e n n /0-=9. 范德瓦尔斯方程采用相互作用的刚性球分子模型，对于1mol 气体RT b V V ap m m=-+))((2 10. 气体分子的平均自由程λ==11. 输运过程 内摩擦dS dz du df z 0)(η-=， 1133mn ηλρλ==v v 热传导dSdt dz dT dQ z 0)(κ-= 13v c κρλ=v 扩散dSdt dz d D dM z 0)(ρ-= 13D λ=v三、习题选解4-1 一根铜棒的两端分别与冰水混合物和沸水接触，经过足够长的时间后，系统也可以达到一个宏观性质不随时间变化的状态。

《空气动力学基础》重点梳理（2013年6月 陈辰编）第一章 引述一、空气动力学基本变量1．压强——作用在单位面积上的正压力dAdFp dA 0lim→=（0dA dA →）其中：L dA l <<<0，l 为分子间距，L 为特征长度（如弦长、展长、直径等）压强具有点的属性：无粘流体，流体内部任意一点的压强均是各向同性的，即压强值与受压面的方位无关。

2．密度——单位体积内的质量dvdmdv 0lim→=ρ（dv 不能趋向于0）密度具有点的属性。

3．温度kT KE 23=温度具有点的属性。

4．流动速度 5．切应力6．完全气体状态方程 （1）所用假设①它的分子是一种完全弹性的微小球粒； ②分子除彼此碰撞瞬间外没有作用力；③分子的体积可以忽略不计（微粒的实有总体积和气体所占空间相比可忽略不计）。

（2）完全气体状态方程R 为通用气体常数，其数值为)/(831522K s m ⋅；m 为所研究气体的相对分子质量；T 为绝对温度(K)。

如将m R /改为R R 为气体常数。

7．单位二、空气动力及力矩 1．空气动力的来源（1）物体表面的压力分布；（2）物体表面的剪应力（摩擦应力）分布。

压力垂直作用在物体表面，剪应力相切作用在物体表面且与运动方向相反。

2．R 的分解（1）投影到风轴系L ：升力（垂直于∞V ）；D ：阻力（平行于∞V ） （2）投影到体轴系N ：轴向力（垂直于弦长c ）；A ：法向力（平行于弦长c ） （3）风轴系与体轴系之间关系⎩⎨⎧+=-=ααααcos sin sin cos A N D A N L （迎角α——弦长c 与来流速度∞V 之间的夹角） 3．空气动力与力矩表达式 （1）单位展长的法向力与轴向力：()()⎰⎰-++-='TELE l l l TE LEu u u ds p ds p N θτθθτθsin cos sin cos()()⎰⎰+++-='TELE l l l TELEu u u ds p ds p A θτθθτθcos sin cos sin （2）单位展长的前缘力矩：()()[]⎰--+='TELEu u u u u LEds y p x p M θτθθτθsin cos sin cos ()()[]⎰+-+-+TELEl l l l l ds y p x p θτθθτθcos sin sin cos4．力与力矩的无量纲系数 （1）动压的定义221∞∞∞=V q ρ，∞∞V ,ρ为物体远前方的密度和速度。

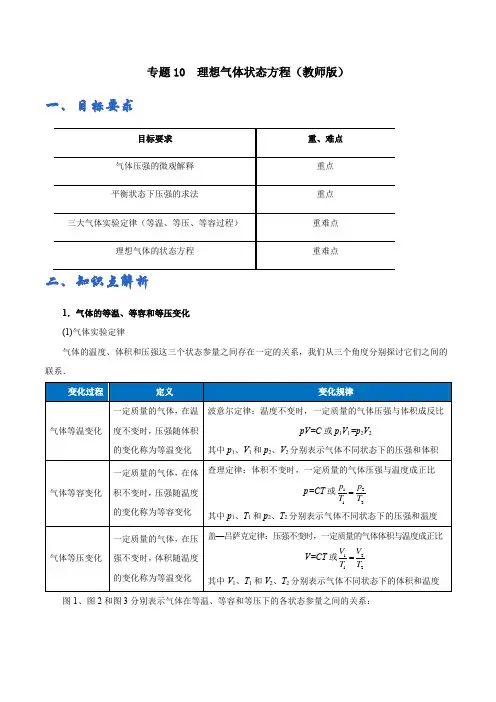
专题10 理想气体状态方程（教师版）一、目标要求二、知识点解析1．气体的等温、等容和等压变化(1)气体实验定律气体的温度、体积和压强这三个状态参量之间存在一定的关系，我们从三个角度分别探讨它们之间的联系．图1、图2和图3分别表示气体在等温、等容和等压下的各状态参量之间的关系：注意：只有取开尔文温标时，等容变化和等压变化的正比关系才成立． 2.气体压强的微观解释①压强：从微观角度来看，气体对容器的压强是由于大量气体分子对容器的撞击引起的，气体的温度越高，气体分子的密集程度（单位体积内的分子数）越大，气体对容器的压强越大；注意：与气体对容器的压强不同，大气压强是由地球的吸引产生的； ②微观理解a ．一定质量的气体温度不变时，平均动能不变，压缩体积使得气体分子密集程度增大，则压强增大；b ．一定质量的气体体积不变时，升高温度使得气体分子的平均动能增加，在相同密集程度下撞击容器时的作用力更大，则压强增大；c ．一定质量的气体压强不变时，升高温度，分子平均动能增大，为使气体的压强不变，气体只能减小分子的密集程度，即体积增大．3．理想气体状态方程 (1)理想气体①定义：气体实验定律只有在温度变化不大（相比室温）、压强变化不大（相比大气压）的情况下才成立，为研究方便，假设一种气体，在任何温度和任何压强下都符合实验定律，这种气体被称为理想气体；实际气体在温度变化不大（相比室温）、压强变化不大（相比大气压）时可以视作理想气体；②性质：理想气体中的分子忽略自身体积，可视作质点；不考虑分子间的作用力，即分子运动时做匀速直线运动，且不计分子势能；分子与分子、分子与容器的碰撞都是完全弹性的；(2)理想气体状态方程设一定质量的理想气体在1状态时的温度、压强和体积分别为T 1、p 1、V 1，在2状态时的温度、压强和体积分别为T 2、p 2、V 2，则有：112212p V p V T T理论表明，考虑理想气体的数量关系，理想气体状态方程为：pV=nRT 其中n 为理想气体的物质的量．三、考查方向图1图2图3题型1：气体压强的微观解释典例一：（2017•朝阳区二模）科学精神的核心是对未知的好奇与探究，小君同学想寻找教科书中“温度是分子平均动能的标志”这一结论的依据，他以氦气为研究对象进行了一番研究，经查阅资料得知：第一，理想气体的模型为气体分子可视为质点，分子间除了相互碰撞外，分子间无相互作用力；第二，一定质量的理想气体，其压强p 与热力学温度T 的关系式为p nkT =，式中n 为单位体积内气体的分子数，k 为常数。

气体状态方程 热力学定律理想气体的状态方程：（1）理想气体：能够严格遵守气体实验定律的气体，称为理想气体。

理想气体是一种理想化模型。

实际中的气体在压强不太大，温度不太低的情况下，均可视为理想气体。

（2）理想气体的状态方程：C TPVT V P T V P ==或222111 一定质量的理想气体的状态发生变化时，它的压强和体积的乘积与热力学温度的比值保持不变。

即此值为—恒量。

热力学第一定律:（1）表达式为:ΔE=W+Q1.改变内能的两种方式：做功和热传递都可以改变物体的内能。

2.做功和热传递的本质区别：做功和热传递在改变物体内能上是等效的。

但二者本质上有差别。

做功是把其他形式的能转化为内能。

而热传递是把内能从一个物体转移到另一个物体上。

3.功、热量、内能改变量的关系——热力学第一定律。

①内容：在系统状态变化过程中，它的内能的改变量等于这个过程中所做功和所传递热量的总和。

②实质：是能量转化和守恒定律在热学中的体现。

③表达式：∆E W Q=+ ④为了区别不同情况，对∆E 、W 、Q 做如下符号规定： ∆E > 0 表示内能增加∆E < 0 表示内能减少Q > 0 表示系统吸热 Q < 0 表示系统放热 W > 0 表示外界对系统做功W < 0 表示系统对外界做功能的转化和守恒定律：1.物质有许多不同的运动形式，每一种运动形式都有一种对应的能。

2.各种形式的能都可以互相转化，转化过程中遵守能的转化和守恒定律。

3.能的转化和守恒定律：能量既不能凭空产生，也不会凭空消失，它只能从一种形式转化为别的形式，或者从一个物体转移到别的物体。

应注意的问题：1.温度与热量：①温度：温度是表示物体冷热程度的物理量。

从分子动理论观点看，温度是物体分子平均动能的标志。

温度是大量分子热运动的集体表现，含有统计意义，对个别分子来说，温度是没有意义的。

温度高低标志着物体内部的分子热运动的剧烈程度。

理想气体状态方程理想气体的压强体积和温度关系理想气体状态方程是描述理想气体性质的基本方程，它揭示了理想气体压强、体积和温度之间的关系。

该方程由三个参数组成，分别是压强P、体积V和温度T。

理想气体状态方程可以表示为P×V =n×R×T，其中n是气体的物质量，R是气体常数。

理想气体状态方程起源于理想气体模型，这个模型假设气体分子之间不存在相互作用力，气体分子体积可以忽略不计。

在这个模型下，理想气体的状态完全由其压强、体积和温度决定，而与气体的化学性质无关。

首先我们来推导理想气体状态方程。

根据达尔顿气体定律，气体的总压强等于各种气体分子的部分压强之和。

设有一理想气体在一个封闭的容器中，假设此气体由n个分子组成，每个分子的质量为m。

根据牛顿第二定律，气体分子会受到来自容器壁以及其他分子的撞击力，这些力使得气体分子发生变速度，从而改变其动量。

根据运动学知识可知，分子的动量变化与力的大小和分子作用时间的乘积成正比。

因此，气体的压强可以定义为单位面积上分子碰撞引起的动量变化率。

假设容器的底面积为A，那么单位时间内容器底面积上总的分子撞击次数为naV，其中na为单位体积中分子的数目，V为容积。

由于分子在单位时间内碰撞的次数与分子的速度和体积成正比，我们可以得到p = \frac{naV}{A} = n\frac{m}{V} \frac{v}{4}\，其中v为分子的平均速度。

等式右边第一个项表示单位体积中分子的数目，即分子的物质量n除以体积V。

第二个项表示分子速度v的平方对分子平均速度v的平方的比值。

根据动理学理论可知，分子的平均动能与温度成正比。

因此，我们可以用kT代替分子的平均动能，其中k为玻尔兹曼常数。

将平均速度v表示为平均动能kT与分子质量m之间的关系，我们可以得到v =\sqrt{\frac{{2kT}}{{m}}}\。

将此式代入压强的表达式中，我们可以得到p = \frac{1}{4}na\sqrt{\frac{{2kT}}{{m}}}\。

气体的理想气体状态方程从气球到天气预报的物理学原理气体是物质存在的一种形态，它是由大量微观粒子组成的，具有可压缩性和可扩散性的特点。

在研究气体的物理性质和行为时，理解气体状态方程是非常重要的。

本文将从气球的实例入手，探讨气体的理想气体状态方程，并解释其在天气预报中的物理学原理。

一、气球中的气体行为我们经常看到气球会渐渐膨胀起来，这是由于气球内外压力不平衡所导致的。

根据理想气体状态方程，气体的压强与体积、温度有关。

在气球中，气体的温度保持不变，而压强随着气体的体积变化而变化。

公式表示如下：P × V = n × R × T其中，P表示气体的压强，V表示气体的体积，n表示气体的物质量（单位为摩尔），R为气体常数，T表示气体的温度（单位为开尔文）。

当我们把气球充满气体时，气体分子会与气球内壁碰撞，产生弹性碰撞力。

越多的气体分子在单位面积上与气球壁碰撞，产生的压强就越大。

而当气体分子增加时，体积相对减小，气体分子与壁碰撞的频率增加，压强也随之增大，导致气球膨胀。

二、理想气体状态方程的推导在理想气体状态方程中，我们研究的是气体在理想条件下的行为。

它基于下面两个假设：1. 气体分子与分子之间没有相互作用力；2. 气体分子的体积可以忽略不计，只考虑其点状质量。

根据这两个假设，我们可以推导出理想气体状态方程。

首先，考虑到气体的分子质量为m，速度为v，根据牛顿第二定律，我们有：F = m × a其中，F表示受力，m表示质量，a表示加速度。

既然气体分子没有相互作用力，那么受力只能来自于气体分子与容器壁之间的碰撞，即：F = Δp / Δt其中，Δp表示气体分子的动量变化，Δt表示时间变化。

由于气体分子的质量可以忽略不计，我们可以将动量变化表示为：Δp = mv - mu其中，v表示气体分子的末速度，u表示气体分子的初速度。

将以上两个等式相等并整理得出：mv - mu = Δp = F × Δt进一步整理得到：m(v - u) = F × Δt根据动能定理，气体分子的动能可以表示为：Ek = (1/2)mv^2由于气体分子在不相互作用的情况下，动能守恒，即：(1/2)mu^2 = (1/2)mv^2代入前面的等式中，我们得到：(1/2)m(v - u)^2 = F × Δt将力F表示为压强P，并将时间变化Δt表示为体积变化ΔV/V，其中ΔV表示体积的变化量，V表示初始体积，我们得到：(1/2)m(v - u)^2 = P × ΔV根据气体的物质量公式n = m / M，其中M表示气体的摩尔质量，n 表示气体的物质量（单位为摩尔），我们可以得到：(1/2)nM(v - u)^2 = P × ΔV再通过平均动能公式K = (3/2)kT，其中k为玻尔兹曼常数，T为气体的温度（单位为开尔文），我们得到：(1/2)nM(v - u)^2 = (2/3)P × (4/3)π (R + ΔR)^3 - (2/3)P × (4/3)π R^3其中R表示气球的半径，ΔR表示体积的变化量。

理想气体状态方程与气体动力学模型气体是一种物态，它的分子之间存在着松散的排列和高度运动的特性。

研究气体的性质和行为对于理解自然界和工程实践中的很多现象至关重要。

在过去的几个世纪里，科学家们通过实验和理论研究，总结出了一系列关于气体的基本规律和模型，其中包括理想气体状态方程和气体动力学模型。

一、理想气体状态方程理想气体状态方程是描述气体物理性质的重要方程之一，它描述了气体的状态、体积、压强和温度之间的关系。

根据理想气体状态方程，气体的状态可以用下式表示：PV = nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，R是气体常数，T表示气体的温度。

这个方程是理想气体的基本方程，适用于低密度和高温下的气体。

理想气体状态方程的推导基于几个基本假设。

首先，理想气体被认为是由大量自由运动的点状分子组成，它们之间的相互作用可以忽略不计；其次，这些分子之间的碰撞是完全弹性的，不会有能量损失；最后，气体分子的体积极小，可以看作是点状的。

理想气体状态方程的应用非常广泛。

在热力学和工程领域，该方程被用于计算气体的压强、体积和温度之间的关系。

在化学反应和工业生产中，理想气体状态方程可以用于计算气体的物质的量、温度和压强的变化。

二、气体动力学模型气体动力学是研究气体运动和行为的科学分支。

在气体动力学模型中，气体被看作是由大量分子组成的，这些分子之间存在相互作用和碰撞。

气体动力学模型可以用于描述气体在等温、等压、等容等条件下的运动和变化。

在气体动力学模型中，分子之间的碰撞和相互作用是非常重要的。

根据动力学理论，气体分子的平均动能与温度成正比，而与气体的性质和组成无关。

这种关系被称为气体的平均动能定理。

根据平均动能定理，可以推导出气体分子的速率分布和平均速率之间的关系。

气体动力学模型还可以用于研究气体的压强和体积之间的关系。

根据气体动力学理论，气体的压强与分子的速率和碰撞频率有关。

当气体的温度升高时，气体分子的速率增加，碰撞频率也增加，从而导致气体的压强增加。

气体动力学1.理想气体运动的基本方程组理想气体：无粘性、无导热性雷诺数：度量粘性效应的相对大小的量纲一的数R e=ρVLμ=惯性力粘性力●要确定理想气体的流场，一般需要知道六个参数：速度V的三个分量，压力p，密度ρ和温度T。

因此理想气体动力学要建立六个独立的基本方程，连同初边值条件，以构成定解问题。

●基本方程所依据的是三个方面的物理定律，即运动学方面的质量守恒定律，动力学方面的牛顿定律和热力学方面的第一、第二定律以及气体热状态方程。

●建立基本方程时首先面临着这么一个问题：怎样选取流体物质形态的模型作为研究对象。

有两种流体模型可供选择。

一种是随体观点的模型，它认定某个有确定质量的流体团，称为封闭系统，其特点是：(1) 系统的体积τ(t)和界面积σ(t)随流体运动而随时变化；(2) 在系统的界面上，只有能量交换，没有质量交换。

一种是当地观点的模型，它在流体空间认定一个固定的控制面所包围的区域，称为开口系统，其特点是：(1) 系统的体积τ和界面积σ是固定不变的；(2) 在系统的界面上，既有能量交换，也有质量交换。

对于上述两种流体模型，即封闭系统和开口系统，还有两种数学表达形式。

一种是选取有限质量（体积）的系统，写成积分形式的基本方程。

另一种是选取微元质量（体积）的系统，写成微分形式的基本方程。

微分形式的方程适用于连续流程，便于探讨流场各处的参数分布规律。

积分形式的方程便于从总体上研究问题，而且可以用来求解系统中有间断面存在的情况。

综上所述，理想气体运动的基本方程组的要点可归为：六个方程、三个方面、两种观点、两种形式。

1.1 连续性方程质量守恒方程（当地观点、微分形式）微元体的质量平衡式：微元体内质量的增加率=进入微元体的质量净流率微元体内质量的增加率：ððt (ρδxδyδz)=ðρðtδxδyδz进入微元体的质量流率的净变化率：通过微元体每一个表面的质量流率等于密度、速度分量和面积的乘积。