勾股定理2

勾股定理逆定理一． 知识归纳８.．勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论．９.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决． 常见图形：A B C 30°D CB A AD B CCB D A题型二：应用勾股定理建立方程例２.⑴ 在ABC ∆中，90ACB ∠=︒，5AB =cm ，3BC =cm ，CD AB ⊥于D ，CD ＝⑵ 已知直角三角形的两直角边长之比为3:4，斜边长为15，则这个三角形的面积为⑶ 已知直角三角形的周长为30cm ，斜边长为13cm ，则这个三角形的面积为分析：在解直角三角形时，要想到勾股定理，及两直角边的乘积等于斜边与斜边上高的乘积．有时可根据勾股定理列方程求解例３.如图ABC ∆中，90C ∠=︒，12∠=∠， 1.5CD =， 2.5BD =，求AC 的长21E DCBA分析：此题将勾股定理与全等三角形的知识结合起来题型三：实际问题中应用勾股定理例5.如图有两棵树，一棵高8cm ，另一棵高2cm ，两树相距8cm ，一只小鸟从一棵树的树梢飞到另一棵数的树梢，至少飞了 mAB CD E题型四：应用勾股定理逆定理，判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ，b ，c ，判定ABC ∆是否为Rt ∆① 1.5a =，2b =， 2.5c = ②54a =，1b =，23c =例7.三边长为a ，b ，c 满足10a b +=，18ab =，8c =的三角形是什么形状？题型五：勾股定理与勾股定理的逆定理综合应用 例8.已知ABC ∆中，13AB =cm ，10BC =cm ，BC 边上的中线12AD =cm ，求证：AB AC =证明：D CB A。

3.1勾股定理（2）【学习目标】1．经历探索勾股定理的过程，发展合情推理的水平，体会数形结合思想．2．经历用多种拼图方法验证勾股定理的过程，发展用数学的眼光观察现实世界和有条理地思考与表达的水平，感受勾股定理的文化价值．3．能说出勾股定理，并能用勾股定理解决简单问题．【学习重点】1．经历探索勾股定理的过程，发展合情推理的水平，体会数形结合思想．2．经历用多种拼图方法验证勾股定理的过程，发展用数学的眼光观察现实世界和有条理地思考与表达的水平，感受勾股定理的文化价值．【学习难点】通过拼图验证勾股定理的过程，使学生获得一些研究问题与合作交流的方法与经验。

【自主预习】P80【合作探究】实践探索一1．我国古代把直角三角形中较短的直角边称为勾，较长的称为股，斜边称为弦．图（1）称为“弦图”，最早是由三国时期的数学家赵爽在《周髀算经》中给出的．图（2）是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就. 你能用不同方法表示大正方形的面积吗？图（1）图（2）2．剪四个完全相同的直角三角形，然后将它们拼成如下图的图形．大正方形的面积能够表示为_______，又能够表示为____________.比照两种表示方法，看看能不能得到勾股定理的结论．用上面得到的完全相同的四个直角三角形，还能够拼成如下列图所示的图形，与上面的方法类似，也能说明勾股定理是准确的方法（请逐一说明）．归纳其共有的证明思路：利用图形的割补，借助前后的面积相等形成关于三边的数量关系．3．大家能够在课后继续研究更多的证明方法，自己阅读课本88页“勾股定理的证明”．实践探索二P81，如图，把火柴盒放倒，在这个过程中，也能验证勾股定理，你能利用这个图验证勾股定理吗？把你的想法与大家交流一下．,实践探索三1．观察下列图的△ABC 和△DEF ，它们是直角三角形吗？2．观察图，并分别以△ABC 和△DEF 的各边为边向外作正方形，其中2个小正方形的面积的和等于大正方形的面积吗？【课堂检测】1．如图，长2.5m 的梯子靠在墙上，梯子的底部离墙角1.5m ，求梯子的顶端与地面的距离h .2．完成课本P82的练习．3.课本 P82/3.44.补充习题 P47h 2.51.5A B CD E F。

勾股定理（2）第二课时一、引入回顾上节课所学习的勾股定理的验证方法。

二、动手操作，合作探究1．利用五巧板拼“青朱出入图”（教师利用课件介绍“青朱出入图”的历史）。

你能利用“青朱出入图”验证勾股定理吗？（给学生提供充分实践、探索和交流的时间，鼓励他们积极思考解决问题的方法，并与他人进行合作与交流。

）2．教师可以利用课件介绍一些国外的勾股定理验证方法，重点介绍意大利文艺复兴时代著名画家达·芬奇对勾股定理的验证方法。

步骤：（1）在一张长方形的纸板上画两个边长分别为a 、b 的正方形，并连结BC 、FE 。

（2）沿ABCDEF 剪下，得两个大小相同的纸板Ⅰ、Ⅱ。

（3）将纸板Ⅱ翻转后与Ⅰ拼成其它的图形。

（4）比较两个多边形ABCDEF 和F E D C B A ''''''的面积，你能验证勾股定理吗？（给学生充足的时间，进行独立思考，鼓励学生交流合作，教师巡视帮助，引导学习困难的学生。

最后，验证方法让学生进行讲解、板演、叙述，教师做简单的总结。

）你还想了解其他的验证方法吗？三、课堂总结1．从两节课的课题学习中你有哪些收获？2．你学到了哪些数学方法和数学思想？（给出学生两个问题，让学生充分讨论、交流，得出结论，最后教师小结本课题。

）四、巩固教科书第179页，习题第2题。

勾股定理有着悠久的历史，古巴比伦人和中国人看出了这个关系，古希腊毕达哥拉斯学派首先验证了这个关系。

同学们，你们对勾股定理感兴趣吗？你想尝试自己验证勾股定理吗？请发挥你的才智，去探索勾股定理、去研究勾股定理吧！。

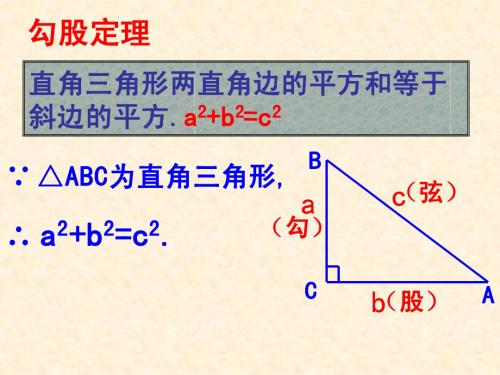
全章要点勾股定理：1、勾股定理定义：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾：直角三角形较短的直角边股：直角三角形较长的直角边弦：斜边2、勾股数：满足a2＋b2＝c2的三个正整数叫做勾股数（注意：若a，b，c、为勾股数，那么ka，kb，kc同样也是勾股数组。

）*附：常见勾股数：3,4,5； 6,8,10； 9,12,15； 5,12,13勾股定理的逆定理：：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。

（经典直角三角形：勾三、股四、弦五）其他方法：（1）有一个角为90°的三角形是直角三角形。

（2）有两个角互余的三角形是直角三角形。

用它判断三角形是否为直角三角形的一般步骤是：（1）确定最大边（不妨设为c）；（2）若c2＝a2＋b2，则△ABC是以∠C为直角的三角形；若a2＋b2＜c2，则此三角形为钝角三角形（其中c为最大边）；若a2＋b2＞c2，则此三角形为锐角三角形（其中c为最大边）注意：（1）直角三角形斜边上的中线等于斜边的一半（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

（3）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

3、勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n的线段例题讲解例1．△ABC中，AB=AC=25cm，高AD=20cm,则BC= ，S△ABC= 。

解：30cm，300cm2例2．△ABC中，若∠A=2∠B=3∠C，AC=32cm，则∠A= 度，∠B= 度,∠C= 度，BC= ，S△ABC= 。

解：90，60，30，4，23例3．△ABC 中，∠C=90°，AB=4，BC=32，CD ⊥AB 于D ，则AC= ，CD= ，BD= ，AD= ,S △ABC = 。

勾股定理复习(2)学习目标1.掌握直角三角形的边、角之间所存在的关系，熟练应用直角三角形的勾股定理和逆定理来解决实际问题．2.经历反思本单元知识结构的过程，理解和领会勾股定理和逆定理．3.熟悉勾股定理的历史，进一步了解我国古代数学的伟大成就，激发爱国主义思想，培养良好的学习态度．重点：掌握勾股定理以及逆定理的应用．难点：应用勾股定理以及逆定理．考点一、已知两边求第三边1．在直角三角形中,若两直角边的长分别为1cm ，2cm ，则斜边长为______．2．已知直角三角形的两边长为3、2，则另一条边长是________________．3．在数轴上作出表示10的点．4．已知，如图在ΔABC 中，AB=BC=CA=2cm ，AD 是边BC 上的高． 求 ①AD 的长；②ΔABC 的面积．考点二、利用列方程求线段的长1．如图，铁路上A ，B 两点相距25km ，C ，D 为两村庄，DA ⊥AB 于A ，CB ⊥AB 于B ，已知DA=15km ，CB=10km ，现在要在铁路AB 上建一个土特产品收购站E ，使得C ，D 两村到E 站的距离相等，则E 站应建在离A 站多少km 处？2.如图，某学校（A 点）与公路（直线L ）的距离为300米，又与公路车站（D 点）的距离为500米，现要在公路上建一个小商店（C 点），使之与该校AAD E BC及车站D 的距离相等，求商店与车站之间的距离．考点三、判别一个三角形是否是直角三角形1.分别以下列四组数为一个三角形的边长：（1）3、4、5（2）5、12、13（3）8、15、17（4）4、5、6，其中能够成直角三角形的有2.若三角形的三别是a 2+b 2,2ab,a 2-b 2(a>b>0),则这个三角形是 .3.如图1，在△ABC 中，AD 是高，且，求证：△ABC 为直角三角形。

考点四、灵活变通1.在Rt △ABC 中， a ，b ，c 分别是三条边，∠B=90°，已知a=6，b=10，则边长c=2.直角三角形中，以直角边为边长的两个正方形的面积为72cm ，82cm ，则以斜边为边长的正方形的面积为_________2cm ．3.如图一个圆柱，底圆周长6cm ，高4cm ，一只蚂蚁沿外壁爬行，要从A 点爬到B 点，则最少要爬行 cm4.如图：带阴影部分的半圆的面积是 （π取3）5.一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A 点沿纸箱爬到 B 点，那么它所爬行的最短路线的长是CD BD AD 2⋅=6.若一个三角形的周长123c m,一边长为33c m,其他两边之差为3c m,则这个三角形是______________________．7.如图：在一个高6米，长10米的楼梯表面铺地毯，则该地毯的长度至少是 米。

A B C D ①②③④⑤E A B C D E ①②③④⑤④③②①⑤C B A A B C E a b c a b c第二课时时间：20090925课题：勾股定理（二）目标：经历用多种拼图方法验证勾股定理的过程，发展用数学的眼光观察现实世界和有 条理地思考与表达的能力，感受勾股定理的文化价值。

重点：勾股定理难点：对验证勾股定理的探索过程的理解教程：（全课内容用演示文稿展示）一、复习1．请说出勾股定理：直角三角形两直角边的平方和等于斜边的平方。

2．△ABC 中，∠A=90°，根据以下条件，求第三边和长（1）a=15,b=12；（2）b=10,c=24；（3）c=7,a=25.3．作业讲评、查家作二、实验、探究1．将P 43章头图中的①②③④⑤剪开拼成大正方形ABDE 。

拼图说明：直角三角形两条直角边的平方和等于斜边的平方。

这也是验证勾股定理的一种方法。

分析;通过多媒体演示如何拼图，从而得出结论。

2．早在公元3世纪，我国数学家赵爽说用4个直角三角形拼成 如图所示的图形，证明了勾股定理，这个图形称为“弦图”。

拼图说明，△ABC 中，∠C=90°，BC 2+AC 2=AB 2为什么？你看出来了吗？ （4×1／2ab+(b-a)2=c 2，即a 2+b 2=c 2）3．如图，把火柴盒放倒，在这个过程中也能验证勾股定理S 梯形ACDE =S △ABC +S △BDE +S △ABE 即1／2（a+b ）（a+b ）=1／2 ab+1／2 ab+1／2c 2所以a 2+b 2=c 2CB A A BCD 勾股定理的证明方法：有记载的就有几百种三、思考锐角三角形、钝角三角形三边之间也有这样的等量关系吗？注意：不是直角三角形没有这个结论可演示《教学光盘》动画资料库 第二章动画—4四、再探索（1）用4张直角三角形纸片拼成如图形状，图中的3个正方形的面积之间有何关系？请用a 、b 、c 将所得的关系表示出来。