贵州2014届高三上学期寒假作业 数学(5) Word版 含答案

【原创】高三数学寒假作业（二）一、选择题，每小题只有一项是正确的。

1.设集合{}{}212,log 2A x x B x x =-≤=<，则A B ⋃=A. []1,3-B. [)1,4-C. (]0,3D. (),4-∞ 2.已知函数sin ,0,()(1),0,x x f x f x x π≤⎧=⎨->⎩那么)32(f 的值为 A. 21- B. 23- C. 21 D. 23 3.已知函数f (x)＝267,0,100,,x x x x x ++<≥⎧⎪⎨⎪⎩ 则 f (0)＋f (-1)＝ （ ） (A) 9 (B)7110 (C) 3 (D) 1110 4.已知函数()22x f x =-，则函数|()|y f x =的图像可能是………………………………..（ ）5.若互不相等的实数c b a ,,成等差数列，b a c ,,成等比数列，且103=++c b a ，则=a （ ）A. 4B. 2C. -2D. -46.下列各式中值为的是（ ）A ． sin45°cos15°+cos45°sin15°B ． sin45°cos15°﹣cos45°sin15°C ． cos75°cos30°+sin75°sin30°D ．7.设实数x ，y 满足条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,00820104y x y x y x ,若目标函数z ＝ax ＋by(a ＞0，b ＞0)的最大值为12，则23a b +的最小值为()8.已知函数()f x 满足1()()f x f x =, 当[]1,3x ∈时,()ln f x x =,若在区间1,33⎡⎤⎢⎥⎣⎦内,曲线()()g x f x ax =-与x 轴有三个不同的交点,则实数a 的取值范围是 ( ) A.10,e ⎛⎫ ⎪⎝⎭ B.10,2e ⎛⎫ ⎪⎝⎭ C.ln 31,3e ⎡⎫⎪⎢⎣⎭ D.ln 31,32e ⎡⎫⎪⎢⎣⎭9.圆心在直线y ＝x 上，经过原点，且在x 轴上截得弦长为2的圆的方程为() A ．(x －1)2＋(y －1)2＝2B ．(x －1)2＋(y ＋1)2＝2C ．(x －1)2＋(y －1)2＝2或(x ＋1)2＋(y ＋1)2＝2D ．(x －1)2＋(y ＋1)2＝或(x ＋1)2＋(y －1)2＝2二、填空题10.已知集合{}|1A x x =≤，{}|B x x a =≥，且A B R ⋃=，则实数a 的取值范围是__________ .11.理：已知集合{}0,2>==x x y y M ，{})2lg(2x x y x N -==，则=N M .12.已知等差数列{}n a 的前n 项和为n S ，且1533a a a +=，1014a =，则12S =13.抛物线241x y -=上的动点M 到两定点（0，-1）、（1，-3）的距离之和的最小值为三、计算题14.（本小题满分13分） 已知函数)12(log )(21--=x ax x f (a 为常数).(1)若常数2a <且0a ≠,求()f x 的定义域;(2)若()f x 在区间(2,4)上是减函数,求a 的取值范围.15.（本小题满分12分）已知直三棱柱111C B A ABC -中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝1AA ，D 、E 、F 分别为A B 1、C C 1、BC 的中点．（1）求证：DE ∥平面ABC ；（2）求证：F B 1⊥平面AEF ；（3）求二面角F AE B --1的余弦值．16.（本小题满分12分）已知椭圆()2222:10x y C a b a b+=>>的离心率为2，短轴端点到焦点的距离为2。

【KS5U 首发】贵州2013—2014学年高一寒假作业（5）数学 Word 版含答案.doc第I 卷（选择题）请点击修改第I 卷的文字说明 评卷人 得分 一、选择题(题型注释）1。

已知R n m ∈,，则“0≠m ”是“0≠mn "的( ）A ．充分但不必要条件B ．必要但不充分条件C ．充要条件D ．既不充分也不必要条件2。

在ABC ∆中，若bB a A cos sin =，则B 的值为（ ) A ． 30 B ． 45C ． 60D ．903。

集合},0|),{(},2|),{(R x y y x B y y x A x∈>===之间的关系是 （ ） A ．AB B ．A BC ．A=BD ．A ∩B=φ4.函数x y -=2的图象经过怎样的变换可以得到121+=+-x y 的图象（ ）A 、向左平移1个单位,再向下平移1个单位B 、向左平移1个单位,再向上平移1个单位C 、向右平移1个单位，再向上平移1个单位D 、向右平移1个单位,再向下平移1个单位5。

设1()lg ,||1,1x f x x x -=<+则323()13x x f x++等于 ( ） A ．2()f x B ．3()f x C ．2()f xD ．3()f x6.已知数列{}n a 满足)(,,*1221N n a a a b a a a n n n ∈-===++。

{}n n a S 是的前n 项的和， 则20042004S a +等于 （ ）A ．a b +B ．a b -C ．a b -+D ．a b --7。

设2)(1=x f ，x x x f 2cos sin )(2+=，x x x f 2cos 2sin )(3+=，24sin )(x x f =，上述函数中，周期函数的个数是(A ） 1 (B ） 2 （C) 3 （D ） 48。

已知a ，b 是两个相互垂直的单位向量，而13||=c ,3=⋅a c ，4=⋅b c 。

贵州2013-2014学年高一寒假作业（3）数学 Word 版含答案.doc第I 卷（选择题） 请点击修改第I 卷的文字说明 评卷人 得分 一、选择题（题型注释）1.非空集合S {},,5,4,3,2,1⊆且若,S a ∈则必有S a ∈-6，则所有满足上述条件的集合S 共有（ ）．A ．6个B ．7个C ．8个D ．9个2.3log 2=a ，6log 4=b ，9log 8=c ，则下列关系中正确的是A ．c b a >>B ．b c a >>C ．a b c >>D ．b a c >>3.果奇函数)(x f 在区间［1，4］上是增函数且最大值是5，那么)(x f 在区间［-4，-1］上是 （ ）（A ）增函数且最大值为-5 （B ）增函数且最小值为-5（C ）减函数且最大值为-5 （D ）减函数且最小值为-54.若函数y =f (x +1)的定义域是［－2,3］,则y =f (2x －1)的定义域为 （ ）A ．［0,25］ B ．［－1,4］ C ．［－5,5］ D ．［－3,7］5.若函数x x x f 2sin 2cos 811)(--=的最大值为a ，最小值为b ，则b a 1-等于（ ）（A ）18 （B ）6 （C ）5 （D ）06.如果 A A tan 1tan 1+-= 4+5，那么cot （A +4π）的值等于 ( ) A -4-5 B 4+5 C -541+ D 541+7.已知︱︱=1，︱︱=,=0,点C 在∠AOB 内，且∠AOC =30°，设=m +n (m 、n ∈R )，则等于A. B.3 C.D.8.如图，一个空间几何体的正视图，左视图，俯视图均为全等的等腰直角三角形，如果直角三角形的直角边长都为1，那么这个几何体的体积为（ ）A ．61B ．31C ．21D ．1正视图左视图 俯视图第II 卷（非选择题） 评卷人 得分 二、填空题（题型注释）9.已知向量a ＝(23)，，b ＝(12)，，且(a ＋λb )⊥(a －b )，则λ=____10.在ABC ∆中，如果sin A ∶sin B ∶sin C =5∶6∶8，那么此三角形最大角的余弦值是 .11.若数列｛a n ｝由a 1=2，a n+1=a n +2n(n ≥1)确定，求通项公式a n ==________12.在公差不为零的等差数列{}n a 中，有23711220a a a -+=，数列{}n b 是等比数列，且77b a =，则68b b =13.设a （0＜a ＜1）是给定的常数，f （x ）是R 上的奇函数，且在（0，+∞）上递减。

贵州2013-2014学年高三寒假作业（6）数学 Word 版含答案.doc第I 卷（选择题）一、选择题（题型注释） 1.已知F 1，F 2分别是双曲线的左、右焦点，过点F 2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ，若点M 在以线段F 1F 2为直径的圆外，则双曲线离心率的取值范围是 (A) (B) (C) (D) 2.定义在R 上的偶函数0)(log ,0)21(,),0[)(41<=+∞=x f f x f y 则满足且上递减在的x 的集合为（）A ．),2()21,0(+∞⋃B ．)2,1()1,21(⋃C ．),2()1,21(+∞⋃ D ． ),2()21,(+∞⋃-∞3.一个几何体的三视图如图所示，则该几何体的体积为_______________.4.{}2312,n n a S n a a a =已知数列为等比数列，是其前项和，若47552=4a a S 且与的等差中项为，则 ．5.设全集{}1,2,3,4,5U =,集合{}2,3,4A =,{}2,5B =,则()U B C A =（ ）（A ）{}5 （B ） {}125， ， （C ） {}12345， ， ， ， （D ） ∅6.已知i 是虚数单位，a ，b ∈R ，且(i)i 2i a b +=-，则a ＋b ＝（ ）（A ）1（B ）－1 （C ）－2 （D ）－37.已知l 、m 是两条不同的直线，α是个平面，则下列命题正确的是 （ ）（A ）若l //α，m //α, 则//l m (B) 若l //α，m ⊥α,，则l m ⊥ (C) 若l m ⊥，m ⊥α,则l //α (D) 若l m ⊥，m //α, 则α⊥l8.已知两个集合{})2ln(|2++-==x x y x A ，⎭⎬⎫⎩⎨⎧≤-+=012|x e x x B ，则B A ⋂ (A) ⎪⎭⎫⎢⎣⎡221-， (B)⎥⎦⎤ ⎝⎛21-1-， (C) ()e ，1- (D)()e ,29.右图中，321,,x x x 为某次考试三个评阅人对同一道题的独立评分，p 为该题的最终得分，当126,9,9.5x x p ===时，3x 等于(A) 10(B) 9(C) 8(D) 710.函数1()e (0,)ax f x a b b=-＞＞0的图象在0x =处的切线与圆221x y +=相切，则a b +的最大值是( )（A ） 4 （B ） （C （D ）2第II 卷（非选择题）二、填空题（题型注释）11.已知角θ的顶点为坐标原点，始边为x 轴的正半轴.若),4(y p 是角θ终边上一点，且552sin -=θ，则=y ______________.12.设R x ∈，向量)1,(x a =，)2,1(-=b =x ______________ . 13.函数43)1ln()(2+--+=x x x x f 的定义域为_________________.14.一个四面体所有棱长都为2,四个顶点在同一球面上，则此球表面积为 。

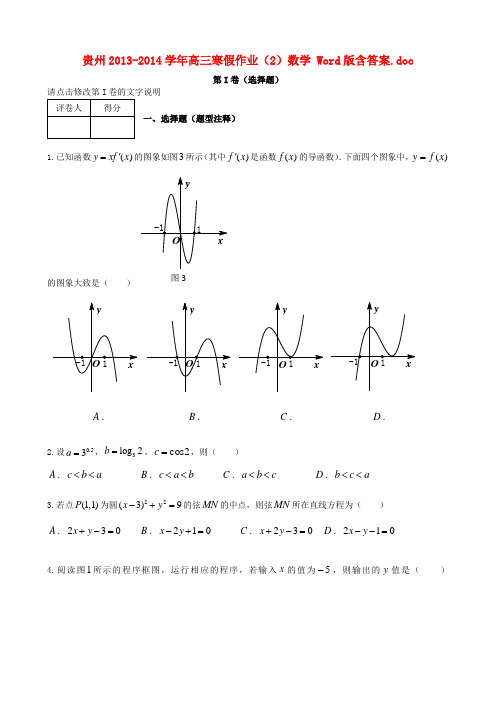
贵州2013-2014学年高三寒假作业（2）数学 Word 版含答案.doc第I 卷（选择题）一、选择题（题型注释）1.已知函数()y xf x ='的图象如图3所示（其中()f x '是函数)(x f 的导函数）．下面四个图象中，)(x f y =的图象大致是（ ）A ．B ．C ．D ．2.设0.53a =，3log 2b =，2cos =c ，则（ ）A ．c b a <<B ．c a b <<C ．a b c <<D ．b c a <<3.若点(1,1)P 为圆22(3)9x y -+=的弦MN 的中点，则弦MN 所在直线方程为（ ）A ．230x y +-=B ．210x y -+=C ．230x y +-=D ．210x y --=4.阅读图1所示的程序框图，运行相应的程序，若输入x 的值为5-，则输出的y 值是（ ）A ．1-B ．1C ．2D ．415.等差数列}{n a 的前n 项和为n S ，已知6,835==S a ，则9a =（ ）A ．8B ．12C ．16D ．246.已知x 为实数，条件p ：x x <2，条件q ：x12>，则p 是q 的( ) A ．充要条件 B ．必要不充分条件 C ．充分不必要条件 D ．既不充分也不必要条件7.若数列{}n a 的通项为2(2)n a n n =+，则其前n 项和n S 为（ ）A ． 112n -+B ．31121n n --+C ．31122n n --+D ．311212n n --++8.设函数)(x f 对任意y x ,满足)()()(y f x f y x f +=+，且4)2(=f ，则)1(-f 的值为（ ） A ．3-B ．2-C ．2D ．39.双曲线)0,0(12222>>=-b a bx a y 的一条渐近线为2y x =，则该双曲线的离心率等于（ ）A ．25 B ．5 C ．6D ．26图1是输出y x =|x -3||x |>3输入x 开始10.设集合2{|6<0}M x x x =--,2{|=log (1)}N x y x =-，则N M 等于（ ）A ．(1,2)B ．(1,2)-C ．(1,3)D ．(1,3)-第II 卷（非选择题）二、填空题（题型注释）11.已知等比数列}{n a 中，⎰-=62)232(dx x a ，2433=a ，若数列}{n b 满足n n a b 3log =，则数列}1{1+n n b b 的前n 项和=n S ．12.5(+1)(12)x x -展开式中，3x 的系数为 （用数字作答）．13.过点(2,2)P -且与曲线33y x x =-相切的直线方程是（ ）（A ）916y x =-+ （B ）920y x =- （C ）2y =- （D ）916y x =-+或2y =-三、解答题（题型注释）15.（满分12分）设数列{}n a 的前n 项和为n S .已知11a =，131n n a S +=+，n *∈N 。

贵州2013-2014学年高三寒假作业（4）数学 Word 版含答案.doc第I 卷（选择题）一、选择题（题型注释）1.若,(0,2]x y ∈且2xy =,使不等式2a x y +（）≥(2)(4)x y --恒成立，则实数a 的取值范围为（ ）A ．a ≤12 B ．a ≤2 C ．a ≥2 D ．a ≥122.已知椭圆2222:1(0)x y E a b a b +=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为(1,1)-,则E 的方程为（ ）A ．2214536x y +=B ．2213627x y +=C ．2212718x y +=D ．221189x y += 3.已知函数y=f(x)的图像是下列四个图像之一,且其导函数'()y f x =的图像如右图所示,则该函数的图像是（ ）A . B. C. D.4.向量a ，b 1=，23=，a 与b 的夹角为= ( ) A.13 B.12 C.15 D.145.已知αβ、为锐角，3cos5α=，1tan()3αβ-=-，则tanβ的值为（）A．13B．3 C．913D．1396.一个几何体的三视图如图所示，其中俯视图是菱形，则该几何体的侧面积为（）A.63+ B.53+ C.62+ D.52+7.等比数列{}n a的前n项和为n s，且41a，22a，3a成等差数列. 若1a=1，则4s=( )A.15B.7 B.8 D.168.执行右图程序框图，如果输入的N是6，那么输出的p是（）A.120B.720C.1440D.50409.B10.已知复数i iz1)3(tan--=θ,则“3πθ=”是“z是纯虚数”的（）A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件第II 卷（非选择题）二、填空题（题型注释）11.已知变量x ,y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则y x z +=的最大值是 .12.若曲线2ln yax x =-在点(1,)a 处的切线平行于x 轴,则a =________.13.某校高三年级的学生共1000人，一次测验成绩的分布直方图如图所示，现要按右图所示的4个分数段进行分层抽样，抽取50人了解情况，则在80～90分数段应抽取人数为 ．14.D三、解答题（题型注释）15.（本小题满分10分）在平面直角坐标系xoy 中，直线l 的参数方程为：⎩⎨⎧+=+=ααsin 2cos 1t y t x （t 为参数）.以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C 的极坐标方程为：θρsin 6=. （I ）求曲线C 的直角坐标方程；（II ）若曲线C 与直线l 交于A ，B 两点，点)2,1(P ，求PB PA +的最小值.16.（本小题满分10分）如图，在ABC ∆中，CD 是ACB ∠的角平分线，ACD ∆的外接圆交BC 于E ，AC AB 2=.（I ）求证：AD BE 2=；（II ）若1=AC ，2=EC ，求AD 的长.17.（本小题满分12分）设a 为实数，函数a x e x f x 22)(+-=，R x ∈.（I ）求)(x f 的单调区间与极值；（II ）求证：当12ln ->a 且0>x 时，122+->ax x e x .18.(本小题满分12分)已知双曲线C ：12222=-b y a x )0,0(>>b a 的焦距为4，以原点为圆心，实半轴长为半径的圆和直线06=+-y x 相切.（Ⅰ）求双曲线C 的方程；（Ⅱ）设点F 为双曲线C 的左焦点，试问在x 轴上是否存在一定点M ，过点M 任意作一直线l 与双曲线C 交于P ，Q 两点，使得⋅为定值？若存在，求出此定值及点M 的坐标；若不存在，请说明理由.19.（本小题满分12分）如图，在直三棱柱111ABC A B C -中，12=2AA AC AB ==，且11BC A C ⊥． （Ⅰ)求证：平面1ABC ⊥平面11A ACC ；（Ⅱ)设D 是11A C 的中点，判断并证明在线段1BB 上是否存在点E ，使DE ‖平面1ABC ；若存在，求三棱锥1E ABC -的体积．20.(本小题满分12分) 某市对该市小微企业资金短缺情况统计如下表：(I)试估计该市小微企业资金缺额的平均值；(II)某银行为更好的支持小微企业健康发展，从其第一批注资的A行业3家小微企业和B行业的2家小微企业中随机选取3家小微企业，进行跟踪调研．求选取的3家小微企业中A行业的小微企业至少有2家的概率．试卷答案1.D2.D3.C4.B5.B6.C7.A8.B9.B10.C11.512.2113.20人14.15.（1）9)3(22=-+y x；..................5分 (2)72...................10分16.（1）⇒DA DE =，BDE ∆∽BCA ∆，⇒AD BE 2=；.........5分(2)由BC BE BABD ⋅=⋅⇒21=AD ............10分17.（1）)(x f 在()2ln ,∞-上单调递减，在()+∞,2ln 上单调递增， a f x f 22ln 22)2(ln )(+-==极小值，无极大值；.........5分（2）令)12()(2+--=ax x ex g x ，a x e x g x 22)('+-=，......7分 由（1）知：≥)('x g a 22ln 22+-，因为12ln ->a ，所以0)('>x g ，....9分所以)(x g 在[)+∞,0上单调递增，所以0)0()(=≥g x g ，.........11分 即当12ln ->a 且0>x 时，122+->ax x e x ...............12分18.（1）1322=-y x ；................4分（2）当直线l 的斜率存在时，设直线l ：)(m x k y -=，33±≠k ， 代入双曲线C 的方程1322=-y x ，0)1(36)13(22222=++--k m x mk x k ， 得：1362221-=+k mk x x ，133322221-+=⋅k k m x x ，013222>+-k k m ，.......6分 所以，131)15122(222--++=⋅k k m m ，......8分 当3151222=++m m 时，1=⋅，解得：， 检验：33+-=m 不合题意，33--=m 满足0>∆.......10分当直线l 的不斜率存在时，直线l ：33--=x ，1=⋅， 所以)0,33(--M ，1=⋅.......12分19. （1）⇒⊥C A 1平面1ABC ，所以平面1ABC ⊥平面11A ACC ；.......5分（2）分别取1BB ，1AA 的中点E ，F ，连接EF ，DE ，DF⇒平面EFD ∥平面1ABC ，⇒DE ‖平面1ABC ，.......8分⇒⊥11A C 平面11A ABB ，......................10分分20. （1）平均值为：602.0903.07035.0501.03005.010=⨯+⨯+⨯+⨯+⨯；.......................5分（2）设A 行业3家小微企业为：1A ，2A ，3A ；设B 行业2家小微企业为：1B ，2B .5家小微企业随机选取3家有10种可能：321A A A ，121B A A ，131B A A ，221B A A ， 231B A A ，211B B A ，132B A A ，232B A A ，212B B A ，213B B A ，................8分选取的3家小微企业中A 行业的小微企业至少有2家的有7种可能，..........10分 所以概率为107P . .............................12分。

贵州2013-2014学年高三寒假作业（7）数学 Word 版含答案.doc第I 卷（选择题）一、选择题（题型注释）1.已知函数()x f 为偶函数，若将()x f 的图像向右平移一个单位又得到一个奇函数，若()12-=f ，则()()()201321f f f +++ 等于 ( )（A ）1- （B ）0 （C ）1003- （D ）10032.函数|1|2)(||log 2x x x f x --=的图像大致是 ( )3.若ABC ∆为锐角三角形，则下列不等式中一定能成立的是（ ） （A ）0sin cos log cos >B A C （B ）0cos cos log cos >B A C （C ）0sin sin log sin >B A C （D ）0cos sin log sin >B A C4.某公司新招聘进8名员工，平均分给下属的甲、乙两个部门，其中两名英语翻译人员不能分给同一个部门；另三名电脑编程人员也不能分给同一个部门.则不同的分配方案有 （ ）（A ） 36种 （B ）38种 （C ）108种 （D ） 114种5.已知全集{1,2,3,4,5}U =,集合{1,2}A =,{2,3,4}B =,则B A C u ⋂)(= （ ） A.}2{ B.}4,3{ C.}5,4,1{ D.}5,4,3,2{6.在三棱锥ABC S -中，22,====⊥SC SA BC AB BC AB ，，二面角B AC S --的余弦值是33-，若C B A S ,,,都在同一球面上，则该球的表面积是( )（A ）68 （B ）π6 （C ）π24 （D ） 6π7.设n S 为等差数列}{n a 的前n 项和,184a S =,27-=a ，则9a = （ ）A.6-B.4-C.2-D.28.已知()()()f x x a x b =--（其中b a <），若()f x 的图象如图（1）所示，则函数()x g x a b =+的图象是( )9.函数2()ln f x x x=-的零点所在的区间是（ ） A ．(1,2) B ．(,3)e C ． (2,)eD ．(3,)+∞10.三个数0.377,0.3,ln0.3a b c ===大小的顺序是 （ ）A ．a b c >> B. a c b >> C ．b a c >> D. c a b >>第II 卷（非选择题）二、填空题（题型注释）11.等差数列{}n a 的前n 项和为n S ，且936S =-,13104S =-，等比数列{}n b 中，55b a =，77b a =，则6b = ．12.5(+1)(12)x x -展开式中，3x 的系数为 （用数字作答）．13.如图, 设A 、B 、C 、D 为球O 上四点，若AB 、AC 、AD 两两互相垂直，且AB AC =2AD =，则A 、D 两点间的球面距离 ．14. 已知函数3,1,(),1,x x f x x x ⎧≤=⎨->⎩若()2f x =，则x = .三、解答题（题型注释）15.已知函数f (x )＝ax 2＋(b －8)x －a －ab ，当x ∈(－3,2)时，f (x )＞0，当x ∈(－∞，－3)∪(2，＋∞)时，f (x )＜0.(1)求f (x )在0,1内的值域；(2)c 为何值时，ax 2＋bx ＋c ≤0的解集为R?16.已知集合A ＝{x | x 2－3x －11≤0}，B ＝{x | m ＋1≤x ≤2m －1}，若A ⊇B 且B ≠ο/，求实数m 的取值范围。

某某省某某市第一中学2014届高三数学第五次月考试卷 理（命题:某某市第一中学高三年级数学备课组）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1页至第2页，第Ⅱ卷第3页至第4页。

考试结束后，请将本试卷和答题卡一并交回。

满分150分，考试用时120分钟。

第Ⅰ卷（选择题60分）注意事项：1、答题前，考生务必用黑色碳素笔将自己的某某、某某号、考场号、座位号在答题卡上填写清楚。

2、每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

在试题卷上作答无效。

一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1、设集合{}sin ,A y y x x R ==∈，集合{}lg B x y x ==，则()R C A B =（ ）(1,)A +∞、[)1,B +∞、[]1,1C -、(,1)(1,)D -∞-+∞、2、已知i 为虚数单位，复数122iz i-=-，则复数z 的虚部是（ ） A 、35i -B 、35-C 、45i D 、45由资料可知y 和x 呈线性相关关系,由表中数据算出线性回归方程ˆˆˆy bx a =+中的ˆ123,b =.据此估计,使用年限为10年时的维修费用是（ ）万元.A 、12.18B 、12.28C 、12.38D 、12.484、若某棱锥的三视图(单位：cm)如图所示， 则该棱锥的体积等于（ ）A 、10 cm 3B 、20 cm354 3C 、30 cm 3D 、40 cm 35、已知,m n 为异面直线，m ⊥平面α，n ⊥平面β,直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄，则以下命题正确的个数是（ ）（1）α∥β且l ∥α（2）αβ⊥且l β⊥（3）α与β相交，且交线垂直于l （4）α与β相交，且交线平行于lA 、0个B 、1 个C 、2个D 、3个6、若111a b<<，则下列结论中不正确的是( ) log log a b A b a >、log log 2a b B b a +>、2(log )1b C a <、log log log log a b a b D b a b a +>+、7、已知y x ,满足⎪⎩⎪⎨⎧≤+≥≥511y x y x 时，)0(>≥+=b a b y a x z 的最大值为1，则b a +的最小值为（ ）A 、7B 、8C 、9D 、108、如图所示，用模拟方法估计圆周率π的程序框图， P 表示估计结果，则图中空白框内应填入（ ）A 、1000N P =B 、41000NP = C 、1000M P =D 、41000MP =9、在ABC ∆中，,,a b c 分别是角,,A B C 的对边， 若2222014a b c +=，则2tan tan tan (tan tan )A BC A B ⋅+的值为( )A 、0B 、1C 、2013D 、201410、平行四边形ABCD 中，AB ·BD =0，沿BD 折成直二面角A BD C --，且22421AB BD +=，则三棱锥A BCD -的外接球的表面积为（ ）A 、2πB 、4πC 、48πD11、已知椭圆:22221(,0)x y a b a b+=>和圆O :222b y x =+,过椭圆上一点P 引圆O 的两条切线,切点分别为B A ,. 若椭圆上存在点P ,使得0PA PB ⋅=,则椭圆离心率e 的取值X 围是（ ）A 、)1,21[B 、]22,0(C 、]22,21[D 、)1,22[12、已知R 上的函数()y f x =，其周期为2，且(]1,1x ∈-时2()1f x x =+，函数1sin (0)()11(0)x x g x x xπ+>⎧⎪=⎨-<⎪⎩，则函数()()()h x f x g x =-在区间[]5,5-上的零点的个数为（ ）A 、11B 、10C 、9D 、8第Ⅱ卷（非选择题，共90分）注意事项：本卷包括必考题和选考题两部分。

2013—2014学年度上学期高三一轮复习数学（理）单元验收试题（5）【新课标】命题范围：数列说明：本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150分；答题时间120分钟。

第Ⅰ卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（本大题共12个小题，每小题5分，共60分）。

1．已知数列{a n }的前4项分别为2,0,2,0，则下列各式不可以作为数列{a n }的通项公式的一项是( )．A ．a n ＝1＋(－1)n+1B ．a n ＝2sin n π2C ．a n ＝1－cos n πD ．a n ＝⎩⎪⎨⎪⎧2，n 为奇数0，n 为偶数2．（2013年高考江西卷（理））等比数列x ,3x +3,6x +6,..的第四项等于（ ）A ．-24B ．0C ．12D ．243．已知n S 为等差数列{}n a 的前n 项的和，254,a a +=，721S =，则7a 的值为（ ）A ． 6B ．7C ．8D ．9 4．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）等比数列{}n a 的前n 项和为n S ,已知12310a a S +=,95=a ,则=1a （ ） A ．31 B ．31- C ．91D ．91-5．（2013年高考新课标1（理））设等差数列{}n a 的前n 项和为11,2,0,3n m m m S S S S -+=-==,则m = ( )A ．3B ．4C ．5D ．66．a 、b ∈R ，且|a|<1,|b|<1，则无穷数列：1,(1+b)a,(1+b+b 2)a 2,…,(1+b+b 2+…+b n －1)a n －1…的和为（ ） A ．)1)(1(1b a -- B ．ab -11 C ．)1)(1(2ab a -- D ．)1)(1(1ab a --7．若钝角三角形三内角的度数成等差数列，且最大边长与最小边长的比值为m ，则m 的范围是（ ） A ．（1，2）B ．（2，+∞）C ．[3，+∞)D ．（3，+∞）8．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））下面是关于公差0d >的等差数列()n a 的四个命题:{}1:n p a 数列是递增数列； {}2:n p na 数列是递增数列；3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列；{}4:3n p a nd +数列是递增数列； 其中的真命题为( )A ．12,p pB ．34,p pC ．23,p pD ．14,p p9．若数列{a n }前8项的值各异，且a n +8=a n 对任意n ∈N *都成立，则下列数列中可取遍{a n }前8项值的数列为（ ）A ．{a 2k +1}B ．{a 3k +1}C ．{a 4k +1}D ．{a 6k +1} 10．在数列{}n a 中,21n n a =-,若一个7行12列的矩阵的第i 行第j 列的元素,i j i j i j a a a a a =⋅++,(1,2,,7;1,2,,12i j ==)则该矩阵元素能取到的不同数值的个数为( )A ．18B ．28C ．48D ．6311．设n n n A B C ∆的三边长分别为,,n n n a b c ，n n n A B C ∆的面积为n S ，1,2,3,n =，若11111,2b c b c a >+=，111,,22n n nnn n n n c a b a a a b c +++++===，则（ ） A ．{S n }为递减数列 B ．{S n }为递增数列C ．{S 2n -1}为递增数列,{S 2n }为递减数列D ．{S 2n -1}为递减数列,{S 2n }为递增数列12．（2013年普通高等学校招生统一考试安徽数学（理）试题）函数=()y f x 的图像如图所示,在区间[],a b 上可找到(2)n n ≥个不同的数12,...,,n x x x 使得1212()()()==,n nf x f x f x x x x 则n 的取值范围是()A ．{}3,4B ．{}2,3,4C ．{}3,4,5D ．{}2,3第Ⅱ卷二、填空题：请把答案填在题中横线上（本大题共4个小题，每小题4分，共16分）。