设计洪峰流量计算

适用于流域面积不大于10km 2的小流域洪峰流量计算
重现期（年）
200100502010C 20.0560.0530.050.0460.044深圳地区
K P 3.05 2.74 2.42 1.988 1.661
举例：计算龙岗5km 2集雨面积，50年一遇洪峰流量Q P （m 3
/s）84.18
举例：计算宝安2km 2集雨面积，10年一遇洪峰流量
Q P （m 3/s）22.24
深圳地区宝安市区及龙岗
盐田大鹏半岛深汕合作区 H 24（mm）170
180
200
220230
深圳地区
C V
一般取0.50.55
广东省洪峰流量经验公式：Q P =C 2×H 24P ×F 0.84 式中：C 2—根据重现期而定；H 24P =H 24×K P ,H 24查“广东省年最大24小时点雨量均值等值线图”，K P 根据重现期和C V 值而定(查广东省洪峰流量经验公式皮尔逊Ⅲ型曲线KP值表)，C V 查“广东省年最大24小时点雨量变差系数等值线图（C S /C V =3.5）”。

重现期而定；H24P=H24
据重现期和C V值而定
东省年最大24小时点
550
0.0410.05
1.326
2.59。

•铁路与公路•西宁成都铁路隆务河设计洪峰流量的计算龙(中铁第一勘察设计院集团有限公司，陕西西安710043)【摘要】设计洪峰流量是确定铁路桥涵高程、跨度的重要指标。

文章以新建西宁至成都铁路中隆务河设计洪峰流量的计算为背景，分别运用院编壹桥8212公式、地方经验公式及数理统计法三种计，对的 流量进行计算，并对计算结果进行了对比分析。

结果表明，桥8212 式计算结果与其他两种方法的结果十分接近，说式对于隆务河乃至该地区流量的计算具有一定的适用性，从而为今后该地区的河流的流量设计提供了理论依据。

【关键词】设计流量；院编壹桥8212公式；经验公式；数理统计法【中图分类号】U442.3 +4修建经常需要架设桥梁以跨越河流、沟谷。

如果桥梁（是高程)设计不当就会造成严重水毁，不仅给带来损失，而 车的行车安全[14。

由多数地区的河测径料不够，不能满足设计，因此河流域的设计洪水般采用推理公式法计算[4]。

式均以式推求设计，并以水形成原理为基础，建立起来。

目前，我国西北地区铁路桥涵设计的计算方法[5]仍以院院编公式为主，且停留在20 ~30前的水平。

随着自然地理条件的、化以及降料的增加，原计算公式的性有待进验证。

本文主要以河["](河河一，发泽库乡境内多禾茂乡加仓村若恰山区，源头海拔4 042 m，出境处的海拔2 160 m，总落差为1 882 m，隆 河全长156. 8km，流域积 4 960 km2，区河流。

并设有同仁、隆务河口两个水文站）洪峰的计算为例，验计算公式在当前的 ，从而为以后该地区的水文计算理论依据。

1洪峰流量计算新建西宁至成都铁路于青海省同仁县跨越隆务河，本文河同仁水文站处设计洪峰采院院编壹桥8212 [7]《河峰设计/(黄河上游地区）计算公式(以下统称“壹桥8212计算公式”）、地方经验公式及数理统计法进行计算，三种方法计算结果进比 。

11壹桥8212计算公式(1)域平均海 2 500 m以下的泾北洛、渭河，清水河，祖历河，洮河，河，庄浪河下游河段以及湟水'支流，计算公式1A"B/.167/.2丑曰6.56(1)(2)流域平均海拔在2 500 m以上的洮河，大夏河上游段干，庄浪河上游，湟水部分支流和西宁以上干流，黄河积石关以上小支流，其计算公式1A"B/.167/.2'日6.7(2)式中i A i为多年平均（m3/S);B为与自然地理条【文献标志码】A件、流域物理特征有关的系数;！1为流域主河槽平均坡度(1);/为流域形状，/=6/52,5为域长度（km);'为流域历平均值(mm);6为流域面积（km2)。

推理公式法计算设计洪峰流量推理公式法是基于暴雨形成洪水的基本原理推求设计洪水的一种方法. 1.推理公式法的基本原理推理公式法计算设计洪峰流量是联解如下一组方程)6.7.8(278.0)5.7.8(,278.0)4.7.8(,278.04/13/11mc cn cp m c n p Q mJ L t F t t SQ t F S =<⎪⎪⎭⎫⎝⎛-=≥⎪⎪⎭⎫⎝⎛--τττμτμτ便可求得设计洪峰流量Q p ，即Q m ,及相应的流域汇流时间τ.计算中涉及三类共7个参数，即流域特征参数F 、L 、J ；暴雨特征参数S 、n ；产汇流参数μ、m 。

为了推求设计洪峰值，首先需要根据资料情况分别确定有关参数.对于没有任何观测资料的流域,需查有关图集.从公式可知，洪峰流量Q m 和汇流时间τ互为隐函数，而径流系数ψ对于全面汇流和部分汇流公式又不同，因而需有试算法或图解法求解。

1. 试算法该法是以试算的方式联解式（8。

7.4）（8。

7。

5)和（8。

7.6）,步骤如下：① 通过对设计流域调查了解，结合水文手册及流域地形图，确定流域的几何特征值F 、L 、J ，设计暴雨的统计参数（均值、C V 、C s / C V ）及暴雨公式中的参数n (或n 1、n 2），损失参数μ及汇流参数m 。

图8。

7.1 推理公式法计算设计洪峰流量流程图② 计算设计暴雨的S p 、x TP ，进而由损失参数μ计算设计净雨的T B 、R B 。

③ 将F 、L 、J 、R B 、T B 、m 代入式（8。

7。

4）（8.7.5）和（8.7。

6），其中仅剩下Q m 、τ、R s ，τ未知,但R s,τ与τ有关，故可求解.④ 用试算法求解。

先设一个Q m ,代入式（8。

7。

6）得到一个相应的τ，将它与t c 比较,判断属于何种汇流情况，再将该τ值代入式（8.7。

4)或式（8。

7。

5），又求得一个Q m ，若与假设的一致(误差不超过1%），则该Q m 及τ即为所求;否则,另设Q m 仿以上步骤试算，直到两式都能共同满足为止。

小流域洪峰流量计算的公式1、推理公式f Q n sm τψ278.0=当τ≥c t ，时，n su τψ-=1 当τc t ，时，nc t n -⎪⎭⎫ ⎝⎛=1τψn H s -=12424n--=410ψττ()nnnsF L mJ ----⎪⎪⎭⎫ ⎝⎛=414431410278.0τ()nc s n t 11⎥⎦⎤⎢⎣⎡-=μm Q ——设计频率的洪峰流量（m 3/s ）ψ——洪峰径流系数τ——汇流历时(h)S ——暴雨雨力(mm/h)n ——暴雨衰减指数，其分界点为1小时，当t<1，取n=n 1，当t 1，取n=n 2μ——产流历时内流域内的平均入渗率（mm/h ）c t ——产流历时24H ——设计频率的最大24小时雨量（mm ）计算步骤1、根据地形图确定流域的特征参数F 、L 、J2、由公式4131FJ L =θ计算θ值，并根据相关公式计算汇流参数m3、由暴雨μ的参数等值线图确定设计流域的暴雨参数特征值24H 、C V 、C S 、n 1或n 2，并由皮尔逊Ⅲ型，结合频率查表，确定指定频率下的K p 值，由()241224H K s K S n p p p -== 4、有《四川省水文手册》，查出n-44的值，并根据ns m -⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44410383.0θτ计算0τ值5、查表确定μ值，并计算n sτμ，查图由n 、n sτμ两坐标的焦点值，确定洪峰径流系数ψ6、根据《四川省水文手册》，查出n-41的值，计算流域汇流时间n--=41ψττ，计算τ值2、水利水电科学研究院的经验公式 适用于流域面积小于100km 2.32ksFQ m =洪峰流量参数K 可有下表3、公路科学研究所nm kFQ =指数n 为面积指数，当101≤≤F 时，K 值如下表梯形断面830)'(189.1⎥⎦⎤⎢⎣⎡-=i m m nQ h ，)1(2200m m h b -+=，212'm m +=。

第二节设计洪峰流量及设计洪量的推求由流量资料推求设计洪峰及不同时段的设计洪量，可以使用数理统计方法，计算符合设计标准的数值，一般称为洪水频率计算。

一、资料审查在应用资料之前，首先要对原始水文资料进行审查，洪水资料必须可靠，具有必要的精度，而且，具备频率分析所必须的某些统计特性，例如洪水系列中各项洪水相互独立，且服从同一分布等。

除在第三章谈到审查资料的可靠性之外，还要审查资料的一致性和代表性。

为使洪水资料具有一致性，要在调查观测期中，洪水形成条件相同，当使用的洪水资料受人类活动如修建水工建筑物、整治河道等的影响有明显变化时，应进行还原计算，使洪水资料换算到天然状态的基础上。

洪水资料的代表性，反映在样本系列能否代表总体的统计特性，而洪水的总体又难获得。

一般认为，资料年限较长，并能包括大、中、小等各种洪水年份，则代表性较好。

此可见，通过古洪水研究，历史洪水调查，考证历史文献和系列插补延长等增加洪水列的信息量方法，是提高洪水系列代表性的基本途径。

根据我国现有水文观测资料情况，SL44—93规定坝址或其上下游具有较长期的实测水资料(一般需要30年以上)，并有历史洪水调查和考证资料时，可用频率分析法计算计洪水。

二、样本选取河流上一年内要发生多次洪水，每次洪水具有不同历时的流量变化过程，如何从历洪水系列资料中选取表征洪水特征值的样本，是洪水频率计算的首要问题。

根据SL44—93规定，应采用年最大值原则选取洪水系列，即从资料中逐年选取一个大流量和固定时段的最大洪水总量，组成洪峰流量和洪量系列。

固定时段一般采用l、3、5、7、15、30天。

大流域、调洪能力大的工程，设计时段可以取得长一些；小流域、调洪能力小的工程，可以取得短一些。

在设计时段以内，还必须确定一些控制时段，即洪水过程对工程调洪后果起控制作用的时段，这些控制时段洪量应具有相同的设计频率。

同一年内所选取的控制时段洪量，可发生在同一次洪水中，也可不发生在同一次洪水中，关键是选取其最大值。

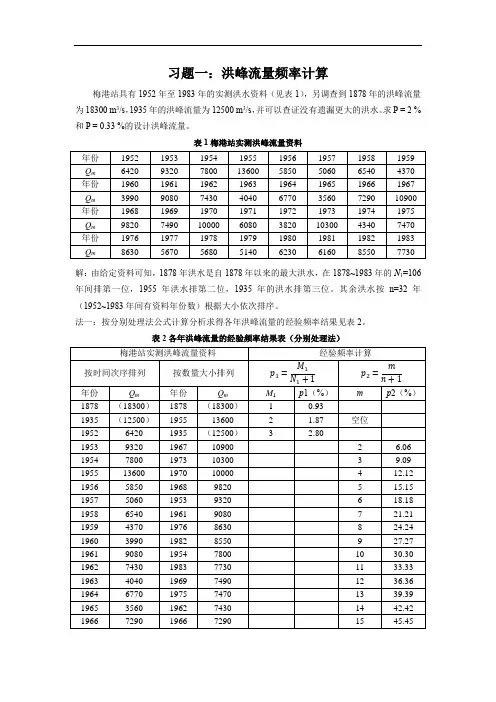
习题一：洪峰流量频率计算梅港站具有1952年至1983年的实测洪水资料（见表1），另调查到1878年的洪峰流量为18300 m3/s，1935年的洪峰流量为12500 m3/s，并可以查证没有遗漏更大的洪水。

求P = 2 %和P = 0.33 %的设计洪峰流量。

表1梅港站实测洪峰流量资料解：由给定资料可知，1878年洪水是自1878年以来的最大洪水，在1878~1983年的N1=106年间排第一位，1955年洪水排第二位，1935年的洪水排第三位。

其余洪水按n=32年（1952~1983年间有资料年份数）根据大小依次排序。

法一：按分别处理法公式计算分析求得各年洪峰流量的经验频率结果见表2。

表2各年洪峰流量的经验频率结果表（分别处理法）根据表2中的流量数据和计算的经验频率，点绘经验点据，如图1中圆形点据所示。

图1分别处理法求得的频率曲线经过调整，参数最终选用Q̅=7146.25 m3/s， C v=0.38，C s=1.32 ，拟合度达96.79%。

经检验，当P = 2 %时的设计洪峰流量为14408.97 m3/s>13900 m3/s，故成果合理。

据此组参数求得P = 2 %和P = 0.33 %的设计洪峰流量分别为14408.97 m3/s和18227.16 m3/s。

法二：按统一处理法公式计算分析求得各年洪峰流量的经验频率结果见表3。

表3各年洪峰流量的经验频率结果表（统一处理法）根据表3中的流量数据和计算的经验频率，点绘经验点据，如图2中圆形点据所示。

图2统一处理法绘制的频率曲线经过调整，参数最终选用Q̅=7080.47 m3/s， C v=0.38，C s=1.33 ，拟合度达96.70%。

经检验，当P = 2 %时的设计洪峰流量为14286.92 m3/s>13900 m3/s，故成果合理。

据此组参数求得P = 2 %和P = 0.33 %的设计洪峰流量分别为14286.92 m3/s和18085.61 m3/s。

附表三：涵洞水力计算洪水量采用公路科学研究所经验公式(适用于汇水面积小于10 Km2))：Q p =KpF mQp——设计洪峰洪量(m3/s）K p——流量模数，根据地区划分及设计标准（广州地区属东南沿海，重现期采用25年一遇时， Kp=22)F—汇水面积（Km2)) ,m——面积指数，当F≤1Km2时，m=1;当1<F<10 Km2时，m=0.751、K6+140～K6+220 2-4x3m箱涵汇水面积：F=0.45+0.50+1.31=2.26（Km2)) Q p=K p F m =22* 2.340.75 =40.5(m3/s）2-4x3m箱涵，坡度为0.001,箱涵过水流量为52(m3/s）> 40.5(m3/s），因此K6+140～K6+220 2-4x3m箱涵可满足排洪要求。

2、K6+700 3-Φ1.5m圆管涵汇水面积：F=0.50（Km2)) Q p=K p F m =22* 0.501 =11(m3/s）3-Φ1.5m圆管涵，坡度为0.004,管涵过水流量为13.44(m3/s）> 11(m3/s），因此K6+700 3-Φ1.5m圆管涵可满足排洪要求。

3、K6+923.2 1-3x2.5m箱涵汇水面积：F=0.45（Km2)) Q p=K p F m =22* 0.451 =9.9(m3/s）1-3x2.5m箱涵，坡度为0.003,箱涵过水流量为19.2(m3/s）> 9.9(m3/s），因此K6+923.2 1-3x2.5m箱涵可满足排洪要求。

4、K8+675.3 2-4x2m箱涵汇水面积：F=1.10（Km2)) Q p=K p F m =22* 1. 10.75=23.6(m3/s）2-4x2m箱涵，坡度为0.003,箱涵过水流量为46.8(m3/s）> 23.6(m3/s），因此K8+675.3 2-4x2m箱涵可满足排洪要求。

面积比拟法计算洪峰流量洪峰流量是指在一定时间内，河流或水库中流量达到最高峰值的流量。

洪峰流量的计算对于水利工程建设和防洪减灾具有重要意义。

而面积比拟法是一种常用的计算洪峰流量的方法。

面积比拟法是一种基于流量连续性原理的计算方法。

其基本思想是将河道或水库划分为若干个断面，通过测量每个断面的水位和横截面积，计算出每个断面的流量，然后将各个断面的流量相加，即可得到整个河道或水库的流量。

这种方法的优点是计算简单、精度较高，适用于各种类型的河道和水库。

具体来说，面积比拟法的计算步骤如下：1. 划分断面：根据河道或水库的实际情况，将其划分为若干个断面。

一般来说，断面的数量越多，计算结果越精确。

2. 测量水位：在每个断面处，测量水位。

水位可以通过水位计、液压计等工具进行测量。

3. 计算横截面积：根据测量得到的水位，计算出每个断面的横截面积。

横截面积可以通过测量断面的宽度和深度来计算。

4. 计算流量：根据流量连续性原理，通过每个断面的横截面积和水位，计算出每个断面的流量。

具体计算公式为：Q=AV，其中Q表示流量，A表示横截面积，V表示流速。

5. 求和计算：将各个断面的流量相加，即可得到整个河道或水库的流量。

需要注意的是，在实际计算中，还需要考虑一些因素，如水流速度的变化、水流的非均匀性等。

这些因素会对计算结果产生一定的影响，因此需要进行适当的修正。

面积比拟法的优点在于计算简单、精度较高，适用于各种类型的河道和水库。

但是，也存在一些局限性。

例如，该方法假设水流速度在各个断面上是相同的，但实际情况下，水流速度会随着河道或水库的形状、水深、水位等因素的变化而发生变化。

因此，在实际应用中，需要根据具体情况进行修正。

面积比拟法是一种常用的计算洪峰流量的方法，其基本思想是将河道或水库划分为若干个断面，通过测量每个断面的水位和横截面积，计算出每个断面的流量，然后将各个断面的流量相加，即可得到整个河道或水库的流量。

该方法计算简单、精度较高，适用于各种类型的河道和水库，但也存在一定的局限性，需要根据具体情况进行修正。