1洪峰流量计算

案例一 水文统计频率曲线图某站有24年的实测年径流量资料，见表1，使用目估线推求年径流量平率曲线的三个参数，并会出曲线图。

表1 （1）经验频率计算①将原始资料填入表2，并且将原始资料按从小到大的排序也填入表2中。

②用公式100%1m Pn 计算经验频率，并将其列入表2中，并将x 和p 对应的点绘制在频率格纸上（图1），本案例分析中n=24.③计算序列的多年平均流量ni 1()/366.395i X x n 平 (m 3/s)④计算各项的模比系数按供公式ilx K x 平计算，并计入表2中，其总和应等于n 。

⑤计算各项（K i -1）,列入表2中，其总和应为零。

⑥计算（K i -1）2，并列入表2中，可以求C v,,i 1(1)(K 1)0.261ni i vK C n⑦计算（K i -1）3，并列入表2中，可求C s ,1(1)^30.05(3)^3ni i sv k C n C计算经验参数平均值X 、变差系数C u 、偏态系数C s 如下表2.表2（2）频率格纸绘制及适线根据表2计算出来的 Cv =,Cs的经验取值为，查《工程水文》教材的附录1，进行配线，计算结果如表3.v1.0 可编辑可修改75522520904304329538239099304318表3根据两次配线结果，选取拟合较好的配线数组：第一次的配线，所画出的曲线偏离经验频率点较大，则重新配线；最后选取第二次配线Cv =，Cs==，配线的频率图如下图1.图1.年流量频率曲线案例二设计年径流分析资料：某水利工程的设计站，有1954-1971年的实测径流资料。

其下游有一参证站，有1939-1971年的年径流系列资料，如表1所示，其中1953-1954年、1957-1978年和1959-1960年，分别被选定为P=50%、P=75%和P=95%的代表年，其年内的逐月径流分配如表2所示。

表1.设计站与参证站年径流系列要求：（1）根据参证站系列，将设计站的年径流系列延长至1939-1971年。

洪峰流量计算8.7.3推理公式法计算设计洪峰流量推理公式法是基于暴雨形成洪水的基本原理推求设计洪水的一种方法。

1.推理公式法的基本原理推理公式法计算设计洪峰流量是联解如下一组方程X便可求得设计洪峰流量Qp，即Qm，及相应的流域汇流时间τ。

计算中涉及三类共7个参数，即流域特征参数F、L、J；暴雨特征参数S、n；产汇流参数μ、m。

为了推求设计洪峰值，首先需要根据资料情况分别确定有关参数。

对于没有任何观测资料的流域，需查有关图集。

从公式可知，洪峰流量Qm和汇流时间τ互为隐函数，而径流系数ψ对于全面汇流和部分汇流公式又不同，因而需有试算法或图解法求解。

1. 试算法该法是以试算的方式联解式（8.7.4）（8.7.5）和（8.7.6），步骤如下：①通过对设计流域调查了解，结合水文手册及流域地形图，确定流域的几何特征值F、L、J，设计暴雨的统计参数（均值、C V、Cs / C V）及暴雨公式中的参数n（或n1、n2），损失参数μ及汇流参数m。

②计算设计暴雨的Sp、X TP，进而由损失参数μ计算设计净雨的T B、R B。

③将F、L、J、T B、R B、m代入式（8.7.4）（8.7.5）和（8.7.6），其中仅剩下Q m、τ、Rs,τ未知，但Rs,τ与τ有关，故可求解。

④用试算法求解。

先设一个Q m，代入式（8.7.6）得到一个相应的τ，将它与t c比较，判断属于何种汇流情况，再将该τ值代入式（8.7.4）或式（8.7.5），又求得一个Q m，若与假设的一致（误差不超过1%），则该Q m及τ即为所求；否则，另设Q m仿以上步骤试算，直到两式都能共同满足为止。

试算法计算框图如图8.7.1。

图8.7.1 推理公式法计算设计洪峰流量流程图2. 图解交点法该法是对（8.7.4）（8.7.5）和（8.7.6）分别作曲线Q m~τ及τ~ Q m，点绘在一张图上，如图8.7.2所示。

两线交点的读数显然同时满足式（8.7.4）（8.7.5）和（8.7.6），因此交点读数Q m、τ即为该方程组的解。

河道系统治理设计洪水计算分析摘要：在河道治理防洪设计过程中，设计洪水计算是必不可少的，其结果为河道断面尺寸拟定、建筑物布置、岸坡防护等各项参数的确定提供依据，洪水分析成果的合理性对整个项目影响甚大。

不同于水库设计洪水计的计算，河道系统治理需要对一条河从河源至入河口的整条河道进行分析。

由于河道水面线的推求一般采用河道分段恒定非均匀流方法，河道的设计流量相应地根据沿流程支流汇入的情况分段给出，汇总各段河道的设计流量得到整条河的设计流量。

本次以清水河设计洪水分析计算为例，分析计算河道设计流量和水面线的计算步骤、方法及成果。

关键词：河道;系统治理;设计洪水;水面线引言清水河流域无长系列的流量及降雨资料，因此无法直接推求河道设计洪水，本次分析流域特点及情况，采用经地方刊布的洪水计算办法进行间接计算。

1、流域划分及流域参数根据清水河流域及支流情况，将清水河分为水库、余家河渡槽、枣木河口及清水河口四个节点，并根据流域1:10000地形图及实测流域1:1000地形图分析计算各节点流域参数。

经分析水库坝址以上流域面积 5.4km2；水库至余家河渡槽区间流域面积37.4km2；水库至枣木河口流域面积73.0km2；支流枣木河流域面积67.2km2；清水河口以上流域面积145.6km2。

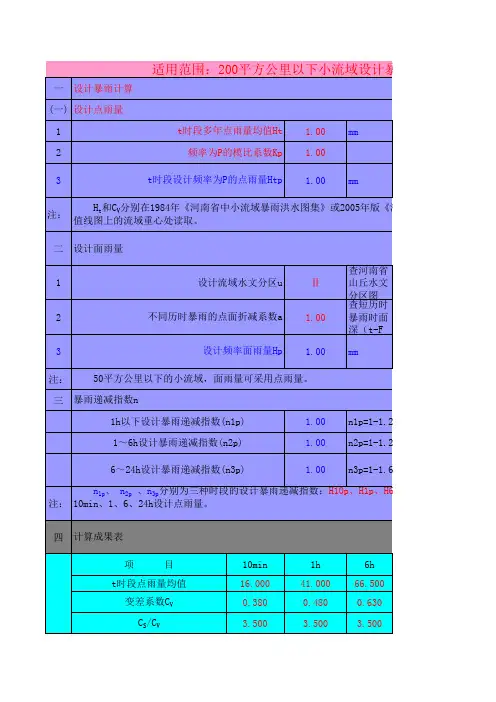
2、设计洪水分析根据《安徽省暴雨参数等值线图、山丘区产汇流分析成果和山丘区中、小面积设计洪水计算办法》以及流域参数查图及表格确定流域1h及24h时段点雨量均值及Cv、Cs，以及模比系数Kp及点面折减系数等，由此推求流域设计面暴雨量。

本次工程流域属于江淮地区浅山～丘陵区，利用该办法计算面净雨量时，应扣除相应损失量。

成果见表1。

表1清水河洪水计算主要参数成果表分析河道流域内水工建筑物情况，河道上游建有一座小1型水库，故河道洪水主要由两部分组成，分别为：①水库下泄洪水；②河道自身区间汇水，包括干流汇水及其支流枣木河汇水。

因此需对水库调洪后的下泄流量及河道自身区间流量分别进行分析计算，之后对成果进行叠加方得最终洪水流量。

洪水计算㈠、洪水设计标准大乐亭水库属小（二）型水利工程，其等级划分按照《水利水电工程等级划分及洪水标准》（SL252—2000），该工程为五等五级建筑，对山区、丘陵区水利水电工程永久性水工建筑的洪水标准其重视期按30—20年一遇设计，300—200年一遇校核，因此，洞甲水库采用防洪标准按30年一遇设计，300年一遇校核。

㈡、洪水复核大乐亭水库坝址以上集雨面积为1.35km2，由于集雨面积及其上下游无水文站，无法取得确切的水文资料，其洪水计算采用《贵州省暴雨洪水计算实用手册（修订本）小汇水流域部分》中简化公式进行计算。

①、洪峰流量的计算采用公式QP=ψp″F0.89式中：Qp—相应频繁下的洪峰流量（m3/S）ψp″—经验性系数（设计时为23.8，校核时为43.0）F—坝址以上集雨面积km2即设计洪峰流量为16.89m3/S，校核洪峰流量为30.51 m3/S，②、洪峰总量的计算采用公式W p=0.1CH24F式中：W p—洪水总量（万m3）C—径流系数（设计时0.86，校核时为0.88）H24—最在24小时降雨量（设计时254mm，校核时为390mm）F—集雨面积即设计洪水总量为14.85万m3，校核洪水总量为23.34万m3㈢、水库调洪计算水库流域面积小，库容也很小，暴雨汇流时间短，无合适的流量过程线可套用，因此，采用三角形概化法进行水库的调洪计算。

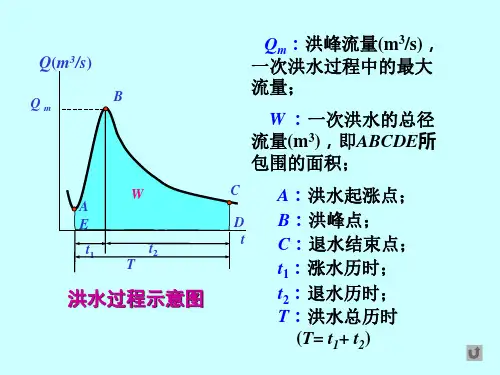
水库的泄洪流量按下式计算：q=MEBH3/2式中：m—流量系数，取m=0.36E—侧收缩系数，E=0.95B—溢流堰宽，B=7.6mH—堰上水头（m）水库水量平衡用下式计算：（Q1+Q2）/2▽t-（q1+q2）/2▽t=V2-V1=▽V式中：Q1、Q2—进段▽t始、未的入库流量（m3/S）q1、q2—时段▽t始、未的水库蓄水量m3▽t—计算时段（秒）水库泄流方程式：q=f（V）联解水量平衡方程和泄流高程，用公式算法，即可求得最大泄洪流量和最高洪水位，详见附表2、附表3、附表4，设计洪洪水过程公式的推求：洪水过程线采用概化三角形线，洪水历时采用下式计算：T=2W p/Q m小时式中：W—洪水总量（m3）Qm—洪峰流量（m3/S）涨洪历时t1与退洪历时t2的比例，即：t1：t2=2据此作出洪水过程线图。

精心整理水利专业常用计算公式一、枢纽建筑物计算1、进水闸进水流量计算：Q=B 0δεm （2gH 03）1/2式中：m —堰流流量系数 ε—堰流侧收缩系数最为常见。

求解明渠恒定缓变流水面曲线，宜采用逐段试算法，对棱柱体和非棱柱渠道均可应用。

逐段试算法的基本公式为△x=f21112222i -i 2g v a h 2g v a h ⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+式中：△x ——流段长度（m ）；g ——重力加速度（m/s2）；h 1、h 2——分别为流段上游和下游断面的水深（m ）； v 1、v 2——分别为流段上游和下游断面的平均流速（m/s ）； a 1、a 2——分别为流段上游和下游断面的动能修正系数； f i ——流段的平均水里坡降，一般可采用⎪⎭⎫ ⎝⎛+=-2f 1f -f i i 21i 或⎪⎪⎭⎫⎝⎛+=∆=3/4222224/312121f f v n R v n 21x h i R n 1=n 2 0.2m ； （6）进口断面河吼道断面间的水平距离与其高度之比：l/P=0.7—0.9； 6、最大负压值出现在吼道断面定点a 处，a 点的最大负压值按下式确定： 式中：Z —前池内正常水位与最低水位之间的高差（m ）；h 0—吼道断面高度（m ）；∑wh—从进水口断面至吼道断面间的水头损失（m ）；γ/p *—因法向加速度所产生的附加压强水头（m ）。

附加压强水头按下式计算：式中：0γ—吼道断面中心半径（m ） 计算结果，须满足下列条件：式中： h a —计算断面处的大气压强水柱高（m ）； H v —水的气化压强水柱高（m ） 最小淹没深度S ，可按下式估算：式中：0γF —吼道断面的水流弗劳德数，000gh /V F =γ。

B —坝址处的河谷宽度(相当于坝顶的部仪)，m 。

L —蓄水后库区延伸长度(回水长度)，km(公里)。

H —最大坝前水深，m 。

K —按库尾蓄水断面与坝址蓄水断面之比采用的系数： l:lO 时，K=32；1:5时，K=27（2）根据淹没面积初估： V=HA/KV—水库总库容，104·m3(万立米)。

水利专业常用计算公式一、枢纽建筑物计算1、进水闸进水流量计算：Q=B 0δεm（2gH 03）1/2式中：m —堰流流量系数ε—堰流侧收缩系数2、 明渠恒定均匀流的基本公式如下：流速公式：u ＝ RiC 流量公式Q ＝Au ＝A RiC 流量模数K ＝A RC 式中：C —谢才系数，对于平方摩阻区宜按曼宁公式确定，即C ＝6/1n 1RR —水力半径（m ）；i —渠道纵坡；A —过水断面面积（m 2）；n —曼宁粗糙系数，其值按SL 18确定。

3、水电站引水渠道中的水流为缓流。

水面线以a1型壅水曲线和b1型落水曲线最为常见。

求解明渠恒定缓变流水面曲线，宜采用逐段试算法，对棱柱体和非棱柱渠道均可应用。

逐段试算法的基本公式为△x=f21112222i -i 2g v a h 2g v a h ⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+ 式中：△x ——流段长度（m ）；g ——重力加速度（m/s ²）；h 1、h 2——分别为流段上游和下游断面的水深（m ）；v 1、v 2——分别为流段上游和下游断面的平均流速（m/s ）；a 1、a 2——分别为流段上游和下游断面的动能修正系数；f i ——流段的平均水里坡降，一般可采用⎪⎭⎫ ⎝⎛+=-2f 1f -f i i 21i 或⎪⎪⎭⎫ ⎝⎛+=∆=3/4222224/312121f f v n R v n 21x h i R式中：h f ——△x 段的水头损失（m ）； n 1、n 2——分别为上、下游断面的曼宁粗糙系数，当壁面条件相同时，则n 1=n 2=n ； R 1、R 2——分别为上、下游断面的水力半径（m ）；A 1、A 2——分别为上、下游断面的过水断面面积（㎡）；4、各项水头损失的计算如下：（1）沿程水头损失的计算公式为⎪⎪⎭⎫ ⎝⎛+∆=3/4222223/412121f v n v n 2x h R R （2）渐变段的水头损失，当断面渐缩变化时，水头损失计算公式为：L f 2122c f c i g 2v g 2v f h h h -+⎪⎪⎭⎫ ⎝⎛-=+=ω 5、前池虹吸式进水口的设计公式（1）吼道断面的宽高比：b 0/h 0=1.5—2.5；（2）吼道中心半径与吼道高之比：r 0/h 0=1.5—2.5；（3）进口断面面积与吼道断面面积之比：A 1/A 0=2—2.5；（4）吼道断面面积与压力管道面积之比：A 0/A M =1—1.65；（5）吼道断面底部高程（b 点）在前池正常水位以上的超高值：△z=0.1m —0.2m ；（6）进口断面河吼道断面间的水平距离与其高度之比：l/P=0.7—0.9；6、最大负压值出现在吼道断面定点a 处，a 点的最大负压值按下式确定：γανp *w 20a h g 2h h -+++Z +∆Z =∑、B式中：Z —前池内正常水位与最低水位之间的高差（m ）；h 0—吼道断面高度（m ）；∑w h—从进水口断面至吼道断面间的水头损失（m ）； γ/p *—因法向加速度所产生的附加压强水头（m ）。

计算说明书━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━工程名称：工程1计算类型：同频率缩放设计洪水过程线一、计算原理1.适用范围在已知典型洪水过程线、设计洪峰流量及各种历时设计洪量时，计算、打印并绘制典型设计洪水过程线。

本程序采用放大倍比K值函数新方法，具有计算速度快、能精确控制各时段设计洪量、保持设计过程基本不变形，并自行精确计算典型洪水各种时段最大洪量等特点。

同时对典型过程时间坐标可任意摘录，缩放后的设计洪水过程时间坐标和典型过程相同，从面能很好地控制设计洪水过程线的形状，并能按要求输出等时距的设计洪水过程。

2.计算方法和公式(1)典型洪水时段最大洪量计算图1所示为一典型洪水过程线，T时段长的最大洪量必须满足(1)式必要条件，但不是充分条件：加入图形因此计算的关键是求出间距为T的等流量点（即A，B两点）。

而洪水过程线可概化为两种形式：Q i+1-Q i>0或Q i+1-Q i<0（少数Q i+1-Q i=0，暂不考虑）。

令A点的斜率为K A[K A=（Q2-Q1）/（t2-t1）]，B点斜率为K B[K B=（Q4-Q3）/（t4-t3）]，则A，B两点的斜率只可能是同号工异号（它们可组合成四种形式出现），对于K A，K B同号，如同时有（Q3-Q2）*（Q4-Q1）≤0，即可能出现等流量点（时间上必须满足t3-t1≥T和t3-t2≤T）。

令式(2)方程组（4）只有X，Y两个未知数，解之可得X，Y，即可计算出相应的t A，t B，Q A，Q B，统计出t A至t B内的洪量，求出过程线内所有满足式（1）要求的洪量，取其最大值，即为T时段段长的最大洪量。

(2)设计洪水过程线的缩放该方法认为放大倍比是关于时间的连续函数，在某一时间区间内放大倍比可表达为某个二次函数，该函数满足其与典型洪水流量的乘积之积分等于该时段内的设计洪量。

洪水削峰率计算公式(一)洪水削峰率计算公式什么是洪水削峰率洪水削峰率是指洪水调度措施对洪峰流量削减的程度，通常用百分比表示。

洪水削峰率越高，即洪峰流量削减越大，对于减轻洪水灾害和保护生态环境具有重要作用。

洪水削峰率的计算公式洪水削峰率计算公式主要基于流量的比较和计算，常用的计算公式有：1.洪水削峰率（Simple Peak Rate）：洪水削峰率（%）= (洪峰流量 - 出口流量) / 洪峰流量× 100%这个公式是基于洪峰流量与出口流量的差异来计算洪水削峰率的，结果为百分比。

例如：洪峰流量为10000立方米/秒，出口流量为2000立方米/秒，那么洪水削峰率为(10000 - 2000) / 10000 × 100% = 80%。

2.洪水削峰率（RRI）：洪水削峰率（%）= (洪峰流量 - 出口流量) / 洪峰流量× 100%这个公式与Simple Peak Rate公式相同，也是基于洪峰流量与出口流量的差异来计算洪水削峰率的，结果为百分比。

例如：洪峰流量为10000立方米/秒，出口流量为2000立方米/秒，那么洪水削峰率为(10000 - 2000) / 10000 × 100% = 80%。

3.洪水削峰率（Original Peak Reduction Ratio）：洪水削峰率（%）= (洪峰流量 - 削减后的洪峰流量) / 洪峰流量× 100%这个公式是基于洪峰流量与削减后的洪峰流量的差异来计算洪水削峰率的，结果为百分比。

例如：洪峰流量为10000立方米/秒，削减后的洪峰流量为2000立方米/秒，那么洪水削峰率为(10000 - 2000) / 10000 × 100% = 80%。

4.洪水削峰率（Effective Peak Reduction Ratio）：洪水削峰率（%）= ((洪峰流量 - 水库出口流量) *流量比例 + (洪峰流量 - 水库排洪流量)) / 洪峰流量× 100%这个公式是基于洪峰流量、水库出口流量和水库排洪流量之间的相关比例来计算洪水削峰率的，结果为百分比。