(优选)第六章协整检验与模型

格式：ppt
大小：788.50 KB
文档页数：25

下载文档原格式

协整检验方法

观察数据的趋势图 5-7 可以看出，货币供应量 y 和国民收入 x 的发展趋势相同，表明两者之间可能存在着协整关系。
6
图 5-7 1 ．单整性检验
表 5-3 变量 1 2 3 4 5 6 ly ly △ ly lx lx △ lx
货币供应量和国民收入的趋势图
货币供应量和国民收入的单位根检验输出结果（ c ， t ， m ） ADF 检验值（ c，t ， 2 ）（ 0 ，0 ， 3 ）（ c， 0 ，2 ）（ c，t ， 3 ）（ c， 0 ，2 ）（c ，0 ， 3 ） -6.0789 2.3528 -3.1570 -6.4965 -1.4727 -5.6712 1% 临界值 -4.80 -2.75 -4.06 -4.89 -4.00 -4.12 5% 临界值 -3.79 -1.97 -3.12 -3.83 -3.10 -3.14 10% 临界值 -3.34 -1.60 -2.70 -3.36 -2.69 -2.71
3
含有常数项、趋势项和滞后阶数；如（ c ， 0 ， 0 ）表示检验方程中含有常数项、不含趋势项、滞后阶数为 0 ，即利用第二种方程进行 DF 检验。检验过程中的滞后阶数是在 EViews 5 中用 SIC 准则自动确定。 3 ．协整性的 EG 检验（ 1 ）键入命令 LS SH C SZZ ，在输出的方程窗口菜单上点击 Procs\ Make residual series ，然后在弹出的对话框中输入残差的变量名并点击 OK ，系统将自动生成回归模型的残差序列。（ 2 ）打开残差序列窗口，在窗口菜单上点击 View \ Unit Root Test ，选择同时带有常数项、趋势项的检验方程（即方程 5-4 ）进行检验。图 5-3 和图 5-4 分别给出了 EViews 3 、 EViews 5 的 ADF 检验结果；检验结果表明，在 5% 显著水平上可以拒绝残差序列存在单位根的假设（实际上只要取显著水平为 0.0168 即可）；所以，根据 EG 两步法的检验原理，上证综指 SH 和深证综指 SZZ 是协整的，即在所考察时期内，两者存在稳定的比例关系，长期关系可以用协整回归模型描述。

协整检验

伪回归：如果一组非平稳时间序列之间不存在协整关系，则这一组变量构造的回归模型就是伪回归。

残差序列是一个非平稳序列的回归被称为伪回归，这样的一种回归有可能拟合优度、显著性水平等指标都很好，但是由于残差序列是一个非平稳序列，说明了这种回归关系不能够真实的反映因变量和解释变量之间存在的均衡关系，而仅仅是一种数字上的巧合而已。

伪回归的出现说明模型的设定出现了问题，有可能需要增加解释变量或者减少解释变量，抑或是把原方程进行差分，以使残差序列达到平稳。

伪回归是回归方程时间序列数据中涉及的一个概念。

该问题通俗来讲，就是：本来两个变量之间是不存在任何经济关系的，但是因为这两个时间序列数据表现出的变化趋势是一致的，所以，当你对其进行回归时候会得到一个很高的可决系数，让你误以为这一回归关系显著成立。

其实这一回归关系是错的，即伪回归。

要想避免伪回归，应首先对变量进行平稳性检验，接下联进行协整检验。

若变量之间存在协整关系，这一回归才算成立。

负相关negative correlation在回归与相关分析中，因变量值随自变量值的增大(减小)而减小(增大)的现象。

在这种情况下，表示相关程度的相关系数为负值。

相关程度用相关系数r表示，-1≤r<1，r的绝对值越大，表示变量之间的相关程度越高，r为负数时，表示一个变量的增加可能引起另一个变量的减少，此时，叫做负相关。

统计学中常用相关系数r来表示两变量之间的相关关系。

r的值介于-1与1之间,r为正时是正相关，反映当x增加(减少)时,y随之相应增加(减少)；呈正相关的两个变量之间的相关系数一定为正值，这个正值越大说明正相关的程度越高。

当这个正值为1时就是完全正相关的情形，如点子排为一条直线，为完全正相关。

正相关虽然意思明确，其实是个模糊的概念，不可以量化，只是定性说法。

如果有明确的关系，例如y=2x，这叫y与x成正比，如果只是大体上，x、y的变化方向一样，例如x上升，y也上升或者x下降，y也下降，那么，这叫正相关。

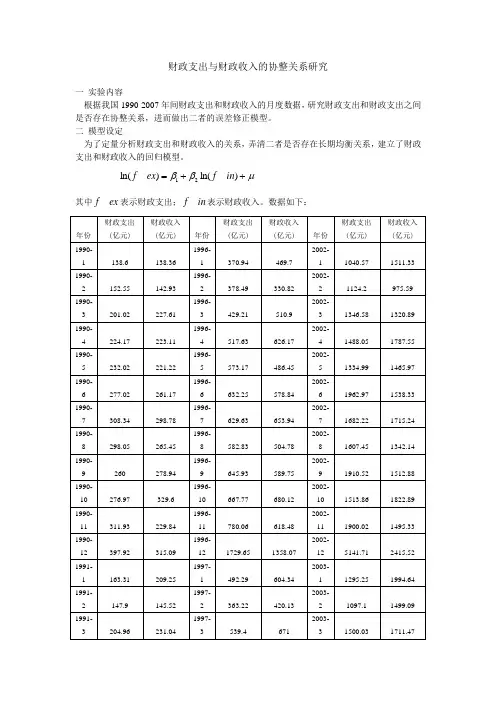
协整检验和误差修正模型

财政支出与财政收入的协整关系研究一实验内容根据我国1990-2007年间财政支出和财政收入的月度数据，研究财政支出和财政支出之间是否存在协整关系，进而做出二者的误差修正模型。

二模型设定为了定量分析财政支出和财政收入的关系，弄清二者是否存在长期均衡关系，建立了财政支出和财政收入的回归模型。

μββ++=)_ln()_ln(21in f ex f其中ex f _表示财政支出；in f _表示财政收入。

数据如下：数据来源：统计年鉴三、实证分析 1、数据处理由数据结构可以看出，数据存在季节波动。

首先利用X-12季节调整方法对这两个指标进行季节调整，消除季节因素，然后去对数。

2、单位根检验经济时间序列数据往往出现非平稳的情况，如果直接对数据建立回归模型，可能会出现伪回归的现象，因此在做回归之前，运用ADF 方法，对数据进行单位根检验。

对ln(ex f _)、ln(in f _)及其一阶差分进行单位根检验，具体检验结果如下所示：ln(ex f _)原值单位根检验Null Hypothesis: LNF_EX has a unit rootExogenous: ConstantLag Length: 5 (Automatic based on SIC, MAXLAG=14)t-StatisticProb.*Augmented Dickey-Fuller test statistic 0.519686 0.9871 Test critical values: 1% level -3.4614785% level -2.87512810% level -2.574090*MacKinnon (1996) one-sided p-values.f_)一阶差分单位根检验ln(exNull Hypothesis: D(LNF_EX) has a unit rootExogenous: ConstantLag Length: 4 (Automatic based on SIC, MAXLAG=14)t-Statistic Prob.* Augmented Dickey-Fuller test statistic -10.83446 0.0000 Test critical values: 1% level -3.4614785% level -2.87512810% level -2.574090*MacKinnon (1996) one-sided p-values.f_)原值单位根检验ln(inNull Hypothesis: LNF_IN has a unit rootExogenous: ConstantLag Length: 11 (Automatic based on SIC, MAXLAG=14)t-Statistic Prob.* Augmented Dickey-Fuller test statistic 0.763850 0.9932 Test critical values: 1% level -3.4624125% level -2.87553810% level -2.574309*MacKinnon (1996) one-sided p-values.f_)一阶差分单位根检验ln(inNull Hypothesis: D(LNF_IN) has a unit rootExogenous: ConstantLag Length: 10 (Automatic based on SIC, MAXLAG=14)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -8.161494 0.0000Test critical values:1% level -3.462412 5% level -2.87553810% level-2.574309*MacKinnon (1996) one-sided p-values.汇总检验结果如下表所示：财政收入和财政支出的对数的原值和一阶差分的单位根检验结果指标 ADF 值P 值ln(ex f _) 0.519686 0.9871 ln(ex f _)的一阶差分-10.83446 0.0000 ln(in f _) 0.763850 0.9932 ln(in f _)的一阶差分 -8.1614940.0000从上表中的ADF 值和P 值可以看出：当显著性水平为0.05时，对ln(ex f _)和ln(in f _)的原值进行检验时，检验结果都表明不能拒绝“存在单位根”的原假设；而当对ln(ex f _)和ln(in f _)的一阶差分进行检验时，检验结果都表明拒绝“存在单位根”的原假设。

时间序列分析中的协整模型构建与检验

时间序列分析中的协整模型构建与检验时间序列分析是一种常用的统计方法，可用于揭示随时间变化的数据的模式和趋势。

而协整模型是时间序列分析中的一种重要工具，它用于分析两个或多个变量之间的长期关系。

本文将探讨协整模型的构建与检验方法，并介绍其在实际应用中的意义。

一、协整模型的构建方法在介绍协整模型的构建方法之前，我们需要先了解一个重要概念——平稳性。

对于一个时间序列，如果其均值、方差和自协方差不随时间变化而变化，我们就称其为平稳时间序列。

在构建协整模型时，我们需要确保所选择的变量都是平稳的。

协整模型的构建步骤如下：1.选择合适的变量：在实际应用中，我们首先需要选择一组有关联的变量，这些变量之间具有一定的相关性。

2.进行单位根检验：单位根检验是确定所选择的变量是否平稳的一种常用方法。

常见的单位根检验方法有ADF检验、PP检验等。

3.若变量不平稳，则进行差分处理：如果单位根检验的结果表明所选择的变量不是平稳的，我们可以对其进行差分处理，即对变量的一阶差分进行分析。

差分后的序列通常会变得平稳。

4.构建协整模型：在变量平稳之后，我们可以使用最小二乘法来估计协整模型的参数。

协整模型通常采用向量自回归模型（VAR）来描述变量之间的长期关系。

二、协整模型的检验方法构建协整模型后，我们需要对其进行检验，以验证模型是否具有统计意义。

常用的协整模型检验方法包括：1.残差序列的平稳性检验：我们首先需要分析协整模型的残差序列。

如果残差序列是平稳的，说明协整模型中的变量可以较好地解释其之间的关系。

2.格兰杰因果检验：格兰杰因果检验用于确定协整关系的方向，即变量之间的因果关系。

在协整模型中，如果变量X的残差序列对变量Y的残差序列具有显著的因果影响，则可以说X是Y的因变量。

3.阶梯回归检验：此方法用于确定模型中的协整向量个数。

在协整模型中，协整向量是变量之间长期关系的表示。

通过阶梯回归检验，我们可以确定协整模型中具有统计意义的协整向量个数。

是我看过的最容易懂的协整检验的归纳课件

NKS
[ 感谢观看 ]
协整检验的基本原理和步骤
01
02
协整检验的基本原理：基于单位根检验和回归分析，通过观察时间序列数据的趋势和周期性变化，判断它们是否存在长期均衡关系。
协整检验的步骤
03
04
05
1. 对每个时间序列进行单位根检验，以判断其是否具有单位根。
2. 如果存在单位根，则对每个时间序列进行差分，以消除单位根。
Engle-Granger两步法
两步法的原理
Engle-Granger两步法是一种协整检验的方法，它首先对数据进行OLS回归，然后对回归残差进行单位根检验，以判断残差是否平稳，从而判断序列是否存在协整关系。
VS
优点与局限性
两步法简单易行，但其局限性在于可能会忽略某些重要的解释变量，导致回归结果失真。
是我看过的最容易懂的协整检验的归纳课件
CONTENTS 目录
• 协整检验的基本概念 • 协整检验的数学模型与算法 • 协整检验的应用场景与实例 • 协整检验的注意事项与展望 • 总结与回顾
CHAPTER 01
协整检验的基本概念
什么是协整检验
协整检验是一种用于研究时间序列数据的统计方法
它用于检验两个或多个时间序列是否存在长期均衡关系
3. 对差分后的时间序列进行回归分析，以判断它们之间是否存在长期均衡关系。
CHAPTER 02
协整检验的数学模型与算法
数据的预处理和单位根检验
数据的平稳性检验
在协整检验之前，需要对数据进行平稳性检验，以确定数据是否满足协整检验的前提条件。
单位根检验
单位根检验是检验时间序列数据是否具有平稳性的常用方法，通过检验数据的差分项是否平稳来判断序列是否平稳。

时间序列的协整检验与误差修正模型讲义

时间序列的协整检验与误差修正模型讲义时间序列的协整检验与误差修正模型是在经济学和金融学中广泛使用的方法，用于分析两个或多个变量之间的长期稳定关系。

本讲义将介绍协整检验的基本概念和步骤，并讨论误差修正模型的理论背景和实际应用。

一、协整检验1. 概念与原理协整是指两个或多个变量之间存在长期稳定的关系，即它们的线性组合是平稳的。

协整关系可以用来解释一个变量对另一个变量的影响，并提供长期均衡关系的信息。

协整检验的基本原理是利用单位根检验方法，测试变量是否存在单位根（非平稳性）。

如果变量存在单位根，则它们是非平稳的；如果变量不存在单位根，则它们是平稳的。

如果变量之间存在协整关系，它们的线性组合将是平稳的。

2. 协整检验的步骤协整检验的一般步骤如下：- 收集数据并绘制时间序列图，观察变量之间的趋势和关系；- 进行单位根检验，常用的方法包括ADF检验、Phillips-Perron检验等；- 如果变量存在单位根，则进行差分，直到变量变为平稳的；- 应用最小二乘法等方法，估计协整关系方程；- 进行残差平稳性检验，确保协整关系的合理性；- 如果协整关系存在，可以进行模型的进一步分析与应用。

二、误差修正模型（Error Correction Model, ECM）1. 概念与原理误差修正模型是一种动态模型，用于解释协整关系的调整速度和误差纠正机制。

在误差修正模型中，除了协整关系的线性组合外，还引入了误差修正项，用于捕捉变量之间的短期非平衡关系。

误差修正项反映了系统离开长期均衡后的调整速度，通过估计误差修正项的系数，可以判断系统是否有趋向于均衡的能力。

当误差修正项的系数为负数且显著时，表示系统具有自我修复的能力；当系数为零时，表示系统处于长期均衡状态；当系数为正数时，表示系统趋向于进一步偏离均衡。

2. ECM模型的应用误差修正模型可以用于解释和预测时间序列数据的长期和短期动态变化。

它在经济学和金融学中有广泛的应用，如货币供给与通货膨胀、利率与消费支出、汇率与经济增长等领域。

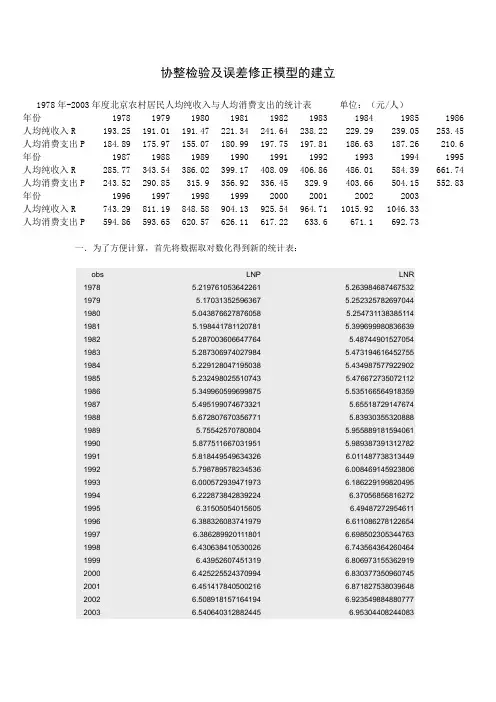
协整检验及误差修正模型的建立

协整检验及误差修正模型的建立1978年-2003年度北京农村居民人均纯收入与人均消费支出的统计表单位：（元/人）年份1978 1979 1980 1981 1982 1983 1984 1985 1986 人均纯收入R 193.25 191.01 191.47 221.34 241.64 238.22 229.29 239.05 253.45 人均消费支出P 184.89 175.97 155.07 180.99 197.75 197.81 186.63 187.26 210.6 年份1987 1988 1989 1990 1991 1992 1993 1994 1995 人均纯收入R 285.77 343.54 386.02 399.17 408.09 406.86 486.01 584.39 661.74 人均消费支出P 243.52 290.85 315.9 356.92 336.45 329.9 403.66 504.15 552.83 年份1996 1997 1998 1999 2000 2001 2002 2003人均纯收入R 743.29 811.19 848.58 904.13 925.54 964.71 1015.92 1046.33人均消费支出P 594.86 593.65 620.57 626.11 617.22 633.6 671.1 692.73 一．为了方便计算，首先将数据取对数化得到新的统计表：obs LNP LNR1978 5.219761053642261 5.2639846874675321979 5.17031352596367 5.2523257826970441980 5.043876627876058 5.2547311383851141981 5.198441781120781 5.3996999808366391982 5.287003606647764 5.487449015270541983 5.287306974027984 5.4731946164527551984 5.229128047195038 5.4349875779229021985 5.232498025510743 5.4766727350721121986 5.349960599699875 5.5351665649183591987 5.495199074673321 5.655187291476741988 5.672807670356771 5.839303553208881989 5.75542570780804 5.9558891815940611990 5.877511667031951 5.9893873913127821991 5.818449549634326 6.0114877383134491992 5.798789578234536 6.0084691459238061993 6.000572939471973 6.1862291998204951994 6.222873842839224 6.370568568162721995 6.31505054015605 6.494872729546111996 6.388326083741979 6.6110862781226541997 6.386289920111801 6.6985023053447631998 6.430638********* 6.7435643642604641999 6.43952607451319 6.8069731553629192000 6.425225524370994 6.8303773509607452001 6.451417840500216 6.8718275380396482002 6.508918157164194 6.9235498848807772003 6.540640312882445 6.95304408244083二．检验时间序列的平稳性5.005.255.505.756.006.256.506.757.0078808284868890929496980002LNPLNR从图中发现，LNP 和LNR 有大致相同的增长和变化趋势，说明二者可能存在协整关系。

时间序列协整检验与误差修正模型讲义

二、协整检验—EG检验
1、两变量的Engle-Granger检验
• 为了检验两变量Yt,Xt是否为协整，Engle和Granger于1987年提出两步检验法，也称为EG检验。
第一步，用OLS方法估计方程 Yt=0+1Xt+t
并计算非均衡误差，得到：
Yˆt ˆ0 ˆ1 X t
eˆt Yt Yˆt 称为协整回归(cointegrating)或静态回归(static regression)。
• 如果X与Y间的长期均衡关系正确，该式表述的非均衡误差应是一平稳时间序列，并且具有零期望值，即是具有0均值的I(0)序列。
• 非稳定的时间序列，它们的线性组合也可能成为平稳的。称变量X与Y是协整的（cointegrated）。
3、协整
• 如果序列{X1t,X2t,…,Xkt}都是d阶单整，存在向量 =(1,2,…,k)，使得Zt=XT ~ I(d-b)，其中，b>0，X=(X1t,X2t,…,Xkt)T，则认为序列 {X1t,X2t,…,Xkt}是(d,b)阶协整，记为Xt~CI(d,b)，为协整向量（cointegrated vector）。
一定是I(0)序列。
由于vt象t一样，也是Z、X、Y、W四个变量的线性组合，由此vt 式也成为该四变量的另一稳定线性组合。
（1, -0,-1,-2,-3）是对应于t 式的协整向量，（1,0-0,-1,1,-1）是对应于vt式的协整向量。
• 检验程序：
–对于多变量的协整检验过程，基本与双变量情形相同，即需检验变量是否具有同阶单整性，以及是否存在稳定的线性组合。
ADF临界值还要小。
– MacKinnon(1991)通过模拟试验给出了协整检验的临界值。

时间序列：协整与ECM模型

USA LOG(GDP) 16.0 LOG(CONS)
LOG(GDP )
LOG(CONS )
7 6 55 60 65 70 75 80 85 90 95 00
14.5 80 82 84 86 88 90 92 94 96 98 00 02
对数的中国 GDP 与宏观消费序列
对数的美国 GDP 与宏观消费序列
file:7chapter7
第7章单方程误差修正模型
14 12 BETA1B Normal BETA1A Normal
7.1.2 EG 两步法的优点 8 ⑴ 每一步只需作单方程估计； 6 ⑵ 全部参数估计量都具有一致性。 4 ⑶ 方法简便，只在第二步才开始引入动态项； 2 ⑷ 在第一步完成的同时也得到了检验协整性的统计量。0
中国对数的进口与出口关系
.3 .2 .1 .0 -.1 -.2 -.3 -.4 -.5 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 00 02 04 06 08
.12
铜的日期货（qcu）和现货（xcu）价格关系
1 1 ut vt
(6.22) (6.23)
(6.24)
(6.25) (6.26)
因为 xt 和 yt 分别与 ut 有线性关系， ut 是随机游走过程（见 (6.22)式），根据 (6.25) 和 (6.26) 式，yt, xt I(1)。因为 vt 是平稳的（见 6.23 式），所以（yt - xt） I(0)，即具有协整关系。(1 - )' 是协整向量。yt = xt 是长期均衡关系。
第6章协整与ECM模型

协整分析与误差修正模型ppt课件

.
⒉协整
如果序列{X1t,X2t,…,Xkt}都是d阶单整，存在向量 =(1,2,…,k)，使得
Zt= XT ~ I(d-b) 其中，b>0，X=(X1t,X2t,…,Xkt)T，则认为序列{X1t,X2t,…,Xkt} 是(d,b)阶协整，记为Xt~CI(d,b)，为协整向量（cointegrated vector）。
.
1、长期均衡
经济理论指出，某些经济变量间确实存在着长期均衡关系，这种均衡关系意味着经济系统不存在破坏均衡的内在机制，如果变量在某时期受到干扰后偏离其长期均衡点，则均衡机制将会在下一期进行调整以使其重新回到均衡状态。
假设X与Y间的长期“均衡关系”由式描述
Yt 01Xtt
式中:t是随机扰动项。
这也解释了尽管这两时间序列是非稳定的，但却可以用经典的回归分析方法建立回归模. 型的原因。
• 从这里，我们已经初步认识到：检验变量之间的协整关系，在建立计量经济学模型中是非常重要的。
而且，从变量之间是否具有协整关系出发选择模型的变量，其数据基础是牢固的，其统计性质是优良的。
.
二、协整检验
因此，一个重要的假设就是:随机扰动项t必须是平稳序列。
显然，如果t有随机性趋势（上升或下降），则会导致Y对其均衡点的任何偏离都会被长期累积下来而不能被消除。
.
式Yt=0+1Xt+t中的随机扰动项也被称为非均衡误差
（disequilibrium error），它是变量X与Y的一个线性组合：
t Yt 01Xt
第二步，检验 e t 的单整性。如 e 果 t 为稳定序列，则认为变量 Y t,X t 为 (1,1)阶协整；如果 e t 为 1阶单整，则认为变量 Y t,X t为 (2,1)阶协整； … 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Johanson协整检验：Var预测.wfl 考察中国GDP,宏观消费cons与基本建设投资inves的协整关系
最大特征值检验
即：至多有r个协整关系
协整方程的形式与单变量时间序列可能出现非零均值、包含确定性趋势
或随机趋势一样，协整方程也可以包含截距和确定性趋势。可能会出现如下情况（Johansen，1995）：
(1) 序列(1式) 没有确定趋势，协整方程没有截距：
Πyt1 HX t αβyt1
(2) 序列没有确定趋势，协整方程有截距项 0：
Γi Φ j j i 1
i1
п称之为压缩矩阵或影响矩阵（impact matrix)
先假定y是向量单位根过程----I(1)
由于I(1)过程经过差分变换将变成I(0)过程，即上式中的
Δyt–j (j=1,2,…,p) 都是I(0)变量构成的向量，那么只要 yt-1 是
I(0)的向量，即 y1,t-1，y2,t-1，…，yk,t-1 之间具有协整关系，就能保证Δyt是平稳过程。可以证明变量y1,t-1，y2,t-1, …，yk,t-1 之
Πyt1 HXt α(βyt1 ρ0 ρ1t) γ0 γ1t
还有一些需要注意的细节： (1) Johansen协整检验的临界值对 k =10 的序列都是有效的。而且临界值依赖于趋势假设，对于包含其他确定性回归量的模型可能是不适合。 (2) 迹统计量和最大特征值统计量的结论可能产生冲突。对这样的情况，建议检验估计得到的协整向量(产生协整向量并检验其平稳性)，并将选择建立在协整关系的解释能力上。
Πyt1 HX t α( βyt1 ρ0 )
(3) 序列有确定性线性趋势，但协整方程只有截距：
Πyt1 HXt α(βyt1 ρ0 ) γ0
(4) 序列和协整方程都有线性趋势，协整方程的线性趋势
表示为 1t ：
Πyt1 HXt α(βyt1 ρ0 ρ1t) γ0
(5) 序列有二次趋势，协整方程仅有线性趋势：
y2,t-1，…，yk,t-1 之间协整向量的个数与形式。称为协整向量矩阵，r 为协整向量的个数。
这r个协整关系将同时出现在每个变量的误差修正表达式中
矩阵的每一行 i 是出现在第 i 个方程中的 r 个协整组
合的一组权重，故称为调整参数矩阵，与前面介绍的误差修
正模型的调整系数的含义一样。而且容易发现和并不是惟一的，因为对于任何非奇异 r r 矩阵 H ，乘积和 H (H 1 ) 都等于。
协整检验在EViews软件中的实现
为了实现协整检验，从VAR对象或Group(组)对象的工具栏中选择View/Cointegration Test… 即可。协整检验仅对已知非平稳的序列有效，所以需要首先对VAR模型中每一个序列进行单位根检验。然后在Cointegration Test Specification的对话框（下图）中将提供关于检假设
可选部分关于协整方程假设
不能确定如何选择，则
选择此项
滞后设定是指在辅助回归中的一阶差分的滞后项，不是指原序列。例如，如果在编辑栏中键入“1 2”，协整检验用 yt 对 yt-1，yt2 和其他指定的外生变量作回归，此时与原序列 yt 有关的最大的滞后阶数是3。对于一个滞后阶数为1 的协整检验，在编辑框中应键入 “0 0”。
下面介绍JJ检验的基本思想。任意一个VAR(p)模型
yt Φ1yt1 Φpyt p εt
t 是 k 维扰动向量。首先给出上式的一种等价形式(hamilton,667)
Φ j j = 1,K p 为k×k维矩阵
p 1
yt Πyt 1 Γi yt i εt (1)
i 1
p
p
其中 Π Φi I
将 yt 的协整检验变成对矩阵的分析问题，这就是 Johansen协整检验的基本原理。因为矩阵的秩等于它的
非零特征根的个数，因此可以通过对非零特征根个数的检验
来检验协整关系和协整向量的秩。略去关于的特征根的求解方法，设矩阵的特征根为 1 2 … k。
Johansen协整检验的两种形式特征根迹检验(trace检验)
的 yt 为 I(1) 过程相矛盾，所以必然有 r < k。
② 如果 r = 0，意味着 = 0，y1,t-1，y2,t-1，…，yk,t-1之间
是不具有协整关系。 ③ 下面讨论 0< r < k 的情形：
0< r < k 表示存在 r 个协整关系。在这种情况下，可以分解成两个列满秩的( k r )阶矩阵和的乘积：
Π αβ
其中rk ( )= r，rk ( )= r。
如果变量间存在协整关系，则无法通过差分形式的有限阶VAR模型进行表示(hamilton 699)
将式п的表达式带入模型(1),即
p1
yt αβyt1 Γiyti εt
向量误差修正模型的表达式VECM
i 1
上式要求 yt-1 的每一行为一个 I(0) 向量，其每一行都是 I(0) 组合变量(yt-1元素的线性组合)，矩阵决定了y1,t-1，
（优选）第六章协整检验与模型
Johansen协整检验
第4章最后一部分的协整检验和误差修正模型主要是针对单方程而言，本节将推广到VAR模型。而且前面所介绍的协整检验是基于回归的残差序列进行检验，本节介绍的Johansen协整检验基于回归系数的协整检验，有时也称为JJ(Johansen-Juselius)检验。 Johansen在1988年及在1990年与Juselius一起提出的一种以VAR模型为基础的检验回归系数的方法，是一种进行多变量协整检验的较好的方法。
间是否具有以及具有什么规模的协整关系主要依赖于矩阵，
且变量间线性无关的协整向量个数即为矩阵的秩(证明略)。设
的秩为 r，则存在 3 种情况: r = k，r = 0，0< r < k：
① 如果 r = k，显然只有当 y1,t-1，y2,t-1，…，yk,t-1 都是 I(0)
变量时，才能保证 yt-1 是 I(0) 变量构成的向量。而这与已知