下载文档原格式
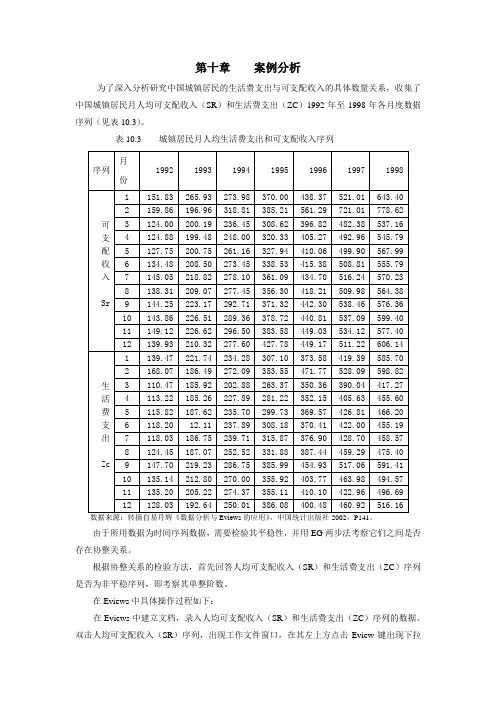
第十章案例分析为了深入分析研究中国城镇居民的生活费支出与可支配收入的具体数量关系，收集了中国城镇居民月人均可支配收入（SR）和生活费支出（ZC）1992年至1998年各月度数据序列（见表10.3）。
表10.3 城镇居民月人均生活费支出和可支配收入序列序列月份1992 1993 1994 1995 1996 1997 1998可支配收入Sr 1 151.83 265.93 273.98 370.00 438.37 521.01 643.402 159.86 196.96 318.81 385.21 561.29 721.01 778.623 124.00 200.19 236.45 308.62 396.82 482.38 537.164 124.88 199.48 248.00 320.33 405.27 492.96 545.795 127.75 200.75 261.16 327.94 410.06 499.90 567.996 134.48 208.50 273.45 338.53 415.38 508.81 555.797 145.05 218.82 278.10 361.09 434.70 516.24 570.238 138.31 209.07 277.45 356.30 418.21 509.98 564.389 144.25 223.17 292.71 371.32 442.30 538.46 576.3610 143.86 226.51 289.36 378.72 440.81 537.09 599.4011 149.12 226.62 296.50 383.58 449.03 534.12 577.4012 139.93 210.32 277.60 427.78 449.17 511.22 606.14生活费支出Zc 1 139.47 221.74 234.28 307.10 373.58 419.39 585.702 168.07 186.49 272.09 353.55 471.77 528.09 598.823 110.47 185.92 202.88 263.37 350.36 390.04 417.274 113.22 185.26 227.89 281.22 352.15 405.63 455.605 115.82 187.62 235.70 299.73 369.57 426.81 466.206 118.20 12.11 237.89 308.18 370.41 422.00 455.197 118.03 186.75 239.71 315.87 376.90 428.70 458.578 124.45 187.07 252.52 331.88 387.44 459.29 475.409 147.70 219.23 286.75 385.99 454.93 517.06 591.4110 135.14 212.80 270.00 355.92 403.77 463.98 494.5711 135.20 205.22 274.37 355.11 410.10 422.96 496.6912 128.03 192.64 250.01 386.08 400.48 460.92 516.16数据来源：转摘自易丹辉《数据分析与Eviews的应用》，中国统计出版社2002，P141。
协整与误差修正模型的研究第一部分协整理论概述 (2)第二部分误差修正模型介绍 (4)第三部分协整与误差修正关系 (7)第四部分模型构建与检验方法 (9)第五部分实证分析应用案例 (13)第六部分结果解释与经济含义 (16)第七部分模型局限性与改进方向 (18)第八部分研究展望与未来趋势 (22)第一部分协整理论概述协整理论概述在经济学和金融学中，我们常常遇到时间序列数据之间的长期均衡关系。
然而，在实际经济活动中，这种均衡关系并不总是能够得到严格的保持，而是存在着一定程度的波动和偏差。
为了解决这一问题，经济学家们提出了协整理论。
协整理论是指两个或多个非平稳的时间序列之间存在一种长期稳定的关系。
换言之，即使各时间序列本身是随机游走的过程，它们之间也可能存在一个稳定的线性组合，使得这个组合呈现出平稳性质。
协整理论的发展为研究经济变量之间的长期动态关系提供了一个强有力的工具。
协整理论的核心思想是由 Engle 和Granger 于1987 年提出的。
他们认为，如果两个非平稳的时间序列之间存在协整关系，则这两个时间序列可以通过一个线性组合达到长期均衡状态，且这个线性组合具有零均值、有限方差和恒定自相关等特性。
在这个意义上，我们可以将协整关系看作是一种长期均衡关系的表现形式。
为了检验两个时间序列之间是否存在协整关系，Engle 和 Granger 提出了一种两步法：首先检验每个时间序列是否为非平稳过程；然后，如果这两个时间序列都是非平稳过程，再通过回归分析来检验它们之间是否存在协整关系。
这种方法被称为 Engle-Granger 两步协整检验。
除了 Engle-Granger 两步协整检验之外，还有许多其他的方法可以用来检验协整关系，例如 Johansen 检验和 Pedroni 检验等。
这些方法都可以有效地帮助我们确定不同时间序列之间的协整关系。
协整理论不仅用于检验不同时间序列之间的长期均衡关系，还可以用于构建误差修正模型。
实验报告（二）——误差修正模型(ECM)的建立与分析一、单位根检验：1、绘制cons与GDP的时间序列图：从时间序列图中可以看出，cons与GDP随时间增加都呈上升趋势，表现出非平稳性。
2、对cons进行单位根检验：先选择对原序列（level）进行单位根检验，根据cons与GDP的时间序列图的走势，选择trend and intercept的检验方法，在maximum lags中填写ADF 检验方法的滞后期为0，从上表中可以看出，P值为0.9888，大于0.05的显著性水平，说明原序列是非平稳的。
选择cons的一阶差分（1st）和trend and intercept,从上表中可以看出，经过一阶差分后，P值（=0.5099）仍然没有通过0.05的置信水平检验，说明是不平稳的，需要继续改进。
再试用ADF检验，在滞后期（maximum lags）中填入8，选择一阶差分和trend and intercept，得出上表，可以看出P值=0.0801，大于0.05，没有通过0.05的置信水平检验，说明是不平稳的，需要继续改进。
再试用ADF检验，在滞后期（maximum lags）中填入6，选择二阶差分和trend and intercept，得出上表，可以看出P值=0.0137，小于0.05，通过0.05的置信水平检验，说明是平稳的。
3、对GDP进行单位根检验：先选择对原序列（level）进行单位根检验，根据cons与GDP的时间序列图的走势，选择trend and intercept的检验方法，在maximum lags中填写ADF 检验方法的滞后期为0，从上表中可以看出，P值为1.0000，大于0.05的显著性水平，说明原序列是非平稳的。
选择GDP的一阶差分（1st）和trend and intercept,从上表中可以看出，经过一阶差分后，P值（=0.5574）仍然没有通过0.05的置信水平检验，说明是不平稳的，需要继续改进。
协整分析与误差修正模型1.协整分析协整分析用于找到两个或多个非平稳时间序列之间的长期关系。
当两个变量之间存在协整关系时，它们的线性组合将是平稳的。
协整关系可以解释为变量之间长期的平衡关系，即存在一种平衡机制使得变量保持在一个相对稳定的范围内。
协整分析的步骤如下：1）对非平稳时间序列进行单位根检验，例如ADF检验。
2）如果两个或多个时间序列都是非平稳的，那么可以进行线性组合，得到一个平稳的时间序列，通过单位根检验确定这个线性组合是否是平稳的。
3）如果线性组合是平稳的，那么就可以认为存在协整关系。
协整分析的优点是可以探索多个非平稳时间序列之间的关系，并且提供了具体的数值关系，能够描述长期平衡关系。
但是，协整分析不能提供因果关系，只能提供关联关系。
2.误差修正模型(ECM)误差修正模型是一种用于描述非平稳变量之间长期关系的模型。
它是在协整分析的基础上发展而来的。
误差修正模型的基本思想是，如果两个变量之间存在协整关系，那么它们之间的误差会随着时间的推移逐渐修正，回归到长期平衡关系。
因此，误差修正模型可以用来分析变量之间的动态行为。
基本的误差修正模型可以表示为：△Y_t=α+βX_t-1+γE_t-1+ε_t其中，△表示时间差分，Y_t和X_t分别表示被解释变量和解释变量，E_t表示长期误差修正项，ε_t表示短期误差项。
α、β和γ分别表示模型的截距和参数。
误差修正模型的步骤如下：1）进行协整分析，确定变量之间的协整关系。
2）构建误差修正模型，通过估计模型参数来描述长期关系。
3）进行模型检验，包括参数显著性检验、拟合优度检验等。
4）根据模型结果进行解释和预测。
误差修正模型的优点是能够同时分析长期和短期关系，提供了关于变量之间回归到长期平衡的速度信息。
同时，误差修正模型还可以用于预测和政策分析等方面。
但是，误差修正模型的局限性在于假设模型中的所有变量都是线性关系，不能很好地处理非线性关系。
综上所述，协整分析和误差修正模型是非平稳时间序列分析中常用的方法，它们能够揭示非平稳变量之间的长期关系，并对其动态行为进行建模和分析。
关于协整与误差修正模型的建立摘要：由于我国的特殊国情，导致所需数据序列并非平稳，经济变量本身是非稳定的时间序列，如果用传统的单方程计量经济模型并不能全面的反映经济变量间的关系。
本文对协整的概念、单位根检验、及误差修正模型的建立进行分析总结，建立在协整基础上的误差修正模型既能反映序列的长期均衡关系，又能反映其偏离均衡的短期调整机制。
关键词：协整误差修正模型单位根About cooperates entire and the error correction model establishmentAi Yunhui Guo WenjuanAbstract:As a result of our country s special national condition,causes to need the data sequence to be by no means steady,economical variable itself right and wrong stable time series,if measures the economic with the traditional single equation not to be able the comprehensive reflection during economical variable relations.This article to cooperates the entire concept,the unit root examination,and the error correction model establishment carries on the analysis to summarize,establishes in cooperates in the entire foundation the error correction model both to be able to reflect the sequence the long term balanced relations,and can reflect its deviation balanced short term adjustment mechanism.Keywords:Cooperates the entire Error correction model Unit root【中图分类号】F014【文献标识码】C【文章编号】1009-9646(2009)1-0007-03非稳定序列转化为稳定序列数据变量的平稳性是传统的计量经济分析的基本要求之一。
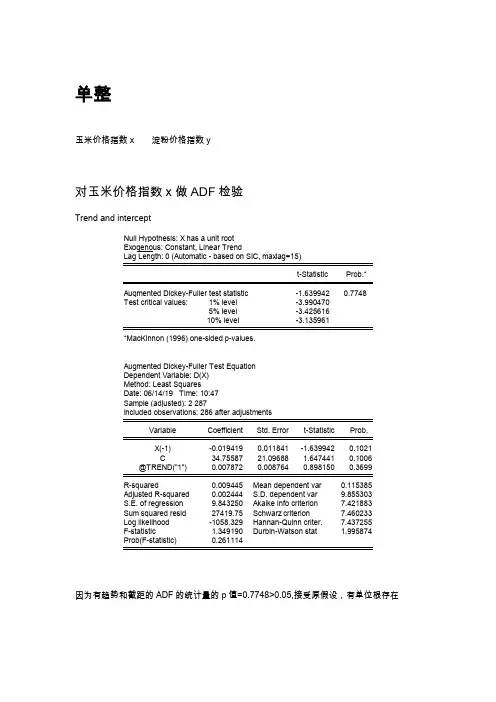
单整玉米价格指数x 淀粉价格指数y对玉米价格指数x做ADF检验Trend and intercept因为有趋势和截距的ADF的统计量的p值=0.7748>0.05,接受原假设，有单位根存在InterceptNone有截距和无截距，也无趋势的ADF统计量值的p值都大于0.05，接受原假设，存在单位根，原有时间序列非平稳。
一阶差分Trend and intercept一阶差分既有趋势又有截距的ADF统计量的p值<0.05，拒绝原假设，一阶差分是平稳的，即玉米价格指数x是一阶单整。
对淀粉价格指数y做ADF检验Trend and intercept因为有趋势和截距的ADF的统计量的p值=0.7817>0.05,接受原假设，有单位根存在interceptNone有截距和无截距，也无趋势的ADF统计量值的p值都大于0.05，接受原假设，存在单位根。
原有时间序列非平稳。
一阶差分Trend and intercept一阶差分既有趋势又有截距的ADF统计量的p值<0.05，拒绝原假设，一阶差分是平稳的，即淀粉价格指数y是一阶单整。
由于，玉米价格指数x，淀粉价格指数y都是一阶单整，所以可能存在协整关系协整检验首先将玉米价格指数x对淀粉价格指数y做回归从图中可知，玉米价格指数x对淀粉价格指数有显著的解释意义，两者之间是正相关关系。
玉米价格指数每增加一个单位，导致淀粉价格指数增加1.438个单位。
AEG检验对得到的残差进行单位根检验Trend and intercept残差的有趋势和截距的ADF的统计量为-2.568>-2.87,有单位根存在，非平稳。
intercept截距的ADF的统计量的p值为0.1362>0.05,接受原假设，有单位根存在，非平稳。
.None’无截距，无趋势的ADF的统计量的p值为0.015<0.05,拒绝原假设，序列平稳。
说明残差序列是I（0），平稳的。
时间序列的协整检验与误差修正模型讲义时间序列的协整检验与误差修正模型是在经济学和金融学中广泛使用的方法，用于分析两个或多个变量之间的长期稳定关系。
本讲义将介绍协整检验的基本概念和步骤，并讨论误差修正模型的理论背景和实际应用。
一、协整检验1. 概念与原理协整是指两个或多个变量之间存在长期稳定的关系，即它们的线性组合是平稳的。
协整关系可以用来解释一个变量对另一个变量的影响，并提供长期均衡关系的信息。
协整检验的基本原理是利用单位根检验方法，测试变量是否存在单位根（非平稳性）。
如果变量存在单位根，则它们是非平稳的；如果变量不存在单位根，则它们是平稳的。
如果变量之间存在协整关系，它们的线性组合将是平稳的。
2. 协整检验的步骤协整检验的一般步骤如下：- 收集数据并绘制时间序列图，观察变量之间的趋势和关系；- 进行单位根检验，常用的方法包括ADF检验、Phillips-Perron检验等；- 如果变量存在单位根，则进行差分，直到变量变为平稳的；- 应用最小二乘法等方法，估计协整关系方程；- 进行残差平稳性检验，确保协整关系的合理性；- 如果协整关系存在，可以进行模型的进一步分析与应用。
二、误差修正模型（Error Correction Model, ECM）1. 概念与原理误差修正模型是一种动态模型，用于解释协整关系的调整速度和误差纠正机制。
在误差修正模型中，除了协整关系的线性组合外，还引入了误差修正项，用于捕捉变量之间的短期非平衡关系。
误差修正项反映了系统离开长期均衡后的调整速度，通过估计误差修正项的系数，可以判断系统是否有趋向于均衡的能力。
当误差修正项的系数为负数且显著时，表示系统具有自我修复的能力；当系数为零时，表示系统处于长期均衡状态；当系数为正数时，表示系统趋向于进一步偏离均衡。
2. ECM模型的应用误差修正模型可以用于解释和预测时间序列数据的长期和短期动态变化。
它在经济学和金融学中有广泛的应用，如货币供给与通货膨胀、利率与消费支出、汇率与经济增长等领域。
