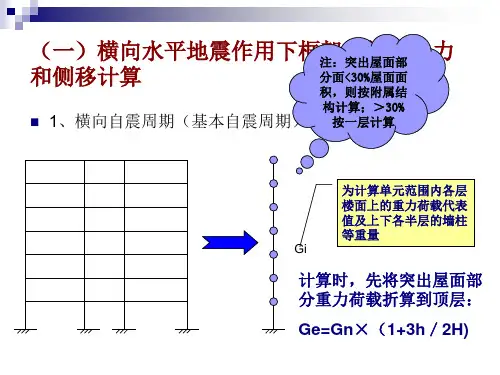
3 水平荷载作用下结构的内力分析为了求得框架-剪力墙结构（计算简图如图3-1所示）在水平力作用下的内力，在近似法中采用了连续化方法，即将各层总连梁离散为沿楼层高度均匀分布的连续连杆。
将连杆切开，则总剪力墙成为静定结构（竖向悬臂墙），如图3-2所示，它受连续连杆的未知约束力F p 和分布外荷载P(x)的作用。
其中F p 可有总框架的抗推刚度f C 与结构变形曲线的二阶导数表示，即22F f d y P C d x=；b C 为总连梁的约束刚度。
b C 与f C 的具体计算见刚度参数的计算。
根据梁的弯曲理论，竖向悬臂墙的荷载与挠度的微分关系可有：（3-1）式中，w EJ 为总剪力墙的抗弯刚度。
当外力可表示为简单的函数形式时，则可方便地通过求解微分方程得到总剪力墙和总框架的变形方程，进而由变形和内力的微分关系可以求出总剪力墙、总框架、总连梁的内力。
连续化方法是一种十分巧妙的做法，无论实际的框架剪力墙是多少层，结构的变形方程形式都不变，因而便于手算。
为了获得简便的变形方程，需要将水平荷载等效地转换成三种典型的形式（倒三角形荷载、均布荷载、顶点集中荷载），风荷载，水平地震作用的具体转换见前面一章。
3.1总剪力墙、总框架、总连梁的内力计算由式（3-1）可推导出总剪力墙分别在三种典型水平荷载作用下的计算公式如下： 倒三角形分布荷载作用下2322111[(1)()()]226f qH sh sh ch Sh y C ch λλλλξλξλξλλλλλ-=+-+--- （3-2a ）221[(1)()]22w qH sh sh ch M sh ch λλλλξλλξξλλλλ=+---- (3-2b) 221[(1)()1]22w qH sh sh sh V ch ch λλλλλξλλλξλλλλ=+---- (6-2b) 均布荷载作用下2221[()(1)(1)]2f qH sh y ch sh C ch λλξλξλλξλξλλ+=-+- （3-3a ）4242()w F b d y d y EJ P x p C d x d x=-+221[()1]w qH sh M ch sh ch λλλξλλξλλ+=-- (3-3b)221[()]w qH sh V ch sh ch λλλλξλξλλ+=- (3-3c) 顶点集中荷载作用下33321[()(1)]w PH sh y ch sh EJ ch λξλξλξλλλλ=--+ (3-4a)1()w sh M PH ch sh ch λλξλξλλλ=- (3-4b) ()w sh V P ch sh ch λλξλξλ=- (3-4c) 式中 y------总剪力墙、总框架的侧移；w M -------总剪力墙的总弯矩； w V --------总剪力墙的总剪力；ξ-------相对坐标，坐标原点在固定端，x Hξ=3.1.1 铰接计算体系的内力计算在铰接计算体系中，各典型水平荷载单独作用下总剪力墙的w M 、w V 可直接由式（3-2）~（3-4）算出。
总框架的总剪力按下式计算：()()()f P W V V V ξξξ=- (3-5)式中 ()f V ξ------总框架的总剪力；()P V ξ-----结构在ξ处由外荷载引起的总剪力，与荷载形式有关。
倒三角形荷载 20()(1)2p q HV ξξ=- (3-5a) 均布荷载 ()(1)p V qH ξξ=- (3-5b) 顶点集中荷载 ()p V F ξ= (3-5c) 式中 0q 、q--------分别为倒三角形荷载的最大荷载集度和均布荷载集度； F-------顶点集中荷载。
当外荷载由几种典型水平荷载组合时，则其总内力为各单一典型水平荷载作用下内力的叠加。
应用式（3-2）~（3-5）计算w M 、w V 、f V 时，建议采用EXECEL 直接由各自的表达式列成如表3-1的形式计算。
比查计算图表精确、方便、条理清楚。
总剪力墙及总框架的内力计算表 表3-13.1.2总框架内力的调整在水平地震作用下，框架-剪力墙结构所求出的总框架各层总剪力fV ，需要按照以下的方法进行调整：如果计算出的总框架的总层剪力00.2f V V ≥,则f V 可按计算值采用；如果00.2f V V <，设计时，f V 取max 1.5f V 和0.2o V 中较小值计算框架梁、柱的弯矩和剪力，但柱的轴力仍按未调整的f V 计算。
其中，o V 为结构底部总地震剪力；max f V 为主体结构各层框架总剪力中的最大值。
对于风荷载引起的总框架的总剪力f V 不需要调整。
3.2各片墙、各榀框架、各根连梁的内力计算3.2.1 各根连梁内力计算在铰接体系中b C =0，总连杆的弯矩和剪力均为零。
连梁与框架柱相连端的弯矩可按一下方法计算：先由D 值法求出与连梁相连柱的柱端弯矩；将连梁看成一端固定（与剪力墙相连端），一端刚接（与柱相连端），考虑连梁与柱相连端的转动刚度，由节点平衡求出梁端弯矩。
3.2.2 各片剪力墙内力计算在进行剪力墙设计时，一般取楼板标高处的弯矩M 、剪力V 作为设计内力。
因此，根据3.1节求出的总剪力墙在各楼层处的内力()w M ξ、()w V ξ后，无论是铰接体系还是刚接体系均应按照各片剪力墙的等效抗弯刚度进行再分配，其计算公式如下：1.eqiWij Wij k eqii EI M M EI ==∑1.eqiWij Wij keqii EI V V EI ==∑(3-17)式中 Wij M ------第i 片剪力墙j 楼层处的弯矩；Wij V -------第i 片剪力墙j 楼层处的弯矩。
由(3-17)求出、Wij M WijV 之后，还需要根据各片剪力墙的具体情况，按照下面方法计算剪力墙墙肢的内力： 3.2.2.1 整截面剪力墙若没有连梁与该片剪力墙相连，则由式（3-17）计算出的WijM 、WijV 就是第i 片剪力墙j 楼层处的弯矩和剪力。
若该片剪力墙与连梁直接相连，则需要考虑连梁对剪力墙弯矩的影响。
设第j 层第i 根连梁的1端与剪力墙相连，则对第i 片剪力墙在第j 层楼盖上、下方的剪力墙截面弯矩u WijM及l WijM 可近似按下式计算：,12/2u Wij Wij i M M M =+ （3-18a ） ,12/2l Wij Wij i M M M =- （3-18b ）式中，,12i M 为第j 层第i 根连梁1端（与剪力墙相连端）在剪力墙轴线处的集中约束弯矩，按式（3-13）计算。
3.2.2.2 小开口整体剪力墙若没有连梁与该片剪力墙相连，则由式（3-17）计算出的WijM 、WijV 就是第i 片剪力墙j楼层处的弯矩和剪力，则小开口墙第K 个墙肢的弯矩kWij M 、剪力kWij V 和轴力k WijN的标准值，可近似由下式计算。
0.850.15k kkWij WijWij KI I M M M II =+∑ （3-19） 0.85k k kWij WijA y N M I= （3-20）k kWij WijKA V V A =∑ （3-21） 式中 k W i j M 、k Wij V 、kWij N ----------整体小开口墙中第k 个墙肢第j 层标高处的弯矩、剪力、轴力；k A 、k I 、k y ------第k 个墙肢的截面面积、惯性矩、截面形心到组合截面形心的距离；I-------组合截面惯性矩。
若有连梁与该片剪力墙相连，则由式（3-17）计算出的WijM 、WijV 后，应仿照（3-18）那样，对弯矩进行修正。
小开口整体剪力墙中第k 个墙肢的弯矩kWij M、剪力k WijV和轴力k Wij N 的标准值，仍按（3-19）~（3-21）计算，不同的只是分别用u Wij M 、l Wij M 代替Wij M ，得出第k 个墙肢j 楼层上、下截面的内力，作为内力标准值。
3.2.2.2 联肢（双肢、多肢）剪力墙对于联肢剪力墙，由式（3-17）计算出该片剪力墙的弯矩和剪力后，还需要进一步求出每个墙肢和连梁的内力，但是这些内力不能直接由WijM 、WijV 分配得到，而应根据联肢墙所受的力，通过联肢墙的分析求解得到。
对此，可采用如下近似处理方法：先由式（3-17）计算出墙顶和墙底的弯矩nWijM、0WijM及剪力n WijV、0WijV,再根据墙顶和墙底的弯矩和剪力等效的原则，求得其“相当荷载”，据此求出联肢墙的每个墙肢和连梁的内力。
根据框架-剪力墙结构中，单片剪力墙的受力特点，“相当荷载”可由倒三角形荷载（g ）、 均布荷载（q ）和顶点集中荷载（F ）组成，并且它们产生的联肢墙顶端剪力、底部剪力和弯矩与总剪力墙分配到该联肢墙相应截面的剪力、弯矩应相等，据此有：墙顶剪力 nWijF V= （3-22）墙底剪力 0/2WijgH gH F V++= （3-23）墙底弯矩 220/3/2WijgH gH FH M ++= （3-24）墙顶弯矩的条件自然满足。
式(3-22)~(3-24)中的n WijV、0Wij V、0Wij M已知，求解联立方程即可求出g 、q 和F 的值。
最后按联肢墙内力计算方法计算荷载g 、q 和F 分别作用下各墙肢的内力，再叠加起来就得到该墙肢拟求的内力，即联肢墙各墙肢的弯矩、剪力、轴力以及连梁的弯矩、剪力。
具体计算可参阅高层建筑结构设计教材相关内容。
3.2.2 各榀框架内力计算框架-剪力墙结构中的总框架包括普通框架和壁式框架，框架梁、柱的内力计算方法仍然采用D 值法。
将3.1节中经过调整后的总框架在各楼层处的总剪力()f V ξ，按各柱的D 值进行分配，便可得到各柱在各楼层处的剪力，但计算太烦琐，在近似法中叶无必要，通常是近似取该柱上下端两层楼板标高处剪力的平均值，作为该柱该层的剪力Cij V 。
第i 根柱（共有m 根）第j 层的剪力为：11().2fj fj iCij mii V V D V D-=+=∑ （3-25）然后，确定出普通框架柱和壁式框架柱的反弯点高度（具体可参阅高层建筑结构设计教材有关内容），便可以计算出柱端弯矩。
再根据节点平衡条件可求出梁端弯矩，进而可以计算框架梁的剪力和柱的轴力，左后作出内力图。
4向荷载作用下结构的内力分析作用在结构上的坚向荷载主要是恒荷载(结构白重)和楼面活荷载(使用荷载)，其值按5.1节所述方法确定。
计算框架—剪力墙结构在竖向荷载作用下的内力时，可忽略各抗侧力构件之间的联系，根据楼盖结构的平面布置，将竖向荷载传递给每相框架及每片墙。
各片墙、各榀框架再技各自的负荷面积确定荷载，进行内力计算。
高层民用建筑楼面活荷载一般不大(1.5~2.02/KN m )，仅占全部坚向荷载的10％~15％。
