山东省德州市2019年中考数学一轮复习第六章圆第21讲与圆有关的计算过预测练习

要题加练4 与圆有关的角度计算姓名：________ 班级：________ 用时：______分钟1．(2018·眉山中考改编)如图，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C，连接BC，若∠P＝36°，求∠B的度数．2．(2018·台湾中考改编)如图，I点为△ABC的内心，D点在BC上，且ID⊥BC，若∠B＝44°，∠C＝56°，求∠AID的度数．3．(2018·陇南中考改编)如图，⊙A过点O(0，0)，C(3，0)，D(0，1)，点B是x轴下方⊙A上的一点，连接BO，BD，求∠OBD的度数．4．(2018·陕西中考改编)如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°，作CD∥AB，并与⊙O相交于点D，连接BD，求∠DBC的度数．5.如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E在⊙O上．(1)若∠AOD＝52°，求∠DEB的度数；(2)若OC＝3，OA＝5，求AB的长．6．(2018·沈阳中考)如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C.(1)若∠ADE＝25°，求∠C的度数；(2)若AB＝AC，CE＝2，求⊙O半径的长．参考答案1．解：∵PA切⊙O于点A，∴∠OAP＝90°.∵∠P＝36°，∴∠AOP＝54°，∴∠B＝27°.2．解：如图，连接CI.在△ABC 中，∵∠B＝44°，∠ACB＝56°， ∴∠BAC＝180°－∠B－∠ACB＝80°. ∵I 点为△ABC 的内心，∴∠CAI＝12∠BAC＝40°，∠ACI＝∠DCI＝12∠ACB＝28°，∴∠AIC＝180°－∠CAI－∠ACI＝112°. 又∵ID⊥BC，∴∠CID＝90°－∠DCI＝62°，∴∠AID＝∠AIC＋∠CID＝112°＋62°＝174°.3.解：如图，连接DC. ∵C(3，0)，D(0，1)，∴∠DOC＝90°，OD ＝1，OC ＝3，∴∠DCO＝30°，∴∠OBD＝30°.4．解：∵AB＝AC ，∠BCA＝65°，∴∠CBA＝∠BCA＝65°，∠A＝50°.∵CD∥AB，∴∠ACD＝∠A＝50°.又∵∠ABD＝∠ACD＝50°，∴∠DBC＝∠CBA－∠ABD＝15°.5．解：(1)∵AB 是⊙O 的一条弦，OD⊥AB， ∴AD ︵＝BD ︵，∴∠DEB＝12∠AOD＝12×52°＝26°.(2)根据勾股定理得AC ＝OA 2－OC 2＝52－32＝4. ∵AB 是⊙O 的一条弦，OD⊥AB，∴AB＝2AC ＝2×4＝8.6．解：(1)如图，连接OA.∵AC 是⊙O 的切线，OA 是⊙O 的半径， ∴OA⊥AC，∴∠OAC＝90°.∵AE ︵＝AE ︵，∠ADE＝25°，∴∠AOE ＝2∠ADE＝50°，∴∠C＝90°－∠AOE＝90°－50°＝40°.(2)∵AB＝AC ，∴∠B＝∠C.∵AE ︵＝AE ︵，∴∠AOC＝2∠B，∴∠AOC＝2∠C. ∵∠OAC＝90°，∴∠AOC＋∠C＝90°， ∴3∠C＝90°，∴∠C＝30°，∴OA＝12OC.设⊙O 的半径为r.∵CE＝2，∴r＝12(r ＋2)，解得r ＝2，∴⊙O 的半径为2.。

一是把不规则图形，通过割补转化为规则图形，二是通过规则图形的面积的和差 来求解．
6．[2018·山西]如图，正方形ABCD内接于 ⊙O，⊙O的半径为2，以点A为圆心，以AC长 为半径画弧交AB的延长线于点E，交AD的延长 线于点F，则图中阴影部分的面积是( A )
类型
圆锥的侧面积
7．[2018·聊城]用一块圆心角为216°的扇形铁皮，做一个高 为40cm的圆锥形工件(接缝忽略不计)，那么这个扇形铁皮的半 径是 50 cm. 8．[2018·宿迁]已知圆锥的底面半径为3cm，高为4cm，则圆锥 的侧面积是 15π cm2.
正多边形每一边所对的④ 圆心角 都相等，这个 ⑤圆心角 叫做正多边形的中心角
2.正n边形的有关计算 正n边形的边长为a，半径为R，边心距为r，中心角为α，外角为β. (1)正n边形的边数n与其外角β的关系：n＝⑥ . (2)R和边组成n个全等的⑦ 三角形，R，r和边的一半组成2n个 全等的⑧ 三角形． 等腰 (3)可以通过勾股定理或三角函数表示R，r，a，α之间的数量关系． 直角
类型
正多边形有关的计算
1．[2018·宜宾]刘徽是中国古代卓越的数学家之一，他在《九章算 术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来
近似计算圆的面积，设圆O的半径为1，若用圆O的外切正六边形的
面积来近似估计圆O的面积，则S＝ ．(结果保留根号)
解题要领：①正多边形外接圆半径、内切圆半径与半弦组成的直角三角形，是计算正
考点弧长与扇形6来自5考1．弧长公式：在半径为R的圆中，因为360°的圆心角所对的弧长就 等于圆周长C＝2πR，所以n°圆心角所对的弧长l＝① ＝ .
2．扇形面积公式：在半径为R的圆中，因为360°的圆心角所对的扇 形的面积等于圆面积S＝πR2，所以n°圆心角所对的扇形面积S＝ ② ＝ .

∴sin∠COB＝
∴∠COB＝60°， ∴∠B＝30°， ∴OC＝ 1 OB＝2，
2
∴S扇形OCE＝ S△OCB＝ ∴S阴影＝S△OCB－S扇形OCE＝
类型三 圆与类似的综合 圆与类似的综合主要体现在圆与类似三角形的综合，
一般结合切线的判定与性质综合考查，求线段长或半径． 一般的解题思路是利用切线的性质构造角相等，进而构造 类似三角形，利用类似三角形对应边成比例求出所求线段 或半径．
∵CD是⊙O的切线，∴∠ODC＝90°， ∴∠BDC＋∠ODB＝90°. ∵AB是⊙O的直径， ∴∠ADB＝90°，∴∠A＋∠ABD＝90°. ∵OB＝OD，∴∠OBD＝∠ODB， ∴∠A＋∠ODB＝90°，∴∠A＝∠BDC.
(2)∵CM平分∠ACD，∴∠DCM＝∠ACM. ∵∠A＝∠BDC， ∴∠A＋∠ACM＝∠BDC＋∠DCM. 即∠DMN＝∠DNM. ∵∠ADB＝90°，DM＝1，∴DN＝DM＝1， ∴MN＝
1．(202X·白银)如图，AN是⊙M的直径，NB∥x轴，AB交 ⊙M于点C. (1)若点A(0，6)，N(0，2)，∠ABN＝30°，求点B的坐标； (2)若D为线段NB的中点，求证：直线CD是⊙M的切线．
(1)解：∵A(0，6)，N(0，2)，∴AN＝4. ∵∠ABN＝30°，∠ANB＝90°， ∴AB＝2AN＝8. 由勾股定理可知NB＝
【分析】 (1)连接OD，由切线的性质可得∠CDB＋∠ODB＝ 90°，由AB是直径，可得∠ADB＝90°，进而可得∠A＋ ∠ABD＝90°，进而求得∠A＝∠BDC；(2)由角平分线及三 角形外角性质可得∠A＋∠ACM＝∠BDC＋∠DCM，即∠DMN＝ ∠DNM，再根据勾股定理求得MN的长． 【自主解答】 (1)如图，连接OD，
【分析】 (1)根据直径所对的圆周角为直角，利用勾股定

第六单元圆专题2 与圆有关的位置关系考点1 点和圆、直线和圆的位置关系1.已知平面内有⊙O和点A,B,若⊙O半径为2cm,线段OA=3cm,OB=2cm,则直线AB与⊙O的位置关系为( )A.相离B.相交C.相切D.相交或相切2.点P是非圆上一点，若点P到⊙O上的点的最小距离是4cm，最大距离是9 cm，则⊙O 的半径是___________.3.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点.若以1cm为半径的⊙O与直线a相切,则OP的长为___________.考点2 切线的性质与判定1.如图,AB是⊙O的直径,BC是⊙O的切线,若∠BAC=35°,则∠ACB的大小为( )A.35°B.45°C.55°D.65°2.如图,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D.下列结论不一定成立的是( )A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A，B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线3.如图,菱形OABC的顶点A,B,C在⊙O上，过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )A.1B.2C.√2C.√34.如图,在▱ABCD中,AD=12,以AD为直径的⊙O与BC相切于点E,连接OC.若OC=AB,则▱ABCD 的周长为____________.5.如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC，AC.当△OAC是直角三角形时，其斜边长为_____________.6.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=___________.7.如图，PA是以AC为直径的⊙O的切线,切点为A,过点A作AB⊥OP,交⊙O于点B. (1)求证:PB是⊙O的切线;,求PO的长.(2)若CC=6,cos∠CCC=358.如图,AB为⊙O的直径,四边形ABCD内接于⊙O,对角线AC,BD交于点E,⊙O的切线AF交BD的延长线于点F,切点为A,且∠CAD=∠ABD.(1)求证:AD=CD;(2)若AB=4,BF=5,求sin∠BDC的值.̂上一点，连接AE并延长至点C，使9.已知:如图,AB是⊙O的直径,E为⊙O上一点，D是AE∠CBE=∠BDE,BD与AE交于点F.(1)求证:BC是⊙O的切线;(2)若BD平分∠ABE,求证:AD²=DF· DB.考点3 三角形的外接圆与内切圆1.如图,已知点O是△ABC的外心,∠A=40°,连接BO,CO,则∠BOC的度数是( )A.60°B.70°C.80°D.90°2.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD是⊙O的直径,若AD=3,则CC=( )C.2√3C.3√3 C.3D.43.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h，r，R，则下列结论不正确的是( )A.h=R+rB.R=2rC.C=√34C C.C=√33C4.如图,△ABC内接于⊙O,∠A=50°,点D是BC的中点,连接OD,OB,OC,则∠BOD=_______.5.如图所示的网格由边长为1个单位长度的小正方形组成，点A，B，C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为_____________.6.已知△ABC的三边a,b,c满足b+|c-3|+C2−8C=4√C−1−19,则△ABC的内切圆半径=____________.专题检测一、选择题(每小题4分，共40分)1.平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )A.点P在⊙O外B.点P在⊙O上C.点P在⊙O内D.无法判断2.已知⊙O的半径为5，点O到直线l的距离为3，则⊙O上到直线l的距离为2的点共有( )A.1个B.2个C.3个D.4个3.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )A.75°B.70°C.65°D.60°̂上一点，则∠EPF的4.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是DF度数是( )A.65°B.60°C.58°D.50°5.如图,PA,PB是⊙O的切线,A,B是切点,若∠P=70°,则∠ABO=( )A.30°B.35°C.45°D.55°6.如图,长方形ABCD中,AB=4,AD=3,圆B 半径为1，圆A与圆B内切，则点C、D与圆A的位置关系是( )A.点C在圆A外，点D在圆A内B.点C在圆A外，点D在圆A外C.点C在圆A上，点D在圆A内D.点C在圆A内，点D在圆A外7.如图,在等腰△ABC中, AB=AC=2√5,BC=8,按下列步骤作图：①以点A为圆心，适当的长度为半径作弧,分别交AB,AC于点E,F,再分EF的长为半径作弧相交于点H，作射线AH；别以点E，F为圆心，大于12AB的长为半径作弧相交于点M,N,作直线②分别以点A，B为圆心，大于12MN,交射线AH于点O;③以点O为圆心，线段OA长为半径作圆.则⊙O的半径为( )A.2√5B.10C.4D.58.如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,若OB=6 cm,OC=8cm,则BE+CG的长等于( )A.13 cmB.12 cmC.11 cmD. 10 cm9.如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD与⊙O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于( )A.35B.23C.34D.4510.如图，点A的坐标为(-3，2),⊙A的半径为1,P为坐标轴上一动点,PQ切⊙A于点Q,在所有P点中，使得PQ长最小时，点P的坐标为( )A.( 0,2)B.( 0,3)C.( -2,0)D.( -3,0)二、填空题(每小题4分，共24分)11.点A(0,3),点B(4,0),则点O(0,0)在以AB为直径的圆 (填“内”“上”或“外”).12.如图,在△ABC中,D是边BC上的一点，以AD为直径的⊙O交AC于点E,连接DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为___________.13.点O是△ABC的外心,若∠BOC=110°,则∠BAC为 .14.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .15.如图,PA,PB是⊙O的切线,A,B是切点.若∠P=50°,则∠AOB= .16.如图，两个圆都是以点O为圆心，大圆的弦AB是小圆的切线，点P为切点，AB=10，则图中圆环的面积为 .三、解答题(共36分)17.(12分)阅读下列材料:平面上两点P₁(x₁,y₁),P₂(x₂,y₂)之间的距离表示为|P1P2|=√(x1−x2)2+(y1−y2)2,称为平面内两点间的距离公式，根据该公式，如图，设P(x，y)是圆心坐标为C(a，b)、半径为r的圆上任意一点，则点P适合的条件可表示为√(x−a)2+(y−b)2=r,变形可得 (x-a)²+(y-b)²=r², 我们称其为圆心为C(a，b)，半径为r的圆的标准方程.例如：由圆的标准方程(x-1)²+(y-2)²=25 可得它的圆心为(1,2),半径为5.根据上述材料，结合你所学的知识，完成下列各题.(1)圆心为C(3,4),半径为2的圆的标准方程为 ;(2)若已知⊙O的标准方程为(x-2)²+y²=2²,圆心为C，请判断点A(3,-1)与⊙O的位置关系.18.(12分)已知△ABC内接于⊙O,AB=AC,∠BAC=42°,点D是⊙O上一点.(1)如图①,若BD为⊙O的直径,连接CD,求∠DBC和∠ACD的大小;(2)如图②,若CD∥BA,连接AD,过点D作⊙O的切线,与OC的延长线交于点E，求∠E的大小.19.(12分)如图,在△ABC中,∠ACB=90°,BO为△ABC的角平分线，以点O为圆心，OC为半径作⊙O与线段AC交于点D.(1)求证:AB为⊙O的切线;,AD=2,求BO的长.(2)若tanA=34参考答案考点1 点和圆、直线和圆的位置关系1.D ⊙O的半径为2 cm,线段OA=3cm,OB=2cm，即点A到圆心O的距离大于圆的半径，点B 到圆心O的距离等于圆的半径，∴点A在⊙O外,点B在⊙O上,∴直线AB 与⊙O的位置关系为相交或相切.2.6.5cm或2.5cm 分为两种情况:①当点在圆内时，如图1，∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,∴直径AB=4+9=13(cm),∴半径r=6.5 cm;②当点在圆外时，如图2，∵点到圆上的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=9-4=5(cm),∴半径r=2.5cm.3.3cm或5cm ∵直线a⊥b,O为直线b上一动点，∴⊙O与直线a相切时,切点为H,∴OH=1 cm. 当点O在点H的左侧，⊙O与直线a相切时，OP=PH-OH=4-1=3(cm);当点O在点H的右侧，⊙O与直线a相切时，OP=PH+OH=4+1=5(cm);∴⊙O与直线a相切,OP的长为3cm或5cm.考点2 切线的性质与判定1.C ∵BC是⊙O的切线,AB是⊙O的直径,∴AB⊥BC,∴∠ABC=90°,∴∠ACB=90°-∠BAC=90°-35°=55°.2.B 由切线长定理,得PA=PB,∴△BPA 是等腰三角形，故A正确；由圆的对称性可知AB⊥PD，但不一定平分，故B不一定正确；如图，连接OB，OA，由切线的性质，得∠OBP=∠OAP=90°,∴点A,B,P在以OP为直径的圆上，故C正确；∵△BPA是等腰三角形,PD⊥AB,∴PC为△BPA的边AB上的中线,故D正确.3.D 如图,连接OB.∵四边形OABC是菱形.∴OA=AB.∵OA=OB,∴OA=AB=OB,∴∠AOB=60°.∵BD是⊙O的切线,∴∠DBO=90°.∵OB=1,∴BD=√3OB=√3.4.24+6√5如图,连接OE,过点C作CF⊥AD交AD于点F,∵四边形ABCD为平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠EOD+∠OEC =180°,∵⊙O与BC相切于点E,∴OE⊥BC,∴∠OEC=90°,∴∠EOD=90°,∵CF⊥AD,∴∠CFO=90°,∴四边形OECF为矩形,∴FC=OE,OD=3,∵AD为直径,AD=12,∴FC=OE=OD= 12在Rt△OFC中，由勾股定理得OC²=OF²+FC²=3²+6²=45.∴AB=OC=3√5,∴平行四边形ABCD的周长为12+12+3√5+3√5=24+6√5.5.2√3或2√2连接OB,∵BC是⊙O的切线,∴∠OBC=90°.∵BC=OA,∴OB=BC=2,∴△OBC是等腰直角三角形，∴∠BCO=45°,∴∠ACO≤45°.当△OAC是直角三角形时，①若∠AOC=90°,∴OC=√2OB=2√2,∴AC=√OA2+OC2=√22+(2√2)2=2√3;②若∠OAC=90°,∵BC是⊙O的切线,∴∠CBO=∠OAC=90°.∵BC=OA=OB,∴△OBC是等腰直角三角形，∴OC= 2√2.6.27°∵ PA切⊙O于点A,∴∠OAP=90°.∵∠P=36°, ∴∠AOP=54°. ∴∠B=12∠AOP=27 ∘.7.(1)证明连接OB,如图,∵PA是以AC为直径的⊙O的切线，切点为A,∴∠PAO=90°, ∵OA=OB,AB⊥OP,∴∠POA=∠POB,在△PAO和△PBO中, {AO=BO,∠POA=∠POB,OP=OP,∴△PAO≌△PBO(SAS),∴∠PBO=∠PAO=90°,即OB⊥PB,又∵OB为⊙O的半径,∴PB是⊙O的切线;(2)解设OP与AB交于点D.∵AB⊥OP,AB=6,∴DA=DB=3,∠PDA =∠PDB=90°,∵cos∠PAB=35=DAPA=3PA,∴PA=5,∴PD=√PA2−AD2=√52−32=4,在Rt△APD和Rt△APO中,cos∠APD= PDPA ,cos∠APO=PAPO,8.(1)证明∵∠CAD=∠ABD,∠ABD=∠ACD,∴∠ACD=∠CAD,∴AD=CD;(2)解∵AF是⊙O的切线,∴∠FAB=90°.∵AB是⊙O的直径,∴∠ACB=∠ADB=∠ADF=90°,∴∠ABD+∠BAD=∠BAD+∠FAD=90°. ∴∠ABD=∠FAD.∵∠ABD=∠CAD,∠CAD=∠EAD,∴∠FAD=∠EAD.∵AD=AD,∴△ADF≌△ADE(ASA).∴AF=AE,DF=DE.∵AB=4,BF=5,∴AF =√BF 2−AB 2=3,∴AE=AF=3. ∵S △ABF =12AB ⋅AF =12BF ⋅AD, ∴AD =AB⋅AF BF=4×35=125,∴DE =√AE 2−AD 2=√32−(125)2=95, ∴BE =BF −2DE =75.∵∠AED=∠BEC,∠ADE=∠BCE=90°.∴△BEC ∽△AED. ∴BEAE =BCAD , ∴BC =BE⋅AD AE=2825, ∴sin ∠BAC =BC AB =725.∵∠BDC=∠BAC,∴sin ∠BDC =725.9.证明 (1)∵AB 是⊙O 的直径,∴∠AEB=90°,∴∠EAB+∠EBA=90°. ∵∠CBE=∠BDE,∠BDE=∠EAB,∴∠EAB=∠CBE,∴∠EBA+∠CBE=∠EBA+∠EAB=90°,即∠ABC=90°,∴CB ⊥AB. ∵AB 是⊙O 的直径,∴BC 是⊙O 的切线. (2)∵BD 平分∠ABE,∴∠ABD=∠DBE. ∵∠DAF=∠DBE,∴∠DAF=∠DBA.∵∠ADB=∠FDA,∴△ADF ∽△BDA, ∴ADBD =DFAD ,∴AD ²=DF ·DB. 考点3 三角形的外接圆与内切圆1.C ∵点O 为△ABC 的外心,∠A=40°, ∴∠A =12∠BOC,∴∠BOC =2∠A =80 ∘. 2.C 过点O 作OE ⊥BC 于点E,如图所示:∵∠BAC=120°,AB=AC,∴∠ABC=∠ACB=30°,又 ∵AB̂对应的圆周角为∠ACB 和∠ADB,∴∠ACB=∠ADB=30°, 而BD 为直径,∴∠BAD=90°,在Rt △BAD 中,∠ADB=30°,AD=3, ∴cos30 ∘=ADBD =3BD =√32,∴BD =2√3,∴OB =√3,又∵∠ABD=90°-∠ADB=90°-30°=60°,∠ABC=30°,∴∠OBE=30°. 又∵OE ⊥BC,∴△OBE 为直角三角形. ∴cos ∠OBE =cos30 ∘−BEOB =√3=√32, ∴BE =32.由垂径定理可得BC=2BE= 2×32=3.3.C 如图,∵△ABC是等边三角形.∴△ABC的内切圆和外接圆是同心圆，圆心为O. 设OE=r,AO=R,AD=h,∴h=R+r,故A正确;∵AD⊥BC,∴∠DAC=12∠BAC=12×60°=30°.在Rt△AOE中,∴R=2r,故B正确;∵OD=OE=r,AB=AC=BC=a,∴AE=12AC=12a,∴(12a)2+r2=(2r)2,(12a)2+(12R)2=R².∴r=√36a,R=√33a,故C错误，D正确.4.50°∵∠A=50° ,∴∠BOC=100°.∵OB=OC,∴△OBC为等腰三角形,又∵D为BC 中点，∴OD为BC上的中线，根据等腰三角形三线合一性质可得OD为∠BOC的平分线∴∠BOD=12∠BOC=50∘.5.(2,3) 根据A,B,C三点的坐标建立如图所示的坐标系.根据题意，得AB=√62+32=3√5,AC=√42+82=4√5,BC=√102+52=5√5.∵AB²+AC²=BC².∴∠BAC=90°.设BC的函数表达式为y=kx+b，代入B( -3,3),C(7,-2).得{3=−3k+b,−2=7k+b,解得{k=−12,b=32,∴BC的函数表达式为y=−12x+32.当y=0时,x=3,即G(3,0),∴点A与点G关于BD对称，射线BD是∠ABC的平分线.设点M为三角形的内心，内切圆的半径为r,在BD上找一点M,过点M作ME⊥AB,过点M作MF⊥AC,且ME=MF=r.∵∠BAC=90°,∴四边形MEAF为正方形, S ABC=12AB×AC=12AB×r+12AC×r+12BC×r,解得r=√5,即AE=EM=√5,∴BE=3√5−√5=2√5,∴BM=√BE2+EM2=5,∵B( -3,3),∴M(2,3).∴△ABC内心M的坐标为(2,3).6.1 ∵b+|c−3|+a2−8a=4√b−1−19，∴|c−3|+(a−4)2+(√b−1−2)2= 0,∴c=3,a=4,b=5.∵3²+4²=25=5²,∴c²+a²=b²,∴△ABC是直角三角形,∠ABC=90°.设内切圆的半径为r.根据题意，得S△ABC=12×3×4=12×3×r+12×4×r+12×r×5,∴r=1.(或者r=3+4−52=1)专题检测1.C2.C 如图,∵⊙O的半径为5,点O到直线l 的距离为3,∴CE=2,过点D作AB⊥ OC,垂足为D,交⊙O于A,B两点,且DE=2,∴⊙O上到直线l的距离为2的点为A，B，C，∴⊙O上到直线l的距离为2的点有3个.3.B4.B5.B 如图,连接OA.∵PA,PB是⊙O的切线,A,B是切点,∴∠PBO=∠PAO=90°,∵∠P=70°,∴∠BOA=360°—∠PBO—∠PAO-∠P=110°,∵OA=OB,∴∠ABO=∠BAO=12(180∘−∠BOA)=12(180 ∘−110 ∘)=35 ∘.6.C 两圆内切，圆心距等于半径之差的绝对值,设圆A的半径为R,则AB=R-1,∵AB =4,圆B半径为1,∴R=5,即圆A的半径等于5,∵AB=4,BC=AD=3,由勾股定理可知AC=5,∴AC=5=R,AD=3C在圆上，点D在圆内.7.D 如图,连接OC,设OA交BC于点T.∵AB=AC=2√5,AO平分∠BAC,∴AO⊥BC,BT=TC=4,∴AT=√AC2−CT2=√(2√5)2−42=2.在Rt△OCT中.有r²=(r-2)²+4²,解得r=5.8.D9.D 连接OC、OD、CD,CD交PA于点E,如图,∵PC,PD与⊙O相切,切点分别为C,D,∴OC⊥CP,PC=PD,OP平分∠CPD.∴OP⊥CD,∴CB̂=DB̂,∴∠COB=∠DOB,∵∠CAD=12∠COD,∴∠COB=∠CAD,在Rt△OCP中, OP=√OC2+PC2=√32+42=5,∴sin∠COP=PCOP =45,∴sin∠CAD=45.10.D 连接AQ、PA,如图,∵PQ切⊙A于点Q,∴AQ⊥PQ,∴∠AQP=90°,∴PQ=√AP2−AQ2=√AP2−1,当AP的长度最小时，PQ的长度最小，∵AP⊥x轴时,AP的长度最小,∴AP⊥x轴时,PQ的长度最小,∵A(-3,2),∴此时P点坐标为(-3,0).11.上 12.55°13.55°或125°分两种情况:(1)点A 与点O 在BC 边同侧时,如图1:∵∠BOC=110°,∴∠BAC =110 ∘×12=55 ∘. (2)点A 与点O 在BC 边两侧时,如图2:∵∠BOC=110°,即BĈ所对的圆心角为110°,∴BDC ̂所对的圆心角为：360°—110°=250°. ∴∠BAC =12×250 ∘=125 ∘. 14.4415.130° ∵PA,PB 是⊙O 的切线,A,B 是切点,∴OA ⊥PA,OB ⊥PB,∴∠OAP=∠OBP=90°,∵∠OAP+∠AOB+∠OBP +∠P=360°,∴∠AOB=360°—90°—90°-50°=130°. 16.25π 如图,连接OP 、OA,∵大圆的弦AB 是小圆的切线,∴OP ⊥AB, ∴AP=BP= 12AB =5, 由勾股定理得OA ²-OP ²=AP ²=25, ∴圆环的面积=π×OA ²-π×OP ²=π×(OA ²-OP ²)=25π.17.解 (1)圆心为C(3,4),半径为2的圆的标准方程为(x-3)²+( y-4)²=4.故答案为：(x-3)²+(y-4)²=4. (2)由题意得圆心为C(2.0),∵A (3,−1),∴AC =√(3−2)2+12= √2<2,∴点A 在⊙C 内部.18.解 (1)∵AB=AC,∴∠ABC=∠ACB= 12(180 ∘−∠BAC)=12×(180 ∘−42 ∘)=69 ∘,∵BD 为直径,∴∠BCD=90°,∵∠D=∠BAC=42°,∴∠DBC=90°-∠D=90°-42°=48°; ∴∠ACD=∠ABD=∠ABC-∠DBC=69°-48°=21°; (2)如图,连接OD,∵CD ∥AB,∴∠ACD=∠BAC=42°,∵四边形ABCD 为⊙O 的内接四边形，∴∠B+∠ADC=180°, ∴∠ADC=180°-∠B=180°-69°=111°,∴∠CAD=180°-∠ACD-∠ADC=180°-42°-111°=27°,∴∠COD=2∠CAD=54°, ∵DE 为切线,∴OD ⊥DE,∴∠ODE=90°,∴∠E=90°-∠DOE=90°-54°=36°. 19.(1)证明如图,过点O 作OH ⊥AB 于点H.∵∠ACB=90°,∴OC ⊥BC.∵BO 为△ABC 的角平分线,OH ⊥AB,∴OH=OC,即OH 为⊙O 的半径. ∵OH ⊥AB,∴AB 为⊙O 的切线.(2)解设⊙O 的半径为3x,则OH=OD=OC=3x.在Rt △AOH 中,∵tanA =34, ∴OHAH =34,∴3xAH =34,∴AH=4x, ∴AO =√OH 2+AH 2=√(3x )2+(4x )2=5x,∵AD=2,∴AO=OD+AD=3x+2,∴3x+2=5x,∴x=1,∴OA=3x+2=5,OH=OD=OC=3x=3 . ∴AC=OA+OC=5+3=8.在Rt △ABC 中, ∵tanA =BCAC ,∴BC =AC ⋅tanA =8×34=6, ∴OB =√OC 2+BC 2=√32+62=3√5.。

2 ∴CF= OC 2 OF = 2 =0.8(m),∴CD=1.6 m. 12 0.6
考点二
圆心角、弧、弦的关系
l︵ l︵
l︵
BC =
例2 如图,D,E分别是☉O的半径OA,OB上的点,CD⊥OA,CE⊥
OB,CD=CE,则 AC 与 BC的大小关系是
AC
l︵
.
解析 ∵CD⊥OA,CE⊥OB,
1.定义:四个顶点都在同一个圆上的四边形叫做圆内接四边形. 2.性质:圆内接四边形的对角
泰安考点聚焦
考点一 垂径定理及其推论
考点二
考点三 考点四
圆心角、弧、弦的关系
圆周角定理及其推论 圆内接四边形的性质
考点一
垂径定理及其推论
中考解题指导 大部分求圆中弦或线段长度或者出现弦的中点
的题目都要用到垂径定理,我们要熟记垂径定理的“两条件三结 论”,并熟练运用定理本身和它的推论.
考点三
例3 ( D )
圆周角定理及其推论
(2017泰安)如图,△ABC内接于☉O,若∠A=α ,则∠OBC等于
A.180°-α B.2α C.90°+α D.90°-α
解析 连接OC,则∠BOC=2∠A=2α ,
∵OB=OC,
1 ∴∠OBC=∠OCB= (180°-2α )=90°-α . 2
2.垂径定理及其推论
(1)定理:垂直于弦的直径平分 弦所对的两条弧 . 弦 ,并且平分
(2)推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
. 温馨提示 优 弧;(5)平分弦所对的劣弧,这五条结论中的任意两条成立,那么其 他的结论也成立. (1)过圆心;(2)垂直于弦;(3)平分弦;(4)平分弦所对的

第二节与圆相关的地点关系姓名： ________班级：________用时：______分钟1．( 2018·湘西州中考 ) 已知⊙O 的半径为 5 cm，圆心 O到直线 l 的距离为 5 cm，则直线l 与⊙O 的地点关系为()A．订交B．相切C．相离D．没法确立2 ． ( 2019·改编题 ) 设⊙O 的半径为3，点O到直线l的距离为d，若直线l与⊙O起码有一个公共点，则d 应知足的条件是()A． d＝ 3B．d≤3C． d＜ 3D． d＞ 33．( 2019·改编题) 如下图，是一块三角形的草坪，现要在草坪上建一凉亭供大家歇息，要使凉亭到草坪三条边的距离相等，凉亭的地点应选在()A．△ ABC的三条中线的交点B．△ ABC三边的中垂线的交点C．△ ABC三条角均分线的交点D．△ ABC三条高所在直线的交点4．( 2018·深圳中考 ) 如图，一把直尺， 60°的直角三角板和光盘如图摆放， A 为 60°角与直尺交点，AB ＝ 3，则光盘的直径是( )A． 3B．33C． 6D．635．( 2018·重庆中考 A 卷 ) 如图，已知AB是⊙O的直径，点P在BA的延伸线上，PD与⊙O 相切于点D，过点 B 作PD的垂线交PD的延伸线于点C，若⊙O 的半径为4， BC＝ 6，则PA 的长为 ()A． 4B．23C． 3D． 2.56．( 2018·台州中考 ) 如图， AB 是⊙O 的直径，点 C 是⊙O 上的点，过点 C 作⊙O 的切线交 AB 的延伸线于点 D. 若∠ A＝32°，则∠ D＝ ________度．7． ( 2018·连云港中考 ) 如图， AB 是⊙O 的弦，点 C 在过点 B 的切线上，且OC⊥O A， OC交 AB 于点 P. 已知∠ OAB＝22°，则∠ OCB＝ __________．8．( 2018·湖州中考 ) 如图，已知△ ABC 的内切圆⊙O 与 BC边相切于点 D，连结OB， OD.若∠ ABC＝40°，则∠ BOD 的度数是 __________ ．9．( 2018·娄底中考 ) 如图，已知半圆O与四边形 ABCD的边 AD， AB，BC都相切，切点分别为 D， E， C，半径 OC＝ 1，则 AE·BE＝ ______．10．( 2019·改编题 ) 已知：如图， AB是⊙O的直径， AC是弦，直线EF 是过点 C的⊙O的切线，∠ BAC＝∠ CAD.(1)求证： AD⊥EF；(2)若∠ B＝30°， AB＝ 12，求 AD的长．11．( 2018·常德中考) 如图，已知⊙O 是等边三角形ABC的外接圆，点D在圆上，在CD的延伸线上有一点F，使 DF＝DA，AE∥BC 交 CF于点 E.(1)求证： EA是⊙O的切线；(2)求证： BD＝ CF.12．( 2018·重庆中考 B 卷 ) 如图，△ ABC 中，∠ A＝30°，点 O是边 AB 上一点，以点O为圆心，以OB为半径作圆，⊙O 恰巧与 AC相切于点D，连结 BD.若 BD均分∠ ABC， AD＝ 2 3 ，则线段CD的长是 ( )33A． 2 B. 3 C. 2 D.2 313．( 2018·无锡中考 ) 如图，矩形 ABCD 中， G是 BC的中点，过 A， D， G三点的⊙O 与边AB， CD分别交于点 E，点 F，给出以下说法：(1)AC 与 BD的交点是⊙O 的圆心； (2)AF 与DE的交点是⊙O 的圆心； (3)BC 与⊙O 相切．此中正确说法的个数是( )A． 0B． 1C． 2D． 314．( 2018·泸州中考 ) 在平面直角坐标系内，以原点O为圆心， 1 为半径作圆，点 P 在直线 y＝3x＋2 3上运动，过点P 作该圆的一条切线，切点为A，则 PA的最小值为 ()A． 3B． 2 C. 3 D. 215．( 2018·南京中考 ) 如图，在矩形ABCD中， AB＝ 5， BC＝ 4，以 CD为直径作⊙ O.将矩形ABCD绕点 C旋转，使所得矩形A′B′CD′的边 A′B′与⊙O相切，切点为 E，边 CD′与⊙O订交于点 F，则 CF 的长为________．16．( 2019·原创题 ) 如下图，在Rt△ABC中，以斜边 AB 为直径作⊙ O，延伸 BC 至点 D，恰巧使得 AD＝AB，过点 C作 CE⊥AD，延伸 DA交⊙O 于点 F.(1)求证： CE是⊙O的切线；(2)若 AB＝10， CE＋EA＝ 4，求 AF 的长度．17．( 2018·德城区一模 ) 已知 AB 是⊙O 的直径， AT 是⊙O 的切线，∠ ABT＝50°，BT 交⊙O 于点 C， E 是AB上一点，延伸CE交⊙O 于点 D.(1)如图 1，求∠T 和∠ CDB的大小；(2)如图 2，当 BE＝ BC时，求∠ CDO的大小．18．( 2019·创新题 ) 阅读资料：|Ax ＋ By ＋ C|在平面直角坐标系 xOy 中，点 P(x ， y ) 到直线 Ax＋By＋ C＝ 0 的距离公式为00d＝A2＋B2.00比如：求点 P (0 ， 0) 到直线 4x＋3y－ 3＝0 的距离．解：由直线 4x＋ 3y－ 3＝ 0 知， A＝ 4， B＝ 3， C＝－ 3，|4 ×0＋3×0－ 3|3∴点 P0(0 ， 0) 到直线 4x＋ 3y－ 3＝ 0 的距离为 d＝42＋ 32＝5.依据以上资料，解决以下问题：35问题 1：点 P1(3 ， 4) 到直线 y＝－4x＋4的距离为 __________；3问题 2：已知⊙C 是以点 C(2， 1) 为圆心， 1 为半径的圆，⊙C 与直线 y＝－4x＋ b 相切，务实数 b 的值；问题 3：如图，设点 P 为问题 2 中⊙C上的随意一点，点A， B为直线 3x＋ 4y＋ 5＝ 0 上的两点，且 AB＝ 2，恳求出 S△ABP的最大值和最小值．参照答案【基础训练】1． B 2.B 3.C 4.D 5.A6． 267.44 °8.70 °9.110． (1) 证明：如图，连结OC.∵E F 是过点 C 的⊙O的切线，∴ OC⊥EF，∴∠ OCA＋∠ ACD＝90°.∵O C＝ OA，∴∠ OCA＝∠ BAC＝∠CAD，∴∠ CAD＋∠ ACD＝90°，∴AD⊥EF.(2)解：∵ OB＝ OC，∴∠ B＝∠ OCB＝30°.又∵∠ AOC 是△ BOC的外角，∴∠ AOC＝∠ B＋∠ OCB＝60°.又∵ OA＝ OC，1∴△ AOC为等边三角形，∴ AC＝2AB＝ 6.1又∵∠ ACD＝30°，∴ AD＝2AC，∴AD＝ 3.11．证明： (1) 如图，连结OA.∵⊙O是等边三角形ABC的外接圆，∴∠ OAC＝30°，∠ BCA＝60°.∵AE∥BC，∴∠ EAC＝∠ BCA＝60°，∴∠ OAE＝∠ OAC＋∠ EAC＝30°＋ 60°＝ 90°，∴EA 是⊙O的切线．(2)∵△ ABC 是等边三角形，∴AB＝ AC，∠ BAC＝∠ ABC＝60°.∵A， B， C， D 四点共圆，∴∠ ADF＝∠ ABC＝60°.∵AD＝ DF，∴△ ADF 是等边三角形，∴AD＝ AF，∠ DAF＝60°，∴∠ BAC＋∠ CAD＝∠ DAF＋∠ CAD，即∠ BAD＝∠ CAF.在△ BAD和△ CAF中，AB＝ AC，∵ ∠BAD＝∠ CAF，AD＝ AF，∴△ BAD≌△ CAF，∴ BD＝ CF.【拔高训练】12． B 13.C 14.D15． 416． (1) 证明：∵ OB＝ OC，∴∠ ABC＝∠ OCB.∵AB＝ AD，∴∠ ABC＝∠ ADB，∴∠ OCB＝∠ ADB，∴ OC∥AD.∵CE⊥AD，∴∠ AEC＝∠ OCE＝90°，∴CE是⊙O的切线．(2)解：如图，过点 O作 OH⊥AF 于点 H，则∠ OCE＝∠ CEH＝∠ OHE＝90°，∴四边形OCEH是矩形，∴OC＝ EH，OH＝ CE.设 AH＝ x.∵CE＋ AE＝4， OC＝ 5，∴AE＝ 5－ x， OH＝ 4－ (5 － x) ＝ x－ 1.在 Rt△AOH中，由勾股定理得222 AH＋ OH＝ OA，即 x2＋ (x － 1) 2＝52，解得 x1＝ 4，x2＝－ 3( 不切合题意，舍去) ，∴AH＝ 4.1∵OH⊥AF，∴ AH＝ FH＝2AF，∴AF＝ 2AH＝2×4＝ 8.17．解： (1) 如图，连结AC.∵AB 是⊙O的直径， AT 是⊙O 的切线，∴A T⊥AB，即∠ TAB＝90°.∵∠ ABT＝50°，∴∠ T＝90°－∠ ABT＝40°.由AB 是⊙O的直径得∠ACB＝90°，∴∠ CAB＝90°－∠ ABC＝40°，∴∠ CDB＝∠ CAB＝40°.(2)如图，连结 AD.在△ BCE中， BE＝ BC，∠ EBC＝50°，∴∠ BCE＝∠ BEC＝65°，∴∠ BAD＝∠ BCD＝65°.∵OA＝ OD，∴∠ ODA＝∠ OAD＝65°.∵∠ ADC＝∠ ABC＝50°，∴∠ CDO＝∠ ODA－∠ ADC＝15°.【培优训练】18．解：问题1： 4提示：直线方程整理得3x ＋4y－ 5＝ 0，故 A＝ 3， B＝ 4， C＝－ 5，35∴点 P1(3 ， 4) 到直线 y＝－4x＋4的距离为|3 ×3＋4×4－ 5|d＝32＋42＝4.3问题 2：直线 y＝－4x＋ b 整理得 3x＋ 4y－ 4b＝ 0，故 A＝ 3， B＝ 4， C＝－ 4b.∵⊙C与直线相切，∴点 C 到直线的距离等于半径，|3 ×2＋4×1－ 4b|＝ 1，即32＋ 42515整理得 |10 － 4b| ＝ 5，解得 b＝4或 b＝4 .问题 3：如图，过点 C 作 CD⊥AB 于点 D.∵在 3x＋ 4y＋ 5＝ 0 中， A＝ 3，B＝ 4， C＝5，∴圆心 C(2， 1) 到直线 AB 的距离|3 ×2＋4×1＋ 5|CD＝＝ 3，32＋ 42∴⊙C 上的点到直线AB的最大距离为3＋1＝ 4，最小距离为3－ 1＝ 2，1∴S△ ABP的最大值为2×2×4＝4，1最小值为2×2×2＝ 2.。

5．（3 分）（2015•徐州模拟）如图，AB 是⊙O 的直径，弦 CD⊥AB，垂足为 E，如果 AB=10，CD=8，那么线段 OE 的长为（ ）
A．5 B．4 C．3 D．2 【考点】垂径定理；勾股定理．菁优网版权所有 【分析】连接 OC，由垂径定理求出 CE 的长，再根据勾股定理得出线段 OE 的长． 【解答】解：连接 OC
北辰教育学科教师辅导教案
在读学校： 学员姓名：
授课类型 星级 教学目的 授课日期及时段
年
月
年 级： 辅导科目： C-2019 年中考数学一轮备考： 《圆专题》 ★★★★★
日 教学内容
一、选择题
1.（3 分）（2015•徐州）下列四个几何体中，主视图为圆的是（ ）
A．
B．
C．
D．
课 时 数： 3 学科教师：
7．（3 分）(2014 年江苏徐州)半径为 4cm，圆心角为 60°的扇形的面积为 π cm2．
考点： 扇形面积的计算． 分析： 直接利用扇形面积公式求出即可．
解答： 解：半径为 4cm，圆心角为 60°的扇形的面积为：
= π（cm2）．
故答案为： π． 点评： 此题主要考查了扇形的面积公式应用，熟练记忆扇形面积公式是解题关键．
代入扇形弧长公式 l nπr ， 180
即 2π=
，
解得 n=120， 即扇形圆心角为 120 度． 故选 C． 【点评】本题综合考查有关扇形和圆锥的相关计算．解题思路：解决此类问题时要紧紧抓住两者之间的两个对应关系： （1）圆锥的母线长等于侧面展开图的扇形半径；（2）圆锥的底面周长等于侧面展开图的扇形弧长．正确对这两个关 系的记忆是解题的关键． 二、填空题
A．30°
B．45°
C．60°

第六章圆第21讲圆的有关性质A组基础题组一、选择题1.(xx浙江衢州)如图,点A,B,C在☉O上,∠ACB=35°,则∠AOB的度数是( )A.75°B.70°C.65°D.35°2.(xx菏泽)如图,在☉O中,OC⊥AB,垂足为E,∠ADC=32°,则∠OBA的度数是( )A.64°B.58°C.32°D.26°3.(xx甘肃凉州)如图,☉A过点O(0,0),C(,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是( )A.15°B.30°C.45°D.60°4.(xx江苏苏州)如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的☉O交AB于点D,E是☉O上一点,且的长=的长,连接OE,过点E作EF⊥OE,交AC的延长线于点F,则∠F 的度数为( )A.92°B.108°C.112°D.124°5.(xx潍坊)如图,四边形ABCD为☉O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )A.50°B.60°C.80°D.85°二、填空题6.(xx北京)如图,点A,B,C在☉O上,的长=的长,∠CAD=30°,∠ACD=50°,则∠ADB=.7.(xx江苏南京)如图,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE,若∠D=78°,则∠EAC=.8.(xx湖北黄冈)如图,△ABC内接于☉O,AB为☉O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .9.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交☉O于D,连接BE.设∠BEC=α,则sin α的值为.三、解答题10.已知△ABC,以AB为直径的☉O分别交AC于D,BC于E,连接ED.若ED=EC.(1)求证:AB=AC;(2)若AB=4,BC=2,求CD的长.11.如图所示,AD是△ABC外角∠EAC的平分线,AD与△ABC外接☉O交于点D,N为BC延长线上一点,且CN=CD,DN交☉O于点M.求证:(1)DB=DC;(2)DC2=CM·DN.B组提升题组一、选择题1.(xx浙江衢州)如图,AC是☉O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8 cm,AE=2 cm,则OF的长度是( )A.3 cmB. cmC.2.5 cmD. cm2.如图所示,在☉O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )A.19B.16C.18D.203.如图,AB是半圆O的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则=( )A. B. C.1- D.二、填空题4.在☉O中,AB是☉O的直径,AB=8 cm,的长=的长=的长,M是AB上一动点,CM+DM的最小值是cm.三、解答题5.(xx江苏无锡)如图,四边形ABCD内接于☉O,AB=17,CD=10,∠A=90°,cos B=,求AD的长.第六章圆第21讲圆的有关性质A组基础题组一、选择题1.B2.D3.B4.C 在Rt△ACB中,∠ACB=90°,∠A=56°,∴∠B=34°.∵的长=的长,∴∠COE=2∠B=68°.∵EF⊥OE,∴∠OEF=90°.又∵∠OCF=90°,∴∠F=180°-68°=112°.5.C 由圆内接四边形的性质,得∠ADC+∠ABC=180°.又∠ABC+∠GBC=180°,∴∠ADC=∠GBC=50°.又∵AO⊥CD,∴∠DAE=40°.延长AE交☉O于点F.由垂径定理,得的长=的长, ∴∠DBC=2∠DAE=80°.二、填空题6.答案70°解析∵的长=的长,∴∠BAC=∠CAD=30°.又∵∠BDC=∠BAC=30°,∠ACD=50°,∴∠ADB=180°-30°-30°-50°=70°.7.答案27°解析∵四边形ABCD是菱形,∠D=78°,∴∠ACB=∠DCB=(180°-∠D)=51°.∵四边形AECD是圆内接四边形,∴∠AEB=∠D=78°,∴∠EAC=∠AEB-∠ACE=27°.8.答案2解析连接BD,因为AB为☉O的直径,所以∠ADB=90°,因为∠CAB=60°,弦AD平分∠CAB,所以∠BAD=30°,因为=cos 30°,所以AB===4.在Rt△ABC中,AC=AB×cos 60°=4×=2.9.答案解析如图,连接BC.∵AB是半圆的直径,∴∠ACB=90°.在Rt△ABC中,AC=8,AB=10,∴BC==6.∵OD⊥AC,∴AE=CE=AC=4.在Rt△BCE中,BE==2,∴sin α===.三、解答题10.解析(1)证明:∵ED=EC,∴∠CDE=∠C.又∵四边形ABED是☉O的内接四边形,∴∠CDE=∠B,∴∠B=∠C,∴AB=AC.(2)连接AE,则AE⊥BC.∴BE=EC=ED=BC.在△ABC与△EDC中,∠C=∠C,∠CDE=∠B,∴△ABC∽△EDC,∴=,∴DC==.由AB=4,BC=2,得DC==.11.证明(1)∵AD平分∠EAC,∴∠EAD=∠DAC=∠DBC.∵四边形ABCD内接于☉O,∴∠EAD=∠DCB,∴∠DBC=∠DCB.∴DB=DC.(2)∵∠DMC=180°-∠DBC=180°-∠DCB=∠DCN,且∠CDM=∠NDC,∴△DMC∽△DCN.∴=.∴DC·CN=CM·DN.∵CN=DC,∴DC2=CM·DN.B组提升题组一、选择题1.D 连接OB,∵AC是☉O的直径,弦BD⊥AO于E,BD=8 cm,AE=2 cm,在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2,解得OE=3 cm,∴OB=3+2=5 cm,∴EC=5+3=8.在Rt△EBC中,BC===4 cm, ∵OF⊥BC,∴∠OFC=∠CEB=90°,又∵∠C=∠C,∴△OFC∽△BEC,∴=,即=,解得OF= cm,故选D.2.D 延长AO交BC于D,作OE⊥BC于E.∵∠A=∠B=60°,∴∠ADB=60°,∴△ADB为等边三角形,∴BD=AD=AB=12,∴OD=4.又∵∠ADB=60°,∴DE=OD=2,∴BE=10,∴BC=2BE=20.故选D.3.D 连接AE,CE,OC,作AD∥CE,交BE于D. ∵点E是弧AC的中点∴可设AE=CE=1,根据平行线的性质得∠ADE=∠CED=45°.∴△ADE是等腰直角三角形,则AD=,BD=AD=.∴BE=+1.再根据两角对应相等得△AEF∽△BEA,∴EF==-1,BF=2.∴=.故选D.二、填空题4.答案8解析如图,作点C关于AB的对称点C',连接C'D与AB相交于点M,此时,点M为CM+DM为最小值时的位置,由垂径定理,得的长=的长,∴的长=的长,∵的长=的长=的长,AB为直径,∴C'D为直径,∴CM+DM的最小值是8 cm.三、解答题5.解析如图所示,过点C作AD延长线的垂线CE,垂足为E,过点C作CF⊥AB于点F,∵四边形ABCD是圆内接四边形,∴∠CDE=∠B.∵cos B=,CD=10,∴cos ∠CDE===,∴DE=6,∴CE=8,∵∠A=∠AEC=∠CFA=90°,∴四边形AFCE是矩形,∴AF=CE=8.∵AB=17,∴BF=9,∴cos B===,∴BC=15,∴CF=12,∴AE=12,∴AD=12-6=6.11 / 11文档可自由编辑打印。

第六章 圆 第21讲 与圆有关的计算
考向正多边形相关的计算
1．[2018·昆明]如图，正六边形ABCDEF 的边长为1，以点A 为圆心，AB 的长为半径，作扇形ABF ，则图中阴影部分的面积为332－13π. (结果保留根号和π)
第1题图 第2题图
2．[2018·烟台]如图，点O 为正六边形ABCDEF 的中心，点M 为AF 中点．以点O 为圆心、以OM 的长为半径画弧得到扇形MON ，点N 在BC 上；以点E 为圆心、以DE 的长为半径画弧得到扇形DEF .把扇形MON 的两条半径OM ，ON 重合，围成圆锥，将此圆锥的底面半径记为r 1，将扇形DEF 以同方法围成的圆锥的底面半径记为r 2.则r 1∶r 2
考向与圆相关的阴影部分的面积
3．[2018·扬州]如图，在△ABC 中，AB ＝AC ，AO ⊥BC 于点O ，OE ⊥AB 于点E ，以点O 为圆心，OE 为半径作半圆，交AO 于点F .
(1)求证：AC是⊙O的切线；
(2)若点F是OA的中点，OE＝3，求图中阴影部分的面积；
(3)在(2)的条件下，点P是BC边上的动点，当PE＋PF取最小值时，直接写出BP的长．。

考点聚焦---点与圆的位置关系
【问题】视察图中点A,点B,点C与⊙O的位置关系？
点A在圆外 点B在圆上 点C在圆内
d＞r A
d＝r
d＜r(或0≤d＜r)
C
·O r
B
注意：已知点的位置可以确定该点到圆心距离与半径的关系，反 过来，已知点到圆心距离与半径的关系也可以确定该点与圆的位 置关系.
当堂训练
当堂训练
1.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连接
BC,若∠P=36º,则∠B等于( A ) A.27º B.32º C.36º D.54º
当堂训练
2.如图,AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,
过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则
1.一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径
是( C )
A.1.5cm B.7.5cm C.1.5cm或7.5cm D.3cm或15cm
2.在Rt△ABC中,∠C=90º,BC=3,AC=4,点P
在以C为圆心,5为半径的圆上,连接 PA,PB.若PB=4,则PA的长为_3_或___7_3_
P2
B
P1
C
A
目录
点与圆的位置关系
直线与圆的位置关系
圆的切线的性质及判定
切线长定理
三角形的内切圆、外接圆
典型例题
【例2】Rt△ABC中,∠C=90º,AC=3cm,BC=4cm,以C为圆心,r为半
径作圆,若⊙aC与直线AB相切,则r的值为( B )
A.2cm B.2.4cm
C.3cm
D.4cm
考点聚焦---直线与圆的位置关系

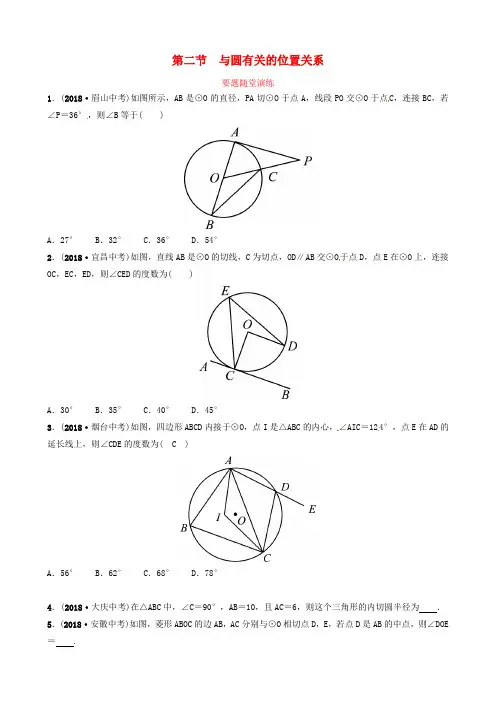
第二节与圆有关的位置关系要题随堂演练1．(2018·眉山中考)如图所示，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C，连接BC，若∠P＝36°，则∠B等于( )A．27° B．32° C．36° D．54°2．(2018·宜昌中考)如图，直线AB是⊙O的切线，C为切点，OD∥AB交⊙O于点D，点E在⊙O上，连接OC，EC，ED，则∠CED的度数为( )A．30° B．35° C．40° D．45°3．(2018·烟台中考)如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC＝124°，点E在AD的延长线上，则∠CDE的度数为( C )A．56° B．62° C．68° D．78°4．(2018·大庆中考)在△ABC中，∠C＝90°，AB＝10，且AC＝6，则这个三角形的内切圆半径为．5．(2018·安徽中考)如图，菱形ABOC的边AB，AC分别与⊙O相切点D，E，若点D是AB的中点，则∠DOE ＝ .6．(2018·济南中考)如图，AB是⊙O的直径，PA与⊙O相切于点A，BP与⊙O相交于点D，C为⊙O上一点，分别连接CB，CD，∠BCD＝60°.(1)求∠ABD的度数；(2)若AB＝6，求PD的长度．7．(2018·聊城中考)如图，在Rt△A BC中，∠C＝90°，BE平分∠ABC交A C于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．(1)求证：AC是⊙O的切线；(2)已知⊙O的半径为2.5，BE＝4，求BC，AD的长．参考答案1．A 2.D 3.C4．2 5.606．解：(1)如图，连接AD.∵∠BCD和∠BAD为同弧所对的圆周角，∴∠BAD＝∠BCD＝60°.∵AB是⊙O的直径，∴∠ADB＝90°，∴∠ABD＝90°－60°＝30°.(2)在Rt△ABD中，∵AB＝6，∠BAD＝60°，∴BD＝3 3.∵AB 是⊙O 的直径且AP 是⊙O 的切线， ∴AB⊥AP，∴∠PAB＝90°.∵AB＝6，∠ABD＝30°，∴PB＝43，∴PD＝PB －BD ＝ 3.7．(1)证明：如图，连接OE.∵OB＝OE ，∴∠OB E ＝∠OEB.∵BE 平分∠A BC ，∠OBE＝∠EBC，∴∠OEB＝∠EBC，∴OE∥BC.又∵∠C＝90°，∴∠OEA＝90°，即AC⊥OE. 又∵OE 是⊙O 的半径，∴AC 是⊙O 的切线．(2)解：在△BCE 与△BED 中，∵∠C＝∠BED＝90°，∠EBC＝∠DBE， ∴△BC E∽△BED，∴BE BD ＝BC BE ，即BC ＝BE 2BD. ∵BE＝4，BD 是⊙O 的直径，即BD ＝5，∴BC＝165. 又∵OE∥BC，∴AO AB ＝OE BC. ∵AO＝AD ＋2.5，AB ＝AD ＋5，∴AD ＋2.5AD ＋5＝2.5165，45 7.解得AD＝。

第六单元《圆》中考知识点梳理第21讲圆的基本性质知识点一：圆的有关概念关键点拨与对应举例1.与圆有关的概念和性质（1）圆：平面上到定点的距离等于定长的所有点组成的图形．如图所示的圆记做⊙O.（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦.（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧.（4）圆心角：顶点在圆心的角叫做圆心角.（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角.（6）弦心距：圆心到弦的距离.（1）经过圆心的直线是该圆的对称轴，故圆的对称轴有无数条；（2）3点确定一个圆，经过1点或2点的圆有无数个.（3）任意三角形的三个顶点确定一个圆，即该三角形的外接圆.知识点二：垂径定理及其推论2.垂径定理及其推论定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形.推论(1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧；(2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧.延伸根据圆的对称性，如图所示，在以下五条结论中：①弧AC=弧BC;②弧AD=弧BD；③AE=BE;④AB⊥CD;⑤CD是直径.只要满足其中两个，另外三个结论一定成立，即推二知三.知识点三：圆心角、弧、弦的关系3.圆心角、弧、弦的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立.推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．知识点四：圆周角定理及其推论4.圆周角定理及其推论（1）定理：一条弧所对的圆周角等于它所对的圆心角的一半. 如图a,∠A=1/2∠O.图a 图b 图c( 2 )推论：①在同圆或等圆中，同弧或等弧所对的圆周角相等.如图b，∠A=∠C.②直径所对的圆周角是直角.如图c,∠C=90°.③圆内接四边形的对角互补.如图a，∠A+∠C=180°，∠ABC+∠在圆中求角度时，通常需要通过一些圆的性质进行转化.比如圆心角与圆周角间的转化；同弧或等弧的圆周角间的转化；连直径，得到直角三角形，通过两锐角互余进行转化等.例：如图，AB是⊙O的直径，C，D是⊙O上ADC=180°. 两点，∠BAC=40°，则∠D的度数为130°．第22讲与圆有关的位置关系知识点一：与圆有关的位置关系关键点拨及对应举例1.点与圆的位置关系设点到圆心的距离为d.(1)d<r⇔点在⊙O内；(2)d＝r⇔点在⊙O上；(3)d>r⇔点在⊙O外．判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可.2.直线和圆的位置关系位置关系相离相切相交由于圆是轴对称和中心对称图形，所以关于圆的位置或计算题中常常出现分类讨论多解的情况.例：已知：⊙O的半径为2，圆心到直线l的距离为1，将直线l沿垂直于l的方向平移，使l与⊙O相切，则平移的距离是1或3.图形公共点个数0个1个2个数量关系d＞r d＝r d＜r知识点二：切线的性质与判定3.切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）.（2）到圆心的距离等于半径的直线是圆的切线.（3）经过半径外端点并且垂直于这条半径的直线是圆的切线.切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径.4.切线的性质（1）切线与圆只有一个公共点.（2）切线到圆心的距离等于圆的半径.（3）切线垂直于经过切点的半径.利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题.*5.切线长（1）定义：从圆外一点作圆的切线，这点与切点之间的线段长叫做这点到圆的切线长.（2）切线长定理：从圆外一点可以引圆的两条切线，两切线长相等，圆心与这一点的连线平分两条切线的夹角.例：如图，AB、AC、DB是⊙O的切线，P、C、D为切点，如果AB=5，AC=3，则BD的长为2.知识点四：三角形与圆5.三角形的外接圆图形相关概念圆心的确定内、外心的性质内切圆半径与三角形边的关系：（1）任意三角形的内切圆（如图a），设三角形的周长为C，则S△ABC=1/2Cr.（2）直角三角形的内切圆（如图b）①若从切线长定理推导，可得r=1/2(a+b+c);若从面积推导，则可得r=.这两种结论可在做选择题和填空题时直接应用.例：已知△ABC的三边长a=3，b=4，c=5，则它的外切圆半径是2.5.经过三角形各定点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形三角形三条垂直平分线的交点到三角形的三个顶点的距离相等6.三角形的内切圆与三角形各边都相切的圆叫三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫圆的外切三角形到三角形三条角平分线的交点到三角形的三条边的距离相等第23讲与圆有关的计算知识点一：正多边形与圆关键点拨与对应举例1.正多边形与圆（1）正多边形的有关概念：边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.（2）特殊正多边形中各中心角、长度比：中心角=120°中心角=90°中心角=60°，△BOC为等边△a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2例：(1) 如果一个正多边形的中心角为72°，那么这个正多边形的边数是5.(2)半径为6的正四边形的边心距为32，中心角等于90°，面积为72.知识点二：与圆有关的计算公式2.弧长和扇形面积的计算扇形的弧长l＝180n rπ；扇形的面积S＝2360n rπ＝12lr例：已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为3π.3.圆锥与侧面展开图（1）圆锥侧面展开图是一个扇形，扇形的半径等于圆锥的母线，扇形的弧长等于圆锥的底面周长.（2）计算公式：,S侧==πrl在求不规则图形的面积时，注意利用割补法与等积变化方法归为规则图形，再利用规则图形的公式求解.例：如图，已知一扇形的半径为3，圆心角为60°，则图中阴影部分的面积为。

2019中考数学一轮复习第一部分教材同步复习第六章圆第23讲圆的相关概念及性质权威预测
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019中考数学一轮复习第一部分教材同步复习第六章圆第23讲圆的相关概念及性质权威预测）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019中考数学一轮复习第一部分教材同步复习第六章圆第23讲圆的相关概念及性质权威预测的全部内容。

第一部分第六章第23讲
1．如图，在半径为4的⊙O中,弦AB∥OC，∠BOC＝30°，则AB的长为（ D ）
A．2 B．2错误!
C．4 D．4错误!
2．如图，AB是⊙O的直径，C,D为圆上两点．若∠AOC＝130°，则∠D等于（ B )
A．20°B．25°
C．35°D．50°。

2019中考数学一轮复习第一部分教材同步复习第六章圆第25讲与圆有关的计算权威预测编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019中考数学一轮复习第一部分教材同步复习第六章圆第25讲与圆有关的计算权威预测）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019中考数学一轮复习第一部分教材同步复习第六章圆第25讲与圆有关的计算权威预测的全部内容。

第一部分第六章第25讲1．圆的面积为94π，则60°的圆心角所对的弧长是( B )A．错误!B．错误!C．错误!D．错误!2．如图，以AD＝2为直径的半圆⊙O中,B，E是半圆弧的三等分点，则图中阴影部分的面积为（ D )A．错误!B．错误!C．错误!D．错误!3．如图，在等腰△ABC中，AB＝BC,以AB为直径的⊙O与AC相交于点D，过点D作DE⊥BC交AB的延长线于点E，垂足为点F.（1）证明：DE是⊙O的切线；(2)若BE＝4，∠E＝30°，求由错误!、线段BE和线段DE所围成图形(阴影部分)的面积．(1）证明：连接BD，OD，∵AB是⊙O的直径，∴∠BDA＝90°.∵AB＝BC,∴∠A＝∠C．又∵AO＝DO，∴OD∥BC,∴∠A＝∠ODA，∴∠C＝∠ODA，∵DE⊥BC，∴OD⊥DE，∴DE是⊙O的切线．（2)解：设⊙O的半径为x，则OB＝OD＝x,在Rt△ODE中，OE＝4＋x，∠E＝30°，∴错误!＝错误!，解得x＝4,∴DE＝4错误!，∴S△ODE＝错误!×4×4错误!＝8错误!，∴S扇形ODB＝错误!＝错误!,则S阴影＝S△ODE－S扇形ODB＝83－错误!。