完整520四年级奥数算式谜一加减法
- 格式:doc
- 大小:25.88 KB
- 文档页数:4

四年级奥数题精选200题一、算式谜1.在下面的数中间填上“+”、“-”;使计算结果为100。
1 2 3 4 5 6 7 8 9=1002. ABCD+ACD+CD=1989;求A、B、C、D。
3. □4□□-3□89=3839。
4. 1ABCDE×3=ABCDE1;求A、B、C、D、E。
二、找规律5.找找规律填数76;2;75;3;74;4;( ); ( );2;3;4;5;8;7;( );( );2;1;4;1;8;1;( );( )。
6.在( )内填入适当的数1;1;2;3;5;8;( );( );1;1;1;3;5;9;( );( );0;1;2;3;6;11;( );( );7.找规律在( )内填上合适的数(1)0;1;3;8;21;55;( );(2)2;6;12;20;30;42;( );(3)1;2;4;7;11;16;( )。
(1)1;6;7;12;13;18;19;( );8.选择一个锐角三角形的一个内角是44度;其余两个角可能是()36度和100度90度和46度75度和61度18度和96度9.简便计算12×102-2469×56+32×56-5613×94+13×10-13×410.解决问题一个三角形的三个内角分别为∠1;∠2和∠3;∠2=2∠1;∠3=∠2;求∠1=?三、排列组合11.小华、小花、小马三个好朋友要在一起站成一排拍一张照片。
三个人争着要站在排头;无法拍照了。
后来照相师傅想了一个办法;说:"我给你们每人站在不同位置都拍一张;好不好?"这下大家同意了。
那么;照相师傅一共要给他们拍几张照片呢?12.二(1)班的小平、小宁、小刚、小超4人排了一个小块板;准备"六、一"演出。
在演出过程中;队形不断变化。
(都站成一排)算算看;他们在演出小快板过程中;一共有多少种队形变化形式?13."69"顺倒过来看还是"69";我们把这两个顺倒一样的数;称为一对数。


5-1-2-1.加減法數字謎教學目標數字謎從形式上可以分為橫式數字謎與豎式數字謎,從運算法則上可以分為加減乘除四種形式的數字謎。
橫式與豎式亦可以互相轉換,本講中將主要介紹數字謎的一般解題技巧。
主要涉及小數、分數、循環小數的數字謎問題,因此,會需要利用數論的知識解決數字謎問題知識點撥一、數字迷加減法1.個位數字分析法2.加減法中的進位與退位3.奇偶性分析法二、數字謎問題解題技巧1.解題的突破口多在於豎式或橫式中的特殊之處,例如首位、個位以及位數的差異;2.要根據不同的情況逐步縮小範圍,並進行適當的估算;3.題目中涉及多個字母或漢字時,要注意用不同符號表示不同數字這一條件來排除若干可能性;4.注意結合進位及退位來考慮;模組一、加法數字謎【例 1】 “華杯賽”是為了紀念和學習我國傑出的數學家華羅庚教授而舉辦的全國性大型少年數學競賽.華羅庚教授生於1910年,現在用“華杯”代表一個兩位數.已知1910與“華杯”之和等於2004,那麼“華杯”代表的兩位數是多少?0191杯华2040+【考點】加法數字謎 【難度】1星 【題型】填空【關鍵字】華杯賽,初賽,第1題【解析】 由0+“杯”=4,知“杯”代表4(不進位加法);再由191+“華”=200,知“華”代表9.因此,“華杯”代表的兩位數是94.【答案】94【例 2】 下麵的算式裏,四個小紙片各蓋住了一個數字。
被蓋住的四個數字的總和是多少?1+49【考點】加法數字謎 【難度】2星 【題型】填空【關鍵字】華杯賽,初賽,第5題【解析】 149的個位數是9,說明兩個個位數相加沒有進位,因此,9是兩個個位數的和,14是兩個十位數的和。
於是,四個數字的總和是14+9=23。
【答案】23【例 3】 在下邊的算式中,被加數的數字和是和數的數字和的三倍。
問:被加數至少是多少?例題精講【考點】加法數字謎 【難度】3星 【題型】填空【關鍵字】第四屆,華杯賽,初賽,第2題【解析】 從“被加數的數字和是和的數字和的三倍”這句話,可以推斷出兩點:①被加數可以被3整除。

学生姓名学生年级学校上课时间辅导老师科目教学重点数学加减法的竖式谜题教学目标训练学生数字加减计算的敏感度开场:1.行礼;2.晨读;3.检查作业;4.填写表格新课导入解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
新课内容考点一:在下面空格中填入适当的数字使算式成立基础练习:□ 9 1 □ 8 2+ □ 1 □ + □ 1 □□ 9 1 □□ 9 0 □□ 7 □□ 9 □+ □ 1 4 + □ 1 1 □ 8 □□□ 7 1 □1 □□ 8 7+ □□ 5 + 9 □ 5 □□□ 4 □ 8 5 26 4 □□□□ 3+ □□ 7 8 + 2 □□ 0 2 6 □□□ 2□□□□□□- □ 8 5 - □ 8 56 37 5 4 8□□□□□□- □ 8 7 - 2 □ 57 3 7 7 3 75 6 □□ 2- □□ 7 - 2 □□ 9 4 2 44 9 □□ 2 □- □□ 7 - □□ 81 7 5 5 3 6□ 8 □ 6 3 □□+ □ 6 □ 3 + □□ 7 8□□ 1 2 8 □ 0 2 6提升训练:□ 8 □□ 1+ 4 □ 2 + □ 9 □□□□□□□ 9 □- □□□ - □□□1 □ 5□ 7 □□ 2 □+ 6 □ 4 - □□ 5□□□□ 7 3 7- □□ 5 + □ 8 □8 □ 0 □ 8考点二:在方格中填上0-9十个数字,不能重复,使等式成立基础练习:□□ 4 □□□□+ 2 8 □ + □ 6□□□ 3 □□ 4 □□□□□- □ 9 □□□ 7提升训练:请你把1,2,3,4,5,6,7,8,9这9个数字分别填到如图所示的方框内,要求图中每个数位上的数字第二排比第一排大,第三排比第二排大。

数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【考点】加法数字谜 【难度】1星 【题型】填空 【关键词】华杯赛,初赛,第1题 【解析】 由0+“杯”=4,知“杯”代表4(不进位加法);再由191+“华”=200,知“华”代表9.因此,“华杯”代表的两位数是94.【答案】94【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?例题精讲知识点拨教学目标5-1-2-1.加减法数字谜1+49【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】华杯赛,初赛,第5题 【解析】 149的个位数是9,说明两个个位数相加没有进位,因此,9是两个个位数的和,14是两个十位数的和。
于是,四个数字的总和是14+9=23。
【答案】23【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】第四届,华杯赛,初赛,第2题 【解析】 从“被加数的数字和是和的数字和的三倍”这句话,可以推断出两点:①被加数可以被3整除。

算式谜(一)一、知识要点“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。
解决这类问题,可以根据已学过的知识,运用正确的分析推理方法,确定算式中的未知数字和运用符号。
由于这类题目的解答过程类似全平时进行的猜谜语游戏,所以,我们把这类题目称为“算式谜题”。
解答算式谜问题时,要先仔细审题,分析数据之间的关系,找到突破口,逐步试验,分析求解,通常要运用倒推法、凑整法、估值法等。
二、精讲精练【例题1】在下面算式的括号里填上合适的数。
【思路导航】根据题目特点,先看个位:7+5=12,在和的个位()中填2,并向十位进一;再看十位,()+4+1的和个位是1,因此,第一个加数的()中只能填6,并向百位进1;最后来看百位、千位,6+()+1的和的个位是2,第二个加数的()中只能填5,并向千位进1;因此,和的千位()中应填8。
练习1:(1)在括号里填上合适的数。
(2)在方框里填上合适的数。
(3)下面的竖式里,有4个数字被遮住了,求竖式中被盖住的4个数字的和。
【例题2】下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字,相同的汉字代表相同的数字。
当它们各代表什么数字时,下列的算式成立。
【思路导航】先看个位,3个“飞”相加的和的个位数字是1,可推知“飞”代表7;再看十位,3个“腾”相加,再加上个位进来的2,所得的和的个位是0,可推知“腾”代表6;再看百位,两个“龙”相加,加上十位进上来的2,所得和的个位是0,“龙”可能是4或9,考虑到千位上的“巨”不可能为0,所以“龙”只能代表4,“巨”只能代表1。
练习2:【例题3】下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个,相同的汉字代表相同的数字。
这些汉字各代表哪些数字?【思路导航】这道题应以“卒”入手来分析。
“卒”和“卒”相加和的个位数字仍然是“卒”,这个数字只能是0。
确定“卒”是0后,所有是“卒”的地方,都是0。
注意到百位上是“兵”+“兵”=“卒”,容易知道“兵”是5,“车”是1;再由十位上的情况可推知“马”是4,进而推得“炮”是2。


数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【考点】加法数字谜 【难度】1星 【题型】填空 【关键词】华杯赛,初赛,第1题【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?1+49例题精讲知识点拨教学目标5-1-2-1.加减法数字谜【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】华杯赛,初赛,第5题【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】第四届,华杯赛,初赛,第2题【例 4】 两个自然数,它们的和加上它们的积恰为34,这两个数中较大数为( ). 【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】走美杯,3年级,初赛【例 5】 下面的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?1991+【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】华杯赛,初赛,第11题【例 6】 在下边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数tavs =______s t v av t s t t t v t t +【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】迎春杯,五年级,初赛,第5题【巩固】 下面的字母各代表什么数字,算式才能成立?DD D +ACDEE B EC B A【考点】加法数字谜 【难度】2星 【题型】填空【巩固】 右面算式中每一个汉字代表一个数字,不同的汉字表示不同的数字.当它们各代表什么数字时算式成立?+啊好是真好是真好啊好【考点】加法数字谜 【难度】2星 【题型】填空【巩固】 下面算式中,相同汉字代表相同数字,不同汉字代表不同数字,求“数学真好玩”代表的数是几?+爱好真知数学更好数学真好玩 【考点】加法数字谜 【难度】2星 【题型】填空【关键词】走美杯,初赛,六年级,第3题【例 7】 下图是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字.已知BAD 不是3的倍数,GOOD 不是8的倍数,那么ABGD 代表的四位数是多少?B A DB A D G O O D+【考点】加法数字谜 【难度】3星 【题型】填空【例 8】 在下面的算式中,汉字“第、十、一、届、华、杯、赛’,代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛’’所代表的7个数字的和等于 .+届赛6一杯0十华02第【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】华杯赛,初赛【例 9】在下边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++☆=_______.+☆☆【考点】加法数字谜 【难度】3星 【题型】填空【例 10】 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A +B +C +D +E +F +G = 。

四年级算式谜在四年级的学习中,我们遇到了很多有趣的算式谜题,这些谜题让我们不仅学习了数学知识,还锻炼了我们的思维能力和解决问题的能力。
其中,最简单的一种算式谜题是“×”和“÷”的问题。
这类问题通常会给出一些数字和运算符,让我们通过运算得到答案。
比如,有一个问题问我们:10÷5=?这个问题很简单,只要把10分成两半,就得到了答案2。
除了“×”和“÷”的问题,还有一种常见的算式谜题是“+”和“-”的问题。
这类问题通常会让我们通过加法和减法来得到答案。
比如,有一个问题问我们:10+5-3=?这个问题需要我们先计算10+5=15,然后再从15中减去3,就得到了答案12。
除了这些基本的算式谜题,还有一些更复杂的问题。
比如,有一个问题问我们:有一个数列,第一项是1,第二项是2,第三项是3,以此类推,第n项是多少?这个问题需要我们找到数列的规律,然后计算出第n项的值。
通过这个问题,我们不仅学习了数列的概念,还了解了数列的规律和计算方法。
四年级的算式谜题是我们学习数学的重要内容之一。
通过这些谜题,我们不仅学习了数学知识,还锻炼了我们的思维能力和解决问题的能力。
在未来的学习中,我们还会遇到更多有趣的谜题,让我们不断探索和学习。
一年级的图文算式,是孩子们学习数学的基础。
它通过直观的图形和数字,帮助孩子们理解加减乘除等基本运算。
图文算式的形式使得孩子们更容易理解数学概念。
对于刚刚接触数学的一年级学生来说,纯数字的运算可能会让他们感到困惑。
而图文算式则通过具体的图形和数字,帮助他们更好地理解问题。
例如,在计算“8+5=?”时,老师可以在黑板上画出8个苹果,然后再画5个苹果,让学生数出总共有多少个苹果。
这样,孩子们就可以通过具体的图形来理解加法的概念。
图文算式还能够帮助孩子们提高解决问题的能力。
在解决实际问题时,孩子们需要将数学概念与实际问题起来。
而图文算式则可以帮助他们更好地理解问题的背景和条件,从而更好地解决问题。

第五周算式谜(一)专题简析:“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。
解决这类问题,可以根据已学过的知识,运用正确的分析推理方法,确定算式中的未知数字和运用符号。
由于这类题目的解答过程类似全平时进行的猜谜语游戏,所以,我们把这类题目称为“算式谜题”。
解答算式谜问题时,要先仔细审题,分析数据之间的关系,找到突破口,逐步试验,分析求解,通常要运用倒推法、凑整法、估值法等。
例1:在下面算式的括号里填上合适的数。
7 6 () 5+ () 4 7()2 1 ()分析:根据题目特点,先看个位:7+5=12,在和的个位()中填2,并向十位进一;再看十位,()+4+1的和个位是1,因此,第一个加数的()中只能填6,并向百位进1;最后来看百位、千位,6+()+1的和的个位是2,第二个加数的()中只能填5,并向千位进1;因此,和的千位()中应填8。
练习一(1)在括号里填上合适的数。
(2)在方框里填上合适的数。
6 ()()□0 □□+2()1 5 -3()1 7()0 9 1 2 8 5 6 (3)下面的竖式里,有4个数字被遮住了,求竖式中被盖住的4个数字的和。
□□+ □□1 6 9例2:下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字,相同的汉字代表相同的数字。
当它们各代表什么数字时,下列的算式成立。
腾飞龙腾飞+巨龙腾飞2 0 0 1分析:先看个位,3个“飞”相加的和的个位数字是1,可推知“飞”代表7;再看十位,3个“腾”相加,再加上个位进来的2,所得的和的个位是0,可推知“腾”代表6;再看百位,两个“龙”相加,加上十位进上来的2,所得和的个位是0,“龙”可能是4或9,考虑到千位上的“巨”不可能为0,所以“龙”只能代表4,“巨”只能代表1。
练习二(1) C D (2)式谜(3)澳门A C D 填式谜澳门归+A B C D +巧填式谜+庆澳门归1 9 8 9 1 9 9 5 1 9 9 9例3:下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个,相同的汉字代表相同的数字。
算式谜四年级奥数题算式谜是一种让人在解题中体会到乐趣的数学游戏。
四年级的奥数题则是需要学生们有一定数学基础和思维能力的挑战。
在本文中,我们将结合这两个主题,探讨一下四年级的奥数题中的算式谜。
首先,我们来看一道典型的四年级奥数题:小明有一些糖果,他把这些糖果平分给他的三个朋友,每个朋友得到5颗糖果,还剩下4颗糖果。
如果他再多买10颗糖果,那么他就可以平分给4个朋友。
请问小明原来有多少颗糖果?这道题需要学生们运用到一些基本的数学概念和计算方法,如除法、乘法、加法和减法等。
但是,如果我们把这个问题变成一个算式谜,会不会更加有趣呢?我们可以这样设计一个算式谜:有一个三位数,它除以3余1,再加上10可以被4整除。
请问这个数是多少?这个算式谜与原来的题目是等价的,但是通过这种方式,我们可以让学生们在解题中更加享受到数学的乐趣。
他们需要运用到除法、加法和取模等知识,同时也需要有一定的逻辑思维能力。
除了这个例子,还有许多其他的算式谜可以用来挑战四年级学生的数学能力。
例如:1. 有一个两位数,它的十位数和个位数的和是9,它的十位数比个位数多2,这个数是多少?2. 有一个三位数,它的百位数是4,个位数是2,如果把它的百位数和个位数交换,得到一个比原来的数小66,这个数是多少?3. 小明有一些钱,他花掉了三分之一,还剩下20元。
请问他原来有多少钱?这些算式谜都需要学生们有一定的数学基础和思维能力,但是它们也能带来一定的乐趣和挑战。
通过这种方式,我们可以让学生们更加积极地学习数学,培养他们的逻辑思维和解决问题的能力。
总之,算式谜是一种非常有趣的数学游戏,可以让学生们在解题中享受到数学的乐趣。
四年级的奥数题则需要学生们有一定的数学基础和思维能力,通过将这两个主题相结合,我们可以让学生们更加积极地学习数学,培养他们的逻辑思维和解决问题的能力。
数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?1+49例题精讲知识点拨教学目标5-1-2-1.加减法数字谜【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【例 4】 两个自然数,它们的和加上它们的积恰为34,这两个数中较大数为( ).【例 5】 下面的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?1991+【例 6】 在下边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数tavs =______s t v av t s t t t v t t +【巩固】 下面的字母各代表什么数字,算式才能成立?DD D +AC DEE B ECBA【巩固】 右面算式中每一个汉字代表一个数字,不同的汉字表示不同的数字.当它们各代表什么数字时算式成立?+啊好是真好是真好啊好【巩固】 下面算式中,相同汉字代表相同数字,不同汉字代表不同数字,求“数学真好玩”代表的数是几?+爱好真知数学更好数学真好玩【例 7】 下图是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字.已知BAD 不是3的倍数,GOOD 不是8的倍数,那么ABGD 代表的四位数是多少?B A DB A D G O O D +【例 8】 在下面的算式中,汉字“第、十、一、届、华、杯、赛’,代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛’’所代表的7个数字的和等于 .+届赛6一杯0十华02第【例 9】 在下边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++ ☆=_______.+☆☆【例 10】 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A +B +C +D +E +F +G = 。
星云站备课教员:***第二讲算式谜(加减法)一、教学目标: 1. 熟知“和、差、积、商”的位数特征。
2. 四年级寒假奥数教案第2讲:算式谜(加减法)。
二、教学重点:巧填方框里的数,通过运算法则,把不完整的算式补充完整。
三、教学难点:巧解数字谜,通过找关键位置进行突破推理出不同的汉字或字母表示的数,使算式成立。
四、教学准备:PPT五、教学过程:第一课时(40分钟)一、外星游记(5分钟)师:同学们,玩过数学里面的踩地雷游戏吗?生:没有。
师:老师带你们去体验下吧。
师:老师在里面设置了猜谜语游戏、地雷、和奖励,踩到地雷的人将要接受小小的惩罚,(老师写一些小纸条,上面写一些好玩有趣的活动,让学生参与)猜到谜语的将可以获得奖励。
要不要一起试一试?生:要。
1. 一加一不是二(打一字)一加一不是二:王2. 一减一不是零(打一字)一减一不是零:三3. 旭日东升(打一数字)旭日东升,旭字中日字升起来,走了,留下"九"。
4. 八分之七。
(打一成语)七上八下因为是7/8,七在上面,八在下方啊。
5. 二三四五六七八九。
(打一成语)缺了衣(一)少了食(十)所以是缺衣少食。
师:数学中也有许多有趣的谜语,这节课老师将带你们去数学迷宫探索算式谜,一起去吧。
[板书课题:算式谜(加减法)]二、星海遨游(30分钟)(一)星海遨游1(10分钟)在下面算式的括号里填上合适的数。
师:根据题目特点,我们先看哪一位?生:先看个位。
师:5+9等于多少?生:14。
师:所以个位上填多少?生:在和的个位()中填4,并向十位进1;师:十位怎么算呢?生:()+4+1的和个位是1,因此,第一个加数的()中只能填6,并向百位进1;师:百位,千位怎么解决呢?生:6+()+1的和个位是2,第二个加数的()中只能填5,并向千位进1,因此,千位上()中应填9。
板书:(一)星海历练1(5分钟)在□里填上适当的数。
分析:根据题目特点,先看个位,3-□=4,个位3减4不够,所以被减数个位要向前借一,13-4=9,减数个位为9,被减数十位□-1-8=9,十位为8,百位为8-1-7=□,所以差的百位为0,千位上□-6=8,被减数千位借一,所以,被减数千位为4,减数的万位就为1。
巧算加减法及加减法的竖式数字谜巧算加减法一、加法加法交换律:两个数相加,交换加数的位置,他们的和不变。
即:a+b=b+a其中a,b各表示任意一数.例如,7+8=8+7=15.总结:多个数相加,任意交换相加的次序,其和不变.加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变。
即:a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).总结:多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变。
二、减法在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”。
如:a+b-c=a+(b-c)a-b+c=a-(b-c)a-b-c=a-(b+c)三、加减法中的速算与巧算速算巧算的核心思想和本质:凑整1、分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.2、加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.4、“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)例题精讲一、加减速算【例1】计算:57911131517192123.【例 2】计算:(1)117+229+333+471+528+622(2)(1350+249+468)+(251+332+1650)(3)756-248-352(4)894-89-111-95-105-94【巩固】同学们,你们有什么好办法又快又准的算出下面各题的答案?把你的好方法讲一讲!也当一次小老师!⑴1847192862813664⑵1234567887661594322⑶200077415923⑷617271438315771二、加补凑整【例 3】计算:(1)298+396+495+691+799+21(2)195+196+197+198+199+15(3)98-96-97-105+102+101(4)399+403+297-501【例 4】199+298+397+496+595+20=___________。
算式谜(一)“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。
解答算式谜问题时,要先仔细审题,分析数据之间的关系,找到突破口,逐步试验,分析求解,通常要运用倒推法、凑整法、估值法等。
例1:在下面算式的括号里填上合适的数。
7 6 () 5+ () 4 7() 2 1 ()分析:根据题目特点,先看个位:7+5=12,在和的个位()中填2,并向十位进一;再看十位,()+4+1的和个位是1,因此,第一个加数的()中只能填6,并向百位进1;最后来看百位、千位,6+()+1的和的个位是2,第二个加数的()中只能填5,并向千位进1;因此,和的千位()中应填8。
练习(1)在括号里填上合适的数。
(2)在方框里填上合适的数。
6 ()()□ 0 □□+ 2 () 1 5 -3 () 1 7() 0 9 1 2 8 5 6(3)下面的竖式里,有4个数字被遮住了,求竖式中被盖住的4个数字的和。
□□+ □□1 6 9例2:下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字,相同的汉字代表相同的数字。
当它们各代表什么数字时,下列的算式成立。
腾飞龙腾飞+巨龙腾飞2 0 0 1分析:先看个位,3个“飞”相加的和的个位数字是1,可推知“飞”代表7;再看十位,3个“腾”相加,再加上个位进来的2,所得的和的个位是0,可推知“腾”代表6;再看百位,两个“龙”相加,加上十位进上来的2,所得和的个位是0,“龙”可能是4或9,考虑到千位上的“巨”不可能为。
1“巨”只能代表,4,所以“龙”只能代表0.练习:(1) C D (2)式谜(3)澳门A C D 填式谜澳门归+A B C D +巧填式谜 +庆澳门归1 9 8 9 1 9 9 5 1 9 9 9例3:下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个,相同的汉字代表相同的数字。
这些汉字各代表哪些数字?兵炮马卒+ 兵炮车卒车卒马兵卒分析:这道题应以“卒”入手来分析。
四年级奥数:数字谜(一)我们在三年级已经学习过一些简单的数字谜问题.这两讲除了复习巩固学过的知识外,还要学习一些新的内容.例1 在下面算式等号左边合适的地方添上括号,使等式成立:5+7×8+12÷4-2=20.分析:等式右边是20,而等式左边算式中的7×8所得的积比20大得多.因此必须设法使这个积缩小一定的倍数,化大为小.从整个算式来看,7×8是4的倍数,12也是4的倍数,5不能被4整除,因此可在7×8+12前后添上小括号,再除以4得17,5+17-2=20.解:5+(7×8+12)÷4-2=20.例2把1~9这九个数字填到下面的九个□里,组成三个等式(每个数字只能填一次):分析与解:如果从加法与减法两个算式入手,那么会出现许多种情形.如果从乘法算式入手,那么只有下面两种可能:2×3=6或2×4=8,所以应当从乘法算式入手.因为在加法算式□+□=□中,等号两边的数相等,所以加法算式中的三个□内的三个数的和是偶数;而减法算式□-□=可以变形为加法算式□=□+□,所以减法算式中的三个□内的三个数的和也是偶数.于是可知,原题加减法算式中的六个数的和应该是偶数.若乘法算式是2×4=8,则剩下的六个数1,3,5,6,7,9的和是奇数,不合题意;若乘法算式是2×3=6,则剩下的六个数1,4,5,7,8,9可分为两组:4+5=9,8-7=1(或8-1=7);1+7=8,9-5=4(或9-4=5).所以答案为与例3下面的算式是由1~9九个数字组成的,其中“7”已填好,请将其余各数填入□,使得等式成立:□□□÷□□=□-□=□-7.分析与解:因为左端除法式子的商必大于等于2,所以右端被减数只能填9,由此知左端被除数的百位数只能填1,故中间减式有8-6,6-4,5-3和4-2四种可能.经逐一验证,8-6,6-4和4-2均无解,只有当中间减式为5-3时有如下两组解:128÷64=5-3=9-7,或164÷82=5-3=9-7.例4 将1~9九个数字分别填入下面四个算式的九个□中,使得四个等式都成立:□+□=6,□×□=8,□-□=6,□□÷□=8.分析与解:因为每个□中要填不同的数字,对于加式只有两种填法:1+5或2+4;对于乘式也只有两种填法:1×8或2×4.加式与乘式的数字不能相同,搭配后只有两种可能:(1)加式为1+5,乘式为2×4;(2)加式为2+4,乘式为1×8.对于(1),还剩3,6,7,8,9五个数字未填,减式只能是9-3,此时除式无法满足;对于(2),还剩3,5,6,7,9五个数字未填,减式只能是9-3,此时除式可填56÷7.答案如下:2+4=6,1×8=8,9-3=6,56÷7=8.例2~例4都是对题目经过初步分析后,将满足题目条件的所有可能情况全部列举出来,再逐一试算,决定取舍.这种方法叫做枚举法,也叫穷举法或列举法,它适用于只有几种可能情况的题目,如果可能的情况很多,那么就不宜用枚举法.例5 从1~9这九个自然数中选出八个填入下式的八个○内,使得算式的结果尽可能大:[○÷○×(○+○)]-[○×○+○-○].分析与解:为使算式的结果尽可能大,应当使前一个中括号内的结果尽量大,后一个中括号内的结果尽量小.为叙述方便,将原式改写为:[A÷B×(C+D)]-[E×F+G-H].通过分析,A,C,D,H应尽可能大,且A应最大,C,D次之,H再次之;B,E,F,G应尽可能小,且B应最小,E,F次之,G再次之.于是得到A=9,C=8,D=7,H=6,B=1,E=2,F=3,G=4,其中C与D,E与F的值可互换.将它们代入算式,得到[9÷1×(8+7)]-[2×3+4-6]=131.练习91.在下面的算式里填上括号,使等式成立:(1)4×6+24÷6-5=15;(2)4×6+24÷6-5=35;(3)4×6+24÷6-5=48;(4)4×6+24÷6-5=0.2.加上适当的运算符号和括号,使下式成立:1 2 3 4 5 =100.3.把0~9这十个数字填到下面的□里,组成三个等式(每个数字只能填一次):□+□=□,□-□=□,□×□=□□.4.在下面的□里填上+,-,×,÷,()等符号,使各个等式成立:4□4□4□4=1,4□4□4□4=3,4□4□4□4=5,4□4□4□4=9.5.将2~7这六个数字分别填入下式的□中,使得等式成立:□+□-□=□×□÷□.6.将1~9分别填入下式的九个□内,使算式取得最大值:□□□×□□□×□□□.7.将1~8分别填入下式的八个□内,使算式取得最小值:□□×□□×□□×□□.第10讲数字谜(二)例1 把下面算式中缺少的数字补上:分析与解:一个四位数减去一个三位数,差是一个两位数,也就是说被减数与减数相差不到100.四位数与三位数相差不到100,三位数必然大于900,四位数必然小于1100.由此我们找出解决本题的突破口在百位数上.(1)填百位与千位.由于被减数是四位数,减数是三位数,差是两位数,所以减数的百位应填9,被减数的千位应填1,百位应填0,且十位相减时必须向百位借1.(2)填个位.由于被减数个位数字是0,差的个位数字是1,所以减数的个位数字是9.(3)填十位.由于个位向十位借1,十位又向百位借1,所以被减数十位上的实际数值是18,18分解成两个一位数的和,只能是9与9,因此,减数与差的十位数字都是9.所求算式如右式.由例1看出,考虑减法算式时,借位是一个重要条件.例 2 在下列各加法算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字,求出这两个算式:分析与解:(1)这是一道四个数连加的算式,其特点是相同数位上的数字相同,且个位与百位上的数字相同,即都是汉字“学”.从个位相同数相加的情况来看,和的个位数字是8,有两种可能情况:2+2+2+2=8与7+7+7+7=28,即“学”=2或7.如果“学”=2,那么要使三个“数”所代表的数字相加的和的个位数字为8,“数”只能代表数字6.此时,百位上的和为“学”+“学”+1=2+2+1=5≠4.因此“学”≠2.如果“学”=7,那么要使三个“数”所代表的数字相加再加上个位进位的2,和的个位数字为8,“数”只能代表数字2.百位上两个7相加要向千位进位1,由此可得“我”代表数字3.满足条件的解如右式.(2)由千位看出,“努”=4.由千、百、十、个位上都有“努”,5432-4444=988,可将竖式简化为左下式.同理,由左下式看出,“力”=8,988-888=100,可将左下式简化为下中式,从而求出“学”=9,“习”=1.满足条件的算式如右下式.例2中的两题形式类似,但题目特点并不相同,解法也不同,请同学们注意比较.例 3 下面竖式中每个汉字代表一个数字,不同的汉字代表不同的数字,求被乘数.分析与解:由于个位上的“赛”ד赛”所得的积不再是“赛”,而是另一个数,所以“赛”的取值只能是2,3,4,7,8,9.下面采用逐一试验的方法求解.(1)若“赛”=2,则“数”=4,积=444444.被乘数为444444÷2=222222,而被乘数各个数位上的数字各不相同,所以“赛”≠2.(2)若“赛”=3,则“数”=9,仿(1)讨论,也不行.(3)若“赛”=4,则“数”=6,积=666666.666666÷4得不到整数商,不合题意.(4)若“赛”=7,则“数”=9,积=999999.被乘数为999999÷7=142857,符合题意.(5)若“赛”=8或9,仿上讨论可知,不合题意.所以,被乘数是142857.例4 在□内填入适当的数字,使左下式的乘法竖式成立.分析与解:为清楚起见,我们用A,B,C,D,…表示□内应填入的数字(见右上式).由被乘数大于500知,E=1.由于乘数的百位数与被乘数的乘积的末位数是5,故B,C中必有一个是5.若C=5,则有6□□×5=(600+□□)×5=3000+□□×5,不可能等于□5□5,与题意不符,所以B=5.再由B=5推知G=0或5.若G=5,则F=A=9,此时被乘数为695,无论C为何值,它与695的积不可能等于□5□5,与题意不符,所以G=0,F=A=4.此时已求出被乘数是645,经试验只有645×7满足□5□5,所以C=7;最后由B=5,G=0知D为偶数,经试验知D=2.右式为所求竖式.此类乘法竖式题应根据已给出的数字、乘法及加法的进位情况,先填比较容易的未知数,再依次填其余未知数.有时某未知数有几种可能取值,需逐一试验决定取舍.例5 在□内填入适当数字,使左下方的除法竖式成立.分析与解:把左上式改写成右上式.根据除法竖式的特点知,B=0,D=G=1,E=F=H=9,因此除数应是99的两位数的约数,可能取值有11,33和99,再由商的个位数是5以及5与除数的积是两位数得到除数是11,进而知A=C-9.至此,除数与商都已求出,其余未知数都可填出(见右式).此类除法竖式应根据除法竖式的特点,如商的空位补0、余数必须小于除数,以及空格间的相互关系等求解,只要求出除数和商,问题就迎刃而解了.例 6 把左下方除法算式中的*号换成数字,使之成为一个完整的式子(各*所表示的数字不一定相同).分析与解:由上面的除法算式容易看出,商的十位数字“*”是0,即商为.因为除数与8的积是两位数,除数与商的千位数字的积是三位数,知商的千位数是9,即商为9807.因为“除数×9”是三位数,所以除数≥12;又因为“除数×8”是两位数,所以除数≤12.推知除数只能是12.被除数为9807×12=117684.除法算式如上页右式.练习101.在下面各竖式的□内填入合适的数字,使竖式成立:2.右面的加法算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.问:“小”代表什么数字?3.在下列各算式中,不同的汉字代表不同的数字相同的汉字代表相同的数字.求出下列各式:4.在下列各算式中,相同的字母代表相同的数字,不同的字母代表不同的数字.这些算式中各字母分别代表什么数字?答案练习91.(1)4×(6+24)÷6-5=15;(2)4×(6+24÷6)-5=35;(3)4×6+24÷(6-5)=48;(4)4×[(6+24)÷6-5]=0.2.(1×2+3)×4×5=100.3.3+6=9,8-7=1,4×5=20.(填法不唯一)4.(4+4)÷(4+4)=1,(4+4+4)÷4=3,(4×4+4)÷4=5,4+4+4÷4=9.5.6+7-3=5×4÷2.6.941×852×763=611721516.提示:按下面两个原则填数:①将较大的数填在高数位上;②各乘数之间的差尽量小.7.15×26×37×48=692640.练习102.9.提示:“生”=“学”+1.提示:(1)由千位知A=B+1,再由个位知C=9.十位减法需向百位借1,由百位知A=8,从而B=7.(2)由除式特点知D=0,A=9,C=1,依次推出G=2,F=5.。
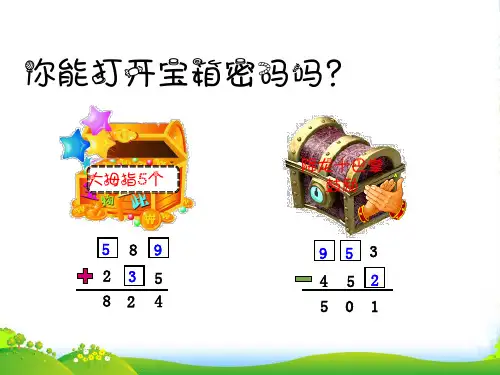
算式谜(一)
“算式谜”一般是指那些含有未知数字或缺少运算符号的算式。
解答算式谜问题时,要先仔细审题,分析数据之间的关系,找到突破口,逐步试验,分析求解,通常要运用倒推法、凑整法、估值法等。
例1:在下面算式的括号里填上合适的数。
7 6 () 5
+ () 4 7
() 2 1 ()
分析:根据题目特点,先看个位:7+5=12,在和的个位()中填2,并向十位进一;再看十位,()+4+1的和个位是1,因此,第一个加数的()中只能填6,并向百位进1;最后来看百位、千位,6+()+1的和的个位是2,第二个加数的()中只能填5,并向千位进1;因此,和的千位()中应填8。
练习
(1)在括号里填上合适的数。
(2)在方框里填上合适的数。
6 ()()□ 0 □□
+ 2 () 1 5 -3 () 1 7
() 0 9 1 2 8 5 6
(3)下面的竖式里,有4个数字被遮住了,求竖式中被盖住的4个数字的和。
□□
+ □□
1 6 9
例2:下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字,相同的汉字代表相同的数字。
当它们各代表什么数字时,下列的算式成立。
腾飞
龙腾飞
+巨龙腾飞
2 0 0 1
分析:先看个位,3个“飞”相加的和的个位数字是1,可推知“飞”代表7;再看十位,3个“腾”相加,再加上个位进来的2,所得的和的个位是0,可推知“腾”代表6;再看百位,两个“龙”相加,加上十位进上来的2,所得和的个位是0,“龙”可能是4或9,考虑到千位上的“巨”不可能为。
1“巨”只能代表,4,所以“龙”只能代表0.
练习:
(1) C D (2)式谜(3)澳门
A C D 填式谜澳门归
+A B C D +巧填式谜 +庆澳门归
1 9 8 9 1 9 9 5 1 9 9 9
例3:下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个,相同的汉字代表相同的数字。
这些汉字各代表哪些数字?
兵炮马卒
+ 兵炮车卒
车卒马兵卒
分析:这道题应以“卒”入手来分析。
“卒”和“卒”相加和的个位数字仍然是“卒”,这个数字只能是0。
确定“卒”是0后,所有是“卒”的地方,都是0。
注意到百位上是“兵”+“兵”=“卒”,容易知道“兵”是5,“车”是1;再由十位上的情况可推知“马”是4,进而推得“炮”是2。
练习:
(1) B A (2) A B C (3)炮兵兵炮
A B + C D C -兵马兵
+ A B A B C D 马兵马
C A A
三、【巩固练习】
1、在下面算式的括号里填上合适的数。
(1)() 6 ()()(2)() 0 ()()
+ 2 () 1 5 - 3 () 1 6
8 0 9 1 4 8 5 7
2、A、B、C、D分别代表4个不同的数字,相同的字母代表相同的数字,求使得下面算式成立A、B、C、D各自代表的数字。
A B C D
A C D
+ C D
1 9 8 9
3、A、B、C、D分别代表不同的数字,它们各是什么数字时同上面的算式成立?
A B C D
- C D C
A B C
4、在□里填上适当的数,使等式成立。
3 □(1)□ 6 4 (2) □□□ 3 - □ 7
8 + 4 8 □ 0 4 2
□、下面算式中不同的图形代表不同的数,不同的字母代表不同的数,请将算式中的图形或字母还原5 成数字。
(2) A B C D ○ 2 □(1) 1 + A B E D □ 1 △-
E D C A D
○ 3 ○
6、在□里填上适当的数。
6 3 □□□□ 8 □
+ + 9 1 □□ 7 8
3 □+ 6 □
0 2 6
□□□□ 1 2 8
□□
□□ 5 □ 2 6 □ 0 0 □□ 9
□- □ - □- 6 0 7 9 □
4 9
□1 7 6
□9
7、下列算式中不同的字母代表不同的数字,求出下列字母所代表的数字。
A B C A B 8 B B A A C
+ A C A B C A C A -9 +
A B A 2 2 6
8 8 8
B
四、【课堂总结】五、【课后作业】.
1、在下面算式的空格内各填入一个合适的数字,使算式成立 9 □□ 7 □
□□ 8 2
1 1 1 4 □+ □□ 1 + □+
□ 7 1 □ 8 □□□ 9 0 □□
2、在下面的算式内,各填上一个合适的数字,使等式成立。
□□□□□□□□□ 5 8 7 □- 8 5 □- - 2 □
7 3 7 8 3 7 5 4 8
、在下面的算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
3习奥运会学好香港
+申办成功-学习好归港香
+学好归港香庆 1
0 2 0
7 9 9 1
4、在空格内填入适当数字使竖式成立。
□□□□□□□□□□□+ □- □□
7 7 7 78 8 8 8。