时变电磁场(电磁场与电磁波).

第六章时变电磁场有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场之中，如题图所示。

滑片的位置由确定，轨道终端接有电阻，试求电流i.解穿过导体回路abcda的磁通为故感应电流为一根半径为a的长圆柱形介质棒放入均匀磁场中与z轴平行。

设棒以角速度绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。

解介质棒内距轴线距离为r处的感应电场为故介质棒内的极化强度为极化电荷体密度为极化电荷面密度为则介质体积内和表面上同单位长度的极化电荷分别为平行双线传输线与一矩形回路共面，如题图所示。

设、、，求回路中的感应电动势。

解由题给定的电流方向可知，双线中的电流产生的磁感应强度的方向，在回路中都是垂直于纸面向内的。

故回路中的感应电动势为式中故则有一个环形线圈，导线的长度为l，分别通过以直流电源供应电压U0和时变电源供应电压U（t）。

讨论这两种情况下导线内的电场强度E。

解设导线材料的电导率为，横截面积为S，则导线的电阻为而环形线圈的电感为L，故电压方程为当U=U0时，电流i也为直流，。

故此时导线内的切向电场为当U=U（t）时，，故即求解此微分方程就可得到。

一圆柱形电容器，内导体半径为a，外导体内半径为b，长为l。

设外加电压为，试计算电容器极板间的总位移电流，证明它等于电容器的传导电流。

解当外加电压的频率不是很高时，圆柱形电容器两极板间的电场分布与外加直流电压时的电场分布可视为相同（准静态电场），即故电容器两极板间的位移电流密度为则式中，是长为l的圆柱形电容器的电容。

流过电容器的传导电流为可见由麦克斯韦方程组出发，导出点电荷的电场强度公式和泊松方程。

解点电荷q产生的电场满足麦克斯韦方程和由得据散度定理，上式即为利用球对称性，得故得点电荷的电场表示式由于，可取，则得即得泊松方程试将麦克斯方程的微分形式写成八个标量方程：（1）在直角坐标中；（2）在圆柱坐标中；（3）在球坐标中。

解（1）在直角坐标中（2）在圆柱坐标中（3）在球坐标系中已知在空气中，求和。

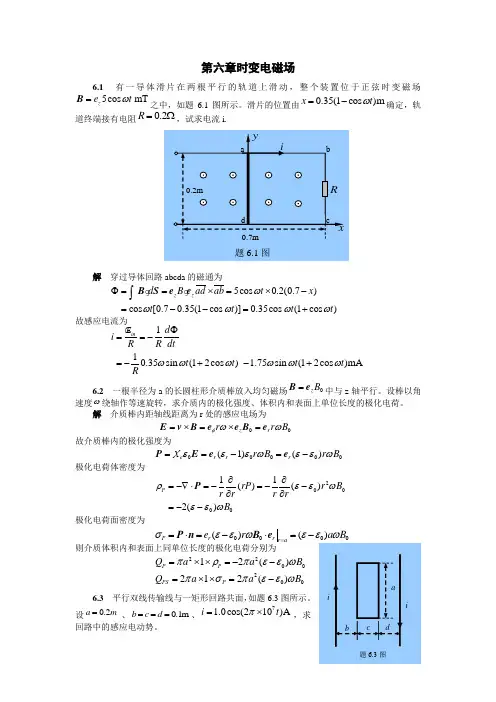
第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场5cos mT z e t ω=B 之中，如题6.1图所示。

滑片的位置由0.35(1cos )m x t ω=-确定，轨道终端接有电阻0.2R =Ω，试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。

设棒以角速度ω绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。

解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面，如题6.3图所示。

设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯，求回路中的感应电动势。

特性：1）电场和磁场互为对方的涡旋（旋度）源。

在空E和§6－3 坡印廷定理及坡印廷矢量1、坡印廷定理能量的流动是时变场中出现的一个重要现象 流动的能量同空间媒质所消耗的能量以及电磁储能之间应满足能量守 恒定律，即Poynting定理，也称能流定理v v v ⎛ ∂ B ⎞ v ⎛ v ∂D ⎞ v v v v v v Q ∇ ⋅ (E × H ) = H ⋅ (∇ × E ) − E ⋅ (∇ × H ) = H ⋅ ⎜ − ⎜ ⎟ ⎜ ∂t ⎟ − E ⋅ ⎜ J + ∂t ⎟ ⎟ ⎝ ⎠ ⎝ ⎠ v v v ∂H v v v ∂E = − μH ⋅ − E ⋅ σ E − εE ⋅ ∂t ∂t 1 ω m = μH 2 ∂ ⎛1 ∂ ⎛1 ⎞ ⎞ 2 = − ⎜ μH 2 ⎟ − σE 2 − ⎜ εE 2 ⎟ ∂t ⎝ 2 ∂t ⎝ 2 1 ⎠ ⎠ ω e = εE 2 ∂ 2 v v = − (ω m + ω e ) − p p = E ⋅ J = σE 2 ∂t假定：媒质是线性、各向同性的，且不随时间变化；无外加源Chap.6 时变电磁场 —— §6－3 坡印廷定理及坡印廷矢量v v ∂ ∇ ⋅ (E × H ) = − (ωm + ωe ) − p ∂t v v v v ∂ 令 S = E × H，得 − ∇ ⋅ S = (ω m + ω e ) + p ∂t单位时间内流入单 位体积中的能量坡印廷定理微分形式 单位体积内焦耳热损耗单位体积内电场能量和磁场能量的增加率 坡印廷定理积分形式取体积分，应用高斯定律得：v v d − ∫ S ⋅ ds = s dt∫ (ωVm+ ω e )dv + ∫ pdvV体积V内变为焦耳 热损耗的功率体积V内电场能量和磁场能量每秒的增加量 由于假设体积V内无外加源，根据能量守恒定律，等式左 端即为单位时间内穿过闭合面S进入体积V中的能量Chap.6 时变电磁场 —— §6－3 坡印廷定理及坡印廷矢量坡印廷定理物理意义： v ∂ 微分形式： − ∇ ⋅ S = ∂t (ω m + ω e ) + p外界向电磁场某点提供的电磁功率密度，等于该点电磁场能量密 度的时间增加率，与对这点自由电荷提供的功率密度之和v v d 积分形式： − ∫s S ⋅ ds = dt ∫V (ω m + ω e )dv + ∫V pdv 某时刻外界通过闭合面进入其所包围体积V中的电磁功率，等于V 内电磁场能量的时间增加率与体积内焦耳热损耗的瞬时功率之和Poynting定理是电磁场中的能量守恒与转换定律 它清楚地表明电磁场是能量的携带者与传播者Chap.6 时变电磁场 —— §6－3 坡印廷定理及坡印廷矢量2、坡印廷矢量v v v v v 由坡印廷定理可知， S ⋅ ds = ∫ (E × H )⋅ ds表示通过闭合面S的总瞬时功率 ∫s s定义:v v v S = E×H为坡印廷矢量，也称能流密度矢量。

《电磁场与电磁波》（第四版）习题集：第4章时变电磁场第4章时变电磁场在时变的情况下，电场和磁场相互激励，在空间形成电磁波，时变电磁场的能量以电磁波的形式进行传播。

电磁场的波动方程描述了电磁场的波动性，本章首先对电磁场的波动方程进行讨论。

在时变电磁场的情况下，也可以引入辅助位函数来描述电磁场，使一些复杂问题的分析求解过程得以简化。

本章对时变电磁场的位函数及其微分方程进行了讨论。

电磁能量一如其它能量服从能量守恒原理，本章将讨论电磁场的能流和表征电磁场能量守恒关系的坡印廷定理。

本章在最后讨论了随时间按正弦函数变化的时变电磁场，这种时变电磁场称为时谐电磁场或正弦电磁场。

4. 1 波动方程由麦克斯韦方程可以建立电磁场的波动方程，揭示了时变电磁场的运动规律，即电磁场的波动性。

下面建立无源空间中电磁场的波动方程。

在无源空间中，电流密度和电荷密度处处为零，即0ρ=、0=J 。

在线性、各向同性的均匀媒质中，E 和H 满足的麦克斯韦方程为t ε=?EH （4.1.1） tμ=-?HE （4.1.2） 0?=H （4.1.3） 0?=E （4.1.4）对式（4.1.2）两边取旋度，有()()tμ=-E H 将式（4.1.1）代入上式，得到22()0t με+=?EE利用矢量恒等式2()()=??-?E E E 和式（4.1.4），可得到2220tμε??-=?EE （4.1.5）此式即为无源区域中电场强度矢量E 满足的波动方程。

同理可得到无源区域中磁场强度矢量H 满足的波动方程为2220tμε??-=?H H （4.1.6）无源区域中的E 或H 可以通过求解式（4.1.5）或式（4.1.6）的波动方程得到。

在直角坐标系中，波动方程可以分解为三个标量方程，每个方程中只含有一个场分量。

例如，式（4.1.5）可以分解为222222220x x x xE E E E x y z tμε++-= （4.1.7） 222222220yyyyE E E E x y z t με++-= （4.1.8）222222220z z z zE E E E x y z t με++-= （4.1.9）在其它坐标系中分解得到的三个标量方程都具有复杂的形式。

第七章 时变电磁场重点和难点通过位移电流的引入，导出全电流定律，说明时变电场可以产生时变磁场。

详细讲解麦克斯韦方程的积分形式和微分形式，说明时变电磁场是有旋有散的，时变电场的方向与时变磁场的方向处处相互垂直，以及麦克斯韦对于人类文明和进步的伟大贡献。

讲解时变电磁场的边界条件时，应与静态场进行比较，尤其要介绍理想导电体的边界条件。

讲解位函数时，应强调罗伦兹条件的重要性。

详细讲解位函数解的物理意义，强调没有滞后效应就不可能有辐射。

指出位函数的积分解仅适用于均匀线性各向同性的媒质。

能量密度容易理解，着重讲解能流密度矢量。

时变电磁场的惟一性定理证明可以略去，但是其物理意义及其重要性必须介绍。

讲解正弦电磁场的复矢量表示方法时，应强调仅适用于频率相同的场量之间的运算。

此外，还应指出该教材使用的时间因子是e j ω t ，而不是e -i ωt 。

对于复能流密度矢量，应着重介绍其实部和虚部的物理意义，以及电场和磁场之间的相位差对于复能流密度矢量的影响。

重要公式位移电流密度：td ∂∂=DJ 全电流连续性原理：0d )( =⋅+⎰SS J J d 0)(=+⋅∇d J J全电流定律：S DJ l H d )(d ⋅∂∂+=⋅⎰⎰SlttD J H ∂∂+=⨯∇ 麦克斯韦方程：积分形式：S DJ l H d )(d ⋅∂∂+=⋅⎰⎰SltS Bl E d d ⋅∂∂-=⋅⎰⎰S l t0d =⋅⎰SS B q S=⋅⎰ d S D微分形式： t ∂∂+=⨯∇D J H t∂∂-=⨯∇B E 0=⋅∇B ρ=⋅∇D电荷守恒原理：V tSV d d ⎰⎰∂∂-=⋅ρS J t∂∂-=⋅∇ρJ 媒质特性方程： E D ε=H B μ=J E J '+= σ一般边界条件：1，0)(12=-⨯E E e n ，式中n e 为由媒质①指向媒质②的边界法向单位矢量。

对于各向同性的线性媒质，221 1εεttD D =2，0)(12=-⋅B B e n 。