受弯构件的变形挠度验算

简述受弯构件挠度验算的最小刚度原则受弯构件是常见的工程结构，其在受到外力作用下会发生弯曲变形。

挠度验算是评估受弯构件变形程度的重要方法之一。

挠度验算的最小刚度原则是指在进行受弯构件的挠度验算时，应根据最小刚度原则，选择合适的验算方法和参数，确保构件在工作状态下的变形满足设计要求。

受弯构件挠度验算的最小刚度原则主要包括以下几个方面：1. 选择合适的验算方法：挠度验算方法有解析法和数值法两种。

解析法适用于简单和理想化的构件情况，可以得到解析解；数值法适用于复杂和实际工程中的构件，可以通过有限元分析等方法得到数值解。

在进行挠度验算时，应根据具体情况选择合适的验算方法。

2. 考虑多种载荷情况：在进行挠度验算时，需考虑不同工作状态下的载荷情况，包括常规荷载、临时荷载、地震作用等。

根据不同载荷情况进行挠度验算，确保结构在各种工作状态下的变形满足设计要求。

3. 确定适当的验算参数：在进行挠度验算时，需确定合适的验算参数，包括构件的刚度、截面性能等。

刚度是指受弯构件抵抗外力作用时的刚性程度，是影响挠度的主要因素之一。

根据构件的实际情况和设计要求，选择适当的刚度参数，进行挠度验算。

4. 参考相关规范和标准：在进行挠度验算时，应参考相关的规范和标准，确保验算结果的准确性和合理性。

例如，中国的《建筑结构荷载标准》（GB 50009-2012）和《钢结构设计规范》（GB 50017-2003）等，提供了受弯构件挠度验算的相关要求和参数。

通过以上几个方面的考虑和参考，可以有效地进行受弯构件的挠度验算。

在实际工程中，挠度验算的结果对于受弯构件的设计和施工具有重要指导意义。

通过合理选择验算方法和参数，确保受弯构件在工作状态下的变形控制在允许范围内，提高结构的安全性和可靠性。

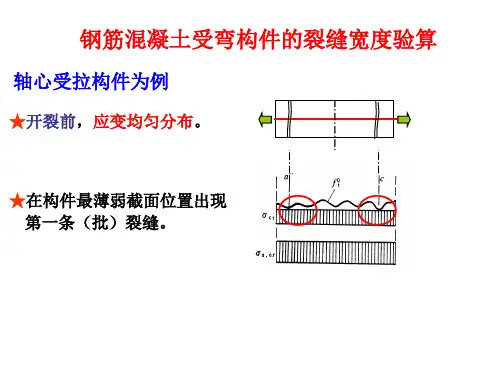
第十章受弯构件的裂缝与变形验算第一节概述1.一、钢筋混凝土受弯构件在使用阶段的计算特点：1.使用阶段一般指梁带裂缝工作阶段。

2.使用阶段计算是按照构件使用条件对已设计的构件进行计算，以保证在使用情况下的应力、裂缝和变形小于正常使用极限状态的限值。

当构件验算不满足要求时，必须按承载能力极限状态要求对已设计好的构件进行修正、调整，直至满足两种极限状态的设计要求。

3.使用阶段计算中涉及到的内力，是各种使用荷载在构件截面上各自产生的同类型内力，按荷载组合原则简单叠加，不带任何荷载系数。

二、结构按正常使用极限状态设计采用的两种效应组合：1 1.作用短期效应组合。

永久作用标准值效应与可变作用频遇值效应相组合，其效应组合表达式为：2 2.作用长期效应组合。

永久作用标准值效应与可变作用准永久值效应相组合，其效应组合表达式为：第二节换算截面一、基本假定二、截面变换三、换算截面的几何特性表达式一、基本假定1.平截面假定。

2.弹性体假定。

3.受拉区出现裂缝后，受拉区的混凝土不参加工作，拉应力全部由钢筋承担。

4.同一强度等级的混凝土，其拉、压弹性模量视为同一常值，不随应力大小而变，从而钢筋的弹性模量和混凝土的弹性模量之比值为一常数值，即/。

与混凝土的强度等级有关。

《公桥规》规定钢筋混凝土构件的截面换算系数。

二、截面变换将截面受拉区纵向受拉钢筋的截面面积换算成假想的能承受拉应力的混凝土截面面积，如图。

并满足：1、虚拟混凝土块仍居于钢筋的重心处且应变相同，即2、虚拟混凝土块与钢筋承担的内力相同，即由虎克定律(Hookelaw)得：根据换算截面面积承受拉力的作用应与原钢筋的作用相同的原则可得所以，上式表明，截面面积为的纵向受拉钢筋的作用相当于截面面积为的受拉混凝土的作用，即称为钢筋的换算截面面积。

<top>三、换算截面的几何特性表达式（一）、单筋矩形截面1、换算截面面积：2、换算截面对中性轴的静矩：2、换算截面对中性轴的静矩：受压区：受拉区：3、换算截面对中性轴的惯性矩4、受压区高度ｘ：对于受弯构件，开裂截面的中性轴通过其换算截面的形心轴，即若将符号（受压区相对高度）及（配筋率）代入上式，则可得到5、受压区边缘混凝土应力6、受拉钢筋应力（二）、双筋矩形截面对于双筋矩形截面，截面换算的方法就是将受拉钢筋的截面和受压钢筋截面分别用两个虚拟的混凝土块代替，形成换算截面。

8.2 受弯构件挠度验第8.2.1条钢筋混凝土和预应力混凝土受弯构件在正常使用极限状态下的挠度，可根据构件的刚度用结构力学方法计算。

在等截面构件中，可假定各同号弯矩区段内的刚度相等，并取用该区段内最大弯矩处的刚度。

当计算跨度内的支座截面刚度不大于跨中截面刚度的两倍或不小于跨中截面刚度的二分之一时，该跨也可按等刚度构件进行计算，其构件刚度可取跨中最大弯矩截面的刚度。

受弯构件的挠度应按荷载效应标准组合并考虑荷载长期作用影响的刚度B进行计算，所求得的挠度计算值不应超过本规范表3.3.2规定的限值。

第8.2.2条矩形、T形、倒T形和I形截面受弯构件的刚度B,可按下列公式计算：B=Mk /Mq(θ-1)+MkBs(8.2.2)式中Mk--按荷载效应的标准组合计算的弯矩，取计算区段内的最大弯矩值；Mq--按荷载效应的准永久组合计算的弯矩，取计算区段内的最大弯矩值；Bs--荷载效应的标准组合作用下受弯构件的短期刚度，按本规范第8.2.3条的公式计算；θ--考虑荷载长期作用对挠度增大的影响系数，按本规范第8.2.5条取用。

第8.2.3条在荷载效应的标准组合作用下，受弯构件的短期刚度Bs可按下列公式计算：1钢筋混凝土受弯构件B s =EsAsh2/1.15ψ+0.2+6αEρ/1+3.5γ'f(8.2.3-1)2预应力混凝土受弯构件1)要求不出现裂缝的构件B s =0.85EcI(8.2.3-2)2)允许出现裂缝的构件B s =0.85EcI/kcr+(1-kcr)ω(8.2.3-3)k cr =Mcr/Mk(8.2.3-4)ω=(1.0+0.21/αE ρ)(1+0.45γf)-0.7 (8.2.3-5)M cr =(σpc+γftk)W(8.2.3-6)γf =(bf-b)hf/bh(8.2.3-7)式中ψ--裂缝间纵向受拉钢筋应变不均匀系数，按本规范第8.1.2条确定；αE --钢筋弹性模量与混凝土弹性模量的比值：αE=Es/Ec;ρ--纵向受拉钢筋配筋率：对钢筋混凝土受弯构件，取ρ=As /(bh);对预应力混凝土受弯构件，取ρ=(Ap+As)/(bh);I--换算截面惯性矩；γf--受拉翼缘截面面积与腹板有效截面面积的比值；b f 、hf--受拉区翼缘的宽度、高度；K cr --预应力混凝土受弯构件正截面的开裂弯矩Mcr与弯矩Mk的比值，当kcr >1.0时，取kcr=1.0;σpc--扣除全部预应力损失后，由预加力在抗裂验算边缘产生的混凝土预压应力；γ--混凝土构件的截面抵抗矩塑性影响系数，按本规范第8.2.4条确定。

一、受弯构件（一）在主平面内受弯的实腹式构件抗弯强度应符合下列规定1、翼缘板弯曲正应力满足下列要求：双向受弯的实腹式构件：f d ≥γ0(M y W y,eff +M z W z,eff )式中：γ0——结构重要性系数；M y 、M z ——计算截面的弯矩设计值；W y,eff 、W z,eff ——有效截面相对于y 轴和z 轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。

2、腹板剪应力应满足下列要求。

闭口截面腹板剪应力应按剪力流理论计算。

γ0τ≤f vd式中：γ0——结构重要性系数；τ——剪应力；f vd ——钢材的抗剪强度设计值。

3、平面内受弯实腹式构件腹板在正应力 σx 和剪应力 τ 共同作用时，应满足下列要求。

γ0√(σx f d )2+(τf vd)2≤1 式中：σx ——x 方向正应力；f d ——钢材的抗拉、抗压和抗弯强度设计值。

（二）受弯构件的整体稳定性应符合下列规定1、等截面实腹式受弯构件，应按下列规定验算整体稳定。

γ0(βm,yM y χLT,y M Rd,y +M z M Rd,z )≤1 γ0(M y M Rd,y +βm,z M z χLT,z M Rd,z)≤1 M Rd,y =W y,eff f dM Rd,z =W z,eff f dλLT,y =√W y,eff f y M cr,y ，λLT,z =√W z,eff f y M cr,z式中： M y 、M z ——构件最大弯矩；βm,y、βm,z——等效弯矩系数；χLT,y、χLT,z——M y和M z作用平面内的弯矩单独作用下，构件弯扭失稳模态的整体稳定折减系数；λ̅̅̅LT,y、λLT,z——弯扭相对长细比；W y,eff、W z,eff——有效截面相对于y轴和z轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。

M cr,y、M cr,z——M y和M z作用平面内的弯矩单独作用下，考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩，可采用有限元方法计算。

第五章 整体分析验算5.1 一般规定5.1.1 局部受压稳定折减系数钢桥在验算受压稳定性时，一般结构在屈曲前后仍在小变形假设范围内处于弹性状态，即弹性屈曲。

对于局部受压的板件，由于构件的弹性屈曲，对构件材料的标准值有所影响。

在计算时，需要考虑弹性屈曲引起的局部稳定折减，局部稳定折减系数ρ应按下列规定计算[3]：()020.4=1110.4=112p λρλρελ⎧≤⎪⎪⎧⎨⎪>++⎨⎪⎪⎪⎩⎩时：时： （5-1）()00.80.4p ελ=- （5-2）1.05p p b t λ⎛== ⎝ （5-3） 式中：p λ——相对宽厚比； t ——加劲板的母板厚度；y f ——屈服强度； E——弹性模量；cr σ——加劲板弹性屈曲欧拉应力；p b ——加劲板局部稳定计算宽度，对开口刚性加劲肋，按加劲肋的间距 b i计算；对闭口刚性加劲肋，按加劲肋腹板间的间距计算；对柔性加劲肋，按腹板间距或腹板至悬臂端的宽度i b 计算；k ——加劲板的弹性屈曲系数，可参考规范《公路钢结构桥梁设计规范》附录B 计算，计算如下。

参考规范《公路钢结构桥梁设计规范》附录B 规定，加劲肋和加劲板对弹性屈曲系数k 有很大的影响。

对纵向加劲肋等间距布置且无横向加劲肋布置的顶板和底板，其弹性屈曲系数k 可由式5-4、5-5计算：*4l l k γγ≥=时： (5-4)()()(()2202*011211l l l l l n a k n b a k n b αγαααδγγααδ⎧++⎛⎫⎪==≤ ⎪⎪+⎝⎭⎪<⎨⎪⎛⎫==>⎪ ⎪+⎝⎭⎪⎩时: （5-5）式中：n ——受压板被纵向加劲肋分割的板元数，1l n n =+； l n ——等间距布置纵向加劲肋根数；a ——加劲板的计算长度（横隔板或刚性横向加劲肋的间距）；b——加劲板的计算宽度（腹板或刚性纵向加劲肋的间距）；α——加劲板的长宽比，按时5-6计算：abα=（5-6） l δ——单根纵向加劲肋的截面面积与母板的面积之比, 按式5-7计算：l l Abtδ= （5-7）t ——加劲板的厚度；l A ——单根纵向加劲肋的截面面积；l γ——纵向加劲肋相对刚度，按式5-8计算：l l EIbDγ= （5-8）l I ——单根纵向加劲肋对加劲板的抗弯惯性矩；D——单宽板刚度，按式5-9计算：()32121Et D ν=- （5-9） ν——泊松比； t ——加劲板的厚度；E——弹性模量。