曲线积分中参数方程和极坐标方程
- 格式:docx
- 大小:11.95 KB
- 文档页数:2

曲线积分的基本概念与运算曲线积分是微积分中重要的一部分。
它主要处理的问题是沿着曲线的积分。
在工程、物理、计算机图形学等领域都有广泛的应用。
曲线积分的基本概念和运算是学习曲线积分的前提,本文将对曲线积分的基本概念和运算进行阐述。
一、曲线积分的基本概念曲线积分是一种重要的线积分,指函数沿着曲线的积分。
对于一条曲线C,其方程可以表示为:C:r(t) = x(t)i + y(t)j 0 ≤ t ≤ 1其中,i和j分别表示x轴和y轴的单位向量,x(t)和y(t)分别表示C上点的横坐标和纵坐标,t表示C上点的参数。
设f(x,y)是在曲线C上连续定义的函数,则曲线积分的定义为:∫C f(x,y) ds其中,ds表示曲线C上的长度元素,即:ds = || r'(t) || dt其中,|| r'(t) || 表示 r(t) 的切向量的模长,也称作速度。
上述式子中,f(x,y)是被积函数,称为速度函数或微分形式。
曲线积分根据路径有向或路径无向分为有向曲线积分和无向曲线积分。
对于有向的曲线C,其有向曲线积分表示为:∫C f(x,y) ds其中,ds的各项都为正,表示沿着曲线从一个端点到另一个端点的积分。
如果积分方向和C的方向相反,则有向曲线积分变为负数。
对于无向曲线C,其无向曲线积分表示为:∫C f(x,y) ds无向曲线积分只考虑积分路径,不考虑积分方向。
二、曲线积分的运算1. 曲线积分的计算曲线积分的计算需要求出函数f(x,y)在曲线C上的值,并将其乘以曲线C的长度。
可以先将曲线C的参数限定在[0,1]区间上,并将积分区间划分为n个小区间,则:∫C f(x,y) ds = lim∑f(xk,yk) ∆s其中,∆s是C上相邻两点之间的距离,即:∆s = || r(tk) - r(tk-1) || = || r'(tk) ||∆t其中,∆t表示曲线C的参数t的步长(∆t=1/n),r'(tk) 表示曲线C在参数t=tk处的切向量。

曲线积分的计算方法曲线积分是数学中重要的概念,用于描述沿着曲线的函数积分。
在本文中,将介绍曲线积分的定义、计算方法以及一些常见的应用。
一、曲线积分的定义曲线积分可以分为第一类曲线积分和第二类曲线积分两种形式。
1. 第一类曲线积分设曲线C为参数方程r(t)=(x(t), y(t)), a≤t≤b,函数f(x, y)在C上有定义,则第一类曲线积分的定义为:∮C f(x, y) ds = ∫[a,b] f(x(t),y(t)) |r'(t)| dt其中,ds表示曲线C上的线元素,|r'(t)|表示r(t)的速度。
2. 第二类曲线积分设曲线C为参数方程r(t)=(x(t), y(t)), a≤t≤b,函数P(x, y)、Q(x, y)在C上有定义,则第二类曲线积分的定义为:∮C P dx + Q dy = ∫[a,b] [P(x(t), y(t)) x'(t) + Q(x(t), y(t)) y'(t)] dt其中,dx和dy表示曲线C上的x和y方向的线元素,x'(t)和y'(t)分别表示x(t)和y(t)对于t的导数。
二、曲线积分的计算方法曲线积分的计算方法与具体的曲线形式和函数形式有关。
以下将介绍几种常见的曲线积分计算方法。
1. 直线积分如果曲线C为一条直线段,可以通过参数方程或直线段的斜率来计算曲线积分。
当曲线C为一条直线段时,可将曲线积分转化为定积分。
2. 圆弧积分如果曲线C为一条圆弧,可使用参数方程或极坐标方程来计算曲线积分。
对于圆弧积分,通常需要将曲线参数化,然后进行曲线积分的计算。
3. 闭合曲线积分如果曲线C为一条闭合曲线,即起点和终点重合,可以通过参数方程或极坐标方程来计算曲线积分。
在计算闭合曲线积分时,需要注意曲线方向的选择,通常选择沿着曲线的正向方向。
三、曲线积分的应用曲线积分在物理学、工程学等领域有广泛的应用。
1. 流量计算曲线积分可以用来计算流体通过曲线边界的流量。

参数方程与极坐标参数方程是指用参数表示的一组函数方程,极坐标则是用角度和半径来表示点的坐标系统。
这两种坐标系统在数学和物理等领域中具有广泛应用。
本文将介绍参数方程和极坐标的概念、性质以及它们的应用领域。
一、参数方程1. 参数方程的概念参数方程是指将变量用参数表示的函数方程。
通常用参数t表示,例如在二维平面上,一个曲线的参数方程可以表示为:x = f(t), y = g(t)2. 参数方程的性质参数方程具有以下性质:- 参数方程可以表示一些常规方程无法表示的图形,如螺旋线等。
- 参数方程可以简化复杂的曲线方程,将其分解为一系列简单的参数方程。
- 参数方程可以描述随时间变化的物体运动,例如质点的运动轨迹。
- 参数方程适用于描述具有对称性的图形,如心形线等。
3. 参数方程的应用参数方程在多个领域中都有应用,包括数学分析、物理学和计算机图形学等。
例如在物理学中,参数方程可以用来描述粒子在电场和磁场中的运动轨迹;在计算机图形学中,参数方程可以用来生成平滑的曲线和曲面。
二、极坐标1. 极坐标的概念极坐标系统是用角度和半径来表示二维平面上的点的坐标系统。
一个点的极坐标可以表示为(r, θ),其中r为点到极坐标原点的距离,θ为点与极坐标正半轴的夹角。
2. 极坐标的性质极坐标具有以下性质:- 极坐标可以用于描述圆形、半径为r的圆、螺旋线等曲线。
- 极坐标可以简化极坐标下复杂函数的表示,例如指数函数在极坐标下具有较简单的形式。
- 极坐标下的积分和微分计算更加方便,适用于某些特定的数学问题。
3. 极坐标的应用极坐标在多个领域中都有应用。
在物理学中,极坐标可用于描述粒子在强磁场中的运动;在地理学中,极坐标可用于描述地球表面上的某点的位置;在工程学中,极坐标可用于描述旋转机械中的运动。
三、参数方程与极坐标的关系参数方程与极坐标是可以相互转换的。
对于平面曲线的参数方程,可以通过参数方程的参数化形式得到极坐标的形式,反之亦然。

第一类曲线积分的极坐标形式曲线积分是微积分中的一个重要概念,它描述了沿着一条曲线的积分过程。
在曲线积分中,第一类曲线积分是最基本的一种类型,它描述了沿着曲线的标量场积分。
而在极坐标系下,第一类曲线积分的计算方法也有其独特的形式。
首先,我们来回顾一下第一类曲线积分的定义。
设曲线L为参数方程r(t)=(x(t),y(t)),其中a≤t≤b,f(x,y)为定义在曲线L上的标量场,则曲线L上f(x,y)的第一类曲线积分为:∫L f(x,y)ds = ∫b_a f(x(t),y(t))√[x'(t)²+y'(t)²]dt其中,ds表示曲线L上的弧长元素,x'(t)和y'(t)分别表示x(t)和y(t)对t 的导数。
接下来,我们来看第一类曲线积分在极坐标系下的形式。
在极坐标系下,曲线L可以表示为r(θ)=(r(θ)cosθ,r(θ)sinθ),其中a≤θ≤b,r(θ)为极径函数。
此时,曲线L上f(x,y)的第一类曲线积分可以表示为:∫L f(x,y)ds = ∫b_a f(r(θ)cosθ,r(θ)sinθ)√[r'(θ)²+r(θ)²]dθ其中,ds表示曲线L上的弧长元素,r'(θ)表示r(θ)对θ的导数。
通过上述公式,我们可以看出,在极坐标系下,第一类曲线积分的计算方法与直角坐标系下有所不同。
在直角坐标系下,我们需要计算曲线L上的弧长元素ds,而在极坐标系下,我们需要计算曲线L上的弧度元素dθ。
此外,由于极坐标系下的曲线L是由极径函数r(θ)和极角θ共同确定的,因此在计算曲线积分时,我们需要将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。
总之,第一类曲线积分是微积分中的一个重要概念,它描述了沿着曲线的标量场积分。
在极坐标系下,第一类曲线积分的计算方法也有其独特的形式,需要注意弧度元素dθ的计算和将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。

极坐标与参数方程极坐标和参数方程是数学中常用的两种描述曲线的方式,它们在不同情况下都具有相应的优势和应用。
极坐标是一种用极径和极角来描述平面上点的坐标系统。
在极坐标中,一个点的坐标表示为(r,θ),其中r表示点到原点的距离,θ表示与正x轴的夹角。
通过改变r和θ的取值,可以描述出各种曲线形状。
极坐标的优势在于可以简洁地描述出圆形、扇形等对称图形,以及螺旋线等特殊曲线形状。
参数方程是用参数来表示曲线上的每个点的坐标的方程。
在参数方程中,一个曲线可以通过一个或多个参数来定义。
曲线上的每个点的位置由参数给出。
参数方程的优势在于可以精确地描述出复杂的曲线形状,如心形线、滑轮线等非对称图形。
极坐标和参数方程在不同情况下使用不同。
以下分别从几何图形、计算和物理学的角度来探讨这两种方法的应用。
从几何图形的角度来看,极坐标适合描述对称图形。
例如,圆形的方程可以用r=a表示,其中a为常数。
而在参数方程中,圆形的方程可以用x=a*cos(t),y=a*sin(t)表示,其中t为参数。
极坐标可以简单地描述出圆形的对称性,而参数方程则更加灵活,可以描述出圆形上每个点的具体位置。
在计算中,极坐标和参数方程都有其应用价值。
在微积分中,极坐标常用于描述极坐标下的曲线与坐标轴围成的封闭曲线的面积,或者用于描述极坐标下的曲线的弧长。
参数方程常用于求参数方程所表示的曲线与坐标轴之间的面积,或者求参数方程所表示的曲线的弧长。
在物理学中,极坐标和参数方程也被广泛应用。
在力学中,极坐标可以方便地描述转动系统中物体相对于转轴的位置。
在电磁学中,参数方程可以用于描述电荷在电场中的运动轨迹。
在天文学中,参数方程可以用于描述行星、彗星等天体的轨道。
总的来说,极坐标和参数方程在不同情况下都有其应用价值。
极坐标适合描述对称图形,参数方程适合描述复杂的非对称图形。
无论是从几何图形、计算还是物理学的角度来看,选择哪种方式取决于具体的应用需求。
曲线积分极坐标公式
曲线积分极坐标公式是数学中的一个重要概念,它是描述曲线上某个向量场沿着曲线的积分值的公式。
在极坐标系下,曲线积分的计算可以更加简便,因为极坐标系下的曲线方程更加简单,而且极坐标系下的向量场也更加容易处理。
在极坐标系下,曲线积分的公式可以表示为:
∫C F(r,θ)·ds = ∫a^b F(r(θ),θ)·r'(θ) dθ
其中,C表示曲线,F(r,θ)表示向量场,r(θ)表示曲线在极坐标系下的参数方程,s表示曲线上的弧长,a和b分别表示曲线的起点和终点。
这个公式的意义是,将曲线C分成许多小段,每一小段的长度为ds,然后将每一小段上的向量场F(r,θ)与ds做点积,最后将所有小段的点积相加,就得到了整个曲线上的积分值。
这个公式的应用非常广泛,例如在物理学中,可以用它来计算电场或磁场沿着曲线的积分值;在工程学中,可以用它来计算流体沿着曲线的流量;在计算机图形学中,可以用它来计算曲线上的曲率等等。
需要注意的是,极坐标系下的曲线积分公式只适用于平面曲线,而不适用于空间曲线。
此外,如果曲线C是闭合曲线,即起点和终点
重合,那么曲线积分的值可能会受到曲线方向的影响,因此需要特别注意。
曲线积分极坐标公式是数学中的一个重要概念,它可以用来描述曲线上某个向量场沿着曲线的积分值。
在极坐标系下,曲线积分的计算更加简便,因为极坐标系下的曲线方程更加简单,而且极坐标系下的向量场也更加容易处理。
参数方程积分平面直角坐标系中,如果曲线上任意一点的坐标x、y都是某个变数t的函数。
曲线的极坐标参数方程ρ=f(t),θ=g(t)。
圆的参数方程 x=a+r cosθ y=b+r sinθ(θ∈ [0,2π) ) (a,b) 为圆心坐标,r 为圆半径,θ为参数,(x,y) 为经过点的坐标。
椭圆的参数方程 x=a cosθ y=b sinθ(θ∈[0,2π)) a 为长半轴长 b为短半轴长θ为参数。
双曲线的参数方程 x=a secθ(正割) y=b tanθ a为实半轴长 b为虚半轴长θ为参数。
抛物线的参数方程 x=2pt^2 y=2pt p表示焦点到准线的距离 t 为参数。
直线的参数方程 x=x'+tcosa y=y'+tsina,x',y'和a表示直线经过(x',y'),且倾斜角为a,t为参数。
参数曲线即用参数方程表示的曲线,参数方程和函数很相似:它们都是由一些在指定的集的数,称为参数或自变数,以决定因变数的结果。
例如在运动学,参数通常是“时间”,而方程的结果是速度、位置等。
如果函数f(x)及F(x)满足:1、在闭区间[a,b]上连续;2、在开区间(a,b)内可导;3、对任一x∈(a,b),F'(x)≠0。
那么在(a,b)内至少有一点ζ,使等式[f(b)-f(a)]/[F(b)-F(a)]=f'(ζ)/F'(ζ)成立。
柯西简洁而严格地证明了微积分学基本定理即牛顿-莱布尼茨公式。
他利用定积分严格证明了带余项的泰勒公式,还用微分与积分中值定理表示曲边梯形的面积,推导了平面曲线之间图形的面积、曲面面积和立体体积的公式。
极坐标与参数方程的区别和联系公式一、区别极坐标和参数方程是数学中常用的两种表示曲线的方法。
它们在描述曲线形状、定位和计算等方面有着不同的特点。
1. 极坐标极坐标是一种使用角度和距离来表示点在平面上位置的方法。
它将点的位置与极坐标轴建立的原点和正极坐标轴之间的距离和夹角联系起来。
在极坐标中,一个点的位置由两个值来确定:极径(表示点到原点的距离,记作r)和极角(表示与正极坐标轴的夹角,记作θ)。
极坐标的表达形式为(r, θ)。
极坐标适用于描述对称、环形或以某个中心为中心的曲线。
它可以简化复杂曲线的表达和运算,并且常用于极坐标图形的绘制以及极坐标系下的积分和微分计算。
2. 参数方程参数方程是一种使用参数表示点在平面上位置的方法。
它通过给定一个或多个参数值来确定曲线上的点的坐标。
在参数方程中,点的坐标由一个或多个参数所决定。
常见的参数方程形式为x = f(t)和y = g(t),其中t为参数,f(t)和g(t)为关于参数t的函数。
参数方程可以描述曲线上每一个点的位置,对于复杂的曲线形状和曲线上的变化,参数方程更加灵活。
它在计算曲线长度、曲线的切线和法线等方面具有优势。
二、联系公式虽然极坐标和参数方程有着不同的表示方式,但它们之间存在一定的联系和转换关系。
1. 极坐标转参数方程将极坐标(r, θ)转换为参数方程(x(t), y(t))时,可以使用以下联系公式:•x(t) = r * cos(θ)•y(t) = r * sin(θ)其中,cos和sin为三角函数,r为极径,θ为极角,(x(t), y(t))为参数方程。
2. 参数方程转极坐标将参数方程(x(t), y(t))转换为极坐标(r, θ)时,可以使用以下联系公式:•r = √(x(t)^2 + y(t)^2)•θ = arctan(y(t) / x(t))其中,√为求平方根,arctan为反正切函数,(x(t), y(t))为参数方程,r为极径,θ为极角。
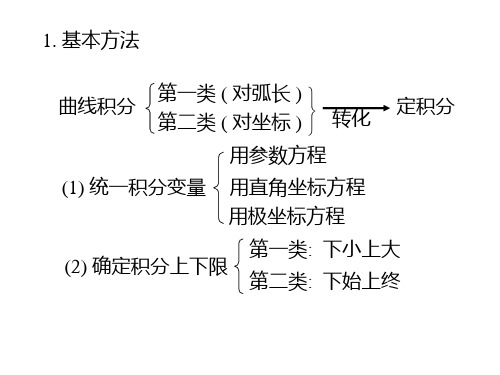
曲线积分中参数方程和极坐标方程在曲线积分中,有两种常用的参数化方式:参数方程和极坐标方程。
参数方程:参数方程使用一个或多个参数来描述曲线上的点的坐标。
通常,一个参数对应于曲线上的一个自变量(例如时间),而每个参数的取值范围定义了曲线的范围。
参数方程的一般形式可以表示为:
x = f(t)
y = g(t)
z = h(t)
这里,x、y、z是曲线上的点的坐标,t是参数。
通过改变参数t的值,可以得到曲线上的不同点。
例如,单位圆的参数方程可以表示为:
x = cos(t)
y = sin(t)
这个参数方程描述了一个圆,其中t的取值范围是[0, 2π]。
在曲线积分中,参数方程可以用于描述曲线的路径,并根据参数来定义被积函数。
曲线积分的计算可以根据参数方程进行参数化积分。
极坐标方程:极坐标方程使用极坐标系统中的角度和半径来描述曲线上的点的位置。
一般而言,极坐标方程的形式为:
r = f(θ)
这里,r是距离原点的距离,θ是与极轴的夹角。
通过改变θ的值,可以得到曲线上的不同点。
例如,单位圆的极坐标方程可以表示为:
r = 1
这个极坐标方程描述了一个圆,其中r的取值始终为1,θ的取值范围是[0, 2π]。
在曲线积分中,极坐标方程可以用于描述曲线的路径,并根据极坐标来定义被积函数。
曲线积分的计算可以根据极坐标方程进行极坐标积分。