几何画板教程:绘制正方体
- 格式:doc
- 大小:271.50 KB
- 文档页数:7

画法几何制图换面法画法几何制图是建筑、机械和电子等设计领域必备的技能。
它的一个重要部分就是“换面法”,它是通过将一个多面体拆分成多个简单的平面形状,然后再用这些形状来绘制其三维图形的方法。
本文将为你介绍如何运用换面法来画一个简单的多面体。
准备工作在开始绘制之前,需要准备以下工具:•笔和铅•直尺•三角尺•绘画纸步骤一:绘制立方体首先,我们要绘制一个基本的多面体,例如一个立方体。
为了做到这一点,我们可以绘制一个正方形(底面),并且在各个角上画上垂直于底面的线段(高),使这些线段接到正方形相应角点处,最后将所有线段相互连接即可形成一个立方体。
注意,在纵向和横向线段的描绘上,需要保持符合比例。
步骤二:拆分面以上述步骤绘制出来的立方体为例,我们需要将其所有的面分成矩形或正方形。
为此,我们需要通过连接每个相邻的面的棱角,将多面体拆解,并且用铅笔标上每个矩形或正方形的上下左右面,使得它们更加容易被识别。
步骤三:绘制每个面在拆分面后,我们可以将每个面单独绘制出来。
为此,我们需要将每个面放在纸上,并用三角尺和直尺来绘制它们。
对于不同的矩形,我们可以采用不同的绘制方法。
例如,对于一条平行于底面的直线,我们可以在每个与之相交的四边形上绘制这条直线,并保持符合比例。
在绘制完每个面后,我们应该标记好它们的相对位置。
步骤四:组成三维图形通过绘制每个面,我们可以将它们组合起来形成多面体的三维图形。
为此,我们应该将每个面按照它的相对位置粘贴到一张透明的塑料纸上,并对其进行调整,使得它们适当地重叠在一起。
这将帮助我们清晰地了解多面体的整体形状。
在这篇文章中,我们介绍了一个基本的画法几何制图技巧——换面法,以及如何使用这个技巧来画一个简单的多面体。
换面法可以帮助我们将多面体拆分成更简单的形状,并在绘制每个形状后重新组装它们来形成三维图形。
这个技巧在建筑、机械和电子等领域的设计工作中都得到了广泛应用。


几何画板中旋转正方体的做法
有许多学生在学习是有思想创新的,他们经常想用几何画板来进行抽象思维上的训练。
其
中最常见的例子就是“旋转正方体”。
首先,我们需要从几何画板中把整个正方体拉出来,包括左右、前后和上下三个方向。
下
一步,就是在这三个方向上采用某种特定的角度来旋转正方体,比如45度,90度,180
度或者其他任意度数。
接下来,我们可以选择要把正方体放在哪一个角度里,然后我们看到的又是一种新的正方
体结构。
我们可以做的是变换它的旋转角度,同时又不失灵活性,从而让我们自己来体会
不同的抽象想法。
最后,这时我们可以用调节正方体角度的视觉来审视它,看看它呈现出来的结构是否正确。
如果每一个角都位于合适的位置,我们就可以判断此旋转正方体的组合是完美的,这便是
我们最终想要达到的最完美的结果。
因此,要在几何画板中旋转正方体是一个很有趣的运动,它可以帮助我们通过调节角度,让我们的抽象思维创新、让我们的数学思维能力得到充分的锻炼。
通过学习,我们可以发现自己形成一种新的思维模式,而这块几何画板又能帮助我们来实践它。

中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系”菜单命令,在操作区建立直角坐标系。


如何画一个正方形?简介正方形是一个具有四条相等边和四个直角的几何图形。
在绘制正方形时,有几种方法可以帮助我们确保边长相等且角度为直角。
方法一:使用直尺和编译器1. 使用直尺绘制一条直线段作为正方形的一条边。
2. 确保直线段的两个端点对齐。
3. 使用直尺在其中一个端点处绘制一条与第一条边相交的直线段。
4. 确保这两条直线段的交点为直角。
5. 测量第一条边的长度。
6. 在交点处绘制一个与第一条边相等的直线段。
7. 使用直尺连接第一条边的另一个端点和新绘制的直线段的端点。
8. 确保所得到的图形的四条边长度相等,并且四个角度为直角。
方法二:使用定规和铅笔1. 使用定规测量出等于所需正方形边长的长度。
2. 将定规的一端放在纸上,从一端开始向另一端绘制一条直线段。
3. 将定规的另一端放在已绘制直线段的末端,以相同长度绘制一条与前一条直线段垂直的直线段。
4. 确保两条直线段相交的地方为直角。
5. 重复上述步骤,绘制另外两条边。
方法三:使用正方形模板1. 在纸上或卡纸上制作一个正方形模板,确保其边长等于所需正方形边长。
2. 将模板放在纸上,使其边与纸的边对齐。
3. 使用铅笔沿着模板的边界轮廓绘制正方形。
注意事项- 在绘制正方形时要确保边长相等,可以使用测量工具(如直尺或定规)来辅助。
- 为了确保角度为直角,可以使用工具(如直尺或定规)来绘制垂直线段。
- 绘制一个正方形不依赖于特定的软件或编译器,因此可以在纸上进行练。
以上是绘制正方形的几种方法,您可以选择适合自己的方法进行尝试。
记得仔细测量和确保边长和角度的准确性。
祝您绘制成功!。



中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系"菜单命令,在操作区建立直角坐标系.单击工具箱上的“文本”工具,移动光标至圆点,当变成一只小黑手时,单击鼠标左键,然后再双击鼠标左键,将标签修改为“A".同法,给单位点加注标签为“1”。

简单的正方体上色简笔画图片教程步骤正六面体是一种侧面和底面均为正方形的直平行六面体,即棱长都相等的六面体。
那么简单的正方体的简笔画要怎么画呢?小编今天教大家画简单的正方体,步骤很简单,一起来学习吧!简单的正方体的简笔画成品图:简单的正方体的简笔画步骤如下:关于正方体的作文:关于正方体的作文一有一天,我和弟弟一起玩拼地垫的游戏,正方形的地垫铺在地上可以拼出好多图形呢。
突然弟弟想要搭成小房子可以躲在里面。
你们猜我是怎样搭的?当时我想了想,学着爸爸以前搭过的样子,让弟弟站在一块地垫上,然后把四块地垫竖起来围住了他,再用一块地垫盖在上面当屋顶,搭成了一个方块形的房子(如图一)。
弟弟藏在里面玩捉迷藏的游戏,特别开心。
爸爸让我仔细观察一下它,看有多少个面、多少条棱。
我数了一数,它有6个正方形的面,有12条一样长的棱,我知道这就叫“正方体”(如图二a)。
爸爸让我想想“长方体”,它有几个面、每个面是不是都是长方形。
家里有不少长方体的东西,比如鞋盒、微波炉、衣柜、牛奶盒,我观察它们,发现,长方体和正方体一样也是有6个面,但是它的面不一定都是长方形。
如图二b长方体,每个面都是长方形;而如图二c长方体,有一组对面对的2个面是正方形、其他4个面都是长方形。
爸爸告诉我,正方体其实是一种特殊的长方体,当长方体的6个面都变成正方形时就变成正方体啦。
哦,原来是这样。
我觉得正方体很奇妙,我会继续发现它们更多的秘密。
生活中我们会遇到很多立体图形:正方体、长方体、圆柱体、球体……我们一起寻找并观察它们吧!关于正方体的作文二上个星期五,我们的素描老师交给我们一样作业,画正方体,要画出阴影效果。
开始画了,我把一张白色的纸夹在我的画板上,我手握着笔,看着电脑上怎么画。
先构图,构图有几个方法:①上紧下松。
②不大不小。
③左右均衡。
我按照这些方法,把正方形的位置定好,然后,我照着电脑上的画法画了起来,先定最高点,再定最低点……我把这些点连了起来。
正方体与长方体的画法
正方体与长方体是常见的几何体,正方体是十二边相等的六面体,长方体则是正方体的加长版,通过观察分析正方体与长方体的每个面,可以掌握物体的明暗关系。
正方体画法步骤:
正方体照片
第一步:画出正方体中间竖棱,线条画竖直。
第二步:把握好右边棱的角度
第三步:把握好左边棱的角度
第四步:注意棱与水平线的夹角越大,则画短些,反之则画长些,以此来确定好左右两根竖线的位置。
第五步:定出正方体的高度,画出向右消失的透视线。
第六步:画出向左消失的透视线。
第七步:画出上面两根透视线,注意透视状态。
第八步:画出正方体结构线。
第九步:根据前后两个角位置,定出正方体的投影。
第十步:暗部整体上一遍调子,注意线条排列均匀,力度不能太重。
第十一步:从明暗交界线处画起,依次向反光处过渡,投影注意前重后轻。
第十二步:加深明暗交界线,并注意上重下轻,右重左轻的变化。
第十三步:进一步深入塑造,注意色彩变化规律,注意灰面的力度把握。
第十三步:调整完成。
《几何画板》在立体几何中的应用一、绘制正方体方法一、斜二侧画法第1步,启动几何画板,单击工具箱上的“直尺”工具,按住“shift”键不放,在操作区作出一条水平线段AB。
第2步,单击工具箱上的“选择箭头”工具,选中点A,依次单击“变换”→“标记中心”菜单命令,将点A标记为中心点。
选中点B和线段AB,依次单击“变换”→“旋转”菜单命令,弹出对话框,在“固定角度”框种填入“90.0”度,单击“旋转”,即可得到线段AB旋转90.0度后的线段AB'。
单击工具箱上“文本”工具,改标签“B'”为“D”。
用同样方法,以点D为中心点旋转AD,作出线段DC。
选中点C和点B,按快捷键“ctrl+L”,作出线段CB,即得到正方形ABCD的前侧面。
第3步,移光标至点A,双击鼠标左键,标记中心点。
同时选中线段AB和点B,依次单击“变换”→“旋转”菜单命令,在对话框“固定角度”框中填入“45”度,单击“旋转”按钮,作出线段AB按逆时针旋转45度的线段AB'。
选中线段AB和点B,依次单击“变换”“缩放”菜单命令,弹出对话框,设置参数缩放比为1/2后,单击“确定”按钮,作出线段AB'缩小一半的线段AB''。
第4步,单击工具箱上的“文本”工具,将标前“B''”改为“A'”。
单击工具箱上的“选择箭头”工具,选中线段AB'和点B',依次单击“显示”→“隐藏”菜单命令,将其隐藏。
第5步,同样方法,以点B为中心点,将线段BC和点C旋转-45度,并将旋转后的线段缩小一半,绘制出线段BB',同理形成这样的图形。
第6步,单击工具箱上的“选择箭头”工具,选中点A'、点B'、点C'、点D',按快捷键“ctrl+L”,作出正方体的后侧面。
即得到正方体。
D'DCBD' D方法二、正等侧画法二、转动的正方体方法一、椭圆模拟法(轴测投影)使用计算器中的画板作动态直观图的基本方法和使用原画板相同,在此简单介绍如下;1.用椭圆上点和圆上点的对应做出转动的平面或多面体的底面.方法是:以平面上一点O为圆心、两条给出的线段m、n为半径作两个同心圆;在大圆上取动点A,在小圆上取动点B;连结OA,作射线OB交大圆于C;过B作OA的平行线与过C作OA的垂线相交于M,则M关于B的轨迹就是一个椭圆,点M是圆上点C在椭圆上的对应点;把点B以O为中心旋转90得到点D,用同样的方法作D在椭圆上的对应点N;把M、N以O为心旋转180得到点E、F,连接四边形MNEF。
例1、作出长方形绕其一边旋转成圆柱体的过程。
1、用自定义工具画一个椭圆(中心为O),在椭圆上任取一点A;1)绘制一个圆,圆心为O,并在圆周上取一点B。
同时选中O和B点,单击“构造/直线”构造直线BO;2)构造圆与直线交点于C;3)在圆上任取一点E,过E构造直线BC垂线,垂线与直线将于F点;4)中EF一,两点。
构造线段EF;5)选取EF,“构造/中点”于G点;6)同时选中G点和E点,单击“构造/轨迹”,构造出椭圆L。
2、选中点O和A,将它们向下平移适当的距离,得到点O’和A’,画出四边形内部,连结AA’,并跟踪AA’;3、作点A在椭圆上的动画,并隐藏椭圆,点击动画按纽以,观看效果。
例2、从正方体上切下一个小三棱锥1、如图,作一个正方体,点A、B、C是图中正方体上三边上的任三个点;2、任作一点S’,让S’点分别按标记向量SA、SB、SC平移得到点A’,B’,C’ ;3、在点C’的旁边画一点M,分别作点C’向点C、点C’向点M移动的动画按纽;4、用不同颜色标出立体图形的侧面,隐藏多余的图形。
例3、作正六边形在平面内的投影1、如图,点O为旋转中心,点A旋转60度生成点B,点B旋转60度生成点C,……;作正六边形A BCDEF的内部,任选一点M,连结DM、BM,作直线AB;2、在正六边形内部(边沿)选一点N,过N分别作NN’垂直直线AB于点N’,NP平行于DM,过N’作N’P平行于BM,BM交NP于点P;3、选中点N和点P,点击轨迹命令,隐藏多余的图形,拖动点M可改变投影的形状。
例4、作一个旋转的正方体1、作线段a、b,选中a、b标记线段比;2、作圆O,作一条经过点O的直线l,在圆O上取一点A,让它以O为中心旋转90度得A’;3、作AC垂直直线l于点C,标记点C,,让点A按标记比缩放得点B,同理将点A’缩放得到点D,作点A在圆O上和动画,隐藏多余的图形;4、让点B和D绕点O旋转180度得点E和F,作四边形BDEF,让四边形BDEF向上平移适当距离,连结对应顶点。
数学立方体画法
画数学立方体的方法可以概括为以下步骤:
1.构图。
首先确定立方体的最高点和最低点,然后根据长宽比例确定最左点和最右点。
确保构图上紧下松,大小适宜,满足立方体一比一的长宽比例关系。
2.定位角点。
确定立方体中间的角点位置及田字中间的横竖十字交叉点位置。
这些点应位于田字外框的中间,竖向位置在田字高度的约四分之一处,横向位置在田字宽度的约五分之二处。
3.画棱边。
从十字交叉点出发,画出立方体的左右两条棱边,注意这两条棱边与画面水平线形成的倾斜角度关系。
接着顺势画出立方体的下沿和上沿两条棱边,形成一个完整的立方体形象。
4.细画外轮廓线。
调整外轮廓线,使离我们近的棱边画得实一些,重一些,离我们远的或看不见的棱边画得虚一些,轻一些,以呈现立方体的立体感和空间感。
5.调整完成。
运用近视远虚的绘画原理,调整画面,使立方体呈现一定的立体感和空间感。
这些步骤可以帮助你画出一个具有立体感和空间感的立方体。
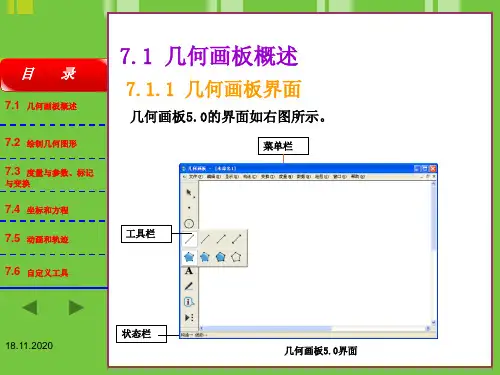
几何画板教程:绘制正方体
————————————————————————————————作者:————————————————————————————————日期:
几何画板教程:绘制正方体
空间立体图形比平面图形更直观,正方体是立体几何中经常出现的一种立体图形,在利用几何画板绘制立体图形时,要注意边与角度的关系。
几何画板绘制正方体的操作步骤如下:
1.首先绘制一个正方形。
ﻫ利用
几何画板绘制正方形
2.双击点A,标记为中心点。
选中线段AB和点B,单击“变换”——“旋转”菜单命令,选择“固定角度”,框中填入“45”度,单击“旋转”按钮,作出线段AB按逆时针旋转45度的线段AB’。
将线段AB以A为中心旋转45度
3.选中线段AB’和点B’,依次单击“变换”——“缩放”菜单命令,弹出对话框,选择“固定比”,设置为1/2,单击“确定”按钮,作出线段AB'缩小一半的线段AB”。
ﻫ将线
段AB’缩放1/2得到线段AB”
4.利用“文本”工具,将标签“B””改为“A’”。
选中线段AB’和点B’,依次单击“显示”——“隐藏”菜单命令,将其隐藏。
修改标签并隐藏线段AB”
5.同样方法,以点B为中心点,将线段BC和点C旋转-45度,并将旋转后的线段缩小一半,绘制出线段BB’。
将线段AB旋转-45度并进行缩放得到线段BB’
6.相同的方法分别以C点和D点为中心将BC和AD旋转135度,再利用缩放得到C’和D’点。
采用相同的方法对线段进行旋转和缩放得到点C’、D’
7.选中点A’、点B’、点C’、点D’,按快捷键“Ctrl+L”,作出正方体的后侧面。
即得到正方体,如图所示。
选中点A’、点B’、点C’、点D’构造四边形
以上内容向大家介绍了几何画板正方体的绘制方法,更多立体图形,比如几何画板棱柱的绘制方法,可以参考图片水印的内容。