第3章平面应力和平面应变
- 格式:ppt
- 大小:6.83 MB
- 文档页数:98



试述平面应力问题和平面应变问题的特点。
平面应力问题和平面应变问题是固体力学中的两个重要概念,用于描述材料在二维平面内受力和变形的行为。
它们具有以下特点:
平面应力问题特点:
1.二维平面:平面应力问题假设材料在一个平面内受力,即只考虑材料在平
面内的应力分布,忽略沿垂直于该平面的应力分量。
2.平行应力:在平面应力问题中,只考虑平行于平面的应力分量,即沿着平
面的两个方向上的应力分量。
3.垂直应力:由于假设材料在平面外的应力分量为零,因此平面应力问题中
不考虑垂直于平面的应力分量。
4.线性弹性:平面应力问题通常基于线性弹性理论,即假设材料的应力-应
变关系是线性的。
平面应变问题特点:
1.二维平面:与平面应力问题类似,平面应变问题假设材料在一个平面内变
形,只考虑材料在平面内的应变分布,忽略垂直于该平面的应变分量。
2.平行应变:平面应变问题中,只考虑平行于平面的应变分量,即沿着平面
的两个方向上的应变分量。
3.垂直应变:与平面应力问题不同,平面应变问题中考虑垂直于平面的应变
分量。
4.线性弹性:平面应变问题通常基于线性弹性理论,假设材料的应力-应变
关系是线性的。
这些问题的特点使得对材料在二维平面内受力和变形行为进行简化和分析成为可能。
它们在工程学和材料科学中有广泛的应用,例如在结构力学、材料设计和应力分析中的应用。


平面应力问题和平面应变问题
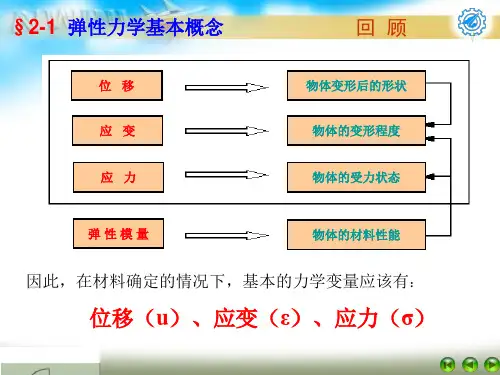
平面应力和平面应变是力学研究中的一个重要内容,它们主要涉及到应力和应变的表达、状态的判断以及它们之间的联系。
首先,平面应力是指施加在平面上的外力,它以牛顿力/
千克为单位来表示。
应力分为正应力和负应力,当施加的外力为正时,应力也是正的,反之亦然。
应力的大小由施加的外力的大小决定,如果外力越大,应力越大,反之亦然。
其次,平面应变是指在应力作用下物体的形变,它以百分比表示,一般用“δ”表示。
应变可以分为正应变和负应变,正
应变表示物体受力时膨胀,负应变表示物体受力时压缩,应变的大小与应力的大小成正比,如果应力越大,应变也越大,反之亦然。
最后,平面应力和应变之间的关系是对称的,它们的关系可以用应力-应变曲线来表示,一般来说,应力和应变的关系
是线性的,也就是说,如果应力增加一倍,应变也会增加一倍。
总之,平面应力和平面应变是力学研究中的一个重要内容,它们主要涉及到应力和应变的表达、状态的判断以及它们之间的联系。
应力和应变之间的关系可以用应力-应变曲线来表示,一般来说,应力和应变的关系是线性的,应力增加一倍,应变也会增加一倍。




试比较平面应力和平面应变问题的异同点下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!比较平面应力和平面应变问题的异同点在工程学和材料力学中,平面应力和平面应变问题是常见的分析对象。

平面应变问题和平面应力问题的异同点1. 前言在我们讨论材料力学时,平面应变和应力这两个概念就像两个兄弟,性格各异却又密不可分。
想象一下,平面应变就像个爱静的书呆子,而平面应力则是那个热爱社交的朋友。
今天就来聊聊这两个家伙的异同,看看他们在我们生活中是怎么“打交道”的。
2. 平面应变问题2.1 定义与特征首先,平面应变问题指的是在某些条件下,材料在某个平面上的变形情况。
简单来说,就是我们常见的“拉伸”和“压缩”情景。
想象一下,像橡皮泥被捏扁了,表面看起来光滑,但内部却可能发生了复杂的变形。
在这种情况下,材料的某一方向的变形被假设为零,这样我们就能简单地处理问题。
2.2 应用场景说到应用,这平面应变可不简单!它常常出现在一些工程问题中,比如桥梁、隧道建设等,特别是在大规模的结构中。
想象一下,一个大桥的承重结构,所有的力都集中在某个平面上,这时应变问题就浮出水面了。
工程师们可得好好研究这个问题,才能保证桥梁的安全性。
3. 平面应力问题3.1 定义与特征转到平面应力问题,哎呀,这家伙可就热闹多了!它主要讨论在一个平面内的应力状态,简单来说,就是材料受到的各种力作用下的反应。
想象你在拥挤的地铁里被挤来挤去,那种“被压力包围”的感觉就是平面应力的典型表现。
这个时候,虽然我们也考虑了材料的厚度,但更关注的是在某个面上的力的分布。
3.2 应用场景在实际应用中,平面应力同样是不可或缺的。
很多时候,我们在设计零件,比如汽车车身或飞机机翼时,就会用到这个概念。
设计师们可得深思熟虑,确保在高速行驶时,这些材料能承受得住压力,绝不能让人有“毛毛的感觉”。
4. 异同点总结4.1 相似之处好啦,现在我们来看看这两个概念的相似之处。
首先,平面应变和应力都涉及到材料如何在外力作用下变形或反应,都是力学的基础。
其次,它们都为工程师提供了重要的分析工具,帮助他们设计出安全可靠的结构,真是一对“亲密无间”的兄弟。
4.2 不同之处不过,这两者的不同也挺明显的。
1. 脆性断裂:断裂前,材料未发生明显的宏观塑性变形的断裂,或指断裂应力低于材料屈服强度的断裂2. 包申格效应:是指金属材料经预先加载产生少量塑性变形(残余应力小于4%),而后再同向加载,规定残余伸长应力(屈服强度、弹性极限)增加,反向加载,规定残余伸长(屈服强度、弹性极限)应力降低的现象。
3. 应力状态软性系数:应力状态中最大切应力和最大正应力的比值4. 刚度:在弹性变形范围内,构件抵抗变形的能力。
5.热疲劳:由周期变化的热应力或热应变引起的材料破坏称为热疲劳。
6.蠕变:材料在长时间的恒温、恒载荷作用下缓慢地产生塑性变形的现象。
7.疲劳强度:在指定疲劳寿命下,材料能承受的上限循环应力。
8.断裂韧度:裂纹失稳扩展的临界状态所对应的应力场强度因子称为材料的断裂韧度9.技术磁化:铁磁材料在外加磁场的作用下所产生的磁化称为技术磁化。
10.允带:电子可以具有的能级所组成的能带称为允带。
1. 韧性:是指材料在断裂前吸收塑性变形功和断裂功的能力。
4.松弛稳定性:材料抵抗应力松弛的能力称为松弛稳定性。
7.低温脆性:材料随着温度下降,脆性增加,当其低于某一温度时,材料由韧性状态变为脆性状态,这种现象为低温脆性。
8.解理断裂:材料在拉应力的作用下原于间结合破坏,沿一定的结晶学平面(即所谓“解理面”)劈开的断裂过程。
6. 破损安全:构件内部即使存在裂纹也不导致断裂的情况。
7.平面应力:只在一个平面内存在应力的现象。
10. △K th :疲劳裂纹扩展的门槛值,表征材料阻止疲劳裂纹开始扩展的能力1. 解释形变强化的概念,并阐述其工程意义。
答:材料进入塑性变形阶段后,随着变形量增大,形变应力不断提高的现象称为形变强化。
(2分)形变强化是金属材料最重要的性质之一,其工程意义在于:1)形变强化可使材料或零件具有抵抗偶然过载的能力,阻止塑性变形的继续发展,保证材料安全。
2)形变强化是工程上强化材料的重要手段,尤其对于不能进行热处理强化的材料,形变强化成为提高其强度的非常重要的手段。
平面应力和平面应变1. 平面应力在三维应力分布中,如果作下列假定无关与z 、、xy y x yz xz z τσσττσ0=== 1-1就得到了平面应力问题。
这种情况发生在薄板边界处受到平行于板面、并且沿厚度均匀分布的力作用的时候如图。
这时,在板的上下表面处,z σ、xz τ、yz τ为零(z 为板的法向),并认为沿着整个厚度方向它们也等到于零(因为厚度很小)。
应力状态只须用仅与x 、y 有关的x σ、y σ、xy τ来描述,称为平面应力情况。
此时,这三个应力分量与z 无关,即沿着板厚度保持不变。
平面应力问题的所有方程可以从相应的三维方程并结合式1-1得到:平衡方程 ⎪⎪⎭⎪⎪⎬⎫=+∂∂+∂∂=+∂∂+∂∂00y y xy x xy x f y x f y x σττσ 1-2 边界条件 ⎪⎭⎪⎬⎫+=+=--y xy xy x m l Y m l X σττσ 1-3 应变--位移方程 ⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂=∂∂=∂∂=x v y u y v x u xy y x γεε 1-4 应力--应变方程 ()()⎪⎭⎪⎬⎫=-=-=G E v E v xy xy x y y y x x τγσσεσσε 1-5 这里()v E G +=12是剪切模量,在结构的矩阵分析中,常把1-5式写成矩阵形式。
即()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧xy y x xy y x v v E τσσγεε1201011称对 1-6 或者,反之用应变表示应力,则有⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧xy y x xy y x v v vE γεετσσ21010112称对 或记: {}[]{}εσD = 1-7其中: []⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--=21010112v v v E D 称对 1-8 协调方程 y x x y xy y x ∂∂∂=∂∂+∂∂γεε22222 1-9 此外,还必须注意下面两点:1) 在平面应力状态中0=z σ,而0≠z ε,事实上有()⎪⎪⎭⎪⎪⎬⎫==+-=00yz xzy x z E v γγσσε 2)平面应力假定下,方程式1-1是违背了某些协调条件的。