激光器速率方程
- 格式:ppt
- 大小:283.00 KB
- 文档页数:21



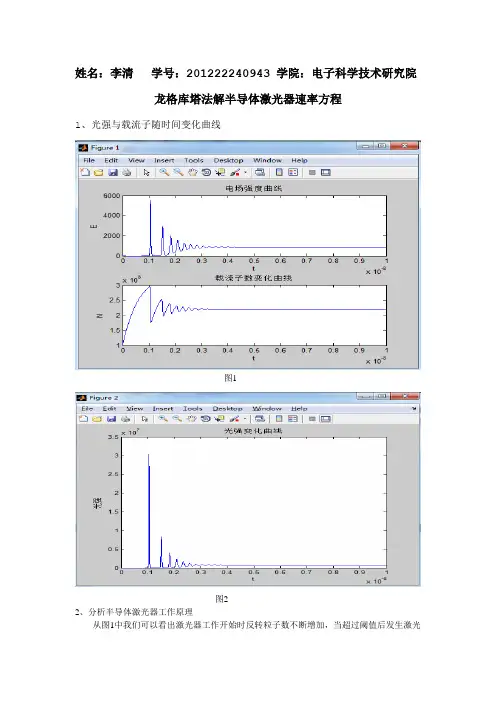
姓名:李清学号:************ 学院:电子科学技术研究院龙格库塔法解半导体激光器速率方程1、光强与载流子随时间变化曲线图1图22、分析半导体激光器工作原理从图1中我们可以看出激光器工作开始时反转粒子数不断增加,当超过阈值后发生激光的激射。
同时,观察图2我们还可以发现,当发生激射后,反转粒子数还在不断增加,激光光强不断增加。
由于激光的产生是以消耗反转粒子数为代价的,因此载流子数开始减少,小于阈值后便不会继续产生激光。
接着反转粒子数被不断激励,数目增加,超过阈值后又发生激光激射,这就是半导体激光器的工作原理。
3、使用稳态分析推导阈值电流的大小在稳态时,增益等于损耗,也就是G=r,同时电场和载流子数均不随时间变化,将这些带入第二个方程,即可解得结果如下,与之电流为0.058417067A。
4、源程序:t0=0;h=1e-12;tn=1e-8;n=(tn-t0)/h+1;E=zeros(1,n);N=zeros(1,n);E(1)=0.1;N(1)=1e8;t=t0:h:tn;for i=1:n-1E1=f1(N(i),E(i));E2=f1(N(i)+h/2,E(i)+E1*h/2);E3=f1(N(i)+h/2,E(i)+E2*h/2);E4=f1(N(i)+h,E(i)+E3*h);E(i+1)=E(i)+(E1+2*E2+2*E3+E4)*h/6;N1=f2(E(i),N(i));N2=f2(E(i)+h/2,N(i)+N1*h/2);N3=f2(E(i)+h/2,N(i)+N2*h/2);N4=f2(E(i)+h,N(i)+N3*h);N(i+1)=N(i)+(N1+2*N2+2*N3+N4)*h/6;endNn=N(n);In=abs(E(n)).*abs(E(n));N0=1.5e8;g=3.6e3;r=252e9;Nx=r/g+N0;q=1.6e-19;re=1.66e9;I0=re*Nx*q+r*q*E(n);subplot(211)plot(t,abs(E))title('电场强度曲线')xlabel('t')ylabel('E')subplot(212)plot(t,N)title('载流子数变化曲线')xlabel('t')ylabel('N')figure(2),plot(t,abs(E).*abs(E)) title('光强变化曲线')xlabel('t')ylabel('光强')function f1=f1(N,E)a=3;g=3.6e3;N0=1.5e8;G=g*(N-N0);r=252e9;f1=0.5*(1+1i*a)*(G-r)*E;function f2=f2(E,N)I=90e-3;q=1.6e-19;re=1.66e9;g=3.6e3;N0=1.5e8;G=g*(N-N0);f2=I/q-re*N-G*(abs(E))^2;。

matlab对半导体激光器速率方程进行求解文章标题:深入探讨Matlab对半导体激光器速率方程的求解1. 简介半导体激光器作为一种重要的光电器件,在通信、医疗、材料加工等领域具有广泛的应用。
而速率方程是描述半导体激光器内部过程的重要数学模型,通过对速率方程的求解,可以更好地理解半导体激光器的工作原理和特性。
在本文中,我将结合Matlab软件,就如何利用Matlab对半导体激光器速率方程进行求解展开深入探讨。
2. 半导体激光器速率方程简介半导体激光器速率方程是描述半导体激光器内部电子和光子之间相互作用的重要数学模型。
其一般形式如下:\[ \frac{dn}{dt} = G - \frac{n}{\tau_{n}} - \frac{nI}{I_{s}} \]\[ \frac{dI}{dt} = \frac{e\eta V}{q}n - (\alpha+g)nI \]其中,n为激子数密度,I为激光光强,G为外界注入的光子数密度,τn为激子寿命,I s为饱和光子密度,η为激子与光子的电荷,V为激光器波导体积,q为电子电荷量,e为元电荷,α为损耗系数,g为增益系数。
3. Matlab在对半导体激光器速率方程求解中的应用Matlab作为一种强大的科学计算软件,提供了丰富的数学建模和仿真工具,非常适合用于对半导体激光器速率方程的求解。
利用Matlab,可以通过编写相应的数学模型和算法,实现对速率方程的数值求解。
Matlab提供了丰富的绘图和数据分析功能,可以对求解结果进行直观展示和分析。
4. 在Matlab中编写半导体激光器速率方程求解程序在使用Matlab对半导体激光器速率方程进行求解时,首先需要编写相应的数学模型和算法。
可以利用Matlab的ODE求解器对速率方程进行数值求解。
还可以结合Matlab的优化工具,对速率方程的参数进行拟合和优化,得到更准确的结果。
在编写程序时,应注意处理数值求解的收敛性和稳定性,避免出现数值不稳定或发散的情况。




半导体激光器速率方程求解半导体激光器是一种利用电流驱动产生激光的器件,广泛应用于通信、激光打印、医疗和科学研究等领域。
了解和理解半导体激光器的工作原理对于设计和优化激光器具有重要意义。
在本文中,我们将介绍半导体激光器速率方程以及如何使用MATLAB进行求解。
半导体激光器速率方程半导体激光器速率方程描述了半导体激光器内部发生的光与电子相互作用的过程。
速率方程包含了四个关键项:电子注入项I in,非辐射复合项R nr,自发辐射项R sp和受激辐射项R spon。
方程可以写成如下形式:dN dt =I ineV−Nτnr+Nτsp+Nτspon其中,N表示激光器内的载流子密度,t表示时间,e为元电荷,V为激光器的有效体积,τnr为非辐射寿命,τsp为自发辐射寿命,τspon为受激辐射寿命。
使用MATLAB求解速率方程MATLAB是一种功能强大的数值计算软件,适合用于求解微分方程。
我们可以利用MATLAB的ODE求解器来求解半导体激光器速率方程。
首先,我们需要定义速率方程的函数形式。
在MATLAB中,我们可以定义一个函数文件,例如rate_equation.m,其中包含速率方程的定义:function dNdt = rate_equation(t, N)% 参数定义I_in = 1; % 电子注入项V = 1; % 有效体积tau_nr = 1; % 非辐射寿命tau_sp = 2; % 自发辐射寿命tau_spon = 0.5; % 受激辐射寿命% 速率方程求解dNdt = (I_in / (e * V)) - (N / tau_nr) + (N / tau_sp) + (N / tau_sp on);end然后,我们可以使用MATLAB的ODE求解器对速率方程进行求解。
例如,可以使用ode45求解器来得到方程的数值解。
% 定义时间范围和初始载流子密度tspan = [010]; % 时间范围N0 = 0; % 初始载流子密度% 求解速率方程[t, N] = ode45(@rate_equation, tspan, N0);% 绘制载流子密度随时间变化的曲线plot(t, N);title('半导体激光器载流子密度随时间变化');xlabel('时间');ylabel('载流子密度');运行以上MATLAB代码,我们可以得到半导体激光器载流子密度随时间变化的曲线图。


第二章 光注入半导体激光器的速率方程模型2.1 光反馈半导体激光器光反馈或光注入半导体激光器的速率方程是分析和模拟系统特性的理论基础,本节先推导光反馈半导体激光器的电场速率方程―Lang-Kobayashi 方程[29],并分析了振荡条件。
为方便分析,将半导体激光器的参量及各参量的关系分别列入表2-1和表2-2。
表2-1 激光器参量的意义符号 物理量 单位 电量 C 有源区体积 m 3 载流子寿命 ns 光子寿命 ps 限制因子 --- 阈值载流子密度 m -3 透明载流子密度 m -3 增益饱和系数 m 3 线宽增强因子 --- 微分增益 m 3s -1 自发辐射因子 --- 端面强度反射率 ---波长nm表2-2 参量之间的关系Table 2-2 Relationships of parameters2.1.1 图2-1 光反馈Fabry-Perot 谐振腔示意图图2-1为光反馈的示意图,激光谐振腔两端面的反射率分别为1R 、2R ,腔长为L ,外部反射镜的反射率为e R 、距离为/2e L c τ=,τ为激光在外腔中环行一次的时间。
E +、E-分别表示正向、负向传播的时变电场的复振幅。
激光的动态变化行为取决于增益,因此可以将增益作为算子。
激光在腔内环行一次的增益为int 2())r G i kL Γg L α=-+- (2-1)将其变为指数形式,上式可变为int exp(2())r m G i kL Γg L αα=-+-- (2-2)其中/k n c ω=为波数。
实际上,激光器有源区内载流子密度()N t 随时间的变化将导致介质折射率和振荡频率的变化。
因此将波数在无光反馈阈值点(th n ,th ω)展开()()g th th th th th n n n nN N c c c N cωωωωω∂≈+-+-∂ (2-3) 其中,g th nn n ωω∂=+∂为介质的群折射率。
将(2-3)式代入(2-2)中,并将r G 分解成1r G G G ω=,其中:频率无关项1int exp[()]exp((2/)())m th th nG Γg L i L c N N Nααω∂=----∂ (2-4) 频率相关项22exp[()]g th th th n Ln L G ii c cωωωω=--- (2-5) 由于2th th n L c ω是2π的整数倍,并且角频率为ω的单色波电场满足关系式di dtω=,G ω可改写为算子exp()exp()th L LdG i dtωωττ=- (2-6) 由于激光器振荡频率在阈值附近,即th ωω≈,因此对时变复电场()e t 可引入慢变化复电场振幅()|()|exp(())E t E t i Φt =,即()()exp()th e t E t i t ω= (2-7)其中th d dtΦωω=-。
第二章 光注入半导体激光器的速率方程模型2.1 光反馈半导体激光器光反馈或光注入半导体激光器的速率方程是分析和模拟系统特性的理论基础,本节先推导光反馈半导体激光器的电场速率方程―Lang-Kobayashi 方程[29],并分析了振荡条件。
为方便分析,将半导体激光器的参量及各参量的关系分别列入表2-1和表2-2。
表2-1 激光器参量的意义符号 物理量 单位 电量 C 有源区体积 m 3 载流子寿命 ns 光子寿命 ps 限制因子 --- 阈值载流子密度 m -3 透明载流子密度 m -3 增益饱和系数 m 3 线宽增强因子 --- 微分增益 m 3s -1 自发辐射因子 --- 端面强度反射率 ---波长nm表2-2 参量之间的关系Table 2-2 Relationships of parameters2.1.1 图2-1 光反馈Fabry-Perot 谐振腔示意图图2-1为光反馈的示意图,激光谐振腔两端面的反射率分别为1R 、2R ,腔长为L ,外部反射镜的反射率为e R 、距离为/2e L c τ=,τ为激光在外腔中环行一次的时间。
E +、E-分别表示正向、负向传播的时变电场的复振幅。
激光的动态变化行为取决于增益,因此可以将增益作为算子。
激光在腔内环行一次的增益为int 2())r G i kL Γg L α=-+- (2-1)将其变为指数形式,上式可变为int exp(2())r m G i kL Γg L αα=-+-- (2-2)其中/k n c ω=为波数。
实际上,激光器有源区内载流子密度()N t 随时间的变化将导致介质折射率和振荡频率的变化。
因此将波数在无光反馈阈值点(th n ,th ω)展开()()g th th th th th n n n nN N c c c N cωωωωω∂≈+-+-∂ (2-3) 其中,g th nn n ωω∂=+∂为介质的群折射率。
将(2-3)式代入(2-2)中,并将r G 分解成1r G G G ω=,其中:频率无关项1int exp[()]exp((2/)())m th th nG Γg L i L c N N Nααω∂=----∂ (2-4) 频率相关项22exp[()]g th th th n Ln L G ii c cωωωω=--- (2-5) 由于2th th n L c ω是2π的整数倍,并且角频率为ω的单色波电场满足关系式di dtω=,G ω可改写为算子exp()exp()th L LdG i dtωωττ=- (2-6) 由于激光器振荡频率在阈值附近,即th ωω≈,因此对时变复电场()e t 可引入慢变化复电场振幅()|()|exp(())E t E t i Φt =,即()()exp()th e t E t i t ω= (2-7)其中th d dtΦωω=-。
光纤激光器速率方程 matlab程序光纤激光器速率方程是描述光纤激光器中光强变化随时间演化的数学模型。
光纤激光器是一种利用光纤作为传输介质的激光器,具有高功率、高效率、窄线宽等优点,在通信、材料加工、医疗等领域有着广泛的应用。
了解光纤激光器速率方程对于优化激光器设计和提高激光器性能具有重要意义。
光纤激光器速率方程描述了光纤激光器中光强的时域演化过程。
光纤激光器中的光强受到多种因素的影响,包括增益、损耗、自发辐射、受激辐射等。
光纤激光器速率方程可以通过对这些因素的定量描述,得到光强随时间的变化规律。
光纤激光器速率方程的基本形式为:dE/dt = (G - α)E - βEL其中,E为激光场强度,t为时间,G为增益系数,α为损耗系数,β为非线性系数,L为光纤长度。
这个方程可以看作是对光强的变化率进行描述,右侧第一项表示增益和损耗对光强的影响,第二项表示非线性效应对光强的影响。
在实际应用中,为了更准确地描述光纤激光器中光强的演化,可以考虑其他因素的影响,如色散、自相位调制等。
这些因素的引入可以使光纤激光器速率方程更加准确地描述光强的变化规律。
为了求解光纤激光器速率方程,可以使用数值方法进行仿真计算。
其中,最常用的方法是有限差分法。
有限差分法将时间和空间离散化,将连续的方程转化为离散的差分方程,然后通过迭代求解差分方程,得到光强随时间的变化。
在MATLAB中,可以通过编写相应的程序来求解光纤激光器速率方程。
首先,需要定义方程中的各个参数和初始条件。
然后,通过差分方法离散化方程,并利用迭代算法求解离散化后的方程。
最后,根据得到的结果,可以绘制光强随时间的变化曲线,以及其他感兴趣的物理量。
光纤激光器速率方程的求解对于优化光纤激光器的设计和改进激光器性能具有重要意义。
通过求解方程,可以获得光纤激光器中光强随时间的变化规律,进而分析和优化激光器的工作状态。
此外,光纤激光器速率方程的求解也为理论研究提供了重要的工具,可以用于研究激光器的非线性效应、自脉冲形成等现象。