浙江省数学中考专题复习专题七动态型问题训练1

1.如图，平行四边形ABCD中，AB= cm，BC=2cm，∠ABC=45°，点P从点B出发，以1cm/s的速度沿折线BC→CD→DA运动，到达点A为止，设运动时间为t(s)，△ABP的面积为S(cm2)，则S与t的大致图象是（）A. B. C. D.【答案】A【解析】：分三种情况讨论：①当0≤t≤2时，过A作AE⊥BC于E．∵∠B=45°，∴△ABE是等腰直角三角形．∵AB= ，∴AE=1，∴S= BP×AE= ×t×1= t；②当2＜t≤ 时，S= = ×2×1=1；③当＜t≤ 时，S= AP×AE= ×（-t）×1= （-t）．故答案为：A．【分析】根据题意分三种情况讨论：①当0≤t≤2时，过A作AE⊥BC于E；②当2＜t≤ 2 +时；③当 2 + ＜t≤ 4 +时，分别求出S与t的函数解析式，再根据各选项作出判断，即可得出答案。

2.如图，边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )A. B. C. D.【答案】B【解析】：连接BD∵四边形ABCD是菱形，∴AB=AD，∵∠DAB=60°，∴△ABD是等边三角形，∴AB=DB，∠BDF=60°∴∠A=∠BDF又∵AE+CF=a，∴AE=DF，在△ABE和△DBF中，∴△ABE≌△DBF（SAS），∴BE=BF，∠ABE=∠DBF，∴∠EBF=∠ABD=60°，∴△BEF是等边三角形．∵E是异于A、D两点的动点,F是CD上的动点,要使△BEF的周长最小，就是要使它的边长最短∴当BE⊥AD时，BE最短在Rt△ABE中，BE==∴△BEF的周长为【分析】根据等边三角形的性质及菱形的性质，证明∠A=∠BDF，AE=DF，AB=AD，就可证明△ABE≌△DBF，根据全等三角形的性质，可证得BE=BF，∠ABE=∠DBF，再证明△BEF是等边三角形，然后根据垂线段最短，可得出当BE⊥AD时，BE最短，利用勾股定理求出BE的长，即可求出△BEF的周长。

初中数学动态问题复习题初中数学动态问题复习题数学是一门需要动脑筋的学科，其中的动态问题更是让人头痛不已。

动态问题是指涉及时间、速度、距离等变量的数学问题。

在初中数学中，动态问题常常出现在应用题中，需要我们通过建立方程、列式子等方法来解决。

下面，我们来复习一些初中数学中常见的动态问题。

1. 小明骑自行车从A地到B地，全程100公里。

他开始时以每小时20公里的速度骑行，过了一段时间后，他加快了速度，以每小时30公里的速度骑行。

问小明骑行了多长时间到达B地？解析：设小明骑行了x小时后加快速度，那么他骑行了(100-20x)公里后加快速度。

根据速度等于路程除以时间，我们可以列出方程：20x + 30(100-20x) = 100解方程得到 x = 2。

所以小明骑行了2小时后加快速度，总共用时2 + (100-20*2)/30 = 4小时。

2. 甲、乙两辆汽车同时从A地出发，分别以每小时60公里和每小时80公里的速度相向而行，相距240公里时，一只鸟从甲车上飞到乙车上，然后再飞回甲车上，如此往复直到两车相遇。

问这只鸟飞了多少公里？解析：设鸟飞行的时间为t小时，那么两车相遇时，甲车行驶了60t公里，乙车行驶了80t公里。

根据题目中的条件，我们可以列出方程：60t + 80t = 240解方程得到 t = 2。

所以鸟飞行了2小时，飞行距离为60*2 = 120公里。

3. 甲、乙两辆汽车同时从A地出发，分别以每小时50公里和每小时70公里的速度相向而行，相距200公里时，一只兔子从甲车上跳到乙车上，然后再跳回甲车上，如此往复直到两车相遇。

问这只兔子跳了多少公里？解析：设兔子跳行的时间为t小时，那么两车相遇时，甲车行驶了50t公里，乙车行驶了70t公里。

根据题目中的条件，我们可以列出方程：50t + 70t = 200解方程得到 t = 2。

所以兔子跳行了2小时，跳行距离为50*2 = 100公里。

通过以上的复习题，我们可以看到，解决动态问题的关键是建立方程或列式子，并通过解方程或计算来得到答案。

第40讲实验与动向型问题动向型问题是指以三角形、四边形、圆等几何图形或函数图象为载体，设计动向变化，并对变化过程中陪伴着的等量关系、变量关系、图形的特别状态、内容图形间的特别关系等进行实验、察看、猜想和概括，进行推理的一类问题，特征这种问题信息量大，灵巧多变，出现的结果常常有多种状况．波及到平行线、相像三角形的性质，锐角三角函数，方程、不等式及函数的知识，以及几何变换，数形联合，分类议论，函数与方程，特别与一般的思想.解决此类问题需要运用运动和变化的看法，掌握运动和变化的全过程，动中解题取静，静中求动，抓住运动中的某一瞬时，抓住变化过程中的特别情况，确策略定运动变化过程中的数目关系、图形地点关系，进而成立方程、不等式、函数、几何模型，找到解决问题的门路.解题时利用方程与函数的思想、转变思想、数形联合思想、分类议论思想，基本适合地使用剖析综合法，发掘题目的隐含条件，将复杂问题分解为基本问题，思想逐一击破，进一步获得新的结论.种类一由点运动产生的问题例1(2017·丽水)如图1，在△ABC中，∠A＝30°，点P从点A出发以2cm/s的速度沿折线A－C－B运动，点Q从点A出发以a(cm/s)的速度沿AB运动，P，Q两点同时出发，2当某一点运动到点B时，两点同时停止运动．设运动时间为x(s)，△APQ的面积为y(cm)，y对于x的函数图象由C1，C2两段构成，如图2所示．1求a的值；求图2中图象C2段的函数表达式；当点P运动到线段BC上某一段时△APQ的面积大于当点P在线段AC上随意一点时△APQ的面积，求x的取值范围．【解后感悟】解题的重点是从运动图与描绘图中获守信息，依据图象确立x的运动时间与面积的关系，同时关注图象不一样状况的议论．这种问题常常研究点在运动变化过程中的变化规律，如等量关系、图形的特别地点、图形间的特别关系等，且表现分类议论和数形联合的思想．1．(2016·白银)如图，△ABC是等腰直角三角形，∠ A＝90°，BC＝4，点P是△ABC边上一动点，沿B→A→C的路径挪动，过点P作PD⊥BC于点D，设BD＝x，△BDP的面积为y，则以下能大概反应y与x函数关系的图象是()2．(1)如图，在平面直角坐标系中，点A在抛物线y＝x2－2x＋2上运动，过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为.2(2) (2016·舟山)如图，在直角坐标系中，点A，B分别在x轴，y轴上，点A的坐标为(－1，0)，∠ABO＝30°，线段动一周，同时另一端点Q随之在周时，点Q运动的总行程为PQ的端点P从点O出发，沿△OBA的边按O→B→A→O运x轴的非负半轴上运动，假如PQ＝3，那么当点P运动一.种类二由线运动产生的问题例2(2015·无锡)如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M.(1)若∠AOB＝60°，OM＝4，OQ＝1，求证：CN⊥OB；当点N在边OB上运动时，四边形OMPQ一直保持为菱形．①问：1－1的值能否发生变化？假如变化，求出其取值范围；假如不变，请说明原因；OMON②设菱形OMPQ的面积为1，△NOC的面积为2S1S S，求的取值范围．2S【解后感悟】解答这种问题时要用运动与变化的看法去察看和研究图形，掌握直线或曲线变化的全过程，此题中PQ∥OA，PM∥OB，波及相像三角形的判断与性质，抓住等量关系，特别注意一些不变量、不变关系或特别关系．3．(1)(2016·长春市南关区模拟)如图，在平面直角坐标系中，矩形ABCD的边BC在x轴的正半轴上，点B在点C的左边，直线y＝kx经过点A(3，3)和点P，且OP＝62.将直线y＝kx沿y轴向下平移获得直线y＝kx＋b，若点P落在矩形ABCD的内部，则b的取值范围是()3A．0<b<3B．－3<b<0C．－6<b<－3D．－3<b<3 (2)(2016·合肥模拟)在平面直角坐标系的第一象限内，边长为1的正方形ABCD的边均平行于坐标轴，4与此正方形的边有交点，A点的坐标为(a，a)．如图，若曲线y＝(x>0)x则a的取值范围是.(3) (2016·新昌模拟)已知Rt△ABC的极点坐标为A(1，2)，B(2，2)，C(2，1)，若抛物线y＝ax2与该直角三角形无公共点，则a的取值范围是.(4) (2016·海陵模拟)如图，等腰直角三角形的斜边长AB＝8，向来线l绕极点B随意旋转，过A向l作垂线，垂足为H，则线段C H长的取值范围是.种类三由图形运动产生的问题例3 (2016·金华)由6根钢管首尾按序铰接而成六边形钢架ABCDEF，相邻两钢管能够转动．已知各钢管的长度为AB＝DE＝1米，BC＝CD＝EF＝FA＝2米．(铰接点长度忽视不计)(1)转动钢管获得三角形钢架，如图1，则点A，E之间的距离是米；转动钢管获得如图2所示的六边形钢架，有∠A＝∠B＝∠C＝∠D＝120°，现用三根钢条连结极点使该钢架不可以活动，则所用三根钢条总长度的最小值是米．4【解后感悟】由图形变化产生的问题包含由点惹起的图形变化，图形的平移、旋转、翻转等；图形在变化过程中，抓住不变的图形和量；以三角形、四边形和圆的变化为常有的一种题型．此题的重点是增添协助线结构特别三角形以及平行四边形．4．(2016·金华)如图，Rt△ABC纸片中，∠C＝90°，AC＝6，BC＝8，点D在边BC上，以AD为折痕折叠△ABD获得△AB′D，AB′与边BC交于点E.若△DEB′为直角三角形，则BD的长是.5．(2016·宁波)如图，在平面直角坐标系中，O为坐标原点，点A的坐标为(5，0)，4菱形OABC的极点B，C都在第一象限，tan∠AOC＝3，将菱形绕点A按顺时针方向旋转角α(0°＜∠α＜∠AOC)获得菱形FADE(点O的对应点为点F)，EF与OC交于点G，连结AG.求点B的坐标；当OG＝4时，求AG的长；求证：GA均分∠OGE；连结BD并延伸交x轴于点P，当点P的坐标为(12，0)时，求点G的坐标．【动点实验题】用如图1，2所示的两个直角三角形(部分边长及角的度数在图中已标出)，达成以下两个研究问题：5研究一：将以上两个三角形如图3拼接(BC和ED重合)，在BC边上有一动点P.(1)当点P运动到∠CFB的角均分线上时，连结AP，求线段AP的长；当点P在运动的过程中出现PA＝FC时，求∠PAB的度数．研究二：如图4，将△DEF的极点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连结MN.在旋转△DEF的过程中，△AMN的周长能否存在有最小值？若存在，求出它的最小值；若不存在，请说明原因．【方法与对策】此题是几何综合题，运用认识直角三角形、勾股定理、全等三角形、二次函数最值等知识点．第(3)问，由发现并证明△AMD≌△CND获得解题的打破点，再利用勾股定理和二次函数的性质求出最小值．这种题型要注意问题的前后关系，要利用前方方法来指导后边的问题，要利用特别到一般的思想，这是中考常有题型．【没有绘图和动向剖析，以致问题剖析不全】k如图，已知△ABC三个极点的坐标分别为A(1，4)，B(4，1)，C(1，1)，若双曲线y＝x(x＞0)与△ABC有公共点，则k的取值范围是________．6精选文档第40讲实验与动向型问题【例题精析】111例1(1)如图1，作PD⊥AB于D，∵∠A＝30°，∴PD＝2AP＝x，∴y＝2AQ·PD＝2ax2，1121由图象可知，当x＝1时，y＝2，∴2×a×1＝2，解得a＝1；(2)如图2，作PD⊥AB于D，7PB ＝5×2－2x ＝10－2x ，PD ＝PB ·sin B ＝(10－2x)·sin B ，∴y ＝ 1由图象可知，2×AQ ×PD 1 4 1 42x ×(10－2x)·sin B ，∵当x ＝4时，y ＝3，∴2×4×(10－2×4)·sin B ＝3，解得，sin B1 1 1 1 25 1 2 1 25 ＝，∴y ＝x ×(10－2x)×3＝－x ＋x ；(3)x ＝－x ＋x ，解得，x 1＝0，x 2＝2，由图3233233象可知，当1 2 有最大值，最大值是 12125 ＝3，x ＝2时，y ＝2x2×2＝2，－3x ＋3x ＝2，解得，x1x 2＝2，∴当2＜x ＜3时，点P 运动到线段 BC 上某一段时△APQ 的面积大于当点 P 在线段AC上随意一点时△APQ 的面积．例2(1)过P 作PE ⊥OA 于E ，∵PQ ∥OA ，PM ∥OB ，∴四边形 OMPQ 为平行四边形．∴PM313＝OQ ＝1，∠PME ＝∠AOB ＝60°，∴PE ＝PM ·sin 60°＝2，ME ＝2，∴CE ＝OC －OM －ME ＝2，∴tan ∠PCE ＝PE 3 ＝，∴∠PCE ＝30°，∴∠CPM ＝90°，又∵PM ∥OB ，∴∠CNO ＝∠CPM ＝CE390°，即CN ⊥OB.11OM ＝x ，ON ＝y.∵四边形OMPQ 为菱形，∴(2)① －的值不发生变化．原因以下：设OMONOQ ＝QP ＝OM ＝x ，NQ ＝y －x.∵PQ ∥OA ，∴∠NQP ＝∠O.又∵∠QNP ＝∠ONC ，∴△NQP ∽△NOC ，QPNQxy －x 111111∴＝，即＝ ，∴6y －6x ＝xy.两边都除以6xy ，得－＝，即－ ＝.②过POC ON6yxy6OMON61S 1x ·PE作PE ⊥OA 于E ，过N 作NF ⊥OA 于F ，则S 1＝OM ·PE ，S 2＝OC ·NF ，∴＝.∵PM ∥OB ，2S3NF2PECM6－xSx （6－x ）∴∠PMC ＝∠O.又∵∠PCM ＝∠NCO ，∴△CPM ∽△CNO.∴ ＝ ＝.∴ 1＝－6 ＝ 18NFCO S 2121S 1(x －3)＋.∵0＜x ＜6，由这个二次函数的图象可知， 0＜ 1.≤18 2 S 2 28例3(1)如图1中，∵FB＝DF，FA＝FE，∴∠FAE＝∠FEA，∠B＝∠D，∴∠FAE＝∠B，∴AE∥BD，∴AE AF AE288＝，∴＝，∴AE＝，故答案为.(2)如图2中，作BN⊥FA于N，延DB FB43333长AB、DC交于点M，连结BD、AD、BF、CF.在Rt△BFN中，∵∠BNF＝90°，BN＝2，FN＝1522AN＋AF＝2＋2＝2，∴BF＝BN＋NF＝7，同理获得AC＝DF＝7，∵∠ABC＝∠BCD＝120°，∴∠MBC＝∠MCB＝60°，∴∠M＝60°，∴CM＝BC＝BM，∵∠M＋∠MAF＝180°，∴AF∥DM，∵AF＝CM，∴四边形AMCF是平行四边形，∴CF＝AM＝3，∵∠BCM＝∠CBD＋∠CDB＝60°，22∠CBD＝∠CDB，∴∠CBD＝∠CDB＝30°，∵∠M＝60°，∴∠MBD＝90°，∴BD＝DM－BM＝23，BE＝22BD＋DE＝13，∵7<3<23＜13，∴用三根钢条连结极点使该钢架不可以活动，∴连结AC、BF、DF即可，∴所用三根钢条总长度的最小值为37，故答案为37.【变式拓展】1．B2. (1)1(2)413.(1)C(2)2≤a≤3(3)a<0或a>2或0<a<(4)0≤CH≤844.2或55．(1)如图1，过点B作BH⊥x轴于点H，∵四边形OABC为菱形，∴OC∥AB，∴∠BAH＝∠COA∵.tan∠AOC＝4，∴tan∠BAH＝4.又∵在直角△BAH中，AB＝5，∴BH＝4AB＝4，AH 3353＝5AB＝3，∴OH＝OA＋AH＝5＋3＝8，∴点B的坐标为(8，4)；(2)如图1，过点A作AM⊥OC443于点M，在直角△AOM中，∵tan∠AOC＝，OA＝5，∴AM＝OA＝4，OM＝OA＝3，∵OG＝4，355∴GM＝OG－OM＝4－3＝1，∴AG＝222217；(3)如图1，过点A作AN⊥EF AM＋GM＝4＋1＝AOM＝∠F，于点N，∵在△AOM与△AFN中，OA＝FA，∴△AOM≌△AFN(AAS)，∴AM＝AN，AMO＝∠ANF＝90°，∴GA均分∠OGE.(4)如图2，过点G作GQ⊥x轴于点Q，由旋转可知：∠OAF＝∠BAD＝α.∵AB9＝AD ，∴∠ABP ＝180°－α，∵∠AOT ＝∠F ，∠OTA ＝∠GTF ，∴∠OGF ＝∠OAF ＝α，∴∠OGA2＝∠EGA ＝180°－α，∴∠OGA ＝∠ABP ，又∵∠GOA ＝∠BAP ，∴△GOA ∽△BAP ，∴GQOA2＝ ，BH AP5 20 4 20 3 15 15 20∴GQ ＝7×4＝7.∵tan ∠AOC ＝3，∴OQ ＝7×4＝7，∴G7，7.【热门题型】【剖析与解】研究一：(1)依题意画出图形，如图 1所示：由题意，得∠CFB ＝60°，FP为角均分线，则∠CFP ＝30°.∴CF ＝BC ·tan 30°＝3×3 3.∴CP ＝CF ·tan ∠CFP ＝33＝31 3313＝1.过点A 作AG ⊥BC 于点G ，则AG ＝2BC ＝2，∴PG ＝CG －CP ＝2－1＝2.在Rt △APG 中，22321210由勾股定理得：AP ＝ AG ＋PG ＝ （2） ＋（2）＝2. (2)由(1)可知，FC ＝ 3，如 图2所示，以点A 为圆心，以FC ＝3长为半径画弧，与BC 交于点P 、P ，则AP ＝AP ＝3.1 2 1 2313cos ∠P 1AG ＝ AG 23 过点A 作AG ⊥BC 于点G ，则AG ＝BC ＝，在Rt △AGP 1中， ＝ ＝ 2，∴∠2 2AP 1 3P 1AG ＝30°.∴∠P 1AB ＝45°－30°＝15°.同理求得，∠P 2AG ＝30°，∠P 2AB ＝45°＋30°＝75°.∴∠PAB 的度数为15°或75°.研究二：△AMN 的周长存在最小值．如图3所示，连结AD ，∵△ABC 为等腰直角三角形，点D 为斜边BC 的中点，∴AD ＝CD ，∠C ＝∠MAD ＝ ∠MAD ＝∠C ，45°.∵∠EDF ＝90°，∠ADC ＝90°，∠MDA ＝∠NDC ∵.在△AMD 与△CND 中，AD ＝CD ，∠MDA ＝∠NDC ，∴△AMD ≌△CND(ASA)．∴AM ＝CN.设AM ＝x ，则CN ＝x ，AN ＝AC －CN ＝2 BC －CN ＝32－x ，2 2在Rt △AMN 中，由勾股定理得：MN ＝2223 2 229AM ＋AN ＝x ＋（2－x ） ＝2x －3 2x ＋2＝3 2293 23 2 292（x －4）＋4，∴△AMN 的周长为：AM ＋AN ＋MN ＝2 ＋2（x －4）＋4.当x ＝3232 93＋323＋32时，有最小值，最小值为＋＝.∴△AMN 周长的最小值为.424 2210【错误警告】如图2，若双曲线与△ABC有公共点，则双曲线向下最多到点C，向上最多到与直线AB只有一个交点，当过点C时，解得k＝1；当双曲线与直线AB只有一个交点时，设直线AB4＝a＋b，a＝－1，∴直线AB的分析分析式为y＝ax＋b，∵A(1，4)，B(4，1)，∴解得1＝4a＋b，b＝5，k式为y＝－x＋5，∴y＝x，∴x2－5x＋k＝0，则该方程有两个相等的实数根，∴＝y＝－x＋5，225250，即(－5)－4k＝0，解得k＝4，∴k的取值范围为：1≤k≤4.11。

2022-2023学年浙教版八年级数学下册精选压轴题培优卷专题07 动态几何问题（一元二次方程的应用）姓名：___________班级：___________考号：___________ 评卷人得分一、选择题(每题2分，共20分) 1．(本题2分)（2022秋·河南郑州·九年级校考期中）如图，矩形ABCD 中，2cm 3cm AB BC ==，，点E 从点B 出发，沿BC 以 2cm/s 的速度向点C 移动，同时点F 从点C 出发，沿CD 以1cm/s 的速度向点D 移动，当E ，F 两点中有一点到达终点时，另一点也停止运动．当AEF △是以AF 为底边的等腰三角形时，则点E 运动时间为( )A ．631B ．631C ．6D ．631或6312．(本题2分)（2022秋·山东德州·九年级统考阶段练习）如图，在Rt ABC △中，90C ∠=︒，12AC =cm ，9BC =cm ．现有动点P 从点A 出发，沿AC 向点C 方向运动，动点Q 从顶点C 出发，沿线段CB 向点B 方向运动，如果点P 的速度是2cm/s ，点Q 的速度是1cm/s ，它们同时出发，当有一点到达所在线段的端点时，就停止运动，当P ，Q 两点运动( )秒时，Rt CPQ △的面积等于5cm 2．A ．1B ．3C ．3或5D ．1或53．(本题2分)（2022秋·广东韶关·九年级统考期中）如图，在△ABC 中，∠ABC ＝90°，AB ＝8cm ，BC ＝6cm ．动点P ，Q 分别从点A ，B 同时开始移动，点P 的速度为1cm/秒，点Q 的速度为2cm/秒，点Q 移动到点C 后停止，点P 也随之停止运动．下列时间瞬间中，能使△PBQ 的面积为15cm 2的是（ ）A ．2秒钟B ．3秒钟C ．3秒钟或5秒钟D ．5秒钟4．(本题2分)（2022秋·全国·九年级专题练习）如图所示，A ，B ，C ，D 为矩形的四个顶点，AB =16cm ，AD =8cm ，动点P ，Q 分别从点A ，C 同时出发，点P 以3cm/s 的速度向B 移动，一直到达B 为止；点Q 以2cm/s 的速度向D 移动．当P ，Q 两点从出发开始几秒时，点P 和点Q 的距离是10cm ．(若一点到达终点，另一点也随之停止运动)（ ）A ．2s 或235sB ．1s 或225sC ．225sD ．2s 或225s 5．(本题2分)（2023春·八年级课时练习）如图，在ABC 中，90,8cm,6cm ABC AB BC ∠=︒==，动点P ，Q 分别从点A ，B 同时开始移动（移动方向如图所示），点P 的速度为1cm/s ，点Q 的速度为2cm/s ，点Q 移动到C 点后停止，点P 也随之停止运动，当PBQ 的面积为215cm 时，则点P 运动的时间是（ ）A ．3sB ．3s 或5sC ．4sD ．5s6．(本题2分)（2022秋·九年级课时练习）如图，在Rt ABC △中，AC 50m =，CB 40m =，90C ∠=︒，点P 从点A 开始沿AC 边向点C 以2m /s 的速度移动，同时另一个点Q 从点C 开始沿CB 以3m /s 的速度移动，当PCQ △的面积等于2450m 时，经过的时间是（ ）A ．10s 或15sB ．10sC ．15sD ．20s7．(本题2分)（2023春·浙江·八年级专题练习）在ABC 中，906cm 8cm ABC AB BC ∠︒＝，＝，＝，动点P 从点A 沿线段AB 向点B 移动，一动点Q 从点B 沿线段BC 向点C 移动，两点同时开始移动，点P 的速度为1cm/s ，点Q 的速度为2/s cm ，当Q 到达点C 时两点同时停止运动．若使PBQ 的面积为25cm ，则点P 运动的时间是（ ）A ．1sB ．4sC ．5s 或1sD ．4s 或1s8．(本题2分)（2023春·浙江·八年级专题练习）如图，在ABC 中，=90=8cm =6cm ABC AB BC ∠︒，，，动点P ，Q 分别从点A ，B 同时开始移动（移动方向如图所示），点P 的速度为1cm/s ，点Q 的速度为2cm/s ，点Q 移动到C 点后停止，点P 也随之停止运动，当PBQ 的面积为212cm 时，则点P 运动的时间是（ ）A ．2sB ．2s 或7sC ．7sD ．3s9．(本题2分)（2022秋·九年级课时练习）在平面直角坐标系中，一次函数4y x =--的图像上有一点P ，过点P 分别向坐标轴作垂线段，若两垂线段与坐标轴围成面积为5的矩形，则符合条件的点P 个数为 （ ）A ．2B ．3C ．4D ．无数个10．(本题2分)（2022秋·九年级课时练习）如图，AB ⊥BC ，AB ＝10 cm ，BC ＝8 cm ，一只蝉从C 点沿CB 方向以每秒1 cm 的速度爬行，蝉开始爬行的同时，一只螳螂由A 点沿AB 方向以每秒2 cm 的速度爬行，当螳螂和蝉爬行x 秒后，它们分别到达了M ，N 的位置，此时，△MNB 的面积恰好为24 cm2，由题意可列方程( )A ．2x ·x ＝24B ．(10－2x)(8－x)＝24C ．(10－x)(8－2x)＝24D ．(10－2x)(8－x)＝48评卷人得分二、填空题(每题2分，共20分) 11．(本题2分)（2022秋·福建宁德·九年级校考阶段练习）如图，在Rt ABC △中，90B ，6cm AB =，8cm BC =，点P 从A 点开始沿AB 边向点B 以1cm/s 的速度移动，点Q 从B 点开始沿BC 边向点C 以2cm /s 的速度移动，则P 、Q 分别从A 、B 同时出发，经过________秒钟，使PBQ 的面积等于28cm ．12．(本题2分)（2023春·八年级课时练习）如图，20AO OB == cm ，OC 是一条射线，OC AB ⊥，一只蚂蚁由A 点以1cm/s 速度向B 点爬行，同时另一只蚂蚁由O 点以2cm/s 的速度沿OC 方向爬行，则_______秒钟后，两只蚂蚁所处位置与O 点组成的三角形面积为1002cm ．13．(本题2分)（2022秋·甘肃武威·九年级校联考阶段练习）如图，在矩形ABCD 中，10cm,8cm AB AD ==，点P 从点A 出发沿AB 以2cm /s 的速度向点B 运动，同时点Q 从点B 出发沿BC 以1cm/s 的速度向点C 运动，点P 到达终点后，P 、Q 两点同时停止运动，则__秒时，BPQ ∆的面积是26cm ．14．(本题2分)（2022秋·九年级课时练习）如图，在Rt ABC 中，50m AC =，40m CB =，90C ∠=︒，点P 从点A 开始沿AC 边向点C 以2m /s 的速度移动，同时另一个点Q 从点C 开始沿CB 以3m /s 的速度移动，当△PCQ 的面积等于450m 2时，经过的时间是____．15．(本题2分)（2022秋·全国·九年级专题练习）如图，在等腰Rt ABC 中，90,42cm C AC ∠=︒=，动点P 从点A 出发沿折线AC CB -向点终B 2cm/s 的速度运动，PQ AB ⊥于点Q ．设运动时间为(s)t ，当t =_______s 时，APQ △的面积为24cm ．16．(本题2分)（2022秋·山东菏泽·九年级校考阶段练习）如图，在Rt ABC 中，90ACB ∠=︒，10cm AC =，15cm BC =，点P 从A 出发沿AC 向C 点以1厘米/秒的速度匀速挪动；点Q 从C 出发沿CB 向B 点以2厘米/秒的速度匀速挪动点P 、Q 分别从起点同时出发，挪动到某一位置时所需时间是为t 秒，当t =______时，PCQ △的面积等于216cm ．17．(本题2分)（2022秋·辽宁沈阳·九年级统考期中）如图，在Rt ABC ∆中，90C ∠=︒，30cm AC =，21cm BC =，动点P 从点C 出发，沿CA 方向运动，动点Q 从点B 出发，沿BC 方向运动，如果点P ，Q 同时出发，P ，Q 的运动速度均为1cm/s ．那么运动 _____秒时，它们相距15cm ．18．(本题2分)（2022春·山东淄博·八年级校考期中）如图，一艘船以40km/h 的速度沿既定航线由西向东航行，途中接到台风警报，某台风中心正以20km/h 的速度由南向北移动，距台风中心200km 的圆形区域（包括边界）都属台风影响区，当这艘轮船接到台风警报时，它与台风中心的距离BC ＝500km ，此时台风中心与轮船既定航线的最近距离BA ＝300km ，如果这艘轮船会受到台风影响，那么从接到警报开始，经过______小时它就会进入台风影响区．19．(本题2分)（2022春·浙江绍兴·八年级校联考阶段练习）如图，在△ABC 中，AB ＝6cm ，BC ＝7cm ，∠ABC ＝30°，点P 从A 点出发，沿射线AB 方向以1cm/s 的速度移动，点Q 从B 点出发，沿射线BC 方向以2cm/s 的速度移动．如果P 、Q 两点同时出发，问：经过_________________秒后△PBQ 的面积等于4cm 2．20．(本题2分)（2023春·八年级课时练习）如图，已知AG ∥CF ，AB ⊥CF ，垂足为 B ，AB =BC =3 ，点 P 是射线AG 上的动点 （点 P 不与点 A 重合），点 Q 是线段 CB 上的动点，点 D 是线段 AB 的中点，连接 PD 并延长交BF 于点 E ，连接PQ ，设AP =2t ，CQ =t ，当△PQE 是以 PE 为腰的等腰三角形时，t 的值为_____．评卷人得分三、解答题(共60分) 21．(本题6分)（2023春·浙江·八年级专题练习）如图，在Rt ABC △中，6AB =厘米，12BC =厘米，点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动，点Q 从点B 开始沿BC 边向点C 以2厘米/秒的速度移动，如果P ，Q 分别是从A ，B 同时出发，设时间为x 秒．(1)经过几秒时，PBQ 的面积等于8平方厘米？(2)经过几秒时，PBQ 的面积等于直角三角形面积的112？22．(本题6分)（2022秋·江西南昌·九年级校联考期中）如图，在矩形ABCD 中，12cm AB =，6cm BC ．点P 沿AB 边从点A 开始向点B 以2cm/s 的速度移动，点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动．如果P 、Q 同时出发，用t （s ）表示移动的时间（0≤t ≤6）．那么当t 为何值时，QAP 的面积等于82cm ？23．(本题8分)（2022秋·山东济南·九年级校考阶段练习）如图，在Rt ABC △中，24cm AC =，7cm BC =，点P 在BC 上，从点B 到点C 运动（不包括点C ），点P 运动的速度为2cm/s ；点Q 在AC 上从点C 运动到点A （不包括点A ），速度为5cm/s ．若点P ，Q 分别从B ，C 同时运动，请解答下面的问题，并写出探索的主要过程．(1)经过几秒，P ，Q 两点的距离为52cm ？(2)经过几秒，PCQ △的面积为215cm ？24．(本题8分)（2022秋·江苏连云港·九年级校考阶段练习）如图，已知等腰三角形ABC ，6cm AC BC ==，120ACB ∠=︒，点P 从点A 出发，沿A C B →→的方向以2cm /s 的速度向终点B 运动，同时点Q 从点B 出发，沿B A →3cm /s 的速度向终点A 运动，当点P 运动到点B 时，两点均停止运动，运动时间记为t 秒，请解决下列问题：(1)若点P 在边AC 上，当t 为何值时，90AQP ∠=︒？(2)是否存在这样的t 值，使APQ △的面积为243cm 若存在，请求出t 的值，若不存在，请说明理由．。

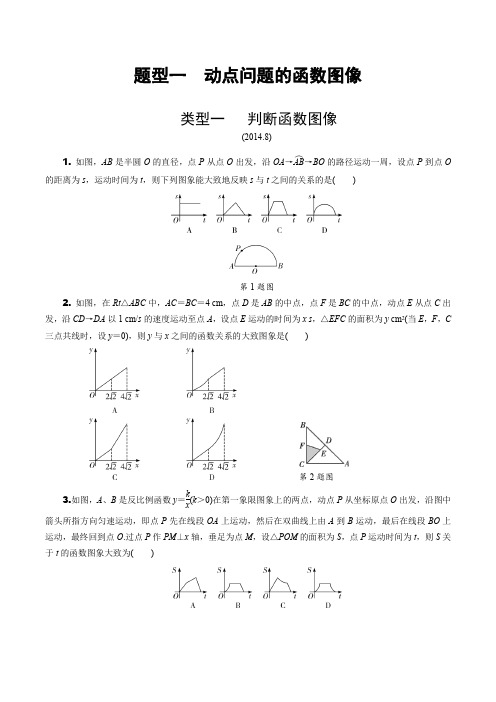
题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图，AB 是半圆O 的直径，点P 从点O 出发，沿OA →AB ︵→BO 的路径运动一周，设点P 到点O的距离为s ，运动时间为t ，则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图，在Rt △ABC 中，AC ＝BC ＝4 cm ，点D 是AB 的中点，点F 是BC 的中点，动点E 从点C 出发，沿CD →DA 以1 cm/s 的速度运动至点A ，设点E 运动的时间为x s ，△EFC 的面积为y cm 2(当E ，F ，C 三点共线时，设y ＝0)，则y 与x 之间的函数关系的大致图象是( )第2题图3.如图，A 、B 是反比例函数y ＝k x(k ＞0)在第一象限图象上的两点，动点P 从坐标原点O 出发，沿图中 箭头所指方向匀速运动，即点P 先在线段OA 上运动，然后在双曲线上由A 到B 运动，最后在线段BO 上运动，最终回到点O .过点P 作PM ⊥x 轴，垂足为点M ，设△POM 的面积为S ，点P 运动时间为t ，则S 关于t 的函数图象大致为( )第3题图4.如图，在菱形ABCD中，∠B＝60°，AB＝2，动点P从点B出发，以每秒1个单位长度的速度沿折线BA→AC运动到点C，同时动点Q从点A出发，以相同速度沿折线AC→CD运动到点D，当一个点停止运动时，另一个点也随之停止.设△APQ的面积为y，运动时间为x秒，则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图，在矩形ABCD中，对角线AC与BD交于点O，点M为线段AC上一个动点，过点M作EF∥BD 交AD(或DC)于点E，交AB(或BC)于点F，已知AC＝5，设AM＝x，EF＝y，则y关于x的函数图象大致为()第5题图6. (2019衢州)如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C 移动至终点C，设点P经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①，点P从矩形ABCD的顶点B出发，沿射线BC的方向以每秒1个单位长度的速度运动，过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象，其中点Q是第一段曲线(抛物线的一部分)的最高点，则AB的长度是()第1题图A. 2B. 3C. 4D. 232.(2019郑州模拟)如图①，四边形ABCD中，AB∥CD，∠B＝90°，AC＝A D.动点P从点B出发，沿折线B－A－D－C方向以 1 cm/s的速度匀速运动，在整个运动过程中，△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示，则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①，菱形ABCD中，∠B＝60°，动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B，同时动点Q以每秒2个单位的速度自点B出发沿折线B－C－D运动到点D.图②是点P、Q运动时，△BPQ的面积S随时间t变化关系图象，则a的值是()第3题图A. 2B. 2.5C. 3D. 234.如图①，在正方形ABCD中，动点E从点A出发，沿A－B－C运动，当点E到达点C时停止运动，过点E作EF⊥AE，交CD于点F，设点E运动的路程为x，FC＝y(当点A，E重合时，点D，F重合；当点C，E重合时，不妨设y＝0)，y与x的函数关系的大致图象如图②，当点E在BC上运动时，FC的最大长度是1，则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①，在矩形ABCD中，动点P从点A出发，沿A→B→C运动，设P A＝x，点D到直线P A的距离为y，且y关于x的函数图象如图②所示，则当△PCD和△P AB的面积相等时，y的值为.第5题图6.如图①，已知点E，F，G，H是矩形ABCD各边的中点，动点M从点E出发，沿E→F→G匀速运动，设点M运动的路程为x，点M到矩形顶点B的距离为y，如果表示y关于x函数关系的图象如图②所示，那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中，s 随着t 的增大而增大，点P 在AB ︵上运动时，s ＝OP ＝12AB (定值)，点P 在OB 上从点B 向点O 运动的过程中，s 随着t 的增大而减小． 2. A 【解析】∵在Rt △ABC 中，AC ＝BC ＝4，∴AB ＝42，AD ＝CD ＝22，CF ＝2，当点E 在CD 上时，CE ＝x ，点E 到BC 的距离h 1＝22x ，∴y ＝12×2×22x ＝22x (0≤x ≤22)；当点E 在AD 上时，BE ＝BD ＋DE ＝CD ＋DE ＝x ，∴点E 到FC 的距离h 2＝22BE ＝22x ，∴y ＝12×2×22x ＝22x (22≤x ≤42)． 3. D 【解析】设∠AOM ＝α，点P 运动的速度为a ，当点P 从点O 运动到点A 的过程中，S ＝12OM ·PM ＝12at ·cos α·at ·sin α＝12a 2·cos α·sin α·t 2，由于α及a 均为常量，从而可知图象本段应为抛物线，且S 随着t 的增大而增大；当点P 从A 运动到B 时，由反比例函数性质可知△OPM 的面积为12k ，保持不变，本段图象应为与x 轴平行的线段；同理可得，当点P 从B 运动到O 过程中，S 也是t 的二次函数，且S 随着t 的增大而减小．4. B 【解析】∵四边形ABCD 为菱形，且∠B ＝60°，AB ＝2，∴当0＜t ＜2时，△APQ 的面积y ＝12t ·(2－t )·sin60°＝－34t 2＋32t ，函数图象为开口向下的一段抛物线，且当t ＝1时，y 最大值为34；当2＜t ＜4时，△APQ 的面积y ＝12(t －2)·(t －2)·sin60°＝34(t －2)2，函数图象为开口向上的一段抛物线，且当t ＝4时，y 最大值为3，故选B .5. B 【解析】当0≤x ≤2.5时，如解图①，∵四边形ABCD 是矩形，∴OA ＝OB ＝OC ＝OD ，∴∠OAD ＝∠ODA ，∵EF ∥BD ，∴∠ODA ＝∠MEA ，∴∠OAD ＝∠MEA ，∴ME ＝MA ，同理可得AM ＝MF ，∴EM ＝AM ＝MF ，∴EF ＝2AM ，即y ＝2x ；当2.5<x ≤5时，如解图②，由题意知CM ＝AC －AM ＝5－x ，∵ME＝MC ＝MF ，∴EF ＝2MC ，即y ＝2(5－x )＝10－2x .综上所述，y ＝⎩⎪⎨⎪⎧2x （0≤x ≤2.5）10－2x （2.5<x ≤5）.图① 图②第5题解图6. C 【解析】∵AB ＝4，点E 是AB 的中点，∴AE ＝BE ＝2，当0≤x ≤2时，如解图①，y ＝S △CPE ＝12PE·BC＝2x，∴此段函数图象是正比例函数的一部分；当2<x≤6时，如解图②，y＝S△CPE＝S正方形ABCD－S△BCE －S△APE－S△PCD＝42－12×4×2－12×2×(x－2)－12×4×[4－(x－2)]＝x＋2，∴此段函数图象是一次函数的一部分；当6<x≤10时，如解图③，y＝S△CPE＝12PC·BC＝12(10－x)×4＝－2x＋20，∴此段函数图象是一次函数的一部分，综上所述，根据各段图象及x的取值范围，可得函数图象如选项C所示．图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得：当点P 运动到点C 的位置时，CG ＝0，∴BC ＝4.当点P运动到线段BC 的中点时，CG ＝43.∵∠B ＝90°，∴∠BAP ＋∠APB ＝90°，∵PG ⊥AP ，∴∠APG ＝90°，∴∠APB ＋∠CPG ＝90°，∴∠BAP ＝∠CPG ，又∵∠ABP ＝∠PCG ＝90°，∴△ABP ∽△PCG ，∴AB PC ＝BP CG，当点P 为BC 的中点时，BP ＝PC ＝2，∴AB 2＝243，解得AB ＝3. 2. B 【解析】结合图形分析函数图象可得，当t ＝3时，点P 到达A 处，即AB ＝3；如解图，过点A作AE ⊥CD 于点E ，则四边形ABCE 为矩形，∵AC ＝AD ，∴DE ＝CE ＝12CD .当S ＝15时，点P 到达点D 处，则S ＝12CD ·BC ＝12·2AB ·BC ＝3×BC ＝15，则BC ＝5，在Rt △ABC 中，由勾股定理得，AD ＝AC ＝AB 2＋BC 2＝34.第2题解图3. D 【解析】由题图②得，t ＝4时两点停止运动，∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒，∴AB ＝4，∵点Q 运动到点C 之前和之后，△BPQ 面积算法不同，即t ＝2时，S 的解析式发生变化，∴题图②中点M 对应的横坐标为2，此时P 为AB 中点，点C 与点Q 重合，如解图，连接AC ，∵菱形ABCD 中，AB ＝BC ＝4，∠B ＝60°，∴△ABC 是等边三角形，∴CP ⊥AB ，BP ＝12AB ＝2，∴CP ＝BC 2－BP 2＝42－22＝23，∴a ＝12BP ·CP ＝12×2×23＝2 3.第3题解图4. C 【解析】如解图，设AB ＝a ，当点E 在BC 上运动时(不与点B 、C 重合)，∵AE ⊥EF ，∴△EFC∽△AEB ，∴EC AB ＝FC EB ，即2a －x a ＝y x －a ，∴y ＝－1a x 2＋3x －2a ，－1a <0，当x ＝－32×（－1a ）＝32a 时，y 取得最大值，此时点E 为BC 的中点，y ＝1，把(32a ，1)代入y ＝－1ax 2＋3x －2a ，解得a ＝4，即AB ＝4，故正方形ABCD 的面积为4×4＝16.第4题解图5. 121313【解析】当P 点在AB 上运动时，D 点到AP 的距离不变，始终是AD 长，从图象可以看出AD ＝4，当P 点到达B 点时，从图象看出x ＝3，即AB ＝3.当△PCD 和△P AB 的面积相等时，P 点在BC 中点处，此时△ADP 面积为12×4×3＝6，在Rt △ABP 中，AP ＝AB 2＋BP 2＝13，则12AP ·y ＝6，解得y ＝121313. 6. 24 【解析】如解图，连接BD ，EG ，FH ，∵点E ，F ，G ，H 是矩形ABCD 各边的中点，∴EF ∥BD ∥GH ，EF ＝GH ＝12BD ，∴四边形EFGH 是平行四边形，又∵EF ＝EH ，∴平行四边形EFGH 是菱形，由题图②得BE ＝3，点M 运动到点G 时，运动路程为10，又∵EF ＝FG ，则可知菱形的边长为5，即EF ＝FG ＝GH ＝HE ＝5，∴AF ＝4，AD ＝8，∴S 菱形EFGH ＝12EG ·FH ＝24.第6题解图。

专题七几何图形动点运动问题【考题研究】几何动点运动问题，是以几何知识和具体的几何图形为背景，渗透运动变化的观点，通过点、线、形的运动，图形的平移、翻折、旋转等把图形的有关性质和图形之间的数量关系位置关系看作是在变化的、相互依存的状态之中，要求对运动变化过程伴随的数量关系的图形的位置关系等进行探究．对学生分析问题的能力，对图形的想象能力，动态思维能力的培养和提高有着积极的促进作用．动态问题，以运动中的几何图形为载体所构建成的综合题，它能把几何、三角、函数、方程等知识集于一身，题型新颖、灵活性强、有区分度，受到了人们的高度关注，同时也得到了命题者的青睐，动态几何问题，常常出现在各地的中考数学试卷中．【解题攻略】几何动点运动问题通常包括动点问题、动线问题、面动问题，在考查图形变换(含三角形的全等与相似)的同时常用到的不同几何图形的性质，以三角形四边形为主，主要运用方程、函数、数形结合、分类讨论等数学思想．【解题类型及其思路】动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

利用动点（图形）位置进行分类，把运动问题分割成几个静态问题，然后运用转化的思想和方法将几何问题转化为函数和方程问题,利用函数与方程的思想和方法将所解决图形的性质（或所求图形面积）直接转化为函数或方程。

解题类型：几何动点运动问题常见有两种常见类型：(1)利用函数与方程的思想和方法将所解决图形的性质直接转化为函数或方程；(2)根据运动图形的位置分类，把动态问题分割成几个静态问题，再将几何问题转化为函数和方程问题【典例指引】类型一【探究动点运动过程中线段之间的数量关系】【典例指引1】在△ABC中，∠ACB＝45°，点D为射线BC上一动点（与点B、C不重合），连接AD，以AD为一边在AD右侧作正方形ADEF．（1）如果AB＝AC，如图1，且点D在线段BC上运动，判断∠BAD∠CAF（填“＝”或“≠”），并证明：CF⊥BD（2）如果AB≠AC，且点D在线段BC的延长线上运动，请在图2中画出相应的示意图，此时（1）中的结论是否成立？请说明理由；（3）设正方形ADEF的边DE所在直线与直线CF相交于点P，若AC＝42，CD＝2，求线段CP的长．【举一反三】如图1，点C在线段AB上，（点C不与A、B重合），分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE，连接AE、BD交于点P（1）观察猜想：①线段AE与BD的数量关系为_________；②∠APC的度数为_______________（2）数学思考：如图2，当点C在线段AB外时，（1）中的结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明（3）拓展应用：如图3，分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE，其中∠ACD=∠BCE=90°，CA=CD，CB=CE，连接AE=BD交于点P，则线段AE与BD的关系为________________类型二【确定动点运动过程中的运动时间】【典例指引2】已知：如图，在平面直角坐标系中，长方形OABC的项点B的坐标是(6,4).（1）直接写出A点坐标（______，______），C点坐标（______，______）；P m，且四边形OADP的面积是（2）如图，D为OC中点.连接BD，AD，如果在第二象限内有一点(),1∆面积的2倍，求满足条件的点P的坐标；ABC（3）如图，动点M从点C出发，以每钞1个单位的速度沿线段CB运动，同时动点N从点A出发.以每秒2t>，在M，个单位的連度沿线段AO运动，当N到达O点时，M，N同时停止运动，运动时间是t秒()0N运动过程中.当5MN=时，直接写出时间t的值.【举一反三】如图，▱ABCD 的对角线AC 、BD 相交于点O ，AB ⊥AC ，AB ＝3，BC ＝5，点P 从点A 出发，沿AD 以每秒1个单位的速度向终点D 运动．连结PO 并延长交BC 于点Q ．设点P 的运动时间为t 秒． （1）求BQ 的长，（用含t 的代数式表示）（2）当四边形ABQP 是平行四边形时，求t 的值（3）当点O 在线段AP 的垂直平分线上时，直接写出t 的值．类型三 【探究动点运动过程中图形的形状或图形之间的关系】【典例指引3】已知矩形ABCD 中，10cm AB =，20cm BC =，现有两只蚂蚁P 和Q 同时分别从A 、B 出发，沿AB BC CD DA =--方向前进，蚂蚁P 每秒走1cm ，蚂蚁Q 每秒走2cm ．问：（1）蚂蚁出发后△PBQ 第一次是等腰三角形需要爬行几秒?（2）P 、Q 两只蚂蚁最快爬行几秒后，直线PQ 与边AB 平行?如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（AO<AB）且AO、AB的长分别是一元二次方程x2-3x+2=0的两个根，点C在x轴负半轴上，且AB：AC=1:2.（1）求A、C两点的坐标；（2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．类型四【探究动点运动过程中图形的最值问题】【典例指引4】如图，抛物线y＝ax2﹣34x+c与x轴相交于点A（﹣2，0）、B（4，0），与y轴相交于点C，连接AC，BC，以线段BC为直径作⊙M，过点C作直线CE∥AB，与抛物线和⊙M分别交于点D，E，点P 在BC下方的抛物线上运动．（1）求该抛物线的解析式；（2）当△PDE是以DE为底边的等腰三角形时，求点P的坐标；（3）当四边形ACPB的面积最大时，求点P的坐标并求出最大值．已知：如图.在△ABC中.AB=AC=5cm，BC=6cm.点P由B出发，沿BC方向匀速运动.速度为1cm/s.同时，点Q从点A出发，沿AC方向匀速运动.速度为1cm/s，过点P作PM⊥BC交AB于点M，过点Q作QN⊥BC，垂足为点N，连接MQ，若设运动时间为t(s)(0<t<3)，解答下列问题：（1）当t为何值时，点M是边AB中点?（2）设四边形PNQM的面积为y(cm2)，求出y与t之间的函数关系式；（3）是否存在某一时刻t，使S四边形PNQM:S△ABC=4:9?若存在，求出此时t的值；若不存在，说明理由；（4）是否存在某一时刻t，使四边形PNQM为正方形?若存在，求出此时t的值；若不存在，请说明理由.【新题训练】1．如图①，△ABC是等边三角形，点P是BC上一动点（点P与点B、C不重合），过点P作PM∥AC交AB于M，PN∥AB交AC于N，连接BN、CM．（1）求证：PM+PN＝BC；（2）在点P的位置变化过程中，BN＝CM是否成立？试证明你的结论；（3）如图②，作ND∥BC交AB于D，则图②成轴对称图形，类似地，请你在图③中添加一条或几条线段，使图③成轴对称图形（画出一种情形即可）．2．如图，在矩形ABCD中，AB=18，AD=12，点M是边AB的中点，连结DM，DM与AC交于点G，点E，F分别是CD与DG上的点，连结EF，(1)求证：CG=2AG.(2)若DE=6，当以E，F，D为顶点的三角形与△CDG相似时，求EF的长.(3)若点E从点D出发，以每秒2个单位的速度向点C运动，点F从点G出发，以每秒1个单位的速度向点D运动.当一个点到达，另一个随即停止运动.在整个运动过程中，求四边形CEFG的面积的最小值.3．知识链接：将两个含30°角的全等三角尺放在一起，让两个30°角合在一起成60°，经过拼凑、观察、思考，探究出结论“直角三角形中，30°角所对的直角边等于斜边的一半”．如图，等边三角形ABC的边长为4cm，点D从点C出发沿CA向A运动，点E从B出发沿AB的延长线BF 向右运动，已知点D、E都以每秒0.5cm的速度同时开始运动，运动过程中DE与BC相交于点P，设运动时间为x秒．(1)请直接写出AD长．（用x的代数式表示）(2)当△ADE为直角三角形时，运动时间为几秒？(3)求证：在运动过程中，点P始终为线段DE的中点．4．如图所示，已知抛物线2(0)y ax a =≠与一次函数y kx b =+的图象相交于(1,1)A --，(2,4)-B 两点，点P 是抛物线上不与A ，B 重合的一个动点.（1）请求出a ，k ，b 的值；（2）当点P 在直线AB 上方时，过点P 作y 轴的平行线交直线AB 于点C ，设点P 的横坐标为m ，PC 的长度为L ，求出L 关于m 的解析式；（3）在（2）的基础上，设PAB ∆面积为S ，求出S 关于m 的解析式，并求出当m 取何值时，S 取最大值，最大值是多少？5．已知：如图，在矩形ABCD 中，AC 是对角线，AB ＝6cm ，BC ＝8cm ．点P 从点D 出发，沿DC 方向匀速运动，速度为1cm /s ，同时，点Q 从点C 出发，沿CB 方向匀速运动，速度为2cm /s ，过点Q 作QM ∥AB 交AC 于点M ，连接PM ，设运动时间为t （s ）（0＜t ＜4）．解答下列问题：（1）当t 为何值时，∠CPM ＝90°；（2）是否存在某一时刻t ，使S 四边形MQCP ＝ABCD 1532S 矩形？若存在，求出t 的值；若不存在，请说明理由； （3）当t 为何值时，点P 在∠CAD 的角平分线上．6．在等边三角形ABC中，点D是BC的中点，点E、F分别是边AB、AC（含线段AB、AC的端点）上的动点，且∠EDF＝120°，小明和小慧对这个图形展开如下研究：问题初探：（1）如图1，小明发现：当∠DEB＝90°时，BE+CF＝nAB，则n的值为；问题再探：（2）如图2，在点E、F的运动过程中，小慧发现两个有趣的结论：①DE始终等于DF；②BE与CF的和始终不变；请你选择其中一个结论加以证明．成果运用:（3）若边长AB＝8，在点E、F的运动过程中，记四边形DEAF的周长为L，L＝DE+EA+AF+FD，则周长L取最大值和最小值时E点的位置?7．如图，在矩形ABCD中，AB＝8cm，BC＝16cm，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．(1)当t为何值时，四边形ABQP是矩形；(2)当t为何值时，四边形AQCP是菱形；(3)分别求出(2)中菱形AQCP的周长和面积．8．如图，O为菱形ABCD对角线的交点，M是射线CA上的一个动点（点M与点C、O、A都不重合），过点A、C分别向直线BM作垂线段，垂足分别为E、F，连接OE，OF．（1）①依据题意补全图形；②猜想OE与OF的数量关系为_________________.（2）小东通过观察、实验发现点M在射线CA上运动时，（1）中的猜想始终成立．小东把这个发现与同学们进行交流，通过讨论，形成了证明（1）中猜想的几种想法：想法1：由已知条件和菱形对角线互相平分，可以构造与△OAE全等的三角形，从而得到相等的线段，再依据直角三角形斜边中线的性质，即可证明猜想；想法2：由已知条件和菱形对角线互相垂直，能找到两组共斜边的直角三角形，例如其中的一组△OAB和△EAB，再依据直角三角形斜边中线的性质，菱形四边相等，可以构造一对以OE和OF为对应边的全等三角形，即可证明猜想．……请你参考上面的想法，帮助小东证明（1）中的猜想（一种方法即可）．（3）当∠ADC=120°时，请直接写出线段CF，AE，EF之间的数量关系是_________________．9．（1）（问题情境）小明遇到这样一个问题：如图①，已知ABC ∆是等边三角形，点D 为BC 边上中点，60ADE ∠=︒，DE 交等边三角形外角平分线CE 所在的直线于点E ，试探究AD 与DE 的数量关系．小明发现：过D 作//DF AC ，交AB 于F ，构造全等三角形，经推理论证问题得到解决．请直接写出AD 与DE 的数量关系，并说明理由． （2）（类比探究）如图②，当D 是线段BC 上（除,B C 外）任意一点时（其他条件不变）试猜想AD 与DE 的数量关系并证明你的结论． （3）（拓展应用）当D 是线段BC 上延长线上，且满足CD BC =（其他条件不变）时，请判断ADE ∆的形状，并说明理由．10．如图，直线y =﹣23x +4与x 轴交于点C ，与y 轴交于点B ，抛物线y =ax 2+103x +c 经过B 、C 两点． （1）求抛物线的解析式；（2）如图，点E 是直线BC 上方抛物线上的一动点，当△BEC 面积最大时，请求出点E 的坐标； （3）在（2）的结论下，过点E 作y 轴的平行线交直线BC 于点M ，连接AM ，点Q 是抛物线对称轴上的动点，在抛物线上是否存在点P ，使得以P 、Q 、A 、M 为顶点的四边形是平行四边形？如果存在，请直接写出点P 的坐标；如果不存在，请说明理由．11．如图，边长为4的正方形ABCD 中，点P 是边CD 上一动点，作直线BP ，过A 、C 、D 三点分别作直线BP 的垂线段，垂足分别是E 、F 、G ．（1）如图（a ）所示，当CP ＝3时，求线段EG 的长；（2）如图（b ）所示，当∠PBC ＝30°时，四边形ABCF 的面积；（3）如图（c ）所示，点P 在CD 上运动的过程中，四边形AECG 的面积S 是否存在最大值？如果存在，请求出∠PBC 为多少度时，S 有最大值，最大值是多少？如果不存在，请说明理由．12．已知：如图，在四边形ABCD 中，//AB CD ，90ACB ∠=︒，10cm AB =，8cm BC =，OD 垂直平分A C .点P 从点B 出发，沿BA 方向匀速运动，速度为1cm/s ；同时，点Q 从点D 出发，沿DC 方向匀速运动，速度为1cm/s ；当一个点停止运动，另一个点也停止运动.过点P 作PE AB ⊥，交BC 于点E ，过点O 作//QF AC ，分别交AD ，OD 于点F ，G .连接OP ，EG .设运动时间为()t s ()05t <<，解答下列问题：(1)当t 为何值时，点E 在BAC ∠的平分线上？ (2)设四边形PEGO 的面积为()2mS c ，求S 与t 的函数关系式.(3)连接OE ，OQ ，在运动过程中，是否存在某一时刻t ，使OE OQ ⊥？若存在，求出t 的值；若不存在，请说明理由.13．已知：如图1，矩形OABC 的两个顶点A ，C 分别在x 轴，y 轴上，点B 的坐标是（8，2），点P 是边BC 上的一个动点，连接AP ，以AP 为一边朝点B 方向作正方形P ADE ，连接OP 并延长与DE 交于点M ，设CP ＝a （a ＞0）．（1）请用含a 的代数式表示点P ，E 的坐标．（2）连接OE ，并把OE 绕点E 逆时针方向旋转90°得EF ．如图2，若点F 恰好落在x 轴的正半轴上，求a 与EMDM的值． （3）①如图1，当点M 为DE 的中点时，求a 的值．②在①的前提下，并且当a ＞4时，OP 的延长线上存在点Q ，使得EQ +22PQ 有最小值，请直接写出EQ +22PQ 的最小值．14．如图，边长为6的正方形ABCD 中，,E F 分别是,AD AB 上的点，AP BE ⊥，P 为垂足． （1）如图①， AF =BF ，AE =23，点T 是射线PF 上的一个动点，则当△ABT 为直角三角形时，求AT 的长；（2）如图②，若AE AF =，连接CP ，求证：CP FP ⊥．15．边长相等的两个正方形ABCO 、ADEF 如图摆放，正方形ABCO 的边OA 、OC 在坐标轴上，ED 交线段OC 于点G ，ED 的延长线交线段BC 于点P ，连AG ，已知OA 长为3. （1）求证：AOG ADG ∆≅∆;（2）若12∠=∠，AG =2，求点G 的坐标；（3）在（2）条件下，在直线PE 上找点M ，使以M 、A 、G 为顶点的三角形是等腰三角形，求出点M 的坐标.16．定义：有一组邻角相等的凸四边形叫做“梦想四边形”。

2019-2020年中考数学备考专题复习七动态几何变化问题检测动态几何题已成为中考试题的一大热点题型。

在近几年各地的中考试卷中，以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中，考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力。

解决动态几何题的策略是：把握运动规律，寻求运动中的特殊位置；在“动”中求“静”，在“静”中探求“动”的一般规律。

通过探索、归纳、猜想，获得图形在运动过程中是否保留或具有某种性质。

下面就动点型、动线型、动面型等几何题作一简要分析。

一. 动点型1.单动点型例1. 如图1，在矩形ABCD中，AD=12，AB=5，P是AD边上任意一点， PE⊥BD，PF⊥AC，E，F 分别是垂足，求 PE+PF的长。

分析与略解： P 是 AD 边上任意一点，不妨考虑特殊点的情况，即在“动”中求“静”。

当 P 点在 D（或 A ）处时，过 D 作 DG⊥AC，垂足为 G，则PE=0，PF=DG，故PE+PF=DG，在 Rt△ADC 中，AC AD 2DC 21225213由面积公式有：DG AD DC 60，AC 13再有“静”寻求“动”的一般规律，得到 PE+PF=DG= 60。

13图 12.双动点型例2. （2003年吉林省）如图2，在矩形ABCD中，AB=10cm，BC=8cm，点 P 从 A 出发，沿 A→B→C→D 路线运动，到 D 点停止；点Q 从 D 点出发，沿 D→C→B→ A 路线运动，到 A 停止。

若点 P、 Q 同时出发，点 P 的速度为每秒 1cm，点 Q 的速度为每秒 2cm，a 秒时点 P、点 Q 同时改变速度，点 P 的速度变为每秒 bcm，点 Q 的速度为每秒 dcm。

图 3 是点 P 出发 x 秒后△ APD 的面积S1(cm2)与 x（秒）的函数关系图象，图4 是点Q 出发x 秒后△AQD 的面积S2(cm2)与x （秒）的函数关系图象。

课后练习40 实验与动态型问题A 组1．(2015·大庆)已知点A (－2，0)，B 为直线x ＝－1上一个动点，P 为直线AB 与双曲线y ＝1x的交点，且AP ＝2AB ，则满足条件的点P 的个数是( )第1题图A ．0个B ．1个C ．2个D ．3个2．(2015·南京市玄武区模拟)如图，水平线l 1∥l 2，铅垂线l 3∥l 4，l 1⊥l 3，若选择l 1、l 2其中一条当成x 轴，且向右为正方向，再选择l 3、l 4其中一条当成y 轴，且向上为正方向，并在此平面直角坐标系中画出二次函数y ＝ax 2－ax －a 的图象，则下列关于x 、y 轴的叙述，正确的是( )第2题图A ．l 1为x 轴，l 3为y 轴B ．l 1为x 轴，l 4为y 轴C ．l 2为x 轴，l 3为y 轴D ．l 2为x 轴，l 4为y 轴3．已知：在△ABC 中，BC ＝10，BC 边上的高h ＝5，点E 在边AB 上，过点E 作EF ∥BC ，交AC 边于点F .点D 为BC 上一点，连结DE 、DF .设点E 到BC 的距离为x ，则△DEF 的面积S 关于x 的函数图象大致为( )第3题图4．(2016·泰兴模拟)如图，A(0，1)，M(3，2)，N(4，4)．动点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线l：y＝－x＋b也随之移动，设移动时间为t秒．若点M，N位于直线l的异侧，则t的取值范围是.B组5．如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连结AD1、BC1.若∠ACB＝30°，AB＝1，CC1＝x，△ACD与△A1C1D1重叠部分的面积为S，则下列结论：第5题图①△A1AD1≌△CC1B；②当x＝1时，四边形ABC1D1是菱形；③当x＝2时，△BDD1为等边三角形；④S＝(x－2)2(0＜x＜2)；其中正确的是(填序号)．6．(2017·衢州)在直角坐标系中，过原点O及点A(8，0)，C(0，6)作矩形OABC，连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF.已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．第6题图(1)如图1，当t＝3时，求DF的长；(2)如图2，点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值；(3)连结AD，当AD将△DEF分成的两部分的面积之比为1∶2时，求相应的t的值．C组7．(2015·河北)如图，点A，B为定点，定直线l∥AB，P是l上一动点．点M，N分别为PA，PB的中点，对于下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是( )第7题图A ．②③B ．②⑤C ．①③④D ．④⑤参考答案课后练习40 实验与动态型问题A 组1．B 2.A 3.D 4.4<t <7B 组5．①②③④6．(1)当t ＝3时，点E 为AB 的中点，∵A (8，0)，C (0，6)，∴OA ＝8，OC ＝6，∵点D 为OB 的中点，∴DE ∥OA ，DE ＝12OA ＝4，∵四边形OABC 是矩形，∴OA ⊥AB ，∴DE ⊥AB ，∴∠OAB ＝∠DEA ＝90°，又∵DF ⊥DE ，∴∠EDF ＝90°，∴四边形DFAE 是矩形，∴DF ＝AE ＝3；(2)∠DEF 的大小不变；理由如下：作DM ⊥OA 于M ，DN ⊥AB 于N ，如图2所示：∵四边形OABC 是矩形，∴OA ⊥AB ，∴四边形DMAN 是矩形，∴∠MDN ＝90°，DM ∥AB ，DN ∥OA ，∴BD DO ＝BN NA ，DO BD＝OM MA ，∵点D 为OB 的中点，∴M 、N 分别是OA 、AB 的中点，∴DM ＝12AB ＝3，DN ＝12OA ＝4，∵∠EDF ＝90°，∴∠FDM ＝∠EDN ，又∵∠DMF ＝∠DNE ＝90°，∴△DMF ∽△DNE ，∴DF DE ＝DM DN ＝34，∵∠EDF ＝90°，∴tan ∠DEF ＝DF DE ＝34； (3)作DM ⊥OA 于M ，DN ⊥AB 于N ，若AD 将△DEF 的面积分成1∶2的两部分，设AD 交EF 于点G ，则点G 为EF 的三等分点；①当点E 到达中点之前时，如图3所示，NE ＝3－t ，由△DMF ∽△DNE 得：MF ＝34(3－t )，∴AF ＝4＋MF ＝－34t ＋254，∵点G 为EF 的三等分点，∴G ⎝ ⎛⎭⎪⎫3t ＋7112，23t ，设直线AD 的解析式为y ＝kx ＋b ，把A (8，0)，D (4，3)代入得：⎩⎪⎨⎪⎧8k ＋b ＝0，4k ＋b ＝3，解得：⎩⎪⎨⎪⎧k ＝－34，b ＝6，∴直线AD 的解析式为y ＝－34x ＋6，把G ⎝⎛⎭⎪⎫3t ＋7112，23t 代入得：t ＝7541； ②当点E 越过中点之后，如图4所示，NE ＝t －3，由△DMF ∽△DNE 得：MF ＝34(t －3)，∴AF ＝4－MF ＝－34t ＋254，∵点G 为EF 的三等分点，∴G ⎝⎛⎭⎪⎫3t ＋236，13t ，代入直线AD 的解析式y ＝－34x ＋6得：t ＝7517；综上所述，当AD 将△DEF 分成的两部分的面积之比为1∶2时，t 的值为7541或7517.第6题图 C 组7．B。