正比例函数、一次函数、反比例函数的性质及图象
- 格式:doc
- 大小:54.00 KB
- 文档页数:2


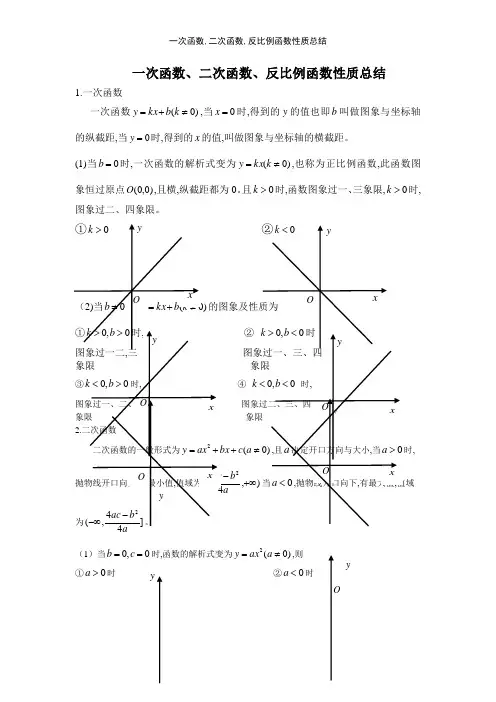
一次函数、二次函数、反比例函数性质总结1.一次函数一次函数)0(≠+=k b kx y ,当0=x 时,得到的y 的值也即b 叫做图象与坐标轴的纵截距,当0=y 时,得到的x 的值,叫做图象与坐标轴的横截距。
(1)当0=b 时,一次函数的解析式变为)0(≠=k kx y ,也称为正比例函数,此函数图象恒过原点)0,0(O ,且横,纵截距都为0。
且0>k 时,函数图象过一、三象限,0>k 时,图象过二、四象限。
② k (≠a )+∞(1)当0,0==c b 时,函数的解析式变为)0(2≠=a ax y ,则 ①0>a 时 ②0<a 时(2)b a ,决定二次函数的对称轴与开口方向②0,0,0=<>c b a 时③ 0,0,0=><c b a 时 ④ 0,0,0=<<c b a 时(3)c a ,决定开口方向与与y 轴的截距①0,0,0=>>b c a 时 ②a③0,0,0=>b c a 时 ④0,0,0=<<b c a 时y yOxx yOOyyOxxxxy y OOx xOOy(3)对于一般的二次函数,c b a ,,共同来决定其函数图像与性质,故通常采用配方的方法 )0(2≠++=a c bx ax y c aba b x a b x a c x a b x a +-++=++=))2()2(()(2222 c a b a b x a +-+=]4)2[(222=c a b a b x a +-+4)2(22 =ab ac a b x a 44)2(22-++ 我们称abx 2-=为二次函数的对称轴,坐标)44,2(2a b ac a b --为二次函数的顶点坐标,此时我们也称其解析式为二次函数的顶点式,并可设其解析式为)0()(2≠+-=a k h x a y 。
若知道二次函数与x 轴的两个交点坐标,可设其解析式为)0)()((21≠--=a x x x x a y 。


1、正比例函数
定义:
形如y=kx(k为常数,且k≠0),我们就说y是x的正比例函数。
正比例函数是特殊的一次函数【一次函数的一般形式为y=kx+b(b不为0,k为常数)】。
图象作法:
a.列表(待定系数)
b.描点
c.连线
正比例函数的图象是一条直线,一定经过坐标的原点;
当k>0时,图象经过一、三象限,y随x的增大而增大;
当k<0时,图象经过二、四象限,y随x的增大而减小。
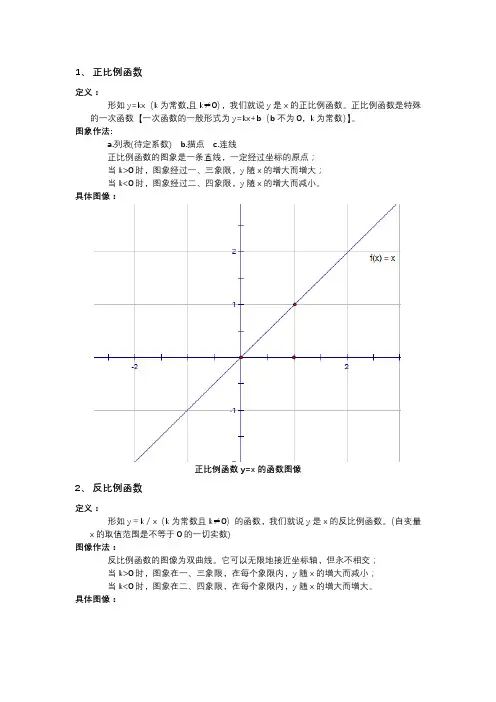
具体图像:
正比例函数y=x的函数图像
2、反比例函数
定义:
形如y=k/x(k为常数且k≠0)的函数,我们就说y是x的反比例函数。
(自变量x的取值范围是不等于0的一切实数)
图像作法:
反比例函数的图像为双曲线。
它可以无限地接近坐标轴,但永不相交;
当k>0时,图象在一、三象限,在每个象限内,y随x的增大而减小;
当k<0时,图象在二、四象限,在每个象限内,y随x的增大而增大。
具体图像:
反比例函数y=1/x的函数图像。
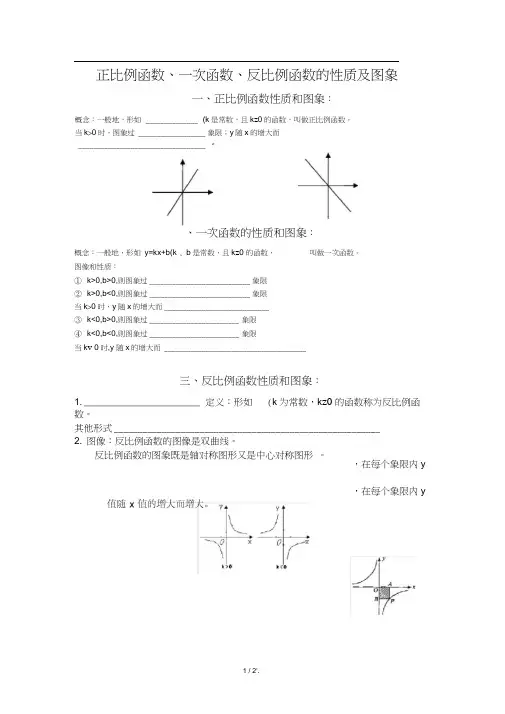
正比例函数、一次函数、反比例函数的性质及图象、一次函数的性质和图象:概念:一般地,形如y=kx+b(k , b是常数,且k z0 的函数,叫做一次函数。
图像和性质:①k>0,b>0,则图象过___________________________ 象限②k>0,b<0,则图象过___________________________ 象限当k>0时,y随x的增大而____________________________③k<0,b>0,则图象过________________________ 象限④k<0,b<0,则图象过________________________ 象限当k v 0时,y 随x的增大而 ______________________________________三、反比例函数性质和图象:1. ______________________ 定义:形如 (k为常数,k z0的函数称为反比例函数。
其他形式________________________________________________________2. 图像:反比例函数的图像是双曲线。
反比例函数的图象既是轴对称图形又是中心对称图形。
,在每个象限内y,在每个象限内y一、正比例函数性质和图象:概念:一般地,形如______________ (k是常数,且k z0的函数,叫做正比例函数。
当k>0时,图象过 __________________ 象限;y随x的增大而__________________________________ 。
3. _________________________________________________ 性质:当k >0时双曲线的两支分别位于_______________________________________值随x值的增大而减小。


初中高中数学七大函数的性质图像1.一次函数(包括正比例函数)最简单最常见的函数,在平面直角坐标系上的图象为直线。
定义域(下面没有说明的话,都是在无特殊要求情况下的定义域):R值域:R奇偶性:无周期性:无平面直角坐标系解析式(下简称解析式):①ax+by+c=0[一般式]②y=kx+b[斜截式](k为直线斜率,b为直线纵截距,正比例函数b=0)③y-y1=k(x-x1)[点斜式](k为直线斜率,(x1,y1)为该直线所过的一个点)④(y-y1)/(y2-y1)=(x-x1)/(x2-x1)[两点式]((x1,y1)与(x2,y2)为直线上的两点)⑤x/a-y/b=0[截距式](a、b分别为直线在x、y轴上的截距)解析式表达局限性:①所需条件较多(3个);②、③不能表达没有斜率的直线(平行于x轴的直线);④参数较多,计算过于烦琐;⑤不能表达平行于坐标轴的直线和过圆点的直线。
倾斜角:x轴到直线的角(直线与x轴正方向所成的角)称为直线的倾斜角。
设一直线的倾斜角为a,则该直线的斜率k=tg(a)。
2.二次函数:题目中常见的函数,在平面直角坐标系上的图象是一条对称轴与y轴平行的抛物线。
定义域:R值域:(对应解析式,且只讨论a大于0的情况,a小于0的情况请读者自行推断)①[(4ac-b^2)/4a,正无穷);②[t,正无穷)奇偶性:偶函数周期性:无解析式:①y=ax^2+bx+c[一般式]⑴a≠0⑵a>0,则抛物线开口朝上;a<0,则抛物线开口朝下;⑶极值点:(-b/2a,(4ac-b^2)/4a);⑷Δ=b^2-4ac,Δ>0,图象与x轴交于两点:([-b+√Δ]/2a,0)和([-b+√Δ]/2a,0);Δ=0,图象与x轴交于一点:(-b/2a,0);Δ<0,图象与x轴无交点;②y=a(x-h)^2+t[配方式]此时,对应极值点为(h,t),其中h=-b/2a,t=(4ac-b^2)/4a);3.反比例函数在平面直角坐标系上的图象为双曲线。

正比例与反比例函数的性质正比例函数和反比例函数是数学中常见的两种函数类型。
它们在数学和实际生活中都有着重要的应用。
本文将详细介绍正比例函数和反比例函数的性质,并探讨它们在不同领域的用途。
1. 正比例函数的性质正比例函数是指两个变量之间存在线性关系,其中一个变量的值是另一个变量的常数倍。
形式上,正比例函数可以表示为 y = kx,其中 k 是常数。
1.1 直线关系正比例函数的图像是一条直线,且经过原点。
这意味着函数中的变量之间的关系是直接的,一方增大,另一方也相应增大。
1.2 斜率正比例函数的斜率是常数 k。
斜率表示了函数的增长速率,正比例函数的斜率恒定。
1.3 比例常数比例常数 k 是正比例函数的一个重要特征。
它体现了两个变量之间的比例关系。
当 k > 1 时,随着 x 的增加,y 的增加幅度更大;当 0 < k < 1 时,随着 x 的增加,y 的增加幅度更小。
2. 反比例函数的性质反比例函数是指两个变量之间存在反比关系,其中一个变量的值是另一个变量的倒数。
形式上,反比例函数可以表示为 y = k / x,其中 k是常数。
2.1 反比例关系反比例函数的图像通常是一个超越原点的曲线。
这意味着函数中的变量之间的关系是间接的,一方增大,另一方相应减小。
2.2 渐近线反比例函数的图像具有渐近线,其中一条渐近线为横轴 (x 轴),另一条渐近线为纵轴 (y 轴)。
这意味着当 x 趋近于正无穷大或负无穷大时,函数的值趋近于 0。
2.3 比例常数比例常数 k 是反比例函数的一个重要特征。
它体现了两个变量之间的反比关系。
当 k > 0 时,随着 x 的增加,y 的值减小;当 k < 0 时,随着 x 的增加,y 的值增大。
3. 应用领域正比例函数和反比例函数在各个领域都有广泛的应用。
3.1 正比例函数的应用正比例函数常常用于计算比例、比率和百分比。
在经济学中,正比例函数可以用于描述成本、收入和利润之间的关系。

正比例函数和反比例函数的区别(附图)
一:正比例函数
y=kx(k为常数,且k≠0),我们就说y是x的正比例函数,
正比例函数是特殊的一次函数,一次函数的一般形式为y=kx+b(b不为0,k为常数)。
正比例函数的图象是一条直线,一定经过坐标的原点,
当k>0时,图象经过一、三象限,y随x的增大而增大,
当k<0时,图象经过二、四象限,y随x的增大而减小。
二、反比例函数
y=k/x(k为常数且k≠0) 的函数,我们就说y是x的反比例函数 (自变量x的取值范围是不等于0的一切实数) 。
反比例函数的图像为双曲线,它可以无限地接近坐标轴,但永不相交,
当k>0时,图象在一、三象限,在每个象限内,y随x的增大而减小,
当k<0时,图象在二、四象限,在每个象限内,y随x的增大而增大。
高中数学 14种函数图像和性质知识解析新人教A版必修1高中不得不掌握的函数图像与常用性质高中常用函数有14种,它们是:1.正比例函数;2.反比例函数;3.根式函数;4一次函数;5.二次函数;6双勾函数.;7..双抛函数;8.指数函数;9对数函数;10.三角函数;11分段函数.;12.绝对值函数;13.超越函数;14.抽象函数。
而函数的性质常见的有:1.定义域;2.值域;3.单调性;4.奇偶性;5.周期性;6.对称性;7.有界性;8.反函数;9.连续性.高中都是从函数解析式入手画出函数图像,再利用函数图像研究其性质,下面我们就函数的图像和性质做归纳总结。
1.正比例函数解析式图像定义域:值域:单调性:奇偶性:反函数:2.反比例函数解析式图像性质定义域:值域:单调性:奇偶性:反函数:对称性:定义域:值域:单调性:对称性:3根式函数解析式图像定义域:值域:单调性:奇偶性:反函数:4一次函数解析式图像定义域:值域:1 性质性质性质用心爱心专心单调性:反函数:5二次函数解析式图像定义域:值域:单调性:对称性:定义域:值域:单调性:对称性:6.双勾函数解析式图像定义域:值域:单调性:奇偶性:对称性:定义域:值域:单调性:奇偶性:对称性:7.双抛函数解析式图像定义域:值域:单调性:奇偶性:对称性:定义域:性质性质性质用心爱心专心值域:单调性:奇偶性:对称性:8.指数函数解析式图像定义域:值域:单调性:9.对数函数解析式图像定义域:值域:单调性:10.三角函数解析式图像单调性:周期性:奇偶性:有界性:对称性:定义域:值域:单调性:周期性:奇偶性:有界性:对称性:定义域:值域:单调性:周期性:奇偶性:有界性:对称性:定义域:值域:单调性:周期性:奇偶性:有界性:对称性:11.分段函数分段函数是在其定义域的不同子集上,分别用几个不同的式子来表示对应关系的函数,它是一类较特殊的函数。
其图像的画法是按定义域的划分分别作图。
正比例函数、一次函数和反比例函数知识点归纳正比例函数:解析式:y=kx(k为常数,k工0) ,k叫做函数的比例系数;(注意:x的指数为1)图像:过原点的直线;必过点:(0,0 )和(1,k);走向:k>o,图像过一三象限,k<0,图像过二四象限;y yK>0k<0/ \0OJx IV x倾斜度:|k|越大,倾斜度越大,也就是越靠近y轴,|k|越小,倾斜度越小,也就是越靠近x轴;如图:yy=2x//y=xO yx增减性:k>O,y随x的增大而增大;k<0,y随x的增大而减小;一次函数:解析式:y=kx+b(k,b为常数,k^ 0),k叫做函数的比例系数,(注意:x的指数为1,b为直线与y轴交点的纵坐标);正比例函数是一次函数的特殊情况,即b=0时的一种情况;图像:一条直线;必过点:(0,b)(-b/k,0);走向:k>o, b>0,图像过一二三象限,k>0,b<0,图像过一三四象限;y yk>0,b<0O O /x x倾斜度:|k|越大,倾斜度越大,也就是越靠近y轴,|k|越小,倾斜度越小,也就是越靠近x轴;如图:yy=2x /F y=xk>0,b>0k<o,b>0,图像过一二四象限k<o ,b>0,图像过二三四象限增减性:k>O,y 随x 的增大而增大;k<0, y 随x 的增大而减小;平移:y=kx+b,向上平移 m 个单位:y=kx+b+m;向下平移 n 个单位:y=kx+b-n;向左平移 m 个单位:y=k (x+m )+b;向右平移 n 个单位:y=k (x-n )+b;简称:上加下减,左加右减;(注:上加下减到代数式后面,左加右减到x 后面,直接与x进行加减,与系数和指数都没关系);反比例函数:解析式:y=k/x (k 为常数,k z 0) 图像:双曲线(图像无限靠近坐标轴, 所在象限:k>0图像经过一三象限;增减性:k>0,y 随x 的增大而减小;k<0,y 随x 的增大而增大;反比例函数知识点归纳1、基础知识(一)反比例函数的概念但永不相交。
一次函数、二次函数、反比例函数性质总结1.一次函数一次函数一次函数)0(¹+=k b kx y ,当0=x 时,得到的y 的值也即b 叫做图象与坐标轴的纵截距,当0=y 时,得到的x 的值,叫做图象与坐标轴的横截距。
的值,叫做图象与坐标轴的横截距。
(1)当0=b 时,一次函数的解析式变为)0(¹=k kx y ,也称为正比例函数,此函数图象恒过原点)0,0(O ,且横,纵截距都为0。
且0>k 时,函数图象过一、三象限,0>k 时,图象过二、四象限。
时,图象过二、四象限。
①0>k ②0<k(2)当0¹b 时,)0(¹+=k b kx y 的图象及性质为的图象及性质为①0,0>>b k 时,时, ② 0,0<>b k 时 图象过一二,三图象过一二,三 图象过一、三、四图象过一、三、四象限象限 象限象限③0,0><b k 时,时, ④ 0,0<<b k 时,时,图象过一、二、四图象过一、二、四 图象过二、三、四图象过二、三、四象限象限 象限象限yxxy yy OOOO xxyOOy xx2.二次函数二次函数 二次函数的一般形式为)0(2¹++=a c bx ax y ,且a 决定开口方向和大小,当0>a 时,抛物线开口向上,有最小值,值域为),44[2+¥-ab ac 当0<a ,抛物线开口向下,有最大值,值域为]44,(2ab ac --¥。
(1)当0,0==c b 时,函数的解析式变为)0(2¹=a ax y ,则,则 ①0>a 时 ②0<a 时(2)b a ,决定二次函数的对称轴和开口方向决定二次函数的对称轴和开口方向①当0,0,0=>>c b a 时 ②0,0,0=<>c b a 时③ 0,0,0=><c b a 时 ④ 0,0,0=<<c b a 时(3)c a ,决定开口方向和与y 轴的截距轴的截距①0,0,0=>>b c a 时 ②0,0,0=<>b c a 时yyOxxxxyyOOyOxxOyO③0,0,0=><b c a 时 ④0,0,0=<<b c a 时(3)对于一般的二次函数,c b a ,,共同来决定其函数图像和性质,故通常采用配方的方法共同来决定其函数图像和性质,故通常采用配方的方法)0(2¹++=a c bx ax yc a b a b x a b x a c x a bx a +-++=++=))2()2(()(2222c a b a b x a +-+=]4)2[(222=c ab a b x a +-+4)2(22=ab ac a b x a 44)2(22-++我们称ab x 2-=为二次函数的对称轴,坐标)44,2(2a b ac a b--为二次函数的顶点坐标,此时我们也称其解析式为二次函数的顶点式,并可设其解析式为)0()(2¹+-=a k h x a y 。
正比例函数、一次函数、反比例函数的性质及图象
一、正比例函数性质和图象:
概念:一般地,形如(k是常数,且k≠0 )的函数,叫做正比例函数。
当k>0时,图象过象限; y随x的增大而。
当k<0时,图象过象限; y随x的增大而。
:
概念:一般地,形如y=kx+b(k,b是常数,且k≠0 )的函数,叫做一次函数。
图像和性质:
①k>0,b>O,则图象过象限
②k>0,b<0,则图象过象限
当k>0时, y随x的增大而。
③k<0,b>0,则图象过象限
④k<0,b<0,则图象过象限
当k<0时, y随x的增大而。
三、反比例函数性质和图象:
1.定义:形如(k为常数,k≠0)的函数称为反比例函数。
其他形式
2.图像:反比例函数的图像是双曲线。
反比例函数的图象既是轴对称图形又是中心对称图形。
3.性质:当k>0时双曲线的两支分别位于,在每个象限内y
值随x值的增大而减小。
当k<0时双曲线的两支分别位于,在每个象限内y 值随x值的增大而增大。
4.|k|的几何意义:表示反比例函数图像上的点向两坐标轴
所作的垂线段与两坐标轴围成的矩形的面积。
练习题 1、若y =(m -1)x
22m -是正比例函数,则m 的值为( ) A 、1 B 、-1 C 、1或-1 D 、2或-2 2、下列函数中,一次函数为( )
A 、2
5y x = B .2
5y x =-1 C .24
5y x = D .2
5y x
=-
3、下列函数中,反比例函数是( )
A 、y=x+1
B 、y=
C 、=1
D 、3xy=2
4、正比例函数y=kx (k ≠0)函数值y 随x 的增大而增大,则y=kx+k 的图象大致是( )
5、直线44
3--=x y 与两坐标轴围成的三角形面积是( ) A 3 B 4 C 12 D 6
6、函数y 1=kx 和y 2=的图象如图,自变量x 的取值范围相同的是( )
7、若点A(x 1,1)、B(x 2,2)、C(x 3,-3)在双曲线上,( )
A 、x 1>x 2>x 3
B 、x 1>x 3>x 2
C 、x 3>x 2>x 1
D 、x 3>x 1>x 2
8、已知一次函数y=ax+b 图象在一、二、三象限,则反比例函数y=
的函数值随x 的增大而__________。