数学分析不定积分
- 格式:pdf
- 大小:111.32 KB
- 文档页数:5

第6章 不定积分6.1 复习笔记一、不定积分的概念和运算法则1.微分的逆运算——不定积分(1)原函数若在某个区间上,函数F (x )和f (x )成立关系F'(x )=f (x ),则称函数F (x )是f (x )的一个原函数。
(2)不定积分一个函数f (x )的原函数全体称为这个函数的不定积分,记作这里,“”称为积分号,f (x )称为被积函数,x 称为积分变量。
2.不定积分的线性性质若函数f (x )和g (x )的原函数都存在,则对任意常数k 1和k 2,函数k 1f(x )+k 2g (x)的原函数也存在,且有二、换元积分法和分部积分法1.换元积分法(1)在不定积分中,用u=g (x )对原式作变量代换,这时相应地有du=g'(x )dx ,于是,这个方法称为第一类换元积分法,也被俗称为“凑微分法”。
(2)找到一个适当的变量代换x=φ(t )(要求x=φ(t )的反函数t=φ-1(x )存在),将原式化为这个方法称为第二类换元积分法。
2.分部积分法对任意两个可微的函数u (x )、v (x ),成立关系式d[u (x )v (x )]=v (x )d[u (x )]+u(x)d[v (x )],两边同时求不定积分并移项,就有也即这就是分部积分公式。
三、有理函数的不定积分及其应用1.有理函数的不定积分(1)形如的函数称为有理函数,这里和分别是m 次和n 次多项式,n,m 为非负整数。
若m>n ,则称它为真分式;若m≤n,则称它为假分式。
(2)设有理函数是真分式,多项式有k 重实根α即则存在实数λ与多项的次数低于的次数,成立(3)设有理函数是真分式,多项式有l 重共轭复根,即其中则实数和多项式的次数低的次数,成立2.可化成有理函数不定积分的情况(1)类的不定积分。
这里R (u ,v )表示两个变量μ、υ的有理函数(即分子和分母都是关于u ,v的二元多项式)。
对作变量代换,则。

数学分析不定积分知识点总结不定积分是数学分析中的一个重要概念,它是微积分学的基础内容之一。
理解和掌握不定积分的相关知识对于进一步学习高等数学以及解决实际问题都具有重要意义。
下面我们将对不定积分的知识点进行详细总结。
一、不定积分的定义如果在区间\(I\)上,\(F'(x) = f(x)\),则称\(F(x)\)是\(f(x)\)在区间\(I\)上的一个原函数。
\(f(x)\)的原函数的全体称为\(f(x)\)在区间\(I\)上的不定积分,记为\(\int f(x)dx\)。
二、基本积分公式1、\(\int kdx = kx + C\)(\(k\)为常数)2、\(\int x^n dx =\frac{1}{n + 1}x^{n + 1} + C\)(\(n \neq -1\))3、\(\int \frac{1}{x}dx =\ln|x| + C\)4、\(\int e^x dx = e^x + C\)5、\(\int a^x dx =\frac{1}{\ln a}a^x + C\)(\(a >0\),\(a \neq 1\))6、\(\int \sin x dx =\cos x + C\)7、\(\int \cos x dx =\sin x + C\)8、\(\int \sec^2 x dx =\tan x + C\)9、\(\int \csc^2 x dx =\cot x + C\)10、\(\int \sec x \tan x dx =\sec x + C\)11、\(\int \csc x \cot x dx =\csc x + C\)这些基本积分公式是进行积分运算的基础,必须牢记。
三、不定积分的性质1、函数的和的不定积分等于各个函数不定积分的和,即\(\int f(x) + g(x)dx =\int f(x)dx +\int g(x)dx\)。
2、常数乘以函数的不定积分等于常数乘以该函数的不定积分,即\(\int kf(x)dx = k\int f(x)dx\)(\(k\)为常数)。


§3 有理函数和可化为一、有理函数的部分分式分解本节给出了求有理函数等有关类型的四、某些无理函数的不定积分三、三角函数有理式的不定积分二、有理真分式的递推公式有理函数的不定积分不定积分的方法与步骤.返回C x B +i A(ii),p t x =+令22,,p pL r q N M =-=-则2,k 时³111æö432x x x x24910 -++-11d x12x +21(22)1 x x--+对三角函数有理式的不定积分, 在某些条件下还可(iii)(,)(,),tan .R u v R u v t x --==若可作变换(i)(,)(,),cos ;R u v R u v t x -=-=若可作变换(ii)(,)(,),sin ;R u v R u v t x -=-=若可作变换?为什么以上变换可使不定积分简化(i),R 若满足条件由代数学知识可知,存在有理函0,R 数使得选用如下三种变换, 使不定积分简化.因此=--ò2(1cos ,cos )d(cos )R x x x 20(,)(,).R u v R u v u =0(ii),,R R 若满足条件则存在有理函数使得20(,)(,).R u v R u v v =类似可得2(1,)d .R t t t =--ò=òò2(sin ,cos )d (sin ,cos )sin d R x x x R x x x x2sin òx.)0(,d òab x32 31129 x t t-+33d òx22d223 x x x--注1对于本题来说,方法2 显然比方法1 简捷.作业P200:1(2)、(3)、(6);2(1)、(3)、(5)。



第八章不定积分一、不定积分概念与基本积分公式1.原函数与不定积分①定义1:设函数f 与F 在区间I 上都有定义,若F’(x)=f(x),x ∈I ,则称F 为f 在区间I 上的一个原函数。
②定理8.1:若函数f 在区间I 上连续,则f 在I 上存在原函数F ,即F’(x)=f(x),x ∈I 。
·不连续的函数也可以有原函数③定理8.2:设F 是f 在区间I 上的一个原函数,则(i)F+C 也是f 在I 上的原函数,其中C 为任意常量函数;(ii)f 在I 上的任意两个原函数之间,只可能相差一个常数。
④定义2:函数f 在区间I 上的全体原函数称为f 在I 上的不定积分,记作∫f(x)dx 。
·[∫f(x)dx]’=[F(x)+C]’=f(x);·d ∫f(x)dx=d[F(x)+C];⑤不定积分的几何意义:积分曲线2.基本积分表①∫0dx=C ;②∫1dx=∫dx=x+C ;③)0,1(11>-≠++=⎰+x C x dx x αααα;④)0(||ln 1≠+=⎰x C x dx x ;⑤∫e x dx=e x +C ;⑥)0,1(ln >≠+=⎰a C aa dx a xx α;⑦)0(sin 1cos ≠+=⎰αC ax a axdx ;⑧)0(cos 1sin ≠+-=⎰αC ax a axdx ;⑨∫sec 2xdx=tanx+C ;⑩∫csc 2xd1=-cotx+C ;⑪∫secx ·tanxdx=secx+C ;⑫∫cscx ·cotxdx=-cscx+C ;⑬12arccos arcsin 1C x C x x dx+-=+=-⎰;⑭12cot arctan 1C x arc C x x dx +-=+=+⎰。
⑮定理8.3:若函数f 与g 在区间I 上都存在原函数,k 1,k 2为两个任意常数,则k 1f+k 2g 在I 上也存在原函数,且当k 1和k 2不同时为零时,有∫[k 1f(x)+k 2g(x)]dx=k 1∫f(x)dx +k 2∫g(x)dx二、换元积分法与分部积分法1.换元积分法①定理8.4(第一换元积分法/凑微分法):设函数f(x)在区间I 上有定义,φ(t)在区间J 上可导,且φ(J)⊆I 。



数学分析中的积分求解方法在数学分析中,积分是一个重要的概念和工具。
它可以用来计算曲线下面的面积、求解定积分以及解决一些实际问题。
本文将介绍一些常见的积分求解方法,包括不定积分和定积分。
一、不定积分不定积分是指对一个函数进行积分,得到的结果是一个含有未知常数的函数。
不定积分的符号表示为∫f(x)dx,其中f(x)是要求积分的函数。
不定积分的求解方法有很多,下面将介绍其中的几种常见方法。
1. 基本积分法基本积分法是指根据一些已知的基本积分公式,将要求积分的函数转化为基本积分公式中的形式,从而求解积分。
例如,对于函数f(x) = x^n,其中n为任意实数,其基本积分公式为∫x^n dx = (1/(n+1))x^(n+1) + C,其中C为常数。
2. 分部积分法分部积分法是指将要求积分的函数进行分解,然后利用分部积分公式进行求解。
分部积分公式为∫u dv = uv - ∫v du,其中u和v是要求积分的函数。
通过适当选择u和dv,可以将原函数转化为更容易求解的形式。
3. 代换积分法代换积分法是指通过代换变量的方法将要求积分的函数转化为一个更容易求解的形式。
常见的代换变量有三角函数代换、指数函数代换和倒数代换等。
通过选择合适的代换变量,可以简化积分的计算过程。
二、定积分定积分是指对一个函数在给定区间上的积分,得到的结果是一个确定的数值。
定积分的符号表示为∫[a,b]f(x)dx,其中[a,b]表示积分区间。
定积分的求解方法有很多,下面将介绍其中的几种常见方法。
1. 几何解释法几何解释法是指将定积分的计算问题转化为几何问题,通过计算图形的面积或体积来求解定积分。
例如,对于一条曲线y=f(x),其在区间[a,b]上的定积分∫[a,b]f(x)dx可以表示为该曲线下方的面积。
2. 分割求和法分割求和法是指将定积分的区间分割成若干小区间,然后对每个小区间内的函数进行求和,最后将这些求和结果相加得到定积分的近似值。
第八章 不定积分3 有理函数可化为有理函数的不定积分一、有理函数的不定积分有理函数:由两个多项式函数的商所表示的函数,其一般形式为:R(x)=)(Q )P(x x =n1-m 1m 0n1-n 1n 0βx βx βαx αx α+⋯+++⋯++, 其中n,m 为非负整数,α0,α1,…αn 与β0,β1,…βn 都是常数,且α0β0≠0. 若m>n ,则称它为真分式;若m ≤n ,则称它为假分式.注:1、假分式可化为整式与真分式的和;2、真分式可表示为若干个部分分式之和(称为部分分式分解);3、分解部分分式的一般步骤:第一步:对分母Q(x)在实系数内作标准分解:(分解前先化β0=1) Q(x)=(x-a 1)1λ…(x-a s )sλ(x 2+p 1+q 1)1μ…(x 2+p t +q t )tμ,其中λi ,μj (i=1,2,…,s ;j=1,2,…,t)均为自然数,而且∑=s1i iλ+2∑=t1j j μ=m ;p j 2-4q j <0, j=1,2,…,t.第二步:根据分母各因式分别写出与之相应的部分分式。
对于每个形如(x-a)k 的因式,它所对应的部分分式是:a -x A 1+22a)-(x A +…+k k a)-(x A ;对于每个形如(x 2+px+q)k 的因式,它所对应的部分分式是:q px x C x B 211++++2222q)px (x C x B ++++…+k2kk q)px (x C x B +++.第三步:确定待定系数。
将所有部分分式通分相加,所得分式的分母即为原分母Q(x),分子与原分子P(x)恒等。
根据同幂项系数相等,可得一组关于待定系数的线性方程,方程组的解就是需要确定的系数。
例1:对R(x)=8-x 4x 2x 5x x 10-x 9x 4x 2x 2345234+--+++-作部分分式分解.解:Q(x)=x 5+x 4-5x 3-2x 2+4x-8=(x-2)(x+2)2(x 2-x+1), R(x)=2-x A 0+2x A 1++222)(x A ++1x x C Bx 2+-+,两边乘以Q(x)得:2x 4-x 3+4x 2+9x-10 ≡A 0(x+2)2(x 2-x+1)+A 1(x 2-4)(x 2-x+1)+A 2(x-2)(x 2-x+1)+(Bx+C)(x-2)(x+2)2. 根据等式两边同幂项系数相等,得到线性方程组:⎪⎪⎪⎩⎪⎪⎪⎨⎧-10.=8C -2A -4A -4A ,9=4C -8B -3A +4A ,4=2C +4B -3A -3A -A ,-1=C +2B +A +A -3A ,2=B +A +A 2102121021010 解得:A 0=1, A 1=2, A 2=-1, B=-1, C=1. ∴对R(x)作部分分式分解的结果为:R(x)=2-x 1+2x 2+-22)(x 1+-1x x 1-x 2+-.注:对以上待定系数法有时可运用简便方法,如将x=2代入恒等式得: 32-8+16+18-10≡A 0·(2+2)2(4-2+1),∴A 0=1,将x=-2代入恒等式得: 32+8+16-18-10≡A 2(-2-2)(4+2+1),∴A 2=-1,于是化简恒等式得: x 4-3x 3+12+16≡A 1(x 2-4)(x 2-x+1)+(Bx+C)(x-2)(x+2)2,分别令x=0,1,-1可得:⎪⎩⎪⎨⎧+ 8.=C +B -3A 2,=3C 3B +A 4,=2C +A 111 解得:A 1=2, B=-1, C=1.小结:求有理真分式的不定积分可归为以下两种形式的不定积分:(1)∫k a)-(x dx =⎪⎩⎪⎨⎧>+=+ 1.k ;C a)-k)(x -(111,k C ;|a -x |ln 1-k (2)∫k 2q)px (x M Lx +++dx=∫k 22)r (t N Lt ++dt=L ∫k 22)r (t t +dt+N ∫k22)r (t dt+,其中 t=x+2p ,r 2=q-4p 2,N=M-4p L.当k=1时,原式=L ∫22r t t +dt+N ∫22rt dt +=2L ln(t 2+r 2)+ r N arctan r t +C. 当k ≥2时,∫k 22)r (t t +dt =1-k 22)r (t )k 1(21+-+C. I k =∫k 22)r (t dt +=2r 1∫k 22222)r (t t -)r (t ++dt=2r 1I k-1-2r 1∫k 222)r (t t +dt=2r 1I k-1+)1k (2r 12-∫td ⎥⎦⎤⎢⎣⎡+1-k 22)r (t 1=2r 1I k-1+)1k (2r 12-⎥⎦⎤⎢⎣⎡-+1-k 1-k 22I )r (t t=1-k 21-k 222I )1k (2r 3-2k )r (t )1k (2r t -++-.重复计算直至归为计算I 1. 最后换元为x ,就得到最终的结果.例2:求∫2222)2x -(x 1x ++dx. 解:2222)2x -(x 1x ++=2222)2x -(x 1)-x 2(2)x 2(x +++-=22x -x 12++222)2x -(x 1-x 2+∫22x -x dx2+=∫11)-(x 1)-d(x 2+dx=arctan(x-1)+C.∫222)2x -(x 1-x 2+dx=∫2222)2x -(x 2)2x -d(x +++∫221)]1)-[(x 1)-d(x +=-222)2x -(x 1++∫22)1t (dt +. ∫22)1t (dt +=1)2(t t 2++21∫1t dt 2+=1)2(t t 2++21arctant+C=2)2x -2(x 1-x 2++21arctan(x-1)+C. ∴原式= arctan(x-1)-222)2x -(x 1++2)2x -2(x 1-x 2++21arctan(x-1)+C=2)2x -2(x 3-x 2++23arctan(x-1)+C.二、三角函数有理式的不定积分:由u(x),v(x)及常数经过有限次四则运算所得到的函数称为关于u(x),v(x)的有理式,并用R(u(x),v(x))表示.∵sinx=2x tan 12x2tan2+=2t12t +, cosx=2x tan 12xtan -122+=22t 1t -1+, (t=tan 2x ); ∴∫R(sinx,cosx)dx=∫R(2t 12t +,22t 1t -1+)d(2arctant)=∫R(2t 12t +,22t 1t -1+)2t12+d(t). 例3:求∫cosx )sinx (1sinx1++dx.解:∫cosx )sinx (1sinx 1++dx=∫22222t 12)t1t -1(1t 12t t 12t 1+⋅+++++dt =21∫(t+2+t 1)dt=4t 2+t+21ln|t|+C=41tan 22x + tan 2x +21ln|tan 2x|+C.例4:求∫xcos b x sin a dx2222+(ab ≠0).解:∫x cos b x sin a dx 2222+=∫2222b x tan a x sec +dx=∫222b x tan a dtanx +=∫222b t a dt+=ab 1∫1b at bat d 2+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=ab 1arctan b at +C=ab 1arctan batanx +C.三、某些无理根式的不定积分: 1、∫R(x,nd cx b ax ++)dx 型不定积分(ad-bc ≠0),只需令t=n dcx bax ++,化为有理函数的不定积分. 例5:求∫2x 2x x1-+dx. 解:令t=2x 2x -+,则x=1t 22t 22-+,原式=∫22t 1)t(t 22+-d 1t 22t 22-+=∫2222221)2)(t (2t 2)]2t(2t -1)1)[4t(t t(t -++--dt=-2∫1)1)(t (t 2t 222-+dt=-2∫(1t 12++1t 12-)dt=-2arctant-∫(1t 1--1t 1+)dt=ln 1t 1t -+-2arctant +C =ln12x 2x 12x 2x --++-+-2arctan 2x 2x -++C=ln 2x 2x 2x 2x --+-++-2arctan2x 2x -++C =ln 44x 2x 22-+-2arctan 2x 2x -++C=ln|2x+24x 2-|-2arctan 2x 2x -++C.例6:求∫2xx 2x)(1dx-++.解:∫2x x 2x)(1dx-++=∫)x 1)(x 2(x)(1dx+-+=∫x2x1x)(112-++dx. 令t=x 2x 1-+,则x=1t 1-2t 22+,dx=22221)(t 1)-2t(2t -1)4t(t ++dt=221)(t t 6+dt. 1+x=1+1t 1-2t 22+=1t 3t 22+,2x )(11+=422t 91)(t +.原式=∫224221)(t t6t 91)t(t +⋅+dt=32∫t -2dt=-t 32+C=x 1x 232+--+C.2、∫R(x,c bx ax 2++)dx 型不定积分(a>0时b 2-4ac ≠0, a<0时b 2-4ac>0),由于ax 2+bx+c=a[(x+a 2b )2+22a 4b -4ac ],若记u=x+a 2b , k 2=22a4b -4ac ,则此二次三项式必属于以下三种情形之一:|a|(u 2±k 2),|a|(k 2-u 2). 因此上述无理根式的不定积分可化为以下三种类型之一:∫R(u,22k u ±)du ,∫R(u,22u k -)du.分别令u=ktant, u=ksect, u=ksint ,则都化为三角有理式的不定积分.例7:求I=∫3x 2x x dx 2--.解法一:令u=x-1=2sec θ, t=tan 2θ, 则t=1x 3-x +. I=∫41)-(x x 1)-d(x 2-=∫4u )1(u du 2-+=∫1θsec )1(2sec θdsec θ2-+=∫)1θ(2secθtan tan θanθs+d θ=∫12sec θsec θ+d θ=∫cos θ21+d θ=∫222t 1t -12t 12+++dt=2∫3t 12+dt=32∫13t 12+⎪⎪⎭⎫ ⎝⎛d ⎪⎪⎭⎫ ⎝⎛3t=32arctan ⎪⎪⎭⎫⎝⎛3t +C=32arctan ⎪⎪⎭⎫ ⎝⎛+33x 3-x +C. 解法二:令3x 2x 2--=x-t, 则x=)1t (23t 2-+, dx=22)1t (23-t 2t --dt. I=∫⎪⎪⎭⎫ ⎝⎛--+-+--t )1t (23t )1t (23t )1t (23-t 2t 2222dt=-2∫3t 12+dt=-32arctan ⎪⎪⎭⎫ ⎝⎛3t +C =32arctan ⎪⎪⎭⎫⎝⎛---3x 3x 2x 2+C.注:一般地,二次三项式ax 2+bx+c 中若a>0,则可令c bx ax 2++=a x ±t ;若c>0,也可令c bx ax 2++=xt ±a ,这类变换称为欧拉变换.习题求下列不定积分:(1)∫1-x x 3dx ;(2)∫127x -x 2-x 2+dx ;(3)∫3x 1dx +;(4)∫4x1dx+;(5)∫221)1)(x -(x dx +; (6)∫22)1x 2(2x 2-x ++dx ;(7)∫x cos 35dx -;(8)∫xsin 2dx 2+;(9)∫x tan 1dx+; (10)∫22x x 1x -+dx ;(11)∫xx dx 2+;(12)∫x1x-1x 12+dx. 解:(1)∫1-x x 3dx=∫1-x 11x 3+-dx=∫(x 2+x+1)dx+∫1-x 1dx=3x 3+2x 2+x+ln|x-1|+C.(2)127x -x 2-x 2+=4)-3)(x -(x 2-x ≡3-x A +4-x B ;∴x-2≡A(x-4)+B(x-3).当x=3时,解得A=-1;当x=4时,解得B=2.∴原式=∫4-x 2dx-∫3-x 1dx=2ln|x-4|-ln|x-3|+C=ln 3-x 4)-(x 2+C.(3)3x11+=1)x 1)(x (x 12+-+≡1x A ++1x -x C Bx 2++;∴A(x 2-x+1)+(Bx+C)(x+1)≡1. 当x=-1时,解得A=31;由A+B=0,得B=-31;由A+C=1,得C=32. ∴原式=31∫1x 1+dx-31∫1x -x 2-x 2+dx=31ln|x+1|-61∫1x -x 3-1-2x 2+dx=31ln|x+1|-61∫1x -x 1)x -d(x 22+++21∫1x -x 12+dx=61ln 1x -x 1)+(x 22++21∫4321-x 12+⎪⎭⎫ ⎝⎛dx =61ln 1x -x 1)+(x 22++31∫121-x 3221-x 32d 2+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛=61ln 1x -x 1)+(x 22++31arctan 31-x 2+C. (4)∫4x 1dx +=21∫422x 11x -1x +++dx=21∫42x 11x ++dx -21∫42x 11x +-dx=21∫222x 1x x 11++dx-21∫222x 1x x 11+-dx=21∫2x 1x x 1x d 2+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--21∫2x 1x x 1x d 2-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+ =42arctan x 21-x 2-82∫)2x 1(x x 1x d ++⎪⎭⎫ ⎝⎛++82∫)2x 1(x x 1x d -+⎪⎭⎫ ⎝⎛+=42arctan x 21-x 2-82ln 1x 2x 1x 2x 22+-+++C. (5)由221)1)(x -(x 1+≡1-x A +1x C Bx 2+++221)(x EDx ++得:A(x 2+1)2+(Bx+C)(x-1)(x 2+1)+(Dx+E)(x-1)≡1. 当x=1时,解得A=41. ∴41x 4+21x 2+41+Bx 4-Bx 3+Cx 3+Bx 2-Cx 2-Bx+Cx-C+Dx 2-Dx+Ex-E=(41+B)x 4-(B-C)x 3+(21+B-C+D)x 2-(B-C+D-E)x-(C+E-41)≡1. ∴B=-41,C =-41,D=-21,E=-21. 原式=41∫1-x dx -41∫1x 1x 2++dx-21∫221)(x 1x ++dx =41ln|x-1|-81∫1x 1)d(x 22++-41∫1x dx 2+-41∫2221)(x 1)d(x ++-21∫221)(x dx + =81ln 1x 1)(x 22+--41arctanx+)1x (412+-21∫221)(x dx +又∫221)(x dx +=∫221)t (tan dtant +=∫cos 2tdt=21∫(cos2t+1)dt=41∫cos2td2t +21∫dt =41sin2t+21t+C=)1t (tan 2tant 2++21arctanx+C=)1x (2x 2++21arctanx+C.∴原式=81ln 1x 1)(x 22+--41arctanx+)1x (412+-)1x (4x 2+-41arctanx+C=81ln 1x 1)(x 22+--21arctanx+)1x (4x -12++C.(6)∫22)1x 2(2x 2-x ++dx=41∫222)1x 2(2x )1x 2d(2x ++++-25∫22)1x 2(2x dx ++=-)1x 24(2x 12++-5∫22)]11)[(2x 1)d(2x +++=-)1x 24(2x 12++-45[1x 22x 12x 2++++2arctan(2x+1)]+C =-)1x 22(2x 3x 52+++-25arctan(2x+1)+C.(7)∫x cos 35dx -=∫222t 1)t 3(15t 12+--+dt=21∫1t)2(d2t 2+=21arctan2t+C=21arctan(2tan 2x )+C.(8)方法一:∫x sin 2dx 2+=∫22t 1t 22t 12+++dt=∫1t t dt 2++=32∫13132t 3132t d 2+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+ =32arctan ⎪⎭⎫ ⎝⎛+3132t +C=32arctan ⎪⎪⎪⎪⎭⎫ ⎝⎛+3132x 2tan +C. 方法二:∫x sin 2dx 2+=∫x tan x sec 2x dx sec 222+=∫2x tan 3dtanx 2+dt=66∫1x tan 23tanx23d2+=66arctan(tanx 23)+C.(9)∫x tan 1dx +=∫x tanx sec x sec x dx sec 222+=∫1tanx x tan x tan dtanx23+++ =21(∫1tanx dtanx +-∫1x tan tanxdtanx 2++∫1x tan dtanx 2+)=21(ln|tanx+1|-21∫1x tan )1x d(tan 22+++x) =21(ln 1x tan |1tanx |2+++x)+C=21(ln|cosx+sinx|+x)+C. (10)I=∫22xx 1x -+dx=-∫22xx 1x x 1-+-+dx+∫2xx 11)dx (x -++=-∫2x x 1-+dx+∫2xx 11)dx (x -++=-x 2x x 1-+-∫22xx 12x -x 2-+dx+∫2xx 11)dx (x -++=-x 2xx 1-+-I+21∫2xx 1x -+dx+∫2xx 11)dx (x -++=-x 2x x 1-+-I+23∫2xx 132x -++dx. ∴I=-2x x 12x -++43∫2x x 132x -++dx.又∫2x x 132x -++dx=-21∫2x x 1x 21-+-dx+67∫2x x 1dx -+ =-2x x 1-++67∫251-2x 151-2x d ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-2x x 1-++67∫arcsin 51-2x +C. ∴原式=-2x x 12x -+-432x x 1-++87∫arcsin 51-2x +C. (11)令t-x=x x 2+,则x=12t t 2+,dx=d 12t t 2+=21)(2t 1)t(t 2++dt. ∫x x dx 2+=∫12t t t 1)(2t 1)t(t 222+-++dt=∫12t 1)d(2t ++=ln|2t+1|+C=ln|2x x 2++2x+1|+C. (12) ∫x 1x -1x 12+dx=-∫1x11-x 1+d x 1=-∫1t 1-t +dt=-∫1t 1-t 2-dt=-∫1t tdt 2-+∫1t dt 2- =-1t 2-+ln|t+1t 2-|+C=-x x 12-+ln x x 112-++C.。
8.1 不定积分概念与基本积分公式(2学时)
【教学目的】深刻理解原函数与不定积分的概念;牢记基本积分表;掌握不定积分的线形运算法则。
【教学重点】不定积分的概念,基本积分表,不定积分的线形运算法则。
【教学难点】求不定积分的技巧。
【教学过程】
一、原函数与不定积分
(一) 原函数
定义1 设函数与在区间)(x f )(x F I 上有定义。
若
)()(x f x F =′, I x ∈,
则称为在区间)(x F )(x f I 上的一个原函数。
如:331x 是在R 上的一个原函数;2x x 2cos 21−, 12cos 2
1+x ,,等都有是在R 上的原函数——若函数存在原函数,则其原函数不是唯一的。
x 2sin x 2cos −x 2sin )(x f 问题1 在什么条件下必存在原函数?若存在,其个数是否唯一;又若不唯一,则有多少个?
)(x f 问题 2 若函数的原函数存在,如何将它求出?(这是本章的重点内容)。
)(x f 定理1 若在区间)(x f I 上连续,则在)(x f I 上存在原函数。
)(x F (证明在第九章中进行。
)
说明:(1)由于初等函数在其定义域内都是连续的,故初等函数在其定义域内必存在原函数(但其原函数不一定仍是初等函数)。
(2)连续是存在原函数的充分条件,并非必要条件。
定理2 设是在在区间)(x F )(x f I 上的一个原函数,则(1)设是在在区间C x F +)()(x f I 上的原函数,其中C 为任意常量(若存在原函数,则其个)(x f
数必为无穷多个)。
(2)在)(x f I 上的任何两个原函数之间,只可能相差上个常数(揭示了原函数间的关系)。
证:(i)这是因为[]
.),()()(I x x f x F C x F ∈=′=′+(ii)设F 和G 是f 在I 上的任意两个原函数,则有
[]
I x x f x f x G x F C x F ∈=−=′−′=′+,0)()()()()(根据第六章拉格朗日中值定理的推论,知道I x C x G x F ∈≡−,)()(. 口
(二) 不定积分
定义 2 函数在区间)(x f I 上的原函数的全体称为在)(x f I 上的不定积分,记作:
∫dx x f )(
其中∫积分号;被积函数; −−−−)(x f −−dx x f )(被积表达式;−−x 积分变量。
注1: 是一个整体记号;
∫dx x f )(注2:不定积分与原函数是总体与个体的关系,即若是的一个原函数,则的不定积分是一个函数族)(x F )(x f )(x f {}C x F +)(,其中是任意常数,于是,记为:∫=。
C dx x f )(C x F +)(此时称C 为积分常数,它可取任意实数。
故有
——先积后导正好还原;
∫=′)(])([x f dx x f 或 。
∫=dx x f dx x f d )()( ∫——先导后积还原后需加上一个常数(不能完全还原)。
+=′C x f dx x f )()(或 ∫。
+=C x f x df )()(如: C x dx x +=∫332, C x xdx +−=∫2cos 212sin 。
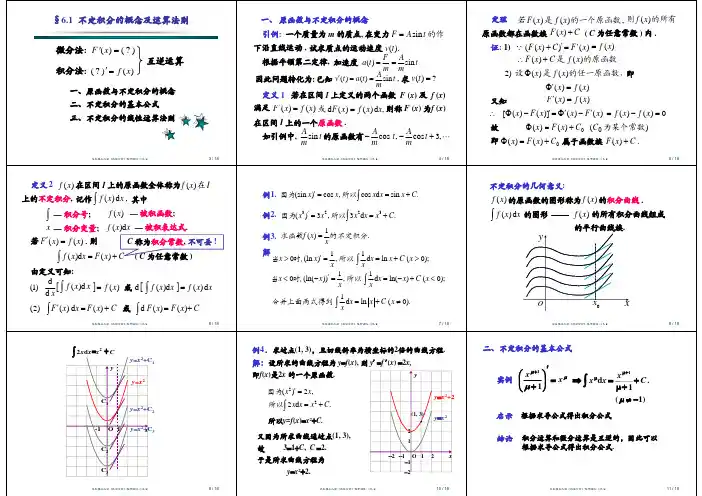
不定积分的风何意义: 若是的一个原函数,则称的图象为的一条积分曲线。
于是,的不定积分在几何上表示的某一条)(x F )(x f )(x F y =)(x f )(x f )(x f
积分曲线沿纵轴方向任意平移所得一载积分曲线组成的曲线族,曲线和在点C x F +)(2)(C x F +x 有相同切线斜率。
如下图。
)(x f
注:在求原函数的具体问题中,往往是先求出全体原函数,然后从中确定一个满足条件00)(y x F =(称之为初始条件,一般由具体问题确定)的原函数,它就是积分曲线族中通过点的那条积分曲线。
),(00y x
二、基本积分表
由于不定积分的定义不象导数定义那样具有构造性,这就使得求原函数的问题要比求导数难得多,因此,我们只能先按照微分法的已知结果去试探。
首先,我们把基本导数公式改写成基本积分公式:
1.;
∫=C dx 02.∫∫;
+==C x dx dx 13.C x dx x ++=∫+11
ααα
,)0,1(>−≠x α; 4.C x dx x
+=∫ln 1,; )0(≠x 5.∫;
+=C e dx e x x 6.C a a dx a x
x
+=∫ln , )1,0(≠>a a ; 7.C ax a
axdx +=∫sin 1cos ,)0(≠a ; 8.C ax a axdx +−=∫cos 1sin ,)0(≠a ;
9.∫;
+=C x xdx tan sec 210.∫;
+−=C x xdx cot csc 211.∫;
+=⋅C x xdx x sec tan sec 12.∫;
+−=⋅C x xdx x csc cot csc 13.
12arccos arcsin 1C x C x x dx +−=+−∫; 14.12cot arctan 1C x arc C x x
dx +−=+=+∫。
注意:上述基本积分公式一定要牢记,因为其它函数的不定积分经运算变形后,最终归结为这些基本不定积分。
另外,还须借助一些积分法则才能求出更多函数的不定积分。
定理3 若函数与在区间)(x f )(x g I 上都存在原函数, 为两个任意常数,也存在原函数,且
21,k k )()(21x g k x f k + ∫∫∫+=+dx x g k dx x f k dx x g k x f k )()()]()([2121(积分的线性性质)。
证明:可由微分法直接验证,因为
[]()()′
+′=′+∫∫∫∫dx x g k dx x f k dx x g k dx x f k )()()()(2121 ).()(21x g k x f k += 口
注:线性法则的一般形式为: 。
∫∑∑∫===n i n
i i i i i dx x f k dx x f k 11)()(根据上述线性运算法则和基本积分公式,可求得一些简单函数的不定积分.
例1、 ,
n n n n a x a x a x a x p ++++=−−1110)(" 则C x a x a x n a x n a dx x p n n n n ++++++=−+∫211102
1)("。
例2、 C x x x dx x x dx x x ++−=++−=++∫∫arctan 23)1
21(113
2224。
例3、 ∫∫∫+=+=dx x x dx x
x x x x x dx )sec (csc sin cos sin cos sin cos 22222222
C x x ++−=tan cot 。
例4、 C x x dx x x xdx x ++−=−=⋅∫∫)2cos 2
14cos 41(21)2sin 4(sin 21sin 3cos C x x +−−=)2cos 4(cos 8
1。
例5、 ∫∫∫−+=−+=−−−−dx dx dx x x x x x x ]2)10()10[()21010()1010(22222 C x x x +−−=−2)1010(10ln 2122。
作业:P182 2,3,4 ,5。