(完整)南京市八年级上学期末数学测试(内含答案),推荐文档

江苏省南京市苏科版八年级数学上 期末测试题（Word 版 含答案）一、选择题1．变量x 、y 有如下的关系，其中y 是x 的函数的是（ ） A ．28y x = B ．||y x =C ．1y x=D ．412x y =2．若分式15x -在实数范围内有意义，则实数x 的取值范围是（ ） A ．5x ≠B ．5x =C ．5x >D ．5x <3．如图，CD 是Rt△ABC 斜边AB 上的高，将△BCD 沿CD 折叠，点B 恰好落在AB 的中点E 处，则∠A 等于( )A ．25°B ．30°C ．45°D ．60°4．如图，∠A ＝30°，∠C ′＝60°，△ABC 与△A′B′C′关于直线l 对称，则∠B 度数为（ ）A ．30B ．60︒C ．90︒D ．120︒ 5．下列各组数不是勾股数的是（ ）A ．3，4，5B ．6，8，10C ．4，6，8D ．5，12，136．一次函数112y x =-+的图像不经过的象限是：（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限7．下列四组数，可作为直角三角形三边长的是A ．456cm cm cm 、、B ．123cm cm cm 、、C ．234cm cm cm 、、D ．123cm cm cm 、、8．如图，一次函数(0)y kx b k =+>的图象过点(0,2)，则不等式20kx b +->的解集是（ ）A ．0x >B ．0x <C ．2x <D ．2x > 9．我们知道，平面内不垂直的两条相交直线是轴对称图形，该图形对称轴条数为（ ） A ．1 B ．2 C ．4 D ．无数 10．直线y=ax+b(a ＜0，b ＞0)不经过( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限二、填空题11．在平面直角坐标系中，过点()5,6P 作PA x ⊥轴，垂足为点A ，则PA 的长为______________.12．如图，在ABC ∆中，AB AC =，点P 为边AC 上一动点，过点P 作PD BC ⊥，垂足为点D ，延长DP 交BA 的延长线于点E ，若10AC =，设CP 长为x ，BE 长为y ，则y 关于x 的函数关系式为__________.（不需写出x 的取值范围）13．如图，函数3y x =-和4y ax =+的图像相交于点A （m ，3），则不等式34x ax ->+的解集为____．14．等边三角形有_____条对称轴．15．已知某地的地面气温是20℃，如果每升高1000m 气温下降6℃，则气温t （℃）与高度h （m ）的函数关系式为_____．16．当直线()223y k x k =-+-经过第二、三、四象限时，则k 的取值范围是_____． 17．如图，已知ABD CBD ∠∠=，若以“SAS”为依据判定ABD ≌CBD ，还需添加的一个直接条件是______．18．若直角三角形斜边上的中线是6cm ，则它的斜边是 ___ cm ．19．若分式2223x x -+的值为零，则x 的值等于___．20．如图①，四边形ABCD 中，//,90BC AD A ∠=︒，点P 从A 点出发，沿折线AB BC CD →→运动，到点D 时停止，已知PAD △的面积s 与点P 运动的路程x 的函数图象如图②所示，则点P 从开始到停止运动的总路程为________.三、解答题21．如图，在ABC ∆中，AD BC ⊥，15AB =，12AD =，13AC =.求BC 的长.22．先化简，再求值：（1﹣11a -）÷2244a a a a-+-，其中a=2+2． 23．（本题满分10分） 如图，直线23y x =+与x 轴相交于点A ，与y 轴相交于点B .(1)求△AOB 的面积；(2)过B 点作直线BP 与x 轴相交于P ，△ABP 的面积是92，求点P 的坐标.24．观察下列等式：112()(2)()(2)22⨯---=-⨯-；4422233⨯-=⨯；111123232⨯-=⨯；……根据上面等式反映的规律，解答下列问题：（1）请根据上述等式的特征，在括号内填上同一个实数：2⨯（）-5=（）5⨯；（2）小明将上述等式的特征用字母表示为：2x y xy-=（x、y为任意实数）.①小明和同学讨论后发现：x、y的取值范围不能是任意实数.请你直接写出x、y不能取哪些实数.②是否存在x、y两个实数都是整数的情况？若存在，请求出x、y的值；若不存在，请说明理由.25．已知甲，乙两名自行车骑手均从P地出发，骑车前往距P地60千米的Q地，当乙骑手出发了1.5小时，此时甲，乙两名骑手相距6千米，因甲骑手接到紧急任务，故甲到达Q地后立即又原路返回P地甲，乙两名骑手距P地的路程y（千米）与时间x（时）的函数图象如图所示．（其中折线O﹣A﹣B﹣C﹣D（实线）表示甲，折线O﹣E﹣F﹣G（虚线）表示乙）（1）甲骑手在路上停留小时，甲从Q地返回P地时的骑车速度为千米/时；（2）求乙从P地到Q地骑车过程中（即线段EF）距P地的路程y（千米）与时间x（时）的函数关系式及自变量x的取值范围；（3）在乙骑手出发后，且在甲，乙两人相遇前，求时间x（时）的值为多少时，甲，乙两骑手相距8千米．四、压轴题26．问题背景：（1）如图1，已知△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：DE＝BD＋CE．拓展延伸：（2）如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC．请写出DE、BD、CE三条线段的数量关系．（不需要证明）实际应用：（3）如图，在△ACB中，∠ACB＝90°，AC＝BC，点C的坐标为(－2，0)，点A的坐标为(－6，3)，请直接写出B点的坐标．27．在平面直角坐标系中点A（m−3，3m+3），点 B（m，m+4）和 D（0，−5），且点 B 在第二象限．（1）点B 向平移单位，再向下平移（用含m 的式子表达）单位可以与点A 重合；（2）若点B 向下移动 3 个单位，则移动后的点B 和点A 的纵坐标相等，且有点 C（m−2，0）．①则此时点A、B、C 坐标分别为、、．②将线段AB 沿y 轴负方向平移n 个单位，若平移后的线段AB 与线段CD 有公共点，求n 的取值范围．③当m<−1 式，连接AD，若线段AD 沿直线AB 方向平移得到线段BE，连接DE 与直线y=−2 交于点F，则点F 坐标为．（用含m 的式子表达）28．已知三角形ABC中，∠ACB＝90°，点D（0，－4），M（4，－4）．（1）如图1，若点C与点O重合，A（－2，2）、B（4，4），求△ABC的面积；（2）如图2，AC经过坐标原点O，点C在第三象限且点C在直线DM与x轴之间，AB分别与x轴，直线DM交于点G，F，BC交DM于点E，若∠AOG＝55°，求∠CEF的度数；（3）如图3，AC经过坐标原点O，点C在第三象限且点C在直线DM与x轴之间，N为AC上一点，AB分别与x轴，直线DM交于点G，F，BC交DM于点E，∠NEC+∠CEF＝180°，求证∠NEF＝2∠AOG．29．在等边△ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D、E处，请问：（1）如图1，在爬行过程中，CD和BE始终相等吗，请证明？（2）如果将原题中的“由A向B和由C向A爬行”，改为“沿着AB和CA的延长线爬行”，EB与CD交于点Q，其他条件不变，蜗牛爬行过程中∠CQE的大小保持不变，请利用图2说明：∠CQE=60°；（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，如图3，则爬行过程中，证明：DF=EF30．如图，在平面直角坐标系中，直线y ＝2x +6与x 轴交于点A ，与y 轴交于点B ，过点B 的直线交x 轴于点C ，且AB ＝BC ．（1）求直线BC 的解析式；（2）点P 为线段AB 上一点，点Q 为线段BC 延长线上一点，且AP ＝CQ ，设点Q 横坐标为m ，求点P 的坐标（用含m 的式子表示，不要求写出自变量m 的取值范围）； （3）在（2）的条件下，点M 在y 轴负半轴上，且MP ＝MQ ，若∠BQM ＝45°，求直线PQ 的解析式．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】 【分析】根据函数的定义：对于x 的每一个取值，y 都有唯一确定的值与之对应即可确定有几个函数． 【详解】A. 28y x =，y 不是x 的函数，故错误；B. ||y x =，y 不是x 的函数，故错误；C. 1y x= ，y 是x 的函数，故正确； D. 412x y =，y 不是x 的函数，故错误； 故选C. 【点睛】主要考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x ，y ，对于x 的每一个取值，y 都有唯一确定的值与之对应，则y 是x 的函数，x 叫自变量．2．A解析：A 【解析】 【分析】根据分式的定义即可求解. 【详解】依题意得50x -≠，解得5x ≠， 故选A. 【点睛】此题主要考查分式的性质，解题的关键是熟知分式的性质.3．B解析：B 【解析】 【分析】先根据图形折叠的性质得出BC=CE ，再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE ，进而可判断出△BEC 是等边三角形，由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论． 【详解】解：∵△ABC 沿CD 折叠B 与E 重合， ∴BC=CE ，∵E 为AB 中点，△ABC 是直角三角形， ∴CE=BE=AE ，∴△BEC 是等边三角形． ∴∠B=60°， ∴∠A=30°， 故选B ． 【点睛】本题考查折叠的性质，直角三角形的性质，等边三角形的判定和性质，解题的关键是熟练掌握折叠的性质：折叠前后的对应边相等，对应角相等.4．C解析：C【分析】由已知条件，根据轴对称的性质可得∠C＝∠C′＝30°，利用三角形的内角和等于180°可求答案．【详解】∵△ABC与△A′B′C′关于直线l对称，∴∠A＝∠A′＝30°，∠C＝∠C′＝60°；∴∠B＝180°−30°-60°＝90°．故选：C．【点睛】主要考查了轴对称的性质与三角形的内角和是180度；求角的度数常常要用到“三角形的内角和是180°．5．C解析：C【解析】【分析】根据勾股数的定义：有a、b、c三个正整数，满足a2+b2=c2，称为勾股数．由此判定即可．【详解】解：A、32+42=52，能构成勾股数，故选项错误；B、62+82=102，能构成勾股数，故选项错误C、42+62≠82，不能构成勾股数，故选项正确；D、52+122=132，能构成勾股数，故选项错误．故选：C．【点睛】本题考查勾股数，解答此题要深刻理解勾股数的定义，并能够熟练运用．6．C解析：C【解析】试题分析：根据一次函数y=kx+b（k≠0，k、b为常数）的图像与性质可知：当k＞0，b＞0时，图像过一二三象限；当k＞0，b＜0时，图像过一三四象限；当k＜0，b＞0时，图像过一二四象限；当k＜0，b＜0，图像过二三四象限.这个一次函数的k=12＜0与b=1＞0，因此不经过第三象限.答案为C考点：一次函数的图像7．D解析：D【解析】根据勾股定理的逆定理对四个选项进行逐一判断即可．【详解】A、∵52+42≠62，∴此组数据不能构成直角三角形，故本选项错误；B、12+22≠32，∴此组数据不能构成直角三角形，故本选项错误；C、∵22+32≠42，∴此组数据不能构成直角三角形，故本选项错误；D、∵12+（2）2=（3）2，∴此组数据能构成直角三角形，故本选项正确．故选：D．【点睛】本题考查的是勾股定理的逆定理，即如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．8．A解析：A【解析】【分析】由图知：一次函数y=kx+b的图象与y轴的交点为（0，2），且y随x的增大而增大，由此得出当x＞0时，y＞2，进而可得解．【详解】根据图示知：一次函数y=kx+b的图象与y轴的交点为（0，2），且y随x的增大而增大；即当x＞0时函数值y的范围是y＞2；因而当不等式kx+b-2＞0时，x的取值范围是x＞0．故选：A．【点睛】本题主要考查的是一次函数与一元一次不等式，在解题时，认真体会一次函数与一元一次不等式（组）之间的内在联系．理解一次函数的增减性是解决本题的关键．9．B解析：B【解析】【分析】直接利用轴对称图形的性质画出对称轴即可．【详解】解：如图所示：平面内不垂直的两条相交直线是轴对称图形，该图形对称轴条数为2条．故选：B．【点睛】此题主要考查了轴对称图形的性质，正确掌握轴对称图形的性质是解题关键．10．C解析：C【解析】【分析】先根据一次函数的图象与系数的关系得出直线y＝ax＋b（a＜0，b＞0）所经过的象限，故可得出结论．【详解】∵直线y＝ax＋b中，a＜0，b＞0，∴直线y＝ax＋b经过一、二、四象限，∴不经过第三象限．故选：C．【点睛】本题考查的是一次函数的图象与系数的关系，即一次函数y＝kx＋b（k≠0）中，当k＜0，b＞0时函数的图象经过一、二、四象限．二、填空题11．【解析】【分析】根据题意得出PA就是P到x轴的距离，即可得出结论．【详解】∵PA⊥x轴，∴PA=|6|=6．故答案为：6．【点睛】本题考查了点到x轴的距离．掌握点到坐标轴的距离是解解析：6【解析】【分析】根据题意得出PA就是P到x轴的距离，即可得出结论．【详解】∵PA⊥x轴，∴PA=|6|=6．故答案为：6．【点睛】本题考查了点到x轴的距离．掌握点到坐标轴的距离是解答本题的关键．12．【解析】【分析】根据等腰三角形的性质和直角三角形两锐角互余得到∠E=∠CPD，再根据对顶角相等得到∠E=∠APE，根据等角对等边得到AE=AP ，即可得到结论．【详解】∵AB=AC，∴∠B解析：20y x =-【解析】【分析】根据等腰三角形的性质和直角三角形两锐角互余得到∠E =∠CPD ，再根据对顶角相等得到∠E =∠APE ，根据等角对等边得到AE =AP ，即可得到结论．【详解】∵AB =AC ，∴∠B =∠C ．∵PD ⊥BC ，∴∠EDB =∠PDC =90°，∴∠B +∠E =90°，∠C +∠CPD =90°，∴∠E =∠CPD ．∵∠APE =∠CPD ，∴∠E =∠APE ，∴AE =AP ．∵AB =AC =10，PC =x ，∴AP =AE =10-x ．∵BE =AB +AE ，∴y =10+10-x =20-x ．故答案为：y =20-x ．【点睛】本题考查了等腰三角形的性质和判定以及直角三角形的性质．解题的关键是得到∠E =∠CPD ．13．x ＜-1．【解析】【分析】由图象可知，在点A 的左侧，函数的图像在的图像的上方，即，所以求出点A 的坐标后结合图象即可写出不等式的解集．【详解】解：∵和的图像相交于点A （m ，3），∴∴∴解析：x ＜-1．【解析】【分析】由图象可知，在点A 的左侧，函数3y x =-的图像在4y ax =+的图像的上方，即34x ax ->+，所以求出点A 的坐标后结合图象即可写出不等式34x ax ->+的解集．【详解】解：∵3y x =-和4y ax =+的图像相交于点A （m ，3），∴33m =-∴1m =-∴交点坐标为A （-1，3），由图象可知，在点A 的左侧，函数3y x =-的图像在4y ax =+的图像的上方，即34x ax ->+∴不等式34x ax ->+的解集为x ＜-1．故答案是：x ＜-1．【点睛】此题主要考查了一次函数与一元一次不等式的关系，用图象法解不等式的关键是找到y 相等时的分界点，观察分界点左右图象的变化趋势，即可求出不等式的解集，重点要掌握利用数形结合的思想．14．3【解析】试题解析：等边三角形有3条对称轴．考点：轴对称图形．解析：3【解析】试题解析：等边三角形有3条对称轴．考点：轴对称图形．15．t=﹣0.006h+20【解析】【分析】根据题意得到每升高1m 气温下降0.006℃，由此写出关系式即可．【详解】∵每升高1000m 气温下降6℃，∴每升高1m 气温下降0.006℃，∴气温解析：t=﹣0.006h+20【解析】【分析】根据题意得到每升高1m 气温下降0.006℃，由此写出关系式即可．【详解】∵每升高1000m 气温下降6℃，∴每升高1m 气温下降0.006℃，∴气温t （℃）与高度h （m ）的函数关系式为t=﹣0.006h+20，故答案为：t=﹣0.006h+20．【点睛】本题考查了函数关系式，正确找出气温与高度之间的关系是解题的关键．16．.【解析】【分析】根据一次函数，，时图象经过第二、三、四象限，可得，，即可求解；【详解】经过第二、三、四象限，∴，，∴，，∴，故答案为.【点睛】本题考查一次函数图象与系数的关系解析：13k <<.【解析】【分析】根据一次函数y kx b =+，k 0<，0b <时图象经过第二、三、四象限，可得220k -<，30k -<，即可求解；【详解】()223y k x k =-+-经过第二、三、四象限，∴220k -<，30k -<，∴1k >，3k <，∴13k <<，故答案为13k <<.【点睛】本题考查一次函数图象与系数的关系；掌握一次函数y kx b =+，k 与b 对函数图象的影响是解题的关键．17．AB=BC【解析】【分析】利用公共边BD以及∠ABD=∠CBD，依据两边及其夹角分别对应相等的两个三角形全等，即可得到需要的条件．【详解】如图，∵在△ABD与△CBD中，∠ABD=∠CBD解析：AB=BC【解析】【分析】利用公共边BD以及∠ABD=∠CBD，依据两边及其夹角分别对应相等的两个三角形全等，即可得到需要的条件．【详解】如图，∵在△ABD与△CBD中，∠ABD=∠CBD，BD=BD，∴添加AB=CB时，可以根据SAS判定△ABD≌△CBD，故答案为AB=CB．【点睛】本题考查了全等三角形的判定．本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．18．12【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半，即可得到答案.【详解】解：∵直角三角形斜边上的中线是6cm，∴则它的斜边是：cm；故答案为：12.【点睛】本题考查了直解析：12【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半，即可得到答案.【详解】解：∵直角三角形斜边上的中线是6cm，⨯=cm；∴则它的斜边是：2612故答案为：12.本题考查了直角三角形的性质，解题的关键是掌握直角三角形斜边上的中线等于斜边的一半.19．【解析】【分析】当分式的值为0时，分式的分子为0，分母不为0，由此求解即可.【详解】解：∵分式的值为零，且∴x ﹣2＝0，解得：x ＝2．故答案为：2．【点睛】本题考查了分式值为0的解析：【解析】【分析】当分式的值为0时，分式的分子为0，分母不为0，由此求解即可.【详解】 解：∵分式2223x x -+的值为零，且2230x +≥ ∴x ﹣2＝0，解得：x ＝2．故答案为：2．【点睛】 本题考查了分式值为0的条件，灵活利用分式值为0的条件是解题的关键.20．11【解析】【分析】根据函数图象可以直接得到AB 、BC 和三角形ADB 的面积，从而可以求得AD 的长，作辅助线CE ⊥AD,从而可得CD 的长，进而求得点P 从开始到停止运动的总路程，本题得以解决.【解析：11【解析】【分析】根据函数图象可以直接得到AB 、BC 和三角形ADB 的面积，从而可以求得AD 的长，作辅助线CE ⊥AD,从而可得CD 的长，进而求得点P 从开始到停止运动的总路程，本题得以解决.解:作CE⊥AD于点E,如下图所示，由图象可知，点P从A到B运动的路程是3，当点P与点B重合时，△PAD的面积是212，由B到C运动的路程为3,∴321 222 AD AB AD⨯⨯==解得，AD=7,又∵BC//AD,∠A=90°，CE⊥AD,∴∠B=90°，∠CEA=90°，∴四边形ABCE是矩形,∴AE=BC=3,∴DE=AD-AE=7-3=4,∴2222345,CD CE DE=+=+=∴点P从开始到停止运动的总路程为: AB+BC+CD=3+3+5=11.故答案为:11【点睛】本题考查了根据函数图象获取信息，解题的关键是明确题意，能从函数图象中找到准确的信息,利用数形结合的思想解答问题.三、解答题21．BC=14.【解析】【分析】根据垂直的性质和勾股定理，先求出线段BD的长度，再求出线段CD的长度，最后求和即可.【详解】解：AD BC⊥，90ADB ADC∴∠=∠=︒∴在Rt ABD∆中，222215129BD AB AD=-=-=∴在Rt ACD∆中，222213125CD AC AD∴=--=9514BC BD CD =+=+=∴【点睛】本题考查了垂直的性质，勾股定理，解决本题的关键是正确理解垂直的性质，熟练掌握勾股定理中三边之间的关系.22．原式=2a a -． 【解析】分析：先根据分式混合运算顺序和运算法则化简原式，再将a 的值代入计算可得． 详解：原式=211(2)(11(1)a a a a a a ---÷---） =22(1)•1(2)a a a a a ---- =2a a -当原式1=． 点睛：本题主要考查分式的混合运算，解题的关键是熟练掌握分式混合运算顺序和运算法则．23．（1）94 ；（2）P(1.5，0) 或 （-4.5,0） 【解析】【分析】（1）分别求直线与x,y 轴交点坐标，再求面积.（2）利用面积，可求得P 点距离A 点的距离，求出P 点坐标.【详解】(1) 由x=0得：y=3，即：B （0，3）．由y=0得：2x+3=0，解得：32x =-∴OA =32,OB =3 . ∴△AOB 的面积: 1393224⨯⨯=. (2) ∵△ABP 的面积是92, OB =3 3922AP ∴= ∴AP =3∴P (1.5，0) 或 （-4.5,0）【点睛】本题考查了一次函数图象上点的坐标特征．24．(1) 53-;(2)①x 不能取-1，y 不能取2；②x=0,y=0；x=1,y=1；x=-3,y=3；x=-2,y=4； 【解析】【分析】（1）设所填数为x,则2x-5=5x ；（2）①假如2x y xy -=，则2,12x y y x x y ==+-，根据分式定义可得；②由①可知21x y x =+或2y x y =-，x≠-1，y≠2，代入尝试可得. 【详解】（1）设所填数为x,则2x-5=5x解得x=53- 所以所填数是53-（2）①假如2x y xy -= 则2,12x y y x x y==+- 所以x≠-1，y≠2即：x 不能取-1，y 不能取2；②存在, 由①可知21x y x =+或2y x y =-，x≠-1，y≠2 所以x,y 可取的整数是：x=0,y=0；x=1,y=1；x=-3,y=3；x=-2,y=4；【点睛】考核知识点：分式的值.理解分式定义是关键.25．（1）1小时，30千米/时；（2）y =24x ﹣24（1≤x ≤3.5）；（3）x =17327【解析】【分析】（1）根据题意结合图象解答即可；（2）求出乙的速度，再利用待定系数法解答即可；（3）根据（2）的结论列方程解答即可．【详解】（1）由图象可知，甲骑手在路上停留1小时，甲从Q 地返回P 地时的骑车速度为：60÷（6﹣4）=30（千米/时），故答案为：1；30．（2）甲从P 地到Q 地的速度为20（千米/时），所以乙的速度为：（6+1.5×20）÷1.5=24（千米/时），60÷24=2.5（小时），设乙从P 地到Q 地骑车过程中（即线段EF ）距P 地的路程y （千米）与时间x （时）的函数关系式为y =24x +b ，则24+b =0，解得b =﹣24．∴乙从P 地到Q 地骑车过程中（即线段EF ）距P 地的路程y （千米）与时间x （时）的函数关系式为y =24x ﹣24（1≤x ≤3.5）．（3）根据题意得，30（x ﹣4）+（24x ﹣24）=60﹣8，解得x =17327． 答：乙两人相遇前，当时间x =17327时，甲，乙两骑手相距8千米． 【点睛】此题考查了一次函数与一元一次方程的综合运用，熟练掌握，即可解题.四、压轴题26．（1）证明见解析；（2）DE ＝BD ＋CE ；（3）B(1，4)【解析】【分析】（1）证明△ABD ≌△CAE ，根据全等三角形的性质得到AE=BD ，AD=CE ，结合图形解答即可；（2）根据三角形内角和定理、平角的定义证明∠ABD=∠CAE ，证明△ABD ≌△CAE ，根据全等三角形的性质得到AE=BD ，AD=CE ，结合图形解答即可；（3）根据△AEC ≌△CFB ，得到CF=AE=3，BF=CE=OE-OC=4，根据坐标与图形性质解答．【详解】（1）证明：∵BD ⊥直线m ，CE ⊥直线m ，∴∠ADB ＝∠CEA ＝90°∵∠BAC ＝90°∴∠BAD ＋∠CAE ＝90°∵∠BAD ＋∠ABD ＝90°∴∠CAE ＝∠ABD∵在△ADB 和△CEA 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△CEA （AAS ）∴AE ＝BD ，AD ＝CE∴DE＝AE＋AD＝BD＋CE即：DE＝BD＋CE（2）解：数量关系：DE＝BD＋CE理由如下：在△ABD中，∠ABD=180°-∠ADB-∠BAD，∵∠CAE=180°-∠BAC-∠BAD，∠BDA=∠AEC，∴∠ABD=∠CAE，在△ABD和△CAE中，ABD CAEBDA AECAB CA∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴△ABD≌△CAE（AAS）∴AE=BD，AD=CE，∴DE=AD+AE=BD+CE；（3）解：如图，作AE⊥x轴于E，BF⊥x轴于F，由（1）可知，△AEC≌△CFB，∴CF=AE=3，BF=CE=OE-OC=4，∴OF=CF-OC=1，∴点B的坐标为B（1，4）．【点睛】本题考查的是全等三角形的判定和性质、坐标与图形性质，掌握全等三角形的判定定理和性质定理是解题的关键．27．（1）左；3；(1-2m)；（2）①（-4，0）；（-1，0）（-3，0）；②当平移后的线段AB 与线段CD 有公共点时，1913n≤≤；③ F9(,2)12m--．【解析】【分析】(1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B点向下平移后，点B和点A的纵坐标相等得到等量关系，可求出m的值，从而求出A、B、C三点坐标；②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设出K点坐标，作KH⊥BM 与H 点，表示出H点坐标，然后利用面积关系ABM AKM BKMS S S∆∆∆=+求出距离；当B'在线段CD 上时，BB'交x 轴于M 点，过B'做B'E⊥OD，利用S△COD = S△OB'C + S△OB'D，求出n的值，从而求出n的取值范围；③通过坐标平移法用m 表示出E 点的坐标，利用D 、E 两点坐标表示出直线DE 的函数关系式，令y=﹣2，求出x 的值即可求出F 点坐标．【详解】解：（1）根据平移规律可得：B 向左平移；m －（m －1）=3，所以平移3个单位；m+4－（3m+3）=1－2m ，所以再向下平移(1-2m )个单位；故答案为：左；3；(1-2m )（2）①点 B 向下移动 3 个单位得：B （m ，m+1）∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A （-4,0）；B （-1,0）；C （-3,0）；②如图 1，过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设 K 点坐标为（-3，a ）M 点坐标为（-1,0）作 KH ⊥BM 与 H 点，H 点坐标为（-1，a ）AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+ ∴222AM BM KC AM KH BM ⨯⨯⨯=+ ∴33323222a ⨯⨯⨯=+ 解得：1a =，∴当线段 AB 向下平移 1 个单位时，线段 AB 和 CD 开始有交点，∴ n ≥ 1，当 B'在线段 CD 上时，如图 2BB'交 x 轴于 M 点，过 B'做 B'E⊥OD,B'M=n-3,B'E=1,OD=5,OC=3∵ S△COD = S△OB'C + S△OB'D∴'' 222 CO OD CO B M OD B E ⨯⨯⨯=+∴353(3)51 222n⨯⨯-⨯=+解得：193n=，综上所述，当平移后的线段 AB 与线段 CD 有公共点时，1913n≤≤．③∵A（m−3，3m+3）， B（m，m+4） D（0，−5）且AD 沿直线 AB 方向平移得到线段BE，∴E点横坐标为：3E点纵坐标为：﹣5+m+4－（3m+3）=﹣4－2m∴E（3，﹣4－2m），设DE：y=kx+b，把D（0，﹣5），E（3，﹣4－2m）代入y=kx+b∴3k+b=42mb=5⎧⎨⎩﹣－﹣∴1-2mk=3b=-5⎧⎪⎨⎪⎩，∴y=12mx53－－，把y=﹣2代入解析式得：﹣2=12mx53－－，x=912m－，∴F9(,2) 12m--．【点睛】本题考查平面直角坐标系中点的平移计算及一次函数解析式求法，解题关键在于理解掌握平面直角坐标系中点平移计算方法以及用待定系数法求函数解析式方法的应用．28．（1）8;（2）145°;（3）详见解析．【解析】【分析】（1）作AD⊥ x轴于D,BE⊥x轴于E,由点A,B的坐标可得出AD=OD=2,BE=EO=4,DE=6,由面积公式可求出答案;（2）作CH∥x轴,如图2,由平行线的性质可得出∠AOG=∠ACH,∠DEC=∠HCE,求出∠DEC+∠AOG=∠ACB=90°,可求出∠DEC=35°,则可得出答案;（3）证得∠NEC=∠HEC,则∠NEF=180°-∠NEH=180°-2∠HEC,可得出结论．【详解】解：（1）作AD⊥x轴于D,BE⊥x轴于E,如图1,∵A（﹣2,2）、B（4,4）,∴AD＝OD＝2,BE＝OE＝4,DE＝6,∴S△ABC＝S梯形ABED﹣S△AOD﹣S△AOE＝12×（2+4）×6﹣12×2×2﹣12×4×4＝8;（2）作CH // x轴,如图2,∵D（0,﹣4）,M（4,﹣4）,∴DM // x轴,∴CH // OG // DM,∴∠AOG＝∠ACH,∠DEC＝∠HCE,∴∠DEC+∠AOG＝∠ACB＝90°,∴∠DEC＝90°﹣55°＝35°,∴∠CEF＝180°﹣∠DEC＝145°;（3）证明：由（2）得∠AOG+∠HEC＝∠ACB＝90°,而∠HEC+∠CEF＝180°,∠NEC+∠CEF＝180°,∴∠NEC＝∠HEC,∴∠NEF＝180°﹣∠NEH＝180°﹣2∠HEC,∵∠HEC＝90°﹣∠AOG,∴∠NEF＝180°﹣2（90°﹣∠AOG）＝2∠AOG．【点睛】本题是三角形综合题,考查了坐标与图形的性质,三角形的面积,平行线的性质,三角形内角和定理,熟练掌握平行的性质及三角形内角和定理是解题的关键．29．（1)相等，证明见解析；（2)证明见解析；（3)证明见解析．【解析】【分析】（1）先证明△ACD≌△CBE，再由全等三角形的性质即可证得CD=BE；（2）先证明△BCD≌△ABE，得到∠BCD=∠ABE，求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC，∠CQE=180°-∠DQB，即可解答；（3）如图3，过点D作DG∥BC交AC于点G，根据等边三角形的三边相等，可以证得AD=DG=CE；进而证明△DGF和△ECF全等，最后根据全等三角形的性质即可证明．【详解】（1）解：CD和BE始终相等，理由如下：如图1，AB=BC=CA，两只蜗牛速度相同，且同时出发，∴CE=AD，∠A=∠BCE=60°在△ACD与△CBE中，AC=CB，∠A=∠BCE，AD=CE∴△ACD≌△CBE（SAS），∴CD=BE，即CD和BE始终相等；（2）证明：根据题意得：CE=AD，∵AB=AC，∴AE=BD，∴△ABC是等边三角形，∴AB=BC，∠BAC=∠ACB=60°，∵∠EAB+∠ABC=180°，∠DBC+∠ABC=180°，∴∠EAB=∠DBC，在△BCD和△ABE中，BC=AB，∠DBC=∠EAB，BD=AE∴△BCD≌△ABE（SAS），∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°，∴∠CQE=180°-∠DQB=60°，即CQE=60°；（3）解：爬行过程中，DF始终等于EF是正确的，理由如下：如图，过点D作DG∥BC交AC于点G，∴∠ADG=∠B=∠AGD=60°，∠GDF=∠E，∴△ADG为等边三角形，∴AD=DG=CE，在△DGF和△ECF中，∠GFD=∠CFE，∠GDF=∠E，DG=EC∴△DGF≌△EDF（AAS），∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质；题弄懂题中所给的信息，再根据所提供的思路寻找证明条件是解答本题的关键．30．（1）y＝﹣2x+6；（2）点P（m﹣6，2m﹣6）；（3）y＝﹣x+3 2【解析】【分析】（1）先求出点A，点B坐标，由等腰三角形的性质可求点C坐标，由待定系数法可求直线BC的解析式；（2）证明△PGA≌△QHC（AAS），则PG＝HQ＝2m﹣6，故点P的纵坐标为：2m﹣6，而点P在直线AB上，即可求解；（3）由“SSS”可证△APM≌△CQM，△ABM≌△CBM，可得∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∠BAM＝∠BCM，由“AAS”可证△APE≌△MAO，可得AE＝OM，PE＝AO＝3，可求m的值，进而可得点P，点Q的坐标，即可求直线PQ的解析式．【详解】（1）∵直线y＝2x+6与x轴交于点A，与y轴交于点B，∴点B(0，6)，点A(﹣3，0)，∴AO＝3，BO＝6，∵AB＝BC，BO⊥AC，∴AO＝CO＝3，∴点C(3，0)，设直线BC解析式为：y＝kx+b，则036k bb=+⎧⎨=⎩，解得：26kb=-⎧⎨=⎩，∴直线BC解析式为：y＝﹣2x+6；（2）如图1，过点P作PG⊥AC于点G，过点Q作HQ⊥AC于点H，∵点Q横坐标为m，∴点Q(m，﹣2m+6)，∵AB＝CB，∴∠BAC＝∠BCA＝∠HCQ，又∵∠PGA＝∠QHC＝90°，AP＝CQ，∴△PGA≌△QHC（AAS），∴PG＝HQ＝2m﹣6，∴点P的纵坐标为：2m﹣6，∵直线AB的表达式为：y＝2x+6，∴2m﹣6＝2x+6，解得：x＝m﹣6，∴点P(m﹣6，2m﹣6)；（3）如图2，连接AM，CM，过点P作PE⊥AC于点E，∵AB＝BC，BO⊥AC，∴BO是AC的垂直平分线，∴AM＝CM，且AP＝CQ，PM＝MQ，∴△APM≌△CQM（SSS）∴∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∵AM＝CM，AB＝BC，BM＝BM，∴△ABM≌△CBM（SSS）∴∠BAM＝∠BCM，∴∠BCM＝∠MCQ，且∠BCM+∠MCQ＝180°，∴∠BCM＝∠MCQ＝∠PAM＝90°，且∠APM＝45°，∴∠APM＝∠AMP＝45°，∴AP＝AM，∵∠PAO+∠MAO＝90°，∠MAO+∠AMO＝90°，∴∠PAO＝∠AMO，且∠PEA＝∠AOM＝90°，AM＝AP，∴△APE≌△MAO（AAS）∴AE＝OM，PE＝AO＝3，∴2m﹣6＝3，∴m＝92，∴Q(92，﹣3)，P(﹣32，3)，设直线PQ的解析式为：y＝ax+c，∴932332a ca c⎧-=+⎪⎪⎨⎪=-+⎪⎩，解得：132ac=-⎧⎪⎨=⎪⎩，∴直线PQ的解析式为：y＝﹣x+32．【点睛】本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质定理以及一次函数的图象和性质，添加辅助线，构造全等三角形，是解题的关键．。

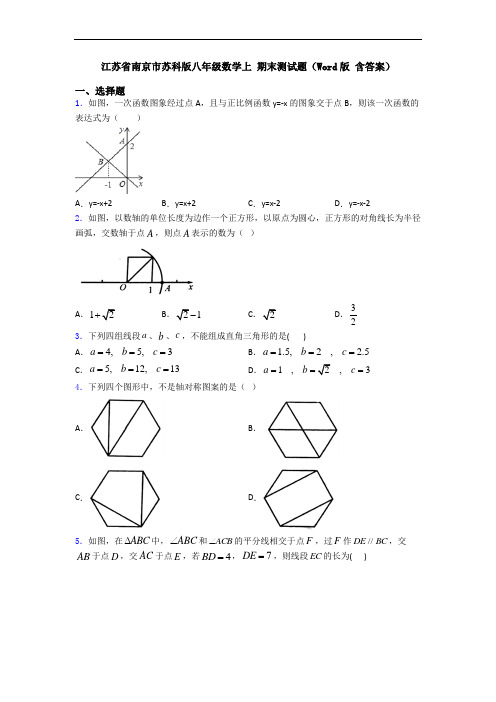
江苏省南京市苏科版八年级数学上 期末测试题（Word 版 含答案）一、选择题1．如图，一次函数图象经过点A ，且与正比例函数y=-x 的图象交于点B ，则该一次函数的表达式为（ ）A ．y=-x+2B ．y=x+2C ．y=x-2D ．y=-x-22．如图，以数轴的单位长度为边作一个正方形，以原点为圆心，正方形的对角线长为半径画弧，交数轴于点A ，则点A 表示的数为（ ）A ．12+B ．21-C ．2D ．323．下列四组线段a 、b 、c ，不能组成直角三角形的是( )A ．4,5,3a b c === B ． 1.5,2, 2.5a b c === C ．5,12,13a b c === D ．1,2,3a b c ===4．下列四个图形中，不是轴对称图案的是（ ）A ．B ．C ．D ．5．如图，在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点F ，过F 作//DE BC ，交AB 于点D ，交AC 于点E ，若4BD =，7DE =，则线段EC 的长为( )A．3 B．4 C．3.5 D．2 6．下列无理数中，在﹣1与2之间的是（）A．﹣3B．﹣2C．2D．5 7． 4的平方根是( )A．2 B．±2 C．16 D．±168．如图，在平面直角坐标系xOy中，直线y＝﹣43x+4与x轴、y轴分别交于点A、B，M是y轴上的点（不与点B重合），若将△ABM沿直线AM翻折，点B恰好落在x轴正半轴上，则点M的坐标为（）A．（0，﹣4 ）B．（0，﹣5 ）C．（0，﹣6 ）D．（0，﹣7 ）9．如图：若△ABE≌△ACD，且AB＝6，AE＝2，则EC的长为（）A．2 B．3 C．4 D．610．某篮球运动员的身高为1.96cm，用四舍五人法将1.96精确到0.1的近似值为（）A．2 B．1.9 C．2.0 D．1.90二、填空题11．如图，在平面直角坐标系中，点P(﹣1，a)在直线y＝2x+2与直线y＝2x+4之间，则a 的取值范围是_____．12．如图，直线l1：y＝﹣12x+m与x轴交于点A，直线l2：y＝2x+n与y轴交于点B，与直线l1交于点P（2，2），则△PAB的面积为_____．13．4的平方根是．14．点(2,1)P关于x轴对称的点P'的坐标是__________．15．已知直角三角形的两边长分别为3、4．则第三边长为________．16．在平面直角坐标系内，一次函数y＝k1x+b1与y＝k2x+b2的图象如图所示，则关于x，y的方程组1122y k x by k x b-=⎧⎨-=⎩的解是________．17．当直线()223y k x k=-+-经过第二、三、四象限时，则k的取值范围是_____．18．已知一次函数1y kx b=+与2y mx n=+的函数图像如图所示，则关于,x y的二元一次方程组0,kx y bmx y n-+=⎧⎨-+=⎩的解是______．19．化简：23(3)2716--+=_____．20．等腰三角形的两边长分别为5cm 和2cm ，则它的周长为_____．三、解答题21．如图，Rt ABC ∆中，90ACB ∠=︒.（1）尺规作图（保留作图痕迹，不写作法与证明）：①作B 的平分线BD 交边AC 于点D ;②过点D 作DE AB ⊥于点E ；（2）在（1）所画图中，若3CD =，8AC =，则AB 长为________________. 22．定义：若两个分式的和为n （n 为正整数），则称这两个分式互为“n 阶分式”，例如分式31x +与31x x +互为“3阶分式”. （1）分式1032x x +与 互为“5阶分式”； （2）设正数,x y 互为倒数，求证：分式22x x y +与22y y x +互为“2阶分式”； （3）若分式24a a b +与222b a b+互为“1阶分式”（其中,a b 为正数），求ab 的值. 23．如图，ABC ∆中，90BAC ∠=，8AC cm =，DE 是BC 边上的垂直平分线，ABD ∆的周长为14cm ，求BC 的长.24．解方程：（1）4x 2﹣8＝0；（2）（x ﹣2）3＝﹣1．25．如图，四边形ABCD 中，CD ∥AB ，E 是AD 中点，CE 交BA 延长线于点F ．（1）试说明：CD ＝AF ；（2）若BC ＝BF ，试说明：BE ⊥CF ．四、压轴题26．如图，直线2y x m =-+交x 轴于点A ，直线122y x =+交x 轴于点B ，并且这两条直线相交于y 轴上一点C ，CD 平分ACB ∠交x 轴于点D ．（1）求ABC 的面积．（2）判断ABC 的形状，并说明理由．（3）点E 是直线BC 上一点，CDE △是直角三角形，求点E 的坐标．27．如图，在平面直角坐标系中，直线y ＝2x ＋4与x 轴交于点A ，与y 轴交于点B ，过点B 的另一条直线交x 轴正半轴于点C ，且OC ＝3．图1 图2（1）求直线BC的解析式；（2）如图1，若M为线段BC上一点，且满足S△AMB＝S△AOB，请求出点M的坐标；（3）如图2，设点F为线段AB中点，点G为y轴上一动点，连接FG，以FG为边向FG右侧作正方形FGQP，在G点的运动过程中，当顶点Q落在直线BC上时，求点G的坐标；28．直角三角形ABC中，∠ACB=90°，直线l过点C．（1）当AC=BC时，如图①，分别过点A、B作AD⊥l于点D，BE⊥l于点E．求证：△ACD≌△CBE．（2）当AC=8，BC=6时，如图②，点B与点F关于直线l对称，连接BF，CF，动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动，同时动点N从点F出发，以每秒3个单位的速度沿F→C→B→C→F向终点F运动，点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D，过点N作NE⊥l于点E，设运动时间为t秒．①CM=，当N在F→C路径上时，CN=．（用含t的代数式表示）②直接写出当△MDC与△CEN全等时t的值．29．如图1中的三种情况所示，对于平面内的点M，点N，点P，如果将线段PM绕点P 顺时针旋转90°能得到线段PN，就称点N是点M关于点P的“正矩点”．（1）在如图2所示的平面直角坐标系xOy 中，已知(3,1),(1,3),(1,3)S P Q ---，(2,4)M -．①在点P ，点Q 中，___________是点S 关于原点O 的“正矩点”；②在S ，P ，Q ，M 这四点中选择合适的三点，使得这三点满足：点_________是点___________关于点___________的“正矩点”，写出一种情况即可； （2）在平面直角坐标系xOy 中，直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，点A 关于点B 的“正矩点”记为点C ，坐标为(,)C C C x y ．①当点A 在x 轴的正半轴上且OA 小于3时，求点C 的横坐标C x 的值；②若点C 的纵坐标C y 满足12C y -<≤，直接写出相应的k 的取值范围．30．如图，在平面直角坐标系中，直线AB 经过点A 332)和B 3，0)，且与y 轴交于点D ，直线OC 与AB 交于点C ，且点C 3．(1)求直线AB 的解析式；(2)连接OA ，试判断△AOD 的形状；(3)动点P 从点C 出发沿线段CO 以每秒1个单位长度的速度向终点O 运动，运动时间为t 秒，同时动点Q 从点O 出发沿y 轴的正半轴以相同的速度运动，当点Q 到达点D 时，P ，Q 同时停止运动．设PQ 与OA 交于点M ，当t 为何值时，△OPM 为等腰三角形？求出所有满足条件的t 值．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】【详解】解：设一次函数的解析式y=kx+b（k≠0），∵一次函数图象经过点A，且与正比例函数y=-x的图象交于点B，∴在直线y=-x中，令x=-1，解得：y=1，则B的坐标是（-1，1）．把A（0，2），B（-1，1）的坐标代入一次函数的解析式y=kx+b得：2{1bk b=-+=，解得2{1bk==，该一次函数的表达式为y=x+2．故选B．2．C解析：C【解析】【分析】先根据勾股定理求出正方形对角线的长，然后根据实数与数轴的关系解答即可.【详解】2211+2，∴点A2.故选C.【点睛】本题考查了勾股定理，以及实数与数轴，主要是数轴上无理数的作法，需熟练掌握．3．D解析：D【解析】【分析】根据勾股定理逆定理，即若三角形中两边到的平方和等于第三边的平方，那么这个三角形是直角三角形，对每项进行计算判断即可.【详解】解：A.2222223491625,525,a b c +=+==+=,B.222221.52 2.254 6.25,2.5 6.25,a b c +=+==+=,C.22222251225144169,13169,a b c +=+==+=,222222123,39,.1D a b c +=+==+≠.【点睛】本题考查了勾股定理的逆定理，解决本题的关键是熟练掌握勾股定理逆定理，正确计算出每项的结果.4．A解析：A【解析】【分析】根据轴对称图形的定义逐项识别即可，一个图形的一部分，以某条直线为对称轴，经过轴对称能与图形的另一部分重合，这样的图形叫做轴对称图形.【详解】A 不是轴对称图形，B 、C 、D 都是轴对称图形.故选A.【点睛】本题考查了轴对称图形的识别，熟练掌握轴对称图形的定义是解答本题的关键.5．A解析：A【解析】【分析】根据△ABC 中，∠ABC 和∠ACB 的平分线相交于点F.求证∠DBF=∠FBC,∠ECF=∠BCF,再利用两直线平行内错角相等，求证出∠DFB=∠DBF ，∠CFE=∠BCF,即BD=DF,FE=CE ，然后利用等量代换即可求出线段CE 的长.【详解】解：∵∠ABC 和∠ACB 的平分线相交于点F,∴∠DBF=∠FBC ，∠ECF=∠BCF,∵DF//BC,交AB 于点D,交AC 于点E.∴∠DFB=∠DBF ，∠CFE=∠BCF ，∴BD=DF=4，FE=CE,∴CE=DE-DF=7-4=3.故选:A.【点睛】本题考查了平行线的性质和角平分线的性质，解决本题的关键是正确理解题意，熟练掌握平行线和角平分线的性质，能够找到相等的量.6．C解析：C【解析】试题分析：A1，故错误；B＜﹣1，故错误；C．﹣1<2，故正确；2，故错误；故选C．【考点】估算无理数的大小．7．B解析：B【解析】【分析】根据平方根的意义求解即可，正数a有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.【详解】∵(±2)2=4,∴4的平方根是±2,即2±.故选B.【点睛】本题考查了平方根的意义，如果个一个数x的平方等于a，即x2=a,那么这个数x叫做a的平方根.8．C解析：C【解析】【分析】设沿直线AM将△ABM折叠，点B正好落在x轴上的C点，则有AB＝AC，而AB的长度根据已知可以求出，所以C点的坐标由此求出；又由于折叠得到CM＝BM，在直角△CMO中根据勾股定理可以求出OM，也就求出M的坐标．【详解】设沿直线AM将△ABM折叠，点B正好落在x轴上的C点，∵直线y＝﹣43x+4与x轴、y轴分别交于点A、B，∴A（3，0），B（0，4），∴AB5，设OM＝m，由折叠知，AC＝AB＝5，CM＝BM＝OB+OM＝4+m，∴OC＝8，CM＝4+m，根据勾股定理得，64+m2＝（4+m）2，解得：m＝6，∴M（0，﹣6），故选：C．【点睛】本题主要考查一次函数的图象，图形折叠的性质以及勾股定理，通过勾股定理，列方程，是解题的关键．9．C解析：C【解析】【分析】根据全等三角形的对应边相等解答即可．【详解】解：∵△ABE≌△ACF，∴AC＝AB＝6，∴EC＝AC﹣AE＝6-2=4，故选：C．【点睛】本题考查的知识点是全等三角形的性质，熟记性质内容是解此题的关键．10．C解析：C【解析】【分析】根据四舍五入法可以将1.96精确到0.1，本题得以解决．【详解】1.96≈2.0（精确到0.1），故选：C．此题主要考查有理数的近似值，熟练掌握，即可解题.二、填空题11．【解析】【分析】计算出当P 在直线上时a 的值，再计算出当P 在直线上时a 的值，即可得答案．【详解】解：当P 在直线上时，，当P 在直线上时，，则．故答案为【点睛】此题主要考查了一次函数与解析：0a 2<<【解析】【分析】计算出当P 在直线y 2x 2=+上时a 的值，再计算出当P 在直线y 2x 4=+上时a 的值，即可得答案．【详解】解：当P 在直线y 2x 2=+上时，()a 212220=⨯-+=-+=，当P 在直线y 2x 4=+上时，()a 214242=⨯-+=-+=，则0a 2<<．故答案为0a 2<<【点睛】此题主要考查了一次函数与一元一次不等式，关键是掌握函数图象经过的点，必能使解析式左右相等．12．【解析】【分析】把点P （2，2）分别代入y ＝﹣x+m 和y ＝2x+n ，求得m ＝3，n ＝﹣2，解方程得到A （6，0），B （0，﹣2），根据三角形的面积公式即可得到结论．【详解】解：把点P （2，解析：【解析】把点P （2，2）分别代入y ＝﹣12x+m 和y ＝2x+n ，求得m ＝3，n ＝﹣2，解方程得到A （6，0），B （0，﹣2），根据三角形的面积公式即可得到结论．【详解】 解：把点P （2，2）分别代入y ＝﹣12x+m 和y ＝2x+n ， 得，m ＝3，n ＝﹣2，∴直线l 1：y ＝﹣12x+3，直线l 2：y ＝2x ﹣2， 对于y ＝﹣12x+3，令y ＝0，得，x ＝6， 对于y ＝2x ﹣2，令x ＝0，得，y ＝﹣2，∴A （6，0），B （0，﹣2），∵直线l 1：y ＝﹣12x+3与y 轴的交点为（0，3）， ∴△PAB 的面积＝12×5×6﹣12×5×2＝10， 故答案为：10．【点睛】本题考查了两直线相交与平行问题，三角形的面积的计算，正确的识别图形是解题的关键． 13．±2．【解析】试题分析：∵，∴4的平方根是±2．故答案为±2．考点：平方根．解析：±2．【解析】试题分析：∵2(2)4±=，∴4的平方根是±2．故答案为±2．考点：平方根．14．（2，-1）【解析】【分析】关于轴对称的点坐标（横坐标不变,纵坐标变为相反数）【详解】点关于轴对称的点的坐标是（2，-1）故答案为：（2，-1）考核知识点：用坐标表示轴对称.解析：（2，-1）【解析】【分析】关于x轴对称的点坐标（横坐标不变,纵坐标变为相反数）【详解】点(2,1)P关于x轴对称的点P'的坐标是（2，-1）故答案为：（2，-1）【点睛】考核知识点：用坐标表示轴对称. 理解：关于x轴对称的点的坐标的特点是：横坐标不变，纵坐标互为相反数；15．5或【解析】试题分析：已知直角三角形两边的长，但没有明确是直角边还是斜边，因此分两种情况讨论：①长为3的边是直角边，长为4的边是斜边时：第三边的长为：；②长为3、4的边都是直角边时：第三边的解析：5【解析】试题分析：已知直角三角形两边的长，但没有明确是直角边还是斜边，因此分两种情况讨论：①长为3的边是直角边，长为4=②长为3、45；∴或5．考点：1．勾股定理；2．分类思想的应用．16．．【解析】【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解．【详解】∵一次函数y＝k1x+b1与y＝k2x+b2的图象的交点坐标为（2，1），∴关于x，y的方程组的解是．解析：21 xy=⎧⎨=⎩．【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解．【详解】∵一次函数y ＝k 1x +b 1与y ＝k 2x +b 2的图象的交点坐标为（2，1），∴关于x ，y 的方程组1122y k x b y k x b -=⎧⎨-=⎩的解是21x y =⎧⎨=⎩． 故答案为21x y =⎧⎨=⎩． 【点睛】本题考查了一次函数与二元一次方程（组）：方程组的解就是两个相应的一次函数图象的交点坐标．17．.【解析】【分析】根据一次函数，，时图象经过第二、三、四象限，可得，，即可求解；【详解】经过第二、三、四象限，∴，，∴，，∴，故答案为.【点睛】本题考查一次函数图象与系数的关系解析：13k <<.【解析】【分析】根据一次函数y kx b =+，k 0<，0b <时图象经过第二、三、四象限，可得220k -<，30k -<，即可求解；【详解】()223y k x k =-+-经过第二、三、四象限，∴220k -<，30k -<，∴1k >，3k <，∴13k <<，故答案为13k <<.【点睛】本题考查一次函数图象与系数的关系；掌握一次函数y kx b =+，k 与b 对函数图象的影响是解题的关键．18．【解析】【分析】根据函数图象交点坐标为两函数解析式组成的方程组的解，从而可得答案．【详解】解：∵一次函数和一次函数的图象交点的坐标为∴方程组的解是： ．故答案为： ．【点睛】本题解析：12x y =-⎧⎨=⎩【解析】【分析】根据函数图象交点坐标为两函数解析式组成的方程组的解，从而可得答案．【详解】解：∵一次函数1y kx b =+和一次函数2y mx n =+的图象交点的坐标为()1,2,-∴方程组00kx y b mx y n -+=⎧⎨-+=⎩的解是：12x y =-⎧⎨=⎩． 故答案为： 12x y =-⎧⎨=⎩． 【点睛】本题主要考查了函数解析式与图象的关系，满足解析式的点就在函数的图象上，在函数的图象上的点，就一定满足函数解析式．函数图象交点坐标为两函数解析式组成的方程组的解．掌握以上知识是解题的关键．19．4【解析】【分析】根据算数平方根和立方根的运算法则计算即可．【详解】解：故答案为4．【点睛】本题主要考查了算数平方根和立方根的计算，熟记运算法则是解题的关键．解析：4【解析】【分析】根据算数平方根和立方根的运算法则计算即可．【详解】=-+=3344故答案为4．【点睛】本题主要考查了算数平方根和立方根的计算，熟记运算法则是解题的关键．20．12cm．【解析】【分析】题目给出等腰三角形有两条边长为5cm和2cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】解：①5cm为腰，2解析：12cm．【解析】【分析】题目给出等腰三角形有两条边长为5cm和2cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】解：①5cm为腰，2cm为底，此时周长为12cm；②5cm为底，2cm为腰，则两边和小于第三边无法构成三角形，故舍去．所以其周长是12cm．故答案为12cm．【点睛】此题主要考查等腰三角形的周长，解题的关键熟知等腰三角形的性质及三角形的构成条件.三、解答题21．（1）①详见解析；②详见解析；（2）10.【解析】【分析】（1）①按角的平分线的作法步骤作图即可；②按垂线的作法步骤作图即可；（2）根据角平分线的性质得到DE=CD．在△AED中利用勾股定理得到AE的长．设AB=x，则BE=AB-AE=x-4．证明Rt△BDC≌Rt△BDE，得到BC=DE=x-4．在Rt△ABC中，利用勾股定理列方程即可得到结论．【详解】（1）①如图，BD 就是所要求作的图形．②如图，DE 就是所要求作的图形．（2）∵∠C =90°，DE ⊥AB ，BD 平分∠ABC ，∴DE =CD =3．∵AC =8，∴AD =AC -DC =8-3=5，∴AE 222253AD DE -=-．设AB =x ，则BE =AB -AE =x -4．在Rt △BDC 和Rt △BDE 中，∵BD =BD ，DC =DE ，∴Rt △BDC ≌Rt △BDE ，∴BC =DE =x -4．在Rt △ACB 中，∵222AC BC AB +=，∴2228(4)x x +-=，解得：x =10．∴AB =10．【点睛】本题考查了基本作图和角平分线的性质以及勾股定理．掌握角平分线的性质是解答本题的关键．22．（1）1532x +；（2）详见解析；（3）12 【解析】【分析】（1）根据分式的加法，设所求分式为A ，然后进行通分求解即可；（2）根据题意首先利用倒数关系，将x ，y 进行消元，然后通过分式的加法化简即可得解； （3）根据1阶分式的要求对两者相加进行分式加法化简，通过通分化简即可得解.【详解】（1）依题意，所求分式为A ，即：10+532x A x =+， ∴1015101015532323232x x x A x x x x+=-=-=++++； （2）∵正数,x y 互为倒数∴1xy =，即1x y= ∴33223332212222222(1)211111x y y y y y x y y x y y y y y y y++=+=+==+++++++ ∴分式22x x y +与22y y x +互为“2阶分式”； （3）由题意得222142a b a b a b +=++，等式两边同乘22(4)(2)a b a b ++ 化简得： 2222(2)2(4)(2)(4)a a b b a b a b a b +++=++即：32232848ab b a b b +=+∴22420a b ab -=，即2(21)0ab ab -= ∴12ab =或0 ∵,a b 为正数 ∴12ab =. 【点睛】 本题主要考查了分式的加减，熟练掌握分式的通分约分运算知识是解决此类问题的关键. 23．10BC =【解析】【分析】由垂直平分线的性质得到BD=CD ，则得到AB+AC=14，然后求出AB ，由勾股定理即可求出BC 的长度.【详解】解：∵DE 是BC 边上的垂直平分线，∴BD=CD ，∵ABD ∆的周长为14cm ，∴AB+AD+DB=14，∴AB+AD+DC=AB+AC=14，∵8AC =，∴1486AB =-=，在Rt △ABC 中，由勾股定理，得10BC =.【点睛】本题考查了垂直平分线的性质定理，勾股定理，解题的关键是掌握由垂直平分线的性质定理，求出AB 的长度.x=24．（1）=x（2）1【解析】【分析】（1）方程整理后，利用平方根定义开方即可求出解；（2）方程利用立方根定义开立方即可求出解．【详解】解：（1）4x2﹣8＝0，移项得：4x2﹣8＝0，即x2＝2，开方得：=x；（2）（x﹣2）3＝﹣1，开立方得：x﹣2＝﹣1，解得：x＝1．【点睛】本题主要考查一元二次方程的解法及立方根，熟练掌握运算法则是解题的关键．25．（1）证明见解析；（2）证明见解析【解析】【分析】（1）由CD∥AB，可得∠CDE＝∠FAE，而E是AD中点，因此有DE＝AE，再有∠AEF＝∠DEC，所以利用ASA可证△CDE≌△FAE，再利用全等三角形的性质，可得CD＝AF；（2）先利用（1）中的三角形的全等，可得CE＝FE，再根据BC＝BF，利用等腰三角形三线合一的性质，可证BE⊥CF．【详解】证明：（1）∵CD∥AB，∴∠CDE＝∠FAE，又∵E是AD中点，∴DE＝AE，又∵∠AEF＝∠DEC，∴△CDE≌△FAE，∴CD＝AF；（2）∵BC＝BF，∴△BCF是等腰三角形，又∵△CDE≌△FAE，∴CE＝FE，∴BE⊥CF（等腰三角形底边上的中线与底边上的高相互重合）．【点睛】本题考查了全等三角形的判定与性质及等腰三角形的性质；证明△CDE ≌△FAE 是正确解答本题的关键．四、压轴题26．（1）5；（2）直角三角形，理由见解析；（3）44,33E ⎛⎫-⎪⎝⎭或82,33E ⎛⎫- ⎪⎝⎭ 【解析】【分析】（1）先求出直线122y x =+与x 轴的交点B 的坐标和与y 轴的交点C 的坐标，把点C 代入直线2y x m =-+，求出m 的值，再求它与x 轴的交点A 的坐标，ABC 的面积用AB 乘OC 除以2得到；（2）用勾股定理求出BC 的平方，AC 的平方，再根据AB 的平方，用勾股定理的逆定理证明ABC 是直角三角形；（3）先根据角平分线求出D 的坐标，再去分两种情况构造全等三角形，利用全等三角形的性质求出对应的边长，从而得到点E 的坐标．【详解】解：（1）令0x =，则10222y =⨯+=， ∴()0,2C ，令0y =，则1202x +=，解得4x =-， ∴()4,0B -，将()0,2C 代入2y x m =-+，得2m =，∴22y x =-+，令0y =，则220x -+=，解得1x =，∴1,0A ，∴5AB =，2OC =，∴152ABC S AB OC =⋅=△；（2）根据勾股定理，222224220BC BO OC =+=+=，22222125AC AO OC =+=+=，且22525AB ==，∴222AB BC AC =+，则ABC 是直角三角形；（3）∵CD 平分ACB ∠， ∴12AD AC BD BC ==， ∴1533AD AB ==， ∴23OD AD OA =-=， ∴2,03D ⎛⎫- ⎪⎝⎭①如图，CED ∠是直角，过点E 作EN x ⊥轴于点N ，过点C 作CM EN ⊥于点M ， 由（2）知，90ACB ∠=︒，∵CD 平分ACB ∠，∴45ECD ∠=︒，∴CDE △是等腰直角三角形，∴CE DE =，∵90NED MEC ∠+∠=︒，90NED NDE ∠+∠=︒，∴MEC NDE ∠=∠，在DNE △和EMC △中，NDE MEC DNE EMC DE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()DNE EMC AAS ≅，设DN EM x ==，EN CM y ==，根据图象列式：DO DN CM EN EM CO +=⎧⎨+=⎩，即232x y x y ⎧+=⎪⎨⎪+=⎩，解得2343x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴43EN CM ==， ∴44,33E ⎛⎫- ⎪⎝⎭；②如图，CDE ∠是直角，过点E 作EG x ⊥轴于点G ，同理CDE △是等腰直角三角形，且可以证得()CDO DEG AAS ≅，∴2DG CO ==，23EG DO ==， ∴28233GO GD DO =+=+=， ∴82,33E ⎛⎫- ⎪⎝⎭，综上：44,33E ⎛⎫-⎪⎝⎭，82,33E ⎛⎫- ⎪⎝⎭． 【点睛】 本题考查一次函数综合，解题的关键是掌握一次函数解析式的求解，与坐标轴交点的求解，图象围成的三角形面积的求解，还涉及勾股定理、角平分线的性质、全等三角形等几何知识，需要运用数形结合的思想去求解．27．（1）443y x =-+；（2）612(,)55M ；（3）23(0,)7G 或(0,-1)G 【解析】【分析】（1）求出点B ，C 坐标，再利用待定系数法即可解决问题；（2）结合图形，由S △AMB ＝S △AOB 分析出直线OM 平行于直线AB ，再利用两直线相交建立方程组求得交点M 的坐标；（3）分两种情形：①当n＞2时，如图2-1中，点Q落在BC上时，过G作直线平行于x 轴，过点F，Q作该直线的垂线，垂足分别为M，N．求出Q（n-2，n-1）．②当n＜2时，如图2-2中，同法可得Q（2-n，n+1），代入直线BC的解析式解方程即可解决问题．【详解】解：（1）∵直线y=2x+4与x轴交于点A，与y轴交于点B，∴A（-2，0），B（0，4），，又∵OC=3，∴C（3，0），设直线BC的解析式为y=kx+b，将B、C的坐标代入得：304k bb+=⎧⎨=⎩，解得：434kb⎧=-⎪⎨⎪=⎩，∴直线BC的解析式为443y x=-+；（2）连接OM，∵S△AMB＝S△AOB，∴直线OM平行于直线AB，故设直线OM解析式为：2y x=,将直线OM的解析式与直线BC的解析式联立得方程组2443y xy x=⎧⎪⎨=-+⎪⎩，解得：65125xy⎧=⎪⎪⎨⎪=⎪⎩故点612(,)55M；（3）∵FA=FB，A（-2，0），B（0，4），∴F （-1，2），设G （0，n ），①当n ＞2时，如图2-1中，点Q 落在BC 上时，过G 作直线平行于x 轴，过点F ，Q 作该直线的垂线，垂足分别为M ，N ．∵四边形FGQP 是正方形，易证△FMG ≌△GNQ ，∴MG=NQ=1，FM=GN=n-2，∴Q （n-2，n-1），∵点Q 在直线443y x =-+上， ∴41(2)43n n -=--+， ∴23=7n , ∴23(0,)7G ． ②当n ＜2时，如图2-2中，同法可得Q （2-n ，n+1），∵点Q 在直线443y x =-+上， ∴4+1(2)43n n =--+， ∴n=-1，∴(0,-1)G ．综上所述，满足条件的点G 坐标为23(0,)7G 或(0,-1)G 【点睛】 本题属于一次函数综合题，考查了待定系数法，三角形的面积，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．28．（1）证明见解析；（2）①CM =8t -，CN =63t -；②t =3.5或5或6.5．【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB ，利用AAS 定理证明△ACD ≌△CBE ；（2）①由折叠的性质可得出答案；②动点N 沿F→C 路径运动，点N 沿C→B 路径运动，点N 沿B→C 路径运动，点N 沿C→F 路径运动四种情况，根据全等三角形的判定定理列式计算．【详解】（1）∵AD ⊥直线l ，BE ⊥直线l ，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，ADC CEB DAC ECB CA CB ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ACD ≌△CBE （AAS ）；（2）①由题意得，AM=t ，FN=3t ，则CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t ；故答案为：8-t ；6-3t ；②由折叠的性质可知，∠BCE=∠FCE ，∵∠MCD+∠CMD=90°，∠MCD+∠BCE=90°，∴∠NCE=∠CMD ，∴当CM=CN 时，△MDC 与△CEN 全等，当点N 沿F→C 路径运动时，8-t=6-3t ，解得，t=-1（不合题意），当点N 沿C→B 路径运动时，CN=3t-6，则8-t=3t-6，解得，t=3.5，当点N 沿B→C 路径运动时，由题意得，8-t=18-3t ，解得，t=5，当点N 沿C→F 路径运动时，由题意得，8-t=3t-18，解得，t=6.5，综上所述，当t=3.5秒或5秒或6.5秒时，△MDC 与△CEN 全等．【点睛】本题考查了折叠的性质，全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．29．（1）①点P ；②见解析；（2）①点C 的横坐标C x 的值为-3；②334k -≤<-【解析】【分析】（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ；②利用新定义得点S 是点P 关于点M 的“正矩点”（答案不唯一）；（2）①利用新定义结合题意画出符合题意的图形，利用新定义的性质证明△BCF ≌△AOB ，则FC=OB 求得点C 的横坐标；②用含k 的代数式表示点C 纵坐标，代入不等式求解即可．【详解】解：（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ，故答案为点P ；②因为MP 绕M 点顺时针旋转90︒得MS ，所以点S 是点P 关于点M 的“正矩点”，同理还可以得点Q 是点P 关于点S 的“正矩点”．（任写一种情况就可以）（2）①符合题意的图形如图1所示，作CE ⊥x 轴于点E ，CF ⊥y 轴于点F ，可得∠BFC=∠AOB=90°．∵直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，∴点B 的坐标为3(0,3),(,0)B A k-在x 轴的正半轴上， ∵点A 关于点B 的“正矩点”为点(,)C C C x y ，∴∠ABC=90°，BC=BA ，∴∠1＋∠2=90°，∵∠AOB=90°，∴∠2＋∠3=90°，∴∠1=∠3．∴△BFC ≌△AOB ，∴3FC OB ==，可得OE ＝3．∵点A 在x 轴的正半轴上且3OA <，0C x ∴<，∴点C 的横坐标C x 的值为－3．②因为△BFC ≌△AOB ，3(,0)A k-，A 在x 轴正半轴上， 所以BF ＝OA ，所以OF ＝OB-OF ＝33k +点3(3,3)C k -+，如图2， -1＜C y ≤2，即：-1＜33k+ ≤2， 则334k -≤<-． 【点睛】本题考查的是一次函数综合运用，涉及到三角形全等、解不等式，新定义等，此类新定义题目，通常按照题设的顺序，逐次求解．30．（1）y 3+2；（2）△AOD 为直角三角形，理由见解析；（3）t ＝2323． 【解析】【分析】（1）将点A 、B 的坐标代入一次函数表达式：y ＝kx +b ，即可求解；（2）由点A 、O 、D 的坐标得：AD 2＝1，AO 2＝3，DO 2＝4，故DO 2＝OA 2+AD 2，即可求解； （3）点C 3，1），∠DBO ＝30°，则∠ODA ＝60°，则∠DOA ＝30°，故点C 31），则∠AOC ＝30°，∠DOC ＝60°，OQ ＝CP ＝t ，则OP ＝2﹣t ．①当OP ＝OM 时，OQ ＝QH +OH 3（2﹣t ）+12（2﹣t ）＝t ，即可求解；②当MO ＝MP 时，∠OQP ＝90°，故OQ ＝12O P ，即可求解；③当PO ＝PM 时，故这种情况不存在． 【详解】解：（1）将点A、B的坐标代入一次函数表达式：y＝kx+b得：33=2023k bk b⎧+⎪⎨⎪=+⎩，解得：3 =32kb⎧⎪⎨⎪=⎩－，故直线AB的表达式为：y＝﹣3x+2；（2）直线AB的表达式为：y＝﹣3x+2，则点D（0，2），由点A、O、D的坐标得：AD2＝1，AO2＝3，DO2＝4，故DO2＝OA2+AD2，故△AOD为直角三角形；（3）直线AB的表达式为：y＝﹣3x+2，故点C（3，1），则OC＝2，则直线AB的倾斜角为30°，即∠DBO＝30°，则∠ODA＝60°，则∠DOA＝30°故点C（3，1），则OC＝2，则点C是AB的中点，故∠COB＝∠DBO＝30°，则∠AOC＝30°，∠DOC＝60°，OQ＝CP＝t，则OP＝OC﹣PC＝2﹣t，①当OP＝OM时，如图1，则∠OMP＝∠MPO＝12（180°﹣∠AOC）＝75°，故∠OQP＝45°，过点P作PH⊥y轴于点H，则OH＝12OP＝12（2﹣t），由勾股定理得：PH＝32（2﹣t）＝QH，OQ＝QH+OH＝32（2﹣t）+12（2﹣t）＝t，解得：t＝23；②当MO＝MP时，如图2，则∠MPO＝∠MOP＝30°，而∠QOP＝60°，∴∠OQP＝90°，故OQ＝12OP，即t＝12（2﹣t），解得：t＝23；③当PO＝PM时，则∠OMP＝∠MOP＝30°，而∠MOQ＝30°，故这种情况不存在；综上，t＝2323．【点睛】本题考查等腰三角形的性质、一次函数解析式、勾股定理、含30°的角的直角三角形的性质等知识点，还利用了方程和分类讨论的思想，综合性较强，难度较大，解题的关键是学会综合运用性质进行推理和计算．。

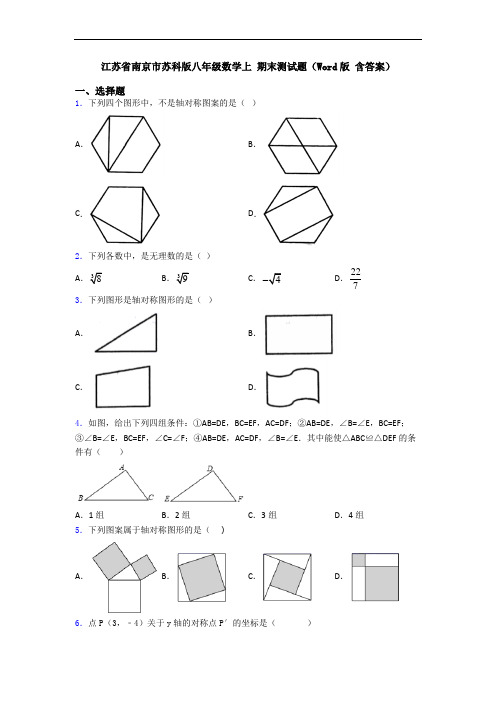
江苏省南京市苏科版八年级数学上期末测试题（Word版含答案）一、选择题1．下列四个图形中，不是轴对称图案的是（）A．B．C．D．2．下列各数中，是无理数的是（）A．38B．39C．4D．22 73．下列图形是轴对称图形的是（）A．B．C．D．4．如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E，BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中能使△ABC≌△DEF的条件有（）A．1组B．2组C．3组D．4组5．下列图案属于轴对称图形的是（）A． B．C．D．6．点P（3，﹣4）关于y轴的对称点P′的坐标是（）A ．（﹣3，﹣4） B ．（3，4） C ．（﹣3，4） D ．（﹣4，3）7．在平面直角坐标系中，将函数3y x =的图象向上平移6个单位长度，则平移后的图象与x 轴的交点坐标为（ ） A ．(2,0) B ．(-2,0) C ．(6,0) D ．(-6,0) 8．下列各数中，无理数的是（ ）A ．0B ．1.01001C ．πD ．49．如图，动点P 在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点()1,1，第2次接着运动到点()2,0，第3次接着运动到点()3,2，···，按这样的运动规律，经过第2020次运动后，动点P 的坐标是（ ）A ．()2020,1B ．()2020,0C ．()2020,2D ．()2019,010．若253x +在实数范围内有意义，则x 的取值范围是（ ） A ．x ＞﹣52B ．x ＞﹣52且x ≠0 C ．x ≥﹣52D ．x ≥﹣52且x ≠0 二、填空题11．如图，已知函数y =x +b 和y =ax +3的图象交点为P ，则不等式x +b ＜ax +3的解集为_____．12．在平面直角坐标系内，一次函数y ＝k 1x +b 1与y ＝k 2x +b 2的图象如图所示，则关于x ，y的方程组1122y k x b y k x b -=⎧⎨-=⎩的解是________．13．如图，直线l 1：y ＝﹣12x +m 与x 轴交于点A ，直线l 2：y ＝2x +n 与y 轴交于点B ，与直线l 1交于点P （2，2），则△PAB 的面积为_____．14．如图，△ABC 中，5BC =，AB 边的垂直平分线分别交AB 、BC 于点D 、E ，AC 边的垂直平分线分别交AC 、BC 于点F 、G ，则△AEG 周长为____．15．若正实数,m n 满足等式222(1)(1)(1)m n m n +-=-+-，则m n ⋅=__________．16．已知，点(,1)A a 和点(3,)B b 关于原点O 对称，则+a b 的值为__________． 17．如图，已知直线3y x b =+与2y ax =-的交点的横坐标为-2，则关于x 的不等式32x b ax +>-的解集为______.18．如图，直线l 上有三个正方形,,a b c ，若,a c 的面积分别为5和11，则b 的面积为__________．19．如图，已知ABD CBD ∠∠=，若以“SAS”为依据判定ABD ≌CBD ，还需添加的一个直接条件是______．20．在平面直角坐标系中，已知线段AB 的两个端点坐标分别是A （-4，-1），B （1,1），将线段AB 平移后得到线段A B ''（点A 的对应点为A '），若点A '的坐标为（-2,2）则点B '的坐标为________________三、解答题21．如图，在77⨯网格中，每个小正方形的边长都为1，画图请加粗加黑. (1)图中格点ABC ∆的面积为______.(2)在图中建立适当的平面直角坐标系，使点(1,3)A ，(2,1)C . (3)画出ABC ∆关于y 轴对称的图形A B C ∆'''.22．如图，四边形ABCD 中，AB CB AD CD ==，，对角线AC ，BD 相交于点O ，,OE AB OF CB ⊥⊥，垂足分别是E 、F ，求证：OE OF =．23．阅读下列材料，然后解答问题： 问题：分解因式：3245x x +-.解答：把1x =带入多项式3245x x +-，发现此多项式的值为0，由此确定多项式3245x x +-中有因式()1x -，于是可设()()322451x x x x mx n +-=-++，分别求出m ，n 的值.再代入()()322451x x x x mx n +-=-++，就容易分解多项式3245x x +-，这种分解因式的方法叫做“试根法”. （1）求上述式子中m ，n 的值；（2）请你用“试根法”分解因式：3299x x x +--.24．小明和小华加工同一种零件，己知小明比小华每小时多加工15个零件，小明加工300个零件所用时间与小华加工200个零件所用的时间相同，求小明每小时加工零件的个数. 25．已知，如图，//AB CD ，E 是AB 的中点，CE DE =，求证：AC BD =．四、压轴题26．问题背景：（1）如图1，已知△ABC 中，∠BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．求证：DE ＝BD ＋CE ．拓展延伸：（2）如图2，将（1）中的条件改为：在△ABC 中，AB ＝AC ，D 、A 、E 三点都在直线m 上，并且有∠BDA ＝∠AEC ＝∠BAC ．请写出DE 、BD 、CE 三条线段的数量关系．（不需要证明）实际应用：（3）如图，在△ACB 中，∠ACB ＝90°，AC ＝BC ，点C 的坐标为(－2，0)，点A 的坐标为(－6，3)，请直接写出B 点的坐标．27．在平面直角坐标系xOy 中，对于点(,)P a b 和点(,)Q a b '，给出如下定义：若1,(2),(2)b a b b a -≥⎧=<⎩'⎨当时当时，则称点Q 为点P 的限变点．例如:点(2,3)的限变点的坐标是(2,2)，点(2,5)--的限变点的坐标是(2,5)-，点(1,3)的限变点的坐标是(1,3)．（1）①点(3,1)-的限变点的坐标是________；②如图1，在点(2,1)A -、(2,1)B 中有一个点是直线2y =上某一个点的限变点，这个点是________；（填“A ”或“B ”）（2）如图2，已知点(2,2)C --，点(2,2)D -，若点P 在射线OC 和OD 上，其限变点Q 的纵坐标b '的取值范围是b m '≥或b n '≤，其中m n >．令s m n =-，直接写出s 的值． （3）如图3，若点P 在线段EF 上，点(2,5)E --，点(,3)F k k -，其限变点Q 的纵坐标b '的取值范围是25b '-≤≤，直接写出k 的取值范围．28．如图1，矩形OACB 的顶点A 、B 分别在x 轴与y 轴上，且点()6,10C ，点()0,2D ，点P 为矩形AC 、CB 两边上的一个点．（1）当点P 与C 重合时，求直线DP 的函数解析式；（2）如图②，当P 在BC 边上，将矩形沿着OP 折叠，点B 对应点B '恰落在AC 边上，求此时点P 的坐标．（3）是否存P 在使BDP ∆为等腰三角形？若存在，直接写出点P 的坐标；若不存在，请说明理由．29．如图所示，在平面直角坐标系xOy 中，已知点A 的坐标(3,2)-，过A 点作AB x ⊥轴，垂足为点B ，过点(2,0)C 作直线l x ⊥轴，点P 从点B 出发在x 轴上沿着轴的正方向运动．（1）当点P 运动到点O 处，过点P 作AP 的垂线交直线l 于点D ，证明AP DP =，并求此时点D 的坐标；（2）点Q 是直线l 上的动点，问是否存在点P ，使得以P C Q 、、为顶点的三角形和ABP ∆全等，若存在求点P 的坐标以及此时对应的点Q 的坐标，若不存在，请说明理由．30．在ABC 中，AB AC =，D 是直线AB 上一点，E 在直线BC 上，且DE DC =． （1）如图1，当D 在AB 上，E 在CB 延长线上时，求证：EDB ACD ∠=∠； （2）如图2，当ABC 为等边三角形时，D 是BA 的延长线上一点，E 在BC 上时，作//EF AC ，求证：BE AD =；（3）在（2）的条件下，ABC ∠的平分线BF 交CD 于点F ，连AF ，过A 点作AH CD ⊥于点H ，当30EDC ∠=︒，6CF =时，求DH 的长度．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】 【分析】根据轴对称图形的定义逐项识别即可，一个图形的一部分，以某条直线为对称轴，经过轴对称能与图形的另一部分重合，这样的图形叫做轴对称图形. 【详解】A 不是轴对称图形，B 、C 、D 都是轴对称图形.故选A.【点睛】本题考查了轴对称图形的识别，熟练掌握轴对称图形的定义是解答本题的关键. 2．B解析：B【解析】【分析】根据无理数的定义结合算术平方根和立方根逐一判断即可得．【详解】2=，为有理数，故该选项错误；D.2-，为有理数，故该选项错误；D. 227，为有理数，故该选项错误.故选B.【点睛】本题考查无理数的定义，立方根，算术平方根.初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．3．B解析：B【解析】【分析】根据轴对称图形的概念，一个图形沿一条直线对折后，直线两旁的部分能够完全重合,这样的图形叫做轴对称图形. 据此进行选择即可.【详解】根据轴对称图形定义，图形A、C、D中不是轴对称图形,而B是轴对称图形.故选B【点睛】本题主要考查了轴对称图形的辨识,解答本题的关键是熟练掌握轴对称图形的概念.4．C解析：C【解析】【分析】根据全等三角形的判定方法：SSS、SAS、ASA及AAS，即可判定．【详解】①满足SSS，能判定三角形全等；②满足SAS，能判定三角形全等；③满足ASA，能判定三角形全等；④的条件是两边及其一边的对角分别对应相等，不能判定三角形全等． ∴能使ABC DEF △≌△全等的条件有3组． 故选：C ． 【点睛】本题考查全等三角形的判定，解题关键是熟练掌握各种判定方法并注意“两边及其一边的对角分别对应相等”不能判定三角形全等．5．D解析：D 【解析】分析：根据轴对称图形的定义，寻找四个选项中图形的对称轴，发现只有D 有一条对称轴，由此即可得出结论．详解：A 、不能找出对称轴，故A 不是轴对称图形； B 、不能找出对称轴，故B 不是轴对称图形； C 、不能找出对称轴，故C 不是轴对称图形； D 、能找出一条对称轴，故D 是轴对称图形． 故选D ．点睛：本题考查了轴对称图形，解题的关键是分别寻找四个选项中图形的对称轴．本题属于基础题，难度不大，解决该题型题目时，通过寻找给定图象有无对称轴来确定该图形是否是轴对称图形是关键．6．A解析：A 【解析】试题解析：∵点P （3，-4）关于y 轴对称点P′， ∴P′的坐标是：（-3，-4）． 故选A ．7．B解析：B 【解析】 【分析】先求出平移后的解析式，继而令y=0，可得关于x 的方程，解方程即可求得答案. 【详解】根据函数图象平移规律，可知3y x =向上平移6个单位后得函数解析式应为36y x =+， 此时与x 轴相交，则0y =， ∴360x +=，即2x =-， ∴点坐标为(-2，0)， 故选B. 【点睛】本题考查了一次函数图象的平移，一次函数图象与坐标轴的交点坐标，先出平移后的解析式是解题的关键.8．C解析：C 【解析】 【分析】根据无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，找出无理数的个数． 【详解】解：A.0是整数，属于有理数； B.1.01001是有限小数，属于有理数； C ．π是无理数；2=，是整数，属于有理数． 故选：C ． 【点睛】本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有ππ的数．9．B解析：B 【解析】 【分析】观察可得点P 的变化规律，“()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++，，， (n 为自然数)”，由此即可得出结论. 【详解】观察， ()()()()()()0123450,01,12,0,3,2,4,0,5,1....P P P P P P ，，，， 发现规律:()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++，，， (n 为自然数) .∵20204505=⨯∴2020P 点的坐标为()2020,0. 故选: B. 【点睛】本题考查了规律型中的点的坐标，解题的关键是找出规律“()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++，，， (n 为自然数)”，本题属于中档题，难度不大，解决该题型题目时，根据点P 的变化罗列出部分点的坐标，再根据坐标的变化找出规律是关键.10．C解析：C【分析】根据二次根式有意义的条件即可确定x的取值范围.【详解】解：由题意得，2x+5≥0，解得x≥﹣52，故选：C．【点睛】a≥时有意义，正确理解二次根式有意义的条件是解题的关键.二、填空题11．x＜1【解析】【分析】当直线y=x+b的图象在直线y=ax+3的上方时，不等式x+b＞ax+3成立；【详解】由于两直线的交点横坐标为：x=1，观察图象可知，当x<1时，x+b<ax+3；解析：x＜1【解析】【分析】当直线y=x+b的图象在直线y=ax+3的上方时，不等式x+b＞ax+3成立；【详解】由于两直线的交点横坐标为：x=1，观察图象可知，当x<1时，x+b<ax+3；故答案为x<1．考点：一次函数与一元一次不等式．12．．【解析】【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解．【详解】∵一次函数y＝k1x+b1与y＝k2x+b2的图象的交点坐标为（2，1），∴关于x，y的方程组的解是．解析：21 xy=⎧⎨=⎩．【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解．【详解】∵一次函数y ＝k 1x +b 1与y ＝k 2x +b 2的图象的交点坐标为（2，1），∴关于x ，y 的方程组1122y k x b y k x b -=⎧⎨-=⎩的解是21x y =⎧⎨=⎩． 故答案为21x y =⎧⎨=⎩． 【点睛】本题考查了一次函数与二元一次方程（组）：方程组的解就是两个相应的一次函数图象的交点坐标．13．【解析】【分析】把点P （2，2）分别代入y ＝﹣x+m 和y ＝2x+n ，求得m ＝3，n ＝﹣2，解方程得到A （6，0），B （0，﹣2），根据三角形的面积公式即可得到结论．【详解】解：把点P （2，解析：【解析】【分析】把点P （2，2）分别代入y ＝﹣12x+m 和y ＝2x+n ，求得m ＝3，n ＝﹣2，解方程得到A （6，0），B （0，﹣2），根据三角形的面积公式即可得到结论．【详解】 解：把点P （2，2）分别代入y ＝﹣12x+m 和y ＝2x+n ， 得，m ＝3，n ＝﹣2，∴直线l 1：y ＝﹣12x+3，直线l 2：y ＝2x ﹣2， 对于y ＝﹣12x+3，令y ＝0，得，x ＝6， 对于y ＝2x ﹣2，令x ＝0，得，y ＝﹣2，∴A （6，0），B （0，﹣2），∵直线l 1：y ＝﹣12x+3与y 轴的交点为（0，3）， ∴△PAB 的面积＝12×5×6﹣12×5×2＝10， 故答案为：10．本题考查了两直线相交与平行问题，三角形的面积的计算，正确的识别图形是解题的关键．14．【解析】【分析】根据线段垂直平分线的性质可得AE=BE，AG=GC，据此计算即可．【详解】解：∵ED，GF分别是AB，AC的垂直平分线，∴AE=BE，AG=GC，∴△AEG的周长为AE解析：【解析】【分析】根据线段垂直平分线的性质可得AE=BE，AG=GC，据此计算即可．【详解】解：∵ED，GF分别是AB，AC的垂直平分线，∴AE=BE，AG=GC，∴△AEG的周长为AE+AG+EG=BE+CG+EG=BC=5．故答案是：5．【点睛】此题主要考查线段的垂直平分线的性质，掌握性质是解题关键．线段的垂直平分线上的点到线段的两个端点的距离相等．15．【解析】【分析】根据整式的完全平方公式将等式两边的式子进行化简，从而求得的值.【详解】∵∴∴∴，故答案为：.【点睛】本题主要考查了整式的乘法公式，熟练掌握完全平方公式及整式的解析：1 2【解析】根据整式的完全平方公式将等式两边的式子进行化简，从而求得m n ⋅的值.【详解】∵2222(1)()2()12221m n m n m n m mn n m n +-=+-++=++--+ 2222(1)(1)2121m n m m n n -+-=-++-+∴222222212121m mn n m n m m n n ++--+=-++-+∴21mn = ∴12mn =， 故答案为：12. 【点睛】本题主要考查了整式的乘法公式，熟练掌握完全平方公式及整式的化简是解决本题的关键. 16．【解析】【分析】根据关于原点对称的点坐标的特点，即可得到答案.【详解】解：∵点和点关于原点对称，∴，，∴；故答案为：.【点睛】本题考查了关于原点对称的点坐标特点，解题的关键是熟记解析：4-【解析】【分析】根据关于原点对称的点坐标的特点，即可得到答案.【详解】解：∵点(,1)A a 和点(3,)B b 关于原点O 对称，∴3a =-，1b =-，∴3(1)4a b +=-+-=-；故答案为：4-.【点睛】本题考查了关于原点对称的点坐标特点，解题的关键是熟记平面直角坐标系中任意一点P （x ，y ），关于原点的对称点是（-x ，-y ），即关于原点的对称点，横纵坐标都变成相反数，比较简单．【解析】【分析】直线y＝3x＋b与y＝ax−2的交点的横坐标为−2，求不等式3x＋b＞ax−2的解集，就是看函数在什么范围内y＝3x＋b的图象在函数y＝ax−2的图象上方．【详解】解析：x＞−2【解析】【分析】直线y＝3x＋b与y＝ax−2的交点的横坐标为−2，求不等式3x＋b＞ax−2的解集，就是看函数在什么范围内y＝3x＋b的图象在函数y＝ax−2的图象上方．【详解】解：从图象得到，当x＞−2时，y＝3x＋b的图象在y＝ax−2的图象上方，∴不等式3x＋b＞ax−2的解集为：x＞−2．故答案为x＞−2．【点睛】本题考查了一次函数与不等式（组）的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．18．16【解析】【分析】运用正方形边长相等，再根据同角的余角相等可得∠ABC=∠DAE，然后证明△ΔBCA≌ΔAED，结合全等三角形的性质和勾股定理来求解即可．【详解】解：∵AB=AD，∠BC解析：16【解析】【分析】运用正方形边长相等，再根据同角的余角相等可得∠ABC=∠DAE，然后证明△ΔBCA≌ΔAED，结合全等三角形的性质和勾股定理来求解即可．【详解】解：∵AB=AD，∠BCA=∠AED=90°，∴∠ABC=∠DAE，∴ΔBCA≌ΔAED(ASA)，∴BC=AE，AC=ED，故AB²=AC²+BC²=ED²+BC²=11+5=16，即正方形b的面积为16.点睛：此题主要考查对全等三角形和勾股定理的综合运用，解题的重点在于证明ΔBCA≌ΔAED，而利用全等三角形的性质和勾股定理得到b=a+c则是解题的关键. 19．AB=BC【解析】【分析】利用公共边BD以及∠ABD=∠CBD，依据两边及其夹角分别对应相等的两个三角形全等，即可得到需要的条件．【详解】如图，∵在△ABD与△CBD中，∠ABD=∠CBD解析：AB=BC【解析】【分析】利用公共边BD以及∠ABD=∠CBD，依据两边及其夹角分别对应相等的两个三角形全等，即可得到需要的条件．【详解】如图，∵在△ABD与△CBD中，∠ABD=∠CBD，BD=BD，∴添加AB=CB时，可以根据SAS判定△ABD≌△CBD，故答案为AB=CB．【点睛】本题考查了全等三角形的判定．本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．20．（3,4）【解析】分析：首先根据点A和点A′的坐标得出平移的方向和平移的数量，然后根据平移法则得出点B′的坐标．详解：∵A的坐标为(－4，－1)，A′的坐标为(－2，2)，∴平移法则为：先向解析：（3,4）【解析】分析：首先根据点A和点A′的坐标得出平移的方向和平移的数量，然后根据平移法则得出点B′的坐标．详解：∵A的坐标为(－4，－1)，A′的坐标为(－2，2)，∴平移法则为：先向右平移2个单位，再向上平移3个单位，∴点B′的坐标为(3，4)．点睛：本题主要考查的是线段的平移法则，属于基础题型．线段的平移法则就是点的平移法则，属于基础题型．三、解答题21．(1)5；(2)见解析；(3)见解析.【解析】【分析】（1）图中格点△ABC的面积=矩形的面积减去3个直角三角形的面积，即可得出结果;（2）由已知点的坐标即可得出点B为坐标原点，即可得出结果;（3）根据关于y轴成轴对称的特点，即对应点到对称轴的距离相等，确定对应点，然后依次连线即可解决.【详解】图中格点△ABC的面积=4×4-11143-21-42=5 222⨯⨯⨯⨯⨯⨯根据点(1,3)A的坐标，向左平移一个单位，向下平移3个单位确定原点坐标，建立坐标系，如图所示根据成轴对称的图形的特点，到对称轴的距离相等，找到对应点并连线如图所示：【点睛】本题考查了割补法求三角形面积，通过坐标找坐标原点确定坐标系，作轴对称图形，解决本题的关键是熟练掌握割补法，将非规则图形转化为规则易解的图形，熟练掌握坐标平移的规律.22．证明见解析．【解析】【分析】欲证明OE=OF ，只需推知BD 平分∠ABC ，所以通过全等三角形△ABD ≌△CBD （SSS ）的对应角相等得到∠ABD=∠CBD ，问题就迎刃而解了．【详解】在△ABD 和△CBD 中，AB CB AD CD BD BD =⎧⎪=⎨⎪=⎩，∴△ABD ≌△CBD （SSS ），∴∠ABD=∠CBD ，∴BD 平分∠ABC ．又∵OE ⊥AB ，OF ⊥CB ，∴OE=OF ．【点睛】本题考查了全等三角形的判定与性质，角平分线的性质，在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．23．（1）5m =，5n =；（2）()()()133x x x ++-【解析】【分析】（1）先找出一个x 的值，进而找出一个因式，再将多项式设成分解因式的形式，即可得出结论；（2）先找出x=-1时，得出多项式的值，进而找出一个因式，再将多项式设成分解因式的形式，即可得出结论．【详解】解：（1）把1x =带入多项式3245x x +-，发现此多项式的值为0，∴多项式3245x x +-中有因式()1x -，于是可设322451xx x x mx n ， 得出：3232451x x x m x n m x n ，∴14m ，0n m，∴5m =，5n =， （2）把1x =-代入3299x x x +--，多项式的值为0，∴多项式3299x x x +--中有因式()1x +，于是可设322329911x x x x x mx n x m x n m x n ，∴11m +=，9n m，9n =- ∴0m =，9n =-，∴3229133991x x x x x x x x【点睛】此题是分解因式，主要考查了试根法分解因式的理解和掌握，解本题的关键是理解试根法分解因式．24．45【解析】【分析】设小明每小时加工零件x 个，则小华每小时加工（x-15）个, 根据时间关系，得30020015x x =- 【详解】 解：设小明每小时加工零件x 个，则小华每小时加工（x-15）个由题意，得30020015x x =- 解得：x ＝45 经检验：x ＝45是原方程的解，且符合题意.答：小明每小时加工零件45个.【点睛】考核知识点：分式方程应用.理解题，根据时间关系列方程是关键.25．见解析【解析】【分析】由CE=DE 易得∠ECD=∠EDC ，结合AB ∥CD 易得∠AEC=∠BED ，由此再结合AE=BE ，CE=DE 即可证得△AEC ≌△BED ，由此即可得到AC=BD.【详解】∵CE DE =，∴ECD EDC ∠=∠，∵//AB CD ，∴AEC ECD ∠=∠，BED EDC ∠=∠，∴AEC BED ∠=∠，又∵E 是AB 的中点，∴AE BE =，在AEC 和BED 中，AE BE AEC BED CE DE =⎧⎪∠=∠⎨⎪=⎩，∴AEC ≌BED ．∴AC BD =．【点睛】熟悉“等腰三角形的性质、平行线的性质和全等三角形的判定方法”是解答本题的关键.四、压轴题26．（1）证明见解析；（2）DE ＝BD ＋CE ；（3）B(1，4)【解析】【分析】（1）证明△ABD ≌△CAE ，根据全等三角形的性质得到AE=BD ，AD=CE ，结合图形解答即可；（2）根据三角形内角和定理、平角的定义证明∠ABD=∠CAE ，证明△ABD ≌△CAE ，根据全等三角形的性质得到AE=BD ，AD=CE ，结合图形解答即可；（3）根据△AEC ≌△CFB ，得到CF=AE=3，BF=CE=OE-OC=4，根据坐标与图形性质解答．【详解】（1）证明：∵BD ⊥直线m ，CE ⊥直线m ，∴∠ADB ＝∠CEA ＝90°∵∠BAC ＝90°∴∠BAD ＋∠CAE ＝90°∵∠BAD ＋∠ABD ＝90°∴∠CAE ＝∠ABD∵在△ADB 和△CEA 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△CEA （AAS ）∴AE ＝BD ，AD ＝CE∴DE ＝AE ＋AD ＝BD ＋CE即：DE ＝BD ＋CE（2）解：数量关系：DE＝BD＋CE理由如下：在△ABD中，∠ABD=180°-∠ADB-∠BAD，∵∠CAE=180°-∠BAC-∠BAD，∠BDA=∠AEC，∴∠ABD=∠CAE，在△ABD和△CAE中，ABD CAEBDA AECAB CA∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴△ABD≌△CAE（AAS）∴AE=BD，AD=CE，∴DE=AD+AE=BD+CE；（3）解：如图，作AE⊥x轴于E，BF⊥x轴于F，由（1）可知，△AEC≌△CFB，∴CF=AE=3，BF=CE=OE-OC=4，∴OF=CF-OC=1，∴点B的坐标为B（1，4）．【点睛】本题考查的是全等三角形的判定和性质、坐标与图形性质，掌握全等三角形的判定定理和性质定理是解题的关键．27．（1）①)3,1；②B；（2）3s=；（3）59k≤≤．【解析】【分析】（1）利用限变点的定义直接解答即可；（2）先利用逆推原理求出限变点(2,1)A-、(2,1)B对应的原来点坐标，然后把原来点坐标代入到2y=，满足解析式的就是答案；（3）先OC OD，的关系式，再求出点P的限变点Q满足的关系式，然后根据图象求出m n，的值，从而求出s即可；（4）先求出线段EF的关系式，再求出点P的限变点Q所满足的关系式，根据图像求解即可．【详解】解：（1）①∵32a=，∴11bb ==-='，∴坐标为：()3,1，故答案为：()3,1； ②∵对于限变点来说，横坐标保持不变，∴限变点(2,1)A -对应的原来点的坐标为：()2,1-或()21--，， 限变点(2,1)B 对应的原来点的坐标为：()2,2，∵()2,2满足2y =，∴这个点是B ，故答案为：B ；（2）∵点C 的坐标为(2,2)--，∴OC 的关系式为：()0y x x =≤，∵点D 的坐标为(2,2)-，∴OD 的关系式为：()0y x x =-≥，∴点P 满足的关系式为：()()00x x y x x ≤⎧⎪=⎨->⎪⎩， ∴点P 的限变点Q 的纵坐标满足的关系式为：当2x ≥时：1b x '=--，当02x <<时：b x x '=-=，当0x ≤时，b x x '==-，图像如下：通过图象可以得出：当2x ≥时，3b '≤-，∴3n =-，当2x <时，0b '≥，∴0m =，∴()033s m n =-=--=；（3）设线段EF 的关系式为：()022y ax c a x k k =+≠-≤≤>-，，， 把(2,5)E --，(,3)F k k -代入得：253a c ka c k -+=-⎧⎨+=-⎩，解得：13a c =⎧⎨=-⎩， ∴线段EF 的关系式为()322y x x k k =--≤≤>-，， ∴线段EF 上的点P 的限变点Q 的纵坐标满足的关系式4(2)|3|3(22)x xb x x x -⎧'=⎨-=--<⎩， 图象如下：当x ＝2时，b ′取最小值，b '＝2﹣4＝﹣2，当b '＝5时，x ﹣4＝5或﹣x +3＝5，解得：x ＝9或x ＝﹣2，当b ′＝1时，x ﹣4＝1，解得：x ＝5，∵ 25b '-≤≤，∴由图象可知，k 的取值范围时：59k ≤≤．【点睛】本题主要考查了一次函数的综合题，解答本题的关键是熟练掌握新定义“限变点”，解答此题还需要掌握一次函数的图象与性质以及最值的求解，此题有一定的难度．28．（1）y=43x+2；（2）（103，10）；（3）存在， P 坐标为（6，6）或（6，7+2）或（6，7）．【解析】【分析】（1）设直线DP 解析式为y=kx+b ，将D 与C 坐标代入求出k 与b 的值，即可确定出解析式；（2）当点B 的对应点B′恰好落在AC 边上时，根据勾股定理列方程即可求出此时P 坐标； （3）存在，分别以BD ，DP ，BP 为底边三种情况考虑，利用勾股定理及图形与坐标性质求出P坐标即可．【详解】解：（1）∵C（6，10）,D（0，2），设此时直线DP解析式为y=kx+b，把D（0，2），C（6，10）分别代入，得2610bk b=⎧⎨+=⎩，解得432kb⎧=⎪⎨⎪=⎩则此时直线DP解析式为y=43x+2；（2）设P（m，10），则PB=PB′=m，如图2，∵OB′=OB=10，OA=6，∴AB′=22OB OA'-=8，∴B′C=10-8=2，∵PC=6-m，∴m2=22+（6-m）2，解得m=103则此时点P的坐标是（103，10）；（3）存在，理由为：若△BDP为等腰三角形，分三种情况考虑：如图3，①当BD=BP1=OB-OD=10-2=8，在Rt△BCP1中，BP1=8，BC=6，根据勾股定理得：CP1228627-=∴AP17P1（6，7）；②当BP2=DP2时，此时P2（6，6）；③当DB=DP3=8时，在Rt△DEP3中，DE=6，根据勾股定理得：P3228627-∴AP 3=AE+EP 3，即P 3（6，+2），综上，满足题意的P 坐标为（6，6）或（6，+2）或（6，）．【点睛】此题属于一次函数综合题，待定系数法确定一次函数解析式，坐标与图形性质，等腰三角形的性质，勾股定理，熟练掌握待定系数法是解题的关键．29．（1）证明见解析；(2,3)D ；（2）存在，(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q -．【解析】【分析】（1）通过全等三角形的判定定理ASA 证得△ABP ≌△PCD ，由全等三角形的对应边相等证得AP ＝DP ，DC ＝PB ＝3，易得点D 的坐标；（2）设P （a ，0），Q （2，b ）．需要分类讨论：①AB ＝PC ，BP ＝CQ ；②AB ＝CQ ，BP ＝PC ．结合两点间的距离公式列出方程组，通过解方程组求得a 、b 的值，得解．【详解】（1）AP PD ⊥90APB DPC ∴∠+∠=AB x ⊥轴90A APB ∴∠+∠=A DPC ∴∠=∠在ABP ∆和PCD ∆中A DPC AB PCABP PCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA ∴∆≅∆AP DP ∴=，3DC PB ==(2,3)D ∴（2）设(,0)P a ，(2,)Q b①AB PC =，BP CQ =223a a b ⎧-=⎪⎨+=⎪⎩，解得03a b =⎧⎨=±⎩或47a b =⎧⎨=±⎩ (0,0)P ∴，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q - ②AB CQ =，BP PC =，322a a b +=-⎧⎨=⎩，解得122a b ⎧=⎪⎨⎪=±⎩ 1(,0)2P ∴-，(2,2)Q -或1(,0)2P -，(2,2)Q - 综上：(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q - 【点睛】 考查了三角形综合题．涉及到了全等三角形的判定与性质，两点间的距离公式，一元一次绝对值方程组的解法等知识点．解答（2）题时，由于没有指明全等三角形的对应边（角），所以需要分类讨论，以防漏解．30．（1）见解析；（2）见解析；（3）3【解析】【分析】（1）根据等腰三角形的性质和外角的性质即可得到结论；（2）过E 作EF ∥AC 交AB 于F ，根据已知条件得到△ABC 是等边三角形，推出△BEF 是等边三角形，得到BE=EF ，∠BFE=60°，根据全等三角形的性质即可得到结论； （3）连接AF ，证明△ABF ≌△CBF ，得AF=CF ，再证明DH=AH=12CF=3． 【详解】解：（1）∵AB=AC ，∴∠ABC=∠ACB ，∵DE=DC ，∴∠E=∠DCE ，∴∠ABC-∠E=∠ACB-∠DCB ，即∠EDB=∠ACD ；（2）∵△ABC 是等边三角形，∴∠B=60°，∴△BEF 是等边三角形，∴BE=EF ，∠BFE=60°，∴∠DFE=120°，∴∠DFE=∠CAD ，在△DEF 与△CAD 中， EDF DCA DFE CAD DE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEF ≌△CAD （AAS ），∴EF=AD ，∴AD=BE；（3）连接AF，如图3所示：∵DE=DC，∠EDC=30°，∴∠DEC=∠DCE=75°，∴∠ACF=75°-60°=15°，∵BF平分∠ABC，∴∠ABF=∠CBF，在△ABF和△CBF中，AB BCABF CBFBF BF=⎧⎪∠=∠⎨⎪=⎩，△ABF≌△CBF（SAS），∴AF=CF，∴∠FAC=∠ACF=15°，∴∠AFH=15°+15°=30°，∵AH⊥CD，∴AH=12AF=12CF=3，∵∠DEC=∠ABC+∠BDE，∴∠BDE=75°-60°=15°，∴∠ADH=15°+30°=45°，∴∠DAH=∠ADH=45°，∴DH=AH=3．【点睛】本题考查了全等三角形的判定与性质，等腰三角形和直角三角形的性质，三角形的外角的性质，等边三角形的判定和性质，证明三角形全等是解决问题的关键．。

八年级数学上学期期末测试一、选择题（每小题2分，共16分）1. 点P ( 2，－3 )关于x 轴的对称点是( )A ． (－2， 3 )B ． (2，3)C ．(－2， 3 )D ．(2，－3 ) 2. 若2=a ,则a 的值为 ( )A.2B.2±C.4D.±43.把0.697按四舍五入法精确到0.01的近似值是 （ ） A. 0.6 B. 0.7 C. 0.67 D. 0.704. 一次函数y ＝2x ＋1的图像不经过( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 5．若440-=m ，则估计m 的值所在的范围是 ( )A ．1＜m ＜2B ．2＜m ＜3C ．3＜m ＜4D ．4＜m ＜56. 若点A （－3，y 1），B （2，y 2），C （3，y 3）是函数2+-=x y 图像上的点，则（ ） A ．321y y y >> B ．321y y y << C ．231y y y << D ．132y y y >>7. 某电视台“走基层”栏目的一位记者乘汽车赴320km 外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y （单位：km ）与时间x （单位：h ）之间的关系如图所示，则下列结论正确的是（ ） A ．汽车在高速公路上的行驶速度为100km/h B ．乡村公路总长为90kmC ．汽车在乡村公路上的行驶速度为60km/hD ．该记者在出发后5h 到达采访地8. 平面直角坐标系中，已知A （8，0），△AOP 为等腰三角形且面积为16，满足条件的P 点有( )A ．4个B ．8个C ．10个D ．12个 二．填空题（每小题2分，共20分） 9. 计算：3－64 ＝ ．10. 若等腰三角形的两边长分别为4和8，则这个三角形的周长为 . 11. 若032=++-y x ，则()2013y x +的值为 ．12. 在平面直角坐标系中，若点M （－1，3）与点N （x ，3）之间的距离是5，则x 的值是 ．（第7题图）13. 如图，已知函数y ＝2x ＋1和y ＝－x －2的图像交于点P ，根据图像，可得方程组⎩⎨⎧2x －y ＋1＝0x ＋y ＋2＝0的解为 .14. 将一次函数y ＝2x ＋1的图像向上平移3个单位长度后，其对应的函数关系式为 ．15. 如图，在△ABC 中，AB ＝1.8，BC ＝3.9，∠B ＝60°，将△ABC 绕点A 按顺时针旋转一定角度得到△ADE ，当点B 的对应点D 恰好落在BC 边上时，则CD 的长为 .16. 如图，在△ABC 中，∠ACB ＝90°，沿CD 折叠△CBD ，使点B 恰好落在AC 边上的点E 处.若 ∠A ＝28°，则∠ADE ＝ °.17. 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A ，B ，C ，D 的面积和是49cm 2 ,则其中最大的正方形S 的边长为 cm. 18. 在平面直角坐标系中，规定把一个正方形先沿着x 轴翻折，再向右平 移2个单位称为1次变换.如图，已知正方形ABCD 的顶点A 、B 的坐 标分别是（－1，－1）、（－3，－1），把正方形ABCD 经过连续7次这样的变换得到正方形A ′B ′C ′D ′，则B 的对应点B ′的坐标是 . 三．解答题（本大题共9小题，共64分） 19. (本题满分8分)(1) (4分) 求出式子中x 的值：9x 2－16＝0. （2）（4分）232)3(8)2(+---20. (本题满分5分) 求一个正数的算术平方根，有些数可以直接求得，如4，有些数则不能直接求得，如5，但可以通过计算器求得. 还有一种方法可以通过一组数的内在联系，运用规律求得，请同学们观察下表：（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表达出来）（2）运用你发现的规律，探究下列问题：已知06.2≈1．435，求下列各数的算术平方根： ①0.0206； ②206； ③20600．（第13题图）（第16题图）（第18题图）（第15题图）21. (本题满分6分)已知关于x 的一次函数y ＝mx ＋2的图像经过点(－2，(1)求m 的值；(2)画出此函数的图像；(3)平移此函数的图像，使得它与两坐标轴所围成的图形的面积为4， 请直接写出此时图像所对应的函数关系式.22. (本题满分8分) 如图，点E 是∠AOB 的平分线上一点，EC ⊥OA ，ED⊥OB ，垂足分别是C 、D ． 求证：（1）∠EDC ＝∠ECD （2）OC ＝OD（3）OE 是线段CD 的垂直平分线23. (本题满分7分)如图，一只小蚂蚁要从A 点沿长方体木块表面爬到B 点处吃蜜糖．已知长方体木块的长、宽、高分别为10cm 、8cm 、6cm ， 试计算小蚂蚁爬行的最短距离．24.(本题满分6分)图l 、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．点A 和 点B 在小正方形的顶点上．(1) 在图1中画出△ABC(点C 在小正方形的顶点上)，使△ABC 为直角三角形 (画一个 即可)；(2) 在图2中画出△ABD(点D 在小正方形的顶点上)，使△ABD 为等腰三角形 (画一个即可)；A（第23题图）第22题图EDBCA O25. (本题满分6分) 一辆客车与一辆出租车分别从甲、乙两地同时出发，相向而行．设客车离甲地的距离为y 1千米，出租车离甲地的距离为y 2千米，两车行驶的时间为x 小时， y 1、y 2关于x 的函数图象如右图所示： （1）根据图像，直接写出y 1、y 2关于x 的函数图象关系式 （2）试计算：何时两车相距300千米？26.(本题满分10分)小丽的爸爸驾车外出旅行，途经甲地到乙地．设他出发第t min 时的速度为 v m/min ，图中的折线表示他从甲地到乙地的驾车速度v 与时间t 之间的函数关系．某学习小组经过探究发现：小丽爸爸前5min 运动的路程在数值上等于长方形AOLB 的面积．由物理学知识还可知：小丽爸爸前n （5＜n ≤10）秒运动的路程在数值上等于矩形AOLB 的面积与梯形BLNM 的面积之和（以后的路程在数值上有着相似的特点）． (1) 小丽的爸爸驾车的最高速度是__ __m/min ；(2) 当45≤t ≤50时，求v 与t 之间的函数关系式，并求出小丽爸爸出发第47min 时的速度； （3）如果汽车每行驶100km 耗油10L ，那么小丽的爸爸驾车从甲地到乙地共耗油多少升？27.(本题满分8分) 在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED=EC. 试探索以下问题：（1）当点E 为AB 的中点时，如图1，请判断线段AE 与DB 的大小关系，请你直接写出结论：AE DB （填“>”“<”或“=”）.（2）当点E 为AB 上任意一点时，如图2，AE 与DB 的大小关系会改变吗？请说明理由.)图2图1ED CBAEDCBA参考答案一、选择题（每小题2分，共16分）二．填空题（每小题2分，共20分）9. －4 10. 20 11. －1 12. －6 或4 13. ⎩⎨⎧x ＝－1y ＝－114. y ＝2x ＋416. 2.1 16. 34 17. 7 18. (11,1) 三．解答题（本大题共9小题，共64分）19.(1) (4分) x 2＝169 …………………………………………………………2分x ＝±43…………………………………………………………………4分(1) 原式＝2－(－2)＋3………………………………………………………………3分 ＝7…………………………………………………………………………4分20．（本题满分5分）（1）被开方数扩大或缩小n210倍，非负数的算术平方根就相应的扩大或缩小n10倍；或者说成被开方数的小数点向左或向右移动2n 位，算术平方根的小数点就向左或向右移动n 位.……………………………………………3分（2）0.1435………………………3分14.35………………………4分； 143.5………………………5分 21.(6分)(1)将x ＝－2,y ＝6代入y ＝mx ＋2得 6＝－2m ＋2, ………………………1分 解得m ＝－2……………………………………………………2分(2)画圈正确…………………………………………………4分(3) y ＝－2x ＋4，y ＝－2x －4…………………………………………6分22.(8分) （1）证DE ＝CE ，则∠EDC ＝∠ECD ．（只要证法对就得分）……………3分（2）全等或等角对等边…………………………………………………6分 （3）用“三线合一”或“垂直平分线”的判断………………………8分23.(7分) A 1B 1＝102＋(8＋6)2 ＝296 …………………………………………2分 A 2B 2＝62＋(8＋10)2 ＝360 …………………………………………4分 A 3B 3＝82＋(6＋10)2 ＝320 …………………………………………6分 ∵296 ＜320 ＜360∴小蚂蚁爬行的最短路线为296 cm ………………………………………7分24.(7分) 分) (1) y 1＝25.(7100x ，y 2＝800－160x …………………………………………2分 (2) ①两车未相遇: (800－160x )－100x ＝300解得x ＝2513………………………………………4分②两车相遇后：100x －(800－160x )＝300解得x ＝5513………………………………………6分 答：2513 h 或5513 h 两车相距300km ……………………………………………7分26.(10分) (1) 1200………………………………………2分(2) 设v ＝kt ＋b （k ≠0），∵函数图象经过点（45，800），（50，0），∴⎩⎨⎧45k ＋b ＝80050k ＋b ＝0 ……………………………4分 解得⎩⎨⎧k ＝－160b ＝8000……………………………5分所以，v 与t 的关系式为v ＝－160t ＋8000……………………………6分 当t ＝47时，v ＝－160×47＋8000＝480(m/min ) ……………………………7分 (2) 行驶的总路程为：400×5＋(400＋1200)×5×12 ＋1200×10＋(1200＋800)×10×12 ＋800×15＋800×5×12＝42000(m)＝42(km ) ……………………………9分 …………10分27.（1）“=” …………………………………………2分（2）AE 与DB 的大小关系不变…………………………………………3分理由：过E 作EF//BC 交AC 于F,FEA因为△ABC 是等边三角形所以∠ABC ＝∠ACB ＝∠BAC ＝60° 所以∠AEF ＝∠ABC ＝60°, ∠AFE ＝∠ACB ＝60° 所以△AEF 是等边三角形……………………………4分 所以AE=EF=AF,又因为AB=AC, 所以BE=CF……………………5分 所以∠DBE ＝∠EFC ＝180°－60°=120°………………6分 在△DBE 和△EFC 中因为⎪⎭⎪⎬⎫==∠=FC BE EFC DBE AEDB 所以△DBE ≌△EFC………………………………………7分所以DB=EF=AE……………………………………………………………………8分。

南京市八年级（上）期末数学试卷（含答案）一、选择题1．如图，在四边形ABCD 中，AB ∥DC ，AD=BC=5，DC=7，AB=13，点P 从点A 出发以3个单位/s 的速度沿AD→DC 向终点C 运动，同时点Q 从点B 出发，以1个单位/s 的速度沿BA 向终点A 运动．当四边形PQBC 为平行四边形时，运动时间为（ ）A ．4sB ．3sC ．2sD ．1s 2．若一次函数(2)1y k x =-+的函数值y 随x 的增大而增大，则（ ） A ．2k < B ．2k > C ．0k >D ．k 0< 3．下列四组线段a ，b ，c ，能组成直角三角形的是（ ） A ．1a =，2b =，3c =B ．1a =，2b =，3c =C ．2a =，3b =，4c =D ．4a =，5b =，6c =4．若1(2,)A y ，2(3,)B y 是一次函数31y x =-+的图象上的两个点，则1y 与2y 的大小关系是( )A ．12y y <B ．12y y =C ．12y y >D ．不能确定 5．已知等腰三角形的两边长分别为3和4，则它的周长为（ ）A ．10B ．11C ．10或11D ．7 6．下列说法中正确的是（ ）A ．带根号的数都是无理数B ．不带根号的数一定是有理数C ．无限小数都是无理数D ．无理数一定是无限不循环小数7．如图，已知AB AD =，下列条件中，不能作为判定ABC ≌ADC 条件的是A ．BC DC =B ．BAC DAC ∠=∠ C ．90BD ︒∠=∠= D ．ACB ACD ∠=∠8．已知正比例函数y ＝kx 的图象经过点（﹣2，1），则k 的值（ ）A ．﹣2B ．﹣12C ．2D ．129．下列调查中，调查方式最适合普查（全面调查）的是（ ）A ．对全国初中学生视力情况的调查B ．对2019年央视春节联欢晚会收视率的调查C ．对一批飞机零部件的合格情况的调查D ．对我市居民节水意识的调查10．如图，直线(0)y kx b k =+≠经过点(1,3)-，则不等式3kx b +≥的解集为（ ）A ．1x >-B ．1x <-C ．3x ≥D ．1x ≥-二、填空题11．已知y 与x 成正比例，当x=8时，y=﹣12，则y 与x 的函数的解析式为_____．12．如图，点A 的坐标为（-2，0），点B 在直线y x =上运动，当线段AB 最短时，点B 的坐标是__________．13．比较大小：10_____3．（填“＞”、“=”或“＜”）14．某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间比原计划生产450台机器所需时间相同，现在平均每天生产___台机器．15．如图，已知ABD CBD ∠∠=，若以“SAS”为依据判定ABD ≌CBD ，还需添加的一个直接条件是______．16．如图，等边△ABC 的周长是18，D 是AC 边上的中点，点E 在BC 边的延长线上．如果DE ＝DB ，那么CE 的长是_____．17．如图，等腰Rt △OAB ，∠AOB ＝90°，斜边AB 交y 轴正半轴于点C ，若A （3，1），则点C 的坐标为_____．18．如图，Rt△ABC中，∠C＝90°，AD是∠BAC的平分线，CD＝4，AB＝16，则△ABD的面积等于_____．19．如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是．20．函数y1=x+1与y2=ax+b的图象如图所示,那么,使y1、y2的值都大于0的x的取值范围是______.三、解答题21．A，B两地相距200千米，甲车从A地出发匀速行驶到B地，乙车从B地出发匀速行驶到A地．乙车行驶1小时后，甲车出发，两车相向而行．设行驶时间为x小时（0≤x≤5），甲、乙两车离A地的距离分别为y1，y2千米，y1，y2与x之间的函数关系图象如图1所示．根据图象解答下列问题：（1）求y1，y2与x的函数关系式；（2）乙车出发几小时后，两车相遇？相遇时，两车离A地多少千米？（3）设行驶过程中，甲、乙两车之间的距离为s千米，在图2的直角坐标系中，已经画出了s与x之间的部分函数图象．①图中点P的坐标为（1，m），则m＝；②求s与x的函数关系式，并在图2中补全整个过程中s与x之间的函数图象．22．已知y 与2x -成正比例，且当1x =时，2y =-．（1）求y 与x 的函数表达式；（2）当12x -<<时，求y 的取值范围．23．一次函数()0y kx b k =+≠的图像为直线l ．（1）若直线l 与正比例函数2y x =的图像平行，且过点（0，−2），求直线l 的函数表达式；（2）若直线l 过点（3，0），且与两坐标轴围成的三角形面积等于3，求b 的值．24．如图，矩形ABCD 中，6AB =，8AD =，点P 从点A 出发，以每秒一个单位的速度沿A B C →→的方向运动；同时点Q 从点B 出发，以每秒2个单位的速度沿B C D →→的方向运动，当其中一点到达终点后两点都停止运动.设两点运动的时间为t 秒.（1）当t =______时，两点停止运动；（2）当t 为何值时，BPQ ∆是等腰三角形？25．已如，在平面直角坐标系中，点A 的坐标为()6,0、点B 的坐标为(0,8)，点C 在y 轴上，作直线AC .点B 关于直线AC 的对称点B ′刚好在x 轴上，连接CB '.（1）写出一点B ′的坐标，并求出直线AC 对应的函数表达式；（2）点D 在线段AC 上，连接DB 、DB '、BB '，当DBB ∆'是等腰直角三角形时，求点D 坐标；（3）如图②，在（2）的条件下，点P 从点B 出发以每秒2个单位长度的速度向原点O 运动，到达点O 时停止运动，连接PD ，过D 作DP 的垂线，交x 轴于点Q ，问点P 运动几秒时ADQ ∆是等腰三角形.四、压轴题26．如图，在△ABC中，AB=AC=18cm，BC=10cm，AD=2BD．（1）如果点P在线段BC上以2cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过2s后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？AB=，27．如图，已知四边形ABCO是矩形，点A，C分别在y轴，x轴上，4 3BC=．（1）求直线AC 的解析式；（2）作直线AC 关于x 轴的对称直线，交y 轴于点D ，求直线CD 的解析式．并结合（1）的结论猜想并直接写出直线y kx b =+关于x 轴的对称直线的解析式；（3）若点P 是直线CD 上的一个动点，试探究点P 在运动过程中，||PA PB -是否存在最大值？若不存在，请说明理由；若存在，请求出||PA PB -的最大值及此时点P 的坐标．28．在平面直角坐标系中点 A （m −3，3m +3），点 B （m ，m +4）和 D （0，−5），且点 B 在第二象限．（1）点 B 向 平移 单位，再向下平移 （用含 m 的式子表达）单位可以与点 A 重合； （2）若点 B 向下移动 3 个单位，则移动后的点 B 和点 A 的纵坐标相等，且有点 C （m −2，0）．①则此时点 A 、B 、C 坐标分别为 、 、 ．②将线段 AB 沿 y 轴负方向平移 n 个单位，若平移后的线段 AB 与线段 CD 有公共点，求 n 的取值范围．③当 m <−1 式，连接 AD ，若线段 AD 沿直线 AB 方向平移得到线段 BE ，连接 DE 与直线y=−2 交于点 F ，则点 F 坐标为 ．（用含 m 的式子表达）29．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC 中，∠ABC 与∠ACB 的平分线交于点P ，∠A ＝64°，则∠BPC ＝ ；（2）如图2，△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E ．其中∠A ＝α，求∠BEC ．（用α表示∠BEC ）；（3）如图3，∠CBM 、∠BCN 为△ABC 的外角，∠CBM 、∠BCN 的平分线交于点Q ，请你写出∠BQC 与∠A 的数量关系，并说明理由；（4）如图4，△ABC 外角∠CBM 、∠BCN 的平分线交于点Q ，∠A=64°，∠CBQ ，∠BCQ 的平分线交于点P ，则∠BPC= ゜，延长BC 至点E ，∠ECQ 的平分线与BP 的延长线相交于点R ，则∠R= ゜．30．在△ABC中，∠BAC=45°，CD⊥AB，垂足为点D，M为线段DB上一动点（不包括端点），点N在直线AC左上方且∠NCM=135°，CN=CM，如图①．（1）求证：∠ACN=∠AMC；（2）记△ANC得面积为5，记△ABC得面积为5．求证：12S ACS AB；（3）延长线段AB到点P，使BP=BM，如图②．探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M，AN=CP始终成立？（写出探究过程）【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】【详解】解：设运动时间为t秒，则CP=12-3t，BQ=t，根据题意得到12-3t=t，解得：t=3，故选B．【点睛】本题考查一元一次方程及平行四边形的判定，难度不大．2．B解析：B【解析】【分析】根据一次函数图象的增减性来确定（k-2）的符号，从而求得k 的取值范围．【详解】∵在一次函数y=（k-2）x+1中，y 随x 的增大而增大，∴k-2＞0，∴k ＞2，故选B.【点睛】本题考查了一次函数图象与系数的关系．在直线y=kx+b （k≠0）中，当k ＞0时，y 随x 的增大而增大；当k ＜0时，y 随x 的增大而减小．3．B解析：B【解析】【分析】根据如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形进行分析即可．【详解】A ．12+22≠32，不能组成直角三角形，故此选项错误；B ．2221+，能组成直角三角形，故此选项正确；C ．32+22≠42，不能组成直角三角形，故此选项错误；D ．42+52≠62，不能组成直角三角形，故此选项错误．故选：B ．【点睛】本题考查了勾股定理逆定理，关键是掌握判断一个三角形是不是直角三角形．必须满足较小两边平方的和等于最大边的平方才能做出判断．4．C解析：C【解析】【分析】根据一次函数的性质，此一次函数系数k ＜0，y 随x 增大而减小，然后观察A 、B 两点的坐标，据此判断即可.【详解】解：∵一次函数1y =+的系数k ＜0，y 随x 增大而减小，又∵两点的横坐标2＜3，∴12y y >故选C.【点睛】本题考查了一次函数的性质，解决本题的关键是理解本题题意，熟练掌握一次函数的增减性.5．C解析：C【解析】【分析】可分3是腰长与底边，两种情况讨论求解即可．【详解】解：①3是腰长时，三角形的三边分别为：3、3、4，能组成三角形，周长=3+3+4=10，②3是底边时，三角形的三边分别为3、4、4，能组成三角形，周长=3+4+4=11，∴三角形的周长为10或11．故选择：C．【点睛】本题考查了等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键，难点在于要分情况讨论．6．D解析：D【解析】【分析】根据无理数的定义判断各选项即可．【详解】A2，是有理数，错误；B中，例如π，是无理数，错误；C中，无限循环小数是有理数，错误；D正确，无限不循环的小数是无理数故选：D【点睛】本题考查无理数的定义，注意含有π和根号开不尽的数通常为无理数．7．D解析：D【解析】【分析】利用全等三角形的判定定理：SSS、SAS、ASA、AAS、HL进行分析即可．【详解】解：A、AB=AD，BC=DC，再加上公共边AC=AC可利用SSS判定△ABC≌△ADC，故此选项不符合题意；B、AB=AD，∠BAC=∠DAC再加上公共边AC=AC可利用SAS判定△ABC≌△ADC，故此选项不合题意；C、AB=AD，∠B=∠D=90°再加上公共边AC=AC可利用HL判定△ABC≌△ADC，故此选项不合题意；D、AB=AD，∠ACB=∠ACD再加上公共边AC=AC不能判定△ABC≌△ADC，故此选项合题意；故选：D．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．8．B解析：B【解析】【分析】将点（﹣2，1）代入y＝kx即可求出k的值.【详解】解：∵正比例函数y＝kx的图象经过点（﹣2，1），∴1＝﹣2k，解得k＝﹣12，故选：B．【点睛】本题考查了正比例函数，熟练掌握求正比例函数解析式的方法是解题的关键.9．C解析：C【解析】【分析】根据普查和抽样调查的特点解答即可．【详解】解：A．对全国初中学生视力情况的调查，适合用抽样调查，不合题意；B．对2019年央视春节联欢晚会收视率的调查，适合用抽样调查，不合题意；C．对一批飞机零部件的合格情况的调查，适合全面调查，符合题意；D．对我市居民节水意识的调查，适合用抽样调查，不合题意；故选：C．【点睛】本题考查了抽样调查和全面调查的知识，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．10．D解析：D【解析】结合函数的图象利用数形结合的方法确定不等式的解集即可．【详解】解：观察图象知：当1x ≥-时，3kx b +≥，故选：D ．【点睛】本题考查了一次函数与一元一次不等式的知识，解题的关键是根据函数的图象解答，难度不大．二、填空题11．y=-x【解析】【分析】根据题意可得y=kx ，再把x=8时，y=-12代入函数，可求k ，进而可得y 与x 的关系式．【详解】设y=kx ，∵当x=8时，y=-12，∴-12=8k ，解得k=解析：y=-32x 【解析】【分析】根据题意可得y=kx ，再把x=8时，y=-12代入函数，可求k ，进而可得y 与x 的关系式．【详解】设y=kx ，∵当x=8时，y=-12，∴-12=8k ，解得k=-32， ∴所求函数解析式是y=-32x ； 故答案为:y=-32x ． 【点睛】 本题考查了待定系数法求函数解析式，解题的关键是理解成正比例的关系的含义．12．【解析】过A作AC⊥直线y=x于C，过C作CD⊥OA于D，当B和C重合时，线段AB最短，推出AC=OC，求出AC、OC长，根据三角形面积公式求出CD，推出CD=OD，即可求出B的坐标．--解析：(1,1)【解析】【分析】过A作AC⊥直线y=x于C，过C作CD⊥OA于D，当B和C重合时，线段AB最短，推出AC=OC，求出AC、OC长，根据三角形面积公式求出CD，推出CD=OD，即可求出B的坐标．【详解】解：过A作AC⊥直线y=x于C，过C作CD⊥OA于D，当B和C重合时，线段AB最短，∵直线y=x，∴∠AOC=45°，∴∠OAC=45°=∠AOC，∴AC=OC，由勾股定理得：2AC2=OA2=4，∴2，由三角形的面积公式得：AC×OC=OA×CD，22=2CD，∴CD=1，∴OD=CD=1，∴B（-1，-1）．故答案为：（-1，-1）．【点睛】本题考查的是一次函数的性质，涉及到垂线段最短，等腰直角三角形的判定与性质，勾股定理等知识点的应用，关键是得出当B和C重合时，线段AB最短，题目比较典型，主要培养了学生的理解能力和计算能力．13．＞．【解析】【分析】先求出3=，再比较即可．【详解】∵32=9＜10，∴＞3，故答案为：＞．【点睛】本题考查了实数的大小比较和算术平方根的应用，用了把根号外的因式移入根号内的方法．解析：＞．【解析】【分析】先求出【详解】∵32=9＜10，3，故答案为：＞．【点睛】本题考查了实数的大小比较和算术平方根的应用，用了把根号外的因式移入根号内的方法．14．200【解析】【分析】【详解】设现在平均每天生产x台机器，则原计划可生产（x﹣50）台，根据现在生产600台机器的时间与原计划生产450台机器的时间相同，等量关系为：现在生产600台机器时解析：200【解析】【分析】【详解】设现在平均每天生产x台机器，则原计划可生产（x﹣50）台，根据现在生产600台机器的时间与原计划生产450台机器的时间相同，等量关系为：现在生产600台机器时间=原计划生产450台时间，从而列出方程：600450x x50=-，解得：x=200．检验：当x=200时，x（x﹣50）≠0．∴x=200是原分式方程的解．∴现在平均每天生产200台机器．15．AB=BC【解析】【分析】利用公共边BD以及∠ABD=∠CBD，依据两边及其夹角分别对应相等的两个三角形全等，即可得到需要的条件．【详解】如图，∵在△ABD与△CBD中，∠ABD=∠CBD解析：AB=BC【解析】【分析】利用公共边BD以及∠ABD=∠CBD，依据两边及其夹角分别对应相等的两个三角形全等，即可得到需要的条件．【详解】如图，∵在△ABD与△CBD中，∠ABD=∠CBD，BD=BD，∴添加AB=CB时，可以根据SAS判定△ABD≌△CBD，故答案为AB=CB．【点睛】本题考查了全等三角形的判定．本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．16．3【解析】【分析】由△ABC为等边三角形，D为AC边上的中点可得∠DBE=30°，由DE=DB得∠E =30°，再证出∠CDE=∠E，得出CD=CE=AC=3即可．【详解】∵△ABC为等边解析：3【解析】【分析】由△ABC为等边三角形，D为AC边上的中点可得∠DBE=30°，由DE=DB得∠E =30°，再证出∠CDE=∠E，得出CD=CE=12AC=3即可．【详解】∵△ABC为等边三角形，D为AC边上的中点，∴BD为∠ABC的平分线，且∠ABC=60°，∴∠DBE=30°，又DE=DB，∴∠E=∠DBE=30°，∵等边△ABC的周长为18，∴AC=6，且∠ACB=60°，∴∠CDE=∠ACB-∠E=30°，∴∠CDE=∠E，∴CD=CE=12AC=3．故答案为：3．【点睛】此题考查了等边三角形的性质、等腰三角形的判定以及三角形的外角性质等知识；熟练掌握等边三角形的性质，证明CD=CE是解题的关键．17．（0，）【解析】【分析】过B作BE⊥y轴于E，过A作AF⊥x轴于F，根据全等三角形的性质得到B（﹣1，3），设直线AB的解析式为y=kx+b，求得直线AB的解析式为y=﹣x+，于是得到结论．解析：（0，52）【解析】【分析】过B作BE⊥y轴于E，过A作AF⊥x轴于F，根据全等三角形的性质得到B（﹣1，3），设直线AB的解析式为y=kx+b，求得直线AB的解析式为y=﹣12x+52，于是得到结论．【详解】过B作BE⊥y轴于E，过A作AF⊥x轴于F，如图所示：∴∠BCO=∠AFO=90°，∵A（3，1），∴OF=3，AF=1，∵∠AOB=90°，∴∠BOC+∠OBC=∠BOC+∠AOF=90°，∴∠BOC=∠AOF，∵OA=OB，∴△BOE≌△AOF（AAS），∴BE=AF=1，OE=OF=3，∴B（﹣1，3），设直线AB的解析式为y=kx+b，∴3 31k bk b-+=⎧⎨+=⎩，解得：1 2 52kb⎧=-⎪⎪⎨⎪=⎪⎩，∴直线AB的解析式为y=﹣12x+52，当x=0时，y=52，∴点C的坐标为（0，52），故答案为：（0，52）．【点睛】此题主要考查全等三角形的判定与性质，解题关键是利用全等得出点坐标进而求得解析式. 18．【解析】【分析】作DH⊥AB于H，如图，根据角平分线的性质得到DH=DC=4，然后利用三角形面积公式计算．【详解】作DH⊥AB于H，如图，∵AD是∠BAC的平分线，∴DH=DC=4，解析：【解析】【分析】作DH⊥AB于H，如图，根据角平分线的性质得到DH=DC=4，然后利用三角形面积公式计算．【详解】作DH⊥AB于H，如图，∵AD是∠BAC的平分线，∴DH=DC=4，∴△ABD的面积=12×16×4=32．故答案为：32．【点睛】本题考查了角平分线的性质及三角形面积公式，熟练掌握“角的平分线上的点到角的两边的距离相等”是解题的关键．19．（﹣4，3）．【解析】试题分析：解：如图，过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，∵OA绕坐标原点O逆时针旋转90°至OA′，∴OA=OA′，∠AOA′=90°，∵∠A′解析：（﹣4，3）．【解析】试题分析：解：如图，过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，∵OA绕坐标原点O逆时针旋转90°至OA′，∴OA=OA′，∠AOA′=90°，∵∠A′OB′+∠AOB=90°，∠AOB+∠OAB=90°，∴∠OAB=∠A′OB′，在△AOB和△OA′B′中，，∴△AOB≌△OA′B′（AAS），∴OB′=AB=4，A′B′=OB=3，∴点A′的坐标为（﹣4，3）．故答案为（﹣4，3）．考点：坐标与图形变化-旋转20．−1<x<2.【解析】【分析】根据x轴上方的图象的y值大于0进行解答．【详解】如图所示,x>−1时,y>0，当x<2时,y>0，∴使y、y的值都大于0的x的取值范围是：−1<x<2.解析：−1<x<2.【解析】【分析】根据x轴上方的图象的y值大于0进行解答．【详解】如图所示,x>−1时,y1>0，当x<2时,y2>0，∴使y1、y2的值都大于0的x的取值范围是：−1<x<2.故答案为：−1<x<2.【点睛】此题考查两条直线相交或平行问题，解题关键在于x轴上方的图象的y值大于0三、解答题21．（1）y1＝50x﹣50，y2＝﹣40x+200；（2）乙车出发259小时后，两年相遇，相遇时，两车离A地8009千米；（3）①160；②当1≤x≤259时，s＝250﹣90x；当259＜x≤5时，s＝90x﹣250；图象详见解析.【解析】【分析】（1）用待定系数法可求解析式；（2）将两个函数表达式组成方程组可求解；（3）①由点P表达的意义可求m的值；②分相遇前和相遇后两种情况分别求解析式．【详解】解：（1）如图1，甲的图象过点（1，0），（5，200），∴设甲的函数表达式为：y1＝kx+b，∴2005k bk b =+⎧⎨=+⎩解得：5050 kb=⎧⎨=-⎩∴甲的函数表达式为：y1＝50x﹣50，如图1，乙的图象过点（5，0），（0，200），∴设乙的函数表达式为：y2＝mx+200，∴0＝5m+200∴m＝﹣40，∴乙的函数表达式为：y2＝﹣40x+200，（2）由题意可得：505040200y xy x=-⎧⎨=-+⎩解得：2598009xy⎧=⎪⎪⎨⎪=⎪⎩答：乙车出发259小时后，两年相遇，相遇时，两车离A地8009千米．（3）①由题意可得乙先出发1小时，且速度为40千米/小时，∴m＝200﹣40×1＝160，故答案为160；②当1≤x≤259时，s＝200﹣40×1﹣（40+50）（x﹣1）＝250﹣90x；当259＜x≤5时，s＝90x﹣250；图象如下：【点睛】本题考查了一次函数的应用，用待定系数法求解析式，理解函数图象是本题的关键．22．（1）y=2x-4；（2）-6＜y＜0．【解析】【分析】（1）设y=k（x-2），把x=1，y=-2代入求出k值即可；（2）把x=-1，x=2代入解析式求出相应的y值，然后根据函数的增减性解答即可．【详解】解：（1）因为y与x-2成正比例，可得：y=k（x-2），把x=1，y=-2代入y=k（x-2），得k（1-2）=-2，解得：k=2，所以解析式为：y=2（x-2）=2x-4；（2）把x=-1，x=2分别代入y=2x-4，可得：y=-6，y=0，∵y=2x-4中y 随x 的增大而增大，∴当-1＜x ＜2时，y 的范围为-6＜y ＜0．【点睛】本题考查了用待定系数法求一次函数的解析式及一次函数的性质，熟练掌握一次函数的性质是解题关键．23．（1）y=2x-2；（2）b=2或-2.【解析】【分析】（1）因为直线l 与直线2y x =平行，所以k 值相等，即k=2，又因该直线过点（0，−2），所以就有-2=2×0+b ，从而可求出b 的值，于是可解；（2）直线l 与y 轴的交点坐标是（0，b ），与x 轴交于（3，0），然后根据三角形面积公式列方程求解即可．【详解】解：（1）∵直线l 与直线2y x =平行，∴k=2，∴直线l 即为y=2x+b ．∵直线l 过点（0，−2），∴-2=2×0+b ，∴b=-2．∴直线l 的解析式为y=2x-2．（2）∵直线l 与y 轴的交点坐标是（0，b ），与x 轴交于（3，0），∴直线l 与两坐标轴围成的三角形面积=132b ⨯⋅． ∴132b ⨯⋅=3， 解得b=2或-2.【点睛】 本题考查了一次函数的有关计算，两条直线平行问题，直线与两坐标轴围成的三角形面积等，难度不大，关键是掌握两条直线平行时k 值相等及求直线与两坐标轴的交点坐标．24．（1）7秒；（2）当t 为2秒或225秒时，BPQ ∆是等腰三角形. 【解析】【分析】（1）分别计算P 、Q 到达终点的时间，根据当其中一点到达终点后两点都停止运动，取时间较短的；（2）分三种情况讨论，利用等腰三角形的定义可求解.【详解】解：（1）∵四边形ABCD 为矩形，6AB =，8AD =，∴6DC AB ==,8BC AD ==，∴点P 运动到终点所需(6+8)÷1=14秒，Q 运动到终点所需(6+8)÷2=7秒，∴当t =7时，两点停止运动；（2）①当t ≤4时，P 点在线段AB 上，Q 点在线段BC 上时，若Rt BPQ ∆是等腰三角形，则BP=BQ,即6-t=2t ，解得t=2秒；②当P 点在线段AB 上，Q 点在线段CD 上时，此时4＜t≤6,如下图,若BPQ ∆是等腰三角形，则PQ=BQ,此时作PE ⊥DC,∵四边形ABCD 为矩形，∴∠C=∠ABC=90°，∴四边形BCEP 为矩形，∴EC=PB=6-t ，EP=BC ，∵PQ=BQ ，∴Rt △EPQ ≌Rt △CBQ （HL ），∴EQ=QC ，即6282t t -=-，解得225t =， ③当P 点在线段BC 上，Q 点在线段CD 上时，此时6＜t≤7如下图，BP=t-6，QC=2t-8,∵当6＜t≤7时，QC-BP=2t-8-(t-6)=t-2>0,∴BQ>QP>QC>BP ，BPQ ∆不可能是等腰三角形，综上所述，当t 为2秒或225秒时，BPQ ∆是等腰三角形. 【点睛】 本题考查矩形的性质和判定，全等三角形的性质和判定，一元一次方程的应用，等腰三角形的定义.掌握方程思想和分类讨论思想是解决此题的关键.25．（1）(4,0)B '-，132y x =-+（2）点D 坐标为(2,2)，（3）点P 运动时间为1秒秒或3.75秒. 【解析】【分析】（1）由勾股定理求出AB=10，即可求出A B '=10，从而可求出(4,0)B '-，设C （0，m ），在直角三角形COB '中，运用勾股定理可求出m 的值，从而确定点C 的坐标，再利用待定系数法求出AC 的解析式即可；（2）由AC 垂直平分BB '可证90BDB ∠'=°，过点D 作DE x ⊥轴于点E ，DF y ⊥轴于点F ，证明FDB EDB ∆∆'≌可得DE=DF ，设D （a ，a ）代入132y x =-+求解即可； （3）分三种情况：①当DQ DA =时，②当AQ AD =时，③当QD QA =时，分类讨论即可得解：【详解】（1）(6,0),(0,8)A B ，6,8OA OB ∴==，90AOB ︒∠=，222OA OB AB ∴+=，22268AB ∴+=，10AB ∴=，点B ′、B 关于直线AC 的对称，AC ∴垂直平分BB '，,10CB CB AB AB ''∴===，(4,0)B '∴-，设点C 坐标为(0,)m ，则OC m =，8CB CB m '∴==-，在Rt COB ∆'中，COB ∠'=90°，222OC OB CB ''∴+=，2224(8),m m ∴+=-3m ∴=，∴点C 坐标为(0,3).设直线AC对应的函数表达式为(0)y kx b k=+≠，把(6,0),(0,3)A C代入，得603k bb+=⎧⎨=⎩，解得123kb⎧=-⎪⎨⎪=⎩，∴直线AC对应的函数关系是为132y x=-+，（2）AC垂直平分BB'，DB DB='∴，BDB∆'∴是等腰直角三角形，90BDB∠'=∴°过点D作DE x⊥轴于点E，DF y⊥轴于点F.90DFO DFB DEB'︒∴∠=∠=∠=，360EDF DFB DEO EOF︒∠=-∠-∠-∠，90EOF︒∠=，90EDF︒∴∠=，EDF BDB'∴∠=∠，BDF EDB'∴∠=∠，FDB EDB∴∆∆'≌，DF DE∴=，∴设点D坐标为(,)a a，把点(,)D a a代入132y x=-+，得0.53a a=-+2a∴=，∴点D坐标为(2,2)，（3）同（2）可得PDF QDE∠=∠又2,90DF DE PDF QDE︒==∠=∠=PDF QDE∴∆∆≌PF QE ∴= ①当DQ DA =时，DE x ⊥∵轴，4QE AE ==∴4PF QE ∴==642BP BF PF ∴=-=-=∴点P 运动时间为1秒.②当AQ AD =时，(6,0),(2,2)A D20,AD ∴=204AQ ∴=-，204PF QE ∴==-6(204)1020BP BF PF ∴=-=--=-∴点P 运动时间为10202-秒.③当QD QA =时，设QE n =，则4QD QA n ==-在Rt DEQ ∆中，90DEQ ∠=°，222DE EQ DQ ∴+=2222(4), 1.5n n n ∴+=-∴=1.5PF QE ∴==6 1.57.5BP BF PF ∴=+=+=∴点P 运动时间为3.75秒.综上所述，点P 运动时间为11020-秒或3.75秒. 【点睛】此题涉及的知识有：待定系数法确定一次函数解析式，坐标与图形性质，等腰三角形的性质，勾股定理，利用了分类讨论的思想，熟练掌握待定系数法是解本题第一问的关键，第三问题要注意分类讨论，不要丢解． 四、压轴题26．（1）①△BPD 与△CQP 全等，理由见解析；②当点Q 的运动速度为125cm /s 时，能够使△BPD 与△CQP 全等；（2）经过90s 点P 与点Q 第一次相遇在线段AB 上相遇．【解析】【分析】（1）①由“SAS”可证△BPD ≌△CQP ； ②由全等三角形的性质可得BP=PC=12BC=5cm ，BD=CQ=6cm ，可求解； （2）设经过x 秒，点P 与点Q 第一次相遇，列出方程可求解．【详解】 解：（1）①△BPD 与△CQP 全等，理由如下：∵AB =AC =18cm ，AD =2BD ，∴AD =12cm ，BD =6cm ，∠B =∠C ，∵经过2s 后，BP =4cm ，CQ =4cm ，∴BP =CQ ，CP =6cm =BD ，在△BPD 和△CQP 中，BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩，∴△BPD ≌△CQP （SAS ），②∵点Q 的运动速度与点P 的运动速度不相等，∴BP ≠CQ ，∵△BPD 与△CQP 全等，∠B =∠C ，∴BP =PC =12BC =5cm ，BD =CQ =6cm ， ∴t =52， ∴点Q 的运动速度=612552=cm /s ，∴当点Q 的运动速度为125cm /s 时，能够使△BPD 与△CQP 全等； （2）设经过x 秒，点P 与点Q 第一次相遇， 由题意可得：125x ﹣2x =36， 解得：x =90， 点P 沿△ABC 跑一圈需要181810232++=（s ） ∴90﹣23×3=21（s ），∴经过90s 点P 与点Q 第一次相遇在线段AB 上相遇．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的性质，一元一次方程的应用，掌握全等三角形的判定是本题的关键．27．（1）y =34-x +3；（2）y =34x -3，y =-kx -b ；（3）存在，4，(8，3) 【解析】【分析】（1）利用4AB =，3BC =，找出A 、C 两点的坐标，设直线解析式，利用待定系数法求出AC 的解析式；（2）由直线AC 关于x 轴的对称直线为CD 可知点D 的坐标，设直线解析式，利用待定系数法求出CD 的解析式，对比AC 的解析式进而写出直线y kx b =+关于x 轴的对称直线的解析式；（3）先判断||PA PB -存在最大值，在P 、A 、B 三点不共线时，P 点在运动过程中，与A 、B 两点组成三角形，两边之差小于第三边，得出结论在P 、A 、B 三点共线时，此时||PA PB -最大，y p = y A =3，求出P 点的纵坐标，最后根据点P 在直线CD 上，将P 点的纵坐标代入直线方程可得横坐标，从而求出P 点坐标．【详解】解：（1）在矩形ABCD 中，OC =AB =4，OA =BC =3，故A (0，3)，C (4，0)，设直线AC 的解析式为：y =kx +b (k ≠0，k 、b 为常数)，点A 、C 在直线AC 上，把A 、C 两点的坐标代入解析式可得：340b k b =⎧⎨+=⎩解得：343k b ⎧=-⎪⎨⎪=⎩， 所以直线AC 的解析式为：y =34-x +3． （2）由直线AC 关于x 轴的对称直线为CD 可知：点D 的坐标为：(0，-3)，设直线CD 的解析式为：y =mx +n (m ≠0，m 、n 为常数)，点C 、D 在直线CD 上，把C 、D 两点的坐标带入解析式可得：-340n m n =⎧⎨+=⎩解得：343m n ⎧=⎪⎨⎪=-⎩， 所以直线CD 的解析式为：y =34x -3， 故猜想直线y kx b =+关于x 轴的对称直线的解析式为：y =-kx -b ．（3）点P 在运动过程中，||PA PB -存在最大值，由题意可知：如图，延长AB 与直线CD 交点即为点P ，此时||PA PB -最大，其他位置均有||PA PB -＜AB （P 点在运动过程中，与A 、B 两点组成任意三角形，两边之差小于第三边），此时，||PA PB -= AB =4，y p = y A =3，点P 在直线CD 上，将P 点的纵坐标代入直线方程可得：34x -3=3， x =8，故P 点坐标为(8，3)，||PA PB -的最大值为x p -x B =8-4=4．【点睛】本题主要考查利用待定系数法求解一次函数解析式及类比推理能力，掌握任意三角形两边之差小于第三边是解题的关键．28．（1）左；3；(1-2m )；（2）①（-4，0）；（-1，0）（-3，0）； ②当平移后的线段 AB 与线段 CD 有公共点时，1913n ≤≤；③ F 9(,2)12m--． 【解析】【分析】(1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B 点向下平移后，点B 和点A 的纵坐标相等得到等量关系，可求出m 的值，从而求出A 、B 、C 三点坐标；②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设出K 点坐标，作 KH ⊥BM 与 H 点，表示出H 点坐标，然后利用面积关系ABM AKM BKM S S S ∆∆∆=+求出距离；当 B '在线段 CD 上时，BB '交 x 轴于 M 点，过 B '做 B 'E ⊥OD ，利用S △COD = S △OB'C + S △OB'D ，求出n 的值，从而求出n 的取值范围；③通过坐标平移法用m 表示出E 点的坐标，利用D 、E 两点坐标表示出直线DE 的函数关系式，令y=﹣2，求出x 的值即可求出F 点坐标．【详解】解：（1）根据平移规律可得：B 向左平移；m －（m －1）=3，所以平移3个单位；m+4－（3m+3）=1－2m ，所以再向下平移(1-2m )个单位；故答案为：左；3；(1-2m )（2）①点 B 向下移动 3 个单位得：B （m ，m+1）∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A （-4,0）；B （-1,0）；C （-3,0）；②如图 1，过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设 K 点坐标为（-3，a ）M 点坐标为（-1,0）作 KH ⊥BM 与 H 点，H 点坐标为（-1，a ）AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+ ∴222AM BM KC AM KH BM ⨯⨯⨯=+ ∴33323222a ⨯⨯⨯=+ 解得：1a =，。

2023-2024学年江苏省南京一中八年级（上）期末数学试卷一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）1．（3分）在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中．轴对称图形是（）A．B．C．D．2．（3分）在平面直角坐标系中，点P（﹣3，m2+1）关于原点的对称点在（）A．第一象限B．第二象限C．第三象限D．第四象限3．（3分）用四舍五入法对数3465983取近似数精确到万位，结果是（）A．347B．3.46C．3.47×106D．3.46×1074．（3分）若，则x的取值范围是（）A．x＞3B．x≥3C．x＜3D．x≤35．（3分）在等腰三角形ABC中，若∠A＝70°，则∠B的度数是（）A．40°B．55°C．70°D．40°或55°或70°6．（3分）若式子+（k﹣2）0有意义，则一次函数y＝（k﹣2）x+2﹣k的图象可能是（）A．B．C．D．7．（3分）△ABC中，BC＝10，AB的垂直平分线与AC的垂直平分线分别交BC于点D，E，且DE＝4，则AD+AE的值为（）A．6B．14C．6或14D．8或128．（3分）如图，设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车原地返回．设x小时后两车间的距离为y千米，y关于x的函数关系如图所示，则乙车的速度为（）A．60千米/小时B．70千米/小时C．75千米/小时D．80千米/小时二、填空题（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）9．（3分）下列实数：，0，，﹣1.5，，2.6161161116…（每两个6之间依次增加一个1），其中无理数有个．10．（3分）实数的算术平方根是．11．（3分）一个等腰三角形两边的长分别为3和8，那么这个三角形的周长是．12．（3分）点P在第二象限，且到x轴，y轴的距离分别为2、3．则点P的坐标是．13．（3分）直线y＝3x+2沿y轴向下平移4个单位，则平移后直线与y轴的交点坐标为．14．（3分）如图，直线y＝kx+b与直线y＝mx+n交于P（1，），则方程组的解是．15．（3分）如图，△ABC中，∠C＝90°，AD平分∠BAC，AB＝10，AC＝6，则BD的长是．16．（3分）如图1，△ABC中，AB＞AC，D是边BC上的动点．设B、D两点之间的距离为x，A、D两点之间的距离为y，表示y与x的函数关系的图象如图2所示，则线段AB的长为．三、解答题（本大题共有10小题，共72分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、推理过程或演算步骤）17．计算：．18．解方程x2﹣9＝0．19．已知：一个正数a的两个不同平方根分别是x+5和4x﹣15．（1）求a的值；（2）求a+1的立方根．20．如图，AC⊥BC，DC⊥EC，AC＝BC，DC＝EC．求证：（1）△ACE≌△BCD；（2）AE⊥BD．21．在如图的正方形网格中，每一个小正方形的边长为1．格点三角形ABC（顶点是网格线交点的三角形）的顶点A、C的坐标分别是（﹣4，6），（﹣1，4）．（1）请在图中的网格平面内建立平面直角坐标系；（2）请画出△ABC关于x轴对称的△A1B1C1；（3）请在y轴上求作一点P，使△PB1C的周长最小，并写出点P的坐标．22．已知y﹣2与x成正比，且当x＝﹣2时，y＝4．（1）求y与x的函数表达式；（2）在坐标系中画出（1）中的函数图象；（3）当y＞0时，直接写出x的取值范围为．23．已知：如图，线段AC和射线AB有公共端点A．（1）①在射线AB取一点P，使△APC是以AC为底边的等腰三角形；②过P作射线PD，使PD∥AC；（以上按要求尺规作图，并保留作图痕迹）（2）若∠BPD＝32°，连接PC，则∠ACP＝°．24．如图，在Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，点D是Rt△ABC外一点，连接DC，DB，且CD＝4，BD＝3．（1）求BC的长；（2）求证：△BCD是直角三角形．25．某商店销售一台A型电脑销售利润为100元，销售一台B型电脑的销售利润为150元．该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的3倍，设购进A型电脑x 台，这100台电脑的销售总利润为y元．（1）求y关于x的函数解析式；（2）该商店购进A型、B型电脑各多少台，才能使销售总利润最大？最大利润为多少？26．如图，直线l1：y＝x﹣4与x轴交于点A，与y轴交于点B，直线l2：y＝kx+b与x轴交于点C（1，0），与y轴交于点D（0，2），直线l1，l2交于点E．（1）求直线l2的函数表达式；（2）试说明CD＝CE．（3）若P为直线l1上一点，当∠POB＝∠BDE时，求点P的坐标．2023-2024学年江苏省南京一中八年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）1．【分析】根据轴对称图形的概念求解．【解答】解：A、不是轴对称图形，故此选项不合题意；B、不是轴对称图形，故此选项不合题意；C、是轴对称图形，故此选项符合题意；D、不是轴对称图形，故此选项不合题意．故选：C．【点评】本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．2．【分析】依据m2+1＞0，即可得出点P（﹣3，m2+1）在第二象限，再根据两个点关于原点对称时，它们的坐标符号相反，即可得出结论．【解答】解：∵m2+1＞0，∴点P（﹣3，m2+1）在第二象限，∴点P（﹣3，m2+1）关于原点的对称点在第四象限，故选：D．【点评】本题主要考查了关于原点对称的两个点的坐标特征，关于原点对称的两个点的横、纵坐标均互为相反数．3．【分析】把千位上的数字5进行四舍五入，然后用科学记数法表示即可．【解答】解：3465983＝3.465983×106中，万位上是6，千位上是5，则精确到万位是3.47×106．故选：C．【点评】本题考查了近似数和科学记数法．解题的关键是掌握近似数和科学记数法的定义．经过四舍五入得到的数称为近似数；用科学记数法保留有效数字，要在标准形式a×10n中a的部分保留，从左边第一个不为0的数字数起，需要保留几位就数几位，然后根据四舍五入的原理进行取舍．4．【分析】根据题意可知x﹣3≥0，直接解答即可．【解答】解：∵，即x﹣3≥0，解得x≥3，故选：B．【点评】考查二次根式的性质与化简，掌握二次根式的化简方法是解题的关键．5．【分析】等腰三角形中已知一个角，求另一个不确定的角，需要分两种情况讨论，得到所有可能的角的度数就是∠B的度数．【解答】解：等腰三角形中已知∠A＝70°，分两种情况讨论：①∠A为底角，那另外两个角为70°和40°，②∠A为顶角，那另外两个角为55°．所以∠B的度数是70°或55°或40°．故选：D．【点评】本题主要考查等腰三角形底角相等的性质，分两种情况讨论是正确解答本题的关键．6．【分析】根据式子+（k﹣2）0有意义，可以求得k的取值范围，然后即可得k﹣2和2﹣k的正负，从而可以一次函数y＝（k﹣2）x+2﹣k的图象经过的象限．【解答】解：∵式子+（k﹣2）0有意义，∴，解得k＞2，∴k﹣2＞0，2﹣k＜0，∴一次函数y＝（k﹣2）x+2﹣k的图象经过第一、三、四象限，故选：B．【点评】本题考查一次函数的图象、零指数幂，解答本题的关键是求出k的取值范围，利用一次函数的性质解答．7．【分析】分两种情况，当BD与CE无重合，当BD与CE有重合．【解答】解：∵AB的垂直平分线与AC的垂直平分线分别交BC于点D，E，∴AD＝BD，AE＝EC，分两种情况：当BD与CE无重合时，∵BC＝10，DE＝4，∴AD+AE＝BD+CE＝BC﹣DE＝10﹣4＝6，当BD与CE有重合时，∵BC＝10，DE＝4，∴AD+AE＝BD+CE＝BC+DE＝10+4＝14，综上所述：AD+AE的值为：6或14，故选：C．【点评】本题考查了线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键，同时渗透了分类讨论的数学思想．8．【分析】根据函数图象中的数据和题意，可以列出相应的二元一次方程组，然后求解即可．【解答】解：设甲车的速度为a千米/小时，乙车的速度为b千米/小时，由图可得：，解得，即甲车的速度为60千米/小时，乙车的速度为70千米/小时，故选：B．【点评】本题考查一次函数的应用、二元一次方程组的应用，利用数形结合的思想是解答本题的关键．二、填空题（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）9．【分析】根据无理数的概念可判断出无理数的个数．【解答】解：是分数，属于有理数；0，，是整数，属于有理数；﹣1.5是有限小数，属于有理数；无理数有：，2.6161161116…（每两个6之间依次增加一个1），共2个．故答案为：2．【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．10．【分析】根据算术平方根的意义可求．【解答】解：∵＝∴的算术平方根为，故答案为：【点评】本题主要考查了平方根、算术平方根概念的运用．如果x2＝a（a≥0），则x是a的平方根．若a＞0，则它有两个平方根，我们把正的平方根叫a的算术平方根；若a＝0，则它有一个平方根，即0的平方根是0.0的算术平方根也是0；负数没有平方根．11．【分析】求等腰三角形的周长，即是确定等腰三角形的腰与底的长求周长；题目给出等腰三角形有两条边长为3和8，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：（1）若3为腰长，8为底边长，由于3+3＜8，则三角形不存在；（2）若8为腰长，则符合三角形的两边之和大于第三边．所以这个三角形的周长为8+8+3＝19．故答案为：19．【点评】本题考查了等腰三角形的性质和三角形的三边关系；题目从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．12．【分析】点P在第二象限，所以横坐标为负数，纵坐标为正数，再根据到x轴，y轴的距离分别为2、3求解即可．【解答】解：∵点P在第二象限，且到x轴，y轴的距离分别为2、3，∴点P坐标为（﹣3，2），故答案为：（﹣3，2）．【点评】本题考查了点的坐标，熟练掌握平面直角坐标系内点的坐标特征是解题的关键．13．【分析】先由直线直线y＝3x+2沿y轴向下平移4个单位可得y＝3x﹣2，再根据一次函数y＝kx+b与y 轴交点为（0，b）可得答案．【解答】解：直线直线y＝3x+2沿y轴向下平移4个单位可得y＝3x+2﹣4，即y＝3x﹣2，则平移后直线与y轴的交点坐标为：（0，﹣2）．故答案为：（0，﹣2）．【点评】此题主要考查了一次函数图象的几何变换，关键是掌握直线y＝kx+b沿y轴平移后，函数解析式的k值不变，b值上移加、下移减．14．【分析】直接根据函数图象交点坐标为两函数解析式组成的方程组的解得到答案．【解答】解：∵直线y＝kx+b与直线y＝mx+n交于P（1，），、∴方程组的解为．故答案为．【点评】本题考查了一次函数与二元一次方程（组）：函数图象交点坐标为两函数解析式组成的方程组的解．15．【分析】作DE⊥AB于E，利用角平分线的性质得CD＝DE，再利用面积法求出CD的长，从而解决问题．【解答】解：作DE⊥AB于E，在Rt△ABC中，由勾股定理得，BC＝，∵AD平分∠BAC，AC⊥DC，DE⊥AB，∴CD＝DE，＝+＝，∴S△ABC∴6CD+10CD＝48，∴CD＝3，∴BD＝BC﹣CD＝8﹣3＝5，故答案为：5．【点评】本题主要考查了勾股定理，角平分线的性质，三角形的面积等知识，运用面积法求出CD的长是解题的关键．16．【分析】从图象看，当x＝1时，y＝，即BD＝1时，AD＝，当x＝7时，y＝，即BD＝7时，C、D重合，此时y＝AD＝AC＝，则CD＝6，即当BD＝1时，△ADC为以点A为顶点腰长为的等腰三角形，进而求解．【解答】解：从图象看，当x＝1时，y＝，即BD＝1时，AD＝，当x＝7时，y＝，即BD＝7时，C、D重合，此时y＝AD＝AC＝，则CD＝6，即当BD＝1时，△ADC为以点A为顶点腰长为的等腰三角形，如图：过点A作AH⊥BC于点H，在Rt△ACH中，AC＝，CH＝DH＝CD＝3，∴AH＝2，在Rt△ABH中，AB＝＝＝2，故答案为：2．【点评】本题考查的是动点问题的函数图象，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．三、解答题（本大题共有10小题，共72分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、推理过程或演算步骤）17．【分析】先计算＝4，＝3，再代入求出即可．【解答】解：原式＝4﹣3，＝1．【点评】本题考查了二次根式和立方根的计算，注意：＝4，＝3．18．【分析】根据直接开方法解方程即可．【解答】解：x2﹣9＝0x2＝9x＝±3x1＝3，x2＝﹣3．【点评】本题考查了直接开方法解一元二次方程，解决本题的关键是掌握直接开方法．19．【分析】（1）根据正数的平方根的性质解决此题．（2）根据立方根的定义解决此题．【解答】解：（1）由题得，x+5+4x﹣15＝0．∴5x＝10．∴x＝2．∴x+5＝7．∴a＝49．（2）由（1）得，a＝49．∴＝8．∴a+1的立方根是2．【点评】本题主要考查立方根、平方根，熟练掌握立方根、平方根是解决本题的关键．20．【分析】（1）由垂直的定义得到∠ACB＝∠DCE＝90°，即得出∠ECA＝∠DCB，即可利用SAS证明△DCB≌△ECA；（2）由（1）得到∠A＝∠B，由∠AGD＝∠BGC，∠B+∠BGC＝90°推出∠A+∠AGD＝90°，可得∠AFG＝90°，即可解决问题．【解答】（1）证明：∵AC⊥BC，DC⊥EC，∴∠ACB＝∠DCE＝90°，∴∠ACB+∠ACD＝∠DCE+∠ACD，即∠ECA＝∠DCB，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS）；（2）证明：如图，AC与BD相交于点G，AE与BD相交于点F，由（1）知，△ACE≌△BCD，∴∠A＝∠B，∵∠AGD＝∠BGC，∠B+∠BGC＝90°，∴∠A+∠AGD＝90°，∴∠AFG＝180°﹣90°＝90°，∴AE⊥BD．【点评】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形全等的条件，灵活运用所学知识解决问题，属于中考常考题型．21．【分析】（1）根据A点坐标建立平面直角坐标系即可；（2）分别作出各点关于x轴的对称点，再顺次连接即可；（3）作出点B关于y轴的对称点B2，连接A、B2交y轴于点P，则P点即为所求．【解答】解：（1）如图所示；（2）如图，即为所求；（3）作点B1关于y轴的对称点B2，连接C、B2交y轴于点P，则点P即为所求．设直线CB2的解析式为y＝kx+b（k≠0），∵C（﹣1，4），B2（2，﹣2），∴，解得，∴直线CB2的解析式为：y＝﹣2x+2，∴当x＝0时，y＝2，∴P（0，2）．【点评】本题考查的是作图﹣轴对称变换，熟知轴对称的性质是解答此题的关键．22．【分析】（1）利用正比例的函数的定义，设y﹣2＝kx，然后把已知的对应值代入求出k，从而得到y与x的函数表达式；（2）利用一次函数解析式确定一次函数x轴和y轴的交点坐标，然后描点画一次函数图象；（3）利用函数图象，找出直线在x轴上所对应的自变量的范围即可．【解答】解：（1）设y﹣2＝kx，把x＝﹣2，y＝4代入得4﹣2＝﹣2k，解得k＝﹣1，∴y﹣2＝﹣x，∴y与x的函数表达式为y＝﹣x+2；（2）当x＝0时，y＝2，则一次函数y轴的交点坐标为（0，2）；当y＝0时，﹣x+2＝0，解得x＝2，则一次函数x轴的交点坐标为（2，0）；如图，（3）当y＞0时，x＜2．故答案为：x＜2．【点评】本题考查了待定系数法求一次函数解析式：求一次函数y＝kx+b，则需要两组x，y的值．也考查了一次函数的性质．23．【分析】（1）①作线段AC的垂直平分线交AB于点P，连接PC，△PAC即为所求；②作∠CPB的角平分线PD即可；（2）利用平行线的性质以及等腰三角形的性质解决问题即可．【解答】解：（1）①如图，△APC即为所求；②如图，射线PD即为所求．（2）∵PD∥AC，∴∠BPD＝∠A＝32°，∵PA＝PC，∴∠ACP＝∠A＝32°，故答案为：32．【点评】本题考查作图﹣复杂作图，线段的垂直平分线的性质，角平分线的定义，等腰三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．24．【分析】（1）在Rt△ABC中，根据勾股定理即可求得BC的长；（2）利用勾股定理逆定理即可证明△BCD是直角三角形．【解答】（1）解：∵Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，∴BC＝＝＝5；（2）证明：∵在△BCD中，CD＝4，BD＝3，BC＝5，∴CD2+BD2＝42+32＝52＝BC2，∴△BCD是直角三角形．【点评】本题考查了勾股定理及其逆定理．勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．掌握定理是解题的关键．25．【分析】（1）根据题意和题目中的数据，可以写出y关于x的函数解析式；（2）根据该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的3倍，可以得到相应的不等式，从而可以得到x的取值范围，再根据（1）中的函数关系式和一次函数的性质，即可得到当购进A型、B型电脑各多少台，才能使销售总利润最大，最大利润为多少．【解答】解：（1）由题意可得，y＝100x+150（100﹣x）＝﹣50x+15000，即y关于x的函数解析式为y＝﹣50x+15000；（2）∵B型电脑的进货量不超过A型电脑的3倍，∴100﹣x≤3x，解得x≥25，∵y＝﹣50x+15000，k＝﹣50＜0，∴y随x的增大而减小，∴当x＝25时，y取得最大值，此时y＝13750，100﹣x＝75，答：该商店购进A型25台、B型电脑75台时，才能使销售总利润最大，最大利润为13750元．【点评】本题考查一次函数的应用、一元一次不等式的应用，解答本题的关键是明确题意，列出相应的函数关系式和不等式，利用一次函数的性质解答．26．【分析】（1）将C（1，0）．D（0，2）代入y＝kx+b即可得出k和b的值；（2）首先求出点E的坐标，过点E作EF⊥x轴于F，利用AAS证明△DOC≌△EFC即可；（3）当点P在点B上方时，则OP∥DE，得直线OP的函数解析式为y＝﹣2x，可求出交点P的坐标，当点P在点B的下方时，设点P关于y轴的对称点为Q，连接OQ交l1为点P'，同理求出直线OQ的函数解析式，从而解决问题．【解答】解：（1）将C（0.5，0）．D（0，2）代入y＝kx+b得，，解得，∴直线l2的函数解析式为y＝﹣2x+2；（2）当﹣2x+2＝x﹣4时，∴x＝2，∴E（2，﹣2），过点E作EF⊥x轴于F，∴EF＝OD＝2，∵∠ODC＝∠CEF，∠DCO＝∠ECF，∴△DOC≌△EFC（AAS），∴CD＝CE；（3）∵∠POB＝∠BDE，∴点P在l1上有两个位置，当点P在点B上方时，如图，∴OP∥DE，∴直线OP的函数解析式为y＝﹣2x，∴﹣2x＝x﹣4，∴x＝，当x＝时，y＝﹣，∴P（，﹣），当点P在点B的下方时，设点P关于y轴的对称点为Q，连接OQ交l1为点P'，∴Q（﹣，﹣），则直线OQ的函数解析式为y＝2x，∴直线OQ与l1的交点为P'（﹣4，﹣8），综上所述：P（，﹣）或（﹣4，﹣8）．【点评】本题是一次函数综合题，主要考查了一次函数图象交点问题，全等三角形的判定与性质，待定系数法求函数解析式等知识，明确两直线平行则k值相等是解题的关键。

江苏省南京市八年级上学期期末数学试卷 （解析版）一、选择题1．在3π-，3127-，7，227-，中，无理数的个数是（ ） A ．1个 B ．2个 C ．3个D ．4个 2．在直角坐标系中,函数y kx =与12y x k =-的图像大数是（ ） A ． B ．C ．D ．3．如图，以Rt ABC ∆的三边为边，分别向外作正方形，它们的面积分别为1S 、2S 、3S ，若12316S S S ++=，则1S 的值为（ ）A ．7B ．8C ．9D ．10 4．如图，已知△ABC 的三条边和三个角，则甲、乙、丙三个三角形中和△ABC 全等的是（ ）A ．甲和乙B ．甲和丙C ．乙和丙D ．只有乙 5．在平面直角坐标系中，把直线23y x =-沿y 轴向上平移2个单位后，所得直线的函数表达式为（ ）A ．22y x =+B ．25y x =-C ．21y x =+D ．21y x =-6．如图，直线(0)y x b b =+>分别交x 轴、y 轴于点A 、B ，直线(0)y kx k =<与直线(0)y x b b =+>交于点C ，点C 在第二象限，过A 、B 两点分别作AD OC ⊥于D ，BE OC ⊥于E ，且8BE BO +=，4=AD ，则ED 的长为（ ）A ．2B ．32C ．52D ．17．如图，若一次函数y ＝﹣2x +b 的图象与两坐标轴分别交于A ，B 两点，点A 的坐标为（0，3），则不等式﹣2x +b ＞0的解集为（ ）A ．x ＞32B ．x ＜32C ．x ＞3D ．x ＜38．下列计算，正确的是（ ）A ．a 2﹣a=aB ．a 2•a 3=a 6C ．a 9÷a 3=a 3D ．（a 3）2=a 6 9．在平面直角坐标系中，点M （﹣3，2）关于y 轴对称的点的坐标为（ ）A ．（﹣3，﹣2）B ．（﹣2，﹣3）C ．（3，2）D ．（3，﹣2） 10．如图，点B 、F 、C 、E 在一条直线上，AB ∥ED ，AC ∥FD ，那么添加下列一个条件后，仍无法判定△ABC ≌△DEF 的是（ ）A ．AB =DE B ．AC =DF C ．∠A =∠D D ．BF =EC二、填空题11．若函数4y kx =-的图象平行于直线2y x =-，则函数的表达式是________．12．如图，在平面直角坐标系中，点P (﹣1，a )在直线y ＝2x +2与直线y ＝2x +4之间，则a 的取值范围是_____．13．如图，已知直线y ＝ax ﹣b ，则关于x 的方程ax ﹣1＝b 的解x ＝_____．14．若等腰三角形的顶角为100︒，则这个等腰三角形的底角的度数__________．15．将一次函数2y x =-的图象平移，使其经过点（2，3），则所得直线的函数解析式是______．16．如图①，四边形ABCD 中，//,90BC AD A ∠=︒，点P 从A 点出发，沿折线AB BC CD →→运动，到点D 时停止，已知PAD △的面积s 与点P 运动的路程x 的函数图象如图②所示，则点P 从开始到停止运动的总路程为________.17．下图所示的网格是正方形网格，BAC ∠________DAE ∠．（填“>”，“=”或“<”）18．如图，已知ABD CBD ∠∠=，若以“SAS”为依据判定ABD ≌CBD ，还需添加的一个直接条件是______．19．已知点M(-1,a)和点N(-2,b)是一次函数y=-2x+1图象上的两点,则a 与b 的大小关系是__________。

江苏省南京市八年级上学期期末数学试卷 （解析版）一、选择题y 1．若点 在 轴负半轴上，则点 的坐标有可能是（ ） P P1,0 0,2 3,00,4A ．B ．C ．D ． D ． 2．在平面直角坐标系中，下列各点位于第四象限的点是( )(2,3) (4,5 ) (1,0)C ．(8,1) A ． B ． 3．如图，△ABC 中，AB ＝AC ，AD 是∠BAC 的平分线．已知 AB ＝5，AD ＝3，则 BC 的长为（）A ．5B ．6C ．8D ．104．某种产品的原料提价，因而厂家决定对产品提价，现有三种方案： % % 方案（一）：第一次提价 p ，第二次提价q ； % % 方案（二）：第一次提价q ，第二次提价 p ；p q% 方案（三）：第一、二次提价均为 ； 2其中 p ， 是不相等的正数. q 有以下说法：①方案（一）、方案（二）提价一样；②方案（一）的提价也有可能高于方案（二）的提价； ③三种方案中，以方案（三）的提价最多；④方案（三）的提价也有可能会低于方案（一）或方案（二）的提价. 其中正确的有（ ） A ．②③B ．①③C ．①④D ．②④5．如图，若一次函数 y ＝﹣2x +b 的图象与两坐标轴分别交于 A ，B 两点，点 A 的坐标为 （0，3），则不等式﹣2x +b ＞0 的解集为（）3 23 2A ．x ＞B ．x ＜C ．x ＞3D ．x ＜3P m 4，m 1一定不在6．如果 m 是任意实数，则点 A ．第一象限B ．第二象限7．下列计算，正确的是（C ．第三象限D ．第四象限）A ．a 2﹣a=aB ．a 2•a =a C ．a ÷a =a3D ．（a 3）2=a 63 69 3 8．在△ABC 中，∠ACB ＝90°，CD ⊥AB 于点 D ，∠A ＝30°，以下说法错误的是（ ）A ．AC ＝2CDB ．AD ＝2CDC ．AD ＝3BD D ．AB ＝2BC ）9．下列各点中，在第四象限且到 x 轴的距离为 3 个单位的点是（A ．（﹣2，﹣3）B ．（2，﹣3）C ．（﹣4，3）D ．（3，﹣4）110．将直线 y ＝ x ﹣1 向右平移 3 个单位，所得直线是（）2 1 A ．y ＝ x +22 1 B ．y ＝ x ﹣421C ．y ＝ x ﹣2 5 21 1 D ．y ＝ x +2 2二、填空题11．若函数 y ＝2x +3﹣m 是正比例函数，则 m 的值为_____． 3x 1 P(m,n) y 的图像上，则 m 2mn n 2 96___________.12．已知点 在一次函数 13．矩形 ABCD 中，其中三个顶点的坐标分别是（0，0）、（5，0）、（5，3），则第四 个顶点的坐标是______．14．等腰三角形中有一个角的度数为 40°，则底角为_____________. 3x y ax 4 的图像相交于点 A （m ，3），则不等式3x a x 4和15．如图，函数 y 的解集为____．16．如图，已知直线 y ＝ax ﹣b ，则关于 x 的方程 ax ﹣1＝b 的解 x ＝_____．A 2,3y 17．点关于 轴对称点的坐标是______.x , y ykx b ymx n 18．已知一次函数 与 的函数图像如图所示，则关于 的二元一12k x y b 0,次方程组 mx y n 0的解是______．19．平行四边形的周长是 20，两条对角线相交于 O ，△AOB 的周长比△BOC 的周长大 2，则 AB 的长为_____．20．计算： 16 =_______．三、解答题21．小丽骑车从甲地到乙地，小明骑车从乙地到甲地，小丽的速度小于小明的速度，两人同时出发，沿同一条公路匀速前进.图中的折线表示两人之间的距离 y(km)与小丽的行驶时 间 x (h)之间的函数关系.请你根据图像进行探究：k m/h ，小明的速度是_________km/h（1）小丽的速度是______ ；（2）求线段 BC 所表示的 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围； （3）若两人相距20km，试求小丽的行驶时间？ 22．求下列各式中 x 的值： （1） 24 0 ；x 2x16 （2） 3 kx23．如图，反比例函数y与一次函数 y=x+b 的图象，都经过点 A （1，2）（1）试确定反比例函数和一次函数的解析式； （2）求一次函数图象与两坐标轴的交点坐标．24．甲、乙两个工程队同时挖掘两段长度相等的隧道，如图是甲、乙两队挖掘隧道长度y x (米)与挖掘时间 (时)之间关系的部分图象.请解答下列问题:1在前2 小时的挖掘中，甲队的挖掘速度为 米/小时，乙队的挖掘速度为 米/小时.22 x 6时，求出 与 之间的函数关系式;x ①当 y 乙 5 ②开挖几小时后，两工程队挖掘隧道长度相差米? / /CD ，E 是 AB 的中点，CE DE，求证： A C BD．25．已知，如图， AB 四、压轴题26．如图，已知 A(3，0)，B(0，-1)，连接 AB ，过 B 点作 AB 的垂线段 BC ，使 BA=BC ，连接 AC（1）如图 1，求 C 点坐标；（2）如图 2，若 P 点从 A 点出发沿 x 轴向左平移，连接 BP ，作等腰直角 BP Q ，连接 CQ ，当点 P 在线段 OA 上，求证：PA=CQ ；（3）在（2）的条件下若 C 、P ，Q 三点共线，直接写出此时∠APB 的度数及 P 点坐标27．直角三角形ABC中，∠ACB=90°，直线l过点C．（1）当AC=BC时，如图①，分别过点A、B作AD⊥l于点D，BE⊥l于点E．求证：△ACD≌△CBE．（2）当AC=8，BC=6时，如图②，点B与点F关于直线l对称，连接BF，CF，动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动，同时动点N从点F出发，以每秒3个单位的速度沿F→C→B→C→F向终点F运动，点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D，过点N作NE⊥l于点E，设运动时间为t秒．①CM=，当N在F→C路径上时，CN=．（用含t的代数式表示）②直接写出当△MDC与△CEN全等时t的值．28．在平面直角坐标系xOy中，若P，Q为某个矩形不相邻的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．图1为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，2）．（1）如图2，点B的坐标为（b，0）．①若b＝﹣2，则点A，B的“相关矩形”的面积是②若点A，B的“相关矩形”的面积是8，则b的值为；．（2）如图3，点C在直线y＝﹣1上，若点A，C的“相关矩形”是正方形，求直线AC的表达式；（3）如图4，等边△DEF的边DE在x轴上，顶点F在y轴的正半轴上，点D的坐标为（1，0）．点M的坐标为（m，2），若在△DEF的边上存在一点N，使得点M，N的“相关矩形”为正方形，请直接写出m的取值范围．29．已知在△ABC中，AB=AC，∠BAC=α，直线l经过点A（不经过点B或点C），点C关于直线l的对称点为点D，连接BD，CD．（1）如图1，①求证：点B，C，D在以点A为圆心，AB为半径的圆上；②直接写出∠BDC的度数（用含α的式子表示）为；（2）如图2，当α=60°时，过点D作BD的垂线与直线l交于点E，求证：AE=BD；（3）如图3，当α=90°时，记直线l与CD的交点为F，连接BF．将直线l绕点A旋转的过程中，在什么情况下线段BF的长取得最大值？若AC=22a，试写出此时BF的值．30．如图，已知直线l：y＝2x+1与坐标轴交于A、C两点，直线l：y＝﹣x﹣2与坐标轴1122交于B、D两点，两直线的交点为P点．(1)求P点的坐标；(2)求△APB的面积；(3)x轴上存在点T，使得S△ATP＝S△APB，求出此时点T的坐标．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】根据y轴上的点的坐标特点，横坐标为0，然后根据题意求解.【详解】解：∵y轴上的点的横坐标为0，又因为点P在y轴负半轴上，∴（0，-2）符合题意故选：B【点睛】本题考查坐标轴上的点的坐标特点，利用数形结合思想解题是本题的解题关键. 2．A解析：A【解析】【分析】根据平面直角坐标系中各象限内点的坐标特征对各选项分析判断即可得解.【详解】解：A.(2,-3)在第四象限，故本选项正确；B.(-4,5)在第二象限，故本选项错误；C.(1,0)在x轴正半轴上，故本选项错误；D.(-8,-1)在第三象限，故本选项错误.故选A.【点睛】本题考查了平面直角坐标系中象限内点的坐标特征，解决本题的关键是熟练掌握每个象限 的坐标特征.3．C解析：C 【解析】 【分析】根据等腰三角形的三线合一得出∠ADB=90°，再根据勾股定理得出 BD 的长，即可得出 BC 的长. 【详解】在△ABC 中，AB ＝AC ，AD 是∠BAC 的平分线， AD BC ，BC=2BD. ∠ADB=90°5 -3 22=4在 Rt △ABD 中，根据勾股定理得：BD= = AB 2 AD 2 BC=2BD=2×4=8. 故选 C. 【点睛】本题考查了等腰三角形的性质及勾股定理，熟练掌握性质定理是解题的关键.4．B解析：B 【解析】 【分析】根据提价方案求出提价后三种方案的价格，得到方案（一）、方案（二）、方案（三）提 价情况，进行对比即可得解. 【详解】∵方案（一）：(1 p %)(1 q %) 1 p % q % p%q %方案（二）：(1q%)(1 p %) 1 q % p % q % p%∴方案（一）、方案（二）提价一样 ∴①对，②错； p q p q p q ∵方案（三）：(1∴可知：%)(1 %) 1 p % q% ( %)2 2 2 2p q p q1 p % q % ( p q %) (1 p % q % p %q %) ( %) p %q %2 2 2 2( %)2 2q ∵ p ， 是不相等的正数p q( %) 0 ∴ 2 2∴方案（三）提价最多∴③对，④错∴①③对故选：B.【点睛】本题主要考查了销售问题中的增长率问题，熟练掌握增长率的相关知识及整式的乘法化简是解决本题的关键.5．B解析：B【解析】【分析】根据点A的坐标找出b值，令一次函数解析式中y=0求出x值，从而找出点B的坐标，观察函数图象，找出在x轴上方的函数图象，由此即可得出结论．【详解】解：∵一次函数y＝﹣2x+b的图象交y轴于点A（0，3），∴b＝3，3令y＝﹣2x+3中y＝0，则﹣2x+3＝0，解得：x＝，23∴点B（，0）．2观察函数图象，发现：3当x＜时，一次函数图象在x轴上方，23∴不等式﹣2x+b＞0的解集为x＜．2故选：B．【点睛】本题考查了一次函数与一元一次不等式，解题的关键是找出交点B的坐标．本题属于基础题，难度不大，解决该题型题目时，根据函数图象的上下位置关系解不等式是关键．6．D解析：D【解析】【分析】求出点P的纵坐标一定大于横坐标，然后根据各象限的点的坐标特征解答．【详解】m 1m 4m 1m 450∵，∴点P的纵坐标一定大于横坐标．．∵第四象限的点的横坐标是正数，纵坐标是负数，∴第四象限的点的横坐标一定大于纵坐标．∴点P一定不在第四象限．故选D．7．D解析：D【解析】【详解】A、a-a，不能合并，故A错误；2B、a•a=a，故B错误；235C、a÷a=a，故C错误；936D、（a）=a，故D正确，3故选D．8．B26解析：B【解析】【分析】在Rt△ABC中，由∠A的度数求出∠B的度数，在Rt△BCD中，可得出∠BCD度数为30°，根据直角三角形中，30°所对的直角边等于斜边的一半，得到BC=2BD，由BD的长求出BC 的长，在Rt△ABC中，同理得到AB=2BC，于是得到结论．【详解】解：∵△ABC中，∠ACB＝90°，∠A＝30°，∴AB＝2BC；∵CD⊥AB，∴AC＝2CD，∴∠B＝60°，又CD⊥AB，∴∠BCD＝30°，在Rt△BCD中，∠BCD＝30°，CD＝3BD，3CD3BD在Rt△ABC中，∠A＝30°，AD＝＝，故选：B．【点睛】此题考查了含30°角直角三角形的性质，以及三角形的内角和定理，熟练掌握性质是解本题的关键．9．B解析：B【解析】【分析】首先确定各点所在象限，再根据到x轴的距离为3个单位可得此点的纵坐标的绝对值为3，进而可得答案．【详解】A、（﹣2，﹣3）在第三象限，故此选项不合题意；B、（2，﹣3）在第四象限，到x轴的距离为3个单位，故此选项符合题意；C、（﹣4，3）在第二象限，故此选项不合题意；D、（3，﹣4）在第四象限，到x轴的距离为4个单位，故此选项不符合题意；故选：B．【点睛】此题主要考查根据象限判定坐标，熟练掌握，即可解题.10．C解析：C【解析】【分析】直接根据“左加右减”的原则进行解答即可．【详解】1由“左加右减”的原则可知，将直线y=x﹣1向右平移3个单位，所得直线的表达式是21y=（x﹣3）﹣1，215即y=x﹣．22故选：C．【点睛】此题主要考查一次函数的平移，熟练掌握平移规律，即可解题.二、填空题11．【解析】【分析】直接利用正比例函数的定义得出答案．【详解】∵函数y=2x+3﹣m是正比例函数，∴3﹣m=0，解得：m=3．故答案为：3．【点睛】本题考查的是正比例函数的定义，一般解析：【解析】【分析】直接利用正比例函数的定义得出答案．【详解】∵函数y=2x+3﹣m是正比例函数，∴3﹣m=0，解得：m=3．故答案为：3．【点睛】y kx（k是常数，k≠0）的函数叫做正比本题考查的是正比例函数的定义，一般地形如例函数．12．1【解析】【分析】直接利用一次函数图象上点的坐标性质直接代入求出即可．【详解】把x=m，y=n代入y=3x-1，可得：n=3m-1，把n=3m-1代入===．故答案为：1.【解析：1【解析】【分析】直接利用一次函数图象上点的坐标性质直接代入求出即可．【详解】把x=m，y=n代入y=3x-1，可得：n=3m-1，把n=3m-1代入9m 6mn n229m 6m(3m 1)(3m 1)==229m 18m 6m 9m 6m 1222=1．故答案为：1.【点睛】此题主要考查了一次函数图象上点的坐标性质，正确代入点的坐标求出是解题关键．13．（0，3）【解析】【分析】画图分析，由矩形的性质求得第四点的坐标，再解答．【详解】如图，根据图形易知第四点的坐标是（0，3）．故填：（0，3）．【点睛】用到的知识点为：矩形的邻边垂直解析：（0，3）【解析】【分析】画图分析，由矩形的性质求得第四点的坐标，再解答．【详解】如图，根据图形易知第四点的坐标是（0，3）．故填：（0，3）．【点睛】用到的知识点为：矩形的邻边垂直，对边平行．本题画出图后可很快求解．14．40°或70°【解析】解：当40°的角为等腰三角形的顶角时，底角的度数=（180°-40°）÷2=70°；当40°的角为等腰三角形的底角时，其底角为40°，故它的底角的度数是70°或40°．故解析：40°或70°【解析】解：当 40°的角为等腰三角形的顶角时，底角的度数=（180°-40°）÷2=70°； 当 40°的角为等腰三角形的底角时，其底角为40°，故它的底角的度数是 70°或 40°． 故答案为：40°或 70°．点睛：此题主要考查学生对等腰三角形的性质这一知识点的理解和掌握，由于不明确40° 的角是等腰三角形的底角还是顶角，所以要采用分类讨论的思想．15．x ＜-1．【解析】【分析】由图象可知，在点 A 的左侧，函数的图像在的图像的上方，即，所以求出点 A 的坐标后结合图象即可写出不等式的解集．【详解】解：∵和的图像相交于点 A （m ，3），∴∴∴解析：x ＜-1．【解析】【分析】由图象可知，在点 A 的左侧，函数 的图像在 y 3x y ax 4 的图像的上方，即 3x ax 4 ，所以求出点 A 的坐标后结合图象即可写出不等式3x ax 4 的解集．【详解】解：∵ y 3x y ax 4和 的图像相交于点 A （m ，3），∴3 3mm 1 ∴ ∴交点坐标为 A （-1，3）， 由图象可知，在点 A 的左侧，函数 的图像在 y 3x y ax 4 的图像的上方， 3x ax 4即 ∴不等式3x a x 4 故答案是：x ＜-1．【点睛】的解集为 x ＜-1． 此题主要考查了一次函数与一元一次不等式的关系，用图象法解不等式的关键是找到y 相 等时的分界点，观察分界点左右图象的变化趋势，即可求出不等式的解集，重点要掌握利 用数形结合的思想． 16．4【解析】【分析】观察图形可直接得出答案.【详解】解：根据图形知，当y＝1时，x＝4，即ax﹣b＝1时，x＝4．故方程ax﹣1＝b的解是x＝4．故答案为4．【点睛】此题考查一次函解析：4【解析】【分析】观察图形可直接得出答案.【详解】解：根据图形知，当y＝1时，x＝4，即ax﹣b＝1时，x＝4．故方程ax﹣1＝b的解是x＝4．故答案为4．【点睛】此题考查一次函数与一元一次方程的联系，渗透数形结合的解题思想．17．（−2，3）【解析】【分析】平面直角坐标系中任意一点P（x，y），关于y轴的对称点的坐标是（−x，y），即关于y轴的对称点，纵坐标不变，横坐标变成相反数．【详解】解：点（2，3）关于y轴对解析：（2，3）【解析】【分析】平面直角坐标系中任意一点P（x，y），关于y轴的对称点的坐标是（−x，y），即关于y 轴的对称点，纵坐标不变，横坐标变成相反数．【详解】解：点（2，3）关于y轴对称的点的坐标是（−2，3），故答案为（−2，3）．【点睛】本题主要考查了平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点：关于y轴对称的点，纵坐标相同，横坐标互为相反数，关于x轴对称的点，横坐标相同，纵坐标互为相反数．18．【解析】【分析】根据函数图象交点坐标为两函数解析式组成的方程组的解，从而可得答案．【详解】解：∵一次函数和一次函数的图象交点的坐标为∴方程组的解是： ．故答案为： ．【点睛】本题x 1 解析： y 2【解析】【分析】根据函数图象交点坐标为两函数解析式组成的方程组的解，从而可得答案．【详解】 1,2 ,的图象交点的坐标为 y kx b 1 y mx n2 解：∵一次函数 和一次函数 k x y b 0x 1 ∴方程组 的解是： ． mx y n 0 y 2 x1 故答案为：．y 2 【点睛】 本题主要考查了函数解析式与图象的关系，满足解析式的点就在函数的图象上，在函数的 图象上的点，就一定满足函数解析式．函数图象交点坐标为两函数解析式组成的方程组的 解．掌握以上知识是解题的关键．19．6【解析】【分析】由已知可得到 AB 比 BC 长 2，根据平行四边形的周长可得到 AB 与 BC 的和，从 而不难求得 AB 的长．【详解】解：∵△AOB 的周长比△BOC 的周长大 2，∴OA+OB+AB -OB-解析：6【解析】【分析】由已知可得到 A B 比 B C 长 2，根据平行四边形的周长可得到 A B 与 BC 的和，从而不难求得A B的长．【详解】解：∵△A O B的周长比△B O C的周长大2，∴O A+O B+A B-OB-O C-BC=2，∵A B C D是平行四边形，∴O A=O C，∴A B-BC=2，∵平行四边形A B C D的周长是20，∴A B+B C=10，∴A B=6．故答案为：6．【点睛】此题主要考查学生对平行四边形的性质的理解及运用，熟记性质是解题的关键．20．4【解析】【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【详解】解：原式==4．故答案为4．【点睛】此题主解析：4【解析】【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【详解】解：原式=42=4．故答案为4．【点睛】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．三、解答题1 30x 30 (1 x 1.5) 21．（1）10；20；（2） y ；（3） 小时或2 小时 3【解析】【分析】（1）根据题意和函数图象中的数据可以分别求得小丽和小明的速度；（2）根据（1）中的结果和图象中的数据可以求得点 C 的坐标，从而可以解答本题（3）根据题意分情况讨论即可求解.【详解】（1）从 可以看出：两人从相距 30 千米的两地相遇用了 1 个小时时间，AB V V 30 则 千米/时，小丽用了 3 个小时走完了 30 千米的全程， 千米/时，小丽小明 ∴ V10 20 小丽 ∴ V 千米/时；小明 故答案为：10；20； （2）C 点的意义是小明骑车从乙地到甲地用了3020 1.5小时，1.51 30 15 此时小丽和小明的距离是 ∴ C 点坐标是(1.5,15). 设 BC 对应的函数表达式为 y k x b ， k b 0 B 1,0 C 1.5,15 则将点 ， 分别代入表达式得 1.5k b 15，k 30 解得： b 30，y 30x 30 (1 x 1.5)，∴ BC 解析式为 1 （3）①当两人相遇前：(30 20) (20 10) （小时）； 3②当两人相遇后：1.5 510 2 （小时）.1 答：小丽出发 小时或2 小时时，两人相距 20 公里. 3【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合 的思想解答． 2 x 2x 2 或 ；（2） 22．（1） x 【解析】【分析】（1）根据平方根的性质解方程即可；（2）根据立方根的性质解方程即可．【详解】解：（1） 24 0xx 2 4 2 x 2 或 解得： x 2x 16 （2） 3 3 8x 2解得： x 【点睛】此题考查的是含平方和立方的方程，掌握平方根的性质和立方根的性质是解决此题的关 键．2 y 23．（1）反比例函数的解析式为 ，一次函数的解析式为 y ＝x ＋1． x（2）（-1,0）与（1,0）．【解析】【分析】k xy （1）将点 A （1，2）分别代入 与 y=x+b 中，运用待定系数法即可确定出反比例解析 式和一次函数解析式．（2）对于一次函数解析式，令 x=0，求出对应 y 的值，得到一次函数与 y 轴交点的纵坐 标，确定出一次函数与 y 轴的交点坐标；令 y=0，求出对应 x 的值，得到一次函数与 x 轴 交点的横坐标，确定出一次函数与 x 轴的交点坐标．【详解】k y 解： （1）∵ 反比例函数 与一次函数 y ＝x ＋b 的图象，都经过点 A （1,2）， x∴ 将 x=1，y=2 代入反比例解析式得：k=1×2=2，将 x=1，y=2 代入一次函数解析式得：b=2－1=1，2 ∴ 反比例函数的解析式为y ，一次函数的解析式为 y ＝x ＋1． x（2）对于一次函数 y=x+1，令 y=0，可得 x=-1；令 x=0，可得 y=1．∴ 一次函数图象与两坐标轴的交点坐标为（-1,0）与（1,0）．y5x 20 z 3 5 ;②挖掘1小时或 小时或 小时后两工程队相距 5 米. 24．(1)10;15; (2) ① 【解析】【分析】(1)分别根据速度=路程除以时间列式计算即可得解;kx b , (2)①设 y 然后利用待定系数法求一次函数解析式解答即可;乙 y -y = 5，y -y =5 ②求出甲队的函数解析式，然后根据 列出方程求解即可. 甲 乙 乙 甲【详解】 606 10米/小时，1 甲队:乙队: 302 15米/小时:故答案为:10,15; 2 2 x 6 y kx b z①当 时，设 ， 2k b 30则， 6k b 50 k 5解得 ， b 202 x 6时， y 5 20;当x z ②易求得:当0 x 2时， y15x z 2 x 6时，5 20 0 x6 y x ， 当;当 时 z y =10x ， 甲 10x 5x 20 4 由解得 x ， 0 x 215x 10x 5 x 1， 1° 当 2°当 解得: x ， ，解得: 5x 20 10x 52 x 4 ，3， 4 x 610 5 20 5 ，x x 3°当 ， 5解得: x 3 5 5 答:挖掘1小时或 小时或 小时后，两工程队相距 米.【点睛】本题考查了一次函数的应用， 主要利用了待定系数法求一-次函数解析式，准确识图获取 必要的信息是解题的关键，也是解题的难点.25．见解析【解析】【分析】由 CE=DE 易得∠ ECD=∠ EDC ，结合 AB ∥ CD 易得∠ AEC=∠ BED ，由此再结合 AE=BE ，CE=DE 即可证得△AEC ≌ △ BED ，由此即可得到 AC=BD.【详解】C E DE ∵ ，EC D ED C ∴ ，//CD ∵ AB ， ∴ ∴ ， AEC EC D BE D EDC ， AEC BE D ，又∵ E 是 AB 的中点，BE ∴ AE ，AE BE AEC BE D C E DE 在 AE C 和 BED 中， ，∴ AE C ≌ ．BE D ∴ AC BD ．【点睛】熟悉“等腰三角形的性质、平行线的性质和全等三角形的判定方法”是解答本题的关键.四、压轴题APB 135 ,P 1, 0 26．（1）(1，-4)；（2）证明见解析；（3） 【解析】【分析】 （1）作 CH ⊥y 轴于 H ，证明△ABO ≌△BCH ，根据全等三角形的性质得到 BH=OA=3， CH=OB=1，求出 OH ，得到 C 点坐标；（2）证明△PBA ≌△QBC ，根据全等三角形的性质得到 PA=CQ ；（3）根据 C 、P ，Q 三点共线，得到∠BQC=135°，根据全等三角形的性质得到∠BPA=∠BQC=135°，根据等腰三角形的性质求出 OP ，得到 P 点坐标．【详解】解：(1)作 CH ⊥y 轴于 H ，则∠BCH+∠CBH=90°，BC 因为 AB ，所以.∠ABO+∠CBH=90°，所以∠ABO=∠BCH ，在△ABO 和△BCH 中，ABOBC H AOB BH CAB BC AB O BCH:BH=OA=3，CH=OB=1，:OH=OB+BH=4，所以 C 点的坐标为（1，-4）；(2)因为∠PBQ=∠ABC=90°，PB Q AB Q ABC ABQ,PBA QB C在△PBA 和△QBC 中， BP B Q PBA QBCBA BCPBA QBC:.PA=CQ ；APB 135 ,P 1,0 (3)BPQ 是等腰直角三角形，:所以∠BQP=45°，当 C 、P ，Q 三点共线时，∠BQC=135°， 由（2)可知，PBA QBC； 所以∠BPA=∠BQC=135°，所以∠ OPB=45°，所以.OP=OB=1，所以 P 点坐标为（1，0) ．【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质，掌握全等三角形的判定定 理和性质定理是解题的关键．27．（1）证明见解析；（2）①CM=8t ，CN=6 3t ；②t=3.5 或 5 或 6.5．【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB ，利用 AAS 定理证明△ACD ≌△CBE ；（2）①由折叠的性质可得出答案；②动点 N 沿 F→C 路径运动，点 N 沿 C→B 路径运动，点 N 沿 B→C 路径运动，点 N 沿 C→F 路径运动四种情况，根据全等三角形的判定定理列式计算．【详解】（1）∵AD ⊥直线l ，BE ⊥直线l ，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中， ADC ＝CEB DAC ＝ECB C A ＝CB ，∴△ACD ≌△CBE （AAS ）；（2）①由题意得，AM=t ，FN=3t ，则 CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t ；故答案为：8-t ；6-3t ；②由折叠的性质可知，∠BCE=∠FCE ，∵∠MCD+∠CMD=90°，∠MCD+∠BCE=90°，∴∠NCE=∠CMD ，∴当 CM=CN 时，△MDC 与△CEN 全等，当点 N 沿 F→C 路径运动时，8-t=6-3t ，解得，t=-1（不合题意），当点 N 沿 C→B 路径运动时，CN=3t -6，则 8-t=3t -6，解得，t=3.5，当点 N 沿 B→C 路径运动时，由题意得，8-t=18-3t ，解得，t=5，当点 N 沿 C→F 路径运动时，由题意得，8-t=3t -18，解得，t=6.5，综上所述，当 t=3.5 秒或 5 秒或 6.5 秒时，△MDC 与△CEN 全等．【点睛】本题考查了折叠的性质，全等三角形的判定和性质，掌握全等三角形的判定定理和性质定 理，灵活运用分情况讨论思想是解题的关键．28．（1）①6；②5 或﹣3；（2）直线 AC 的表达式为：y ＝﹣x+3 或 y ＝x+1；（3）m 的 3 3≤m ≤3．取值范围为﹣3≤m ≤﹣2+ 或 2﹣ 【解析】【分析】（1）①由矩形的性质即可得出结果；②由矩形的性质即可得出结果；（2）过点 A （1，2）作直线 y ＝﹣1 的垂线，垂足为点 G ，则 AG ＝3 求出正方形 AGCH 的 边长为 3，分两种情况求出直线 AC 的表达式即可；1 （3）由题意得出点 M 在直线 y ＝2 上，由等边三角形的性质和题意得出OD ＝OE ＝ DE ＝ 21，EF ＝DF ＝DE ＝2，得出 OF ＝ 3 OD ＝ 3 ，分两种情况：①当点 N 在边 EF 上时，若点 N 与 E 重合，点 M ，N 的“相关矩形”为正方形，则点 M 的 坐标为（﹣3，2）或（1，2）；若点 N 与 F 重合，点 M ，N 的“相关矩形”为正方形，则3 2 3 m 2+ 3 点 M 的坐标为（﹣2+ ， ）；得出 m 的取值范围为﹣ ≤ ≤﹣ 或 2﹣3 ≤m ≤1；②当点 N 在边 DF 上时，若点 N 与 D 重合，点 M ，N 的“相关矩形”为正方形，则点 M 的坐标为（3，2）或（﹣1，2）；若点 N 与 F 重合，点 M ，N 的“相关矩形”为正方形，3 2 2 3 m 3 ≤ ≤ 或 ﹣ 2 则点 M 的坐标为（2﹣ ， ）；得出 m 的取值范围为 ﹣ 3 m 1≤ ≤ ；即可得出结论．【详解】解：（1）①∵b ＝﹣2，∴点 B 的坐标为（﹣2，0），如图 2﹣1 所示：∵点 A 的坐标为（1，2），∴由矩形的性质可得：点 A ，B 的“相关矩形”的面积＝（1+2）×2＝6，故答案为：6；②如图2﹣2所示：由矩形的性质可得：点A，B的“相关矩形”的面积＝|b﹣1|×2＝8，∴|b﹣1|＝4，∴b＝5或b＝﹣3，故答案为：5或﹣3；（2）过点A（1，2）作直线y＝﹣1的垂线，垂足为点G，则AG＝3，∵点C在直线y＝﹣1上，点A，C的“相关矩形”AGCH是正方形，∴正方形AGCH的边长为3，当点C在直线x＝1右侧时，如图3﹣1所示：CG＝3，则C（4，﹣1），设直线AC的表达式为：y＝kx+a，2k a则，14k a1k解得；，a3∴直线AC的表达式为：y＝﹣x+3；当点C在直线x＝1左侧时，如图3﹣2所示：CG＝3，则C（﹣2，﹣1），设直线AC的表达式为：y＝k′x+b，2k b则，12k bk1解得：，b1∴直线AC的表达式为：y＝x+1，综上所述，直线AC的表达式为：y＝﹣x+3或y＝x+1；（3）∵点M的坐标为（m，2），∴点M在直线y＝2上，∵△DEF是等边三角形，顶点F在y轴的正半轴上，点D的坐标为（1，0），1∴OD＝OE＝DE＝1，EF＝DF＝DE＝2，23OD＝3∴OF＝，分两种情况：如图4所示：①当点N在边EF上时，若点N与E重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣3，2）或（1，2）；若点N与F重合，点M，N的“相关矩形”为正方形，3232则点M的坐标为（﹣2+，）或（2﹣，）；∴m的取值范围为﹣3≤m≤﹣2+3或2﹣3≤m≤1；②当点N在边DF上时，若点N与D重合，点M，N的“相关矩形”为正方形，则点M的坐标为（3，2）或（﹣1，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（2﹣3，2）或（﹣2+3，2）；33∴m的取值范围为2﹣≤m≤3或﹣1≤m≤﹣2+；综上所述，m的取值范围为﹣3≤m≤﹣2+3或2﹣3≤m≤3．【点睛】此题主要考查图形与坐标综合，解题的关键是熟知正方形的性质、一次函数的图像与性质及新定义的应用．129．（1）①详见解析；② α；（2）详见解析；（3）当B、O、F 三点共线时BF 最210长，(+)a2【解析】【分析】（1）①由线段垂直平分线的性质可得AD=AC=AB，即可证点B，C，D 在以点A 为圆心，AB 为半径的圆上；②由等腰三角形的性质可得∠BAC=2∠BDC，可求∠BDC 的度数；（2）连接CE，由题意可证△ABC，△DCE 是等边三角形，可得AC=BC，∠DCE=60°=∠ACB，CD=CE，根据“SAS”可证△BCD≌△ACE，可得AE=BD；（3）取AC 的中点O，连接OB，OF，BF，由三角形的三边关系可得，当点O，点B，点F三点共线时，BF 最长，根据等腰直角三角形的性质和勾股定理可求B O10a，O F O C2a，即可求得B F【详解】（1）①连接AD，如图1．∵点C 与点D 关于直线l 对称，∴AC = AD．∵AB= AC，∴AB= AC = AD．∴点B，C，D 在以A 为圆心，AB 为半径的圆上．②∵AD=AB=AC，∴∠ADB=∠ABD，∠ADC=∠ACD，∵∠BAM=∠ADB+∠ABD，∠MAC=∠ADC+∠ACD，∴∠BAM=2∠ADB，∠MAC=2∠ADC，∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α1∴∠BDC=α21故答案为：α．2（2连接CE，如图2．∵∠BAC=60°，AB=AC，∴△ABC是等边三角形，∴BC=AC，∠ACB=60°，1∵∠BDC=α，2∴∠BDC=30°，∵BD⊥DE，∴∠CDE=60°，∵点C关于直线l的对称点为点D，∴DE=CE，且∠CDE=60°∴△CDE是等边三角形，∴CD=CE=DE，∠DCE=60°=∠ACB，∴∠BCD=∠ACE，且AC=BC，CD=CE，∴△BCD≌△ACE（SAS）∴BD=AE，（3）如图3，取AC的中点O，连接OB，OF，BF，，F是以AC为直径的圆上一点，设AC中点为O，∵在△BOF中，BO+OF≥BF，当B、O、F三点共线时BF最长；如图，过点O作OH⊥BC，∵ ∠ BAC=90°，AB=AC=2 2 a ，∴ 2 4 ，∠ ACB=45°，且 OH ⊥BC ， B C AC a ∴ ∠ COH=∠ HCO=45°，∴ OH=HC ，∴ 2 O C HC ，∵ 点 O 是 AC 中点，AC =2 2 a ，∴ O C 2a ， HC a ， ∴ O H∴ BH=3a ，∴ 10a ， B O ∵ 点 C 关于直线 l 的对称点为点 D ，∴ ∠ AFC=90°，∵ 点 O 是 AC 中点，∴ ∴ 2 ， O F O C aBF 10 2 a ， ∴ 当 B 、O 、F 三点共线时 BF 最长；最大值为( 10 + 2 )a ．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理， 三角形的三边关系，灵活运用相关的性质定理、综合运用知识是解题的关键．3 30．（1）P (﹣1，﹣1)；（2） ；（3）T (1，0)或(﹣2，0)． 2【解析】【分析】（1）解析式联立构成方程组，该方程组的解就是交点坐标；（2）利用三角形的面积公式解答；1 1 3（3）求得 C 的坐标，因为 S △ATP ＝S △APB ，S △ATP ＝S △ATC +S △PTC ＝|x + |，所以|x + |＝ ，解 2 2 2 得即可．【详解】 2x 1 x 1 y 解：（1）由 ，解得 ， x 2y 1 y 所以 P （﹣1，﹣1）；（2）令 x ＝0，得 y ＝1，y ＝﹣2 1 2∴A（0，1），B（0，﹣2），13则S△APB＝×（1+2）×1＝；221（3）在直线l：y＝2x+1中，令y＝0，解得x＝﹣，1121∴C（﹣，0），2设T（x，0），1∴CT＝|x+|，2111∵S△ATP＝S△APB，S△ATP＝S△ATC+S△PTC＝•|x+|•（1+1）＝|x+|，22213∴|x+|＝，22解得x＝1或﹣2，∴T(1，0)或(﹣2，0)．【点睛】本题考查一次函数与二元一次方程组，解题的关键是准确将条件转化为二元一次方程组，并求出各点的坐标．。

．．．．．在平面直角坐标系中，在第二象限的点是（）A ．B ．EC BD =AC FD∥A ．9°B ．7．如图，在和AEB △AFC △于点，AB 交FC 于点．下列结论：①M N A ．①②B ．②③D ．①②③．．．二、填空题（本大题共接填写在答题卡相应位置上）9．4的平方根是______15．如图，在平面直角坐标系中，在此坐标系中的第(6,10)C a b --16．如图，在Rt ABC △点．则CD 的长为______D 17．如图，在四边形ABCD 中，的中点，若，6AC =BD =18．如图，和AOB △COD △AD 、BC ．若，1OA =OD 三、解答题（本大题共说明、说理过程或演算步骤）19．（5分）计算4+22．（8分）如图，在平面直角坐标系中，（1）画出关于ABC △23．（8分）已知某种毛线玩具的销售单价下表．x355055⋯y 352015⋯若日销售量是销售单价的一次函数．y x （1）求与之间的函数表达式；y x25．（8分）一辆货车和一辆轿车先后从地出发沿同一直道去地．已知、两地相A B A B 距180km ，轿车的速度为，图中OC 、DE 分别表示货车、轿车离地的距离120km /h A 26．（8分）在中，ABC △BAC ∠（1）如图①，为BC 边上一点，连接D 27．（9分）若一个函数，对于自变量的不同取值范围，该函数有不同的表达式，则这样的（2）正比例函数的图像与函数22y kx =时，的取值范围是______；12y y >x （3）已知点，，函数(2,1)A (1,1)B --变化，直接写出交点个数及对应的的取值范围．k八年级数学答案说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分一、选择题（本大题共8小题，每小题2分，共16分）题号12345678答案B D C B C B A D二、填空题（本大题共10小题，每小题2分，共20分）9．10．3.111．112．2±21y x =-13．>14．915．四16．3217．18．792三、解答题（本大题共9小题，共64分）19．（5分）解：原式2(3)34=+--=-20．（6分）解：（1）；2218x =．29x =．3x =±（2）12x -=-3x =21．（6分）23．（8分）解：（1）设一次函数表达式为y kx =将和代入，得(35,35)(50,20)3550k k +⎧⎨+⎩））方法一：25．（8分）解：（1）60；（2）设OC 的函数表达式为s 所以，160s t =180300 1.5÷=（2）或72(62)27．（9分））：当时，随的增大而增大；性质2：当时，函数有最小值0x ≥y x 0x ≥或；2-02x ≤<时，没有交点；当时，1个交点；12>-112k -<≤-时，2个交点．。

江苏省南京市第一学期八年级数学期末试卷（含解析）一、选择题1．如图，一次函数图象经过点A ，且与正比例函数y=-x 的图象交于点B ，则该一次函数的表达式为（ ）A ．y=-x+2B ．y=x+2C ．y=x-2D ．y=-x-22．下列图书馆的馆徽不是．．轴对称图形的是（ ） A ． B ． C ． D ．3．如图所示的两个三角形全等，图中的字母表示三角形的边长，则1∠的度数为（ ）A ．82°B ．78°C ．68°D ．62°4．已知一次函数y=kx +3（k≠0）的图象经过点A ，且函数值y 随x 的增大而增大，则点A 的坐标可能是（ ）A ．（﹣2，﹣4）B ．（1，2）C ．（﹣2，4）D ．（2，﹣1）5．下列二次根式中属于最简二次根式的是（ ）A 8B 36C ．a b（a ＞0，b ＞0） D 7 6．下列各点中，在函数y=－8x 图象上的是（ ） A ．（﹣2，4）B ．（2，4）C ．（﹣2，﹣4）D ．（8，1） 7．点P （3，﹣4）关于y 轴的对称点P′的坐标是（ ）A ．（﹣3，﹣4）B ．（3，4）C ．（﹣3，4）D ．（﹣4，3） 8．如图， Rt ABC 中，90,B ED ∠=︒垂直平分,AC ED 交AC 于点D ，交BC 于点E .已知ABC 的周长为24,ABE 的周长为14，则AC 的长（ ）A ．10B ．14C ．24D ．159．下列各式成立的是（ ）A ．93=±B ．235+=C ．()233-=±D ．()233-=10．在平面直角坐标系xOy 中，线段AB 的两个点坐标分别为A （﹣1，﹣1），B （1，2）．平移线段AB ，得到线段A ′B ′．已知点A ′的坐标为（3，1），则点B ′的坐标为（ ）A ．（4，4）B ．（5，4）C ．（6，4）D ．（5，3）二、填空题11．“徐宿淮盐”铁路是一条连接徐州与盐城的高速铁路，全长约为316000米.将数据316000用四舍五入法精确到万位，并用科学记数法表示为____________.12．如图，在ABC ∆中，90ACB ∠=︒，点D 为AB 中点，若4AB =，则CD =_______________.13．将一次函数y =2x 的图象向上平移1个单位，所得图象对应的函数表达式为__________．14．若关于x 的分式方程122x x a x x--=--有增根，则a 的值_____________. 15．将一次函数34y x =-的图象向上平移3个单位长度，相应的函数表达式为_____． 16．如图，已知函数y =x +b 和y =ax +3的图象交点为P ，则不等式x +b ＜ax +3的解集为_____．17．如图，在Rt △ABC 中，∠C=90°，AC=3，BC=5，分别以点A 、B 为圆心，大于12AB 的长为半径画弧，两弧交点分别为点P 、Q ，过P 、Q 两点作直线交BC 于点D ，则CD 的长是_____．18．如图,AD 是ABC ∆的角平分线,DE AB ⊥于E ,若18AB =,12AC =,ABC ∆的面积等于30,则DE =_______．19．如图，点P 为∠AOB 内任一点，E ，F 分别为点P 关于OA ，OB 的对称点．若∠AOB ＝30°，则∠E ＋∠F ＝_____°．20．如图，点C 坐标为(0,1)-，直线334y x =+交x 轴，y 轴于点A 、点B ，点D 为直线上一动点，则CD 的最小值为_________.三、解答题21．春节前小明花1200元从市场购进批发价分别为每箱30元与50元的A 、B 两种水果进行销售，分别以每箱35元与60元的价格出售，设购进A 水果x 箱，B 水果y 箱. （1）求y 关于x 的函数表达式；（2）若要求购进A 水果的数量不少于B 水果的数量，则应该如何分配购进A 、B 水果的数量并全部售出才能获得最大利润，此时最大利润是多少？22．如图，一次函数()40y kx k k =+≠的图像与x 轴交于点A ，与y 轴交于点B ，且经过点()2C m ，．(1)当92m =时； ①求一次函数的表达式；②BD 平分ABO ∠交x 轴于点D ，求点D 的坐标；(2)若△AOC 为等腰三角形，求k 的值；(3)若直线42y px p =-+也经过点C ，且24p ≤<，求k 的取值范围．23．（1）如图1，在Rt ABC ∆中，90ACB ∠=︒，60A ∠=︒，CD 平分ACB ∠. 求证：CA AD BC +=.小明为解决上面的问题作了如下思考：作ADC ∆关于直线CD 的对称图形A DC '∆，∵CD 平分ACB ∠，∴A '点落在CB 上，且CA CA '=，A D AD '=.因此，要证的问题转化为只要证出A D A B ''=即可.请根据小明的思考，写出该问题完整的证明过程.（2）参照（1）中小明的思考方法，解答下列问题：如图3，在四边形ABCD 中，AC 平分BAD ∠，10BC CD ==，17AC =，9AD =，求AB 的长.24．一次函数的图象经过点A （2，4）和B （﹣1，﹣5）两点．（1）求出该一次函数的表达式；（2）画出该一次函数的图象；（3）判断（﹣5，﹣4）是否在这个函数的图象上？（4）求出该函数图象与坐标轴围成的三角形面积．25．如图，在△ABC 中，AB =AC =2，∠B =36°，点D 在线段BC 上运动(点D 不与点B 、C 重合)，连接AD ，作∠ADE =36°，DE 交线段AC 于点E ．（1）当∠BDA =128°时，∠EDC = ，∠AED = ；（2）线段DC 的长度为何值时，△ABD ≌△DCE ？请说明理由；（3）在点D 的运动过程中，△ADE 的形状可以是等腰三角形吗？若可以，请直接写出∠BDA 的度数；若不可以，请说明理由．四、压轴题26．（1）在等边三角形ABC 中，①如图①，D ，E 分别是边AC ，AB 上的点且AE=CD ，BD 与EC 交于点F ，则∠BFE 的度数是 度；②如图②，D ，E 分别是边AC ，BA 延长线上的点且AE=CD ，BD 与EC 的延长线交于点F ，此时∠BFE 的度数是 度；（2）如图③，在△ABC 中，AC=BC ，∠ACB 是锐角，点O 是AC 边的垂直平分线与BC 的交点，点D ，E 分别在AC ，OA 的延长线上，AE=CD ，BD 与EC 的延长线交于点F ，若∠ACB=α，求∠BFE 的大小．（用含α的代数式表示）．27．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明． 同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．28．在等腰△ABC 与等腰△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点D 、E 、C 三点在同一条直线上，连接BD ．（1）如图1，求证：△ADB ≌△AEC（2）如图2，当∠BAC ＝∠DAE ＝90°时，试猜想线段AD ，BD ，CD 之间的数量关系，并写出证明过程；（3）如图3，当∠BAC ＝∠DAE ＝120°时，请直接写出线段AD ，BD ，CD 之间的数量关系式为： （不写证明过程）29．如图已知ABC 中，,8B C AB AC ∠=∠==厘米，6BC =厘来，点D 为AB 的中点．如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动，设运动时间为t (秒)．（1）用含t 的代数式表示线段PC 的长度；（2）若点,P Q 的运动速度相等，经过1秒后，BPD △与CQP 是否全等，请说明理由；（3）若点,P Q的运动速度不相等，当点Q的运动速度为多少时，能够使BPD△与CQP全等？（4）若点Q以（3）中的运动速度从点C出发，点v以原来的运动速度从点B同时出发，都顺时针沿三边运动，求经过多长时间，点P与点Q第一次在ABC的哪条边上相遇？30．一次函数y＝kx+b的图象经过点A（0，9），并与直线y＝53x相交于点B，与x轴相交于点C，其中点B的横坐标为3．（1）求B点的坐标和k，b的值；（2）点Q为直线y＝kx+b上一动点，当点Q运动到何位置时△OBQ的面积等于272？请求出点Q的坐标；（3）在y轴上是否存在点P使△PAB是等腰三角形？若存在，请直接写出点P坐标；若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】【详解】解：设一次函数的解析式y=kx+b（k≠0），∵一次函数图象经过点A，且与正比例函数y=-x的图象交于点B，∴在直线y=-x中，令x=-1，解得：y=1，则B的坐标是（-1，1）．把A（0，2），B（-1，1）的坐标代入一次函数的解析式y=kx+b得：2{1bk b=-+=，解得2{1bk==，该一次函数的表达式为y=x+2．故选B．2．D解析：D【解析】【分析】根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．【详解】解：A、是轴对称图形，不符合题意；B、是轴对称图形，不符合题意；C、是轴对称图形，不符合题意；D、因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不是轴对称图形，符合题意；故选：D．【点睛】此题主要考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3．B解析：B【解析】【分析】直接利用全等三角形的性质得出∠1＝∠2进而得出答案．【详解】∵如图是两个全等三角形，∴∠1＝∠2＝180°−40°−62°＝78°．故选：B．【点睛】此题主要考查了全等三角形的性质，正确得出对应角是解题关键．4．A解析：A【解析】【分析】先根据一次函数的增减性判断出k的符号，再对各选项进行逐一分析即可．【详解】∵一次函数y=kx+2(k≠0)的函数值y随x的增大而增大，∴k>0.A. ∵当x=-2，y=-4时，-2k+3=-4，解得k=3.5>0，∴此点符合题意，故本选项正确；B. ∵当x=1，y=2时， k+3=2，解得k=-1<0，∴此点不符合题意，故本选项错误；C. ∵当x=-2，y=4时，-2k+3=4，解得k=−0.5<0，∴此点不符合题意，故本选项错误；D. ∵当x=2，y=−1时，2k+3=−1，解得k=-2<0，∴此点不符合题意，故本选项错误.故答案选A..【点睛】本题考查的知识点是一次函数图像上点的坐标特征，解题的关键是熟练的掌握一次函数图像上点的坐标特征.5．D解析：D【解析】【分析】根据最简二次根式的定义即可求出答案．【详解】解：（A）原式＝2，故A不符合题意；（B）原式＝6，故B不符合题意；（C）ab是分式，故C不符合题意；故选：D．【点睛】本题考查最简二次根式，解题的关键是熟练运用最简二次根式的定义，本题属于基础题型．6．A解析：A【解析】【分析】所有在反比例函数上的点的横纵坐标的积应等于比例系数．本题只需把所给点的横纵坐标相乘，结果是﹣8的，就在此函数图象上【详解】解:-2×4=-8故选:A【点睛】本题考查反比例函数图象上点的坐标特征，掌握反比例函数性质是本题的解题关键．7．A解析：A【解析】试题解析：∵点P（3，-4）关于y轴对称点P′，∴P′的坐标是：（-3，-4）．故选A．8．A解析：A【解析】【分析】首先依据线段垂直平分线的性质得到AE=CE；接下来，依据AE=CE可将△ABE的周长为:14转化为AB+BC=14，求解即可.【详解】∵DE是AC的垂直平分线，∴AE=CE，∴△ABE的周长为:AB+BE+AE=AB+BE+CE=AB+BC∵ABC的周长为24,ABE的周长为14∴AB+BC=14∴AC=24-14=10故选：A【点睛】本题主要考查的是线段垂直平分线的性质，掌握线段垂直平分线的性质是解题的关键. 9．D解析：D【解析】【分析】根据算术平方根的定义对A进行判断；根据二次根式的加减法对B进行判断；根据二次根式的性质对C、D进行判断．【详解】=，所以A选项错误；解：A3B B选项错误；=，所以C选项错误；C3D、(23=，所以D选项正确．故选D.【点睛】此题考查了算术平方根和二次根式的性质以及二次根式的加减，熟练掌握二次根式的性质是解题的关键．10．B解析：B【解析】【分析】由题意可得线段AB平移的方式，然后根据平移的性质解答即可．【详解】解：∵A（﹣1，﹣1）平移后得到点A′的坐标为（3，1），∴线段AB先向右平移4个单位，再向上平移2个单位，∴B（1，2）平移后的对应点B′的坐标为（1+4，2+2），即（5，4）．故选：B．【点睛】本题考查了平移变换的性质，一般来说，坐标系中点的平移遵循：上加下减，左减右加的规律，熟练掌握求解的方法是解题关键．二、填空题11．【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于解析：5⨯3.210【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．316000≈320000=3.2×105．故答案为：3.2×105．【点睛】本题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，正确确定a的值以及n的值是解题的关键．12．【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半即可求出CD．【详解】∵D是AB的中点，∴CDAB=2．故答案为：2．【点睛】本题主要是运用了直角三角形的性质：直角三角形斜解析：2【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半即可求出CD．【详解】∵D是AB的中点，∴CD12AB=2．故答案为：2．【点睛】本题主要是运用了直角三角形的性质：直角三角形斜边上的中线等于斜边的一半．13．y=2x+1．【解析】由“上加下减”的原则可知，将函数y=2x的图象向上平移1个单位所得函数的解析式为y=2x+1，故答案为y=2x+1．解析：y=2x+1．【解析】由“上加下减”的原则可知，将函数y=2x的图象向上平移1个单位所得函数的解析式为y=2x+1，故答案为y=2x+1．14．4【分析】方程第二个分母提取-1变形后，去分母转化为整式方程，表示出方程的解，令方程的解为2，即可求出a 的值．【详解】方程变形得：，去分母得：x+x-a=x-2，解得：x=a-解析：4【解析】【分析】方程第二个分母提取-1变形后，去分母转化为整式方程，表示出方程的解，令方程的解为2，即可求出a 的值．【详解】 方程变形得：+122x x a x x -=--， 去分母得：x+x-a=x-2，解得：x=a-2， ∵方程122x x a x x--=--有增根， ∴x=2，即a-2=2，解得：a=4，故答案为：4．【点睛】 此题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．15．【解析】【分析】根据函数图像平移规律：上加下减常数项，左加右减自变量，变形即可.【详解】解：一次函数的图象向上平移3个单位长度可得：.故答案为：【点睛】本题考查了函数图像平移，解决本解析：31y x =-【解析】根据函数图像平移规律：上加下减常数项，左加右减自变量，变形即可.【详解】解：一次函数34y x =-的图象向上平移3个单位长度可得：34331y x x =-+=-. 故答案为：31y x =-【点睛】本题考查了函数图像平移，解决本题的关键是熟练掌握函数图像的平移规律，要与点的坐标平移区别开.16．x ＜1【解析】【分析】当直线y=x+b 的图象在直线y=ax+3的上方时，不等式x+b ＞ax+3成立；【详解】由于两直线的交点横坐标为：x=1，观察图象可知，当x<1时，x+b<ax+3；解析：x ＜1【解析】【分析】当直线y=x+b 的图象在直线y=ax+3的上方时，不等式x+b ＞ax+3成立；【详解】由于两直线的交点横坐标为：x=1，观察图象可知，当x<1时，x+b<ax+3；故答案为x<1．考点： 一次函数与一元一次不等式．17．【解析】分析：连接AD 由PQ 垂直平分线段AB ，推出DA=DB ，设DA=DB=x ，在Rt△ACD 中，∠C=90°，根据AD2=AC2+CD2构建方程即可解决问题；详解：连接AD ．∵PQ 垂直平 解析：85【解析】分析：连接AD 由PQ 垂直平分线段AB ，推出DA=DB ，设DA=DB=x ，在Rt △ACD 中，∠C=90°，根据AD 2=AC 2+CD 2构建方程即可解决问题；详解：连接AD ．∵PQ 垂直平分线段AB ，∴DA=DB ，设DA=DB=x ，在Rt △ACD 中，∠C=90°，AD 2=AC 2+CD 2，∴x 2=32+（5﹣x ）2， 解得x=175， ∴CD=BC ﹣DB=5﹣175=85， 故答案为85． 点睛：本题考查基本作图，线段的垂直平分线的性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．18．2【解析】【分析】延长AC,过D 点作DF⊥AF 于F ，根据角平分线的性质得到DE=DF,由即可求出.【详解】解：如图延长AC,过D 点作DF⊥AC 于F∵是的角平分线，DE⊥AB，∴DE解析：2【解析】【分析】延长AC ,过D 点作DF ⊥AF 于F ，根据角平分线的性质得到DE=DF,由ABC ABD ACDSS S =+即可求出.【详解】解：如图延长AC ,过D 点作DF ⊥AC 于F∵AD 是ABC ∆的角平分线，DE⊥AB，∴DE =DF∵ABC ABD ACD SS S =+=30 ∴113022AB DE DF AC ⋅+⋅= ∵18AB =,12AC = ，DE =DF ∴1118123022DE DE ⨯⋅+⨯= 得到 DE=2故答案为：2.【点睛】 此题主要考查了角平分线的性质，熟记概念是解题的关键.19．150【解析】【分析】连接OP ，根据轴对称的性质得到，再利用四边形的内角和是计算可得答案.【详解】解：如图，连接OP ，E ，F 分别为点P 关于OA ，OB 的对称点故答案为：1解析：150【解析】【分析】连接OP ，根据轴对称的性质得到60EOF ∠=︒，,,E EPO F FPO ∠=∠∠=∠再利用四边形的内角和是360︒计算可得答案.【详解】解：如图，连接OP ，E ，F 分别为点P 关于OA ，OB 的对称点,,EOA POA POB FOB ∴∠=∠∠=∠30EOA FOB POA POB ∴∠+∠=∠+∠=︒60EOF ∴∠=︒,,E EPO F FPO ∴∠=∠∠=∠360E EPO F FPO EOF ∴∠+∠+∠+∠+∠=︒2()300E F ∴∠+∠=︒150E F ∴∠+∠=︒故答案为：150.【点睛】本题考查了轴对称的性质，四边形的内角和性质，证得60EOF ∠=︒，,,E EPO F FPO ∠=∠∠=∠解本题的关键. 20．【解析】【分析】过点C 作直线AB 的垂线段CD ，利用三角形的面积即可求出CD 的长.【详解】连接AC ，过点C 作CD ⊥AB ，则CD 的长最短，如图，对于直线令y=0，则，解得x=-4，令x=0解析：165【解析】【分析】过点C 作直线AB 的垂线段CD ，利用三角形的面积即可求出CD 的长.【详解】连接AC ，过点C 作CD ⊥AB ，则CD 的长最短，如图，对于直线334y x =+令y=0，则3304x +=，解得x=-4，令x=0，则y=3，∴A(-4，0)，B(0，3)，∴OA=4，OB=3，在Rt △OAB 中，222AB OA OB =+∴22435 ∵C （0，-1），∴OC=1，∴BC=3+1=4， ∴1122ABC S BC AO AB CD ==,即1144=522CD ⨯⨯⨯⨯， 解得，165CD =. 故答案为：165. 【点睛】 此题主要考查了一次函数的应用以及三角形面积公式的运用，解答此题的关键是利用三角形面积相等求出CD 的长.三、解答题21．（1）3245y =-+；（2）应购进A 水果15箱、B 水果15箱能够获得最大利润，最大利润为225元【解析】【分析】（1）根据A 水果总价+B 水果总价=1200列出关于x 、y 的二元一次方程，对方程进行整理变形即可得出结论；（2）设利润为W 元，找出利润W 关于x 的函数关系式，由购进A 水果的数量不得少于B 水果的数量找出关于x 的一元一次不等式，解不等式得出x 的取值范围，再利用一次函数的性质即可解决最值问题.【详解】（1）∵30501200x y∴y 关于x 的函数表达式为：3245y =-+. （2）设获得的利润为w 元，根据题意得510w x y ， ∴240w x =-+∵A 水果的数量不得少于B 水果的数量，∴x y ≥，解得15x ≥.∵10-<，∴w 随x 的增大而减小，∴当15x =时，w 最大225=，此时120315155y -⨯==. 即应购进A 水果15箱、B 水果15箱能够获得最大利润，最大利润为225元.【点睛】本题考查了二元一次方程的应用、一次函数的应用；根据题意得出等量关系列出方程组或得出函数关系式或由不等关系得出不等式是解决问题的关键．22．(1)①334y x =+；②（-32，0）；(2) k =(3) 113k -<≤-. 【解析】【分析】(1)①把x=2,y=92代入4y kx k =+中求出k 值即可； ②作DE ⊥AB 于E ，先求出点A 、点B 坐标，继而求出OA 、OB 、AB 的长度,由角平分线的性质可得到OD=DE,于是BE=OB 可求BE 、AE 的长,然后在Rt AED ∆中用勾股定理可列方程，解方程即可求得OD 的长；(2)求得点A 坐标是（-4，0），点C 坐标是（2，6k ），由△AOC 为等腰三角形,可知OC=OA=4,故2222(6)4k +=,解方程即可；(3) 由直线42y px p =-+经过点C ()2m ，， 得242m p p =-+=22p -+,由（2）知6m k =,故226p k -+=,用k 表示p 代入24p ≤<中得到关于k 的不等式，解不等式即可.【详解】解：(1)当92m =时，点C 坐标是922⎛⎫ ⎪⎝⎭，， ①把x=2,y=92代入4y kx k =+中， 得9242k k =+， 解得34k =， 所以一次函数的表达式是334y x =+；②如图，BD 平分ABO ∠交x 轴于点D ，作DE ⊥AB 于E ，∵在334y x =+中，当x=0时，y=3；当y=0时，x=-4， ∴点A 坐标是（-4，0），点B 坐标是（0，3）， ∴OA=4,OB=3, ∴22345AB +=,∵BD 平分ABO ∠, DE ⊥AB, DO ⊥OB,∴OD=DE,∵BD=BD,∴OBD EBD ∆≅∆,∴BE=OB=3,∴AE=AB-BE=5-3=2,∵在Rt AED ∆中，222AE DE AD +=,∴2222(4)OD OD +=-,∴OD= 32, ∴点D 坐标是（-32，0）， (2) ∵在4y kx k =+中，当y=0时，x=-4；当x=2时，y=6k ， ∴点A 坐标是（-4，0），点C 坐标是（2，6k ）， ∵△AOC 为等腰三角形,∴OC=OA=4,∴2222(6)4k +=,∴13k =,23k =（不合题意，舍去）， ∴3k = (3) ∵直线42y px p =-+经过点C ()2m ，，∴242m p p =-+=22p -+,由（2）知6m k =,∴226p k -+=,∴13p k =-,∵24p ≤<,∴2134k ≤-<,∴113k -<≤-. 【点睛】本题考查了一次函数的综合应用，熟练掌握一次函数的性质及运用数形结合的思想解题是关键.23．（1）证明见解析；（2）21.【解析】 【分析】（1）只需要证明'30A DB B ∠=∠=︒，再根据等角对等边即可证明''A D A B =,再结合小明的分析即可证明；（2）作△ADC 关于AC 的对称图形AD'C ,过点C 作CE ⊥AB 于点E ，则'D E =BE ．设'D E =BE=x ．在Rt △CEB 和Rt △CEA 中，根据勾股定理构建方程即可解决问题.【详解】解：（1）证明：如下图，作△ADC 关于CD 的对称图形△A′DC ，∴A′D=AD ，C A′=CA ，∠CA′D=∠A=60°，∵CD 平分∠ACB ，∴A′点落在CB 上∵∠ACB=90°，∴∠B=90°-∠A=30°，∴∠A′DB=∠CA′D -∠B=30°，即∠A′DB=∠B ，∴A′D=A′B ，∴CA+AD=CA′+A′D=CA′+A′B=CB.（2）如图，作△ADC 关于AC 的对称图形△AD′C ．∴D′A=DA=9，D′C=DC=10，∵AC平分∠BAD，∴D′点落在AB上，∵BC=10，∴D′C=BC，过点C作CE⊥AB于点E，则D′E=BE，设D′E=BE=x，在Rt△CEB中，CE2=CB2-BE2=102-x2，在Rt△CEA中，CE2=AC2-AE2=172-（9+x）2．∴102-x2=172-（9+x）2，解得：x=6，∴AB=AD′+D′E+EB=9+6+6=21．【点睛】本题考查轴对称的性质，勾股定理，等腰三角形的性质，三角形外角的性质.（1）中证明∠A′DB=∠B不是经常用的等量代换，而是利用角之间的计算求得它们的度数相等，这有点困难，需要多注意；（2）中掌握方程思想是解题关键.24．（1）y＝3x﹣2；（2）图象见解析；（3）（﹣5，﹣4）不在这个函数的图象上；（4）23．【解析】【分析】（1）利用待定系数法即可求得；（2）利用两点法画出直线即可；（3）把x＝﹣5代入解析式，即可判断；（4）求得直线与坐标轴的交点，即可求得．【详解】解：（1）设一次函数的解析式为y＝kx+b∵一次函数的图象经过点A（2，4）和B（﹣1，﹣5）两点∴245 k bk b+=⎧⎨-+=-⎩，解得：k3 b2=⎧⎨=-⎩∴一次函数的表达式为y＝3x﹣2；（2）描出A、B点，作出一次函数的图象如图：（3）由（1）知，一次函数的表达式为y＝3x﹣2将x＝﹣5代入此函数表达式中得，y＝3×（﹣5）﹣2＝﹣17≠﹣4∴（﹣5，﹣4）不在这个函数的图象上；（4）由（1）知，一次函数的表达式为y＝3x﹣2令x＝0，则y＝﹣2，令y＝0，则3x﹣2＝0，∴x＝23，∴该函数图象与坐标轴围成的三角形面积为：12×2×23＝23．【点睛】本题考查了待定系数法求一次函数的解析式，一次函数图象上点的坐标特征，一次函数的图象以及三角形的面积，熟练掌握待定系数法是解题的关键．25．（1）16°；52°；（2）当DC=2时，△ABD≌△DCE，理由见解析；（3）当∠BDA的度数为108°或72°时，△ADE的形状是等腰三角形．【解析】【分析】（1）根据三角形内角和定理和等腰三角形的性质，得到答案；（2）当DC＝2时，利用∠DEC+∠EDC＝144°，∠ADB+∠EDC＝144°，得到∠ADB＝∠DEC，根据AB＝DC＝2，证明△ABD≌△DCE；（3）分DA＝DE、AE＝AD、EA＝ED三种情况，根据等腰三角形的性质、三角形内角和定理计算．【详解】（1）∵AB=AC，∴∠C=∠B=36°．∵∠ADE=36°，∠BDA=128°．∵∠EDC=180°﹣∠ADB﹣∠ADE=16°，∴∠AED=∠EDC+∠C=16°+36°=52°．故答案为：16°；52°；（2）当DC=2时，△ABD≌△DCE，理由：∵AB =2，DC =2，∴AB =DC ．∵∠C =36°，∴∠DEC +∠EDC =144°．∵∠ADE =36°，∴∠ADB +∠EDC =144°，∴∠ADB =∠DEC ，在△ABD 和△DCE 中，ADB DEC B CAB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ABD ≌△DCE (AAS)；（3）当∠BDA 的度数为108°或72°时，△ADE 的形状是等腰三角形，①当DA =DE 时，∠DAE =∠DEA =72°，∴∠BDA =∠DAE +∠C =70°+40°=108°；②当AD =AE 时，∠AED =∠ADE =36°，∴∠DAE =108°，此时，点D 与点B 重合，不合题意；③当EA =ED 时，∠EAD =∠ADE =36°，∴∠BDA =∠EAD +∠C =36°+36°=72°；综上所述：当∠BDA 的度数为108°或72°时，△ADE 的形状是等腰三角形．【点睛】本题考查的是等腰三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质，掌握全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键．四、压轴题26．（1）①60°；②60°；（2）∠BFE =α．【解析】【分析】（1）①先证明△ACE ≌△CBD 得到∠ACE=∠CBD ，再由三角形外角和定理可得∠BFE=∠CBD+∠BCF ；②先证明△ACE ≌△CBD 得∠ACE=∠CBD=∠DCF ，再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA ；（2）证明△AEC ≌△CDB 得到∠E=∠D ，则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【详解】（1）如图①中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD，∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°．故答案为60．（2）如图②中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∴∠CAE=∠BCD=′120°∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD=∠DCF，∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°．故答案为60．（3）如图③中，∵点O是AC边的垂直平分线与BC的交点，∴OC=OA，∴∠EAC=∠DCB=α，∵AC=BC，AE=CD，∴△AEC≌△CDB，∴∠E=∠D，∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【点睛】本题综合考查了三角形全等以及三角形外角和定理.27．（1）60°；（2）EF=AF+FC，证明见解析；（3）AF=EF+2DF，证明见解析．【解析】【分析】（1）可设∠BAD＝∠CAD＝α，∠AEC＝∠ACE＝β，在△ACE中，根据三角形内角和可得2α＋60＋2β＝180°，从而有α＋β＝60°，即可得出∠DFC的度数；（2）在EC上截取EG＝CF，连接AG，证明△AEG≌△ACF，然后再证明△AFG为等边三角形，从而可得出EF＝EG＋GF＝AF＋FC；（3）在AF上截取AG＝EF，连接BG，BF，证明方法类似（2），先证明△ABG≌△EBF，再证明△BFG为等边三角形，最后可得出结论．【详解】解：（1）∵AB=AC，AD为BC边上的中线，∴可设∠BAD＝∠CAD＝α，又△ABE为等边三角形，∴AE=AB=AC，∠EAB=60°，∴可设∠AEC＝∠ACE＝β，在△ACE中，2α＋60°＋2β＝180°，∴α＋β＝60°，∴∠DFC=α＋β＝60°；（2）EF=AF+FC，证明如下：∵AB=AC，AD为BC边上的中线，∴AD⊥BC，∴∠FDC=90°，∵∠CFD＝60°，则∠DCF=30°，∴CF＝2DF，在EC上截取EG＝CF，连接AG，又AE=AC，∴∠AEG=∠ACF，∴△AEG≌△ACF（SAS）,∴∠EAG＝∠CAF，AG＝AF，又∠CAF=∠BAD，∴∠EAG=∠BAD，∴∠GAF＝∠BAD+∠BAG=∠EAG+∠BAG=∠60°，∴△AFG为等边三角形，∴EF＝EG＋GF＝AF＋FC，即EF=AF+FC；（3）补全图形如图所示，结论：AF=EF+2DF．证明如下：同（1）可设∠BAD＝∠CAD＝α，∠ACE＝∠AEC＝β，∴∠CAE＝180°－2β，∴∠BAE＝2α＋180°－2β＝60°，∴β－α＝60°，∴∠AFC=β－α＝60°，又△ABE为等边三角形，∴∠ABE=∠AFC=60°，∴由8字图可得：∠BAD＝∠BEF，在AF上截取AG＝EF，连接BG，BF，又AB=BE，∴△ABG≌△EBF（SAS），∴BG＝BF，又AF垂直平分BC，∴BF=CF，∴∠BFA=∠AFC=60°，∴△BFG为等边三角形，∴BG=BF，又BC⊥FG，∴FG=BF=2DF，∴AF＝AG＋GF＝BF＋EF＝2DF＋EF．【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识，解决问题的关键是常用辅助线构造全等三角形，属于中考常考题型．28．（1）见解析；（2）CD2AD+BD，理由见解析；（3）CD3+BD【解析】【分析】（1）由“SAS”可证△ADB≌△AEC；（2）由“SAS”可证△ADB≌△AEC，可得BD＝CE，由直角三角形的性质可得DE＝2AD，可得结论；（3）由△DAB≌△EAC，可知BD＝CE，由勾股定理可求DH＝32AD，由AD＝AE，AH⊥DE，推出DH＝HE，由CD＝DE+EC＝2DH+BD＝3AD+BD，即可解决问题；【详解】证明：（1）∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；（2）CD＝2AD+BD，理由如下：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠BAC＝90°，AD＝AE，∴DE＝2AD，∵CD＝DE+CE，∴CD＝2AD+BD；（3）作AH⊥CD于H．∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠DAE＝120°，AD＝AE，∴∠ADH＝30°，∴AH＝12 AD，∴DH2AD ， ∵AD ＝AE ，AH ⊥DE ，∴DH ＝HE ，∴CD ＝DE +EC ＝2DH +BD+BD ，故答案为：CD+BD ．【点睛】本题是结合了全等三角形的性质与判定，勾股定理等知识的综合问题，熟练掌握知识点，有简入难，层层推进是解答关键.29．（1）6-2t ；（2）全等，理由见解析；（3）83；（4）经过24s 后，点P 与点Q 第一次在ABC 的BC 边上相遇【解析】【分析】（1）根据题意求出BP ，由PC=BC-BP ，即可求得；（2）根据时间和速度的关系分别求出两个三角形中，点运动轨迹的边长，由∠B=∠C ，利用SAS 判定BPD △和CQP 全等即可；（3）根据全等三角形的判定条件探求边之间的关系，得出BP=PC ，再根据路程=速度×时间公式，求点P 的运动时间，然后求点Q 的运动速度即得；（4）求出点P 、Q 的路程，根据三角形ABC 的三边长度，即可得出答案．【详解】（1）由题意知，BP=2t ，则PC=BC-BP=6-2t ，故答案为：6-2t ；（2）全等，理由如下：∵p Q V V =，t=1，∴BP=2=CQ ，∵AB=8cm ，点D 为AB 的中点，∴BD=4（cm ），又∵PC=BC-BP=6-2=4（cm ），在BPD △和CQP 中BD PC B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴BPD △≌CQP （SAS ）故答案为：全等．（3）∵p Q V V ≠，∴BP CQ ≠，又∵BPD △≌CPQ ，∠B=∠C ，∴BP=PC=3cm ，CQ=BD=4cm ，∴点,P Q 运动时间322BP t ==（s ）， ∴48332Q CQ V t===（cm/s ）， 故答案为：83；（4）设经过t 秒时，P 、Q 第一次相遇，∵2/p V cm s =，8/3Q V cm s =， ∴2t+8+8=83t ， 解得：t=24此时点Q 走了824643⨯=（cm ），∵ABC 的周长为：8+8+6=22（cm ），∴6422220÷=，∴20-8-8=4（cm ），经过24s 后，点P 与点Q 第一次在ABC 的BC 边上相遇，故答案为：24s ，在 BC 边上相遇．【点睛】考查了全等三角形的判定和性质，路程，速度，时间的关系，全等三角形中的动点问题，动点的追及问题，熟记三角形性质和判定，熟练掌握全等的判定依据和动点的运动规律是解题的关键，注意动点中追及问题的方向．30．（1）点B （3，5），k ＝﹣43，b ＝9；（2）点Q （0，9）或（6，1）；（3）存在，点P 的坐标为：（0，4）或（0，14）或（0，﹣1）或（0，478） 【解析】【分析】（1）53y x =相交于点B ，则点(3,5)B ，将点A 、B 的坐标代入一次函数表达式，即可求解； （2）OBQ ∆的面积1127||9|3|222OA xQ xB m =⨯⨯-=⨯⨯-=，即可求解； （3）分AB AP =、AB BP =、AP BP =三种情况，分别求解即可．【详解】。