案例6 多边形有效边表填充算法

计算机图形学课程设计设计题目改进的有效边表算法对多边形的填充学院名称信息科学与技术学院专业名称计算机科学与技术学生姓名刘柯学生学号201213030112任课教师梅占勇设计（论文）成绩教务处制2015年9 月28 日目录一、设计内容与要求 (3)1.1设计题目 (3)1.2 设计内容 (3)1.3 设计目标 (3)二、总体设计 (3)2.1 多边形的表示 (3)2.2 x-扫描线算法 (4)2.3 改进的有效边表算法 (4)2.3.1 改进的有效边表算法 (4)2.3.2 有效边表 (5)2.3.3 边表 (6)三、详细设计 (8)3.1 改进的有效边表算法的实现 (8)3.2 有效边表算法程序流程图 (9)四、测试结果 (9)五、总结 (15)六、源代码 (15)参考文献 (26)一、设计内容与要求1.1设计题目用改进的有效边表算法实现多边形的填充1.2 设计内容使用OpenGL实现用改进的有效边表算法填充多边形1.3 设计目标参照课本上改进的有效边表算法的思想，实现该算法的C语言代码，并用该算法搭配OpenGL以像素点的方式绘制出给定顶点坐标的多边形。

二、总体设计2.1 多边形的表示在计算机图形学中，多边形有2种重要的表示方法：顶点表示和点阵表示。

顶点表示用多边形的顶点序列来刻画多边形，这种方法直观、几何意义强，占用内存少，应用普遍，但它没有明确指出哪些像素在多边形内，故不能直接用于面着色。

点阵表示用位于多边形内的像素的集合来刻画多边形。

这种表示法虽然失去了许多重要的几何信息，但便于运用帧缓存表示图形，是面着色所需要的图形表示形式。

大多数图形应用系统采用顶点序列表示多边形，而顶点表示又不能直接用于显示，那么就必须有从多边形的顶点表示到点阵表示的转换，这种转换称为多边形的扫描转换或多边形的填充。

即从多边形的顶点信息出发，求出位于其内部的各个像素，并将其颜色值写入帧缓存的相应单元中。

2.2 x-扫描线算法x-扫描线算法的基本思想是，按照扫描线的顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的像素，即完成填充工作。

实验一：改进的有效边表算法一.实验目的用鼠标描绘几个顶点，画出多边形，用边表桶的填充算法实现多边形的填充。

二.算法思想在处理一条扫描线时，仅对与它相交的多边形的边（有效边）求交，其次利用扫描线的连贯性，考虑到当前扫描线与各边的交点顺序与下一条扫描线各边的交点顺序很可能相同或者相似，因此在当前扫描线处理完毕之后，不必为下一条扫描线从头开始构造交点信息；最后利用多边形边的连贯性，认为若某条边与当前扫描线相交，则它很可能也与下一条扫描线相交且其交点与上一次的交点相交。

三.实现过程1.边表的构造1.首先构造一个纵向链表，链表长度为多边形所占有的最大扫描线数，链表的每个结点，称为，称为一个桶，对应多边形覆盖的每一条扫描线。

2.将每条边的信息装入与该边最小Y坐标（Ymin）相对应的桶中，也就是说，若某条边的较低端点为Ymin,则该边就放在相应的Y=Ymin的扫描线桶中。

3.每条边的数据形成一个结点，内容包括该扫描线与该边的初始交点X（即较低端点的X坐标），该边的最大Y 坐标值Ymax,以及边斜率的倒数1/k.4.同一桶中若干条边按x|ymin 由小到大排序，若x|ymin相等，则按照1/k由小到大排序。

2.扫描线的填充算法1.初始化。

构造边表，AET表设置为空。

2.将第一个不空的ET表中的边与AET表合并。

3.由AET表中取出的交点并进行填充，填充时候设置一个布尔量b（初值为假），令指针有效边表中的第一个结点（交点）到最后一个结点遍历一次，每访问一个结点，把b取反一次，若b为真，则把从当前结点的x值开始到下一个结点的x值结束的区间用多边形色填充，填充之后删除y=ymax的边（需注意，填充时同样为避免多边形区域的扩大化，需要多交点进行与x-扫面线算法相同的处理）。

4.y i+1=y i+1,根据x i+1=x i+1/k计算并修改AET表，同时合并ET表中y=y i+1桶中的边，按次序插入到AET 表中形成新的AET表。

六边形填充多边形算法-概述说明以及解释1.引言1.1 概述在计算机图形学中，六边形填充多边形算法是一种常用的方法，用于在离散的像素网格中填充一个给定的多边形区域。

这个算法主要的思路是利用六边形单元格来填充多边形，通过适当的规则和判断条件来确定哪些六边形单元格应该被填充，从而实现多边形的填充效果。

本文将详细介绍六边形填充多边形算法的原理、步骤以及优缺点，并结合具体的示例进行讲解。

通过深入学习和理解这一算法，读者可以更好地掌握在计算机图形学领域中处理多边形填充的技术手段，从而为实际应用场景中的图形渲染、图像处理等问题提供有效的解决方案。

1.2 文章结构:本文将首先介绍六边形填充多边形算法的概述，包括其背景和基本概念。

接着将详细讲解算法的原理，解释其实现的基本思路和机制。

然后，我们将逐步分析算法的具体步骤，包括算法的实现过程和关键步骤。

接下来，我们将探讨算法的优缺点，评价其在实际应用中的优劣势。

最后，我们将对本文进行总结，讨论六边形填充多边形算法在不同领域的应用前景，并展望未来的研究方向。

通过本文的讲解，读者将对六边形填充多边形算法有一个全面深入的了解。

1.3 目的:本文的目的是介绍六边形填充多边形算法，通过深入解析该算法的原理、步骤以及优缺点，帮助读者了解如何利用六边形填充多边形算法来有效解决填充多边形的问题。

通过本文的阐述，读者可以深入了解该算法的工作原理，从而更好地应用于实际的计算机图形学和几何方面的相关领域。

同时，本文还将探讨该算法的应用领域和未来的发展方向，旨在为读者提供对六边形填充多边形算法的全面了解，以促进该算法在实际应用中的推广和应用。

2.正文2.1 算法原理六边形填充多边形算法是一种基于六边形网格的填充算法，旨在将一个任意形状的多边形以最优方式填充为由六边形组成的图案。

该算法的原理主要包括以下几个步骤：1. 网格初始化：首先将待填充的多边形通过离散化的方式转换为六边形网格，确定网格的大小和分辨率。

带孔多边形填充算法一． 基本原理用自上而下的每一条水平的扫描线扫描多边形，每一条扫描线被多边形分成几段，每一段要么在多边形内，要么在多边形外。

在内的填充，在外的舍弃。

见图1图1二． 基本算法1. 水平扫描线与线段求交点假定当前扫描线y 与多边形的某一条边的交点x 坐标为x,那么下一条扫描线y-1与该边的交点不必从头算起，只要加上一个增量即可。

设增量为dx,显然dx= -(x1-x0)/(y1-y0) 结果是：若y=y i ,x=x i ,则当y=y i -1时，x=x i -(x1-x0)/(y1-y0)图22. 活性边与活性边表为了提高效率，在处理一条扫描线时，仅对与它相交的多边形的边进行求交运算。

我们把与当前扫描线相交的边称为活性边，并把它们按与扫描线交点x 坐标递增的顺序存放在一个链表中，称此链表为活性边表。

由于边的连贯性（即当某条边与当前扫描线相交时，它很可能也与下一条扫描线相交），以及扫描线的连贯性（当前扫描线与各边的交点顺序与下一条扫描线与各边的交点顺序很可能相同或非常类似），在当前扫描线处理完毕之后，我们不必为下一条扫描线从头开始构造活性边表，而只要对当前扫描线的活性边表稍作修改，即可更新得到下一条扫描线的活性边表。

例如,(见图3)扫描线6的活性边表如下：P 6P 1 →P 6P 5→ P 5P 4 →P 4P 3扫描线4的活性边表如下：P 6P 1→P 4P 3扫描线3的活性边表如下：P 6P 1→P 3P 2 (满足上闭下开的原则)。

扫描线2的活性边表如下：P 1P 2→P 2P 3 (满足上闭下开的原则)。

y-1 (x0,y0) (x1,y1) y dx 1图3 3．Y 桶表为了方便活性边表的建立与更新，我们为每一条扫描线建立一个新边表，存放在该扫描线第一次出现的边。

也就是说，若某边的较高端点为Y max ,则该边就放在扫描线Y max 的新边表中。

这样，当我们按扫描线从大到小顺序处理扫描线时，该边在该扫描线第一次出现。

实验三多边形的有效边表填充算法一、实验目的与要求1、理解多边形的扫描转换原理、方法；2、掌握有效边表填充算法；3、掌握链表的建立、添加结点、删除节点的基本方法；3、掌握基于链表的排序操作。

二、实验内容在实验二所实现工程的基础上，实现以下内容并把实现函数封装在类CMyGL 中。

1、C++实现有效边表算法进行多边形扫描转换2、利用1进行多边形扫描转换和区域填充的实现；三、实验原理请同学们根据教材及上课的PPT独立完成。

四、实验步骤（程序实现）。

1、建立并选择工程项目。

打开VC6.0->菜单File 的New 项,在projects 属性页选择MFC AppWizard(exe)项，在Project name 中输入一个工程名,如“Sample”。

单文档。

2、新建一个图形类。

选择菜单InsertNew class，Class type 选择“Generic Class”，Name 输入类名，如“CMyCG。

3、向新建的图形类中添加成员函数（实际就是加入实验要求实现的图形生成算法的实现代码）。

在工作区中直接鼠标右键单击，选择“Add Member Function…”项，添加绘制圆的成员函数。

void PolygonFill(int number, CPoint *p, COLORREF color, CDC* pDC)添加其他成员函数：CreatBucket();CreatET();AddEdge();EdgeOrder();4、成员函数的实现。

实现有效边表填充算法。

这一部分需要同学们去实现。

参考实现：多边形的有效边表填充算法的基本过程为：1、定义多边形：2、初始化桶3、建立边表4、多边形填充1)对每一条扫描线，将该扫描线上的边结点插入到临时AET表中，HeadE.2)对临时AET表排序，按照x递增的顺序存放。

3)根据AET表中边表结点的ymax抛弃扫描完的边结点，即ymax>=scanline4)扫描AET表，填充扫描线和多边形相交的区间。

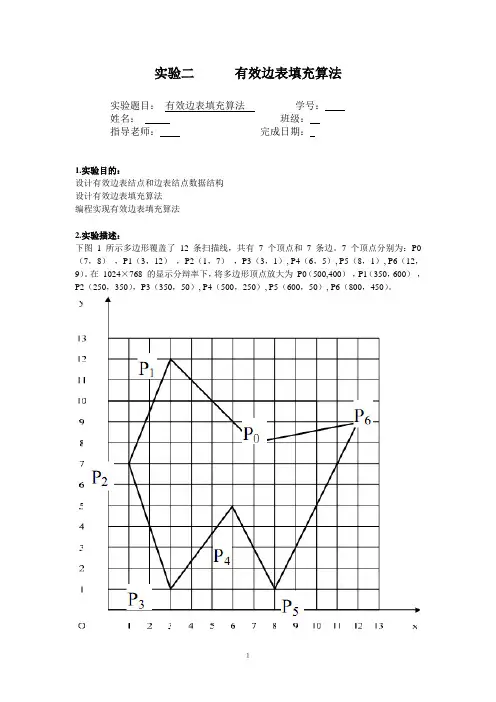
实验二有效边表填充算法实验题目：有效边表填充算法学号：姓名：班级：指导老师：完成日期：1.实验目的：设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述：下图1 所示多边形覆盖了12 条扫描线，共有7 个顶点和7 条边。

7 个顶点分别为：P0（7，8），P1（3，12），P2（1，7），P3（3，1）, P4（6，5）, P5（8，1）, P6（12，9）。

在1024×768 的显示分辩率下，将多边形顶点放大为P0（500,400），P1（350，600），P2（250，350），P3（350，50）, P4（500，250）, P5（600，50）, P6（800，450）。

图1示例多边形图2屏幕显示多边形3.算法设计：多边形的有效边表填充算法的基本原理是按照扫描线从小到大的移动顺序，计算当前扫描线与多边形各边的交点，然后把这些交点按x值递增的顺序进行排序、配对，以确定填充区间，然后用指定颜色点亮填充区间的所有像素，即完成填充工作。

有效边表填充算法通过访问多边形覆盖区间内的每个像素，可以填充凸、凹多边形和环，已成为目前最为有效的多边形填充算法。

4.源程序：1）//AET.h和AET..cppclass AET{public:AET();virtual ~AET();double x;int yMax;double k; //代替1/kAET *next;}2）//Bucket.h和Bucket.cppclass Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;}3) // TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数，顶点存放在整型二维数组Point[N]中class CTestView : public CView{。

实验二2-2一、实验题目给定四个点绘制图4-44所示的不同转角的两个正方形，使用有效边表算法进行填充，填充效果如图4-45所示，注意采用“左闭右开”和“上闭下开”的原则，使得每个正方形的右边界和下边界没有填充。

二、实验思想有效边表填充算法通过维护边表和有效边表，避开了扫描线与多边形所有边求交的复杂运算。

填充原理是按照扫描线从小到大的移动顺序，计算当前扫描线与有效边的交点，然后把这些交点按x值递增的顺序进行排序、配对，以确定填充区间，最后用指定颜色填充区间内的所有像素，即完成填充工作。

三、实验代码void CTestView::GetMaxX()//获得屏幕宽度{CRect Rect;GetClientRect(&Rect);MaxX=Rect.right;}void CTestView::GetMaxY()//获得屏幕高度{CRect Rect;GetClientRect(&Rect);MaxY=Rect.bottom;}void CTestView::ReadPoint()//读入点表函数{//设置第一个正方形的4个顶点int a=160;P1[0]=CP2(MaxX/4-a,MaxY/2+a);//P0P1[1]=CP2(MaxX/4+a,MaxY/2+a);//P1P1[2]=CP2(MaxX/4+a,MaxY/2-a);//P2P1[3]=CP2(MaxX/4-a,MaxY/2-a);//P3//设置第二个正方形的4个顶点int b=ROUND(sqrt(2)*a);P2[0]=CP2(3*MaxX/4,MaxY/2+b);//P0P2[1]=CP2(3*MaxX/4+b,MaxY/2);//P1P2[2]=CP2(3*MaxX/4,MaxY/2-b);//P2P2[3]=CP2(3*MaxX/4-b,MaxY/2);//P3}void CTestView::DrawRect(CDC *pDC,CP2 *P)//绘制正方形函数{CP2 T;CLine line;for(int i=0;i<4;i++)//边循环{if(i==0){line.MoveTo(pDC,P[i]);T=P[0];}else{line.LineTo(pDC,P[i]);;}}line.LineTo(pDC,T);//闭合}void CTestView::OnMENUIFill(){// TODO: Add your command handler code hereCOLORREF FColor;CColorDialog ccd(RGB(255,0,0));if(ccd.DoModal()==IDOK)//调用调色板选取色{FColor=ccd.GetColor();m_Red=GetRValue(FColor);//获得颜色的红色分量m_Green=GetGValue(FColor);//获得颜色的绿色分量m_Blue=GetBValue(FColor);//获得颜色的蓝色分量}RedrawWindow();//刷新屏幕FillRect(P1);//填充正方形1FillRect(P2);//填充正方形2}void CTestView::FillRect(CP2 *P)//填充正方形函数{CFill fill;CPi2 Point[4];for(int i=0;i<4;i++){Point[i].x=P[i].x;Point[i].y=ROUND(P[i].y);Point[i].c=CRGB(double(m_Red)/255.0,double(m_Green)/255.0,double(m_Blue)/255.0);}CDC *pDC=GetDC();fill.SetPoint(Point,4);//填充正方形fill.CreateBucket();fill.CreateEdge();fill.Gouraud(pDC);ReleaseDC(pDC);}四、实验截图。

有效边表填充算法基本思想：⽤⽔平扫描线从上到下（或从下到上）扫描由多条⾸尾相连的线段构成的多边形，每根扫描线与多边形的某些边产⽣⼀系列的交点。

将这些交点按照x坐标排序，将排序后的点两两配对，作为线段的两个端点，以所填的颜⾊画⽔平直线。

步骤1.求交，计算扫描线与多边形的交点。

2.交点排序，对第1步得到的交点按照x从⼩到⼤排序3.颜⾊填充，对排序后的交点两两组成⼀个⽔平线段，以画线段的⽅式进⾏颜⾊填充。

4.完成多边形扫描，就结束算法，否则，继续1有效边多边形与当前扫描线相交的边成为有效边(active edge)。

在处理⼀条扫描线时仅对有效边进⾏求交运算，避免与多边形所有边求交，提⾼效率。

x y max1/k next桶表与边表有效边给出了扫描线与有效边交点的计算⽅法，但没有给出新边出现的位置坐标。

为了确定在哪条扫描线上加⼊了新边，就需要构造⼀个边表（edge table ET),⽤以存放扫描线上多边形各条边出现的信息。

⽔平边本⾝就是扫描线在建⽴边表时可以不予考虑。

桶表与边表的表⽰法桶表是按照扫描线顺序管理边出现的⼀个数据结构。

⾸先，构造⼀个纵向扫描线链表，链表的长度为多边形所占有的最⼤扫描线数，链表的每个节点称为桶(bucket）,对应多边形覆盖的每⼀条扫描线。

将每条边的信息链加⼊该边最⼩y坐标对应的桶处。

对每⼀条扫描线，如果新增多条边，按照x|y min 坐标递增的顺序存放在⼀个链表中，若x|y min 相等，则按照1/k递增，就形成边表。

x|ymin ymax1/k next。

多边形填充算法-有序边表法（扫描线算法）1.算法的基本思想（扫描线连贯性原理）： 对于⼀个给定的多边形，⽤⼀组⽔平(垂直)的扫描线进⾏扫描，对每⼀条扫描线均可求出与多边形边的交点，这些交点将扫描线分割成落在多边形内部的线段和落在多边形外部的线段；并且⼆者相间排列。

于是，将落在多边形内部的线段上的所有象素点赋以给定的⾊彩值。

算法中不需要检验每⼀个象素点，⽽只考虑与多边形边相交的交点分割后的扫描线段。

2.算法求解：对于每⼀条扫描线的处理：1）求交点：⾸先求出扫描线与多边形各边的交点；2）交点排序：将这些交点按X坐标递增顺序排序；3）交点匹配：即从左到右确定落在多边形内部的那些线段；4）区间填充：填充落在多边形内部的线段。

3.求交点的⽅法最简单的办法：将多边形的所有边放在⼀个表中，在处理每条扫描线时，从表中顺序取出所有的边，分别求这些边与扫描线的交点。

不使⽤该⽅法的原因：将做⼀些⽆益的求交点动作，因为扫描线并不⼀定与多边形的边相交，扫描线只与部分甚⾄较少的边相交；因此，在进⾏扫描线与多边形边求交点时，应只求那些与扫描线相交的边的交点。

确定与扫描线相交的边：⽤边表来确定哪些边是下⼀条扫描线求交计算时应该加⼊运算的。

4.边表（ET）：ET的意义在于为扫描线提供待加⼊的新边信息。

建⽴边的分类表ET(Edge Table)，每个结点结构如下：（Ymax ，ΔX ，X Ymin，）Ymax：边的最⼤Y值；ΔX：从当前扫描线到下⼀条扫描线之间的X增量（dX/ dY)；X Ymin：边的下端点的X坐标；next：指针，指向下⼀条边。

边的分类表可以这样建⽴：先按下端点的纵坐标(y值)对所有边作桶分类，再将同⼀组中的边按下端点X坐标递增的顺序进⾏排序, X坐标还相同的按ΔX递增的顺序进⾏排序。

5.活性边表AET把与当前扫描线相交的边称活化边AEL(Active Edge List) 。

组成的表称为活性表AET，其数据域组成如下：Ymax ：存放边的上端点Y坐标；X ：边与当前扫描线交点的X坐标；ΔX ，next指针：同边表。

多边形的边缘填充算法1.实验目的：在一个区域的内部填上不同的灰度或色彩2试验步骤：实验基本思想：逐边向右求补。

可以按任意顺序处理多边形的每条边。

在处理每条边时，首先求出该边与扫描线的交点，然后将每一条扫描线上交点右方的所有像素取补。

多边形的所有边处理完毕之后，填充即完成。

3实验程序（算法思想）：1、找出扫描线的范围2、建立边角桶（1）建立空桶（2）遍历多边形各边，根据边的r较小端输入桶中。

3、扫描填充#include "ggltools.h"void gltRasterText(double x, double y, const char *text, void *font){if(text == NULL) return ;glRasterPos2d(x, y);for(int i=0; text[i] != '\0'; i++){glutBitmapCharacter(font, text[i]);}}void gltLine2d(double x0, double y0, double x1, double y1){glBegin(GL_LINES);glVertex2d(x0, y0);glVertex2d(x1, y1);glEnd();}void gltRect2d(double x0, double y0, double x1, double y1)glBegin(GL_LINE_STRIP);glVertex2d(x0, y0);glVertex2d(x1, y0);glVertex2d(x1, y1);glVertex2d(x0, y1);glVertex2d(x0, y0);glEnd();}char gltClipCode(const GPoint2d &pt, const GPoint2d &top, const GPoint2d &bottom) {char code = 0;if(pt.y() > top.y()) code |= 0x01;else if(pt.y() < bottom.y()) code |= 0x02;if(pt.x() > bottom.x()) code |= 0x04;else if(pt.x() < top.x()) code |= 0x08;return code;}template <class T>void swap(T &a , T &b){T t =a;a=b;b=t;}bool gltLineClip2d(GPoint2d &pt0, GPoint2d &pt1,const GPoint2d &top, const GPoint2d &bottom){char c0,c1;double x,y;while (true){c0=gltClipCode(pt0,top,bottom);c1=gltClipCode(pt1,top,bottom);if (c0 & c1) return false;if (c0==0&&c1==0)return true;if(c0==0){swap(pt0,pt1);swap(c0,c1);}if(c0 & 0x01)//点在yt 上方；{y=top.y();x=pt0.x()+(y-pt0.y())*(pt1.x()-pt0.x())/(pt1.y()-pt0.y());}else if (c0 & 0x02){y=bottom.y();x=pt0.x()+(y-pt0.y())*(pt1.x()-pt0.x())/(pt1.y()-pt0.y());}else if(c0 & 0x04){x=bottom.x();y=pt0.y()+(x-pt0.x())*(pt1.y()-pt0.y())/(pt1.x()-pt0.x());}else if(c0 & 0x08){x=top.x();y=pt0.y()+(x-pt0.x())*(pt1.y()-pt0.y())/(pt1.x()-pt0.x());}pt0.set(x,y);}return false;}4.实验输出结果：。