下载文档原格式
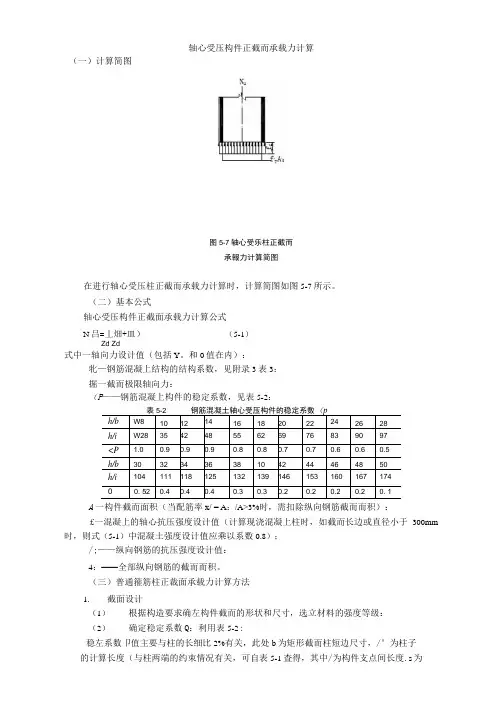
轴心受压构件正截而承载力计算（一）计算简图图5-7轴心受乐柱正截而承報力计算简图在进行轴心受压柱正截而承载力计算时，计算简图如图5-7所示。
（二）基本公式轴心受压构件正截面承载力计算公式N吕=丄畑+皿）（5-1）Zd Zd式中一轴向力设计值（包括Y。
和0值在内）：牝—钢筋混凝上结构的结构系数，见附录3表3：掘一截而极限轴向力：（P——钢筋混凝上构件的稳定系数，见表5-2：A一构件截而面积（当配筋率x/ = A：/A>3%时，需扣除纵向钢筋截而而积）：£一混凝上的轴心抗压强度设计值（计算现浇混凝上柱时，如截而长边或直径小于300mm 时，则式（5-1）中混凝土强度设计值应乘以系数0.8）；/;——纵向钢筋的抗压强度设计值：4：——全部纵向钢筋的截而而积。
（三）普通箍筋柱正裁面承载力计算方法1.截面设计（1）根据构造要求确左构件截而的形状和尺寸，选立材料的强度等级：（2）确定稳定系数Q：利用表5-2 :稳左系数卩值主要与柱的长细比2%有关，此处b为矩形截而柱短边尺寸，/°为柱子的计算长度（与柱两端的约朿情况有关，可自表5-1査得，其中/为构件支点间长度.s为拱轴线的长度）。
（3）计算所需的纵向钢筋截而而积A；：N吕=丄曲/ + “；）Xd X<1（4）选择纵向钢筋钢筋混凝土柱内配置的纵向钢筋常用II级或III级，并应符合下列要求：1）纵向钢筋的根数不得少于4根，每边不得少于2根：直径不应小于12mm,工程中常用钢筋直径为12〜32mm,宜选用根数较少的粗直径钢筋以形成劲性较好的骨架。
2）在轴向受压时沿截面周边均匀布置：在偏心受压时沿截面短边均匀布置。
3）现浇立柱纵向钢筋的净距不应小于50mm,同时中距也不应大于350mm。
在水平位置上浇筑的装配式柱，其净距与梁相同，当偏心受压柱的长边大于或等于600mm时，应在长边中间设宜直径为10〜16mm，间距不大于500mm的纵向构造钢筋，同时相应地设置联系拉筋。
4.2 轴心受压构件承载力计算按照箍筋配置方式不同，钢筋混凝土轴心受压柱可分为两种：一种是配置纵向钢筋和普通箍筋的柱(图4.2.1a)，称为普通箍筋柱；一种是配置纵向钢筋和螺旋筋（图4.2.1b）或焊接环筋(图4.2.1c)的柱，称为螺旋箍筋柱或间接箍筋柱。
需要指出的是，在实际工程结构中，几乎不存在真正的轴心受压构件。
通常由于荷载作用位置偏差、配筋不对称以及施工误差等原因，总是或多或少存在初始偏心距。
但当这种偏心距很小时，如只承受节点荷载屋架的受压弦杆和腹杆、以恒荷载为主的等跨多层框架房屋的内柱等，为计算方便，可近似按轴心受压构件计算。
此外，偏心受压构件垂直于弯矩作用平面的承载力验算也按轴心受压构件计算。
一、轴心受压构件的破坏特征按照长细比的大小，轴心受压柱可分为短柱和长柱两类。
对方形和矩形柱，当≤8时属于短柱，否则为长柱。
其中为柱的计算长度，为矩形截面的短边尺寸。
1．轴心受压短柱的破坏特征配有普通箍筋的矩形截面短柱，在轴向压力N作用下整个截面的应变基本上是均匀分布的。
N较小时，构件的压缩变形主要为弹性变形。
随着荷载的增大，构件变形迅速增大。
与此同时，混凝土塑性变形增加，弹性模量降低，应力增长逐渐变慢，而钢筋应力的增加则越来越快。
对配置HPB235、HRB335、HRB400、RRB400级热轧钢筋的构件，钢筋将先达到其屈服强度，此后增加的荷载全部由混凝土来承受。
在临近破坏时，柱子表面出现纵向裂缝，混凝土保护层开始剥落，最后，箍筋之间的纵向钢筋压屈而向外凸出，混凝土被压碎崩裂而破坏（图4.2.2）。
破坏时混凝土的应力达到棱柱体抗压强度。
当短柱破坏时，混凝土达到极限压应变=0.002，相应的纵向钢筋应力值=E s=2×105×0.002N/mm2=400N/mm2。
因此，当纵向钢筋为高强度钢筋时，构件破坏时纵向钢筋可能达不到屈服强度。
设计中对于屈服强度超过400N/mm2的钢筋，其抗压强度设计值只能取400N/mm2。
轴心受压构件长细比详细计算公式及扩展
长细比的计算公式如下：
λ=L/d
其中，λ为长细比，L为构件的长度，d为构件的截面尺寸（一般指最小截面尺寸，如矩形截面的宽度或圆形截面的直径）。
1.普通钢筋混凝土构件：λ≤60
2.预应力混凝土短期受拉构件：λ≤35
3.预应力混凝土长期受拉构件：λ≤25
以上是常见的构件长细比限制，对于特殊构件或特殊材料，限制值可能有所不同。
在进行具体的构件设计时，需要结合实际情况进行计算和判断。
扩展的长细比计算公式如下：
1.矩形截面长细比计算公式：
-构件为矩形截面，不考虑抗弯预应力，截面面积为A，截面惯性矩为I，截面高度为h，长细比为λ，宽度为b；
-λ=L/d=L/(b/√12)=√12*L/b
-公式中√12是矩形截面抗弯构件的长细比的系数。
2.圆形截面长细比计算公式：
-构件为圆形截面，直径为d，长细比为λ；
-λ=L/d
3.T形截面长细比计算公式：
-构件为T形截面，不考虑抗弯预应力，截面上翼缘的高度为h1，宽度为b1，截面下翼缘的高度为h2，宽度为b2；
-λ=L/d=L/((b1h1+b2h2)/2)
以上是一些常见截面形状的长细比计算公式。
在实际工程设计中，可能还会有其他特殊形状的截面，需要根据具体情况进行计算。
在进行长细比计算时，需要注意以下几点：
1.计算中要考虑截面惯性矩的效应，通常会取截面最不利的惯性矩进行计算。
2.考虑截面的有效高度，对于有孔洞或开口的截面，需要减去孔洞或开口的高度。
3.不同材料的长细比限制值可能有所不同，需要根据不同材料的特性进行计算和判断。
轴心受压构件正截面承载力计算首先，要计算轴心受压构件的正截面承载力，我们需要了解构件的几何参数，例如截面的尺寸和形状，以及构件的材料特性，如弹性模量和抗压强度等。
下面介绍一种常用的计算方法，即欧拉公式。
欧拉公式适用于细长的杆件，可以计算其承载力。
根据欧拉公式，轴心受压构件的正截面承载力可以表示为：Pcr = (π^2 * E * I) / (Lr)^2其中，Pcr 是构件的临界承载力，E 是构件的弹性模量，I 是构件截面的惯性矩，Lr 是约化长度。
对于不同的构件形状，惯性矩I的计算公式也不同。
以下是一些常见形状的惯性矩计算公式：1.矩形截面：I=(b*h^3)/12，其中b是截面的宽度，h是截面的高度；2.圆形截面：I=π*(d^4)/64，其中d是截面的直径；3.方管截面：I=(b*h^3-(b'*h')^3)/12，其中b是外边框的宽度，h是外边框的高度，b'是内边框的宽度，h'是内边框的高度。
约化长度Lr的计算取决于构件的边界条件。
以下是一些常见边界条件的约化长度计算公式：1.双端固定支承：Lr=L；2.一端固定支承、一端支座支承：Lr=0.7*L；3.双端支座支承：Lr=2*L。
通过使用上述公式，我们可以计算出轴心受压构件的正截面承载力。
需要注意的是，上述公式是基于一些理想化假设和条件下推导得出的，实际工程中还需要考虑一些因素，例如构件的稳定性和局部细部构造等。
因此，在实际设计中，应该根据具体情况综合考虑各种因素，并结合相关的规范和标准进行设计和验证，以确保构件的安全性和可靠性。
总之，轴心受压构件正截面承载力计算是工程设计中的重要环节。
通过合理的参数选择和计算，可以确定构件能够安全承受的最大压力，从而保证结构的安全和可靠性。
第四章二、钢梁的强度计算钢梁的强力一般应包括弯应力、剪应力和折算应力的验算。
对弯应力强度的验算如下： 单向弯曲 xx n xMfW=≤σϒ（4-3）双向弯曲 m axyxx n xyn yMMfWW =+≤σϒϒ （4-4）式中xM,yM——绕x 轴和y 轴的计算弯矩，应考虑荷载分项系数；f ——钢材的抗弯强度设计值——（表2-4）；nxW ,n yW ——钢梁对x 轴和y 轴的净截面模量；x ϒ,yϒ——截面塑性发展系数，工字形x ϒ=1.05,yϒ=1.2；其他截面形式的xϒ,yϒ值详见表5-4.当梁的受压翼缘的自由外伸宽度b 与其厚度 1t 之比大于13⨯时（但不超过15⨯），或当梁直接受动力荷载时，都应取1.0x y ==ϒϒ。
钢闸门和拦污栅中的各种梁，按有关现行专门规范规定，仍应采用容许应力计算法。
对应于式（4-3）的验算式为：单向弯曲 []xnxMM =≤σσ（4-5）钢梁剪应力的验算公式为 v wVS f It =≤τ（4-6）式中 V ——梁所受的最大剪力，应考虑荷载分项系数； vf ——钢材的抗剪强度设计值（表2-4）；I——梁的毛截面惯性矩（不考虑螺栓孔削弱）；S ——梁的毛截面在计算剪应力处以上部分对于中和轴的面积矩； wt ——摸板厚度若梁截面在同一点上受到较大的弯应力 σ、局部压应力c σ、和剪应力 τ共同作用时，还应按下式验算其折算应力：ep f=≤σβ （4-7）式中c σ,σ ——以拉应力为正值，压应力为负值；β ——计算折算应力的强度增大系数，当σ与cσ 同号或0c=σ时，取β=1.1，当σ 与cσ 异号时，取β=1.2 。
轧成梁的设计挠度验算。
应按荷载标准值计算梁的挠度：2x w PLw l EL l ⎡⎤=≤⎢⎥⎣⎦β（4-19）式中 β ——系数，根据梁的荷载分布与支承情况而定，例如收均载的简支梁5384=β/，跨度中点受集中荷载P 时，148=β/；P ——梁所受的荷载总值，例如，受均载q 时，P=qL ； x EI ——梁的抗弯刚度；w l ⎡⎤⎢⎥⎣⎦——相对挠度限值，随各类结构的使用要求而定，可由表4-2查得，详见有关规范中的规定。
