轴心受压构件长细比详细计算公式及扩展

!"##年$期 总第$%期 !.."作者简介 樊平 #%$*' 四川人 工学博士 从事公路工程研究轴心受压构件合理长细比理论及确定方法樊(平交通运输部公路科学研究院 北京(#"""77摘(要 在进行轴心受压构件设计时 截面面积一般都通过规范公式进行迭代求解获得 但是迭代法因需反复计算而显繁琐 为解决这一问题 本文通过引入表示构件截面特性参数0使之与构件长细比关联 并与现行规范验算公式联解而直接计算构件的合理长细比 这种方法克服了反复迭代的麻烦 在进行轴心受压构件截面设计时无须假设长细比反复试算 可根据设计已知量直接计算截面尺寸 文中提出方法的理论意义在于 它将轴心受压构件稳定性设计问题由传统的验算过程转变为直接求解过程 对于构件设计具有实用意义 关键词 轴心受压构件 长细比 稳定性 直接设计法中图分类号 .//(((((文献标识码 1!"引言在结构设计过程中 除需满足强度 刚度等要求外 结构构件的稳定性也是必不可少 目前国内外大多数现行规范中 轴心受压构件截面面积都是通过满足规范中给定的正截面强度验算式来确定 式中包含两个未知数 即截面面积和稳定系数 在设计过程中 截面面积的求解一般都采用迭代法进行 即先根据经验拟定结构截面尺寸 然后验算是否满足相关规范对该类构件的稳定性要求 在已选定材料的情况下 如不满足稳定性要求则改变结构截面尺寸 再进行验算 这样反复迭代直到满足要求为止 对于大型受压柱 使用迭代法会出现一些困难 试算次数多 而且会产生较大误差 不能满足目前所提倡的精细化设计的要求 反复迭代设计法的主要不足可归纳为以下几点 # 因需反复计算而显繁琐 ! 计算结果的误差大 虽能满足设计要求 但如需对结构进行比较择优 这种方法显然不能给出满意的结果 本文通过引入表示构件截面特性参数 使之与构件长细比关联 并与现行规范验算公式联解而直接计算构件的合理长细比 这种方法克服了反复迭代的麻烦 在进行轴心受压构件截面设计时可根据设计已知量计算截面尺寸#"轴心受压构件合理长细比#(!"轴心受压构件稳定承载能力设计公式目前不管是混凝土轴心受压构件 钢轴心受压构件或钢管混凝土轴心受压构件 在设计过程中其截面面积的确定都通过设计规范给定的公式 其形式一般如式 #F B #I& 2*#式中 I 为设计轴向力 &为稳定系数 2*为材料强度设计值式 # 可以看出 要得到轴向受压构件截面面积值 需要求解具有两个未知量F #和&的方程 在这种情况下 一般采用迭代法进行求解为了能避免迭代直接得到设计面积 首先应弄清轴心受压构件长细比与所求面积之间的关系 假定任意截面形状 任意材料的轴心受压构件的计算长度和设计轴向力也为任意值 在这种情况下稳定系数与长细比的关系具有如图 # 的曲线形状图#(轴心受压构件稳定系数&与构件长细比的关系从图#可以看出当构件长细比趋向于"时 稳定系数趋向# 随着长细比值的增大 稳定系数在平缓减小 当长细比增大到一定程度 稳定系数趋于一个很小的值 对于一般材料这个值为"0)2"0#* 考虑图#构件长细比与稳定系数的关系 式 # 中轴心桥隧工程#//"!"##年$期 总第$%期受压构件截面面积与长细比的关系则有如图!的趋势从图!可以看出长细比越大 截面面积F #越大 最小截面面积对应的长细比1为" 即当稳定系数&为#时图!(截面面积与长细比的关系通过分析可知 轴心受压构件长细比趋向于"在两种条件下才可能 一是当构件计算长度趋向"时 二是在截面静矩趋向于无穷大时第一种情况是针对极短柱 不涉及失稳的问题 在此无须关注 第二种情况在是需要研究的问题 要满足这种条件 需要在最小的截面面积F 时通过截面调整使得截面惯性矩达到最大 当然也须保证构件截面局部稳定的要求 #(#"构件截面特征从式 # 还可以看出截面面积只与长细比相关 而与截面形状无关 因此可以将截面面积表示为与截面形状相关的表达式 任何形状截面的截面面积都可以表示为很多长方形面积的和 如式 !F !"(;+2+!式中 ;+为第+个截面的宽 2+为第+个截面的厚度首先确定一个截面主要尺寸 如;#为主要尺寸 则截面面积可以表示为F !";!#2#;#&;!!2!;!&"&;!A 2A ;A"CCCCCCC ;!#+#&;!!+!&";!A+A ";!#(;!+;!#++"4;!# )式中 ++"2+;+由轴心受压截面局部稳定条件确定 从式 ) 可以看出截面面积由截面主要尺寸;#和参数4确定 对于简单的情况 如正方形截面4"# 对于圆形截面4"7/对于任意截面可以以同样的方式得到截面最小静矩和主要尺寸之间的关系 如式 /W 3B C"# ; /式中 W 3B C 为截面最小静矩 93B C 截面惯性矩如对于圆形截面#:"0!*截面静矩和构件计算长度 长细比有如下关系 如式 *W 3B C "#"13J e*式中 #"为构件计算长度 13J e为构件最大长细比 根据式 / 和式 * 将截面主要尺寸;表示为;"#"# 13J e&((在将式 & 带入 )F !"4#"# 1()3J e !"4#!#"1()3J e !"(#"1()3J e !$ ("4#!7 #('"轴心受压构件合理长细比公式式 $ 与 7 可以看出轴心受压构件截面面积同长细比的平方成反比 同计算长度成正比 而参数(在取决于构件局部稳定条件和截面形状 将 # 与 $ 表示为图)图)(截面面积与长细比的关系将式 # 代入式 $ 可以得到I & 2*"(#"()1!% ((一般在设计规范都给出了&和1的关系表达式 或表格形式给出二者的关系式 % 即是获得轴心受压构件合理长细比的解析方程 在满足该式的条件下得到的长细比对应的截面面积具有最小值 而且以此得到的构件截面满足整体和局部稳定条件为了进一步说明问题 将式 % 表示为式 #" 的形式 在给定的( #" I 2*和稳定系数的情况下满足该式的长细比为最合理的长细比 (#!"2*& 1 I 1!"# #"((将 % 变换为下式!"##年$期!总第$%期"#/!"1!&!1""(#!"2*I "I !##"((上式的右端为一个无量纲的综合参数I #它取决于设计已知参数和构件截面特征参数($从式!##"可以看出#在设计过程中如事先知道截面特征参数(#则通过其他设计已知参数可以直接获得合理长细比#根据长细比其他截面尺寸则可以很容易求得$'"矩形截面关于稳定性的截面特征参数 的确定((以矩形截面钢管混凝土为例说明截面特征参数(的推导方法#如图/所示矩形截面#高为H #宽为;#钢板壁厚为B$图/(矩形截面示意图矩形截面的面积可以表示为下式&F"F *&F J O J O *"F *#&F J F *O JO ()*"CC H !;H #&F J F *O JO ()*"4(H !!#!"式中&4";H #&F J F *O J O ()*";H #&.JA ()J !#)"相对于?与@轴的截面惯性矩表示为截面主尺寸H 的函数#如下式&C9?*;H )#!&!;B O J O *H !&B ()!!&!O J O *B H )#!";H )##!&#!O J O *B H #&B ()H !&#&B ;O J O []*";H )##!&#&B ;A J #&);H #&B ()H ()[]!!#)J "9@*H ;)#!&!H B O J O *;!&B ()!!&!O J O *B ;)#!"H ;)##!&#!O J O *B ;#&B ();!&#&B H O J O []*"H ;)##!&#&B H A J#&)H ;#&B ();()[]!!#)j "截面静矩表示为&W ?!#/J "W @"H ;H 槡!#/j "#?#*J "#@";H 槡!#*j "因此#矩形截面特征参数为(?"4#!?";H !#&.J A J "!##!&#&B ;A J #&);H #&B ()H()!!#&J "(@"4#!@"#&.J A ()J!;H ##!&#&B H A J #&)H ;#&B ();()!!#&j "((从式!#&"可以看出#当已知含钢率.J#钢和混凝土弹性模量之比A J#截面高宽之比;H#以及钢板厚度与矩形截面宽度之比B ;或厚度与截面高度之比BH后#即可以确定截面特征参数(?和(@$而且可以通过保证截面在?和@方向具有相同的稳定性这样的原则确定截面高宽之比;H $截面宽度之比B;或厚度与截面高度之比BH由钢板的局部稳定条件来确定$由式!#&"得到截面特征参数(后#根据式!##"便可计算轴心受压构件长细比#然后根据所求长细比计算截面其他尺寸$)"结论!#"通过文中理论推导长细比的表达式可以看出#它能够同时满足规范稳定性和满足构件局部稳定性要求#因此称为-合理长细比.$通过该长细比可(下转第!"7页桥隧工程#/-"!"##年$期!总第$%期"!/"施工过程中#加强施工方和第三方监控量测#根据反馈信息及时修正处治方案$*"结语旱莲花隧道为浅埋大跨度公路隧道#地质条件复杂%岩体破碎#节理发育#隧道成洞条件及自稳能力差#导致初支大变形问题$隧道施工大变形主要是由岩性%地下水及施工工法等因素综合影响出现的$通过对隧道大变形原因的综合分析#采取了以地表和洞内注浆加固%稳定后换拱等处治技术措施#顺利解决了隧道浅埋段的大变形问题$采用的技术方案可为类似工程施工提供参考$参考文献/#)(张旭珍0关角隧道大变形处理技术0石家庄铁道大学学报#!"##!"#"0/!)(刘新荣#钟祖良#黄林伟0桃树垭隧道初期支护大变形分析与工程处理0水文地质工程地质#!""7!"/"0/))(谢俊峰#陈建平0火车岭隧道软弱围岩大变形特征及机理分析0武汉科技大学学报#!""$!"&"0//)(王连池#张庆飞0土质隧道大变形浅析0隧道建设#!""##!#!/"""""""""""""""""""""""""""""""""""""""""""""""""0上接第!"#页以计算截面的主要尺寸#再通过主要尺寸计算截面其他尺寸#据此而设计的截面相应也满足构件的整体稳定性和局部稳定性$!!"以矩形截面方钢管混凝土为例推导出了无量纲参数表达式(#(的值取决于截面的相对尺寸#如高宽比%宽厚比%高厚比#以及含钢率%弹性模量比#尺寸之比参数取决于受压构件局部稳定条件和截面各方向保持同一稳定性等要求#而含钢率%弹性模量比则由设计已知量确定$因此#对于同类型结构(表示截面特性#由已知条件计算得出$这样在给定截面形状的和&!1"后#可以直接计算轴心受压构件长细比$!)"文中提出方法的理论意义在于#它将轴心受压构件稳定性设计问题由传统的验算过程转变为直接求解过程#对于构件设计具有实用意义$参考文献/#)(P 1*""#$'!"")#钢结构设计规范0/!)(陈绍蕃0结构设计原理0北京&科学出版社#!""*0/))(王正中0钢压杆稳定设计的直接计算法0力学与实践##%%$##%!*"&)"'))0//)(吴东红0钢轴心受压构件截面的直接计算法0力学与实践##%%7#!"!*"0/*)(钟善铜0钢管混凝土结构0北京&清华大学出版社#!"")0/&)(韩林海#杨有福0现代钢管混凝土结构技术0北京&中国建筑工业出版社#!""$0/$)(F J K J L J M B GH 0=0N O @B L J K P G J QR B E S >?@P T U K U V >E U @>G G A MW U G @C J K P G >B X G U W U G @C U G G >?T J @A M Y K U L U G @>X ?@C >B @U K P G A M S >G ?@C D S W B Z0[S ?O C U ??'B G \>C L J W B Q H /7)(樊平#左新黛0圆钢管混凝土轴心受压构件稳定性直接设计法0建筑结构学报#!""%#V!H。

计算长度、长细比、平面内平面外、回转半径解析计算长度：构件在其有效约束点间的几何长度乘以考虑杆端变形情况和所受荷载情况的系数而得的等效长度，用以计算构件的长细比。

计算焊缝连接强度时采用的焊缝长度。

计算长度是从压杆稳定计算中引出的概念。

计算长度等于压杆失稳时两个相邻反弯点间的距离。

计算长度=K*几何长度。

K为计算长度系数。

记住铰支座可以看成是反弯点，这样两端铰接压杆的计算长度等于两个铰支座的距离，即等于几何长度。

此时，k=1。

K可以大于1，也可小于1.1、在很多教材中规定，不同端部约束条件下轴心受压构件（柱）的计算长度系数：如两端铰接L=1.0；两端固定L=0.5；一端铰支一端固定L=0.7；悬臂L=2.0等2、钢结构规范附录D中柱的计算长度系数，需要根据K1、K2值查表第1条中所列的计算长度系数是理想条件下的；第2条是考虑上下端既不是固定也不是铰接而进行的一种修正。

此外，需要注意国内钢结构的压杆和拉杆都需要按计算长度来计算长细比，实际上拉杆没有失稳的问题，也自然不会有计算长度了，应直接取几何长度。

美国钢结构规范中规定拉杆的长细比直接按几何长度计算，概念正确！平面外与平面内实际上这是钢结构中常用的简化术语。

以钢梁和钢屋架为例，全称应该分别是弯矩作用平面内和弯矩作用平面外，即在竖向平面内失稳的计算长度称为平面内计算长度。

对于三角形钢屋架中央的竖杆还有斜平面计算长度呢，详细看一下有关的参考书吧钢结构杆件截面形心有两个轴，x、y轴，绕这两个轴就有两个回转半径。

受压杆要计算在这两个方向的压杆稳定及纵向弯曲系数，就需要这两个方的计算长度。

在主平面（一般是绕x轴）方向的叫平面内，另一个方向就叫平面外。

例如钢屋架的上弦杆，平面内的计算长度就是节点间的距离，而另方向支撑点间的距离就是平面外的计算长度。

平面内,平面外,举个简单的例子,也就是你在看pkpm的手册里面,特别是关于板这个概念用得多.1、关于板的面内面外,通常刚性板假定面内刚度无穷大,面外刚度为零,面内就是你站在地面,目光平视看到的板的方向就是面内方向,即水平方向的板的刚度,(个人认为)这个时候如果视板为一个构件,简单的认为其轴向刚度无穷大.面外方向就是水平板的垂直方向,就是你站在楼板上,你自身身体的方向,就是面外方向,这个时候视为其抗弯刚度为零(GA和EA一般是不考虑的),也即分析时不考虑.框架结构分析时,特别是在大学期间手算框架时有明显的体现的,2、还有一种是在柱子的计算中提得比较多,即所谓的弯矩作用平面内和弯矩作用平面外.对单向偏压构件,弯矩所在的平面即弯矩作用平面内,是按照压弯构件计算的,弯矩作用平面内就是取一个柱横截面,做一个垂直于柱横截面的平面,弯矩在这个平面内,这个平面就是弯矩作用平面.规范规定在弯矩作用平面外按轴压构件验算,弯矩作用平面外就是与前面所述的包含了弯矩的那个作用面相垂直的平面,当然也垂直于柱截面.(我认为在通常的平面简化计算中这个解释还是比较圆满的)回转半径回转半径是指物体微分质量假设的集中点到转动轴间的距离，它的大小等于转动惯量除总质量后再开平方。

关于609钢管长细比的计算
1、长细比计算步骤
首先计算出惯性矩I ，对于圆管的惯性矩可根据下列公式计算：
)1(64
44
απ-=D I 其中D d /=α，d 为圆管内径，D 为圆管外径。

A I
=
i 其中A 为截面面积，对于圆管截面22)1(4απ-=
D A
长细比λ计算公式: i l
μλ=
式中l 为竿的长度，μ为长度因数，其值由竿端约束情况决定。

例如，两端铰支的细长压杆，μ=1；一段固定、一段自由的细长压杆，μ=2；两端固定的细长压杆，μ=0.5；一段固定一段铰支的细长压杆，μ=0.7。

受压杆件的容许长细比
2、609钢管参数参数
钢管外径D=609mm ，内径d=603mm ，壁厚3mm ，钢材为Q235级钢。

3、长细比计算
钢管惯性矩)1(6444
απ-=D I =3.14*6094*[1-(603/609)
4]/64=262053178.4mm4
截
面面积22
)1(4απ-=D A =3.14*6092*[1-(603/609)]2/4=28.26mm2
A I
=i =3045.15
=2*5916/3045.15=3.9<200
i l
μλ=。

轴心受压构件长细比详细计算公式及扩展-CAL-FENGHAI.-(YICAI)-Company One1关于受压杆件长细比的计算1.对于轴压构件的长细比计算公式如下：l 0=λl l ⋅=μ0A I i =（根据I 的定义，理解i ）其中对各个系数进行详解：A —构件的横截面积。

矩形面积为A=bh 。

对于圆形截面为：42D A π=，圆管截面22)1(4απ-=D A 。

I —构件的截面惯性矩。

对于矩形的截面惯性矩为123bh I =，对于圆形截面来说为644D I π=，对于圆管截面的惯性矩为)1(6444απ-=D I 其中D d /=α，d 为圆管内径，D 为圆管外径。

矩形：24/3232022222bh y b dy b y dA y I h hh =⋅=⋅=⋅=⎰⎰-圆形：64/)22sin (2164)2cos 1(2164sin sin 320420420223220222D D d D d dr r rd r drdA y I DD πθθθθθθθθππππ=-⋅=-⋅==⋅=⋅=⎰⎰⎰⎰⎰⎰（θθ2sin 212cos -=）l 为构件的几何长度，其具体长度又根据混凝土，钢结构，砌体等不同的结构形式而有所不同。

μ为长度因数，其值由竿端约束情况决定。

例如，两端铰支的细长压杆，μ=1；一段固定、一段自由的细长压杆，μ=2；两端固定的细长压杆，μ=；一段固定一段铰支的细长压杆，μ=。

拓展：根据i 的计算公式，很明显，我们可以就算出矩形和圆形的回转半径i ：矩形：12h i =；圆形（实）：4Di =,圆环:4)1(4α-=D i (不用记)钢结构受压杆件的容许长细比。

轴心受压构件长细比详细计算公式及扩展
长细比的计算公式如下：
λ=L/d
其中，λ为长细比，L为构件的长度，d为构件的截面尺寸（一般指最小截面尺寸，如矩形截面的宽度或圆形截面的直径）。

1.普通钢筋混凝土构件：λ≤60
2.预应力混凝土短期受拉构件：λ≤35
3.预应力混凝土长期受拉构件：λ≤25
以上是常见的构件长细比限制，对于特殊构件或特殊材料，限制值可能有所不同。

在进行具体的构件设计时，需要结合实际情况进行计算和判断。

扩展的长细比计算公式如下：
1.矩形截面长细比计算公式：
-构件为矩形截面，不考虑抗弯预应力，截面面积为A，截面惯性矩为I，截面高度为h，长细比为λ，宽度为b；
-λ=L/d=L/(b/√12)=√12*L/b
-公式中√12是矩形截面抗弯构件的长细比的系数。

2.圆形截面长细比计算公式：
-构件为圆形截面，直径为d，长细比为λ；
-λ=L/d
3.T形截面长细比计算公式：
-构件为T形截面，不考虑抗弯预应力，截面上翼缘的高度为h1，宽度为b1，截面下翼缘的高度为h2，宽度为b2；
-λ=L/d=L/((b1h1+b2h2)/2)
以上是一些常见截面形状的长细比计算公式。

在实际工程设计中，可能还会有其他特殊形状的截面，需要根据具体情况进行计算。

在进行长细比计算时，需要注意以下几点：
1.计算中要考虑截面惯性矩的效应，通常会取截面最不利的惯性矩进行计算。

2.考虑截面的有效高度，对于有孔洞或开口的截面，需要减去孔洞或开口的高度。

3.不同材料的长细比限制值可能有所不同，需要根据不同材料的特性进行计算和判断。

轴心受压构件合理长细比理论及确定方法
轴心受压构件是在轴线中心受到拉应力，考虑根据材料安全性要求，其合理长细比受到制约。

要确定轴心受压构件合理长细比，应综合考虑体积、重量、制造、安装等因素，并根据特殊情况采取相应的措施确定，具体方法如下介绍：
（1）按设计所需受压构件设计。

设计轴心受压构件的最重要的原则是按照设计所需的尺寸、强度的要求进行设计，使受压构件能够胜任所承受的作用，保证构件性能、受力安全，并在可行的条件下取得较小的体积和较低的重量。

（2）确定受压构件的型号和材料。

根据构件的受力性能、环境条件以及状况等确定受压构件的型号和材料，确保该结构取得的强度，刚度，耐久度要求。

（3）按受压构件的操作要求确定其合理长细比。

在确定受压构件材料及型号后，根据不同的使用条件，按受压构件的安装、操作要求，采用Rehn伯量法、椭圆矩形法等确定长细比，以确保得到最佳的强度及结构稳定性。

（4）考虑制造及组装要求，确定受压构件的合理尺寸。

考虑构件的制造情况和组装安装要求，确定受压构件的尺寸，以符合制造要求和组装要求。

（5）考虑经济及防腐蚀等因素。

在确定受压构件的尺寸并考虑制造及组装要求后，要考虑构件的经济性，如考虑防腐蚀性及重物等特殊要求，以获得多种可供选择，可以根据上述方法确定轴心受压构件合理长细比。

计算长度、长细比、平面内平面外、回转半径解析计算长度：构件在其有效约束点间的几何长度乘以考虑杆端变形情况和所受荷载情况的系数而得的等效长度，用以计算构件的长细比。

计算焊缝连接强度时采用的焊缝长度。

计算长度是从压杆稳定计算中引出的概念。

计算长度等于压杆失稳时两个相邻反弯点间的距离。

计算长度=K*几何长度。

K为计算长度系数。

记住铰支座可以看成是反弯点，这样两端铰接压杆的计算长度等于两个铰支座的距离，即等于几何长度。

此时，k=1。

K可以大于1，也可小于1.1、在很多教材中规定，不同端部约束条件下轴心受压构件（柱）的计算长度系数：如两端铰接L=1.0；两端固定L=0.5；一端铰支一端固定L=0.7；悬臂L=2.0等2、钢结构规范附录D中柱的计算长度系数，需要根据K1、K2值查表第1条中所列的计算长度系数是理想条件下的；第2条是考虑上下端既不是固定也不是铰接而进行的一种修正。

此外，需要注意国内钢结构的压杆和拉杆都需要按计算长度来计算长细比，实际上拉杆没有失稳的问题，也自然不会有计算长度了，应直接取几何长度。

美国钢结构规范中规定拉杆的长细比直接按几何长度计算，概念正确！平面外与平面内实际上这是钢结构中常用的简化术语。

以钢梁和钢屋架为例，全称应该分别是弯矩作用平面内和弯矩作用平面外，即在竖向平面内失稳的计算长度称为平面内计算长度。

对于三角形钢屋架中央的竖杆还有斜平面计算长度呢，详细看一下有关的参考书吧钢结构杆件截面形心有两个轴，x、y轴，绕这两个轴就有两个回转半径。

受压杆要计算在这两个方向的压杆稳定及纵向弯曲系数，就需要这两个方的计算长度。

在主平面（一般是绕x轴）方向的叫平面内，另一个方向就叫平面外。

例如钢屋架的上弦杆，平面内的计算长度就是节点间的距离，而另方向支撑点间的距离就是平面外的计算长度。

平面内,平面外,举个简单的例子,也就是你在看pkpm的手册里面,特别是关于板这个概念用得多.1、关于板的面内面外,通常刚性板假定面内刚度无穷大,面外刚度为零,面内就是你站在地面,目光平视看到的板的方向就是面内方向,即水平方向的板的刚度,(个人认为)这个时候如果视板为一个构件,简单的认为其轴向刚度无穷大.面外方向就是水平板的垂直方向,就是你站在楼板上,你自身身体的方向,就是面外方向,这个时候视为其抗弯刚度为零(GA和EA一般是不考虑的),也即分析时不考虑.框架结构分析时,特别是在大学期间手算框架时有明显的体现的,2、还有一种是在柱子的计算中提得比较多,即所谓的弯矩作用平面内和弯矩作用平面外.对单向偏压构件,弯矩所在的平面即弯矩作用平面内,是按照压弯构件计算的,弯矩作用平面内就是取一个柱横截面,做一个垂直于柱横截面的平面,弯矩在这个平面内,这个平面就是弯矩作用平面.规范规定在弯矩作用平面外按轴压构件验算,弯矩作用平面外就是与前面所述的包含了弯矩的那个作用面相垂直的平面,当然也垂直于柱截面.(我认为在通常的平面简化计算中这个解释还是比较圆满的)回转半径回转半径是指物体微分质量假设的集中点到转动轴间的距离，它的大小等于转动惯量除总质量后再开平方。

抗震设计中钢结构轴心受压长细比问题的讨论摘要：钢结构的稳定问题是钢结构设计和研究的重要问题，轴心受压问题又是该问题的核心和基础。

在简要阐述钢结构稳定理论的基础上,结合相关规范和试验资料文献,讨论钢结构抗震设计时，轴心受压支撑构件的长细比限值，以及抗震承载力验算时不同钢种的长细比修正问题。

结论表明:在弹性屈曲范围的长细比不应进行钢号修正。

关键词：钢结构；抗震设计；长细比；弹性屈曲1问题的提出构件长细比和板件宽厚比是钢结构设计的两个基本指标,既涉及结构的稳定安全,也与用钢量紧密相关。

关于钢结构抗侧力支撑的长细比限值在《钢结构设计规范( GB 50017 - 2003)》和有关钢结构抗震设计的规范、规程中都有明确规定。

然而,后者规定的构件长细比限值与设计规范在表现形式上却不尽相同,其长细比限值皆以Q235 钢的屈服强度为基准,对其他牌号钢材乘以（为钢材屈服强度) 予以修正。

此外,支撑构件抗震承载力计算时也采用了同样的修正。

这些修正，会在计算和分析时产生矛盾，比如以下这个算例的计算：设有长细比为150 的两个中心支撑构件,其端部支承、几何条件完全相同。

其中,一个采用Q235 钢,另一个采用Q345 钢。

在静力设计时,两者的承载力基本相同;而抗震设计时,需要考虑支撑承载力退化修正后Q345 钢支撑的承载力设计值将小于Q235 钢的设计值。

而若抗震设计规范规定,此两中心支撑的长细比上限值为150,则在此两支撑构件中,由Q235钢制作的构件,满足抗震设计要求;而用Q345 钢制作的构件,则不满足抗震要求,不可应用,需加大其截面直至长细比小于123。

由此，我们可以提出问题：抗震钢结构的中心支撑长细比,究竟是否需要钢号修正? 何种情况下需要修正以及如何修正?2轴心受压构件的长细比和承载力根据已有的力学知识，所谓的长细比是构件的计算长度与构件的截面回转半径i的比值，是用来衡量结构轴心压杆的柔度的，一般的计算长细比的公式如下=，而计算长度和几何长度的关系根据其约束的不同，采取对u取值的不同进行计算，具体算法的可以参考相关的力学资料。

计算长度：构件在其有效约束点间的几何长度乘以考虑杆端变形情况和所受荷载情况的系数而得的等效长度，用以计算构件的长细比。

计算焊缝连接强度时采用的焊缝长度。

计算长度是从压杆稳定计算中引出的概念。

计算长度等于压杆失稳时两个相邻反弯点间的距离。

计算长度=K＊几何长度.K为计算长度系数.记住铰支座可以看成是反弯点,这样两端铰接压杆的计算长度等于两个铰支座的距离,即等于几何长度。

此时，k=1。

K可以大于1,也可小于1.1、在很多教材中规定，不同端部约束条件下轴心受压构件（柱）的计算长度系数：如两端铰接L=1.0；两端固定L=0.5；一端铰支一端固定L=0.7；悬臂L=2.0等2、钢结构规范附录D中柱的计算长度系数，需要根据K1、K2值查表第1条中所列的计算长度系数是理想条件下的；第2条是考虑上下端既不是固定也不是铰接而进行的一种修正。

此外，需要注意国内钢结构的压杆和拉杆都需要按计算长度来计算长细比，实际上拉杆没有失稳的问题，也自然不会有计算长度了,应直接取几何长度。

美国钢结构规范中规定拉杆的长细比直接按几何长度计算，概念正确！平面外与平面内实际上这是钢结构中常用的简化术语。

以钢梁和钢屋架为例,全称应该分别是弯矩作用平面内和弯矩作用平面外，即在竖向平面内失稳的计算长度称为平面内计算长度。

对于三角形钢屋架中央的竖杆还有斜平面计算长度呢,详细看一下有关的参考书吧钢结构杆件截面形心有两个轴，x、y轴,绕这两个轴就有两个回转半径。

受压杆要计算在这两个方向的压杆稳定及纵向弯曲系数，就需要这两个方的计算长度。

在主平面(一般是绕x轴）方向的叫平面内，另一个方向就叫平面外。

例如钢屋架的上弦杆，平面内的计算长度就是节点间的距离,而另方向支撑点间的距离就是平面外的计算长度。

平面内,平面外,举个简单的例子,也就是你在看pkpm的手册里面，特别是关于板这个概念用得多。

1、关于板的面内面外，通常刚性板假定面内刚度无穷大，面外刚度为零，面内就是你站在地面,目光平视看到的板的方向就是面内方向,即水平方向的板的刚度，（个人认为)这个时候如果视板为一个构件，简单的认为其轴向刚度无穷大。

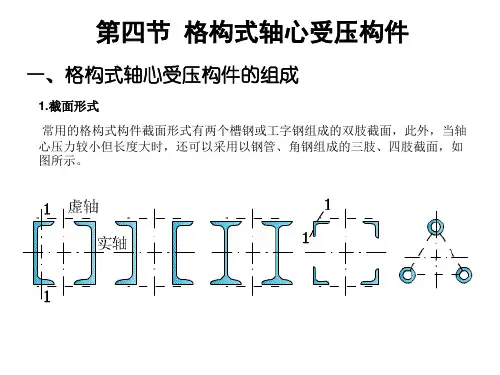
6轴心受力长细比，整体稳定计算
弦杆和腹杆都是由双角钢组合起来的
上弦受压下弦受拉腹杆可能受压也可以受拉
三个拉力固定住，二个压杆相当下面固定，上面铰接，0.8
垫板多少是合适的
5.1.5条
垫板间距中到中距离，节点板取边，垫板取中。

应2012 eg4.3.7 eg4.3.9 （283）
5.3.8受压容许长细比，5.3.9条受拉容许长细比
主要讲三个内容：
1，运输安装中不产生太大的弯曲变形
2，使用中，静力作用下（重力）荷载作用下不产生较大的下挠3，在多震荷载不产生太大的震动
应2012 eg4.3.5 eg4.3.6 （281）
三稳定计算
材料强度
稳定系数弯曲屈曲扭转屈曲弯扭屈曲。