下载文档原格式
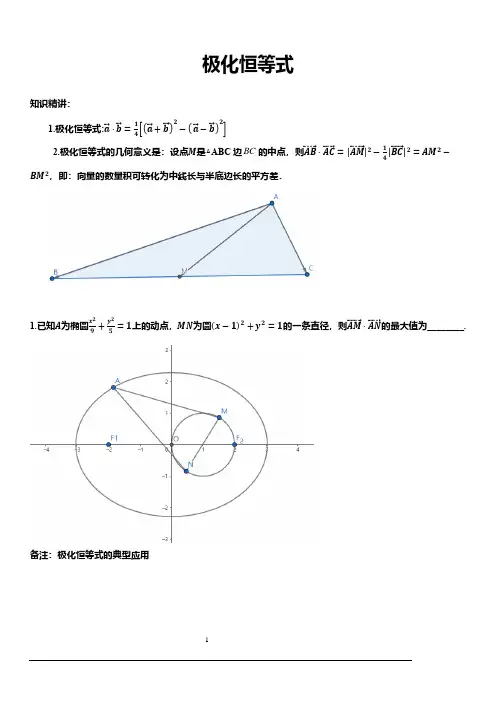
极化恒等式知识精讲：1.极化恒等式:a ⃗ ⋅b ⃗ =14[(a ⃗ +b ⃗ )2−(a ⃗ −b⃗ )2] 2.极化恒等式的几何意义是：设点M 是△ABC 边的中点，则AB⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AM ⃗⃗⃗⃗⃗⃗⃗ |2−14|BC ⃗⃗⃗⃗⃗⃗ |2=AM 2−BM 2，即：向量的数量积可转化为中线长与半底边长的平方差．1.已知A 为椭圆x 29+y 25=1上的动点，MN 为圆(x −1)2+y 2=1的一条直径，则AM ⃗⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的最大值为________.备注：极化恒等式的典型应用BC2. （三星）（2017全国2理）已知ΔABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ⃗⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )的最小值是（ ）A.−2B.−32 C. −43 D.−1 解：方法一：建系法连接OP ，OA⃗⃗⃗⃗⃗⃗ =(0,√3)，OB ⃗⃗⃗⃗⃗⃗ =(−1,0)，OC ⃗⃗⃗⃗⃗⃗ =(1,0). PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(−x,−y )⋅(−x,√3−y) ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =x 2+y 2−√3y =x 2+(y −√32)2−34 ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−34，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32 ∴最小值为−32方法二：均值法∵PC ⃗⃗⃗⃗⃗ +PB⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ 由上图可知：OA ⃗⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗⃗ −PO ⃗⃗⃗⃗⃗⃗ ；两边平方可得3=(PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ∵ (PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2≥−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ，∴ 2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32，∴最小值为−32 解法三：配凑法 ∵PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ∴PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(PO ⃗⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗⃗ )22=(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(AO ⃗⃗⃗⃗⃗⃗ )22≥−32∴最小值为−323．在∆ABC 中，BC 边上的中线AD 的长为2，点P 是∆ABC 所在平面上的任意一点，则PA PB PA PC ⋅+⋅的最小值为 A ．1B ．2C ．-2D ．-1【详解】建立如图所示的平面直角坐标系，使得点D 在原点处，点A 在y 轴上，则A (0,2)．设点P 的坐标为x y (,)，则(,2),(,)PA x y PO x y =−−=−−， 故()22(2)PA PB PA PC PA PB PC PA PO x y y ⋅+⋅=⋅+=⋅=+−22=+−−≥−x y 2[(1)]2222，当且仅当==x y 0,1时等号成立．所以PA PB PA PC ⋅+⋅的最小值为−2．选C ．4. （武汉二中高二）已知圆M:x 2+(y −1)2=1, 圆N:x 2+(y +1)2=1, 直线l 1、l 2分别过圆心M ,且l 1与圆M 相交于A 、B , l 2与圆N 相交于C 、D , P 是椭圆x 23+y 24=1上的任意一动点, 则PA → ⋅PB → +PC → ⋅PD →的最小值为______________.6 备注：用到极化恒等式5．在平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，若BE →=EF →=FG →=GC →，则2AE →∙DC →+AE →∙AF →=_____；若P 为边BC 上一动点，当PA →∙PC →取最小值时，则cos ∠PDC 的值为_____．解：∵平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，∴△ABC 是边长为2的等边三角， 在Rt △ADC 中，AC =2,CD =1，所以∠ACD =60∘，又BE →=EF →=FG →=GC →， ∴E,F,G 是BC 边的四等分点．如图建立坐标系：则：A(0,√3),B (−1,0),C (1,0)， D (32,√32),E (−12,0),F (0,0),G (12,0)， 所以2AE →DC →+AE →AF →=2(−12,−√3)(−12,−√32)+(−12,−√3)(0,−√3)=132，再设P (x,0)，则−1≤x ≤1，∴PA →PC →=(−x,√3)(1−x,0)=x 2−x =(x −12)2−14，显然x =12时，PA →PC →最小，此时P (12，0)，∴cos ∠PDC =cos ⟨DP →，DC →⟩=(−1，−√3)⋅(−1，−√3)(−1)+(−√32)(−12)+(−√32)=5√714．故答案为：132，5√714．6．在△OAB 中，OA =OB =2，AB =2√3，动点P 位于直线OA 上，当PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值时，向量PA ⃗⃗⃗⃗⃗⃗ 与PB ⃗⃗⃗⃗⃗⃗ 的夹角余弦值为（ ）A ．−3√77B ．7C ．−√217D ．√213【详解】∵|AB ⃗⃗⃗⃗⃗⃗ |2=(OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗⃗ )2=OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ ，即8−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =12，∴OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2， 设OP ⃗⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗⃗ (0≤λ≤1)，PA ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ，PB ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −OP ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ ， 所以，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅(OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ )=(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ +λ(λ−1)OA⃗⃗⃗⃗⃗⃗ 2 =−2(1−λ)+4λ(λ−1)=4λ2−2λ−2=(2λ−12)2−94，当λ=14时，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值−94，此时|PA ⃗⃗⃗⃗⃗⃗ |=34|OA ⃗⃗⃗⃗⃗⃗ |=32， |PB ⃗⃗⃗⃗⃗⃗ |2=|OB ⃗⃗⃗⃗⃗⃗ −14OA⃗⃗⃗⃗⃗⃗ |2=116OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−12OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =116×22+22−12×(−2)=214，所以，|PB ⃗⃗⃗⃗⃗⃗ |=√212，则cos <PA⃗⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗⃗ >=PA⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ |PA⃗⃗⃗⃗⃗⃗ |⋅|PB ⃗⃗⃗⃗⃗⃗ |=−9432×√212=−√217. 故选：C.7. （三星）在锐角∆ABC 中已知B= 3，|AB ⃗⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2,则AB ⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的取值范围是__________.解：法一：极化恒等式；法二：以B 为原点，BA 所在直线为x 轴建立坐标系，因为设A（x ，0）因为△ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°，即A 在如图的线段DE 上（不与D ，E 重合），所以1＜x ＜4，则AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ =x 2﹣x=（x ﹣12）2﹣14，所以AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ 的范围为（0，12）．方法2∵∠B=π3， △ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°=a=2由正弦定理可得()−==A B a b csin 120sinA sin 0∴=b ,=−Ac A sin 2sin 1200)( ∴120cos cos AB AC c b A A ===+=+⎝⎭−AA Asin tan 32202)(∵∈tanA0,3)( ∴(0,12AB AC ∈)8.在△ABC 中，AC ＝2BC ＝4，∠ACB 为钝角，M ，N 是边AB 上的两个动点，且MN ＝1，若CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ 的最小值为34，则cos ∠ACB ＝ ． 【答案】1−3√58【解析】取MN 的中点P ，则由极化恒等式得CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ =|CP ⃗⃗⃗⃗⃗ |2−14|MN ⃗⃗⃗⃗⃗⃗⃗ |2=|CP ⃗⃗⃗⃗⃗ |2−14∵CM ⃗⃗⃗⃗⃗⃗ ⋅CN ⃗⃗⃗⃗⃗⃗ 的最小值为34∴|CP ⃗⃗⃗⃗⃗ |min 由平几知识知：当CP ⊥AB 时，CP 最小. 如图，作CH ⊥AB ，H 为垂足，则CH=1 又AC ＝2BC ＝4，所以∠B ＝30o ，sinA=14 所以cos ∠ACB ＝cos （150o －A ）=1−3√58.9.如图所示，矩形ABCD 的边AB=4，AD=2，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧EB ̂ (含端点B 、E)上的一点，则PA → ·PB → 的取值范围是 .H【解析】取AB 的中点设为O ，则， 当O 、P 、C 共线时， PO 取得最小值为PO =2√2−2；当P 与B （或E ）重合时，PO 取得最大值为PO=2， 所以的取值范围是.10.如图，是边长为P 是以C 为圆心，1为半径的圆上的任意一点，则AP⃗⃗⃗⃗⃗⃗ ∙BP ⃗⃗⃗⃗⃗⃗ 最小值是_____.－111.（三星）如图，在△ABC 中，D 是BC 的中点，E,F 是AD 上的两个三等分点，BA ⃗⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =4,BF ⃗⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗ =−1,则BE ⃗⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ 的值是________.备注：极化恒等式的典型应用2221=4PA PB PO AB PO ⋅−=−4PA PB ⋅−[8∆ABC CA BP12.若平面向量a ，b 满足|2a －b|≤3，则a·b 的最小值为________.【解析】根据极化恒等式得：8a ⋅b =(2a +b)2−(2a −b)2=(2a +b)2−9≥−9，故a ⋅b ≥−98，所以a ⋅b 的最小值为−98．13.已知平面向量a ，b ，e 满足|e|＝1，a·e ＝1，b·e ＝－2，|a ＋b|＝2，那么a·b 的最大值为________． 解： 由a·e ＝1，b·e ＝－2得: a·e －b·e ＝3，即（a －b ）·e ＝3，|a －b|cos θ＝3a·b=14[|a ＋b|2－|a －b|2]≤－5414.在中，已知，，则面积的最大值是 ．解：取BC 的中点为D ，则AB ⃗⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =AD 2−BC24，所以AD =√2因为BC 边上的高线长不大于中线长，当中线就是高线时，面积最大，故．15.已知平面向量a ⃗ ,b ⃗ ,c ⃗ 满足|a ⃗ |=1，a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2，|2b ⃗ −c ⃗ |=2，那么b⃗ ⋅c ⃗ 的最小值为________． 【解析】由a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2得2a ⃗ ⋅b ⃗ +a ⃗ ⋅c ⃗ =3，即a ⃗ ⋅(2b ⃗ +c ⃗ )=3 又a ⃗ ⋅(2b ⃗ +c ⃗ )=|a ⃗ ||2b ⃗ +c ⃗ |cos θ（其中θ为向量a ⃗ 与2b ⃗ +c ⃗ 的夹角） 所以|2b⃗ +c ⃗ |=3cos θ所以b⃗ ⋅c ⃗ =18[(2b ⃗ +c ⃗ )2−(2b ⃗ −c ⃗ )2]=18(9cos 2θ−4)≥58.∆ABC =BC 21AB AC •=∆ABC ∆ABC16.已知锐角的外接圆的半径为1， ，则的取值范围为__________．17.已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则PA → ⋅PB →的取值范围是_____.[－2,6]18.在ΔABC 中，AB =3,AC =4,∠BAC =60°，若P 是ΔABC 所在平面内的一点，且AP =2，则PB → ⋅PC →的最大值为_____.10+2√3719.已知点P 是边长为2√3的正三角形ABC 内切圆上的一点，则PA → ⋅PB →的取值范围为_____.[−3,6]20.已知正方形ABCD 的边长为1，中心为O ，直线l 经过中心O ，交AB 于点M ，交CD 于点N ，P 为平面上一点，若2OP → ＝λOB → ＋(1－λ)OC → ，则PM → ·PN →的最小值为__________.−71621.设点P 为正三角形△ABC 的边BC 上的一个动点，当PA → ·PC →取得最小值时，sin ∠PAC 的值为________．√392622.在平面直角坐标系xOy 中，点A ，B 分别在x 轴，y 轴正半轴上移动，AB ＝2，若点P 满足PA → ·PB →＝2，则OP 的取值范围为________．[√3−1,√3+1]23.在△ABC 中，E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB → ·PC →＋BC →2的最小值是__________．4√3∆ABC ∠=πB 6BA BC⋅⎝ ⎛23,3。
向量极化恒等式【要点总结】1.极化恒等式：a ·b ＝14[(a ＋b )2－(a －b )2]几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14.2.平行四边形PMQN ，O 是对角线交点.则： (1)PM →·PN →＝14[|PQ |2－|NM |2](平行四边形模式)；(2)PM →·PN →＝|PO |2－14|NM |2(三角形模式).【典例1】 如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点． BA →·CA →＝4， BF →·CF →＝－1，则BE →·CE →的值为________．【答案】 78【解析】 设BD ＝DC ＝m ，AE ＝EF ＝FD ＝n ，则AD ＝3n.根据向量的极化恒等式，有AB →·AC →＝AD →2－DB →2＝9n 2－m 2＝4， FB →·FC →＝FD →2－DB →2＝n 2－m 2＝－1.联立解得n 2＝58，m 2＝138.因此EB →·EC →＝ED →2－DB →2＝4n 2－m 2＝78.即BE →·CE →＝78.【典例2】如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为2，MN 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦)，P 为正方体表面上的动点，当弦MN 的长度最大时， PM →·PN →的取值范围是________．【答案】 [0,2]【解析】 由正方体的棱长为2，得内切球的半径为1，正方体的体对角线长为2 3.当弦MN 的长度最大时，MN 为球的直径．设内切球的球心为O ，则PM →·PN →＝PO →2－ON →2＝PO →2－1.由于P 为正方体表面上的动点，故OP ∈[1，3]，所以PM →·PN →∈[0,2]． 【典例3】 (1)在△ABC 中，M 是BC 的中点，AM ＝3，BC ＝10，则AB →·AC →＝________.(2)(2018·上海调研)已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则P A →·PB →的取值范围是________. 【答案】 (1)－16 (2)[－2，6]【解析】 (1)因为M 是BC 的中点，由极化恒等式得：AB →·AC →＝|AM |2－14|BC |2＝9－14×100＝－16.(2)取AB 的中点D ，连接CD ，因为三角形ABC 为正三角形，所以O 为三角形ABC 的重心，O 在CD 上，且OC ＝2OD ＝2，所以CD ＝3，AB ＝2 3. 又由极化恒等式得：P A →·PB →＝|PD |2－14|AB |2＝|PD |2－3，因为P 在圆O 上，所以当P 在点C 处时，|PD |max ＝3， 当P 在CO 的延长线与圆O 的交点处时，|PD |min ＝1， 所以P A →·PB →∈[－2，6].【典例4】 (2018·诸暨适应性考试)已知AB 是圆O 的直径，AB 长为2，C 是圆O 上异于A ，B 的一点，P 是圆O 所在平面上任意一点，则(P A →＋PB →)·PC →的最小值为( ) A.－14B.－13C.－12D.－1【答案】 C【解析】 P A →＋PB →＝2PO →，∴(P A →＋PB →)·PC →＝2PO →·PC →，取OC 中点D ，由极化恒等式得，PO →·PC →＝|PD |2－14|OC |2＝|PD |2－14，又|PD |2min ＝0，∴(P A →＋PB →)·PC →的最小值为－12. 【典例5】 如图，在平行四边形ABCD 中，已知AB ＝8，AD ＝5，CP→＝3PD →，AP →·BP →＝2，则AB →·AD →的值是( ) A.44 B.22 C.24 D.72 【答案】 B【解析】 如图，取AB 中点E ，连接EP 并延长，交AD 延长线于F ，AP →·BP →＝（AP →＋BP →）2－（AP →－BP →）24＝（2EP →）2－AB →24＝2，∴EP ＝32，又∵CP →＝3PD →，AE →＝EB →，AB →＝DC →， ∴AE ＝2DP ，即△F AE 中，DP 为中位线，AF ＝2AD ＝10，AE ＝12AB ＝4，FE ＝2PE ＝62，AD →·AB →＝AF →·AE →＝AF 2＋AE 2－EF 22＝100＋16－722＝22.【典例6】 若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为( ) A.2 B.3 C.6 D.8 【答案】 C【解析】 如图，由已知|OF |＝1，取FO 中点E ，连接PE ，由极化恒等式得：OP →·FP →＝|PE |2－14|OF |2＝|PE |2－14，∵|PE |2max＝254，∴OP →·FP →的最大值为6. 【典例7】 已知正方形ABCD 的边长为1，点E 是AB 边上的动点，则DE →·DA →的值为________. 【答案】 1【解析】 取AE 中点O ，设|AE |＝x (0≤x ≤1)，则|AO |＝12x ，∴DE →·DA →＝|DO |2－14|AE |2＝12＋⎝⎛⎭⎫12x 2－14x 2＝1. 【典例8】 (2018·镇海中学模拟)在面积为2的△ABC 中，E ，F 分别是AB ，AC 的中点，点P 在直线EF 上，则PC →·PB →＋BC →2的最小值是________. 【答案】 23【解析】 取BC 的中点为D ，连接PD ，则由极化恒等式得PC →·PB →＋BC →2＝PD →2－BC →24＋BC →2＝PD →2＋3BC →24≥AD →24＋3BC →24此时当且仅当AD →⊥BC →时取等号， PC →·PB →＋BC →2≥AD →24＋3BC →24≥2AD →24·3BC →24＝2 3. 【典例9】 已知在△ABC 中，P 0是边AB 上一定点，满足P 0B ＝14AB ，且对于边AB 上任一点P ，恒有PB →·PC →≥P 0B →·P 0C →，则( ) A ．∠ABC ＝90° B ．∠BAC ＝90° C ．AB ＝AC D ．AC ＝BC【答案】 D【解析】 如图所示，取AB 的中点E ，因为P 0B ＝14AB ，所以P 0为EB 的中点，取BC 的中点D ，则DP 0为△CEB 的中位线，DP 0∥CE.根据向量的极化恒等式，有PB →·PC →＝PD →2－DB →2，P 0B →·P 0C →＝P 0D →2－DB →2. 又PB →·PC →≥P 0B →·P 0C →，则| PD →|≥|P 0D →|恒成立，必有DP 0⊥AB.因此CE ⊥AB ，又E 为AB 的中点，所以AC ＝BC.【典例10】 如图所示，正方形ABCD 的边长为1，A ，D 分别在x 轴，y 轴的正半轴(含原点)上滑动，则OC →·OB →的最大值是________．【答案】 2【解析】 如图，取BC 的中点M ，AD 的中点N ，连接MN ，ON ，则OC →·OB →＝OM →2－14.因为OM≤ON ＋NM ＝12AD ＋AB ＝32，当且仅当O ，N ，M 三点共线时取等号． 所以OC →·OB →的最大值为2.。
以小博大，很多数学老师不知道的极化恒等式，解决6类平面向量问题“曲中求直，蓄而后发，此谓借力打人，四两拨千斤也”。
出自武术大家李亦畲的《五字诀》，用于说明太极之奥义。
今天介绍一个平面向量的极化恒等式，亦有“四两拨千斤”之妙。
一个公式，六种用法，小公式，大力量！求解数量积常用的方法基底法、坐标法和图形法（几何意义法），但有时其解题过程运算复杂、过程繁冗，经常导致错误。
此时若能巧用极化恒等式，往往化繁为简，快速找到解题突破口。
本文以近几年高考、模拟试题为例，对极化恒等式在数量积问题中的应用进行分类整理，有助于学生成绩快速提升！定理：设a，b是平面内的两个向量，则有a·b= 1/4［（a+b）²-（a-b）²］.推导方式比较容易，只需将右侧平方公式打开即可！几何意义：△ABC中，AD为中线。
则有：极化恒等式的几何意义即：向量的数量积可转化为中线长与半底边长的平方差，揭示了三角形中线与边的关系，也可以理解为向量的数量积可表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的1/4。
特征：两个向量必须共起点，点D是两个向量夹角所对第三向量（这两个向量之差）上的中点。
题型一：三角形中数量积【点评】利用极化恒等式构造方程组，从而求出数量积的值。
对于从中线与底边这两个方向寻找基底向量的数量积问题，可以运用极化恒等式，把数量积转化为数量的运算，大大简化计算量！【分析】此题是最值问题，标准答案是坐标法。
计算量较大，此时利用极化恒等式直接将数量积转化，利用均值非常简单。
以下是几道三角形模型适合极化恒等式关于数量积的练习题。
用来给学生练习使用。
题型二四边形中数量积配套练习题型三圆形中数量积配套练习题型四圆锥曲线中数量积配套练习题型五立体几何中的数量积配套练习题型六多动点数量积【分析】此题初看是可以使用极化恒等式求解，但学生一经分析便遇到了两个动点的困难，成了许多学生的“拦路虎”，此题需要结合转化的思想，挖掘静态条件，从而进行突破。
第6节 极化恒等式知识与方法1.平行四边形性质：如下图所示，在平行四边形ABCD 中，()22222AC BD AB AD+=+.2.极化恒等式的平行四边形模式：在平行四边形ABCD 中，()2214AB AD AC BD ⋅=-. 3.极化恒等式的三角形模式：22AB AD AE EB ⋅=-，其中E 为BD 中点.提醒：极化恒等式主要用于解决数量积计算问题，利用极化恒等式，关键是取中点，巧妙之处是可将本身需要夹角才能计算的数量积转化为只需长度即可计算的量.典型例题【例1】（2012·浙江）在ABC 中，M 是BC 中点，3AM =，10BC =，则AB AC ⋅=_______. 【解析】解法1：AB AM MB =+，()()AC AM MC AB AC AM MB AM MC =+⇒⋅=+⋅+ ()2223516AM MB MC AM MB MC =+⋅+⋅+=-=-.解法2：由极化恒等式，22223516AB AC AM BM ⋅=-=-=-.【答案】16- 【例2】（2017·新课标Ⅱ卷）已知ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC⋅+的最小值是（ ） A.2-B.32-C.4-D.1-【解析】解法1：如图，设AC 中点为D ，则3OD =()()22232224PA PB PC PA PO PD ODPD ⎛⎫⋅+=⋅=-=-⎪⎝⎭，所以当0PD =，即点P 与点D 重合时，()PA PB PC ⋅+取得最小值32-.解法2：建立如图所示的坐标系，设(),P x y ，则()1,0B -，()1,0C ，(0,3A ， 所以()3PA x y =-，()1,PB x y =---，()1,PC x y =--，()2,2PB PC x y +=--， 故())()22233232222PA PBPCx y y x y ⎛⋅+=+-=+- ⎝⎭， 所以当03x y =⎧⎪⎨=⎪⎩时，()PA PB PC ⋅+取得最小值32-.【答案】B【例3】正三角形ABC 内接于半径为2的圆O ，E 为线段BC 上一动点，延长AE 交圆O 于点F ，则FA FB ⋅的取值范围为_______.【解析】解法1：建立如图1所示的平面直角坐标系，则可设()2cos ,2sin F θθ62ππθ⎛⎫-≤≤ ⎪⎝⎭，圆的半径为2423sin60ABAB ⇒=⇒=︒，故()3,1A --，)3,1B -，所以()32cos ,12sin FA θθ=----，()32cos ,12sin FB θθ=--，从而[]224cos 34sin 4sin 124sin 0,6FA FB θθθθ⋅=-+++=+∈. 解法2：如图2，设AB 中点为D ，圆的半径为24233sin 60ABAB AD ⇒=⇒=︒由极化恒等式，2223FA FB FD AD FD ⋅=-=-，由图可知当F 与点B 重合时，FD 3F 与点C 重合时，FD 取得最大值3，所以[]230,6FA FB FD ⋅=-∈.【答案】[]0,6【例4】正方形ABCD 的边长为2，以A 为圆心，1为半径作圆与AB 、AD 分别交于E 、F 于两点，若P为劣弧EF 上的动点，则PC PD ⋅的最小值为_______.【解析】解法1：建立如图所示的平面直角坐标系，则()2,2C ，()0,2D ，设()cos ,sin P θθ02πθ⎛⎫≤≤ ⎪⎝⎭，则()2cos ,2sin PC θθ=--，()cos ,2sin PD θθ=--，所以()()()()22cos cos 2sin 54sin 2cos 55PC PD θθθθθθϕ⋅=--+-=--=-+， 其中ϕ为某确定的锐角，022ππθϕθϕϕ≤≤⇒≤+≤+，故当2πθϕ+=时，PC PD ⋅取得最小值为55-.解法2：设CD 中点为G ，由极化恒等式，2221PC PD PG DG PG ⋅=-=-， 由图可知min 151PG AG =-， 所以())2min51155PC PD⋅=-=-【答案】55-强化训练1.（★★★）在平行四边形ABCD 中，2AC =，4BD =，则AB AD ⋅=_______.【解析】由极化恒等式，()()22221124344AB AD AC BD ⋅=-=-=-.【答案】3-2.（★★★）设M 、N 是20x y +-=上的两个动点，且2MN =OM ON ⋅的最小值为（ ）A.1B.2C.52 D.32【解析】解法1：如图，设(),2M x x -，则由2MN =()1,3N x x -- 所以()()()2123266OM ON x x x x x x ⋅=-+--=-+，显然当32x =时，OM ON ⋅取最小值32.解法2：如图，设G 为MN 中点，由极化恒等式，222221142OM ON OG MG OG MN OG ⋅=-=-=-， 显然OG 222-=OM ON ⋅的最小值32. 【答案】D3.（2016·江苏·★★★★）在ABC 中，D 是BC 中点，E 、F 是AD 上两个三等分点，4BA CA ⋅=，1BF CF ⋅=-，则BE CE ⋅的值是_______.【解析】设AE EF FD x ===，BD CD y ==，由极化恒等式，222222222259481318x BA CA AD BD x y BF CF FD BD x y y ⎧=⎧⎪⋅=-=-=⎪⎪⇒⎨⎨⋅=-=-=-⎪⎪⎩=⎪⎩， 故2222748BE CE ED BD x y ⋅=-=-=.【答案】784.（★★★）在ABC 中，60A =︒，2AB =，3AC =，D 在边AC 上运动，则DA DB ⋅的最小值为________.【解析】由余弦定理，2222cos 7BC AB AC AB AC A =+-⋅⋅=，所以7BC 取AB 中点G ，由极化恒等式，2221DA DB DG AG DG ⋅=-=-， 故DG 的长最小时，DA DB ⋅也最小，由图可知当点D 位于图中0D 处时，DG 的长最小， 且012DG BH =，03sin 3BH AB A DG =⋅==，所以DA DB ⋅的最小值为14-.【答案】14-5.（★★★）已知AB 是圆O 的直径，4AB =，C 是圆O 上异于A 、B 的一点，P 是圆O 所在平面内的任意一点，则()PA PB PC +⋅的最小值是________.【解析】如图，设OC 中点为D ， 则()()()22222212PA PBPC PO PC PD OD PD +⋅=⋅=-=-≥-，当且仅当P 、D 重合时取等号， 所以()PA PB PC +⋅的最小值是2-【答案】2-6.（★★★）在半径为1的扇形AOB 中，60AOB ∠=︒，C 为弧AB 上的动点，AB 与OC 交于点P ，则OP BP ⋅的最小值为_______.【解析】如图，设OB 中点为D ，则22214OP BP PD OD PD ⋅=-=-，故当PD 最小时，OP BP ⋅最小，由图可知当P 与0P 重合时，PD 最小，且易求得03DP =，所以OP BP ⋅的最小值为116-.【答案】116-7.（★★★）若O 和F 分别是椭圆22143x y +=的中心和左焦点，P 为椭圆上一点，则OP FP ⋅的最大值是（ ）A.2B.3C.6D.8【解析】如图，由题意，()1,0F -，设OF 中点为D ，则12OD =，由极化恒等式，22214OP FP PD OD PD ⋅=-=-，显然max 52PD =，所以OP FP ⋅的最大值是6.【答案】C8.（★★★）如下图所示，正方形ABCD 的边长为4，AB 为半圆O 的直径，P 为半圆圆弧上的动点，则PC PD ⋅的取值范围为________.【解析】如图，设E 为CD 中点，由极化恒等式，2224PC PD PE DE PE ⋅=-=-，由图可得225PE ≤≤所以PC PD ⋅的取值范围为[]0,16.【答案】[]0,169.（★★★★）四边形ABCD 中，M 是AB 上的点，1MA MB MC MD ====，90CMD ∠=︒,若N 是线段CD 上的动点，NA NB ⋅的取值范围是_______.【解析】M 是AB 上的点且1MA MB MC MD ====⇒C 、D 两点在以AB 为直径的圆上，且圆心为M ，90CMD CMD ∠=︒⇒是等腰直角三角形，由极化恒等式，2221NA NB NM AM NM ⋅=-=-，显然上点N 在CD 21NM ≤≤，所以102NA NB -≤⋅≤.【答案】1,02⎡⎤-⎢⎥⎣⎦10.（★★★★）在ABC 中，3AB =，4AC =，60A =︒，若P 是ABC 所在平面内一点，且2AP =，则PB PC ⋅的最大值是_________.【解析】如图，2AP =⇒点P 在以A 为圆心，2为半径的圆上运动，设BC 中点为D ，由余弦定理，222132cos 1313BC AB AC AB AC A BC CD =+-⋅⋅∠=⇒= 由极化恒等式，222134PB PC PD CD PD ⋅=-=-，由斯特瓦尔特公式，222AB CD AC BD AD BC BD CD BC ⋅+⋅-⋅=⋅⋅，即22213131313341313AD +-解得：37AD =AD 的长），当点P 在圆上运动时，max 3722PD AD =+=+，所以()2max37132102374PB PC⎫⋅=+-=+⎪⎪⎝⎭【答案】10237。
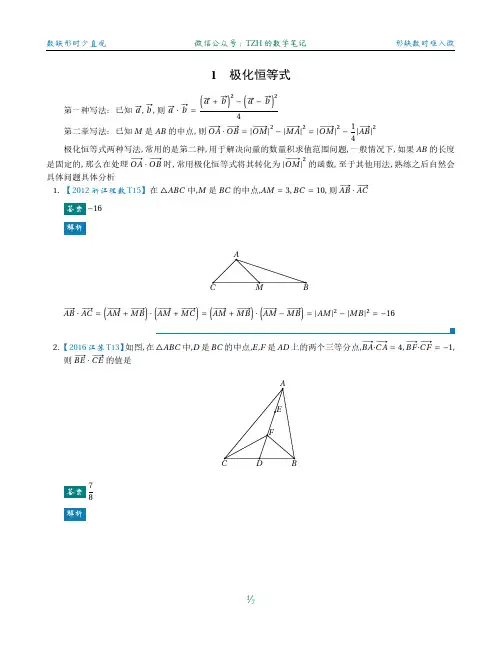
1极化恒等式第一种写法：已知#…a ,#…b ,则#…a ⋅#…b =⒧#…a +#…b ⒭2−⒧#…a −#…b ⒭24第二章写法：已知M 是AB 的中点,则# …OA ⋅# …OB =|# …OM|2−|# …MA|2=|# …OM|2−14|# …AB|2极化恒等式两种写法,常用的是第二种,用于解决向量的数量积求值范围问题,一般情况下,如果AB 的长度是固定的,那么在处理# …OA ⋅# …OB 时,常用极化恒等式将其转化为|# …OM|2的函数,至于其他用法,熟练之后自然会具体问题具体分析1.【2012浙江理数T15】在△ABC 中,M 是BC 的中点,AM =3,BC =10,则# …AB ⋅# …AC−16# …AB ⋅# …AC =⒧# …AM +# …MB⒭⋅⒧# …AM +# …MC ⒭=⒧# …AM +# …MB⒭⋅⒧# …AM −# …MB⒭=|AM|2−|MB|2=−162.【2016江苏T13】如图,在△ABC 中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,# …BA⋅# …C A =4,# …BF⋅# …C F =−1,则# …BE ⋅# …C E的值是78记|BD|=x ,|DF|=y ,則4=# …BA ⋅# …C A =|AD|2−|BD|2=9y 2−x 2−1=# …BF ⋅# …C F =|DF|2−|BD|2=y 2−x 2⎧⎪⎪⎨⎪⎪⎩x 2=138y 2=58从而# …BE ⋅# …C E =|DE|2−|BD|2=4y 2−x 2=783.【2018天津理数T8】如图,在平面四边形ABC D 中,AB⊥BC ,AD⊥C D,∠BAD =120∘,AB =AD =1.若点E 为边C D 上的动点,则# …AE ⋅# …BE 的最小值为A.2116B.32C.2516D.3A取AB 中点F ,则# …AE ⋅# …BE =|# …EF|2−|# …AF|2当EF ⟂C D 时,|# …EF|取得最小值54,比时# …AE ⋅# …BE 取得最小值2116,选A4.【2013浙江理数T7】设△ABC ,P 0是边AB 上一定点,满足# …P 0B =14# …AB ,且对于边AB 上任一点P ,恒有# …PB ⋅# …PC ⩾# …P 0B ⋅# …P 0C ,则A.∠ABC =90∘ B.∠BAC =90∘C.AB =ACD.AC =BCD取AB,BC的中点D,E.则# …PB⋅# …PC=(# …PE+# …EB)⋅(# …PE−# …EB)=|PE|2−|EB|2⩾|P0E|2−|EB|2,所以|PE|⩾|P0E|,则必有P0E⟂AB,从而C D⟂AB,所以AC=BC,选择D5.【2017全国2卷理数T12】已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则# …PA⋅⒧# …PB+PC⒭的最小值是A.−2B.−32C.−43D.−1B取BC中点M,取AM中点N,则# …PA⋅(# …PB+# …PC)=2# …PA⋅# …PM=2⒧PN2−MN2⒭⩾−2MN2=−32,当PN重合时取到,所以所求最小值是−32,选择B6.【2020天津T15】如图,在四边形ABC D中,∠B=60∘,AB=3,BC=6,且# …AD=λ# …BC,# …AD⋅# …AB=−32,则(1)实数λ的最小值为(2)若M,N是线段BC上的动点,且|# …MN|=1,则# …DM⋅# …DN的最小值为A DB M N C(1)16(2)132# …AD⋅# …AB=λ# …BC⋅# …AB=−9λ=−32,所以λ=16.取MN中点E,则# …DM⋅# …DN=|DE|2−|MN|24当DE⟂BC时,取到最小值13 2.7.【2005江苏T18】在△ABC 中,O 为中线AM 上的一个动点,若AM =2,则# …OA ⋅⒧# …OB +# …OC ⒭的最小值为−2设|OM|=x ,则# …OA ⋅(# …OB +# …OC )=2# …OA ⋅# …OM =−2x(2−x)⩾−2,取等条件是x =1,故所求最小值为−28.【2012安徽理数T14】若|2#…a −#…b |⩽3,则#…a ⋅#…b 的最小值是−98#…a ⋅#…b =|2#…a +#…b |2−|2#…a −#…b |28⩾−|2#…a −#…b |28⩾−989.在平行四边形ABC D 中,AD =√2,AB =2.若# …BF =# …FC ,则# …AF ⋅# …DF72# …AF ⋅# …DF =(# …AB +# …BF)⋅(# …AB −# …BF)=|AB|2−|BF|2=7210.已知△ABC 中,AB =8,BC =10,AC =6,P 在平面ABC 内,且# …PB ⋅# …PC =−9,则|# …PA|的取值范围是[1,9]解析11.正方体ABC D −A 1B 1C 1D 1的棱长为2,MN 是它的内切球的一条弦（我们把球面上任意两点之间的线段称为球的弦）,P 为正方体表面上的动点,当弦MN 的长度最大是,# …PM ⋅# …PN 的取值范围是[0,2]解析12.在面积为2的平行四边形ABC D中,点P为直线AD上的动点,则# …PB⋅# …PC+# …BC2的最大值是2√3设M为BC的中点,由题意,# …PB⋅# …PC+BC2=PM2−14BC2+BC2=PM2+34BC2⩾√3⋅PM⋅BC⩾√3⋅2S△PBC=2√3.取等条件为PM=√32BC且PM⟂BC.故所求最小值为2√313.在半径为1的扇形AOB中,∠AOB=60∘,C为弧AB的动点,AB与OC交于点P,则# …OP⋅# …BP的最小值是−1 16解析14.已知正四面体ABC D的棱长为2,P是以棱BC为直径的球面上一动点,则# …PA⋅# …PD的最大值是A.1+√2B.3C.2+√2D.2(√2+1)D取AD中点E,BC中点F,则# …PA⋅# …PD=|PE|2−|AE|2=|# …PF+# …FE|2−1⩽(|# …PF|+|# …FE|)2−1=(1+√2)2−1=2+2√2,选D15.【成都七中23届高三上一诊模拟T16】已知A(2cos15∘,2sin15∘),O(0,0),且|# …OB|=|# …OC|=2,则# …AB⋅# …AC的取值范围[−2,16]如图方法1极化恒等式记M为BC的中点,由极化恒等式可知:# …AB⋅# …AC=# …AM2−# …BM2,易知OM⊥BC,所以# …BM2=# …OB2−# …OM2所以# …AB⋅# …AC=# …AM2−# …BM2=# …AM2+# …OM2−# …OB2=# …AM2+# …OM2−# …OA2由余弦定理可知# …AM 2+# …OM 2−# …OA 2=2|# …MA|⋅|# …MO|cos ∠AMO =2# …MA ⋅# …MO记D 为OA 的中点,再由极化恒等式可知2# …MA ⋅# …MO =2 # …MD 2−# …OD 2因为B ,C 是圆上任意两点(可重合)所以|# …MD|∈[0,3]所以−2⩽# …AB ⋅# …AC ⩽16方法2投影暂无16.【乐山市21届一诊T10】已知△ABC 是边长为2的等边三角形,点P 是△ABC 所在平面的内的一点,且BP =1,则当# …AP ⋅# …C P 取得最小值时,# …BP ⋅# …BC 的值是A.√3B.√32C.−√3D.−√32A 方法1建系建系如图A(0,√3),B(−1,0),C (1,0),设P(−1+cos θ,sin θ)# …AP ⋅# …C P =⒧−1+cos θ,sin θ−√3⒭(−2+cos θ,sin θ)=3−2√3sin ⒧θ+π3⒭当且仅当θ=π6+2kπ时取等,代入# …BP ⋅# …BC =√3方法2向量转换# …AP⋅# …C P=⒧# …AB+# …BP⒭⋅⒧# …C B+# …BP⒭=# …AB⋅# …C B+# …AB⋅# …BP+# …BP⋅# …C B+# …BP2=2√3+1+# …AB⋅# …BP+# …BP⋅# …C B下求# …AB⋅# …BP+# …BP⋅# …BP⋅# …C B的最小值# …AB⋅# …BP+# …BP⋅# …BP⋅# …C B=−2# …BM⋅# …BP=−2|# …BM|⋅|# …BP|cos∠PBM=−2√3cos∠PBM⩾−2√3,当∠PBM=0时取得最小值,代入# …BP⋅# …BC=√3方法3极化恒等式# …AP⋅# …C P=# …PM2−14# …AC2=# …PM2−1⩾3−2√3,当P在线段BM与圆B的交点P′时,取得最小值,代入# …BP⋅# …BC=√3。
