高中数学《极化恒等式》PPT教学课件

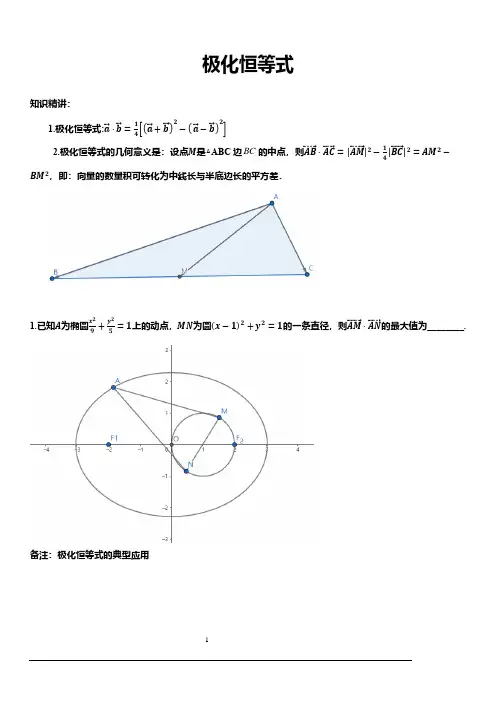
极化恒等式知识精讲：1.极化恒等式:a ⃗ ⋅b ⃗ =14[(a ⃗ +b ⃗ )2−(a ⃗ −b⃗ )2] 2.极化恒等式的几何意义是：设点M 是△ABC 边的中点，则AB⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AM ⃗⃗⃗⃗⃗⃗⃗ |2−14|BC ⃗⃗⃗⃗⃗⃗ |2=AM 2−BM 2，即：向量的数量积可转化为中线长与半底边长的平方差．1.已知A 为椭圆x 29+y 25=1上的动点，MN 为圆(x −1)2+y 2=1的一条直径，则AM ⃗⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的最大值为________.备注：极化恒等式的典型应用BC2. （三星）（2017全国2理）已知ΔABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ⃗⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )的最小值是（ ）A.−2B.−32 C. −43 D.−1 解：方法一：建系法连接OP ，OA⃗⃗⃗⃗⃗⃗ =(0,√3)，OB ⃗⃗⃗⃗⃗⃗ =(−1,0)，OC ⃗⃗⃗⃗⃗⃗ =(1,0). PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(−x,−y )⋅(−x,√3−y) ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =x 2+y 2−√3y =x 2+(y −√32)2−34 ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−34，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32 ∴最小值为−32方法二：均值法∵PC ⃗⃗⃗⃗⃗ +PB⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ 由上图可知：OA ⃗⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗⃗ −PO ⃗⃗⃗⃗⃗⃗ ；两边平方可得3=(PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ∵ (PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2≥−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ，∴ 2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32，∴最小值为−32 解法三：配凑法 ∵PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ∴PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(PO ⃗⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗⃗ )22=(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(AO ⃗⃗⃗⃗⃗⃗ )22≥−32∴最小值为−323．在∆ABC 中，BC 边上的中线AD 的长为2，点P 是∆ABC 所在平面上的任意一点，则PA PB PA PC ⋅+⋅的最小值为 A ．1B ．2C ．-2D ．-1【详解】建立如图所示的平面直角坐标系，使得点D 在原点处，点A 在y 轴上，则A (0,2)．设点P 的坐标为x y (,)，则(,2),(,)PA x y PO x y =−−=−−， 故()22(2)PA PB PA PC PA PB PC PA PO x y y ⋅+⋅=⋅+=⋅=+−22=+−−≥−x y 2[(1)]2222，当且仅当==x y 0,1时等号成立．所以PA PB PA PC ⋅+⋅的最小值为−2．选C ．4. （武汉二中高二）已知圆M:x 2+(y −1)2=1, 圆N:x 2+(y +1)2=1, 直线l 1、l 2分别过圆心M ,且l 1与圆M 相交于A 、B , l 2与圆N 相交于C 、D , P 是椭圆x 23+y 24=1上的任意一动点, 则PA → ⋅PB → +PC → ⋅PD →的最小值为______________.6 备注：用到极化恒等式5．在平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，若BE →=EF →=FG →=GC →，则2AE →∙DC →+AE →∙AF →=_____；若P 为边BC 上一动点，当PA →∙PC →取最小值时，则cos ∠PDC 的值为_____．解：∵平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，∴△ABC 是边长为2的等边三角， 在Rt △ADC 中，AC =2,CD =1，所以∠ACD =60∘，又BE →=EF →=FG →=GC →， ∴E,F,G 是BC 边的四等分点．如图建立坐标系：则：A(0,√3),B (−1,0),C (1,0)， D (32,√32),E (−12,0),F (0,0),G (12,0)， 所以2AE →DC →+AE →AF →=2(−12,−√3)(−12,−√32)+(−12,−√3)(0,−√3)=132，再设P (x,0)，则−1≤x ≤1，∴PA →PC →=(−x,√3)(1−x,0)=x 2−x =(x −12)2−14，显然x =12时，PA →PC →最小，此时P (12，0)，∴cos ∠PDC =cos ⟨DP →，DC →⟩=(−1，−√3)⋅(−1，−√3)(−1)+(−√32)(−12)+(−√32)=5√714．故答案为：132，5√714．6．在△OAB 中，OA =OB =2，AB =2√3，动点P 位于直线OA 上，当PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值时，向量PA ⃗⃗⃗⃗⃗⃗ 与PB ⃗⃗⃗⃗⃗⃗ 的夹角余弦值为（ ）A ．−3√77B ．7C ．−√217D ．√213【详解】∵|AB ⃗⃗⃗⃗⃗⃗ |2=(OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗⃗ )2=OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ ，即8−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =12，∴OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2， 设OP ⃗⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗⃗ (0≤λ≤1)，PA ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ，PB ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −OP ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ ， 所以，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅(OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ )=(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ +λ(λ−1)OA⃗⃗⃗⃗⃗⃗ 2 =−2(1−λ)+4λ(λ−1)=4λ2−2λ−2=(2λ−12)2−94，当λ=14时，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值−94，此时|PA ⃗⃗⃗⃗⃗⃗ |=34|OA ⃗⃗⃗⃗⃗⃗ |=32， |PB ⃗⃗⃗⃗⃗⃗ |2=|OB ⃗⃗⃗⃗⃗⃗ −14OA⃗⃗⃗⃗⃗⃗ |2=116OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−12OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =116×22+22−12×(−2)=214，所以，|PB ⃗⃗⃗⃗⃗⃗ |=√212，则cos <PA⃗⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗⃗ >=PA⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ |PA⃗⃗⃗⃗⃗⃗ |⋅|PB ⃗⃗⃗⃗⃗⃗ |=−9432×√212=−√217. 故选：C.7. （三星）在锐角∆ABC 中已知B= 3，|AB ⃗⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2,则AB ⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的取值范围是__________.解：法一：极化恒等式；法二：以B 为原点，BA 所在直线为x 轴建立坐标系，因为设A（x ，0）因为△ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°，即A 在如图的线段DE 上（不与D ，E 重合），所以1＜x ＜4，则AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ =x 2﹣x=（x ﹣12）2﹣14，所以AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ 的范围为（0，12）．方法2∵∠B=π3， △ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°=a=2由正弦定理可得()−==A B a b csin 120sinA sin 0∴=b ,=−Ac A sin 2sin 1200)( ∴120cos cos AB AC c b A A ===+=+⎝⎭−AA Asin tan 32202)(∵∈tanA0,3)( ∴(0,12AB AC ∈)8.在△ABC 中，AC ＝2BC ＝4，∠ACB 为钝角，M ，N 是边AB 上的两个动点，且MN ＝1，若CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ 的最小值为34，则cos ∠ACB ＝ ． 【答案】1−3√58【解析】取MN 的中点P ，则由极化恒等式得CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ =|CP ⃗⃗⃗⃗⃗ |2−14|MN ⃗⃗⃗⃗⃗⃗⃗ |2=|CP ⃗⃗⃗⃗⃗ |2−14∵CM ⃗⃗⃗⃗⃗⃗ ⋅CN ⃗⃗⃗⃗⃗⃗ 的最小值为34∴|CP ⃗⃗⃗⃗⃗ |min 由平几知识知：当CP ⊥AB 时，CP 最小. 如图，作CH ⊥AB ，H 为垂足，则CH=1 又AC ＝2BC ＝4，所以∠B ＝30o ，sinA=14 所以cos ∠ACB ＝cos （150o －A ）=1−3√58.9.如图所示，矩形ABCD 的边AB=4，AD=2，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧EB ̂ (含端点B 、E)上的一点，则PA → ·PB → 的取值范围是 .H【解析】取AB 的中点设为O ，则， 当O 、P 、C 共线时， PO 取得最小值为PO =2√2−2；当P 与B （或E ）重合时，PO 取得最大值为PO=2， 所以的取值范围是.10.如图，是边长为P 是以C 为圆心，1为半径的圆上的任意一点，则AP⃗⃗⃗⃗⃗⃗ ∙BP ⃗⃗⃗⃗⃗⃗ 最小值是_____.－111.（三星）如图，在△ABC 中，D 是BC 的中点，E,F 是AD 上的两个三等分点，BA ⃗⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =4,BF ⃗⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗ =−1,则BE ⃗⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ 的值是________.备注：极化恒等式的典型应用2221=4PA PB PO AB PO ⋅−=−4PA PB ⋅−[8∆ABC CA BP12.若平面向量a ，b 满足|2a －b|≤3，则a·b 的最小值为________.【解析】根据极化恒等式得：8a ⋅b =(2a +b)2−(2a −b)2=(2a +b)2−9≥−9，故a ⋅b ≥−98，所以a ⋅b 的最小值为−98．13.已知平面向量a ，b ，e 满足|e|＝1，a·e ＝1，b·e ＝－2，|a ＋b|＝2，那么a·b 的最大值为________． 解： 由a·e ＝1，b·e ＝－2得: a·e －b·e ＝3，即（a －b ）·e ＝3，|a －b|cos θ＝3a·b=14[|a ＋b|2－|a －b|2]≤－5414.在中，已知，，则面积的最大值是 ．解：取BC 的中点为D ，则AB ⃗⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =AD 2−BC24，所以AD =√2因为BC 边上的高线长不大于中线长，当中线就是高线时，面积最大，故．15.已知平面向量a ⃗ ,b ⃗ ,c ⃗ 满足|a ⃗ |=1，a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2，|2b ⃗ −c ⃗ |=2，那么b⃗ ⋅c ⃗ 的最小值为________． 【解析】由a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2得2a ⃗ ⋅b ⃗ +a ⃗ ⋅c ⃗ =3，即a ⃗ ⋅(2b ⃗ +c ⃗ )=3 又a ⃗ ⋅(2b ⃗ +c ⃗ )=|a ⃗ ||2b ⃗ +c ⃗ |cos θ（其中θ为向量a ⃗ 与2b ⃗ +c ⃗ 的夹角） 所以|2b⃗ +c ⃗ |=3cos θ所以b⃗ ⋅c ⃗ =18[(2b ⃗ +c ⃗ )2−(2b ⃗ −c ⃗ )2]=18(9cos 2θ−4)≥58.∆ABC =BC 21AB AC •=∆ABC ∆ABC16.已知锐角的外接圆的半径为1， ，则的取值范围为__________．17.已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则PA → ⋅PB →的取值范围是_____.[－2,6]18.在ΔABC 中，AB =3,AC =4,∠BAC =60°，若P 是ΔABC 所在平面内的一点，且AP =2，则PB → ⋅PC →的最大值为_____.10+2√3719.已知点P 是边长为2√3的正三角形ABC 内切圆上的一点，则PA → ⋅PB →的取值范围为_____.[−3,6]20.已知正方形ABCD 的边长为1，中心为O ，直线l 经过中心O ，交AB 于点M ，交CD 于点N ，P 为平面上一点，若2OP → ＝λOB → ＋(1－λ)OC → ，则PM → ·PN →的最小值为__________.−71621.设点P 为正三角形△ABC 的边BC 上的一个动点，当PA → ·PC →取得最小值时，sin ∠PAC 的值为________．√392622.在平面直角坐标系xOy 中，点A ，B 分别在x 轴，y 轴正半轴上移动，AB ＝2，若点P 满足PA → ·PB →＝2，则OP 的取值范围为________．[√3−1,√3+1]23.在△ABC 中，E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB → ·PC →＋BC →2的最小值是__________．4√3∆ABC ∠=πB 6BA BC⋅⎝ ⎛23,3。

第2讲极化恒等式结论：设a b、是两个平面向量，则有恒等式()()2214a b a b a b ⎡⎤=+--⎢⎥⎣⎦ ，在三角形中，也可以用三角形的中线来表示，22AB AC AM MB =- 。

极化恒等式的作用主要在于，它可以将两个向量的数量积转化为这两个向量之和或之差，因此，当两个向量之和或之差为定值时，常常可以考虑利用极化恒等式进行转化求解。

典型例题1．（2012浙江15）在ABC ∆中，M 是BC 的中点，3AM =，10BC =，则AB AC =．法1解：设AMB θ∠=，则AMC πθ∠=-．又AB MB MA =- ，AC MC MA =- ，∴(AB AC = )(MB MA - 2)MC MA MB MC MB MA MA MC MA -=--+，2553cos 35cos()916θπθ=--⨯-⨯-+=-，故答案为16-．法2：极化恒等式22223516AB AC AM MB =-=-=-2．如图，在ABC ∆中，D 是BC 的中点，E ，F 是AD 上的两个三等分点，4BA CA =，1BF CF =- ，则BE CE的值是．法1解：D 是BC 的中点，E ，F 是AD 上的两个三等分点，∴BF BD DF =+ ，CF BD DF =-+ ，3BA BD DF =+ ，3CA BD DF =-+ ，∴221BF CF DF BD =-=- ，2294BA CA DF BD =-= ，∴258DF = ，2138BD = ，又 2BE BD DF =+ ，2CE BD DF =-+，∴22748BE CE DF BD =-= ，故答案为：78法2：极化恒等式FDAD BD FD CF BF BD AD CA BA 3142222=-=-=∙=-=∙分别解出FD ²和BD ²的值，即可求解CMDG O3．已知AB 为圆O 的直径，M 为圆O 的弦CD 上一动点，8AB =，6CD =，则MA MB的取值范围是．法1解：以AB 所在的直线为x 轴，以线段AB 的垂直平分线为y 轴建立平面直角坐标系，如图所示；且圆O 的直径为AB ，设(,)M x y ，则(4,0)A ，(4,0)B -，(4,)MA x y =-- ，(4,)MB x y =--- ，222(4)(4)()16MA MB x x y x y =---+-=+-，又M 是圆O 的弦CD 上一动点，且6CD =，所以2216916x y -+ ，即22716x y + ，其中最小值在CD 的中点时取得，所以MA MB的取值范围是[9-，0]．故答案为：[9-，0]．法2直接使用极化恒等式22MA MB MO OA=-4MO ≤≤ ，4OA =[]9,0MA MB ∴∈-一课一练1．（2013•浙江二模）如图放置的边长为1的正方形ABCD 的顶点A 、D 分别在x 轴、y 轴正半轴上（含原点）上滑动，则OB OC的最大值是．2.（2018•天津）如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==．若点E 为边CD 上的动点，则AE BE的最小值为()A ．2116B ．32C ．2516D ．33、（2017•新课标Ⅱ）已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC +的最小值是()A ．2-B ．32-C ．43-D ．1-参考答案1）法1解：如图令OAD θ∠=，由于1AD =故0cos A θ=，sin OD θ=，如图2BAX πθ∠=-，1AB =，故cos cos()cos sin 2Bx πθθθθ=+-=+，sin()cos 2B y πθθ=-=故(cos sin ,cos )OB θθθ=+同理可求得(sin ,cos sin )C θθθ+，即(sin ,cos sin )OC θθθ=+，∴(cos sin OB OC θθ=+，cos )(sin θθ ，cos sin )1sin 2θθθ+=+，OB OC的最大值是2故答案是2法2：极化恒等式如图，取BC ，AD 中点E ，F ,22214OB OC OE EB OE =-=-根据极化恒等式13122OE OF EF ≤+=+=所以有最大值22）法1解：如图所示，以D 为原点，以DA 所在的直线为x 轴，以DC 所在的直线为y 轴，过点B 做BN x ⊥轴，过点B 做BM y ⊥轴，AB BC ⊥ ，AD CD ⊥，120BAD ∠=︒，1AB AD ==，1cos602AN AB ∴=︒=，3sin 602BN AB =︒=，13122DN ∴=+=，32BM ∴=，3tan 302CM MB ∴=︒=，3DC DM MC ∴=+=，(1,0)A ∴，3(2B ，32，C ，设(0,)E m ，∴(1,)AE m =- ，3(2BE =- ，32m -，0m ，∴22233321(()224216416AE BE m m m =+-=-+-=-+ ，当m =2116．故选：A ．法2：极化恒等式22214EA EB EF FA EF =-=-当EF CD ⊥时，15144EF EK KF =+=+=251214416EA EB ⎛⎫=-=⎪⎝⎭最小3）法1解：建立如图所示的坐标系，以BC 中点为坐标原点，则A ，(1,0)B -，(1,0)C ，设(,)P x y ，则()PA x y =-- ，(1,)PB x y =--- ，(1,)PC x y =--，则22223()222[(]4PA PB PC x y x y +=-+=+--∴当0x =，y =时，取得最小值332(42⨯-=-，故选：B ．法2：极化恒等式222222()()()2PA PB PC PE EA PF FA PE PF +=-+-=+- 当P 位于EF 中点时，有最小值。

极化恒等式1.极化恒等式：a ·b ＝14[(a ＋b )2－(a －b )2].几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14.2.平行四边形ABCD ，M 是对角线交点.则： (1)AD AB ⋅＝14[AC 2－BD 2](平行四边形模式)；(2)AD AB ⋅＝AM 2－14BD 2(三角形模式). 例1.在△ABC 中，M 是BC 的中点，AM ＝3，BC ＝10，则AB→·AC →＝________.例2.在△ABC 中，P 0是边AB 上一定点，满足P 0B ＝14AB ，且对于边AB 上任一点P ，恒有PB →·PC →≥P 0B →·P 0C →，则( ) A.∠ABC ＝90° B.∠BAC ＝90° C.AB ＝ACD.AC ＝BC例3.已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则P A →·PB→的取值范围是________. 1.若点G ABC ∆的重心，且2,=⊥AB GB GA ，则________=⋅CB CA 2.已知ABC ∆的外接圆O 的半径是1，6π=∠B ,则BC BA ⋅的取值范围3.在锐角ABC ∆，已知3π=B ，2||=-AC AB ,则AC AB ⋅的取值范围4.在ABC ∆，60,4,3=∠==BAC AC AB 若点P 是ABC ∆所在平面内的一点，且2=AP ,则PC PB ⋅的最大值为5.在ABC ∆，9,8,7===BC AC AB ，点P 是ABC ∆内的一点，且7-=⋅PC PA ，则||PB 的取值范围课后练习1.已知正方形ABCD 的边长为1，点E 是AB 边上的动点，则DE →·DA →的值为_______.2. 如图所示放置的边长为1的正方形ABCD 的顶点分别在x 轴，y 轴正半轴上(含bMABD原点)滑动，则OB → ·OC →的最大值为________．3.在平面直角坐标系xOy 中，点A ，B 分别在x 轴，y 轴正半轴上移动，AB ＝2，若点P 满足P A → ·PB→ ＝2，则OP 的取值范围为________．4.已知AB 是圆O 的直径，AB 长为2，C 是圆O 上异于A ，B 的一点，P 是圆O 所在平面上任意一点，则(P A →＋PB →)·PC →的最小值为( ) A.－14 B.－13 C.－12 D.－15.如图，BC ，DE 是半径为1的圆O 的两条直径，BF →＝2FO →，则FD →·FE →＝( )A.－34B.－89C.－14D.－496.正ABC ∆的边长等于3，点P 在其外接圆上运动，则PB AP ⋅的 取值范围是（ ）7. 在△ABC 中，E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB→ ·PC → ＋BC → 2的最小值是__________． 8. 已知A (0，1)，曲线M ：y ＝log a x 恒过点B ，若P 是曲线M 上的动点，且AB → ·AP →的最小值为2，则a ＝________． 9. 已知正方形ABCD 的边长为1，中心为O ，直线l 经过中心O ，交AB 于点M ，交CD 于点N ，P 为平面上一点，若2OP → ＝λOB → ＋(1－λ)OC → ，则PM → ·PN → 的最小值为__________.10. 已知A ，B 是圆O ：x 2＋y 2＝1上的两个点，P 是线段AB 上的动点，那么当△AOB 的面积最大时，AO→ ·AP → －AP → 2的最大值是________．。

数学极化恒等式数学极化恒等式是数学中的一个重要概念，它在求解复数运算、多项式拆分和向量运算中起到了至关重要的作用。

本文将从多个角度介绍数学极化恒等式，展示其在数学领域中的广泛应用。

首先，我们来了解一下什么是极化恒等式。

在数学中，极化恒等式是指通过极化恒等式可以将一个向量或数列拆成两个特定的数的和。

它的形式为：\[x = \frac{1}{2} \left( x + \overline{x} \right) +\frac{1}{2i} \left( x - \overline{x} \right)\]其中，\(x\)表示一个复数或向量，\(\overline{x}\)表示其共轭。

数学极化恒等式在求解复数运算中应用广泛。

复数可以表示为实部加上虚部的形式，而极化恒等式可以将复数拆分成实轴和虚轴上的两个数。

例如，对于一个复数\(z = a + bi\)，其中\(a\)为实部，\(b\)为虚部。

根据极化恒等式，可以得到：\[z = \frac{1}{2} \left( a + bi + a - bi \right) +\frac{1}{2i} \left( a + bi - a + bi \right)\]化简后得到：\[z = \frac{1}{2} \left( 2a \right) + \frac{1}{2i}\left( 2bi \right)\]继续化简可得：\[z = a + bi\]这就是复数的极化恒等式。

通过极化恒等式，我们可以将复数的实部和虚部分离出来，更方便进行计算和分析。

极化恒等式在多项式的拆分中也有重要应用。

对于一个多项式\(f(x)\)，它可以表示为一些特定数的和。

根据极化恒等式，可以将其拆分成实数和虚数的和。

例如，对于一个二次多项式\(f(x) = ax^2 + bx + c\)，其中\(a\)、\(b\)、\(c\)均为实数。

根据极化恒等式，可以得到：\[f(x) = \frac{1}{2} \left( ax^2 + bx + c + ax^2 - bx - c \right) + \frac{1}{2i} \left( ax^2 + bx + c - ax^2 + bx + c \right)\]化简后得到：\[f(x) = \frac{1}{2} \left( 2ax^2 \right) + \frac{1}{2i} \left( 2bx \right) + c\]继续化简可得：\[f(x) = ax^2 + bx + c\]这就是多项式的极化恒等式。

2021-2022学年高三一轮复习向量--极化恒等式公式推导()()()()222222222142a b a ab b ab a b a b a b a ab b ⎫+=++⎪⎡⎤⇒=+--⎬⎢⎥⎣⎦⎪-=-+⎭在△ABC 中，D 是边BC 的中点，则22AB AC AD DB=-.如图，由()()222222111222AB AC AB AC AB AC AD CB AD DB ⎡⎤⎡⎤⎛⎫=+--=-=- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭得证.类比初中的“完全平方和”与“完全平方差公式”。

几何意义向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14。

注：平行四边形中AD 2+BC 2=2(AB 2+AC 2)极化恒等式的作用主要在于，它可以将两个向量的数量积转化为这两个向量的“和向量”与“差向量”，因此，当两个向量的“和向量”或“差向量”为定向量时，常常可以考虑利用极化恒等式进行转化.DCBA常见的解决的题型:有中点或能构造中点的积的向量题。

与课本的渊源（1）课本上有：在ABC ∆中，()()11,22AD AB AC BD AC AB =+=-是课本上出现的2个重要的向量三角关系，而极化恒等式无非是这两个公式的逆用，说明极化恒等式源与教材；（2）向量是连接代数与几何的桥梁，由于向量的坐标运算引入，向量与代数的互换已经深入人心，而与几何的运算练习略显单薄，而极化恒等式恰恰弥补了这个缺憾，可以说极化恒等式是把向量的数量积问题用形象的几何图形展示的淋漓尽致。

【典型例题】【例1】已知AB 为圆O 的直径，M 为圆O 的弦CD 上一动点，8AB =，6CD =，则MA MB ⋅的取值范围是 ．【答案】[]9,0-【解析】[]2221164749,0MA MB MO BA MO OC OM OG OM MA MB =-=-≤≤⇒≤≤⇒∈-【例2】(江苏高考题)如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点，4BA CA ⋅=，1BF CF ⋅=- ，则BE CE ⋅的值是________.【答案】78224BA CA AB AC AD BD ⋅=⋅=-=2222119BF CF FB FC FD BD AD BD ⋅=⋅=-=-=- 解得：224513,88AD BD ==，所以22224798BE CE EB EC ED BD AD BD ⋅=⋅=-=-=.【例3】（苏州市2020年高三上学期期中）如图，在四边形ABCD 中，4AC =，12BA BC ⋅=，E 为AC 的中点.（1）若12cos 13ABC ∠=，求ABC ∆的面积ABC S ∆；（2）若2BE ED =，求DA DC ⋅的值.【解析】解：（1）12cos 13ABC ∠=，()0,ABC π∠∈，5sin 13ABC ∴∠==，1212cos ,13BA BC BA BC ABC BA BC ⋅==⋅∠=⋅ 13,BA BC ∴⋅=1155sin 1322132ABC S BA BC ABC ∆∴=⋅∠=⨯⨯=.（2）以E 为原点，AC 所在直线为x 轴，建立如图所示平面直角坐标系，则A (－2,0)，C (2,0)，设D (),x y ，由2BE ED =，可得(2,2)B x y --，则2212(22,2)(22,2)444,BA BCx y x y x y ⋅==-⋅+=-+224,x y ∴+=∴()()222,2,40DA DC x y x y x y ⋅=---⋅--=+-=.【极化恒等式的解法】第二问()()()()()2222222111122412444422BA BC BA BCBA BC BECA BE CABE BE BE ED ED ⎡⎤⎡⎤⋅==+--=-=-=-=⎢⎥⎢⎥⎣⎦⎣⎦⇒==⇒=()()()2222112044DA DC DA DCDA DC DEAC ⎡⎤⎡⎤⋅=+--=-=⎢⎥⎢⎥⎣⎦⎣⎦【例4】如图，在ABC ∆中，已知4,6,60AB AC BAC ==∠=︒，点,D E 分别在边,AB AC 上，且2,3AB AD ACAE ==，若F 为DE 的中点，则BF DE的值为________.【解析】取BD 的中点N ，连接,NF EB ，则BE AE BE ⊥⇒=在DEB ∆中，1//2FN EB FN ⇒=，()2221222144BF DE FB FD FN DB FN BF DE ⎛⎫==-=-⇒= ⎪⎝⎭【例5】如图，在平面四边形ABCD 中，AB BC⊥，AD CD ⊥，60BCD ∠=︒，CB CD ==若点M 为边BC 上的动点，则AM DM ⋅的最小值为 ▲ ．用极化不等式的解法如下：设E 是AD 的中点，作EN BC ⊥于N ，延长CB 交DA 的延长线于F ，由题意可得：6,22,4FD FC CD BF AB FA ====⇒=⇒==55242EN EF AD EN AB FA ⇒=⇒==⇒=. 则 2222252111124AM DM MA MD ME EA ME EN ⎛⎫ = =-=-≥-=-= ⎪⎝⎭，所以 ()min214AM DM=. 【例6】在△ABC 中，已知AB =3C π=，则CA CB的最大值为 .解析：设D 是AB 的中点，连接CD ，点O 是△ABC 的外心，连接DO 并延长交圆O于'C ，由△'ABC是等边三角形，3'2AD C D =⇒=， 则 22222233333'4242CA CB CD DA CD C D ⎛⎫⎛⎫ =-=-≤-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭所以 ()max32CA CB =.【例7】（全国III 卷理科真题）已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC +的最小值是（ ）.2A -3.2B - 4.3C - .1D -解析：取BC 的中点D ，连接AD，PD ，取AD 的中点E ，连接PE ， 由△ABC 是边长为2的等边三角形，E 为中线AD 的中点12AE AD ⇒==则()()222233222220242PA PB PC PA PD PA PD PE EAPE ⎡⎤⎛⎫⎛⎫⎢⎥ += = =-=-≥⨯-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦所以 ()min32PA PB PC ⎡⎤+=-⎣⎦.【例8】如图，在平面四边形ABCD 中，2AC AD ==，120DAC ∠=︒，90ABC ∠=︒， 则BD BC 的最大值为 .PABCDE解析：取CD 的中点E ，连接EA ，EB ， 由2AC AD ==,120,sin 60DACAE CD DE AD ∠=︒⇒⊥=︒=由90,,,ABC AEC A B C E ∠=∠=︒⇒四点共圆，且直径为AC . 则(2222223231BD BC BE ED BE AC =-=-≤-=-=所以 ()max1BD BC=.【例9】(2020南通押题密卷11)如图，已知点O 为△ABC 的重心，OA ⊥OB ，AB 6=，则AC BC ⋅的值为 ．【解析】法1：连结CO 并延长交AB 于点M (如图1)， 则，因为，所以．法2： 以AB 的中点M 为坐标原点，AB 为x 轴建立平面直角坐标系(如图2)，则，， 设，则易得， B ACD()()AC BC AO OC BO OC ⋅=+⋅+2AO BO OC BO OC AO OC =⋅+⋅+⋅+2OC BO OC AO OC =⋅+⋅+()OC BO AO OC =⋅++22OC =26OC OM AB ===72AC BC ⋅=()30A -，()30B ，()C x y ，O()33yx ，因为OA OB ，所以， 从而，化简得，，所以．法3：极化恒等式()()()222222111218672444AC BC AC BCAC BC AMAB ⎡⎤⎡⎤⎡⎤⋅=+--=-=-=⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦.【例10】在平面四边形ABCD 中，O 为BD 的中点，且3OA =，5OC =．若7AB AD =-， 则BC DC 的值是 ． 【答案】9 【解析】()()()()22222221172441237644AB AD AB AD AB AD AO DB DB DB ⎡⎤⎡⎤=-=+--=-⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤=⨯-=-⇒=⎢⎥⎣⎦()()()()22222111225649444BC DC BC DC BC DC OCBD ⎡⎤⎡⎤⎡⎤=+--=-=⨯-=⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦【例11】如图放置的边长为1的正方形ABCD ，顶点,A D 分别在x 轴，y 轴正半轴（含原点）滑动，则OB OC 的最大值为______________.【解析】如图，,BC AD 中点,E F ，⊥0AO BO ⋅=()()()2330333yx x +⋅-+=2281x y +=222(3)(3)972AC BC x x y x y ⋅=+-+=+-=()()()222221112444OB OC OB OC OB OC OEBC OE ⎡⎤⎡⎤=+--=-=-⎢⎥⎢⎥⎣⎦⎣⎦因为1312391244OE OF EF OB OC <+=+=⇒≤-=【例12】（2020南京29中模拟考）在ABC ∆中，点,E F 分别是线段,AB AC 的中点，点P 在直线EF 上，若ABC ∆的面积为2，则2PB PC BC+的最小值是_____________.【解析】取BC 中点2222222133,23444O PB PC PO BC PB PC BC PO BC PO BC PO BC=-⇒+=+≥=()2min13332322ABC PO h PO BC h BC S PB PC BC ∆≥⇒≥==⇒+=【例13】如图，已知正方形ABCD 的边长为2，E 为AB 的中点，以A 为圆心，AE 为半径，作圆交AD 于点F，若P为劣弧EF上的动点，则PC PD 的最小值是____________.【解析】222114PC PD PG CD PG =-=- 当,,A P G 三点共线时PG 最小，此时 ()min''15P G AG AP PC PD=-=⇒=-【巩固训练】1. 在ABC ∆中,60BAC ∠=若2AB =,BC =,D 在线段AC 上运动，DA DB ⋅的最小值为2. 已知AB 是圆O 的直径,AB 长为2,C 是圆O 上异于,A B 的一点,P 是圆O 所在平面上任意一点,则()PA PB PC +⋅的最小值为_________3．在ABC ∆中，3AB =，4AC =，60BAC ∠=，若P 是ABC ∆所在平面内一点，且2AP =，则PB PC ⋅的最大值为4．在Rt ABC ∆，2AC BC ==，已知点P 是ABC ∆内一点，则)(PB PA PC +⋅的最小值是 .5. 已知B A 、是单位圆上的两点，O 为圆心，且MN AOBo ,120=∠是圆O 的一条直径，点C 在圆内，且满足)10()1(<<-+=λλλOB OA OC ，则CN CM ⋅的取值范围是（ ） A ．⎪⎭⎫⎢⎣⎡-1,21 B ．[)1,1- C ．⎪⎭⎫⎢⎣⎡-0,43 D ．[)0,1-6. 正ABC ∆边长等于3，点P 在其外接圆上运动，则PB AP ⋅的取值范围是（ ） A. ⎥⎦⎤⎢⎣⎡-23,23 B. ⎥⎦⎤⎢⎣⎡-21,23 C. ⎥⎦⎤⎢⎣⎡-23,21 D. ⎥⎦⎤⎢⎣⎡-21,217．在锐角ABC ∆中，已知3B π=，2AB AC -=，则AB AC ⋅的取值范围是 ．8. 正方体1111-ABCD A B C D 的棱长为2，MN 是它内切球的一条弦（把球面上任意2个点之间的线段成为球的弦），P 为正方体表面上的动点，当弦MN 最长时，PM PN ⋅的最大值为9. 已知B A 、是单位圆上的两点，O 为圆心，且MN AOBo ,120=∠是圆O 的一条直径，点C 在圆内，且满足)10()1(<<-+=λλλOB OA OC ，则CN CM ⋅的取值范围是 .10. 如图，在△ABC 中，已知AB ＝4，AC ＝6，∠BAC ＝60°，点D ，E 分别在边AB ，AC 上，且AD AB 2=，AE AC3=，点F 为DE 的中点，则DE BF ⋅的值为________．。