极化恒等式
- 格式:pdf
- 大小:278.57 KB
- 文档页数:6

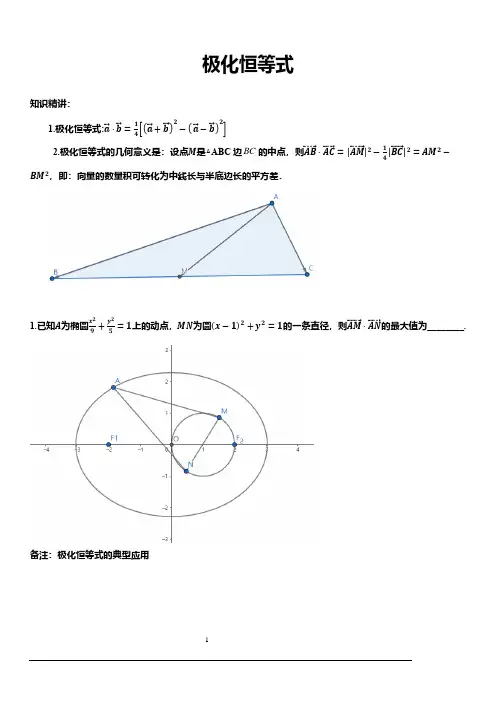
极化恒等式知识精讲:1.极化恒等式:a ⃗ ⋅b ⃗ =14[(a ⃗ +b ⃗ )2−(a ⃗ −b⃗ )2] 2.极化恒等式的几何意义是:设点M 是△ABC 边的中点,则AB⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AM ⃗⃗⃗⃗⃗⃗⃗ |2−14|BC ⃗⃗⃗⃗⃗⃗ |2=AM 2−BM 2,即:向量的数量积可转化为中线长与半底边长的平方差.1.已知A 为椭圆x 29+y 25=1上的动点,MN 为圆(x −1)2+y 2=1的一条直径,则AM ⃗⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的最大值为________.备注:极化恒等式的典型应用BC2. (三星)(2017全国2理)已知ΔABC 是边长为2的等边三角形,P 为平面ABC 内一点,则PA ⃗⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )的最小值是( )A.−2B.−32 C. −43 D.−1 解:方法一:建系法连接OP ,OA⃗⃗⃗⃗⃗⃗ =(0,√3),OB ⃗⃗⃗⃗⃗⃗ =(−1,0),OC ⃗⃗⃗⃗⃗⃗ =(1,0). PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ,∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(−x,−y )⋅(−x,√3−y) ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =x 2+y 2−√3y =x 2+(y −√32)2−34 ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−34,∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32 ∴最小值为−32方法二:均值法∵PC ⃗⃗⃗⃗⃗ +PB⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ,∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ 由上图可知:OA ⃗⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗⃗ −PO ⃗⃗⃗⃗⃗⃗ ;两边平方可得3=(PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ∵ (PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2≥−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ,∴ 2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32,∴最小值为−32 解法三:配凑法 ∵PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ∴PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(PO ⃗⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗⃗ )22=(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(AO ⃗⃗⃗⃗⃗⃗ )22≥−32∴最小值为−323.在∆ABC 中,BC 边上的中线AD 的长为2,点P 是∆ABC 所在平面上的任意一点,则PA PB PA PC ⋅+⋅的最小值为 A .1B .2C .-2D .-1【详解】建立如图所示的平面直角坐标系,使得点D 在原点处,点A 在y 轴上,则A (0,2).设点P 的坐标为x y (,),则(,2),(,)PA x y PO x y =−−=−−, 故()22(2)PA PB PA PC PA PB PC PA PO x y y ⋅+⋅=⋅+=⋅=+−22=+−−≥−x y 2[(1)]2222,当且仅当==x y 0,1时等号成立.所以PA PB PA PC ⋅+⋅的最小值为−2.选C .4. (武汉二中高二)已知圆M:x 2+(y −1)2=1, 圆N:x 2+(y +1)2=1, 直线l 1、l 2分别过圆心M ,且l 1与圆M 相交于A 、B , l 2与圆N 相交于C 、D , P 是椭圆x 23+y 24=1上的任意一动点, 则PA → ⋅PB → +PC → ⋅PD →的最小值为______________.6 备注:用到极化恒等式5.在平面四边形ABCD 中,===AB BC CD 22,∠ABC =60∘,∠ADC =90∘,若BE →=EF →=FG →=GC →,则2AE →∙DC →+AE →∙AF →=_____;若P 为边BC 上一动点,当PA →∙PC →取最小值时,则cos ∠PDC 的值为_____.解:∵平面四边形ABCD 中,===AB BC CD 22,∠ABC =60∘,∠ADC =90∘,∴△ABC 是边长为2的等边三角, 在Rt △ADC 中,AC =2,CD =1,所以∠ACD =60∘,又BE →=EF →=FG →=GC →, ∴E,F,G 是BC 边的四等分点.如图建立坐标系:则:A(0,√3),B (−1,0),C (1,0), D (32,√32),E (−12,0),F (0,0),G (12,0), 所以2AE →DC →+AE →AF →=2(−12,−√3)(−12,−√32)+(−12,−√3)(0,−√3)=132,再设P (x,0),则−1≤x ≤1,∴PA →PC →=(−x,√3)(1−x,0)=x 2−x =(x −12)2−14,显然x =12时,PA →PC →最小,此时P (12,0),∴cos ∠PDC =cos ⟨DP →,DC →⟩=(−1,−√3)⋅(−1,−√3)(−1)+(−√32)(−12)+(−√32)=5√714.故答案为:132,5√714.6.在△OAB 中,OA =OB =2,AB =2√3,动点P 位于直线OA 上,当PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值时,向量PA ⃗⃗⃗⃗⃗⃗ 与PB ⃗⃗⃗⃗⃗⃗ 的夹角余弦值为( )A .−3√77B .7C .−√217D .√213【详解】∵|AB ⃗⃗⃗⃗⃗⃗ |2=(OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗⃗ )2=OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ ,即8−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =12,∴OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2, 设OP ⃗⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗⃗ (0≤λ≤1),PA ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −OP ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ , 所以,PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅(OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ )=(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ +λ(λ−1)OA⃗⃗⃗⃗⃗⃗ 2 =−2(1−λ)+4λ(λ−1)=4λ2−2λ−2=(2λ−12)2−94,当λ=14时,PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值−94,此时|PA ⃗⃗⃗⃗⃗⃗ |=34|OA ⃗⃗⃗⃗⃗⃗ |=32, |PB ⃗⃗⃗⃗⃗⃗ |2=|OB ⃗⃗⃗⃗⃗⃗ −14OA⃗⃗⃗⃗⃗⃗ |2=116OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−12OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =116×22+22−12×(−2)=214,所以,|PB ⃗⃗⃗⃗⃗⃗ |=√212,则cos <PA⃗⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗⃗ >=PA⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ |PA⃗⃗⃗⃗⃗⃗ |⋅|PB ⃗⃗⃗⃗⃗⃗ |=−9432×√212=−√217. 故选:C.7. (三星)在锐角∆ABC 中已知B= 3,|AB ⃗⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2,则AB ⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的取值范围是__________.解:法一:极化恒等式;法二:以B 为原点,BA 所在直线为x 轴建立坐标系,因为设A(x ,0)因为△ABC 是锐角三角形,所以A+C=120°,∴30°<A <90°,即A 在如图的线段DE 上(不与D ,E 重合),所以1<x <4,则AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ =x 2﹣x=(x ﹣12)2﹣14,所以AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ 的范围为(0,12).方法2∵∠B=π3, △ABC 是锐角三角形,所以A+C=120°,∴30°<A <90°=a=2由正弦定理可得()−==A B a b csin 120sinA sin 0∴=b ,=−Ac A sin 2sin 1200)( ∴120cos cos AB AC c b A A ===+=+⎝⎭−AA Asin tan 32202)(∵∈tanA0,3)( ∴(0,12AB AC ∈)8.在△ABC 中,AC =2BC =4,∠ACB 为钝角,M ,N 是边AB 上的两个动点,且MN =1,若CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ 的最小值为34,则cos ∠ACB = . 【答案】1−3√58【解析】取MN 的中点P ,则由极化恒等式得CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ =|CP ⃗⃗⃗⃗⃗ |2−14|MN ⃗⃗⃗⃗⃗⃗⃗ |2=|CP ⃗⃗⃗⃗⃗ |2−14∵CM ⃗⃗⃗⃗⃗⃗ ⋅CN ⃗⃗⃗⃗⃗⃗ 的最小值为34∴|CP ⃗⃗⃗⃗⃗ |min 由平几知识知:当CP ⊥AB 时,CP 最小. 如图,作CH ⊥AB ,H 为垂足,则CH=1 又AC =2BC =4,所以∠B =30o ,sinA=14 所以cos ∠ACB =cos (150o -A )=1−3√58.9.如图所示,矩形ABCD 的边AB=4,AD=2,以点C 为圆心,CB 为半径的圆与CD 交于点E ,若点P 是圆弧EB ̂ (含端点B 、E)上的一点,则PA → ·PB → 的取值范围是 .H【解析】取AB 的中点设为O ,则, 当O 、P 、C 共线时, PO 取得最小值为PO =2√2−2;当P 与B (或E )重合时,PO 取得最大值为PO=2, 所以的取值范围是.10.如图,是边长为P 是以C 为圆心,1为半径的圆上的任意一点,则AP⃗⃗⃗⃗⃗⃗ ∙BP ⃗⃗⃗⃗⃗⃗ 最小值是_____.-111.(三星)如图,在△ABC 中,D 是BC 的中点,E,F 是AD 上的两个三等分点,BA ⃗⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =4,BF ⃗⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗ =−1,则BE ⃗⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ 的值是________.备注:极化恒等式的典型应用2221=4PA PB PO AB PO ⋅−=−4PA PB ⋅−[8∆ABC CA BP12.若平面向量a ,b 满足|2a -b|≤3,则a·b 的最小值为________.【解析】根据极化恒等式得:8a ⋅b =(2a +b)2−(2a −b)2=(2a +b)2−9≥−9,故a ⋅b ≥−98,所以a ⋅b 的最小值为−98.13.已知平面向量a ,b ,e 满足|e|=1,a·e =1,b·e =-2,|a +b|=2,那么a·b 的最大值为________. 解: 由a·e =1,b·e =-2得: a·e -b·e =3,即(a -b )·e =3,|a -b|cos θ=3a·b=14[|a +b|2-|a -b|2]≤-5414.在中,已知,,则面积的最大值是 .解:取BC 的中点为D ,则AB ⃗⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =AD 2−BC24,所以AD =√2因为BC 边上的高线长不大于中线长,当中线就是高线时,面积最大,故.15.已知平面向量a ⃗ ,b ⃗ ,c ⃗ 满足|a ⃗ |=1,a ⃗ ⋅b ⃗ =12,a ⃗ ⋅c ⃗ =2,|2b ⃗ −c ⃗ |=2,那么b⃗ ⋅c ⃗ 的最小值为________. 【解析】由a ⃗ ⋅b ⃗ =12,a ⃗ ⋅c ⃗ =2得2a ⃗ ⋅b ⃗ +a ⃗ ⋅c ⃗ =3,即a ⃗ ⋅(2b ⃗ +c ⃗ )=3 又a ⃗ ⋅(2b ⃗ +c ⃗ )=|a ⃗ ||2b ⃗ +c ⃗ |cos θ(其中θ为向量a ⃗ 与2b ⃗ +c ⃗ 的夹角) 所以|2b⃗ +c ⃗ |=3cos θ所以b⃗ ⋅c ⃗ =18[(2b ⃗ +c ⃗ )2−(2b ⃗ −c ⃗ )2]=18(9cos 2θ−4)≥58.∆ABC =BC 21AB AC •=∆ABC ∆ABC16.已知锐角的外接圆的半径为1, ,则的取值范围为__________.17.已知正三角形ABC 内接于半径为2的圆O ,点P 是圆O 上的一个动点,则PA → ⋅PB →的取值范围是_____.[-2,6]18.在ΔABC 中,AB =3,AC =4,∠BAC =60°,若P 是ΔABC 所在平面内的一点,且AP =2,则PB → ⋅PC →的最大值为_____.10+2√3719.已知点P 是边长为2√3的正三角形ABC 内切圆上的一点,则PA → ⋅PB →的取值范围为_____.[−3,6]20.已知正方形ABCD 的边长为1,中心为O ,直线l 经过中心O ,交AB 于点M ,交CD 于点N ,P 为平面上一点,若2OP → =λOB → +(1-λ)OC → ,则PM → ·PN →的最小值为__________.−71621.设点P 为正三角形△ABC 的边BC 上的一个动点,当PA → ·PC →取得最小值时,sin ∠PAC 的值为________.√392622.在平面直角坐标系xOy 中,点A ,B 分别在x 轴,y 轴正半轴上移动,AB =2,若点P 满足PA → ·PB →=2,则OP 的取值范围为________.[√3−1,√3+1]23.在△ABC 中,E ,F 分别是线段AB ,AC 的中点,点P 在直线EF 上,若△ABC 的面积为2,则PB → ·PC →+BC →2的最小值是__________.4√3∆ABC ∠=πB 6BA BC⋅⎝ ⎛23,3。

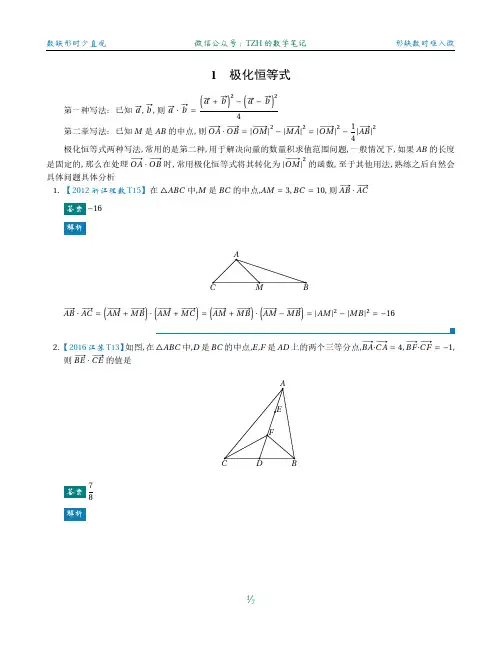
第2讲极化恒等式结论:设a b、是两个平面向量,则有恒等式()()2214a b a b a b ⎡⎤=+--⎢⎥⎣⎦ ,在三角形中,也可以用三角形的中线来表示,22AB AC AM MB =- 。
极化恒等式的作用主要在于,它可以将两个向量的数量积转化为这两个向量之和或之差,因此,当两个向量之和或之差为定值时,常常可以考虑利用极化恒等式进行转化求解。
典型例题1.(2012浙江15)在ABC ∆中,M 是BC 的中点,3AM =,10BC =,则AB AC =.法1解:设AMB θ∠=,则AMC πθ∠=-.又AB MB MA =- ,AC MC MA =- ,∴(AB AC = )(MB MA - 2)MC MA MB MC MB MA MA MC MA -=--+,2553cos 35cos()916θπθ=--⨯-⨯-+=-,故答案为16-.法2:极化恒等式22223516AB AC AM MB =-=-=-2.如图,在ABC ∆中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,4BA CA =,1BF CF =- ,则BE CE的值是.法1解:D 是BC 的中点,E ,F 是AD 上的两个三等分点,∴BF BD DF =+ ,CF BD DF =-+ ,3BA BD DF =+ ,3CA BD DF =-+ ,∴221BF CF DF BD =-=- ,2294BA CA DF BD =-= ,∴258DF = ,2138BD = ,又 2BE BD DF =+ ,2CE BD DF =-+,∴22748BE CE DF BD =-= ,故答案为:78法2:极化恒等式FDAD BD FD CF BF BD AD CA BA 3142222=-=-=∙=-=∙分别解出FD ²和BD ²的值,即可求解CMDG O3.已知AB 为圆O 的直径,M 为圆O 的弦CD 上一动点,8AB =,6CD =,则MA MB的取值范围是.法1解:以AB 所在的直线为x 轴,以线段AB 的垂直平分线为y 轴建立平面直角坐标系,如图所示;且圆O 的直径为AB ,设(,)M x y ,则(4,0)A ,(4,0)B -,(4,)MA x y =-- ,(4,)MB x y =--- ,222(4)(4)()16MA MB x x y x y =---+-=+-,又M 是圆O 的弦CD 上一动点,且6CD =,所以2216916x y -+ ,即22716x y + ,其中最小值在CD 的中点时取得,所以MA MB的取值范围是[9-,0].故答案为:[9-,0].法2直接使用极化恒等式22MA MB MO OA=-4MO ≤≤ ,4OA =[]9,0MA MB ∴∈-一课一练1.(2013•浙江二模)如图放置的边长为1的正方形ABCD 的顶点A 、D 分别在x 轴、y 轴正半轴上(含原点)上滑动,则OB OC的最大值是.2.(2018•天津)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==.若点E 为边CD 上的动点,则AE BE的最小值为()A .2116B .32C .2516D .33、(2017•新课标Ⅱ)已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC +的最小值是()A .2-B .32-C .43-D .1-参考答案1)法1解:如图令OAD θ∠=,由于1AD =故0cos A θ=,sin OD θ=,如图2BAX πθ∠=-,1AB =,故cos cos()cos sin 2Bx πθθθθ=+-=+,sin()cos 2B y πθθ=-=故(cos sin ,cos )OB θθθ=+同理可求得(sin ,cos sin )C θθθ+,即(sin ,cos sin )OC θθθ=+,∴(cos sin OB OC θθ=+,cos )(sin θθ ,cos sin )1sin 2θθθ+=+,OB OC的最大值是2故答案是2法2:极化恒等式如图,取BC ,AD 中点E ,F ,22214OB OC OE EB OE =-=-根据极化恒等式13122OE OF EF ≤+=+=所以有最大值22)法1解:如图所示,以D 为原点,以DA 所在的直线为x 轴,以DC 所在的直线为y 轴,过点B 做BN x ⊥轴,过点B 做BM y ⊥轴,AB BC ⊥ ,AD CD ⊥,120BAD ∠=︒,1AB AD ==,1cos602AN AB ∴=︒=,3sin 602BN AB =︒=,13122DN ∴=+=,32BM ∴=,3tan 302CM MB ∴=︒=,3DC DM MC ∴=+=,(1,0)A ∴,3(2B ,32,C ,设(0,)E m ,∴(1,)AE m =- ,3(2BE =- ,32m -,0m ,∴22233321(()224216416AE BE m m m =+-=-+-=-+ ,当m =2116.故选:A .法2:极化恒等式22214EA EB EF FA EF =-=-当EF CD ⊥时,15144EF EK KF =+=+=251214416EA EB ⎛⎫=-=⎪⎝⎭最小3)法1解:建立如图所示的坐标系,以BC 中点为坐标原点,则A ,(1,0)B -,(1,0)C ,设(,)P x y ,则()PA x y =-- ,(1,)PB x y =--- ,(1,)PC x y =--,则22223()222[(]4PA PB PC x y x y +=-+=+--∴当0x =,y =时,取得最小值332(42⨯-=-,故选:B .法2:极化恒等式222222()()()2PA PB PC PE EA PF FA PE PF +=-+-=+- 当P 位于EF 中点时,有最小值。

极化恒等式
1极化恒等式的推导:
(如图,有向量OA与向量OB,两向量之和为OD,其中E为AB,OD的中点) 2使用条件:共起点内积
3适用于:平面向量,空间向量
3使用方法:找斜边中点,再使用公式代入
4
例1:
解析:取BC的中点E,AD的中点为F
=
−→
−
⋅
−→
−
OC
OB
2
2−→
−
-
−→
−
EC
OE
=2
−→
−
OE
-
2
2
1
⎪
⎭
⎫
⎝
⎛
由三角形两边和大于第三边可以得到:
OE ≤OF+EF
OF 为直角三角形OAD 的中线,所以OF=2
1 EF=1
所以:−→−⋅−→−OC OB 的最大值为2
例2:
我们在此题的基础上增加一点难度:求−→−⋅−→−PD
PC 的最小值和最大值 解答:根据“极化恒等式”的方法,我们找到斜边CD 的中点O 点,则 −→−⋅−→−PD PC =22−→−-−→−OD
PO 其中OD=1
故我们只需要判断PO 的最大值与最小值
根据三角形两边和大于第三边,我们得到:
1)PO ≤AP+AO 2)PO+AO ≥AO
(其中AP=1,AO=5)
所以PO 的最大值为(5+1),最小值为(5-1)
故:−→−⋅−→−PD
PC 的最大值为(5+25),最小值为(5+25)。

极化恒等式的应用极化恒等式(Polarization Identity)是线性代数中的一个重要定理,它对向量空间内的内积和范数的关系进行了深入的探讨和证明。
极化恒等式不仅在线性代数中具有广泛的应用,而且在物理、工程、计算机科学、经济学等多个领域中也有着重要的应用。
本文将介绍极化恒等式的应用,包括其在向量空间的几何意义、特征向量的计算、信号处理、机器学习和经济学等方面的应用。
一、在向量空间的几何意义极化恒等式是向量空间内内积和范数的一个等式,它的几何意义是将内积(或范数)表示为向量之间的内积的线性组合。
极化恒等式表明了向量空间内的任何一个内积可以表示为向量之间的内积的线性组合,这个线性组合的系数是向量空间内的所有向量。
因此,极化恒等式是将内积和范数联系在一起的关键。
具体来说,假设V是一个有限维向量空间,u和v是V中的任意两个向量,则其极化恒等式可以表示为:⟨u,v⟩ = (||u||^2 + ||v||^2 - ||u-v||^2)/2其中,⟨u,v⟩表示u和v的内积,||u||表示u的范数。
这个等式可以表示为u和v之间的距离。
通过极化恒等式,我们可以得到向量空间中的任意两个向量之间的内积和范数的关系,从而为向量空间内的几何结构构建提供了基础。
例如,在计算几何中,利用极化恒等式可以计算任意两个向量之间的夹角,从而计算出向量空间中的长度、角度和曲线等几何问题。
二、特征向量的计算极化恒等式在计算特征向量和特征值方面也具有重要的应用。
这里,特征向量是指一个向量空间中的一个非零向量,其在线性变换下只被缩放,而不改变其方向。
特征向量的计算是线性代数中的一个关键问题,它在信号处理、图像处理和机器学习等领域中有广泛的应用。
通过极化恒等式,我们可以计算特征向量和特征值。
假设A 是一个n*n的实对称矩阵,x是非零向量,λ是实数,则其极化恒等式可以表示为:(Ax)·x = x·(Ax) = λx·x其中,·表示向量之间的内积操作。

极化恒等式补充1极化恒等式:()()2214a b a b a b ⎡⎤⋅=+--⎢⎥⎣⎦极化恒等式的几何意义是:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14,即222214a b AD BC AM BM ⎡⎤⋅=-=-⎣⎦ 2极化恒等式的应用例1ABC M BC AM=3BC=10AB AC=∆⋅ 在中,是的中点,,,则解析:221925162AB AC AM BC ⋅=-=-=- 00001ABC P AB P B=AB AB P 4PB PC P B P C ∆⋅≥⋅ 例2:设,是边上一定点,满足,且对于边上任意一点,恒有,则0.90A ABC ∠=0.90B BAC ∠=.C AB AC =.D AC BC=22022000000BC D PD P D PBC PB PC=PD BD P BC P B P C=P D ,PD P D P D AB AC=BCBD ∆⋅-∆⋅-≥⊥ 解析:取中点,连接,,在内使用极化恒等式得在内使用极化恒等式得由条件知,即,故3ABCD P AB APB PC PD f⋅ 例:设正方形的边长为4,动点在以为直径的圆弧上,则第三题图第四题图解析:[]24,225016.PC PD PE PE PC PD ⎡⎤⋅=-∈⋅∈⎣⎦由图知,,,故,2min ABC 4ABC E F AB AC P EF S =2PC PB+BC =∆⋅ 例:在中,点,分别是线段,的中点,点在直线上,若,则2222222421322,,,44434+BC 23PD BC BC=.43BCPBC PC PB PD BC PC PB BC PD BC h PD BC BC PC PB BC ⋅=-⋅+=+=≥⋅+≥≥⊥ 解析:因此,当且仅当,时等号成立051AOB AOB=60C AB OC P OP BP ∠⋅ 例:如图,在半径为的扇形中,,为弧上的动点,与交于点,则的最小值为解析:如上图所示,213311,PD ,442162OP BP PD OP BP ⎡⎤⎡⎤⋅=-∈⋅∈-⎢⎥⎢⎥⎣⎦⎣⎦ 易知,,则()6ABCD OB OC ⋅ 例:如图放置的边长为1的正方形顶点分别在x轴,y轴正半轴含原点滑动,则的最大值为22111OB OC=OE 12424⎛⎫⋅-≤+-= ⎪⎝⎭ 解析:。

极化恒等式公式1、基本极化恒等式基本极化恒等式又称为Stokes方程,它是理解介质中电磁波传播的基本方程。
它由波动磁场场强E和磁场场强H的外场响应组成,可以概括为:E =εHH=-D其中ε表示极化率,D表示电导率。
我们可以从它推导出其他极化恒等式,如:2、垂直极化恒等式垂直极化恒等式又称为Faraday方程,它是介质中电磁波传播的重要方程,可以根据基本极化恒等式推导而来,它包括垂直极化分量的电离度、垂直极化作用的等效度以及垂直极化圆盘的传播常数等因素,可以表示为:Dtanθ=ε+ηV其中,θ表示极化角,η表示磁导率,V表示电位场的垂直极化分量。
3、水平极化恒等式水平极化恒等式由基本极化恒等式推导而来,它表达了水平极化作用的电离度、极化作用的等效度、电位场的水平极化分量以及水平极化圆盘的传播常数等因素,可以表示为:cosθ=ε+ηV其中,θ表示极化角,η表示磁导率,V表示电位场的水平极化分量。
4、反射极化恒等式反射极化恒等式可以由基本极化恒等式推导而来,用来研究电磁波在介质之间沿极化方向传播时所见到的反射现象。
这个公式可以表达用于反射电离度、等效度、反射圆盘传播常数以及反射角等因素,可以表示为:Et/Es=(ncosθ-μsinθ) / (ncosθ+μsinθ)其中,θ表示反射极化角,n为介质的电离度,μ为介质的等效度,Es 为入射波的强度,Et为反射波的强度。
5、传播极化恒等式传播极化恒等式凝结了电磁波在介质中沿一定方向传播时的电离度、等效度,以及传播极化圆盘的传播常数等因素,它可以由基本极化恒等式推出,可以表示为:H/E=ncosθ/μsinθ其中,θ表示传播极化角,n为介质的电离度,μ为介质的等效度,E 为入射波的强度,H为传播波的强度。

极化恒等式证明
极化恒等式公式为:当H是实空间时,(x,y)=(1/4)(‖x+y‖^2-‖x-y‖^2);当H是复空间时,(x,y)=(1/4)(‖x+y‖^2-‖x-y‖^2+i‖x+iy‖^2-i‖x-iy‖^2)。
极化恒等式(polarization identity)是联系内积与范数的一个重要的等式,是用范数表示内积的公式。
设H是内积空间,‖·‖是由内积(·,·)导出的范数。
对于实内积空间上的双线性埃尔米特泛函以及复内积空间上的双线性泛函φ(x,y)也分别有类似于上述的恒等式。
极化恒等式之恒等式简介:
恒等式(identities),数学概念,恒等式是无论其变量如何取值,等式永远成立的算式。
恒等式成立的范围是左右函数定义域的公共部分,两个独立的函数却各自有定义域,与x在非负实数集内是恒等的,而在实数集内是不恒等的。
恒等式有多个变量的,也有一个变量的,若恒等式两边就一个变量,恒等式就是两个解析式之间的一种关系。
它来源于e^ix=cosx+isinx(复数的三角表示),令x=π就得e^πi + 1 = 0。

平面向量系列极化恒等式一、极化恒等式 极化恒等式:])()[(4122b a b a b a --+=⋅ 极化恒等式的几何意义:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的41,即:2222||||]|||[|41BM AM BC AD b a -=-=⋅,如图:证明:2222||2||)(||||||b b a a b a AD b a AD ++=+=⇒+= 2222||2||)(||||||b b a a b a BC b a BC +-=-=⇒-= 以上两式相减得:22)()(4b a b a b a --+=⋅ ])()[(4122b a b a b a --+=⋅二、例题精析1、(2014,浙江高考理)在三角形ABC 中,M 是BC 的中点,AM=3,BC=10,则AC AB ⋅=_________ [解析]如图所示,由极化恒等式易得:16532222-=-=-=⋅BM AM AC AB2、(2016,长春二模)已知AB 为圆122=+y x 的一条直径,点P 为直线02=+-y x 上任意一点,则PB PA ⋅的最小值是_______[解析]如图所示,由极化恒等式易知,当OP 垂直直线时,PB PA ⋅有最小值,即: 1122222=-=-=⋅OB PO PB PA3、(2013,湖州二模)正方体的棱长为2,MN 是它的内切球的一条弦,P 为正方体表面上的动点,当弦MN 的长度最大时,PN PM ⋅的取值范围是_______[解析] 当弦MN 的长度最大时,即MN 为圆的直径,由极化恒等式得:当点P 在A ,C ,A1,C1任一点时有最大值,当点P 在圆与正方体的切点时有最小值,即:213)(22221max =-=-=⋅MO O C PN PM , 011)(2222min =-=-=⋅MO MO PN PM ,故]2,0[∈⋅PN PM 。
1极化恒等式第一种写法:已知#…a ,#…b ,则#…a ⋅#…b =⒧#…a +#…b ⒭2−⒧#…a −#…b ⒭24第二章写法:已知M 是AB 的中点,则# …OA ⋅# …OB =|# …OM|2−|# …MA|2=|# …OM|2−14|# …AB|2极化恒等式两种写法,常用的是第二种,用于解决向量的数量积求值范围问题,一般情况下,如果AB 的长度是固定的,那么在处理# …OA ⋅# …OB 时,常用极化恒等式将其转化为|# …OM|2的函数,至于其他用法,熟练之后自然会具体问题具体分析1.【2012浙江理数T15】在△ABC 中,M 是BC 的中点,AM =3,BC =10,则# …AB ⋅# …AC−16# …AB ⋅# …AC =⒧# …AM +# …MB⒭⋅⒧# …AM +# …MC ⒭=⒧# …AM +# …MB⒭⋅⒧# …AM −# …MB⒭=|AM|2−|MB|2=−162.【2016江苏T13】如图,在△ABC 中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,# …BA⋅# …C A =4,# …BF⋅# …C F =−1,则# …BE ⋅# …C E的值是78记|BD|=x ,|DF|=y ,則4=# …BA ⋅# …C A =|AD|2−|BD|2=9y 2−x 2−1=# …BF ⋅# …C F =|DF|2−|BD|2=y 2−x 2⎧⎪⎪⎨⎪⎪⎩x 2=138y 2=58从而# …BE ⋅# …C E =|DE|2−|BD|2=4y 2−x 2=783.【2018天津理数T8】如图,在平面四边形ABC D 中,AB⊥BC ,AD⊥C D,∠BAD =120∘,AB =AD =1.若点E 为边C D 上的动点,则# …AE ⋅# …BE 的最小值为A.2116B.32C.2516D.3A取AB 中点F ,则# …AE ⋅# …BE =|# …EF|2−|# …AF|2当EF ⟂C D 时,|# …EF|取得最小值54,比时# …AE ⋅# …BE 取得最小值2116,选A4.【2013浙江理数T7】设△ABC ,P 0是边AB 上一定点,满足# …P 0B =14# …AB ,且对于边AB 上任一点P ,恒有# …PB ⋅# …PC ⩾# …P 0B ⋅# …P 0C ,则A.∠ABC =90∘ B.∠BAC =90∘C.AB =ACD.AC =BCD取AB,BC的中点D,E.则# …PB⋅# …PC=(# …PE+# …EB)⋅(# …PE−# …EB)=|PE|2−|EB|2⩾|P0E|2−|EB|2,所以|PE|⩾|P0E|,则必有P0E⟂AB,从而C D⟂AB,所以AC=BC,选择D5.【2017全国2卷理数T12】已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则# …PA⋅⒧# …PB+PC⒭的最小值是A.−2B.−32C.−43D.−1B取BC中点M,取AM中点N,则# …PA⋅(# …PB+# …PC)=2# …PA⋅# …PM=2⒧PN2−MN2⒭⩾−2MN2=−32,当PN重合时取到,所以所求最小值是−32,选择B6.【2020天津T15】如图,在四边形ABC D中,∠B=60∘,AB=3,BC=6,且# …AD=λ# …BC,# …AD⋅# …AB=−32,则(1)实数λ的最小值为(2)若M,N是线段BC上的动点,且|# …MN|=1,则# …DM⋅# …DN的最小值为A DB M N C(1)16(2)132# …AD⋅# …AB=λ# …BC⋅# …AB=−9λ=−32,所以λ=16.取MN中点E,则# …DM⋅# …DN=|DE|2−|MN|24当DE⟂BC时,取到最小值13 2.7.【2005江苏T18】在△ABC 中,O 为中线AM 上的一个动点,若AM =2,则# …OA ⋅⒧# …OB +# …OC ⒭的最小值为−2设|OM|=x ,则# …OA ⋅(# …OB +# …OC )=2# …OA ⋅# …OM =−2x(2−x)⩾−2,取等条件是x =1,故所求最小值为−28.【2012安徽理数T14】若|2#…a −#…b |⩽3,则#…a ⋅#…b 的最小值是−98#…a ⋅#…b =|2#…a +#…b |2−|2#…a −#…b |28⩾−|2#…a −#…b |28⩾−989.在平行四边形ABC D 中,AD =√2,AB =2.若# …BF =# …FC ,则# …AF ⋅# …DF72# …AF ⋅# …DF =(# …AB +# …BF)⋅(# …AB −# …BF)=|AB|2−|BF|2=7210.已知△ABC 中,AB =8,BC =10,AC =6,P 在平面ABC 内,且# …PB ⋅# …PC =−9,则|# …PA|的取值范围是[1,9]解析11.正方体ABC D −A 1B 1C 1D 1的棱长为2,MN 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦),P 为正方体表面上的动点,当弦MN 的长度最大是,# …PM ⋅# …PN 的取值范围是[0,2]解析12.在面积为2的平行四边形ABC D中,点P为直线AD上的动点,则# …PB⋅# …PC+# …BC2的最大值是2√3设M为BC的中点,由题意,# …PB⋅# …PC+BC2=PM2−14BC2+BC2=PM2+34BC2⩾√3⋅PM⋅BC⩾√3⋅2S△PBC=2√3.取等条件为PM=√32BC且PM⟂BC.故所求最小值为2√313.在半径为1的扇形AOB中,∠AOB=60∘,C为弧AB的动点,AB与OC交于点P,则# …OP⋅# …BP的最小值是−1 16解析14.已知正四面体ABC D的棱长为2,P是以棱BC为直径的球面上一动点,则# …PA⋅# …PD的最大值是A.1+√2B.3C.2+√2D.2(√2+1)D取AD中点E,BC中点F,则# …PA⋅# …PD=|PE|2−|AE|2=|# …PF+# …FE|2−1⩽(|# …PF|+|# …FE|)2−1=(1+√2)2−1=2+2√2,选D15.【成都七中23届高三上一诊模拟T16】已知A(2cos15∘,2sin15∘),O(0,0),且|# …OB|=|# …OC|=2,则# …AB⋅# …AC的取值范围[−2,16]如图方法1极化恒等式记M为BC的中点,由极化恒等式可知:# …AB⋅# …AC=# …AM2−# …BM2,易知OM⊥BC,所以# …BM2=# …OB2−# …OM2所以# …AB⋅# …AC=# …AM2−# …BM2=# …AM2+# …OM2−# …OB2=# …AM2+# …OM2−# …OA2由余弦定理可知# …AM 2+# …OM 2−# …OA 2=2|# …MA|⋅|# …MO|cos ∠AMO =2# …MA ⋅# …MO记D 为OA 的中点,再由极化恒等式可知2# …MA ⋅# …MO =2 # …MD 2−# …OD 2因为B ,C 是圆上任意两点(可重合)所以|# …MD|∈[0,3]所以−2⩽# …AB ⋅# …AC ⩽16方法2投影暂无16.【乐山市21届一诊T10】已知△ABC 是边长为2的等边三角形,点P 是△ABC 所在平面的内的一点,且BP =1,则当# …AP ⋅# …C P 取得最小值时,# …BP ⋅# …BC 的值是A.√3B.√32C.−√3D.−√32A 方法1建系建系如图A(0,√3),B(−1,0),C (1,0),设P(−1+cos θ,sin θ)# …AP ⋅# …C P =⒧−1+cos θ,sin θ−√3⒭(−2+cos θ,sin θ)=3−2√3sin ⒧θ+π3⒭当且仅当θ=π6+2kπ时取等,代入# …BP ⋅# …BC =√3方法2向量转换# …AP⋅# …C P=⒧# …AB+# …BP⒭⋅⒧# …C B+# …BP⒭=# …AB⋅# …C B+# …AB⋅# …BP+# …BP⋅# …C B+# …BP2=2√3+1+# …AB⋅# …BP+# …BP⋅# …C B下求# …AB⋅# …BP+# …BP⋅# …BP⋅# …C B的最小值# …AB⋅# …BP+# …BP⋅# …BP⋅# …C B=−2# …BM⋅# …BP=−2|# …BM|⋅|# …BP|cos∠PBM=−2√3cos∠PBM⩾−2√3,当∠PBM=0时取得最小值,代入# …BP⋅# …BC=√3方法3极化恒等式# …AP⋅# …C P=# …PM2−14# …AC2=# …PM2−1⩾3−2√3,当P在线段BM与圆B的交点P′时,取得最小值,代入# …BP⋅# …BC=√3。

平面向量中的极化恒等式及有关最值(范围)问题知识拓展1.极化恒等式:a ·b =14[(a +b )2-(a -b )2].几何意义:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14.2.平行四边形PMQN ,O 是对角线交点.则:(1)PM →·PN →=14[PQ 2-NM 2](平行四边形模式);(2)PM →·PN →=PO 2-14NM 2(三角形模式).3.平面向量中的最值(范围)问题(1)向量数量积投影、向量的模、夹角的最值(或范围);(2)向量表达式中字母参数的最值(或范围).题型突破题型一 极化恒等式的应用【例1】 (1)在△ABC 中,M 是BC 的中点,AM =3,BC =10,则AB →·AC→=________.(2)已知正三角形ABC 内接于半径为2的圆O ,点P 是圆O 上的一个动点,则P A →·PB→的取值范围是________.解析 (1)因为M 是BC 的中点,由极化恒等式得AB →·AC →=AM 2-14BC 2=9-14×100=-16.(2)取AB 的中点D ,连接CD ,因为三角形ABC 为正三角形,所以O 为三角形ABC 的重心,O 在CD 上,且OC =2OD =2,所以CD =3,AB =2 3.又由极化恒等式得P A →·PB →=PD 2-14AB 2=PD 2-3,因为P 在圆O 上,所以当P 在点C 处时,PD max =3, 当P 在CO 的延长线与圆O 的交点处时,PD min =1,所以P A →·PB→∈[-2,6]. 答案 (1)-16 (2)[-2,6]【训练1】 (1)已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE →·DA→的值为________. (2)若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP →·FP→的最大值为( ) A.2B.3C.6D.8解析 (1)取AE 中点O ,设AE =x (0≤x ≤1),则AO =12x ,∴DE →·DA→=DO 2-14AE 2=12+⎝ ⎛⎭⎪⎫12x 2-14x 2=1. (2)如图,由已知|OF |=1,取FO 中点E ,连接PE ,由极化恒等式得OP →·FP →=|PE |2-14|OF |2=|PE |2-14,∵|PE |2max =254,∴OP →·FP →的最大值为6. 答案 (1)1 (2)C题型二 平面向量中的最值(范围)问题类型1 利用函数型【例2-1】 (1)设θ为两个非零向量a ,b 的夹角,已知对任意实数t ,|b -t a |的最小值为1,则( )A.若θ确定,则|a |唯一确定B.若θ确定,则|b |唯一确定C.若|a |确定,则θ唯一确定D.若|b |确定,则θ唯一确定(2)已知m ,n 是两个非零向量,且|m |=1,|m +2n |=3,则|m +n|+|n|的最大值为( )A. 5B.10C.4D.5解析 (1)由|b -t a |的最小值为1知(b -t a )2的最小值为1,令f (t )=(b -t a )2,即f (t )=b 2-2t a ·b +t 2a 2,则对于任意实数t ,f (t )的最小值为4a 2·b 2-(2a ·b )24a 2=4a 2b 2-(2|a ||b |cos θ)24a2=1,化简得b 2(1-cos 2θ)=1,观察此式可知,当θ确定时,|b |唯一确定,选B.(2)因为(m +2n )2=4n 2+4m ·n +1=9,所以n 2+m ·n =2,所以(m +n )2=m 2+2m ·n +n 2=5-n 2,所以|m +n |+|n |=5-|n |2+|n |.令|n |=x (0<x ≤5),f (x )=5-x 2+x ,则f ′(x )=-2x 25-x 2+1.由f ′(x )=0,得x =102,所以当0<x <102时,f ′(x )>0时,当102<x ≤5时,f ′(x )<0,所以函数f (x )在⎝ ⎛⎭⎪⎫0,102上单调递增,在⎝ ⎛⎦⎥⎤102,5上单调递减,所以f (x )max =f ⎝ ⎛⎭⎪⎫102=10,故选B. 答案 (1)B (2)B【训练2-1】 (1)(2017·浙江卷)已知向量a ,b 满足|a |=1,|b |=2,则|a +b |+|a -b |的最小值是________,最大值是________.(2)如图,在边长为1的正方形ABCD 中,E 为AB 的中点,P 为以A 为圆心,AB 为半径的圆弧(在正方形内,包括边界点)上的任意一点,则AP →·BP→的取值范围是________;若向量AC →=λDE →+μAP →,则λ+μ的最小值为________.解析 (1)由题意,不妨设b =(2,0),a =(cos θ,sin θ)(θ∈[0,2π)), 则a +b =(2+cos θ,sin θ),a -b =(cos θ-2,sin θ).令y =|a +b |+|a -b | =(2+cos θ)2+sin 2θ+(cos θ-2)2+sin 2θ=5+4cos θ+5-4cos θ,则y 2=10+225-16cos 2θ∈[16,20].由此可得(|a +b |+|a -b |)max =20=25,(|a +b |+|a -b |)min =16=4,即|a +b |+|a -b |的最小值是4,最大值是2 5.(2)以点A 为坐标原点,分别以AB ,AD 所在的直线为x 轴、y 轴建立平面直角坐标系,则易得A (0,0),B (1,0),C (1,1),D (0,1),E ⎝ ⎛⎭⎪⎫12,0,P (cos θ,sin θ)⎝ ⎛⎭⎪⎫0≤θ≤π2,则AP →·BP →=(cos θ,sin θ)·(cos θ-1,sin θ)=cos 2θ-cos θ+sin 2θ=1-cosθ,又因为0≤θ≤π2,所以AP →·BP →=1-cos θ∈[0,1].由AC→=λDE →+μAP →得(1,1)=λ⎝ ⎛⎭⎪⎫12,-1+μ(cos θ,sin θ)=⎝ ⎛⎭⎪⎫12λ+μcos θ,-λ+μsin θ,所以⎩⎨⎧12λ+μcos θ=1,-λ+μsin θ=1,解得⎩⎨⎧λ=2sin θ-2cos θ2cos θ+sin θ,μ=32cos θ+sin θ,则λ+μ=2sin θ-2cos θ2cos θ+sin θ+32cos θ+sin θ=2sin θ-2cos θ+32cos θ+sin θ,当θ=π2时,λ+μ=2sin θ-2cos θ+32cos θ+sin θ=5,当θ≠π2时,λ+μ=2sin θ-2cos θ+32cos θ+sin θ=2tan θ-2+3tan 2θ+12+tan θ,设f (x )=2x -2+3x 2+12+x(x ≥0),则f ′(x )=⎝⎛⎭⎪⎫2+3x x 2+1(2+x )-(2x -2+3x 2+1)(2+x )2=6x 2+1+6x -3(2+x )2x 2+1>0(x ≥0),所以函数f (x )=2x -2+3x 2+12+x 在[0,+∞)上单调递增,则当tan θ=0时,λ+μ=2tan θ-2+3tan 2θ+12+tan θ取得最小值12.综上所述,λ+μ的最小值为12.答案 (1)4 25 (2)[0,1] 12类型2 利用不等式型【例2-2】 (1)(2020·浙江名校新高考研究联盟三联)已知边长为1的正方形ABCD ,E ,F 分别是边BC ,DC 上的两个动点,AE→+AF →=xAB →+yAD→,若x +y =3,则|EF →|的最小值为________. (2)(一题多解)(2019·七彩阳光联盟三联)已知平面向量a ,b ,c 满足|a |=|b |=|c |=1,a ·b =0,则|2c -a |+⎪⎪⎪⎪⎪⎪12c -b 的最小值为( ) A.172B.2C.52D. 5(3)(2016·浙江卷)已知向量a ,b ,|a |=1,|b |=2.若对任意单位向量e ,均有|a ·e |+|b ·e |≤6,则a ·b 的最大值是________.解析 (1)因为四边形ABCD 是正方形,以C 为坐标原点建立平面直角坐标系,则A (1,1),B (1,0),C (0,0).设E (a ,0),F (0,b ),则0≤a ,b ≤1.所以AE→=(a -1,-1),AF →=(-1,b -1),因为AE →+AF →=xAB →+yAD→,所以有y =2-a ,x =2-b .因为x +y =3,所以a +b =1.所以|EF →|=a 2+b 2≥(a +b )22=22,所以|EF →|min =22,当且仅当a =b =12时取到最小值.(2)法一 因为|a |=|b |=|c |=1,且a ⊥b .所以通过计算有|2c -a |=|c -2a |,⎪⎪⎪⎪⎪⎪12c -b =⎪⎪⎪⎪⎪⎪c -12b ,所以|2c -a |+⎪⎪⎪⎪⎪⎪12c -b =|c -2a |+⎪⎪⎪⎪⎪⎪c -12b ≥⎪⎪⎪⎪⎪⎪2a -12b =172,故选A. 法二 因为|a |=|b |=|c |=1,且a ⊥b ,所以可设a =(1,0),b =(0,1),c =(x ,y ),则有x 2+y 2=1,所以|2c -a |+⎪⎪⎪⎪⎪⎪12c -b =(2x -1)2+4y 2+14x 2+⎝ ⎛⎭⎪⎫12y -12=4x 2-4x +1+4y2+14x 2+14y 2-y +1=x 2-4x +4+y 2+x 2+y 2-y +14=(x -2)2+y 2+x 2+⎝ ⎛⎭⎪⎫y -122≥22+⎝ ⎛⎭⎪⎫122=172,故选A. (3)由已知可得6≥|a ·e |+|b ·e |≥|a ·e +b ·e |=|(a +b )·e |由于上式对任意单位向量e 都成立.∴6≥|a +b |成立.∴6≥(a +b )2=a 2+b 2+2a ·b =12+22+2a ·b .即6≥5+2a ·b ,∴a ·b ≤12. 答案 (1)22 (2)A (3)12【训练2-2】 (1)(2020·杭州四中仿真)若非零向量a ,b 满足a 2=(5a -4b )·b ,则cos 〈a ,b 〉的最小值为________.(2)(2019·浙江名师预测卷一)已知向量a ,b 满足|b |=1,|a +b |=2|a -b |,则|a |2-|b |2的取值范围是( )A.⎣⎢⎡⎦⎥⎤-89,8B.⎣⎢⎡⎦⎥⎤-19,8 C.⎣⎢⎡⎦⎥⎤-2,19 D.⎣⎢⎡⎦⎥⎤-19,19 (3)(2020·温州适应性测试)已知平面向量a ,b ,c 满足:a ·b =0,|c |=1,|a -c |=|b -c |=5,则|a -b |的最小值为( )A.5B.6C.7D.8解析 (1)由a 2=(5a -4b )·b 得a ·b =15(a 2+4b 2)≥15×2|a |2·4|b |2=45|a |·|b |,则cos 〈a ,b 〉=a ·b |a |·|b |≥45|a |·|b ||a |·|b |=45,当且仅当|a |=2|b |时等号成立,所以cos 〈a ,b 〉的最小值为45.(2)因为|b |=1,所以|(a +b )-(a -b )|=2|b |=2.两边平方得|a +b |2+|a -b |2-2(|a |2-|b |2)=4,又|a +b |=2|a -b |,所以|a |2-|b |2=5|a -b |2-42,又因为|a +b |-|a -b |≤|(a +b )-(a -b )|≤|a +b |+|a -b |,即|a -b |≤2≤3|a-b |,故23≤|a -b |≤2,所以|a |2-|b |2=5|a -b |2-42的取值范围是⎣⎢⎡⎦⎥⎤-89,8,故选A.(3)|a -b |2=|(a -c )-(b -c )|2=(a -c )2-2(a -c )(b -c )+(b -c )2=50-2(a ·b -a ·c -b ·c +1)=48+2(a +b )·c =48+2|a +b |cos θ(其中θ为a +b 与c 的夹角),因为|a -b |=|a +b |,所以|a -b |2=48+2|a -b |cos θ,则由cos θ∈[-1,1],得48-2|a -b |≤|a -b |2≤48+2|a -b |,解得6≤|a -b |≤8,即|a -b |的最小值为6,此时向量a -b 的方向与向量c 的方向相反,故选B.答案 (1)45 (2)A (3)B类型3 利用向量平行(垂直)、向量的投影型【例2-3】 (1)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A ,B ,C ,D 四点均位于图中的“晶格点”处,且A ,B 的位置如图所示,则AB →·CD→的最大值为________.(2)已知|a |=2,|b |=|c |=1,则(a -b )·(c -b )的最大值为________,最小值为________.解析 (1)先建立平面直角坐标系如图,因为正六边形的边长均为1,所以B (0,0),A ⎝ ⎛⎭⎪⎫32,92,当CD →在AB →方向上的投影最大时,AB →·CD →最大,此时取C (0,5),D (-3,0),即(AB →·CD →)max =⎝⎛⎭⎪⎫-32,-92·(-3,-5)=32+452=24.(2)设M =a ·c -a ·b -b ·c ,则(a -b )(c -b )=a ·c -a ·b -b ·c +b 2=1+a ·c-a ·b -b ·c =1+M .而(b -a -c )2=6+2M ,M =-3+12(b -a -c )2,∴当(b -a -c )2=0时,M min =-3,∴[(a -b )(c -b )]min =1-3=-2;当b ,-a ,-c 共线且同向时,M max =-3+12(1+2+1)2=5,∴[(a -b )·(c -b )]max =1+5=6.答案 (1)24 (2)6 -2【训练2-3】 (1)已知向量a ,b ,c 满足|b |=|c |=2|a |=1,则(c -a )·(c -b )的最大值是________,最小值是________.(2)已知|OA →|=|OB →|=|OC →|=2,|OP →|=1,且OA →=BO →,记P A →·PB →+PB →·PC →+PC →·P A →的最大值为M ,最小值为m ,则M +m =( )A.6B.4C.-2D.-4解析 (1)由题意得|a |=12,|b |=|c |=1,则(c -a )·(c -b )=|c |2-c ·b -c ·a+a ·b =|c |2+12(-a -b +c )2-12(|a |2+|b |2+|c |2)=-18+12(-a -b +c )2,则当向量-a ,-b ,c 同向共线时,(c -a )·(c -b )取得最大值-18+12⎝ ⎛⎭⎪⎫12+1+12=3,当-a -b +c =0时,(c -a )·(c -b )取得最小值-18. (2)因为P A →·PB →+PB →·PC →+PC →·P A →=(OA →-OP →)·(OB →-OP →)+(OB →-OP →)·(OC →-OP →)+(OC →-OP →)·(OA →-OP →)=3OP →2-2OP →·OC →-4,令3OP →=OQ →,2OC →=OM →,P A →·PB →+PB →·PC →+PC →·P A →=OP →·MQ →-4,如图,设OC →与OP→夹角为θ(θ∈[0,π]).因为MQ →=OQ →-OM →.所以MQ →·OP →|OP →|=OP →(3OP →-2OC→)=3-4cos θ,又因为cos θ∈[-1,1],所以MQ →在OP →方向上的投影d ∈[-1,7],即M =3,m =-5,所以M +m =-2,故选C.答案 (1)3 -18 (2)C类型4 利用轨迹图形性质(数形结合)型【例2-4】 (1)(一题多解)(2018·浙江卷)已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为π3,向量b 满足b 2-4e ·b +3=0,则|a -b |的最小值是( ) A.3-1 B.3+1 C.2D.2- 3(2)已知向量|a |=3,|b |=6,a ·b =9,则|a +t (b -a )|+|(1-t )(b -a )-13b |(其中t ∈[0,1])的最小值是________.解析 (1)法一 设O 为坐标原点,a =OA→,b =OB →=(x ,y ),e =(1,0),由b 2-4e ·b +3=0得x 2+y 2-4x +3=0,即(x -2)2+y 2=1,所以点B 的轨迹是以C (2,0)为圆心,1为半径的圆.因为a 与e 的夹角为π3,所以不妨令点A 在射线y =3x (x >0)上,如图,数形结合可知|a -b |min =|CA→|-|CB →|=3-1.故选A.法二 由b 2-4e ·b +3=0得b 2-4e ·b +3e 2=(b -e )·(b -3e )=0. 设b =OB →,e =OE →,3e =OF →,所以b -e =EB →,b -3e =FB →,所以EB →·FB →=0,取EF 的中点为C ,则B 在以C 为圆心,EF 为直径的圆上,如图,设a =OA →,作射线OA ,使得∠AOE =π3,所以|a -b |=|(a -2e )+(2e -b )|≥|a -2e |-|2e -b |=|CA→|-|BC →|≥3-1.故选A.(2)由cos 〈a ,b 〉=a ·b |a ||b |=12得a ,b 的夹角为60°,又因为|a |=3,|b |=6,所以△OAB 为直角三角形,B =30°.如图,令a =OA →,b =OB →,∠BOA =60°,AC→=tAB →,DB →=13OB →,则|OA →+tAB →|=|OC →|,⎪⎪⎪⎪⎪⎪(1-t )AB →-13OB →=|CD →|,问题转化为当点C 在线段AB 上运动时,求|OC→|+|CD →|的最小值.作点D 关于线段AB 对称的点G ,连接OG ,则OG 即为所求的最小值.在Rt △BDE 中,∠BED =90°,BD =2,B =30°,则DE =1,DG =2DE =2,在△ODG 中,OD =4,∠ODG =120°,DG =2,由余弦定理得OG =OD 2+DG 2-2OD ·DG cos ∠ODG =27. 答案 (1)A (2)27【训练2-4】 (1)已知|a |=|b |=1,向量c 满足|c -(a +b )|=|a -b |,则|c |的最大值为________.(2)(一题多解)(2019·宁波模拟)已知向量a ,b ,c 满足|a |=1,|b |=2,|c -b |=1,则|a +c |的取值范围为________.解析 (1)由|c -(a +b )|=|a -b |得向量c 的终点的轨迹为以向量a +b 的终点为圆心,|a -b |为半径的圆,则|c |的最大值为|a +b |+|a -b |, 又因为|a +b |+|a -b |≤2[(a +b )2+(a -b )2] =2(|a |2+2a ·b +|b |2+|a |2-2a ·b +|b |2)=22,当且仅当|a +b |=|a -b |,即a ⊥b 时等号成立,所以|c |的最大值为2 2. (2)法一 令m =a +c ,则问题转化为|m |的取值范围.由三角不等式有||m |-|a +b ||≤|m -(a +b )|,则|a +b |-1≤|m |≤1+|a +b |,又||a |-|b ||≤|a +b |≤|a |+|b |,即1≤|a +b |≤3,故0≤|m |≤4,即|a +c |的取值范围为[0,4].法二 如图,由已知,作OB→=b ,分别以点O ,B 为圆心作单位圆,则-a 的终点A 在圆O 上,c 的终点C 在圆B 上,则AC→=c -(-a )=c +a ,故|a +c |=|AC →|表示两圆上两点连线的长,因此,由圆的性质得0≤|AC →|≤4,即|a +c |的取值范围为[0,4].答案 (1)22 (2)[0,4] 补偿训练 一、选择题1.(2013·浙江卷)在△ABC 中,P 0是边AB 上一定点,满足P 0B =14AB ,且对于边AB 上任一点P ,恒有PB →·PC →≥P 0B →·P 0C →,则( ) A.∠ABC =90° B.∠BAC =90° C.AB =ACD.AC =BC解析 取BC 边中点D ,由极化恒等式得PB →·PC →=PD →2-14BC →2,P 0B →·P 0C →=P 0D →2-14BC →2,由PB →·PC →≥P 0B →·P 0C →,得PD →2≥P 0D →2,即|PD →|≥|P 0D →|,D 到AB 的最短距离为P 0D ,∴DP 0→⊥AB →,设AB 的中点为P ′,又P 0B =14AB ,∴DP ∥CP ,∴CP ⊥AB ,故AB =AC . 答案 C2.(2020·诸暨适应性考试)已知AB 是圆O 的直径,AB 长为2,C 是圆O 上异于A ,B 的一点,P 是圆O 所在平面上任意一点,则(P A →+PB →)·PC →的最小值为( )A.-14B.-13C.-12D.-1解析 P A →+PB →=2PO →,∴(P A →+PB →)·PC →=2PO →·PC →,取OC 中点D ,由极化恒等式得PO →·PC →=PD 2-14OC 2=PD 2-14,又PD 2min =0,∴(P A →+PB →)·PC →的最小值为-12. 答案 C3.(一题多解)如图,BC ,DE 是半径为1的圆O 的两条直径,BF →=2FO →,则FD →·FE→=( )A.-34B.-89C.-14D.-49解析 法一 ∵BF →=2FO →,圆O 的半径为1,∴|FO →|=13, ∴FD →·FE →=(FO →+OD →)·(FO →+OE →)=FO →2+FO →·(OE →+OD →)+OD →·OE →=⎝ ⎛⎭⎪⎫132+0-1=-89.法二 OF =13,由极化恒等式得 FD →·FE →=OF 2-14DE 2=19-1=-89. 答案 B4.如图,在△ABC 中,点D ,E 是线段BC 上两个动点,且AD →+AE →=xAB →+yAC →,则1x +4y的最小值为( )A.32 B.2 C.52D.92解析 由图可设AD→=λAB →+(1-λ)AC →,AE →=μAB →+(1-μ)AC →,其中λ,μ∈(0,1),则AD→+AE →=(λ+μ)AB →+(2-λ-μ)AC →.由题知,x =λ+μ,y =2-λ-μ,所以有x +y =2,所以1x +4y =12⎝ ⎛⎭⎪⎫1x +4y (x +y )=12⎝ ⎛⎭⎪⎫5+y x +4x y ≥12⎝ ⎛⎭⎪⎫5+2y x ×4x y =92,当且仅当y =2x ,即x =23,y =43时,取等号,故选D. 答案 D5.在△ABC 中,BC =2,A =45°,B 为锐角,点O 是△ABC 外接圆的圆心,则OA →·BC →的取值范围是( ) A.(]-2,22 B.(]-22,2 C.[]-22,22D.()-2,2解析 依题意得△ABC 的外接圆半径R =12·BCsin 45°=2,|OA→|=2, 如图所示,A 在弧A 1C 上(端点除外),OA 2→与BC →同向,此时OA →·BC →有最大值22, 又OA 1→·BC →=-2,故OA →·BC →∈(]-2,22.故选A. 答案 A6.记max{a ,b }=⎩⎪⎨⎪⎧a ,a ≥b ,b ,a <b .在△AOB 中,∠AOB =90°,P 为斜边AB上一动点.设M =max{OP →·OA →,OP →·OB →},则当M 取最小值时,AP PB =( )A.OAOBB.OA OBC.⎝ ⎛⎭⎪⎫OA OB 2D.⎝ ⎛⎭⎪⎫OA OB 3 解析 M 取最小值时,OP →·OA →=OP →·OB →,即OP →·AB →=0,亦即OP ⊥AB .根据直角三角形的射影定理可得|AP ||PB |=AP ·PB PB 2=⎝ ⎛⎭⎪⎫OP PB 2=⎝ ⎛⎭⎪⎫OA OB 2,故选C.答案 C7.(2019·浙江名师预测卷四)已知a ,b 是单位向量,向量c 满足|c -b +a |=|a +b |,则|c |的最大值为( ) A.2 B.2 2 C.3D.3 2解析 由|c -(b -a )|=|a +b |得向量c 的终点的轨迹为以向量b -a 的终点为圆心,|a +b |为半径的圆,则|c |的最大值为|a +b |+|b -a |. 又因为|a +b |+|b -a |≤2[(a +b )2+(b -a )2]=2(|a |2+2a ·b +|b |2+|b |2-2a ·b +|a |2)=2 2.当且仅当|a +b |=|b -a |,即a ⊥b 时等号成立,所以|c |的最大值为2 2. 答案 B8.(2020·浙江教育绿色评价联盟适考)在矩形ABCD 中,AB =1,AD =2,动点P 在以C 为圆心且与BD 相切的圆上,若BP →=λBA →+μBC→,设λ+2μ的最大值为M ,最小值为N ,则M -N 的值为( )A.2105B.3105C.4105D.10解析 如图,以C 为坐标原点,分别以直线BC ,CD 为x ,y 轴建立平面直角坐标系,则B (-2,0),A (-2,1),由已知,圆C 的方程为x 2+y 2=45,设P⎝ ⎛⎭⎪⎫25cos θ,25sin θ,又BP →=λBA →+μBC →,则⎩⎨⎧25cos θ+2=2μ, 25sin θ=λ,即λ+2μ=25(sin θ+cos θ)+2=225sin ⎝ ⎛⎭⎪⎫θ+π4+2,故M -N =⎝ ⎛⎭⎪⎫225+2-⎝ ⎛⎭⎪⎫-225+2=4105,故选C.答案 C9.(2018·天津卷)如图,在平面四边形ABCD 中,AB ⊥BC ,AD ⊥CD ,∠BAD =120°,AB =AD =1.若点E 为边CD 上的动点,则AE →·BE →的最小值为( )A.2116B.32C.2516D.3解析 以A 为坐标原点,AB 所在直线为x 轴,建立如图的平面直角坐标系,因为在平面四边形ABCD 中,AB =AD =1,∠BAD =120°,所以A (0,0),B (1,0),D ⎝ ⎛⎭⎪⎫-12,32.设C (1,m ),E (x ,y ),所以DC → =⎝ ⎛⎭⎪⎫32,m -32,AD →=⎝ ⎛⎭⎪⎫-12,32,因为AD ⊥CD ,所以⎝ ⎛⎭⎪⎫32,m -32·⎝ ⎛⎭⎪⎫-12,32=0,则32×(-12)+32⎝⎛⎭⎪⎫m -32=0,解得m =3,即C (1,3).因为E 在CD 上,所以32≤y ≤3,由k CE =k CD ,得3-y 1-x =3-321+12,即x =3y -2,因为AE →=(x ,y ),BE →=(x -1,y ),所以AE →·BE →=(x ,y )·(x -1,y )=x 2-x +y 2=(3y -2)2-3y +2+y 2=4y 2-53y +6,令f (y )=4y 2-53y +6,y ∈⎣⎢⎡⎦⎥⎤32,3.因为函数f (y )=4y 2-53y +6在⎣⎢⎡⎦⎥⎤32,538上单调递减,在⎝ ⎛⎦⎥⎤538,3上单调递增,所以f (y )min =4×⎝ ⎛⎭⎪⎫538 2-53×538+6=2116.所以AE →·BE →的最小值为2116,故选A. 答案 A 二、填空题10.在△ABC 中,BC =3,AB →·AC →=4,则BC 边上的中线AM 的长是________.解析 因为AB →·AC →=14[(2AM →)2-BC →2], AM →2=14(4AB →·AC →+BC →2)=254,即|AM →|=52, 所以BC 边上的中线AM 的长为52. 答案 5211.在面积S =2的△ABC 中,E ,F 分别是AB ,AC 的中点,点P 在直线EF 上,则PC →·PB →+BC →2的最小值是________. 解析 取BC 的中点为D ,连接PD ,则由极化恒等式得PC →·PB →+BC →2=PD →2-BC →24+BC →2=PD →2+34BC →2≥h 24+34BC→2(其中h 为A 点向BC 边作的高), 当且仅当PD→⊥BC →时取等号. 由上可知PC →·PB →+BC →2≥h 24+34BC →2≥2h 24·34BC →2≥3S =2 3.答案 2 312.在Rt △ABC 中,CA =CB =2,M ,N 是斜边AB 上的两个动点,且MN =2,则CM →·CN→的取值范围是________. 解析 取MN 的中点为P ,由极化恒等式得CM →·CN →=14[(2CP →)2-MN →2]=CP →2-12.问题转化为求|CP→|的取值范围,当P 为AB 的中点时,|CP →|取最小值为2,则CM →·CN →的最小值为32;当M 与A (或N 与B )重合时,|CP →|取最大值为102,则CM →·CN →的最大值为2,所以CM →·CN →的取值范围是⎣⎢⎡⎦⎥⎤32,2. 答案 ⎣⎢⎡⎦⎥⎤32,2 13.(2020·浙江新高考仿真卷二)在△ABC 中,A =120°,BC =213,AC=2,则AB =________;当|CB→+λCA →|取到最小值时,则λ=________. 解析 在△ABC 中,由余弦定理得BC 2=AC 2+AB 2-2AC ·AB cos A ,即(213)2=22+AB 2-2×2AB cos 120°,解得AB =6,则cos C =BC 2+AC 2-AB 22BC ·AC =(213)2+22-622×213×2=51326,则|CB →+λCA →|2=|CB →|2+λ2|CA →|2+2λCB →·CA →=(213)2+λ2×22+2λ×213×2×51326=4λ2+20λ+52,则当λ=-202×4=-52时,|CB →+λCA →|取得最小值.答案 6 -5214.若非零向量a 和b 满足|a +b |=|b |=2,则|a |的取值范围是________,|a -b |的取值范围是________.解析 因为||a +b |-|b ||≤|a |=|a +b -b |≤|a +b |+|b |=4,又a 是非零向量,所以|a |的取值范围是(0,4],因为|a -b |+|a +b |≥2|b |=|(a +b )-(a -b )|≥||a -b |-|a +b ||,所以-4≤|a -b |-|a +b |≤4,|a -b |+|a +b |≥4,又|a +b |=2,解得|a -b |的取值范围是[2,6].答案 (0,4) [2,6]15.(2020·杭州三校三联)如图,圆O 是半径为1的圆,OA =12,设B ,C 为圆上的任意2个点,则AC →·BC→的取值范围是________.解析 设a =OA →,b =OB →,c =OC →,则有|a |=12,|b |=|c |=1,则AC →·BC →=(c -a )·(c -b )≤|c -a |·|c -b |≤(|c |+|a |)·(|c |+|b |)=32×2=3,当且仅当a ,b 同向共线,且与c 反向共线时,等号成立,所以AC →·BC→的最大值为3.AC →·BC →=(c -a )·(c -b )=1-c ·(a +b )+a ·b ≥1-|c |·|a +b |+a ·b =1-|a +b |+a ·b =1-54+2a ·b +a ·b ,令a ·b =t ,则易得t ∈⎣⎢⎡⎦⎥⎤-12,12,AC →·BC →=(c -a )·(c -b )≥1-54+2t +t ,设f (t )=1-54+2t +t ⎝ ⎛⎭⎪⎫-12≤t ≤12,则f ′(t )=1-154+2t .易得当t =-18时,f (t )=1-54+2t +t 取得最小值-18.综上所述,AC →·BC →的取值范围为⎣⎢⎡⎦⎥⎤-18,3. 答案 ⎣⎢⎡⎦⎥⎤-18,3 16.已知平面向量a ,b ,c 满足|a |=1,|b |=2,|c -a |=|c -b |,则|c |的最小值为________,此时a ·b =________.解析 由|c -a |=|c -b |,得c 2-2a ·c +a 2=c 2-2b ·c +b 2,即2b ·c -2a ·c=b 2-a 2=3,则(b -a )·c =32≤|b -a |·|c |≤(|b |+|a |)·|c |=3|c |,所以|c |≥12,当且仅当a 与b 方向相反且a ,b ,c 共线时等号成立,所以|c |的最小值为12,此时a ·b =|a ||b |cos π=-2.答案 12 -217.已知正三角形ABC 的边长为4,O 是平面ABC 内的动点,且∠AOB =π3,则OC →·AB→的最大值为________. 解析 如图,圆E 2为△ABC 的外接圆,圆E 1与圆E 2关于直线AB 对称,由题意知O 在圆E 1,E 2的优弧AB ︵上(圆E 1,E 2半径相等),设AB 的中点为D ,OC →·AB →=(DC →-DO →)·AB →=BA →·DO →=|BA →|·|DO →|·cos ∠ADO ,易知当∠ADO为锐角,且DO →在BA →方向上的射影最大时,OC →·AB →取得最大值,易知DO→在BA→方向上射影的最大值为△ABO 外接圆的半径,故所求最大值为4×42sin π3=1633.答案 1633 18.(2019·浙江卷)已知正方形ABCD 的边长为1,当每个λi (i =1,2,3,4,5,6)取遍±1时,|λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →|的最小值是________,最大值是________.解析 如图,以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴建立平面直角坐标系,则AB→=(1,0),AD →=(0,1). 设a =λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD → =λ1AB →+λ2AD →-λ3AB →-λ4AD →+λ5(AB →+AD →)+λ6(AD →-AB →) =(λ1-λ3+λ5-λ6)AB →+(λ2-λ4+λ5+λ6)AD → =(λ1-λ3+λ5-λ6,λ2-λ4+λ5+λ6).故|a|=(λ1-λ3+λ5-λ6)2+(λ2-λ4+λ5+λ6)2.∵λi (i =1,2,3,4,5,6)取遍±1,∴当λ1-λ3+λ5-λ6=0,λ2-λ4+λ5+λ6=0时,|λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →|取得最小值0. 考虑到λ5-λ6,λ5+λ6有相关性,要确保所求模最大,只需使|λ1-λ3+λ5-λ6|,|λ2-λ4+λ5+λ6|尽可能取到最大值,即当λ1-λ3+λ5-λ6=2,λ2-λ4+λ5+λ6=4时可取到最大值,∴|λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →|的最大值为4+16=2 5. 答案 0 2 5。
专题2 极化恒等式与向量隐圆知识点1 极化恒等式极化恒等式:2214a ba b a b,我们再之前提到两个向量的数量积,有两个方案,一是知道模和夹角,二是知道两个向量的坐标,极化恒等式的出现,使得向量的数量积有了第三种方案,就是利用中线的平方差,这样无需任何角度和坐标,完全靠长度平方差来解决,向量完全靠模长化解决数量积问题,联想我们学习的极坐标,所谓“极化”,就是完全模长化,这个完全模长化的恒等式就叫极化恒等式.在ABC △中,若AM 是ABC △的BC 边中线,有以下两个重要的向量关系:()()1212AM AC AB BM AC AB ⎧=+⎪⎪⎨⎪=-⎪⎩ 定理1 平行四边形两条对角线的平分和等于两条邻边平分和的两倍.以此类推到三角形,若AM 是ABC ∆的中线,则()22222AB AC AM BM +=+.定理2 在ABC ∆中,若M 是BC 的中点,则有22221.4AB AC AM BC AM BM ⋅=-=- 【例1】(2014•新课标II )设向量a ,b 满足a b +=a b -=a b ⋅等于( ) A .1B . 2C .3D .5【例2】(2020•新课标Ⅰ)设a ,b 为单位向量,且||1a b +=,则||a b -= .【例3】(2022•北京)在△ABC 中,3AC =,4BC =,90C ∠=︒.P 为△ABC 所在平面内的动点,且1PC =,则PA PB ⋅的取值范围是( ) A .[5-,3]B .[3-,5]C .[6-,4]D .[4-,6]【例4】(2020•天津)如图,在四边形ABCD 中,60B ∠=︒,3AB =,6BC =,且AD BC λ=,32AD AB =-,则实数λ的值为 ,若M ,N 是线段BC 上的动点,且||1MN =,则DM DN 的最小值为 .【例5】(2016•江苏卷)如图,在ABC △中,D 是BC 的中点E ,F 是AD 的两个三等分点,4BA CA ⋅=,1BF CF ⋅=-则BE CE ⋅= .【例6】(2018•天津)如图,在平面四边形ABCD 中,BC AB ⊥,CD AD ⊥,︒=∠120BAD ,1==AD AB .若点E 为边CD 上的动点,则AE BE ⋅的最小值为( ) A .2116B .32C .2516D .3【例7】(2016•浙江卷)已知向量,2,1,,==b a b a 若对任意单位向量e ,均有a e b e ⋅+⋅≤则a b ⋅的最大值是 .【例8】(2017•全国II 卷)已知ABC △是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC⋅+的最小值是( ) A .2-B .23-C .34-D .1-【例9】(2022•重庆期末)如图,正六边形的边长为2,半径为1的圆O 的圆心为正六边形的中心,若点M 在正六边形的边上运动,动点A ,B 在圆O 上运动且关于圆心O 对称,则MA MB ⋅的值可能为( )A .32B .52C .3D .72【例10】(2022•淮安月考)如图,在ABC ∆中,6BC =,D ,E 是BC 的三等分点,且4AD AE ⋅=,则()A .2133AE AB AC =+B .1122AD AB AE =+ C .4AB AC ⋅=- D .2228AB AC +=同步训练1.(2022•雨花区开学)已知正方形ABCD 的对角线长为2,EF 是它的内切圆一条弦,点P 为正方形ABCD 四条边上的一个动点,当弦EF 的长度最大时,PE PF ⋅不可能为( ) A .0B .13C .12D .232.(2022•房山区开学)已知ABC ∆是边长为2的等边三角形,AB 为圆M 的直径,若点P 为圆M 上一动点,则PA PC ⋅的取值范围为( ) A .[0,4]B .[1-,3]C .[2-,4]D .[3-,1]3.(2022•南关区期末)在等腰梯形ABCD 中,//AB CD ,24AB CD ==,AD BC ==E 为CD 的中点,F 为线段BC 上的点,则EF BF ⋅的最小值是( )A .0B .95-C .45-D .14.(2022•思明区月考)如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE EA =,2CF FB =.点P 在正方形ABCD 的边上,且16PE PF ⋅=,则满足条件的点P 的个数是( )A .0B .2C .4D .65.(2022•资阳期末)如图,在等腰直角ABC ∆中,斜边为4BC =,M ,N 为BC 上的动点,且1MN =,则AM AN ⋅取值范围为( )A .15[4B .C .15[,6]4D .[4,6]6.(2022•万州区开学)在ABC ∆中,3AC =,4BC =,90C ∠=︒.P 为ABC ∆所在平面内的动点,且1PC =,则PA PB ⋅的取值范围是 .7.(2022•黄浦区开学)如图,ABC ∆中,4AC =,2BC =,ACB ∠为钝角,M 、N 是边AB 上的两个动点,且1MN =,若CM CN ⋅的最小值为34,则cos ACB ∠= .8.(2022•青岛期末)设点P 是边长为2的ABC △三边上的一动点,则()PA PB PC ⋅+的取值范围是 . 9.(2018•浙江联考)如图,在等腰梯形ABCD 中,2=AB ,4=CD ,5=BC ,点E ,F 分别为AD ,BC 的中点.如果对于常数λ,在等腰梯形ABCD 的四条边上,有且只有8个不同的点P ,使得PE PF λ⋅=成立,那么λ的取值范围是( ) A .⎪⎭⎫⎝⎛--209,45B .⎪⎭⎫ ⎝⎛-411,209C .⎪⎭⎫ ⎝⎛--41,209D .511,44⎛⎫- ⎪⎝⎭知识点2 向量的隐圆问题第一类 极化恒等式向量乘积型:PA PB λ=定理 平面内,若B A ,为定点,且PA PB λ=,则P 的轨迹是以AB 中点M 为圆心,241AB +λ为半径的圆. 证明 由PA PB λ=,根据极化恒等式可知,λ=-2241AB PM ,所以λ+=241AB PM ,P 的轨迹是以M 为圆心241AB +λ为半径的圆. 【例11】(2017•江苏)在平面直角坐标系xOy 中,)012(,-A ,)60(,B ,点P 在圆O :5022=+y x 上,若20PA PB ≤,则P 的横坐标范围是 .【例12】已知)32(,A ,)36(-,B ,P 在0343=+-y x 上,若满足20AP BP λ+=的P 有2个,则λ的取值范围是 .第二类 与向量模和矩形相关构成隐圆如图,在矩形ABCD 中,若对角线AC 和BD 交于点O ,P 为平面内任意一点,有以下两个重要的向量关系:①2222PA PC PB PD ;① .PA PCPB PD4⎭根据极化恒等式2a b a b +⎛⎫⋅= ⎪⎝,可得224AC PA PC PO PB PD ⋅=-=⋅ 推广到空间,得到的结论就是:底面是矩形的四棱锥相对侧棱长的平方和以及向量乘积均相等.【例13】(2008•浙江卷)已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足0)()(=-⋅-c b c a ,则||c 的最大值是( )A .1B .2C .2D .【例14】(2013•重庆卷)在平面内,12AB AB ⊥,121OB OB ==,12AP AB AB =+若12OP ,则OA 的取值范围是( )A .0,⎡⎢⎣⎭B. ,⎝⎦C. ,⎝D. ,⎝【例15】(2012•江西卷)在Rt ABC △中,点D 是斜边AB 的中点,点P 为线段CD 的中点,则222PA PB PC +等于( ) A .2B .4C . 5D . 10【例16】(2022•岳麓区月考)已知向量a 、b 、c 满足3a ,2b ,1c ,且(c)(c)0a b ,则a b-的取值范围是 _ .【例16】(2022•安徽模拟)已知||||2a b ==,||1c =,()()0a c b c --=,则||a b -的取值范围是( )A .11]B .C .11]D .第三类 与向量模和向量数量积构成隐圆【例17】(2022•绍兴期中)已知平面向量a ,b ,c 满足对任意x R ∈都有||||a xb a b -≥-,||||a xc a c -≥-成立,||||1a c b c -=-=,||3a b -=,则||a 的值为( )A .1B C .2D .7 【例18】(2022•山东月考)已知向量a ,b ,c ,其中||2a b -=,||1a c -=,b 与c 夹角为60︒,且()()1a b a c --=-.则||a 的最大值为 .【例19】(2018•浙江)已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为3π,向量b 满足2430b e b -⋅+=,则||a b -的最小值是( )A 1B 1C .2D .2【例20】(2016•四川)在平面内,定点A ,B ,C ,D 满足||||||DA DB DC ==,2DA DB DB DC DC DA ⋅=⋅=⋅=-,动点P ,M 满足||1AP =,PM MC =,则2||BM 的最大值是( )A .434B .494C D同步训练10.(2022•海淀开学)已知a ,b 是单位向量,0a b ⋅=,若||1a b c ++=,则||b c -的取值范围是( )A .[0,2]B .[11]C .1-1]D .11]+11.(2022•浙江月考)已知向量,,a b c 满足||1,20,2||||a a b c a c b =+=-=-,则向量c b -与a 夹角的最大值是( ) A .12πB .6π C .4π D .3π 12.(2022•沙坪坝区期末)已知圆22(1)4C x y ++=,过点(0,)M m 的直线交圆于A ,B 两点,下列说法正确的是( )A .当1m =时,||AB 的最小值是 B .当m 时,||AM 的取值范围是[22+C .当2m =时,MA MB ⋅为定值D .当m =-||2||AB AM =时,120ACB ∠=︒13.(2016•四川)已知正三角形ABC 的边长为ABC 内的动点P ,M 满足||1AP =,PM MC =,则2||BM 的最大值是( )A .434B .494C D 14.(2022•祁东县期末)已知向量a ,b ,c 满足||3a =,||1b =,||7a b -=,||2||c c a =-.设()m tb t R =∈,则( )A .||m c -B .||m c -的最小值为2C .||m c -的最大值为2D .||m c -无最大值15.(2022•南京模拟)已知O 为坐标原点,向量,,OA OB OC ,满足||||||1OA OB OC ===,()()0OA OB OB OC -⋅-=,若||4OP =,则||PA PB PC ++的取值范围是( )A .[11,13]B .[8,11]C .[8,13]D .[5,11]16.(2022•仙游期中)已知向量,,a b c 满足:||1,()(),(2)a a c b c a a b =-⊥-⊥-,若37||2b =,||c 的最大值和最小值分别为m ,n ,则m n +等于( )A .32B C D 17.(2022•宝山区开学)已知a ,b 为单位向量,且a b ⊥,向量c 满足||2c a b --=,则||c 的范围为( )A .[1,1B .[2,2C .D .[3-,3+18.(2022•礼泉县开学)已知ABC ∆是边长为2的正三角形,点P 为平面内一点,且||3CP =,则()PC PA PB ⋅+的取值范围为 .19(2022•门头沟期末)已知向量,,a b c ,满足||2a =,||3b a b =⋅=,若2(2)()03c a c b -⋅-=,则||b c -的最小值是( )A .2B .23+C .1D .220.(2022•长沙月考)在平面上,12OB OB ⊥,12|||2MB MB ==12OP OB OB =+.若||1MP <,则||OM 的取值范围是 .21.(2022•浙江期中)已知a ,b 是两个单位向量,与a ,b 共面的向量c 满足2()0c a b c a b -+⋅+⋅=,则||c 的最大值为( )A .B .2CD .122.(2022•余姚期中)设平面向量,,a b c 满足||1a =,||2b =,1a b ⋅=,()()0a c b c -⋅-=,则|2|a c -的最大值为( )A B C D .223.(2022•浙江模拟)设a b c ,,为平面向量,||||2a b ==,若(2)()0c a c b -⋅-=,则c b ⋅的最大值为( )A .2B .94C .174D .524.(2022•苏州月考)已知平面向量a ,b ,c 满足||3a =,||2b =,a ,b 的夹角等于6π,且()()0a c b c --=,则||c 的取值范围是 .25.(2022•昆山月考)已知平面向量a ,b ,c 满足||||1a b ==,(2)a a b ⊥-,(2)()0c a c b --=,则||c 的最大值与最小值的和为 .。
巧用极化恒等式秒杀高考向量题冷世平整理说明:由于前几天,大家经常提到极化恒等式,本人便收集整理了一些相关资料,相对较系统,且加入了群里大家讨论的部分题目,由于相当一部分内容非原创,所以只和大家分享一下自己整理的好东西而已,故不作投稿使用。
高中数学中存在着大量等量关系,如立方差(和)公式、二项展开式、两角和与差公式等.在高中数学中常能见到这些等量关系的身影,这也是高中教学重点关注的对象.但有些等量关系看似冷门,甚至课本上都不出现,但它在问题解决过程中却能起到立竿见影的效果,实现对问题的快速“秒杀”,极化恒等式就是可以“秒杀”高考向量题的一个有力工具。
1.极化恒等式极化恒等式最初出现于高等数学中的泛函分析,它表示数量积可以由它诱导出的范数来表示,把这个极化恒等式降维至二维平面即得:21()()4a b a b a b 2⎡⎤⋅=+--⎣⎦ ,有时也可将其写成。
224()(a b a b a b ⋅=+-- )注:21()()4a b a b a b ⎡⋅=+--⎣ 2⎤⎦表明向量的内积运算可以由向量线性运算的模导出(也是向量内积的另一种定义),是沟通向量内积运算和线性运算的重要公式.若是实数,则恒等式,a b 21()()4a b a b a b ⎡⋅=+--⎣2⎤⎦也叫“广义平方差”公式; 极化恒等式的几何意义是:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14,即222214a b AD BC AM BM ⎡⎤⋅=-=-⎣⎦ (如图)在三角形中,也可以用三角形的中线来表示,22214a b AM BM AM BC ⋅=-=-2,它揭示了三角形的中线与边长的关系。
此恒等式的精妙之处在于建立起了向量与几何长度(数量)之间的桥梁,实现了向量与几何、代数的巧妙结合。
2.极化恒等式的应用自向量引入高中数学以后,由于它独特的性质(代数与几何的桥梁),在近几年全国各地的高考中迅速成为创新题命制的出发点,向量试题有着越来越综合,越来越灵活的趋势,在浙江省数学高考中尤为突出,也出现了一些非常精美的向量题。
例1在ABC ∆中,M 是BC 的中点,3,10AM BC ==,则______AB AC ⋅=(年浙江省数学高考理科试题第15题)2012【分析】该问题就是利用极化恒等式解决的极好范例,因为21925162AB AC AM BC ⋅=-=-=-。
下面我们再来看年浙江省数学高考选择题第题:20137例2设是边0,ABC P ∆AB 上一定点,满足014P B AB =,且对于边AB 上任一点,恒有P00PB PC P B P C ⋅≥⋅.90A ABC ∠= ,则.9B BAC ∠= 0.C AB AC = .D AC BC =(年浙江省数学高考选择题第题)20137【分析】考生普遍反映该题无从入手,笔者认为主要原因有2个:⑴该题呈现方式比较新颖;⑵学生解题工具使用不当,以致费时费力且不得要领。
【解析1】如图,取BC 的中点D ,连接,在内使用极化恒等式得0,PD P D PBC ∆22PB PC PD BD ⋅=- ,在内使用极化恒等式得,由条件知恒有0P BC ∆22BD - 00P C P D ⋅= 0P B 0P D ≥PD ,即,故0P D AB ⊥AC BC =,故选D 。
【解析2】如图,取线段BC 的中点M ,则22224()4()4PB PC PB PC PB PC PM BC ⋅=+--=- ,要使的值最小,只需PB PC ⋅ PM 取得最小值,所以只有当MP AB ⊥时,PM取得最小值,且点与点必须重合,P 0P M 是线段BC 的中点,只有时才能成立,故选AC BC =D 。
很多一线教师都认为这个题目在10个选择题中是最难的,应该放在压轴的位置,笔者却不这样认为,其实这个题目只是在例1的基础上对极化恒等式的应用灵活化,步子迈得更大一些而己,这个题目的姊妹题也出现在年浙江省高中数学联赛中:2013例3如图,已知直线与抛物线交于点为的中点,C 为抛物线上一个动点,若满足AB 24y =x ,,A B M AB 0C {}00A C B CA CB ⋅=⋅min C,则下列一定成立的是( )0.A C M AB ⊥ 0.B C M l ⊥,其中l 为抛物线过点的切线0C 00.C C A C B ⊥ 01.2D C M AB =(20年浙江省高中数学联赛试题)13【解析1】由{}00min C A C B CA CB ⋅=⋅得00CA CB C A C B ⋅≥⋅ 220C M 2y ⑴,由极化恒等式知式⑴等价于,即,即抛物线22CM AM 220C M AM -≥- CM ≥ 4x =上所有点到M 的距离最近的点即,故以0C M 为圆心,0MC 为半径的圆与抛物线内切,故选B 。
【解析2】2244CB CA CM AB ⋅=- ,因为AB 给定,显然要使CB CA ⋅ 最小,只需CM最小,即,其中l 是抛物线过点的切线。
0C M l ⊥0C 需要说明的是,命题组并没有说明l 是一条什么样的直线,其实直线是:当以定点l M 为圆心的圆与抛物线相切时的公切线。
24y =x 例4在正中,ABC ∆D 是BC 上的点,3,1AB BD ==,则______AB AD ⋅=(年上海市数学高考试题第11题)2011【分析】这是极化恒等式的直接变式范例。
【解析】设BD 的中点为E,则222222244AE 44113AB AD BD AO OE BD ⎡⎤⋅=-+-=+-=⎢⎥⎣⎦=,则152AB AD ⋅= 。
例5已知是平面内个互相垂直的单位向量,若向量,a b2c 满足()()a c b c 0-⋅-= ,则c 的最大值是( ).1A .2BC2D (年浙江省数学高考理科试题第题)20089【解析】本题从表面上看似乎和“极化恒等式”并没有关系,事实上,根据“极化恒等式”有,从而224()()()()()()a c b c a c b c a c b c ⎡⎤⎡-⋅-=-+-----⎣⎦⎣ ⎤⎦22()(22a b a b c +--=。
如图,设OA ,且为线段的中点,显然OB ⊥ ,,,OA a OB b OC c D ===AB 21,(222=a b a b a b ODDC c ++-==-=,上式表明,DC 是有固定起点,固定模长的动向量,即点C 的轨迹是以D 为起点,以2为半径的圆,因此,c ,故选C 。
事实上,类似的问题时有看到,只是很多时候用其他的方法取代了“极化恒等式”,或在无意中使用“极化恒等式”。
例6在中,是边ABC ∆2,3,AB AC D ==BC 的中点,则_____AD BC ⋅=(2年天津市数学高考文科试题第15题)007【解析】根据“极化恒等式”有2215()()22AB AC AD BC AC AB AC AB +⋅=⋅-=-=2。
本题的解决涉及到三角形的边及中线的关系,这可以看作是年浙江省数学高考试题第题的最初原型。
20137例7设正方形的边长为,动点在以为直径的圆弧ABCD 4P AB APB 上(如图所示),则 PC PD ⋅的取值范围是【解析】取CD 中点E ,联结,在PE PDC ∆内使用极化恒等式得2222144PC PD PE ED PE CD ⋅=-=-- 2PE = ,由图可知,PE ⎡∈⎣,故。
[]0,16PC PD ⋅∈ 例8在中,点ABC ∆,E F 分别是线段,AB AC 的中点,点在直线P EF 上,若的面积为2,则的最小值是 ABC ∆2PC PB BC ⋅+(年江苏省南京市数学高考模拟试题)2012【分析】如图,取BC 的中点D ,在内使用极化恒等式得PBC ∆22214PC PB PD BD PD ⋅=-=- 2BC ,从而22234PC PB BC PD BC ⋅+=+ ,因为的面积为,所以的高ABC ∆2ABC ∆4h BC =,又EF 为ABC ∆的中位线,故PBC ∆的高为2BC ,从而2PD BC≥,因此22PB BC ⋅+ 2434PC BC BC ≥+≥,BC BC ⊥PD =例9如图,在半径为1的扇形中, AOB 60,AOB C ∠=︒为弧上的动点,与OC 交于点,则的最小值为 AB P OP BP ⋅【解析】如图,取OB 的中点D ,作DE AB ⊥于点E ,根据极化恒等式21()()4a b a b a b 2⎡⎤⋅=+--⎣⎦ 可知,2222211()()(2)4414P PO PO PB PO PB PD BO PD ⎡⎤⎡⎤⋅==+-=-=-⎣⎦⎣⎦ OP B PB ⋅ -,易知,42PD DE ⎡⎤∈=⎢⎣⎦⎣⎦AD ,则2111,4162OP BP PD ⎡⎤⋅=-∈-⎢⎥⎣⎦ OP BP ,故⋅ 的最小值为116-。
其实本题只需要等边三角形的条件,外面的圆弧完全没用,本题还可以求的取值范围。
AOB OP BP ⋅例10如图放置的边长为1的正方形顶点分别在ABCD x 轴,y 轴正半轴(含原点)滑动,则OB 的最大值为 OC ⋅【解析】取BC 中点为点E ,连接,如图所示:,OB OC由极化恒等式可知,222214412OB OC OB OC OB OC OE ⋅=+--=-≤+-= 4(1)18,因而有。
2OB OC ⋅≤3.极化恒等式带来的反思⑴极化恒等式源于教材又高于教材,在ABC ∆中,11(),(22AD AB AC BD AC AB =+=-)是课本上出现的个重要的向量三角关系,而极化恒等式无非就是这个公式的逆用;22⑵具有三角几何背景的数学问题利用极化恒等式考虑尤为简单,让“秒杀向量”成为另一种可能; ⑶向量是连接代数与几何的桥梁,由于向量的坐标运算引入,向量与代数的互换运算可以说是深入人心,而与几何的运算联系略显单薄,而极化恒等式恰恰弥补了这个缺憾,可以说极化恒等式应该是把向量的数量积问题用形象的几何图形展示得淋漓尽致; ⑷实际上,“极化恒等式”在空间中同样可以发挥作用,下面举个例子。
2例11正方体1111ABCD A B C D -的棱长为2,MN 是它内切球的一条弦(把球面上任意个点之间的线段称为球的弦),为正方体表面上的动点,当弦2P MN 最长时,PM PN ⋅的最大值为_【解析】设球心为,球半径为O R ,则1R =,根据极化恒等式,得2244(2)PM PN PO R ⋅=-244PO = -,因为为正方体表面上的动点,所以P PO 的最大值为正方体对角线长的一半,,于是的最大值为。
PM PN ⋅2例12点是棱长为1的正方体P 1111ABCD A B C D -的底面1111A B C D 上一点,则PA PC ⋅的取值范围是 _(年北京市朝阳区高三数学二模试题)2013【解析】设AC 的中点为M ,根据“极化恒等式”得222444PA PC PM AC PM 2⋅=-=- ,因为32≤1PM ≤ ,所以112PA ≤⋅PC ≤。