解三角形应用举例
- 格式:doc
- 大小:489.85 KB
- 文档页数:9


解三角形应用举例一、测量距离问题例1(1)如图,A,B两点在河的同侧,且A,B两点均不可到达,要测出A,B 的距离,测量者可以在河岸边选定两点C,D,若测得CD=32km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为km.答案6 4解析∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,∴∠DAC=60°,∴AC=DC=32km.在△BCD中,∠DBC=180°-∠CDB-∠ACD-∠ACB=45°,由正弦定理,得BC=DCsin∠DBC·sin∠BDC=32sin 45°·sin 30°=64(km).在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BCcos 45°=34+38-2×32×64×22=38.∴AB=64km.∴A,B两点间的距离为64km.(2)如图,为了测量两座山峰上P,Q两点之间的距离,选择山坡上一段长度为300 3 m且和P,Q两点在同一平面内的路段AB的两个端点作为观测点,现测得∠PAB=90°,∠PAQ=∠PBA=∠PBQ=60°,则P,Q两点间的距离为m.答案900解析由已知,得∠QAB=∠PAB-∠PAQ=30°.又∠PBA=∠PBQ=60°,∴∠AQB=30°,∴AB=BQ.又PB为公共边,∴△PAB≌△PQB,∴PQ =PA.在Rt△PAB中,AP=AB·tan 60°=900(m),故PQ=900 m,∴P,Q两点间的距离为900 m.二、测量高度问题例2如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为30°,45°,且A,B 两点间的距离为60 m,则树的高度为m.答案30+30 3解析在△PAB中,∠PAB=30°,∠APB =15°,AB=60 m,sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=22×32-22×12=6-2 4,由正弦定理得PB sin 30°=AB sin 15°, 所以PB =12×606-24=30(6+2), 所以树的高度为PB ·sin 45°=30(6+2)×22=(30+303)(m ). 三、测量角度问题例3 已知岛A 南偏西38°方向,距岛A 3海里的B 处有一艘缉私艇.岛A 处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶,问缉私艇朝何方向以多大速度行驶,恰好用0.5小时能截住该走私船?⎝⎛⎭⎫参考数据:sin 38°≈5314,sin 22°≈3314 解 如图,设缉私艇在C 处截住走私船,D 为岛A 正南方向上一点,缉私艇的速度为x 海里/小时,结合题意知BC =0.5x ,AC =5,∠BAC =180°-38°-22°=120°.由余弦定理可得BC 2=AB 2+AC 2-2AB ·ACcos 120°,所以BC 2=49,所以BC =0.5x =7, 解得x =14.又由正弦定理得sin ∠ABC =AC ·sin ∠BAC BC=5×327=5314, 所以∠ABC =38°,又∠BAD =38°,所以BC ∥AD ,故缉私艇以14海里/小时的速度向正北方向行驶,恰好用0.5小时截住该走私船. 素养提升 数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并且用数学符号或数学术语予以表征.从实际问题中抽象出距离、高度、角度等数学问题,然后利用正弦定理、余弦定理求解,很好地体现了数学抽象的数学素养.。



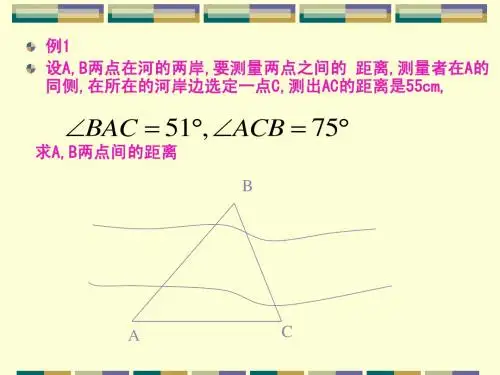
解三角形(4)---解三角形应用举例例1、如图,设A 、B 两点在河的两岸,要测量两点之间的距离,测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离是55m ,∠BAC=︒51,∠ACB=︒75.求A 、B 两点的距离(精确到0.1m )启发提问1:∆ABC 中,根据已知的边和对应角,运用哪个定理比较适当?启发提问2:运用该定理解题还需要那些边和角呢?分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了边AB 的对角,AC 为已知边,再根据三角形的内角和定理很容易根据两个已知角算出AC 的对角,应用正弦定理算出AB 边。
解:根据正弦定理,得ACB AB ∠sin = ABCAC ∠sin AB =ABC ACB AC ∠∠sin sin =ABC ACB ∠∠sin sin 55 = )7551180sin(75sin 55︒-︒-︒︒ =︒︒54sin 75sin 55 ≈ 65.7(m) 答:A 、B 两点间的距离为65.7米变式练习:两灯塔A 、B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东30︒,灯塔B 在观察站C 南偏东60︒,则A 、B 之间的距离为多少?(画图建立数学模型。
答案:2a km )例2、如图,A 、B 两点都在河的对岸(不可到达),设计一种测量A 、B 两点间距离的方法。
分析:这是例1的变式题,研究的是两个不可到达的点之间的距离测量问题.首先需要构造三角形,所以需要确定C 、D 两点.根据正弦定理中已知三角形的任意两个内角与一边既可求出另两边的方法,分别求出AC 和BC ,再利用余弦定理可以计算出AB 的距离.解:测量者可以在河岸边选定两点C 、D ,测得CD=a ,并且在C 、D 两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA =δ,在∆ADC 和∆BDC 中,应用正弦定理得:AC = )](180sin[)sin(δγβδγ++-︒+a = )sin()sin(δγβδγ+++a BC = )](180sin[sin γβαγ++-︒a = )sin(sin γβαγ++a 计算出AC 和BC 后,再在∆ABC 中,应用余弦定理计算出AB 两点间的距离AB =αcos 222BC AC BC AC ⨯-+ 分组讨论:还没有其它的方法呢?变式训练:若在河岸选取相距40米的C、D两点,测得∠BCA=60︒,∠ACD=30︒,∠CDB=45︒,∠BDA =60︒(画图建立数学模型。





解三角形的应用举例主讲:黄冈中学高级教师汤彩仙一、知识概述1、基线:在测量上,根据测量需要适当确定的线段叫做基线.2、仰角和俯角:在视线和水平线所成角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角,如图.3、坡度:坡向与水平向的夹角,如图.4、方位角:指从正北方向顺时针转到目标方向线所成的角,如图中B点的方位角为α.5、方向角:从指定方向线到目标方向线所成的小于90°的水平角,如南偏西60°,指以正南方向为始边,顺时针方向向西旋转60°.如图中∠ABC为北偏东60°或为东偏北30°.二、例题讲解例1、某渔轮在航行中不幸遇险,发出呼叫信号,我海军军舰在A处获悉后,立即测出该渔轮在方位角为45°距离为10海里的C处,并测得渔轮正沿方位角为105°的方向,以9海里/小时的速度向小岛靠拢,我海军军舰立即以21海里/小时的速度前去营救,求军舰的航向和靠近渔轮所需的时间.解:如图,设所需的时间为t小时,则,∠ACB=45°+75°=120°.在中,根据余弦定理,则有:,可得,.解得或(舍).又所以军舰应以方位角为航行,且靠近渔轮需要小时.例2、在某定点A测得一船初始位置B在A的北偏西度,10分钟后船在A的正北,又过了10分钟后船到达A的北偏东度,若船的航向与速度都不变,航向为北偏东度,求的正切值.解:如图,在中,由正弦定理得,又,故,即①在中,由正弦定理得,即②由题意,有,由①②得.整理得..即,∴.例3、如果,某观测站C在城A的南偏西20°的方向上,由A城出发有一公路,走向是南偏东40°,在C 处测得距C为31公里的公路上B处,有一人正沿公路向A城走去,走了20公里后,到达D处,此时C、D间距离为21公里,问此人还需走多少公里到达A城.解:法一:设AD=x,AC=y,则解得x=15(负值舍掉).法二:.法三:作CE⊥AD于E,则,.根据余弦定理,.则.。
第三章三角函数、三角恒等变换及解三角形第8课时解三角形应用举例1. (必修5P11习题4改编)若海上有A、B、C三个小岛,测得A,B两岛相距10海里,∠BAC=60°,∠ABC=75°,则B、C间的距离是________海里.答案:5 6解析:由正弦定理,知BCsin60°=ABsin(180°-60°-75°),解得BC=56(海里).2. (必修5P20练习第4题改编)江岸边有一炮台高30 m,江中有两条船,船与炮台底部在同一水面上,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距________m.答案:10 3解析:如图,OA为炮台,M、N为两条船的位置,∠AMO=45°,∠ANO=60°,OM=AOtan45°=30,ON=AOtan30°=33×30=103,由余弦定理,得MN=900+300-2×30×103×32=300=103(m).3. (必修5P18例1改编)如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40 m的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB 的距离是__________ m.答案:20 6解析:由已知知△BDC为等腰直角三角形,故DB=40;由∠ACB=60°和∠ADB=60°知A、B、C、D四点共圆,所以∠BAD=∠BCD=45°;在△BDA 中,运用正弦定理可得AB =20 6. 4. (必修5P 21习题2改编)某人在C 点测得塔顶A 在南偏西80°,仰角为45°,此人沿南偏东40°方向前进10 m 到D ,测得塔顶A 的仰角为30°,则塔高为________m.答案:10解析:如图,设塔高为h ,在Rt △AOC 中,∠ACO =45°,则OC =OA =h. 在Rt △AOD 中,∠ADO =30°,则OD =3h. 在△OCD 中,∠OCD =120°,CD =10.由余弦定理得OD 2=OC 2+CD 2-2OC·CD cos ∠OCD , 即(3h)2=h 2+102-2h×10×cos120°,∴ h 2-5h -50=0,解得h =10或h =-5(舍).5. 如图,一船在海上自西向东航行,在A 处测得某岛M 的方位角为北偏东α角,前进mkm 后在B 处测得该岛的方位角为北偏东β角,已知该岛周围nkm 范围内(包括边界)有暗礁,现该船继续东行.当α与β满足条件________时,该船没有触礁危险.答案:mcos αcos β>nsin (α-β)解析:∠MAB=90°-α,∠MBC =90°-β=∠MAB+∠AMB=90°-α+∠AMB,∴ ∠AMB =α-β.由题可知,在△ABM 中,根据正弦定理得BM sin (90°-α)=msin (α-β),解得BM =mcos αsin (α-β).要使船没有触礁危险,需要BMsin(90°-β)=mcos αcos βsin (α-β)>n ,所以α与β满足mcos αcos β>nsin (α-β)时船没有触礁危险.1. 用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等. 2. 实际问题中的常用角 (1) 仰角和俯角与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方的角叫仰角,目标视线在水平视线下方的角叫俯角(如图①).(2) 方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°,西偏北60°等.(3) 方位角:指从正北方向顺时针转到目标方向线的水平角,如B 点的方位角为α(如图②).(4) 坡度:坡面与水平面所成的二面角的度数.[备课札记]题型1 测量距离问题例1 要测量河对岸A 、B 两点之间的距离,选取相距 3 km 的C 、D 两点,并且测得∠ACB =75°,∠BCD =45°,∠ADC =30°,∠ADB =45°,求A 、B 之间的距离.解:△ACD 中,∠ACD =120°,∠CAD =∠ADC=30°,∴ AC =CD = 3 km.在△BCD 中,∠BCD =45°,∠BDC =75°,∠CBD =60°,∴ BC =3sin75°sin60°=6+22.在△ABC 中,由余弦定理得AB 2=AC 2+BC 2-2AC·BC·cos ∠ACB =(3)2+⎝ ⎛⎭⎪⎫6+222-2·3·6+22cos75°=5,∴ AB = 5 km.故A 、B 之间的距离为 5 km.变式训练 设A 、B 两点在河的两岸,一测量者在A 所在的河岸边选定一点C ,测出AC 的距离为50m ,∠ACB =45°,∠CAB =105°,求A 、B 两点的距离.解:由题意知∠ABC=30°,由正弦定理AC sin ∠ABC =ABsin ∠ACB ,得AB =AC·sin ∠ACBsin ∠ABC=50×2212=50 2 m.故A 、B 两点的距离为50 2 m. 题型2 测量高度问题例2 某兴趣小组要测量电视塔AE 的高度H(单位:m)如图所示,垂直放置的标杆BC 的高度h =4 m ,仰角∠ABE=α,∠ADE =β.(1) 该小组已测得一组α、β的值,算出了tan α=1.24,tan β=1.20,请据此算出H 的值;(2) 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125 m ,试问d 为多少时,α-β最大?解:(1) 由AB =H tan α,BD =h tan β,AD =H tan β及AB +BD =AD ,得H tan α+h tan β=Htan β,解得H =htan αtan α-tan β=4×1.241.24-1.20=124.因此,算出的电视塔的高度H 是124 m. (2) 由题设知d =AB ,得tan α=Hd.由AB =AD -BD =H tan β-h tan β,得tan β=H -hd,所以tan (α-β)=tan α-tan β1+tan αtan β=h d +H (H -h )d≤h2H (H -h ),当且仅当d =H (H -h )d ,即d =H (H -h )=125×(125-4)=555时,上式取等号.所以当d =555时,tan (α-β)最大.因为0<β<α<π2,则0<α-β<π2,所以当d=555时,α-β最大.故所求的d 是555m.备选变式(教师专享)如图所示,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ,现测得∠BCD=α,∠BDC =β,CD =s ,并在点C 测得塔顶A 的仰角为θ,求塔高AB.解:在△BCD 中,∠CBD =π-α-β,由正弦定理得BC sin ∠BDC =CDsin ∠CBD ,所以BC =CD·sin ∠BDC sin ∠CBD =s·sin βsin (α+β).在Rt △ABC 中,AB =BCtan ∠ACB =s·tan θsin βsin (α+β).题型3 测量角度问题例3 在海岸A 处,发现北偏西75°的方向,距离A 2海里的B 处有一艘走私船,在A 处北偏东45°方向,距离A (3-1)海里的C 处的缉私船奉命以103海里/小时的速度追截走私船.此时,走私船正以10海里/小时的速度从B 向北偏西30°方向逃窜,问缉私船沿什么方向能最快追上走私船?解:由已知条件得,AB =2,AC =3-1,∠BAC =120°,∴ BC =AB 2+AC 2-2AB·AC·cos ∠BAC =4+4-23+23-2= 6.在△ABC 中,AB sin ∠ACB =BCsin ∠BAC ,解得sin ∠ACB =22,∴ ∠ACB =45°, ∴ BC 为水平线,设经过时间t 小时后,缉私船追上走私船,则在△BCD 中, BD =10t ,CD =103t ,∠DBC =120°,sin ∠BCD =BDsin ∠CBDCD =10t ×32103t=12,∴ ∠BCD =30°,∴ 缉私船沿北偏西60°的方向能最快追上走私船. 备选变式(教师专享)如图,渔船甲位于岛屿A 的南偏西60°方向的B 处,且与岛屿A 相距12海里,渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行,若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙,刚好用2 h 追上,此时到达C 处.(1) 求渔船甲的速度; (2) 求sin α的值.解:(1) 依题意知,∠BAC =120°,AB =12海里,AC =10×2=20海里,∠BCA =α.在△ABC 中,由余弦定理,得BC 2=AB 2+AC 2-2AB·AC·cos ∠BAC =122+202-2×12×20×cos120°=784,解得BC =28海里.所以渔船甲的速度为BC2=14海里/小时.(2) 在△ABC 中,因为AB =12海里,∠BAC =120°,BC =28海里,∠BCA =α,由正弦定理,得AB sin α=BCsin120°.即sin α=AB·sin120°BC =12×3228=3314.1. 在△ABC 中,若sin 2A +sin 2B <sin 2C ,则△ABC 的形状是________.答案:钝角三角形解析:由正弦定理可把不等式转化为a 2+b 2<c 2,cosC =a 2+b 2-c22ab<0,所以三角形为钝角三角形.2. 已知△ABC 的三边长成公比为2的等比数列,则其最大角的余弦值为________.答案:-24解析:设最小边为a ,则其他两边分别为2a ,2a.由余弦定理,得最大角的余弦值为cos α=a 2+(2a )2-(2a )22a ×(2a )=-24.3. (2013·上海一模)一人在海面某处测得某山顶C 的仰角为α(0°<α<45°),在海面上向山顶的方向行进m m 后,测得山顶C 的仰角为90°-α,则该山的高度为________m .(结果化简)答案:12mtan2α解析:由题意知∠CAB=α,∠CDB =90°-α,∠CDA =90°+α,且AD =m ,则∠ACD =90°-2α.由正弦定理得AD sin (90°-2α)=AC sin (90°+α),即m cos2α=ACcos α,即AC =mcos αcos2α,所以山高BC =ACsin α=msin αcos αcos2α=12mtan2α.4. 已知△ABC 中,AB 边上的高与AB 边的长相等,则AC BC +BC AC +AB 2BC ·AC 的最大值为________.答案:2 2解析:AC BC +BC AC +AB 2BC ·AC =AC 2+BC 2+AB 2BC ·AC .又AC 2+BC 2=AB 2+2AC·BC·cosC , ∴ 原式=2cosC +2AB 2BC ·AC =2cosC +4S △ABCBC ·AC=2cosC +2BC·AC·sinCBC ·AC=2cosC +2sinC=22sin ⎝⎛⎭⎪⎫C +π4,∴ 当C =π4时,最大值为2 2.1. 某人在汽车站M 的北偏西20°的方向上的A 处(如图所示),观察到C 处有一辆汽车沿公路向M 站行驶,公路的走向是M 站的北偏东40°.开始时,汽车到A 处的距离为31 km ,汽车前进20 km 后,到A 处的距离缩短了10 km.问汽车还需行驶多远,才能到达汽车站M?解:设汽车前进20 km 后到达B 处,在△ABC 中,AC =31,BC =20,AB =21,由余弦定理,得cosC =AC 2+BC 2-AB 22AC ·BC =2331,则sinC =12331.所以sin ∠MAC =sin ()120°-C =sin120°cosC -cos120°sinC =35362.在△MAC 中,由正弦定理,得MC =AC·sin ∠MACsin ∠AMC=31×3536232=35,从而有MB =MC -BC =15 km. 答:汽车还需行驶15 km ,才能到达汽车站M.2. 某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O 北偏西30°且与该港口相距20海里的A 处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v 海里/时的航行速度匀速行驶,经过t 小时与轮船相遇.(1) 若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2) 假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.解:(1) 设相遇时小艇航行的距离为S 海里,则S =900t 2+400-2·30t·20·cos (90°-30°)=900t 2-600t +400 =900⎝ ⎛⎭⎪⎫t -132+300 . 故当t =13时,S min =10 3 海里,此时v =10313=30 3 海里/时.即小艇以303海里/时的速度航行,相遇时小艇的航行距离最小. (2) 设小艇与轮船在B 处相遇,则v 2t 2=400+900t 2-2·20·30t·cos(90°-30°),故v 2=900-600t +400t 2.∵ 0<v≤30,∴ 900-600t +400t 2≤900,即2t 2-3t ≤0,解得t≥23.又t =23时,v =30海里/时.故v =30海里/时时,t 取得最小值,且最小值等于23.此时,在△OAB 中,有OA =OB =AB =20海里,故可设计航行方案如下:航行方向为北偏东30°,航行速度为30海里/时,小艇能以最短时间与轮船相遇.3. 如图,A 、B 是海面上位于东西方向相距5(3+3)海里的两个观测点,现位于A 点北偏东45°、B 点北偏西60°的D 点有一艘轮船发出求救信号,位于B 点南偏西60°且与B 点相距203海里的C 点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D 点需要多长时间?解:由题意知AB =5(3+3)海里,∠DBA =90°-60°=30°,∠DAB =90°-45°=45°,所以∠ADB=180°-(45°+30°)=105°.在△ADB 中,由正弦定理得DBsin ∠DAB =AB sin ∠ADB ,所以DB =AB·sin ∠DAB sin ∠ADB =5(3+3)·sin45°sin105°=5(3+3)·sin45°sin45°cos60°+cos45°sin60°=103海里.又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC =203海里,在△DBC 中,由余弦定理得CD 2=BD 2+BC 2-2BD·BC·cos ∠DBC =300+1 200-2×103×203×12=900,所以CD =30海里,则需要的时间t =3030=1 h .所以救援船到达D 点需要1 h.4. 如图,半圆O 的直径为2,A 为直径延长线上的一点,OA =2,B 为半圆上任意一点,以AB 为一边作等边三角形ABC.问:点B 在什么位置时,四边形OACB 面积最大?解:设∠AOB=α,在△AOB 中,由余弦定理得AB 2=OA 2+OB 2-2×OA×OBcos∠AOB=12+22-2×1×2×cosα=5-4cosα,于是,四边形OACB 的面积为S =S △AOB + S △ABC =12OA ·OBsin α+34AB 2=12×2×1×sin α+34(5-4cosα) =sinα-3cos α+534=2sin ⎝⎛⎭⎪⎫α-π3+534.因为0<α<π,所以当α-π3=π2,α=5π6,即∠AOB=5π6时,四边形OACB面积最大.1. (1) 利用示意图把已知量和待求量尽量集中在有关的三角形中,建立一个解三角形的模型.(2) 利用正、余弦定理解出所需要的边和角,求得该数学模型的解.(3) 应用题要注意作答.2. (1) 测量高度时,要准确理解仰、俯角的概念.(2) 分清已知和待求,分析(画出)示意图,明确在哪个三角形中应用正、余弦定理.(3) 注意竖直线垂直于地面构成的直角三角形.请使用课时训练(A)第8课时(见活页).[备课札记]。