解三角形应用举例
- 格式:doc
- 大小:223.00 KB
- 文档页数:6


解三角形应用举例一、测量距离问题例1(1)如图,A,B两点在河的同侧,且A,B两点均不可到达,要测出A,B 的距离,测量者可以在河岸边选定两点C,D,若测得CD=32km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为km.答案6 4解析∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,∴∠DAC=60°,∴AC=DC=32km.在△BCD中,∠DBC=180°-∠CDB-∠ACD-∠ACB=45°,由正弦定理,得BC=DCsin∠DBC·sin∠BDC=32sin 45°·sin 30°=64(km).在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BCcos 45°=34+38-2×32×64×22=38.∴AB=64km.∴A,B两点间的距离为64km.(2)如图,为了测量两座山峰上P,Q两点之间的距离,选择山坡上一段长度为300 3 m且和P,Q两点在同一平面内的路段AB的两个端点作为观测点,现测得∠PAB=90°,∠PAQ=∠PBA=∠PBQ=60°,则P,Q两点间的距离为m.答案900解析由已知,得∠QAB=∠PAB-∠PAQ=30°.又∠PBA=∠PBQ=60°,∴∠AQB=30°,∴AB=BQ.又PB为公共边,∴△PAB≌△PQB,∴PQ =PA.在Rt△PAB中,AP=AB·tan 60°=900(m),故PQ=900 m,∴P,Q两点间的距离为900 m.二、测量高度问题例2如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为30°,45°,且A,B 两点间的距离为60 m,则树的高度为m.答案30+30 3解析在△PAB中,∠PAB=30°,∠APB =15°,AB=60 m,sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=22×32-22×12=6-2 4,由正弦定理得PB sin 30°=AB sin 15°, 所以PB =12×606-24=30(6+2), 所以树的高度为PB ·sin 45°=30(6+2)×22=(30+303)(m ). 三、测量角度问题例3 已知岛A 南偏西38°方向,距岛A 3海里的B 处有一艘缉私艇.岛A 处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶,问缉私艇朝何方向以多大速度行驶,恰好用0.5小时能截住该走私船?⎝⎛⎭⎫参考数据:sin 38°≈5314,sin 22°≈3314 解 如图,设缉私艇在C 处截住走私船,D 为岛A 正南方向上一点,缉私艇的速度为x 海里/小时,结合题意知BC =0.5x ,AC =5,∠BAC =180°-38°-22°=120°.由余弦定理可得BC 2=AB 2+AC 2-2AB ·ACcos 120°,所以BC 2=49,所以BC =0.5x =7, 解得x =14.又由正弦定理得sin ∠ABC =AC ·sin ∠BAC BC=5×327=5314, 所以∠ABC =38°,又∠BAD =38°,所以BC ∥AD ,故缉私艇以14海里/小时的速度向正北方向行驶,恰好用0.5小时截住该走私船. 素养提升 数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并且用数学符号或数学术语予以表征.从实际问题中抽象出距离、高度、角度等数学问题,然后利用正弦定理、余弦定理求解,很好地体现了数学抽象的数学素养.。


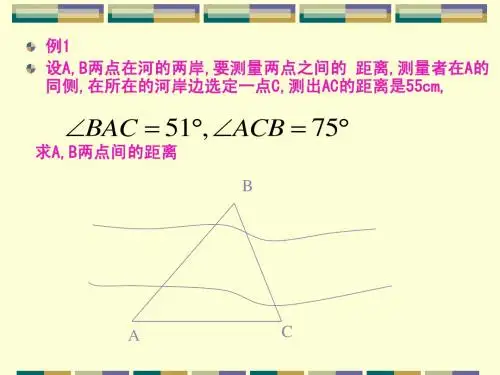
解三角形(4)---解三角形应用举例例1、如图,设A 、B 两点在河的两岸,要测量两点之间的距离,测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离是55m ,∠BAC=︒51,∠ACB=︒75.求A 、B 两点的距离(精确到0.1m )启发提问1:∆ABC 中,根据已知的边和对应角,运用哪个定理比较适当?启发提问2:运用该定理解题还需要那些边和角呢?分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了边AB 的对角,AC 为已知边,再根据三角形的内角和定理很容易根据两个已知角算出AC 的对角,应用正弦定理算出AB 边。
解:根据正弦定理,得ACB AB ∠sin = ABCAC ∠sin AB =ABC ACB AC ∠∠sin sin =ABC ACB ∠∠sin sin 55 = )7551180sin(75sin 55︒-︒-︒︒ =︒︒54sin 75sin 55 ≈ 65.7(m) 答:A 、B 两点间的距离为65.7米变式练习:两灯塔A 、B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东30︒,灯塔B 在观察站C 南偏东60︒,则A 、B 之间的距离为多少?(画图建立数学模型。
答案:2a km )例2、如图,A 、B 两点都在河的对岸(不可到达),设计一种测量A 、B 两点间距离的方法。
分析:这是例1的变式题,研究的是两个不可到达的点之间的距离测量问题.首先需要构造三角形,所以需要确定C 、D 两点.根据正弦定理中已知三角形的任意两个内角与一边既可求出另两边的方法,分别求出AC 和BC ,再利用余弦定理可以计算出AB 的距离.解:测量者可以在河岸边选定两点C 、D ,测得CD=a ,并且在C 、D 两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA =δ,在∆ADC 和∆BDC 中,应用正弦定理得:AC = )](180sin[)sin(δγβδγ++-︒+a = )sin()sin(δγβδγ+++a BC = )](180sin[sin γβαγ++-︒a = )sin(sin γβαγ++a 计算出AC 和BC 后,再在∆ABC 中,应用余弦定理计算出AB 两点间的距离AB =αcos 222BC AC BC AC ⨯-+ 分组讨论:还没有其它的方法呢?变式训练:若在河岸选取相距40米的C、D两点,测得∠BCA=60︒,∠ACD=30︒,∠CDB=45︒,∠BDA =60︒(画图建立数学模型。






解三角形的应用举例主讲:黄冈中学高级教师汤彩仙一、知识概述1、基线:在测量上,根据测量需要适当确定的线段叫做基线.2、仰角和俯角:在视线和水平线所成角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角,如图.3、坡度:坡向与水平向的夹角,如图.4、方位角:指从正北方向顺时针转到目标方向线所成的角,如图中B点的方位角为α.5、方向角:从指定方向线到目标方向线所成的小于90°的水平角,如南偏西60°,指以正南方向为始边,顺时针方向向西旋转60°.如图中∠ABC为北偏东60°或为东偏北30°.二、例题讲解例1、某渔轮在航行中不幸遇险,发出呼叫信号,我海军军舰在A处获悉后,立即测出该渔轮在方位角为45°距离为10海里的C处,并测得渔轮正沿方位角为105°的方向,以9海里/小时的速度向小岛靠拢,我海军军舰立即以21海里/小时的速度前去营救,求军舰的航向和靠近渔轮所需的时间.解:如图,设所需的时间为t小时,则,∠ACB=45°+75°=120°.在中,根据余弦定理,则有:,可得,.解得或(舍).又所以军舰应以方位角为航行,且靠近渔轮需要小时.例2、在某定点A测得一船初始位置B在A的北偏西度,10分钟后船在A的正北,又过了10分钟后船到达A的北偏东度,若船的航向与速度都不变,航向为北偏东度,求的正切值.解:如图,在中,由正弦定理得,又,故,即①在中,由正弦定理得,即②由题意,有,由①②得.整理得..即,∴.例3、如果,某观测站C在城A的南偏西20°的方向上,由A城出发有一公路,走向是南偏东40°,在C 处测得距C为31公里的公路上B处,有一人正沿公路向A城走去,走了20公里后,到达D处,此时C、D间距离为21公里,问此人还需走多少公里到达A城.解:法一:设AD=x,AC=y,则解得x=15(负值舍掉).法二:.法三:作CE⊥AD于E,则,.根据余弦定理,.则.。
东方中学教案
1.知识与技能:
会在各种应用问题中,抽象或构造出三角形,标出已知量、未知量,确定解三角形的方法;搞清利用解斜三角形可解决的各类应用问题的基本图形和基本等量关系;理解各种应用问题中的有关名词、术语,如:坡度、俯角、仰角、方向角、方位角等;通过解三角形的应用的学习,提高解决实际问题的能力
2.过程与方法:
通过巧妙的设疑,顺利的引导新课,为下节课做好铺垫。
结合学生的实际情况,采用“提出问题—引发思考—探索猜想—总结规律—反馈练习”的教学过程,根据大纲要求以及教学内容之间的内在联系,铺开例题,设计变式,同时通过多媒体、图形观察等直观演示,帮助学生掌握在各种应用问题中,抽象或构造出三角形,标出已知量、未知量,确定解三角形的方法。
3.情感、态度与价值观:
实际问题中抽象出一个或几个三角形,然后逐个解三角形,得到实际问题的解。
修改简记教学过程:
一、复习引入:
二、讲解范例:
例1 自动卸货汽车的车箱采用液压结构,设计时需要计算
油泵顶杆BC的长度已知车箱的最大仰角为60°,油泵顶点
B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角
为6°20′,AC长为1.40m,计算BC的长(保留三个有效数字)
分析:求油泵顶杆BC的长度也就是在△ABC内,求边长BC的问题,而根据已知条件,
AC=1.40m,AB=1.95 m,∠BAC=60°+6°20′=66°20′相当于已知△ABC
的两边和它们的夹角,所以求解BC可根据余弦定理解:由余弦定理,得
BC2=AB2+AC2-2AB·AC cos A
=1.952+1.402-2×1.95×1.40×cos66°20′=3.571
∴BC≈1.89 (m)
答:油泵顶杆B C约长1.89 m
评述:此题虽为解三角形问题的简单应用,但关键是把未知边所处的三角形找到,在转
换过程中应注意“仰角”这一概念的意义,并排除题目中非数学因素的干扰,将数量关系
从题目准确地提炼出来
例2某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A处获悉后,立即测出该渔
船在方位角为45°、距离A为10海里的C处,并测得渔船正沿方位角为105°的方向,
以9海里/h的速度向某小岛B靠拢,我海军舰艇立即以21海里/h的速度前去营救,
试问舰艇应按照怎样的航向前进?并求出靠近渔船所用的时间
分析:设舰艇从A 处靠近渔船所用的时间为x h,则利用余弦定理建立方程来解决
较好,因为如图中的∠1,∠2可以求出,而AC 已知,BC 、AB 均可用x表示,故可看成是 一个已知两边夹角求第三边问题
解:设舰艇从A 处靠近渔船所用的时间为xh,则AB =21x海里,BC =9x 海里, AC =10 海里,∠ACB =∠1+∠2=45°+(180°-105°)=120°, 根据余弦定理,可得
AB 2=AC 2+BC 2-2AC ·BC ·cos120°得
(21x)2=102+(9x)2
-2×10×9xcos120°,
即36x2-9x2
×10=0
解得x1=
32,x2=-12
5 (舍去) ∴AB =21x=14,BC =9x=6
再由余弦定理可得
cos ∠BAC =
,9286.010
1426101422
22222=⨯⨯-+=⋅⋅-+AC AB BC AC AB ∴∠BAC =21°47′,45°+21°47′=66°47′
所以舰艇方位角为66°47′,
3
2
小时即40分钟
答:舰艇应以66°47′的方位角方向航行,靠近渔船则需要40分钟
评述:解好本题需明确“方位角”这一概念,方位角是指由正北方向顺时针旋转到目标 方向线的水平角,其范围是(0°,360°)
在利用余弦定理建立方程求出x后,所求舰艇方位角就转化为一个已知三边求角的 问题,故仍然利余弦定理
例3用同样高度的两个测角仪AB 和CD 同时望见气球E 在它们的正西方向的上空,分别 测得气球的仰角是α和β,已知B 、D 间的距离为a ,测角仪的高度是b ,求气球的高度 分析:在Rt △EGA 中求解EG ,只有角α一个条件,需要再有一边长被确定,而△EAC 中 有较多已知条件,故可在△EAC 中考虑EA 边长的求解,而在△EAC 中有角β, ∠EAC =180°-α两角与BD =a 一边,故可以利用正弦定理求解EA 解:在△ACE 中,AC =BD =a ,∠ACE =β,∠AEC =α-β,
根据正弦定理,得AE =
)
sin(sin βαβ
-a
在Rt △AEG 中,EG =AE sin α=
)
sin(sin sin βαβ
α-a
∴EF =EG +b =
)sin(sin sin βαβ
α-a +b ,
答:气球的高度是
)
sin(sin sin βαβ
α-a +b
评述:此题也可以通过解两个直角三角形来解决,思路如下:设 EG =x,在Rt △EGA 中用cot α表示AG ;在Rt △EGC 中,利
用cot β表示CG ,而CG -AG =CA =BD =a ,故可以求出EG ,又 GF =CD =b ,故EF 高度可求
例4如图所示,已知半圆的直径AB =2,点C 在AB 的延长线上,BC =1,点P 为半圆上 的一个动点,以DC 为边作等边△PCD ,且点D 与圆心O 分别在PC 的两侧,求四边形OPDC
面积的最大值
分析:要求四边形OPDC 面积的最大值,这首先需要建立一个面积函数,问题是选谁 作为自变量,注意到动点P 在半圆上运动与∠POB 大小变化之间的联系,自然引入∠POB = θ作为自变量建立函数关系四边形OPDC 可以分成△OPC 与等边△PDC ,S△OPC
可用
2
1
·OP ·OC ·sin θ表示,而等边△PDC 的面积关键在于边长求解,而边长PC 可以 在△POC 中利用余弦定理表示,至于面积最值的获得,则通过三角函数知识解决
解:设∠POB =θ,四边形面积为y,则在△POC 中,由余弦定理得: PC 2=OP 2+OC 2-2OP ·OC cos θ=5-4cos θ
∴y=S△OPC +S△PCD =
θsin 212
1
⨯⨯+43(5-4cos θ) =2sin(θ-
3
π
)+435
∴当θ-
3π=2
π
即θ=65π时,ymax =2+435
评述:本题中余弦定理为表示△PCD 的面积,从而为表示四边形OPDC 面积提供了可能,
可见正、余弦定理不仅是解三角形的依据,一般地也是分析几何量之间关系的重要公式,要 认识到这两个定理的重要性
另外,在求三角函数最值时,涉及到两角和正弦公式sin (α+β)=sin αcos β+ cos αsin β的构造及逆用,应要求学生予以重视
三、课堂练习:
1如图,在海岸A 处发现北偏东45°方向,距A 处(3-1)海里的B 处有一艘走私船在
A 处北偏西75°方向,距A 处2海里的C 处的我方缉私船,奉命以103海里/时的速度
追截走私船,此时走私船正以10海里/时的速度,从B 处向北偏东30°方向逃窜 问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间 解:设辑私船应沿CD 方向行驶t小时,才能最快截获(在D 点)走私船,
则CD =103t海里,BD =10t海里
∵BC 2
=AB 2
+AC 2
-2AB ·AC ·cos A
=(3-1)2+22
-2(3-1)·2cos120°=6, ∴BC =6
22
6120sin 2sin sin sin sin =
︒=⋅=∴=
BC A AC ABC ABC
AC
A BC
∴∠ABC =45°,∴B 点在C 点的正东方向上,
∠CBD =90°+30°=120°
,
21
310120sin 10sin sin sin sin =︒⋅=⋅=∴=
t t CD CBD BD BCD CBD
CD
BCD BD
∠BCD =30°,∴∠DCE =90°-30°=60°
由∠CBD =120°,∠BCD =30°得∠D =30°
∴BD =BC ,即10t=6
∴t=
10
6
(小时)≈15(分钟) 答:辑私船沿北偏东60°的方向行驶,才能最快截获走私船,需时约15分钟 四、小结
通过本节学习,要求大家在了解解斜三角形知识在实际中的应用的同时,掌握由实际 问题向数学问题的转化,并提高解三角形问题及实际应用题的能力。