桁架的有限元分析

桁架的有限元分析问题：已知模型由轨座，桁架以及垫块三个部分组成。

载荷为186吨，加载与距中间400mm 处的轨座上。

材料为Q345钢，密度为33/108.7m kg ⨯，弹性模量为5102⨯MPa ，泊松比为0.3，摩擦系数为0.05。

要求对模型使用ANSYS 进行有限元分析，分析其安全性。

问题分析：模型是对称的，可以简化模型，用模型的四分之一进行ANSYS 有限元分析，可以减少计算量。

需要在两个剖面处施加对称约束，从而保证中间部分不发生位移。

垫块的底部需要添加一个全约束以防止刚体位移。

图1为简化的模型。

图1 模型建模以及运算1将模型导入将所给的模型文件dggl.sat 导入到ANSYS 中，补充完整模型，即添加垫块。

再将模型分割，得到简化后的模型，即图1。

2 划分网格将轨座和桁架分割成规整的方体，使用映射网格来将轨座和桁架划分成六面体网格，可以得到比较规整的网格。

使用扫掠划分将垫块划分成六面体网格，网格大小设定为15mm。

划分结果如图2。

图2 网格化分3 设置单元类型对于实体模型分析，我们可选用8节点SOLID185单元。

整个分析过程有关于非线性接触的问题，所以要设置接触对单元类型。

选择TARGET170和CONTACT174单元。

4接触对创建使用设置接触对向导Contact Manager来设置。

设置轨座下表面和垫块上表面作为接触面，桁架为两接触面所对应的目标面。

其中轨座与桁架的接触对需设置成绑定接触，以防止发生滑移。

创建的接触对如图3所示。

图3 接触对的创建图4 边界条件5 添加约束施加约束，要在整体模型的中间部分施加对称约束以及对垫块施加全约束，从而保证无刚体位移。

如图4所示。

6 添加载荷选择距YOZ平面400毫米处的线，加集中载荷力为1860KN，方向为竖直向下，即Y的负向。

加载结果如图5所示。

图5 添加集中力载荷7 设置材料参数和载荷步在Material Models中，设置弹性模量EX为2e5(单位为兆帕)，泊松比PRXY 为0.3；材料的密度Density为7.8e-9（单位为千克每立方毫米）；摩擦系数Friction coefficient为0.05。

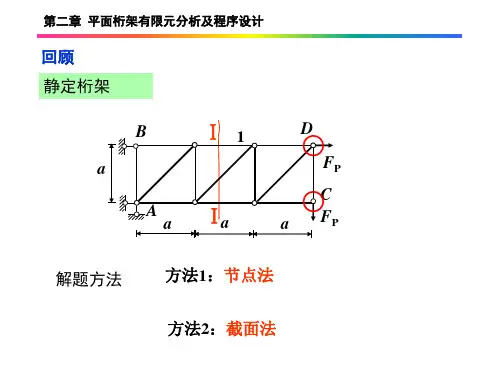
第9章桁架和梁的有限元分析第1节基本知识一、桁架和梁的有限元分析概要1．桁架杆系的有限元分析概要桁架杆系系统的有限元分析问题是工程中最常见的结构形式之一，常用在建筑的屋顶、机械的机架及各类空间网架结构等多种场合。

桁架结构的特点是，所有杆件仅承受轴向力，所有载荷集中作用于节点上。

由于桁架结构具有自然离散的特点，因此可以将其每一根杆件视为一个单元，各杆件之间的交点视为一个节点。

2．梁的有限元分析概要梁的有限元分析问题也是是工程中最常见的结构形式之一，常用在建筑、机械、汽车、工程机械、冶金等多种场合。

梁结构的特点是，梁的横截面均一致，可承受轴向、切向、弯矩等载荷。

根据梁的特点，等截面的梁在进行有限元分析时，需要定义梁的截面形状和尺寸，用创建的直线代替梁，在划分网格结束后，可以显示其实际形状。

二、桁架和梁的常用单元桁架和梁常用的单元类型和用途见表９-1。

通过对桁架和梁进行有限元分析，可得到其在各个方向的位移、应力并可得到应力、位移动画等结果。

第2节 桁架的有限元分析实例一、案例1——2D 桁架的有限元分析图9-1 人字形屋架的示意图 问题人字形屋架的几何尺寸如图9-1所示。

杆件截面尺寸为0.01m 2，试进行静力分析，对人字形屋架进行静力分析，给出变形图和各点的位移及轴向力、轴力图。

条件人字形屋架两端固定，弹性模量为2.0×1011 N/m 2，泊松比为0.3。

解题过程制定分析方案。

材料弹性材料，结构静力分析，属2D 桁架的静力分析问题，选用Link1单元。

建立坐标系及各节点定义如图9-1所示，边界条件为1点和5点固定，6、7、8点各受1000 N 的力作用。

1．ANSYS 分析开始准备工作（1）清空数据库并开始一个新的分析 选取Utility>Menu>File>Clear & Start New ，弹出Clears database and Start New 对话框，单击OK 按钮，弹出Verify 对话框，单击OK 按钮完成清空数据库。

桁架结构的有限元法单元坐标系下的单元平衡方程为单元坐标系下的单元平衡方程为图1. i u v {u v u v u u v v {}u v e u v q u v图2.与位移不同的是，杆的轴向力U 和总体系下的力{,}TU V 是等价的（如图U V eU V U Vq ee K q P K l所示的简单桁架结构。

进行整体桁架结构分析？为说明分析方法，考虑图3所示的简单桁架结构。

总体系下的节点位移和力向量为总体系下的节点位移和力向量为总体平衡方程具有如下形式：总体平衡方程具有如下形式：是数学上定义的，它的重要性质是：只于坐标, (1+注意，本问题中的坐标, (1,,)ix i n = 相当于函数()u x 的定义区间图4 解：单元1的单刚的单刚113133333[]413133333e EA K l éù--êú--êú=êú--êúêú--ëû单元2的单刚的单刚213133333[]413133333e EA K l éù--êú--êú=êú--êúêú--ëû 总刚阵总刚阵1313330033001313[]4003333131320333306EA K l éù--êú--êúêú--êú=êú--êúêú---êú---ëû节点位移向量节点位移向量33{}{0000}T u u v =节点力向量节点力向量22{}{}22T P PP =´´´´故有故有332020642u P EA v P l ìüéùìü=íýíýêúëûîþîþ2Pl62)62)36262) 3。

桁架结构及有限元分析MATLAB桁架结构是一种由杆件和节点连接而成的结构系统。

它的主要特点是具有良好的刚性和承载能力，适用于跨度较大的建筑物或桥梁。

桁架结构的设计和分析是工程领域中重要的课题。

有限元分析是一种常用的方法，用于对桁架结构进行力学和结构分析。

MATLAB是一种强大的数学建模和计算工具，可以方便地进行有限元分析。

在进行桁架结构的有限元分析之前，首先需要进行结构的建模。

可以使用MATLAB中的节点和杆件来建立桁架结构的几何模型。

节点代表结构中的连接点，杆件代表连接节点的杆件。

接下来，需要将结构分割为有限元网格。

在MATLAB中，可以使用二维和三维有限元网格生成函数来生成网格。

生成的网格可以根据需要的精度进行调整。

每个有限元包含一个或多个节点和杆件，用于描述局部的力学行为。

在有限元分析中，需要考虑材料的力学性质。

可以通过定义材料的模量、泊松比和密度等参数来描述材料的本构关系。

在MATLAB中，可以使用材料库函数来定义不同材料的力学性质。

进行有限元分析时，需要考虑结构的边界条件和加载条件。

边界条件包括固定边界和位移约束，加载条件可以是力、压力或扭矩等。

在MATLAB中，可以使用边界条件函数来定义结构的边界条件和加载条件。

在有限元分析的过程中，需要对结构进行求解。

可以使用线性或非线性求解算法来计算结构的位移和应力等。

MATLAB中提供了多种求解器和求解方法，可以根据需要选择适合的求解算法。

完成有限元分析后，可以进行结果的后处理。

可以使用MATLAB中的可视化工具来绘制结构的位移和应力云图，以及显示结构的反应力和形变等。

可以通过对结果进行分析和比较，评估结构的可靠性和安全性。

总之，使用MATLAB进行桁架结构的有限元分析可以帮助工程师深入了解结构的力学行为和性能。

它可以为结构的设计和优化提供依据，并帮助工程师制定提高结构性能的策略。

同时，MATLAB提供了丰富的功能和工具，使得桁架结构的分析和设计更加高效和准确。

平面桁架结构的有限元分析平面桁架结构是一种经常在建筑和工程领域中使用的结构形式。

它由直杆组成，连接在节点上，形成一个稳定的平面结构。

平面桁架结构的设计和分析需要使用有限元分析方法来确定结构的受力状态和稳定性。

本文将介绍平面桁架结构的有限元分析方法，包括模型建立、加载条件、应力和变形分析等。

首先，建立平面桁架结构的有限元模型。

模型应包括杆件和节点两个基本元素。

杆件是结构的主要受力元素，节点是杆件的连接点。

通过连接节点和杆件，可以构建起整个桁架结构。

在有限元模型中，每个节点被赋予一个坐标，每个杆件的长度和截面积也需要定义。

通过这些信息，可以建立结构的有限元模型。

加载条件是进行有限元分析的第二个关键步骤。

加载条件包括结构所承受的外部力和约束条件。

外部力是指作用于结构上的力，包括重力、风力、地震力等。

约束条件是指限制结构自由运动的条件，例如固定节点或滑动支座等。

在有限元分析中，将这些加载条件应用到有限元模型中，以模拟真实结构的受力情况。

然后进行应力和变形分析。

在有限元分析中，结构的应力分布和变形情况可以通过求解有限元方程来得到。

有限元方程是由结构的力平衡和材料的应力-应变关系所组成的方程组。

通过求解有限元方程，可以计算出结构中每个节点的应力和变形情况。

这些结果可以用来评估结构的安全性和稳定性。

在进行有限元分析时，需要注意一些细节。

首先，选择合适的材料模型和参数。

不同的材料具有不同的力学特性，例如弹性模量、屈服强度等。

选择适当的材料模型和参数，以获得准确的分析结果。

其次，进行网格划分和单元类型选择。

将结构划分为小单元，并选择适当的单元类型，以确保每个单元的形状和大小适合结构的几何形状。

最后，进行后处理和结果分析。

得到应力和变形结果后，可以进行结果的可视化和分析，以评估结构的性能。

总之，平面桁架结构的有限元分析是一种有效的工具，可以用于评估结构的受力状态和稳定性。

通过合适的模型建立、加载条件选择以及应力和变形分析等步骤，可以得到准确的分析结果，为结构的设计和优化提供有力支持。

基于ANSYS的26t桁架门式起重机有限元分析ANSYS是一个强大的有限元分析软件，适用于各种结构和材料的工程分析。

本文将结合ANSYS对一种26t桁架门式起重机进行有限元分析。

首先，我们需要建立起重机的CAD模型，并对其中的主要构件进行网格划分。

在此过程中，需要注意选择适当的网格密度以及网格类型，以确保分析结果的准确性和计算效率。

接下来，我们可以使用ANSYS加载程序对起重机进行分析。

在分析过程中，需要考虑外部载荷、材料特性、约束条件等多个因素。

具体来说，一个26t桁架门式起重机外部受力主要包括起重物自重、物体运动时的惯性载荷、环境风力载荷等。

在有限元分析中，我们通常会使用强度计算模型、位移计算模型，以及模态分析模型等多种模型来模拟实际物理情况，并对构件的强度、刚度、自振频率等重要性能进行评估。

在对26t桁架门式起重机进行有限元分析过程中，可以得到以下结果：1. 刚度和强度分布特性：在外部载荷作用下，起重机各部件的刚度和强度分布情况可以得到精确的数值描述，以便进一步计算构件的应力、应变、位移等参数。

2. 位移和变形分布特性：起重机各部件在受力下的变形和位移情况可以得到全面而掌握性的分析结果，帮助了解结构的可操作性和稳定性。

3. 自然频率分布特性：进行模态分析时，可以得到起重机各个部件的自然振动频率以及振动模态分析等信息，帮助了解起重机在使用过程中的自身振动特性和在外部环境影响下的响应。

基于上述分析结果，可以为26t桁架门式起重机的设计、制造和使用提供可靠的依据。

同时，我们还可以在ANSYS上进行优化设计，比如可以在起重机中添加一些支撑结构、加强拉杆等措施，以及选择更优良的材料，来增强其强度和稳定性。

总的来说，利用ANSYS进行26t桁架门式起重机的有限元分析，有助于解决实际施工过程中可能存在的安全隐患，提高施工效率和工程质量。

对于一台26t桁架门式起重机的有限元分析，需要收集的数据包括起重机的CAD模型、材料力学参数、外部载荷等多个方面的数据。

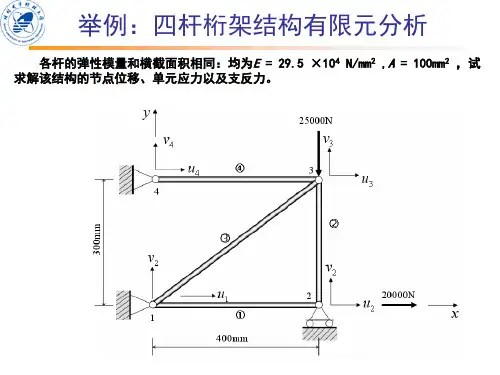
有限元上机分析报告~学院：机械工程专业及班级：机械设计及其自动化08级7班姓名：***学号：题目编号： 2》1.题目概况结构组成和基本数据结构：该结构为一个六根杆组成的桁架结构，其中四根杆组成了直径为800cm的正方形，其他两根杆的两节点为四边形的四个角。

材料：该六根杆截面面积均为100cm2，材料均为Q235，弹性模量为200GPa，对于直径或厚度大于100mm的截面其强度设计值为190Mpa。

载荷：结构的左上和左下角被铰接固定，限制了其在平面内x和y方向的位移，右上角受到大小为2000KN的集中载荷。

结构的整体状况如下图所示：分析任务】该分析的任务是对该结构的静强度进行校核分析以验算该结构否满足强度要求。

2.模型建立物理模型简化及其分析由于该结构为桁架结构，故认为每根杆件只会沿着轴线进行拉压，而不会发生弯曲和扭转等变形。

结构中每根杆为铰接连接，有集中载荷作用于最上方的杆和最右方杆的铰接点。

单元选择及其分析由于该结构的杆可以认为是只受拉压的杆件，故可以使用LINK180单元，该单元是有着广泛工程应用的杆单元，它可以用来模拟桁架、缆索、连杆、弹簧等等。

这种三维杆单元是杆轴方向的拉压单元，每个节点具有三个自由度：沿节点坐标系X、Y、Z方向的平动。

就像铰接结构一样，不承受弯矩。

输入的数据有：两个节点、横截面面积（AREA）、单位长度的质量(ADDMAS)及材料属性。

输出有：单元节点位移、节点的应力应变等等。

由此可见，LINK180单元适用于该结构的分析。

模型建立及网格划分(（1）启动Ansys软件，选择Preferences→Structural，即将其他非结构菜单过滤掉。

（2）选择单元类型：选择Preprocessor→Element Type→Add/Edit/Delete→Add，在出现的对话框中选择Link→3d finit stn 180，即LINK180，点击“OK”（3）选择实常数：选择Preprocessor→Real Constants→Add/Edit/Delete→Add，在出现的对话框中的Cross-sectional area中输入100，点击“OK”。

桁架结构的有限元分析MATLAB桁架结构是一种由直杆或斜杆连接而成的稳定结构，在工程应用中较为常见。

有限元分析（Finite Element Analysis，FEA）是一种利用数值方法解决结构力学问题的工具。

本文将介绍如何使用MATLAB进行桁架结构的有限元分析，并对其进行1200字以上的详细描述。

在进行桁架结构有限元分析前，需要先进行结构建模以及材料属性和加载条件的定义。

这些定义可以通过MATLAB命令行或者编写MATLAB脚本文件实现。

首先，我们需要定义桁架结构的节点和单元。

节点用于表示桁架结构的连接点，单元用于表示相邻节点之间的连接关系。

可以使用MATLAB中的矩阵表示节点和单元，如下所示：nodes = [x1, y1; x2, y2; ...; xn, yn];elements = [n1, n2; n3, n4; ...; nm, np];```其中，`nodes`是一个n行2列的矩阵，表示n个节点的坐标；`elements`是一个m行2列的矩阵，表示m个单元的节点连接关系。

接下来，我们需要定义材料属性和加载条件。

材料属性包括杨氏模量和截面面积等参数，加载条件包括节点的约束和外部加载。

可以使用MATLAB中的矩阵或者结构体表示材料属性和加载条件，如下所示：materials = struct('E', E1, 'A', A1; 'E', E2, 'A', A2; ...);constraints = [n1, d1x, d1y; ...; nm, dmx, dmy];loads = [n1, F1x, F1y; ...; nl, Flx, Fly];```其中，`materials`是一个结构体数组，每个结构体包含材料的杨氏模量（E）和截面面积（A）；`constraints`是一个m行3列的矩阵，表示m个节点的约束，其中d1x和d1y分别表示节点的x方向和y方向位移约束；`loads`是一个l行3列的矩阵，表示l个节点的外部加载，其中F1x和F1y分别表示节点的x方向和y方向外部力。

用ANSYS对一桁架结构进行有限元计算有限元分析是一种常用的结构力学计算方法，其可以有效地分析并预测复杂结构的力学行为。

ANSYS是一款广泛使用的有限元分析软件，其提供了强大的功能和工具，可以对各种类型的结构进行有限元计算。

一桁架结构是一种常见的工程结构，其由一根主梁和多个次梁构成。

这种结构广泛应用于桥梁、建筑物和机械设备等领域。

下面将介绍在ANSYS中对一桁架结构进行有限元计算的步骤和方法。

首先，在ANSYS中创建一个新的工程，并选择适当的工作空间和单位。

然后，使用ANSYS的几何建模工具，如DesignModeler或SpaceClaim，创建一桁架结构的三维模型。

可以通过绘制线段、矩形和圆弧等基本几何形状来构建结构。

此外，还可以导入外部CAD文件或使用ANSYS提供的几何建模功能创建结构。

创建完模型后，需要定义结构的材料属性。

根据具体情况，在ANSYS的材料库中选择适当的材料，并将其属性分配给结构中的各个部分。

可以指定材料的弹性模量、泊松比、密度和屈服强度等参数。

接下来，定义结构的约束条件和加载情况。

可以在结构的关键节点上固定约束或施加位移约束，以模拟实际工况中的支撑条件。

此外，在适当的位置上施加集中载荷、分布载荷或压力等加载，以模拟外部力的作用。

在定义好约束条件和加载情况后，需要进行网格划分。

ANSYS提供了多种网格划分算法和工具，如Tetrahedral、Hexahedral和Prism等。

根据模型的复杂程度和预期计算结果的准确性，可以选择适当的网格划分方法。

完成网格划分后，可以开始进行有限元计算。

在ANSYS中，可以选择适当的有限元求解器，并设定求解器的参数。

然后，进行计算并等待计算结果。

在计算完成后，可以对结果进行后处理。

ANSYS提供了丰富的后处理工具和功能，如显示变形、应力云图、位移云图、剖面图等用于分析和解释计算结果。

可以通过这些后处理工具来评估结构的强度和刚度，并与设计要求进行对比。