实例1 四杆桁架结构有限元分析

实例：2D四杆桁架结构的有限元分析学习有限元方法的一个最佳途径，就是在充分掌握基本概念的基础上亲自编写有限元分析程序，这就需要一个良好的编程环境或平台。

MATLAB软件就是这样一个平台，它以功能强大、编程逻辑直观、使用方便见长。

将提供有限元分析中主要单元完整的MATLAB程序，并给出详细的说明。

1D杆单元的有限元分析MATLAB程序(Bar1D2Node)最简单的线性杆单元的程序应该包括单元刚度矩阵、单元组装、单元应力等几个基本计算程序。

下面给出编写的线性杆单元的四个MATLAB函数。

Bar1D2Node _Stiffness(E,A,L)该函数计算单元的刚度矩阵，输入弹性模量E，横截面积A和长度L，输出单元刚度矩阵k(2×2)。

Bar1D2Node _Assembly(KK,k,i,j)该函数进行单元刚度矩阵的组装，输入单元刚度矩阵k，单元的节点编号i、j，输出整体刚度矩阵KK。

Bar1D2Node _Stress(k,u,A)该函数计算单元的应力，输入单元刚度矩阵k、单元的位移列阵u(2×1)以及横截面积A计算单元应力矢量，输出单元应力stress。

Bar1D2Node_Force(k,u)该函数计算单元节点力矢量，输入单元刚度矩阵k和单元的位移列阵u(2×1)，输出2×1的单元节点力矢量forces。

基于1D杆单元的有限元分析的基本公式，写出具体实现以上每个函数的MATLAB程序如下。

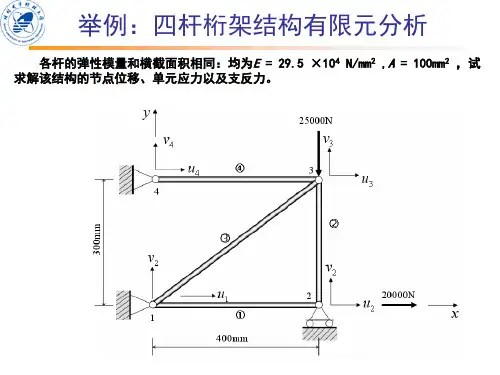
%%%%%%%%%%% Bar1D2Node %% begin %%%%%%%%%function k=Bar1D2Node_Stiffness(E, A, L)%该函数计算单元的刚度矩阵%输入弹性模量E，横截面积A和长度L%输出单元刚度矩阵k(2×2)%---------------------------------------k=[E*A/L -E*A/L; -E*A/L E*A/L];%%%%%%%%%%%%%%%%%%%%%%%%%%function z=Bar1D2Node_Assembly(KK,k,i,j)%该函数进行单元刚度矩阵的组装%输入单元刚度矩阵k，单元的节点编号i、j%输出整体刚度矩阵KK%-----------------------------------DOF(1)=i;DOF(2)=j;for n1=1:2for n2=1:2KK(DOF(n1), DOF(n2))= KK(DOF(n1), DOF(n2))+k(n1, n2);endendz=KK;%------------------------------------------------------------function stress=Bar1D2Node_Stress(k, u, A)%该函数计算单元的应力%输入单元刚度矩阵k, 单元的位移列阵u(2×1)%输入横截面积A计算单元应力矢量%输出单元应力stress%-----------------------------------stress=k*u/A;%-----------------------------------------------------------%%%%%%%%%%%%%%%%%%%%%%%%%function forces=Bar1D2Node_Force(k, u)%该函数计算单元节点力矢量%输入单元刚度矩阵k和单元的位移列阵u(2×1)%输出2×1的单元节点力分量forces%-----------------------------------------forces=k*u;%%%%%%%%%%% Bar1D2Node %% end %%%%%%%%%【四杆桁架结构的有限元分析—数学推导】如图所示的结构，各杆的弹性模量和横截面积都为E=29.54×10N/mm2, A=100mm 2，试求解该结构的节点位移、单元应力以及支反力。

第9章桁架和梁的有限元分析第1节基本知识一、桁架和梁的有限元分析概要1．桁架杆系的有限元分析概要桁架杆系系统的有限元分析问题是工程中最常见的结构形式之一，常用在建筑的屋顶、机械的机架及各类空间网架结构等多种场合。

桁架结构的特点是，所有杆件仅承受轴向力，所有载荷集中作用于节点上。

由于桁架结构具有自然离散的特点，因此可以将其每一根杆件视为一个单元，各杆件之间的交点视为一个节点。

2．梁的有限元分析概要梁的有限元分析问题也是是工程中最常见的结构形式之一，常用在建筑、机械、汽车、工程机械、冶金等多种场合。

梁结构的特点是，梁的横截面均一致，可承受轴向、切向、弯矩等载荷。

根据梁的特点，等截面的梁在进行有限元分析时，需要定义梁的截面形状和尺寸，用创建的直线代替梁，在划分网格结束后，可以显示其实际形状。

二、桁架和梁的常用单元桁架和梁常用的单元类型和用途见表９-1。

通过对桁架和梁进行有限元分析，可得到其在各个方向的位移、应力并可得到应力、位移动画等结果。

第2节 桁架的有限元分析实例一、案例1——2D 桁架的有限元分析图9-1 人字形屋架的示意图 问题人字形屋架的几何尺寸如图9-1所示。

杆件截面尺寸为0.01m 2，试进行静力分析，对人字形屋架进行静力分析，给出变形图和各点的位移及轴向力、轴力图。

条件人字形屋架两端固定，弹性模量为2.0×1011 N/m 2，泊松比为0.3。

解题过程制定分析方案。

材料弹性材料，结构静力分析，属2D 桁架的静力分析问题，选用Link1单元。

建立坐标系及各节点定义如图9-1所示，边界条件为1点和5点固定，6、7、8点各受1000 N 的力作用。

1．ANSYS 分析开始准备工作（1）清空数据库并开始一个新的分析 选取Utility>Menu>File>Clear & Start New ，弹出Clears database and Start New 对话框，单击OK 按钮，弹出Verify 对话框，单击OK 按钮完成清空数据库。

第9章桁架和梁的有限元分析第1节基本知识一、桁架和梁的有限元分析概要1．桁架杆系的有限元分析概要桁架杆系系统的有限元分析问题是工程中最常见的结构形式之一，常用在建筑的屋顶、机械的机架及各类空间网架结构等多种场合。

桁架结构的特点是，所有杆件仅承受轴向力，所有载荷集中作用于节点上。

由于桁架结构具有自然离散的特点，因此可以将其每一根杆件视为一个单元，各杆件之间的交点视为一个节点。

2．梁的有限元分析概要梁的有限元分析问题也是是工程中最常见的结构形式之一，常用在建筑、机械、汽车、工程机械、冶金等多种场合。

梁结构的特点是，梁的横截面均一致，可承受轴向、切向、弯矩等载荷。

根据梁的特点，等截面的梁在进行有限元分析时，需要定义梁的截面形状和尺寸，用创建的直线代替梁，在划分网格结束后，可以显示其实际形状。

二、桁架和梁的常用单元桁架和梁常用的单元类型和用途见表９-1。

表９-1 桁架和梁常用结构实体单元列表通过对桁架和梁进行有限元分析，可得到其在各个方向的位移、应力并可得到应力、位移动画等结果。

第2节 桁架的有限元分析实例一、案例1——2D 桁架的有限元分析图9-1 人字形屋架的示意图问题 人字形屋架的几何尺寸如图9-1所示。

杆件截面尺寸为0.01m 2，试进行静力分析，对人字形屋架进行静力分析，给出变形图和各点的位移及轴向力、轴力图。

条件人字形屋架两端固定，弹性模量为2.0×1011 N/m 2，泊松比为0.3。

解题过程制定分析方案。

材料弹性材料，结构静力分析，属2D 桁架的静力分析问题，选用Link1单元。

建立坐标系及各节点定义如图9-1所示，边界条件为1点和5点固定，6、7、8点各受1000 N 的力作用。

1．ANSYS 分析开始准备工作（1）清空数据库并开始一个新的分析 选取Utility>Menu>File>Clear & Start New ，弹出Clears database and Start New 对话框，单击OK 按钮，弹出V erify 对话框，单击OK 按钮完成清空数据库。

2D四杆桁架结构的有限元分析实例2D四杆桁架结构是一种常见的结构形式，广泛应用于工程领域。

在进行结构设计和分析时，有限元分析是一种常用的方法，可以对结构进行力学性能和应力分布的分析。

下面将以一个具体的例子来介绍2D四杆桁架结构的有限元分析。

```A*/\/\/\*-------*BC```该桁架结构由四根杆件构成，材料为钢，杆件截面可视为圆形。

假设桁架结构的高度为H，宽度为W，杆件的直径为D，且杆件AB和BC的长度为L。

首先，我们需要将该桁架结构离散为有限元网格。

可以采用等距离离散方法，在杆件AB上取N个节点，在杆件BC上取M个节点。

每个节点的坐标可以通过计算得到。

接下来，我们需要确定边界条件。

假设桁架结构的支座在节点A和C 处。

我们可以将节点A和C固定，即其位移为零，这是考虑到节点A和C作为支座点不会产生水平和竖直的位移。

然后，我们需要为杆件的材料属性和截面属性建立数学模型。

假设桁架结构的钢材的弹性模量为E，泊松比为ν。

另外，我们需要确定杆件的截面半径r。

接下来，我们需要确定桁架结构的荷载。

假设在节点B作用一个竖直向下的荷载P。

这个荷载会使得杆件AB和杆件BC受到拉力。

然后，我们可以使用有限元软件进行计算。

在计算中，我们可以采用线性弹性模型进行计算，即假设所有杆件在加载之前是弹性的。

在计算中，我们可以使用有限元方法对每个单元进行力学性能和应力分布的分析。

可以使用线性弹性有限元方法，如直接刚度法或变分法等。

在计算得到每个单元的力学性能和应力分布后，我们可以进一步分析整个桁架结构的强度和刚度。

可以计算整个结构的位移、载荷和应力等。

最后，我们可以通过对结果进行后处理和分析，来评估桁架结构的性能和稳定性。

可以计算结构的应力、变形和应变等。

综上所述，2D四杆桁架结构的有限元分析可以通过离散桁架结构为有限元网格，确定边界条件、材料和截面属性，施加荷载，并使用有限元软件进行计算。

通过对每个单元的力学性能和应力分布进行分析，并综合整个结构的性能和稳定性，可以得到结构的位移、载荷和应力等信息。

四杆桁架结构有限元分析：1 基于图形界面(GUI)的交互式操作(step by step)(1) 进入A NSYS(设定工作目录和工作文件)程序→ANSYS →ANSYS Interactive →Working directory (设置工作目录) →Initial jobname(设置工作文件名): planetruss→Run →OK(2) 设置计算类型ANSYS Main Menu: Preferences… →Structural →OK(3) 选择单元类型ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Del ete…→A dd… →Link：2D spar 1 →OK (返回到E lement Types 窗口) →Close(4) 定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models→Structural →Linear →Elastic→Isotropic: EX:2.95e11 (弹性模量)，PRXY: 0 (泊松比) →OK →鼠标点击该窗口右上角的“U”来关闭该窗口(5) 定义实常数以确定单元的截面积ANSYS Main Menu: Preprocessor →Real Constants… →Add/Edit/Delete →Add →Type 1→OK→RealConstant Set No: 1 (第1号实常数), AREA: 1e-4 (单元的截面积) →OK→Close(6) 生成单元ANSYS Main Menu: Preprocessor →Modeling →Creat→Nodes→In Active CS→Node number 1 →X:0,Y:0,Z:0 →Apply →Node number 2 →X:0.4,Y:0,Z:0 →Apply →Node number 3 →X:0.4,Y:0.3,Z:0 →Apply→Node number 4 →X:0,Y:0.3,Z:0→OKANSYS Main Menu: Preprocessor →Modeling →Create →Elements→Elem Attributes（接受默认值）→User numbered→Thru nodes→OK→选择n ode 1 和n ode2→Apply→选择n ode 2 和n ode3→Apply →选择node 1 和n ode3→Apply→选择n ode 4 和n ode3→Apply→OK (7) 模型施加约束和外载添加位移的约束，分别将1节点X和Y方向、2 节点Y方向、4 节点的X和Y方向位移约束。

桁架结构及有限元分析MATLAB桁架结构是一种由杆件和节点连接而成的结构系统。

它的主要特点是具有良好的刚性和承载能力，适用于跨度较大的建筑物或桥梁。

桁架结构的设计和分析是工程领域中重要的课题。

有限元分析是一种常用的方法，用于对桁架结构进行力学和结构分析。

MATLAB是一种强大的数学建模和计算工具，可以方便地进行有限元分析。

在进行桁架结构的有限元分析之前，首先需要进行结构的建模。

可以使用MATLAB中的节点和杆件来建立桁架结构的几何模型。

节点代表结构中的连接点，杆件代表连接节点的杆件。

接下来，需要将结构分割为有限元网格。

在MATLAB中，可以使用二维和三维有限元网格生成函数来生成网格。

生成的网格可以根据需要的精度进行调整。

每个有限元包含一个或多个节点和杆件，用于描述局部的力学行为。

在有限元分析中，需要考虑材料的力学性质。

可以通过定义材料的模量、泊松比和密度等参数来描述材料的本构关系。

在MATLAB中，可以使用材料库函数来定义不同材料的力学性质。

进行有限元分析时，需要考虑结构的边界条件和加载条件。

边界条件包括固定边界和位移约束，加载条件可以是力、压力或扭矩等。

在MATLAB中，可以使用边界条件函数来定义结构的边界条件和加载条件。

在有限元分析的过程中，需要对结构进行求解。

可以使用线性或非线性求解算法来计算结构的位移和应力等。

MATLAB中提供了多种求解器和求解方法，可以根据需要选择适合的求解算法。

完成有限元分析后，可以进行结果的后处理。

可以使用MATLAB中的可视化工具来绘制结构的位移和应力云图，以及显示结构的反应力和形变等。

可以通过对结果进行分析和比较，评估结构的可靠性和安全性。

总之，使用MATLAB进行桁架结构的有限元分析可以帮助工程师深入了解结构的力学行为和性能。

它可以为结构的设计和优化提供依据，并帮助工程师制定提高结构性能的策略。

同时，MATLAB提供了丰富的功能和工具，使得桁架结构的分析和设计更加高效和准确。

有限元上机分析报告学院：机械工程专业及班级：机械设计及其自动化08级7班姓名：王浩煜学号：20082798题目编号： 21.题目概况1.1 结构组成和基本数据结构：该结构为一个六根杆组成的桁架结构，其中四根杆组成了直径为800cm的正方形，其他两根杆的两节点为四边形的四个角。

材料：该六根杆截面面积均为100cm2，材料均为Q235，弹性模量为200GPa，对于直径或厚度大于100mm的截面其强度设计值为190Mpa。

载荷：结构的左上和左下角被铰接固定，限制了其在平面内x和y方向的位移，右上角受到大小为2000KN的集中载荷。

结构的整体状况如下图所示：1.2 分析任务该分析的任务是对该结构的静强度进行校核分析以验算该结构否满足强度要求。

2.模型建立2.1 物理模型简化及其分析由于该结构为桁架结构，故认为每根杆件只会沿着轴线进行拉压，而不会发生弯曲和扭转等变形。

结构中每根杆为铰接连接，有集中载荷作用于最上方的杆和最右方杆的铰接点。

2.2单元选择及其分析由于该结构的杆可以认为是只受拉压的杆件，故可以使用LINK180单元，该单元是有着广泛工程应用的杆单元，它可以用来模拟桁架、缆索、连杆、弹簧等等。

这种三维杆单元是杆轴方向的拉压单元，每个节点具有三个自由度：沿节点坐标系X、Y、Z方向的平动。

就像铰接结构一样，不承受弯矩。

输入的数据有：两个节点、横截面面积（AREA）、单位长度的质量(ADDMAS)及材料属性。

输出有：单元节点位移、节点的应力应变等等。

由此可见，LINK180单元适用于该结构的分析。

3.3 模型建立及网格划分（1）启动Ansys软件，选择Preferences→Structural，即将其他非结构菜单过滤掉。

（2）选择单元类型：选择Preprocessor→Element Type→Add/Edit/Delete→Add，在出现的对话框中选择Link→3d finit stn 180，即LINK180，点击“OK”（3）选择实常数：选择Preprocessor→Real Constants→Add/Edit/Delete→Add，在出现的对话框中的Cross-sectional area中输入100，点击“OK”。

平面桁架结构的有限元分析平面桁架结构是一种经常在建筑和工程领域中使用的结构形式。

它由直杆组成，连接在节点上，形成一个稳定的平面结构。

平面桁架结构的设计和分析需要使用有限元分析方法来确定结构的受力状态和稳定性。

本文将介绍平面桁架结构的有限元分析方法，包括模型建立、加载条件、应力和变形分析等。

首先，建立平面桁架结构的有限元模型。

模型应包括杆件和节点两个基本元素。

杆件是结构的主要受力元素，节点是杆件的连接点。

通过连接节点和杆件，可以构建起整个桁架结构。

在有限元模型中，每个节点被赋予一个坐标，每个杆件的长度和截面积也需要定义。

通过这些信息，可以建立结构的有限元模型。

加载条件是进行有限元分析的第二个关键步骤。

加载条件包括结构所承受的外部力和约束条件。

外部力是指作用于结构上的力，包括重力、风力、地震力等。

约束条件是指限制结构自由运动的条件，例如固定节点或滑动支座等。

在有限元分析中，将这些加载条件应用到有限元模型中，以模拟真实结构的受力情况。

然后进行应力和变形分析。

在有限元分析中，结构的应力分布和变形情况可以通过求解有限元方程来得到。

有限元方程是由结构的力平衡和材料的应力-应变关系所组成的方程组。

通过求解有限元方程，可以计算出结构中每个节点的应力和变形情况。

这些结果可以用来评估结构的安全性和稳定性。

在进行有限元分析时，需要注意一些细节。

首先，选择合适的材料模型和参数。

不同的材料具有不同的力学特性，例如弹性模量、屈服强度等。

选择适当的材料模型和参数，以获得准确的分析结果。

其次，进行网格划分和单元类型选择。

将结构划分为小单元，并选择适当的单元类型，以确保每个单元的形状和大小适合结构的几何形状。

最后，进行后处理和结果分析。

得到应力和变形结果后，可以进行结果的可视化和分析，以评估结构的性能。

总之，平面桁架结构的有限元分析是一种有效的工具，可以用于评估结构的受力状态和稳定性。

通过合适的模型建立、加载条件选择以及应力和变形分析等步骤，可以得到准确的分析结果，为结构的设计和优化提供有力支持。

超静定桁架的计算分析一．问题描述及数学建模计算分析模型如图所示。

载荷：1.0e8N超静定桁架的计算分析模型按照问题要求，在ANSYS 10.0中先建立四个点，然后建立三条直线并设置约束，然后给整个模型添加载荷。

二．有限元建模选择程序，点击ANSYS 10.0，进入ANSYS的操作界面，依次点击如下选项：Interactive →change the working directory into yours →input Initial jobname: truss→Run。

2.1设置计算类型并进行单元选择在ANSYS的主菜单ANSYS Main Menu下依次选择：Preferences 、Structural ，最后单击OK选项，完成计算类型的设置。

接下来进行单元选择，步骤依次为：Preprocessor →Element Type→Add/Edit/Delete →Add →Link 2D spar 1 →OK →Options… →K3: Plane Strain →OK→Close。

2.2 定义材料参数和实常数弹性模量定义为11，泊松比为0.35。

P reprocessor →Material Props →210Material Models →Structural →Linear →Elastic →Isotropic →EX:2.0e11, PRXY:0.35，最后单击OK就完成了材料参数的定义。

定义实常数按照如下步骤：Preprocessor →Real Constants… →Add… →Type 1→OK→AREA:0.3 →OK →Close。

2.3 生成特征点及桁架设置四个点的坐标依次为：（1、1）、（2、1）、（3、1）、（2、0）。

然后依次选择：Preprocessor、Modeling、Create、Keypoints、In Active CS Modeling，依次输入四个点的坐标：input:1(1,1),2(2,1),3(3,1),4(2,0)，最后单击OK即可在坐标系中生成四个特征点。

matlab桁架结构有限元计算摘要：一、引言二、MATLAB 在桁架结构有限元计算中的应用1.桁架结构的离散化与编号2.组装刚度矩阵3.求解器求解4.后处理三、MATLAB 桁架有限元分析实例1.空间桁架有限元分析2.基于MATLAB 的三维桁架有限元分析3.五杆桁架有限元分析四、用MATLAB 编写程序求解桁架结构内力问题1.静定结构绘制简图2.计算结构力学3.机动分析五、结论正文：一、引言在工程领域中，桁架结构由于其优越的力学性能和简单的结构形式，被广泛应用于桥梁、塔架等大型建筑结构中。

为了确保桁架结构的安全性和稳定性，对其进行有限元分析是非常必要的。

MATLAB 作为一种强大的数学软件，可以方便地进行桁架结构的有限元计算。

本文将介绍如何使用MATLAB 进行桁架结构有限元计算。

二、MATLAB 在桁架结构有限元计算中的应用1.桁架结构的离散化与编号在进行有限元分析之前，首先需要对桁架结构进行离散化处理，将连续的桁架杆件划分为有限个小杆件。

同时，为了方便后续计算，需要对各个杆件和节点进行编号。

2.组装刚度矩阵根据桁架结构的几何参数和材料性能，可以计算出各个杆件的刚度矩阵。

将这些刚度矩阵组装成一个总的刚度矩阵，用于描述整个桁架结构的刚度特性。

3.求解器求解利用MATLAB 的求解器，可以对桁架结构进行有限元求解。

求解器会根据刚度矩阵和施加的边界条件，计算出节点的位移和单元的应力。

4.后处理在求解完成后，需要对计算结果进行后处理。

这包括对计算结果的保存、可视化以及结果的验证等。

三、MATLAB 桁架有限元分析实例1.空间桁架有限元分析例如，可以针对一个空间桁架结构，使用MATLAB 进行有限元分析。

假设该桁架结构由铝制成的垂直和水平部分和钢制成的对角桁架构件组成。

结构承受荷载P，需要计算节点位移、单元应力以及支反力。

2.基于MATLAB 的三维桁架有限元分析还可以利用MATLAB 进行三维桁架有限元分析。

四杆桁架结构的有限元分析在ANSYS 平台上，完成相应的力学分析。

即如图3-8所示的结构，各杆的弹性模量和横截面积都为4229.510N/mm E = , 2100mm A =，基于ANSYS 平台，求解该结构的节点位移、单元应力以及支反力。

1． 基于图形界面的交互式操作(step by step)(1) 进入ANSYS(设定工作目录和工作文件)程序 →ANSYS → ANSYS Interactive →Working directory (设置工作目录) →Initial jobname (设置工作文件名): planetruss →Run → OK(2) 设置计算类型ANSYS Main Menu : Preferences… → Structural → OK(3) 选择单元类型ANSYS Main Menu : Preprocessor →Element Type →Add/Edit/Delete… →Add… →Link ：2D spar 1 →OK (返回到Element Types 窗口) →Close(4) 定义材料参数ANSYS Main Menu : Preprocessor →Material Props →Material Models →Structural →Linear →Elastic → Isotropic: EX:2.95e11 (弹性模量)，PRXY: 0 (泊松比) → OK → 鼠标点击该窗口右上角的“ ”来关闭该窗口(5) 定义实常数以确定单元的截面积ANSYS Main Menu: Preprocessor →Real Constant s… →Add/Edit/Delete →Add →Type 1→ OK →Real Constant Set No: 1 (第1号实常数), AREA: 1e-4 (单元的截面积) →OK →Close(6) 生成单元ANSYS Main Menu: Preprocessor →Modeling →Creat →Nodes → In Active CS →Node number 1 → X:0,Y:0,Z:0 →Apply →Node number 2 → X:0.4,Y:0,Z:0 →Apply →Node number 3 → X:0.4,Y:0.3,Z:0→Apply→Node number 4 →X:0,Y:0.3,Z:0→OKANSYS Main Menu: Preprocessor →Modeling→Create →Elements→Elem Attributes（接受默认值）→User numbered→Thru nodes→OK→选择节点1，2→Apply→选择节点2，3→Apply→选择节点1，3→Apply→选择节点3，4→Apply→OK(7)模型施加约束和外载添加位移的约束，分别将节点1 X和Y方向、节点2 Y方向、节点4的X和Y方向位移约束。

2D四杆桁架结构的有限元分析实例实例：2D四杆桁架结构的有限元分析学习有限元方法的一个最佳途径，就是在充分掌握基本概念的基础上亲自编写有限元分析程序，这就需要一个良好的编程环境或平台。

MATLAB软件就是这样一个平台，它以功能强大、编程逻辑直观、使用方便见长。

将提供有限元分析中主要单元完整的MATLAB程序，并给出详细的说明。

1D杆单元的有限元分析MATLAB程序(Bar1D2Node)最简单的线性杆单元的程序应该包括单元刚度矩阵、单元组装、单元应力等几个基本计算程序。

下面给出编写的线性杆单元的四个MATLAB函数。

Bar1D2Node _Stiffness(E,A,L)该函数计算单元的刚度矩阵，输入弹性模量E，横截面积A和长度L，输出单元刚度矩阵k(2×2)。

Bar1D2Node _Assembly(KK,k,i,j)该函数进行单元刚度矩阵的组装，输入单元刚度矩阵k，单元的节点编号i、j，输出整体刚度矩阵KK。

Bar1D2Node _Stress(k,u,A)该函数计算单元的应力，输入单元刚度矩阵k、单元的位移列阵u(2×1)以及横截面积A计算单元应力矢量，输出单元应力stress。

Bar1D2Node_Force(k,u)收集于网络，如有侵权请联系管理员删除该函数计算单元节点力矢量，输入单元刚度矩阵k和单元的位移列阵u(2×1)，输出2×1的单元节点力矢量forces。

基于1D杆单元的有限元分析的基本公式，写出具体实现以上每个函数的MATLAB程序如下。

%%%%%%%%%%% Bar1D2Node %% begin %%%%%%%%%function k=Bar1D2Node_Stiffness(E, A, L)%该函数计算单元的刚度矩阵%输入弹性模量E，横截面积A和长度L%输出单元刚度矩阵k(2×2)%---------------------------------------k=[E*A/L -E*A/L; -E*A/L E*A/L];%%%%%%%%%%%%%%%%%%%%%%%%%%function z=Bar1D2Node_Assembly(KK,k,i,j)%该函数进行单元刚度矩阵的组装%输入单元刚度矩阵k，单元的节点编号i、j%输出整体刚度矩阵KK%-----------------------------------DOF(1)=i;DOF(2)=j;for n1=1:2for n2=1:2收集于网络，如有侵权请联系管理员删除KK(DOF(n1), DOF(n2))= KK(DOF(n1), DOF(n2))+k(n1, n2);endendz=KK;%------------------------------------------------------------function stress=Bar1D2Node_Stress(k, u, A)%该函数计算单元的应力%输入单元刚度矩阵k, 单元的位移列阵u(2×1)%输入横截面积A计算单元应力矢量%输出单元应力stress%-----------------------------------stress=k*u/A;%-----------------------------------------------------------%%%%%%%%%%%%%%%%%%%%%%%%%function forces=Bar1D2Node_Force(k, u)%该函数计算单元节点力矢量%输入单元刚度矩阵k和单元的位移列阵u(2×1)%输出2×1的单元节点力分量forces%-----------------------------------------forces=k*u;%%%%%%%%%%% Bar1D2Node %% end %%%%%%%%%收集于网络，如有侵权请联系管理员删除【四杆桁架结构的有限元分析—数学推导】如图所示的结构，各杆的弹性模量和横截面积都为E=29.54×10N/mm2,A=100mm 2，试求解该结构的节点位移、单元应力以及支反力。

【MATLAB 算例】3.2.5(2) 四杆桁架结构的有限元分析(Bar2D2Node)如图3-8所示的结构，各个杆的弹性模量和横截面积都为4229.510/E N mm =⨯, 2100A mm =。

试基于MATLAB 平台求解该结构的节点位移、单元应力以及支反力。

图3-8 四杆桁架结构解答：对该问题进行有限元分析的过程如下。

（1） 结构的离散化与编号对该结构进行自然离散，节点编号和单元编号如图3-8所示，有关节点和单元的信息见表3-1~表3-3。

（2）计算各单元的刚度矩阵(基于国际标准单位)建立一个工作目录，将所编制的用于平面桁架单元分析的4个MA TLAB 函数放置于该工作目录中，分别以各自函数的名称给出文件名，即：Bar2D2Node_Stiffness ，Bar2D2Node_Assembly ，Bar2D2Node_Stress ，Bar2D2Node_Forces 。

然后启动MATLAB ，将工作目录设置到已建立的目录中，在MATLAB 环境中，输入弹性模量E 、横截面积A ，各点坐标x1,y1,x2,y2,x3,y3,x4,y4,角度alpha 1, alpha 2和alpha 3,然后分别针对单元1，2，3和4，调用4次Bar2D2Node_Stiffness ，就可以得到单元的刚度矩阵。

相关的计算流程如下。

>>E=2.95e11;>>A=0.0001;>>x1=0;>>y1=0;>>x2=0.4;>>y2=0;>>x3=0.4;>>y3=0.3;>>x4=0;>>y4=0.3;>> alpha1=0;>> alpha2=90;>> alpha3=atan(0.75)*180/pi;>> k1=Bar2D2Node_Stiffness (E,A,x1,y1,x2,y2,alpha1)k1 = 73750000 0 -73750000 00 0 0 0-73750000 0 73750000 00 0 0 0>> k2=Bar2D2Node_Stiffness (E,A,x2,y2,x3,y3,alpha2)k2 = 1.0e+007 *0.0000 0.0000 -0.0000 -0.00000.0000 9.8333 -0.0000 -9.8333-0.0000 -0.0000 0.0000 0.0000-0.0000 -9.8333 0.0000 9.8333>> k3=Bar2D2Node_Stiffness (E,A,x1,y1,x3,y3,alpha3)k3 = 1.0e+007 *3.7760 2.8320 -3.7760 -2.83202.8320 2.1240 -2.8320 -2.1240-3.7760 -2.8320 3.7760 2.8320-2.8320 -2.1240 2.8320 2.1240>> k4=Bar2D2Node_Stiffness (E,A,x4,y4,x3,y3,alpha1)k4 = 73750000 0 -73750000 00 0 0 0-73750000 0 73750000 00 0 0 0（3） 建立整体刚度方程由于该结构共有4个节点，因此，设置结构总的刚度矩阵为KK (8×8)，先对KK 清零，然后四次调用函数Bar2D2Node _Assembly 进行刚度矩阵的组装。