大学物理课件--驻波

设＝1080 Hz，d =15.3 cm，则空气中声速为
u 2d ν 2 0.153 1 080 m s 1 330m s 1
例21.4 一只二胡的“千斤”（弦上方固定点）和“码子” （弦下方固定点）之间的距离是L=0.3m。其上一根弦的质量线密 度为l=3.8×10-4kg/m，拉紧它的张力 F=9.4N。求此弦所发的声 音的基频是多少？此弦的三次谐频振动的节点在何处？
L
2 2
n =3
三次 谐频
3 2
边界情况不同，简正模式也不同：
L= n
n
4
L
L= n
n
2
L
n=1,3… n = 1
基频Βιβλιοθήκη n=1,3… n = 1n
1
1 4
基频
1
1 2
n = 3
三次 谐频
n = 3
3 2
三次 谐频
3
3
3 3 2
末端封闭的笛中的驻波
末端开放的笛中的驻波
一般地说，对于一个驻波体系存在无限多个本征频率和 简正模式。在这一体系中形成的任何实际的振动，都可以看成 是各种简正模式的线性叠加，其中每一种简正模式的位相和所 占比例的大小，则由初始扰动的性质决定。 当周期性驱动力的频率与驻波体系的某一简正频率相同时， 就会使该频率驻波的振幅变得最大，这种现象也称为共振。利 用共振方法可以测量空气中的声速。
2

r1 )
y2 Acos[t
半波损失
2

( r1

2
)]
例题2
一列沿x轴方向传播的入射波的波函数为
t x y Acos 2 ( ) ,在x=0处反射,反射点为一节点 T
求:(1)反射波的波函数. (2)合成波的波函数 (3)波腹,波节 的位置坐标. 解 (1)由于有相位突变,故反射波的波函数为:
x'
2
x'

k ,
x' k

2

,
0
k 0 ,1,2 ,
(x,x'只取负值及零)
五、简正模式 （normal mode） 每个频率对应一种可能的震动方式，每种振动方式称为弦 线振动的简正模式。 波在一定边界内传播时就会形成各种驻波。 如两端固定的弦，形成驻波必须满足以下条件：
21.7 波的叠加
驻波
一、波的叠加原理（独立性原理）
通过对各种波动相遇现象的观察和研究，可总结如下规律：
无论是否相遇， 各列波将保持原有的特性( 频率, 波长和 振动方向等)不变，按照原来的方向继续前进， 就象没
有遇到其他的波一样。
在其相遇区域内，任一点处质点的的振动为各个波单独 存在时所引起的振动的矢量和。 这个规律叫做波的叠加原理或波的独立性原理。 注意：波的叠加原理仅在弱波条件时成立，强冲击波则不成立 。
(3)由
t y 2 Asin(2 )sin(2 ) T
x
形成波腹的各点,振幅最大,即: 亦即:
sin2
x
2 故波腹点坐标为: x k ( 2k 1) , k 0 ,1,2 , 4
形成波节各点,振幅最小,即: 即:
2
x

( 2k 1)


1
sin2
简谐振动的振幅
2

x cost
简谐振动
A' ( x )
x 但是这一函数不含有传播因子 ( t ) ,也不满足 u y(t t , x ut ) y(t , x ) 所以它不是行波。
它表示各点都在作简谐振动，各点振动的 频率相同，是原来波的频率。但各点振幅 随位置的不同而不同。
设有两列相干波，振幅相同，分别沿 x 轴正、负方向 传播，选初相位均为零的表达式为：
y1 Acos(t
y1 t 0 u
2

x)
y2 Acos(t
y2
2

u
x)
t0
x
x
y1 Acos(t
2

x)
y2 Acos(t
2

x)
其合成波称为驻波，其表达式 ：
pm uA
(21.41)
声强，即声波的能流密度
( W / m2 )
p 1 2 2 I A u 2 2 u
炮声的声强约为
2 m
(21.42)
1W / m 2
用聚焦的方法获得的超声波
最大声强可达
10 W / m
n
L
或
n
2
L，n 1,2,3…
2L n n
u n n 2L n
波速
u
—系统的固有频率
u
F
F —弦中的张力 l —弦的线密度
l
每种可能的稳定振动方式称作系统的一个简正模式。 两端固定的弦：
n =1
基频
1 2
n
n
n =2
二次 谐频
2 n 1,2,3 …
2L n n
设有两个频率相同的波源S 1 和S 2
y10 ( s1 , t ) A10cos(t 10 )
s2
r2
y20 ( s2 , t ) A20cos(t 20 )
传播到 P 点引起的振动为：
r1 y1 ( p , t ) A1cos[ ( t ) 10 ] u 2 y1 ( p , t ) A1cos(t 10 r1 )
u 2m 代入,可得: 将 f
所以在两波源的连线上因干涉而静止的点的位置分别为:
x 1,2 ,3 , ,17,18,19m
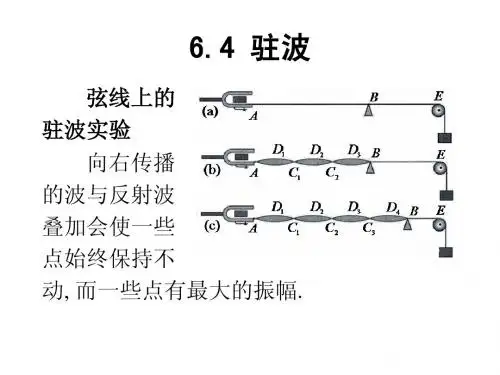
三、驻波：（驻波是干涉的特例）
1、驻波: 两列振幅相同，而传播方向相反的相干波，其合成 波是驻波。 2、驻波的形成 :
.cn:8080/info/yanshi/s hipin/qitihuoyan.html
| 2 Acos
2
x | 0

波腹：振幅最大的点称为波腹。
波腹的位置为： x k k 0 , 1, 2... 2 两相邻波腹间的距离 / 2。 两相邻波节与波腹间的距离/4。 因此可用测量波腹间的距离，来确定波长。
| cos
2
x | 1
即:
2
x k 的各点。
A Amin | A1 A2 |
当两波源的初相位相同时，相干条件可写为： 干涉加强
干涉减弱
r2 r1 (2k 1) k 0,1,2,3,... 2
r2 r1 k
k 0,1,2,3,...
为波 程差。
例题1 在同一媒质中相距为20m 的两平面简谐波源S1 和S2 作同方向，同频率(f=100Hz )的谐振动，振幅均为A= 0.05m， 点S1 为波峰时，点S2 恰为波谷，波速u = 200m / s 。 求：两波源连线上因干涉而静止的各点位置.
疏 u u
密
半波损失
形成的驻波在界面处是波节。
实验 结果： 波疏媒质 波密媒质
波密媒质
界面处是波节
u
2
波疏媒质
u
界面处是 波腹
界面处是波腹
理论结果：
y1 Acos(t

r1 )
y2 Acos(t
无半波损失
2

r1 )
0
u
u
界面处是波节
y1 Acos(t
y y1 y2 Acos(t
2

2
x ) Acos(t
2

x)
利用三角函数关系求出驻波的表达式 ：
y 2 Acos
振幅为 2 Acos 2

x cost
x

各点作频率相同、振幅不同的简谐振动 。
利用三角函数关系求出驻波的表达式：
y 2 Acos
二、波的干涉： 1、干涉现象: 在一定条件下，两波相遇，在媒质中某些位置 的点振幅始终最大，另些位置振幅始终最小， 而其它位置，振动的强弱介乎二者之间，保 持不变，称这种现象为干涉现象。 2、产生干涉的条件：
两波源具有相同的频率。 两波源具有恒定的相位差。 满足上述条件的波称为相干 波。 两波源的振动方向相同。 p r1 3、干涉加强、减弱条件： s1
O

S1
x

P

S2
x
解 选S1 处为坐标原点O，向右为x 轴正方向,设点S1 的振 动初相位为零,由已知条件可得波源S1 和S2 作简谐振动的运 动方程分别为:
y1 Acos(2ft )
y2 Acos(2ft )
S1 发出的向右传播的波的波函数为: y1 Acos[2 ( ft S2 发出的向左传播的波的波函数为:
水槽插入两端开口玻璃管，音叉置于管上端，音叉频率为， 管中空气柱长度 l 通过水面高低调节。水面由管顶端下降到l=a 时，声强第一次达到最大;下降到l=d+a和l=2d+a时，声强第二、 三次最大。声强出现极大，表示音叉频率与管内空气柱固有频 率相同而发生共振。
1 1 1 1 a , a d , a 2d 1 4 2 4 4 d 2 , u , u 2d
t x y2 Acos[2 ( ) ] T
(2)根据波的叠加原理,合成波的波函数为:
t x t x y y1 y2 Acos[2 ( )] Acos[2 ( ) ] T T x t x t 2 Acos(2 )cos(2 ) 2 Asin(2 )sin(2 ) 2 T 2 T