当前位置：文档之家 › 结构力学(第二章)-静定刚架

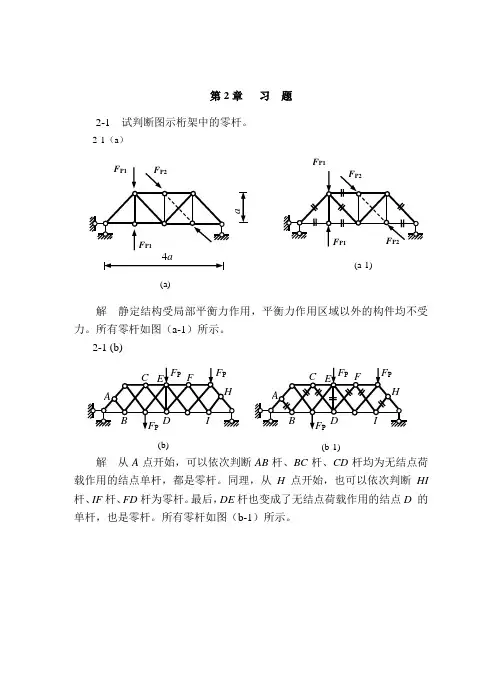
结构力学(第二章)-静定刚架

  • 格式：ppt
  • 大小：1.53 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

结构力学(I)-02-1 结构静力分析篇4(桁架)@@9

结构力学(I)-02-1 结构静力分析篇4(桁架)@@9

4m
15kN 4m
15kN 4m
15kN
F
FNGF
15kN
ME = 0 MF = 0
FNGF = -20 kN FNGE = 25 kN
哈工大 土木工程学院

16 / 53
第二章 静定结构受力分析
有些杆件利用其特殊位置可方便计算
L形结点 结点平面汇交力系中，
除某一杆件外，其它所
结点 单杆
有待求内力的杆件均共 线时，则此杆件称为该 结点的结点单杆。
FN1
FN2 FN
Fy=0 f(FN2 , FN )=0 Fx=0 g(FN2 , FN )=0
38 / 53
FAy
哈工大 土木工程学院

第二章 静定结构受力分析
FP
FP
E b
3
FP
1 2 4
FP D
FP
FP
FP
C
弦杆 斜杆
F F
M
y
x
C
0
0
0
f ( FN 2 , FN ) 0
FN1
FN 2
y
FN 2 FN 0
竖杆
利用对称性取结点D 先求斜杆b，再利用结点E
哈工大 土木工程学院
F F
0 0
FN 4
FN 3
39 / 53
y
第二章 静定结构受力分析
练习求FN1、 FN2 、 FN3
FP
1
FP
2h
对称轴?
3
2
4a
为了使计算简捷应注意： 1）选择一个合适的出发点； 2）选择一个合适的隔离体； 3）选择一个合适的平衡方程。
哈工大 土木工程学院

长沙理工结构力学期末考试题库和答案第二章静定梁与钢架 结构力学超静定

长沙理工结构力学期末考试题库和答案第二章静定梁与钢架 结构力学超静定

长沙理工结构力学期末考试题库和答案第二章静定梁与钢架结构力学超静定第二章静定梁及静定刚架一、判断题1．静定结构在荷载作用下产生的内力与杆件弹性常数、截面尺寸无关。

（ O ）2．计算位移时，对称的静定结构是指杆件几何尺寸、约束、刚度均对称的结构。

（ O ） 3．静定结构在支座移动、变温及荷载分别作用下，均产生位移和内力。

（ X ）4．几何不变体系一定是静定结构。

（ X ）25．图示结构 MK = ql/2（内侧受拉）。

（ X ）q6．图示结构中 AB 杆弯矩为零。

（ X ） q7．图示结构中 |MAC|=|MBD|。

（ O ）|8．图示结构中 |MAC|=|MBD。

（ O ）l9．图示结构 M 图的形状是正确的。

（ X ） M 图 10．图示结构|MC|=0 。

（ O）11．图示结构中 A、B 支座反力均为零。

d二、选择题12．静定结构有变温时：（ C ）A. 无变形，无位移，无内力；B. 有变形，有位移，有内力；C. 有变形，有位移，无内力；D. 无变形，有位移，无内力。

13．静定结构在支座移动时：（ D ）A. 无变形，无位移，无内力；B. 有变形，有位移，有内力；C. 有变形，有位移，无内力； D 无变形，有位移，无内力。

O ）（14．静定结构的内力计算与（ A ）A. EI 无关；B. EI 相对值有关；C. EI 绝对值有关；D. E 无关， I 有关。

15．图示结构MA 、MC （设下面受拉为正）为：（ C ）A.MA =0 ，MC=Pa/2 ；B.MA =2Pa ，MC=2Pa ；C.MA =Pa ，MC=Pa ；D.MA =－Pa，MC=Pa 。

16．图示结构 MA、 MB （设以内侧受拉为正）为：( DA. MA=－Pa ， MB =Pa；B. MA=0 ， MB =－Pa ；C. MA=Pa ，MB =Pa ；D.MA=0 ， MB =Pa 。

17．图示结构 B 点杆端弯矩（设内侧受拉为正）为：( C )A.MBA = Pa, MBC = －Pa ；B.MBA = MBC = 2Pa；C. MBA = MBC = Pa ；D.MBA = MBC = 0 。

结构力学第2章 杆系结构的组成分析

结构力学第2章 杆系结构的组成分析

(c)
图2-14
退出
解： 图2-14a所示体系可视为在图2-14b所示静定结 构的基础上逐次增加两个杆按规则3构成，如 图2-14c所示。也可如图按相反次序依次撤除两 杆，使体系简化后再分析。两种方法分析结果 该体系都是无多余约束的几何不变体系，可作 为静定(构架)结构。
退出
[例题2-2] 试对图2-15所示体系进行几何组成分析。
这些约束的约束数s及相当的单铰、(单)链杆和 单刚结点个数是多少呢？
复铰
复刚结
(d)一铰连接多根杆 (e)一杆连接多根杆 (f)多杆刚结
退出
图2-2 约束
由图2-2可以归纳得到， 连接n个刚片的复铰 相当于(n-1)个单数，相当 于2(n-1)个约束；n个刚 片 之 间 复 刚 结 点 相 当 于 ( n-1) 个 单 刚 结 点 ， 相 当 于 3(n-1)个约束。联结三点的链杆，将原来结点的六 个自由度减少为整体的三个自由度，因而相当于三 个约束，即相当于三根简单链杆。一般说来，联结 n个点的的复杂链杆相当于(2n-3)根简单链杆。
利用加二元体规则，可在一个按上述规则构成 的静定结构基础上，通过增加二元体组成新的静定 结构，如此组成的结构称为主从结构，基础部分称 为主结构或基本部分，后增加的二元体部分称为从 结构或附属部分。图2-13所示之结构均为主从结构。
退出
附属部分
C DF E
A
B
(a)
附属部分
基本部分
(b)
附属部分
基本部分
结构 (几何不变)
静定结构(梁、刚架、拱、桁架、组合结 构) 无多余约束
超静定结构(梁、刚架、拱、桁架、组合 结构) 有多余约束
退出
不同静力特征的结构其分析计算方法是不同的。 因此，要正确分析必须首先准确无误地判断体系的 可变性以及静定和超静定性质。

结构力学二三四章总结

结构力学二三四章总结

第二章静定梁与静定刚架§2-1 单跨静定梁一、概述1、单跨静定梁的结构形式：水平梁、斜梁及曲梁简支梁、悬臂梁及伸臂梁。

2、3个内力分量的规定：图示（注：1、附加增量；2、成对出现：作用力与反作用力；3、正负号统一）轴力N(截面上应力沿杆轴切线方向的合力)：拉力＋，压力－剪力Q(截面上应力沿杆轴法线方向的合力)：以绕截面邻近小段隔离体顺时针旋转为＋，反之为－弯矩M(截面上应力对截面形心的力矩)：弯矩使杆件下部受拉时为正，上侧受拉时为负3、截面法、分离体、平衡方程：求指定截面的内力的基本方法。

图示将指定截面假想截开，切开后截面的内力暴露为外力，取任一局部作为隔离体，作隔离体受力图（荷载、反力、内力组成平面一般力系或平面汇交力系），由隔离体的平衡条件可以确定所求截面的三个内力。

平面一般力系平衡方程的三种形式。

注意：平衡方程的正负和内力的正负是完全不同性质的两套符号系统。

受力平衡条件：平面一般力系，平衡方程不同形式（正负号：同方向同符号）轴力＝截面一边的所有外力沿杆轴切线方向的投影代数和；剪力＝截面一边的所有外力沿杆轴法线方向的投影代数和；弯矩＝截面一边的所有外力对截面形心的力矩代数和。

画隔离体受力图时，注意：(1)隔离体与其周围约束要全部截断，而以相应的约束力代替；(2)约束力要符合约束的性质。

截断链杆以轴力代替，截断受弯构件时以轴力、剪力及弯矩代替，去掉支座时要以相应的支座反力代替。

(3)隔离体是应用平衡条件进行分析的对象。

在受力图中只画隔离体本身所受到的力，不画隔离体施给周围的力；(4)不要遗漏力。

包括荷载及截断约束处的约束力；(5)未知力一般假设为正号方向，已知力按实际方向画。

（6）“三清”：截面左右分清、外力清楚、正负号清楚4、内力图：图示1）定义：表示结构上各截面的内力随横截面位置变化规律的图形。

内力方程式：内力与x（表示横截面位置的变量）之间的函数表达式。

2）几点注意（1）弯矩图画在受拉边、不标明正负，轴力图剪力图画在任一边，标明正负。

04静定刚架--习题

04静定刚架--习题

XC YC
B
YB
M A 2Pm(
)
结构力学电子教程
4 静定刚架
4.9-4.14 计算刚架指定截面内力。 4.9 计算题4-1图刚架结点C各杆截面内力。 2kN/m N CD C 解： Q C D M CD CD
4m
2kN/m
D
A
6m
B
2kN/m
（1）取CB为隔离体
C
M CA QCA N CA
NCE 0, QCE 2P, M CE 2Pa
（右边受拉）
B
结构力学电子教程
4 静定刚架
4.13 计算题4-13图刚架结点D各杆截面内力。 解： 2kN NDC 4 3 4 16kN
3kN/m 4m C D E
QDC 5.33kN
M DC 4 3 3 4 2 5.33 6 68kN m（上边受拉）
M A 0 : 2 5 7.5 YB 10 0
XA
2.08kN
B
5m
YC XC C
XB M B 2.08kN YB 7.5kN
YB 7.5kN( )
0 : 2 5 2.5 YA 8 0
YA 2.5kN( ) X 0 : X A XB 0
A
2m
9kN
2m
C
2m
6.31kN
9.69kN
NEF 0 QEF 8 9.69 1.69kN
M EF 9.69 4 8 2 22.76kN m （下边受拉） NEB 0
1.69kN1.69kN 9kN 22.76kN m 4.26kN m E 9kN 27kN m

结构力学3静定刚架

结构力学3静定刚架
（）
速绘弯矩图
Pa
P
a
2m/3 m/3
m m/3
m 2m/3
a
a
a
a
↑↑↑↑↑
P
Pa a
P Pa
a
qa2/2 l
a
a
P
m
m Pa/2
m
Oa
a
m
m/2 m
m/2a
a
Pa/2
m
m/2a
m
a
m/2
m/2
m/2
0
m/2a
a
a m/2
a
a
P
2Pa Pa
2P
0
Pa
a
a
a
Pa
a
2P
m
2Pa Pa
P
Pa P
h
E

D
B
2q A
2a 2a
4a
4）杆AB
N BA
M BA
B QBA
2q 14qa2
A 8qa
10qa
3)杆BE q
M BE

N BE
QBE 4a
8qa 2
M图NBBiblioteka = 10qa QBA = 0 M BA = 2qa2
x=0
NBE q 4a sin = 0
N BE
=
4qa
1、悬臂刚架
可以不求反力，由自由端开始直接求作内力图。
q
2q
½qL²↓↓↓↓↓↓↓↓↓
qL²
2q
↓↓↓↓↓
L
q
qL²
2m
2m
L
6q
2、简支型刚架弯矩图
简支型刚架绘制弯矩图时，往

长沙理工大学结构力学解答集(学生版)

第一章机动分析一、判断题1．( X ) 2．( X ) 3．( X ) 4．( O )二、选择题5．(B) 6．(D) 7．(C) 8．(A) 9．(A) 10．(A) 11．(C) 12．(B) 13．(A)三、填空题14．几何瞬变15． 或不定值16．两刚片用不完全相交及平行的三根链杆连接而的体系。

17．几何不变且无多余约束。

四、分析与计算题18．几何不变且无多余约束。

19．瞬变。

20．几何不变无多余约束。

21．几何不变无多余约束。

22．瞬变。

23．几何不变无多余约束。

24．可变。

25．几何不变无多余约束。

26．几何不变无多余约束。

27．几何不变，有两个多余约束。

28．几何不变无多余约束。

29．几何不变无多余约束。

30．几何不变无多余约束。

1第二章静定梁与静定刚架一、判断题1．（O）2．（O）3．（X）4．（X）5．（X）6．( X ) 7．( O ) 8．( O ) 9．( X ) 10．( O ) 11．( O )二、选择题12．（C）13．（D）14．（A）15．( C )16．( D )17．( C ) 18．( C )19．（C）20．（B）21．（C ）三、填空题22．不变，零23．无关24．位移，变形，内力25．在任意荷载作用下，所有反力和内力都可由静力平衡条件求得确定的、有限的、唯一的解答。

26．0 ，027．20kN·m ，下28．75kN·m ，右29．2Pa，右30．0.5pa ，上31．Pa, 左四、分析与计算题32．33.20.5q lq l28M图PaPaPaPaPaPaPaM图2334． 35．图(k N m 1616M RA ql H 0M B B ql 0.5( )图M Bql 0.522______A36． 37．1050203050().图 M kN m DC BE Aql20.5ql 2ql20.5图M DC B A38． 39．图M m CA B().图 M kN m 2020AB 5DC40． 41．BCD40120图 M ()kN .m A 408040图M PlPl2Pl ABC D442． 43．().图 M kN m 4441535 图M ql 28ql 223ABDC44． 45．()图 M kN .m AB 151515151515C DE F 1515Pa 2/3图Pa 2/3Pa 2/3Pa 2/3M AB46． 47．Pa 2/3Pa /34AB图MPaPa0.5P a0.5P a图M48． 49．PaPaPaPa图M图M550． 51．ql20.5ql20.5ql20.5ql20.5图M图M mmm m52． 53．P aPa0.5P a0.5P a0.5M 图m0.5m54． 55．mmmmqPM 图56． 57．4040404020kN1k N 1k N3k N1k N Q 图 (3.5)N 图 (3.5)658．PPPQ 图N 图59．qaqa qa /2qaqa qa/2qa /232Q 图 N 图60． 61．PPa 图M ACDB图M qa 22qa 2262．ABC ED F Pa Pa 13237第三章 静 定 拱一、判断题1．（X ） 2．（O ）3． ( O )二、选择题4．（C ）5．（B ） 6．（D ） 7．（B ） 8．( B ) 9．( D )三、填空题10． 0 , 011． 7.5kN ·m , 下四、分析与计算题12． 00K K K M Q N qr ===-13． 20(13)5(31)5(31)K K K M kN m Q kNN kN =-⋅=-=-+14． 100105K K K M kN m Q N kN =-⋅==-8第四章 静定桁架一、判断题1．（O ） 2．（O ） 3．（X ） 4．（X ） 5．（X ） 6．（X ）二、选择题7． ( D ) 8．( D ) 9．( D ) 10．（D ） 11．（D ）三、填空题12． 0 , 013． BC , FG , ED ， DB , DF 14． 1.414P , －2P 15． 0.5P ( 拉 ) 16． P四、分析与计算题17． 18．图M 2Pa2Pa 2Pa Pa6Pa 6ABC D E FG图M 2qa 22qa 22qa 22qa 2qa219．9ABDC806020M ()kN .m 图20． 14/3N P = 21． N 10= N P 22=22． N 1=PN P 22=-23． N 125kN =-N 2=44kNN 310kN =24． N 10= N P 2233=/ 25． N 10= N P 2= N P 322=/ 26． N P 12= N P 22=-27． N P 115=-. N P 2=28． N P 106=. N P 2=29． 1222N P N P =-=30． 1234101052102N N N N =-==-=-kN , kN , kN , kN 31． N P 1=-32．(kN)(kN)(kN)30280/3350/31404050140/3140/320M 图图图Q N 203033．10444().4图 M kN m 链 杆 轴 力， N = -2 kN34．Q 图(kN)1515().图 M kN m 555512.55157.512.52N 图(kN)1535．1502.5272.5452.52150100250250N 图 (kN)903015028026010100Q 图（kN ）图 M (kN .m )11第五章 图 乘 法一、判断题1．( X ) 2．( X ) 3．( X ) 4．( X ) 5．( O )二、选择题6．( C ) 7．( C ) 8．( C ) 9．( C ) 10．( B ) 11．( A ) 12．( A ) 13．( C )三、填空题14．(////)ac ad bd bc l 3636+++⋅ 15．()ql EI 424/ ()→ 16．733ql EI /（）17．5482Pa EI /() （逆 时 针） 18．4Pa/EA （↓） 19．qa EI qa EA 330625/./+四、分析与计算题20． ()()()C EI Pl h Plh EI ϕ=-⋅⋅⋅=-113322//// ()21． ()AVPl EIh l ∆=+22916// （↓）1222． ()AV Pl EI ∆=↓29243/ 23． ()BH EI ∆=-←11340/ 24． A φ=00016.rad （）25． ()CH Pl EI ∆=-←19483/() 26． ()DH ∆=→00084.m27． K D =4860/EI ()28． AB Pl EI ϕ=492/ （）29． AB Pl EI H ∆=35813/() （）30． BVE I 2M l2=∆(31． ()ϕD MlEI =632．ϕB = 15.625( )EI33． ∆AH = - 5 P a 3 / E I ( ← )34． ∆BH = - 8Pa 3/ E I ( ← ) 35． ϕD EI =835/ () 36．ϕD = /2()52P l E I37．3ϕC 左 =13 /162ql EI （）38． ()∆EV ql EI =-↑74324/()39． ϕAB EA =2414. （ ）1340． ()∆CV Pa EA =↓2414.41． ϕC Pa EI P EA =+532752/./（） 42． ∆AV EI EA =+3101875(↓)43． ()ϕC EI EI EI =++=301333408333..（） 44． ∆C D H cm =0795.（）45． ∆∆CH R =-⋅=∑--⋅=()1∆∆ （→）46． ()ϕB R l l =-⋅=--=∑∆∆∆0505././ ()14第六章 力 法一、判断题1．(X) 2．(X) 3．(X) 4．(X) 5．(X) 6．(X) 7．(X)二、选择题8．(B) 9．(D) 10．(A) 11．(C) 12．(C)三、填空题13．6次14． (2+1.414)Pl/EA 15． -256/EI ， 0 16．l EA l EI //()+13123 17．l EA h EI //()+233 18．0 ， 0 ， 0四、分析与计算题20． δ1145=./EI ； ∆1405P EI =-/ 21． 111234/765/P E I E I δ=∆=- 22．152 /2Pl图M PPlPl /2Pl 基 本 体 系PX 123．X 1X 1基 本 体 系 8322432248图M ()kN .m ()分 2()分 324．X 1413431基本体系图 M ()kN .m kN .m4kN .m25．X 1X 14522.5X 2X 2基 本 体 系 图M ()kN .m ()分 2()分 326．16基本体系31.42222.89X 1图 M ()kN .m27．qa /2qa 2/242 /122 /242 /242 /242基本体系qa qa qa qa qa a /21X 图 M ()kN .m /122qa28．X 1X 2=0ql 2/4ql 2/2基本体系 M 图 X 1ql 2/2ql 2/4(2分 )(3分 )29．175050图 M ()kN .m30．q1EI =基 本 体 系X 432720图 M ()kN .m 504231．X 2X 1基 本 体 系图 M ()kN .m 17. 8231. 6826. 6432． 33．M 图1.77P1.77P3PPP3P1.23P 1.23P4.234.23-12.796-12.8-13.870.5340.5346.1337.20.534a-a a -bb c N (k N )a b c =-=-=0755********...34．120.4375 1.417N P N P =-=35．1810kNX 1基本体系( 2分 )3030M 图·()kN m ( 3分)36．X1图M X 2q基 本 体 系8.71 6.773.8716.52 1.87qqqqq37．EI/l X=X =1M 1图图M N 图 1lα1分 )(2分 )(7.521138．l图M X 11=()34EI l θ基 本 体 系39．1922.2X=图M R=kN .m-3.7kN X=1-1(2分 )(4分 )基 本 体 系40．()()()()()()()334164 24hA h EI Ph h EI h Ph h PhEI ∆=⋅⋅-⋅⋅⋅=第七章 位 移 法一、判断题：1．（X ） 2．（X ） 3．（O ） 4．（O ） 5．（O ） 6．（X ）7．（O ） 8．（X ） 9．（X ）二、选择题10．（B ）三、填空题11． 0 12． 4 13． 273EI l / 14． 0 15． -6l 016． -Pl17． r 22 = 4.5 R P 1 = -8 18． r 11 = 13 R P 1 = 020四、分析与计算题19． r EI l 1110=/ R ql P 12316=-/ 20． r 22 = 3EI R P 2 = 021．ql /8ql 2/8M Z 12图22．Z 1101010101010(kN m).M 图23．Z 117.417.47.74(kN m).M 图24．Z 1M Pl/4Pl/4Pl/4Pl/4图25．21Z 1hhhha aM a= Pl/h= Pl/图12432717226．Z 12- Pl+ ql 192962Pl+ql Pl-ql 2192Pl/M 35315图827．P /23 图P /23P /23P /23M28．Z 1/9/9/9/9/9245图Pl Pl Pl Pl M Pl29．2210kN Z 1Z 2基 本 体 系20/320/320/310/3图 (kN m).M30．Z 110kN/m10.665.3320.1314.2111.25 5.33基 本 体 系图 (kN m)M .Z 231．Z 1基 本 体 系=10kN/m 80kNZ 248.648.68037.0362.8125.78图 M ()kN .m q32．Z 1基 本 体 系图(kN m)4kN/mZ 225/1450/775/14M .33．23140/13160/1310kN10kN/m320/1320Z 1Z 2基 本 体 系 M 图 （kN ·m ） 34．7101010M 图 （ 2332ql /） 35．Z 2图 (kN m).=10kN/m5.42.961.481.4811.8311.83简 化 图q M Z 136．2kN/mZ 1Z 2基 本 体 系图 ( N m).1.470.421.262.740.21M 4k37．24P /2P/2Z 1Z 2基 本 体 系5 /185 /18/6/62 /92 /9/18/18M 图Pl Pl PlPlPlPl Pl Pl简 化38．EI 1= 图=11/4 3 /420/320/37.540/3M EI3 3 /8EI3 /8EIZ ∞EI39．图M40．Z 1图 (kN m)1cm193.5918211.5.M第八章力矩分配法一、判断题1．( X ) 2．( O ) 3．( X ) 4．( X )二、选择题5．( B ) 6．( B ) 7．( C ) 8．( C ) 9．( D ) 10．( D )三、填空题11．012．0 , M AB2, MAB13．M/2 下14．8 kN·m15．1/3 ，1/3 ，1/316．0 ，1 ，0.2252617．i EI l =，()μBA i i i =+=34337，μBC =47，μBD =0四、分析与计算题18． μAD =19 , μAC =49 , μAB =49, μBA = 1 , μBE = 0M BE F = －160 kN ·m19． μμAB AC ==3812/,/, μμAD AE ==180/,M k N m M AB AC FF .,,=⋅=750 M M kN m AD AE FF ,==⋅02020． μμμμAD AC FD FG ====05. μμμDA DE DF ===13/，M kN m DF F,=-⋅375 MkN mFDF=-⋅37521． 14.7BC M kN m =-⋅ 22． 40AC M kN m =-⋅ 23． 0.3EB M kN m =⋅ 24． 2BA M kN m =⋅ 25．27MF2 分 ( )M 图 kN m .( )3 分( )2 分( )5 分( )1/21/2-1BA BCCB CD DC0.50.51/32/3-40-2013.3326.67-13.3313.33-6.67-6.67-3.331.111.112.22-1.11-0.56-0.56-7.217.2125.56-25.56-34.4434.44A B CD25.567.217.213.626．BDAC10.8430.8347.0830.83202023.5523.5510.845.425.42对 称 结 构 ， 对 称 荷 载 ， 取 一 半 结 构 计 算M 图 kN m .( )27．28M 图 kN m .( )CABDEBA BE EB μMFDA AD AC AB 11.54-1.62 -2.43 2.5 分 ( )2.5 分( )7 分( )6/133/134/1345-12012034.6217.3123.08-26.31-52.62-78.9212.14 6.078.14.0546.7668.38-115.1381.35-81.3581.3546.7668.38115.1323.3840.680.40.628．μM F5.126.6901234521 23-9090454.238.594.3 4.849.68-2.6-5.21-3.93-1.970.86 1.75+1.975.09-5.0926.5690-90( 2.5 分 )( 2.5 分 )( 7 分 ）0.330.670.570.4310-12.83-25.65-19.35-9.68图 M ()kN .m -26.564345343229．7.4CB M kN m =-⋅30．29对 称 性 取 半 结 构1.891.055.712.86307.8722.138.66A D EFB CAD AB BA BC BEBF 301.5-7.5-22.5-11.251.492.983.980.99 1.79-0.37-1.12-0.560.170.230.060.1-7.87-22.13-8.66 5.71 1.051.89μ 3 分 ( )3 分( )8 分 ( )0.250.750.30610.4082 0.102 0.1837M 图 (kN.m)31． 16.85CB M kN m =⋅ 32．kN m .( )M 图 2.231.934.167.895AD μμAB i AD AB S AB i EI l=i/=i AC i ==6i ,,,,AC μ= 0.257,= 0.446 ,= - 7.5kN m .,DA M = - 3.75kN m .,= 4i 32i =0.297M AD FF,AC S =⨯3,AD S =6i ,1.123033．CD B A EF 56.8518.960图 M ()kN .m 对 称 性 取 半 刚 架 ，u MFCA AC AB BA BF BE EB 0.50.50.40.30.3-4040-60-604866-618189-1.8-3.6-2.7-2.72.70.90.918.9-18.953.43.3-56.7-63.3（ 4 分 ）（ 3 分 ） （ 3 分 ）（8 分 ）53.7 3.1563.1518.934． 3.31DC M kN m =⋅31第九章 影响线及其应用一、判断题1． ( X ) 2．( O ) 3．( X ) 4．( X ) 5．( O ) 6．( X ) 7．( X )二、选择题8．( C ) 9．( B ) 10．( C ) 11．（C ） 12．（C ） 13．（D ） 14．（A ）三、填空题15． 结 构 在 恒 载 及 活 载 作 用 下 ， 各 截 面 内 力 最 大 最 小 值变 化 范 围 图 。

结构力学3静定结构的受力分析-刚架

1 结构力学多媒体课件1、刚架由梁和柱组成的结构，其结点全部或部分是刚结点。

2、刚架的形式2）简支刚架1）悬臂刚架2、刚架的形式3)三铰刚架4)主从刚架3、刚架的特点1）杆数少，净空大，便于使用3、刚架的特点2）刚结点的特点①变形：刚结点处的各杆端不能发生相对移动和相对转动，因而受力变形后，各杆杆端转动了同一角度，即各杆之间的夹角保持不变。

②受力：刚结点可承受和传递弯矩保持角度不变3、刚架的特点3）横梁和竖柱连成整体，使整体刚度增大，弯矩的峰值减少二、刚架中各杆的杆端内力1、支座反力的计算⑴求反力时要先根据支座的性质正确定出反力未知量个数，不能多、不能少。

⑵假定反力方向，由平衡方程确定其数值。

⑶应尽量利用一个平衡方程求一个未知力。

⑷求出反力后要有没有用过的平衡方程校核。

l /2l /2l /2l /2CBAPF AY =0.5PF BY =0.5PF AX=0.75P F BX =0.25P2m 2m 4mCBA4m2kN/mGFEDF AX =1KNF CX =1KNF CY =3KNF BY =7KN2、杆端内力的计算⑴方法：截面法⑵内力符号结点处有不同的杆端截面。

各截面上的内力用该杆两端字母作为下标来表示，并把该端字母列在前面。

——AB杆A端的轴力。

FN AB——AB杆A端的剪力。

FQ AB——AB杆A端的弯矩。

MAB2、杆端内力的计算⑶内力的正负规定轴力FN：以拉力为正，压力为负。

剪力FQ：以绕隔离体顺时针转为正,反之为负。

弯矩M：不规定正负，但弯矩图画在受拉侧。

F N FNF Q F QM AB M BAF NF NF QF Q MBAM AB 竖杆剪力图和轴力图可画在任一侧，但必须标出正负；弯矩图画在受拉一侧，可不标正负。

2、杆端内力的计算 ⑷正确选取脱离体⑸注意结点平衡∑F X =0 ∑F Y =0 ∑M D ＝0一般先求出支座反力及铰结点处的内约束力，然后将刚架拆成杆件，逐杆绘制其内力图，将各杆的内力图合在一起就是刚架的内力图。

(完整版)结构力学解析

第一章平面体系的几何组成分析一判断题1. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。

（×）2. 两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必需满足的条件。

（√)3。

计算自由度W小于等于零是体系几何不变的充要条件.（×）4. 三个刚片由三个铰相联的体系一定是静定结构.（×)5。

有多余约束的体系一定是超静定结构。

(×）6。

平面几何不变体系的三个基本组成规则是可以相互沟通的.（√）7。

三刚片由三个单铰或任意六根链杆两两相联，体系必为几何不变。

（×）8. 两刚片用汇交于一点的三根链杆相联，可组成几何不变体系.（×）9。

若体系计算自由度W〈0，则它一定是几何可变体系。

(×）10。

有多余约束的体系一定是几何不变体系.（×）11。

几何不变体系的计算自由度一定等于零.(×)12。

几何瞬变体系的计算自由度一定等于零。

（×)13. 图中链杆1和2的交点O可视为虚铰。

(×）题13图二选择题1. 图示体系为:（A）A．几何不变无多余约束 B．几何不变有多余约束 C．几何常变 D．几何瞬变题1图题2图2。

图示体系为：（B）A．几何不变无多余约束 B．几何不变有多余约束 C．几何常变 D．几何瞬变3. 图示体系是（B）A．无多余联系的几何不变体系 B．有多余联系的几何不变体系C．几何可变体系 D．瞬变体系题3图4。

图示体系的几何组成为（B）A．几何不变无多余约束 B．几何不变有多余约束 C．瞬变体系 D．可变体系题4图5. 图示平面体系的几何组成为（C)A。

几何不变无多余约束 B。

几何不变有多余约束 C.瞬变体系 D.几何可变体系题5图6. 图示体系为（A）A。

几何不变,无多余约束 B.几何不变,有多余约束 C。

几何常变 D。

几何瞬变题6图题7图7. 图示体系为（D）A。

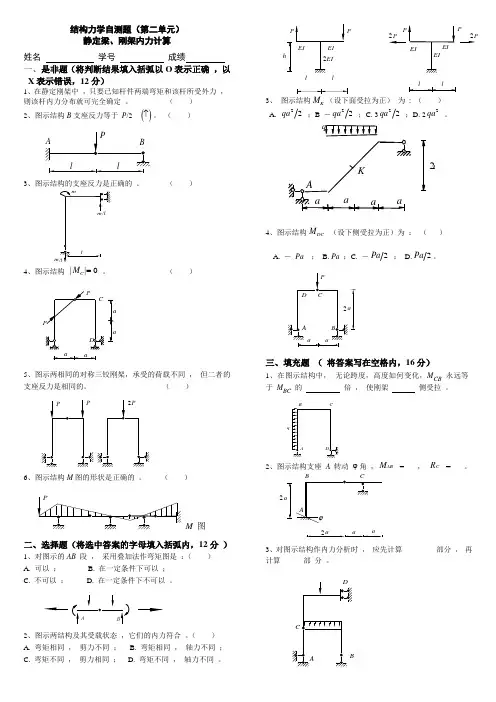
结构力学自测题(第二单元)

结构力学自测题（第二单元） 静定梁、刚架内力计算姓名 学号 成绩 一、 是非题（将判断结果填入括弧以O 表示正确 ，以 X 表示错误，12分）1、在静定刚架中 ，只要已知杆件两端弯矩和该杆所受外力 ， 则该杆内力分布就可完全确定 。

（ ）2、图示结构B 支座反力等于 P /2 ()↑。

（ ）3、图示结构的支座反力是正确的 。

（ ）4、图示结构 ||M C =0 。

（ ）aa5、图示两相同的对称三铰刚架，承受的荷载不同 ， 但二者的支座反力是相同的。

（ ）6、图示结构M 图的形状是正确的 。

（ ）M 图二、选择题（将选中答案的字母填入括弧内，12分 ）1、对图示的AB 段 ， 采用叠加法作弯矩图是 ：（ ） A. 可以 ；B. 在一定条件下可以 ；C. 不可以 ；D. 在一定条件下不可以 。

2、图示两结构及其受载状态 ，它们的内力符合 。

（ ） A. 弯矩相同 ， 剪力不同 ； B. 弯矩相同 ， 轴力不同 ； C. 弯矩不同 ， 剪力相同 ； D. 弯矩不同 ，轴力不同 。

PPll l3、 图示结构K （设下面受拉为正） 为 : （ ）A. qa 2 ；B －qa 22 ；C. 3qa2 ；D. 2qa 2。

2 a4、图示结构M DC （设下侧受拉为正）为 ： （ ）A. － Pa ；B. Pa ；C. －Pa ；D.Pa 2。

aa三、填充题 （ 将答案写在空格内，16分）1、在图示结构中， 无论跨度，高度如何变化，M CB 永远等 于 M BC 的倍 ， 使刚架 侧受拉 。

2、图示结构支座 A 转动 ϕ角 ，M AB = ___， R C = __ 。

BCaaA ϕ2a23、对图示结构作内力分析时 ， 应先计算_________部分 ， 再 计算______部 分 。

4、．图示结构DB 杆的剪力Q DB = _______ 。

5、图示梁支座B 处左侧截面的剪力Q B 左=_ __ 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

N EF 4 P()
F
y
0, NCD 6P()
B
P 0, YA 2P()
3.复合刚架(主从结构)的支座反力(约束力)计算 若附属部分上无 方法:先算附属部分,后算基本 例1: 求图示刚架的支座反力 外力,附属部分上的 部分,计算顺序与几何组成顺序 约束力是否为零? 相反. D
分段 定点 连线
例题1: 作图示结构弯矩图
Pl / 2 Pl / 2 l/2
P
练习: 作弯矩图
P P
l
l/2
l l
Pl / 2
l
2 Pl
Pl
Pl
P
l l
例题1: 作图示结构弯矩图
Pl / 2 Pl / 2 l/2
P
练习: 作弯矩图
P P
l
l/2
l l
Pl / 2
l
2 Pl
P
l/2 l/2
Pl
Pl
结点上无外力偶作用,则两 三. 刚架指定截面内力计算 个杆端的弯矩值相等,方向 与梁的指定截面内力计算方法相同. 相反.
例1: 求图示刚架1,2截面的弯矩
C
P
连接两个杆端的刚结点,若 §2-2 静定刚架受力分析
M1
M
1
2
l 2 l 2
M2
A
B
l 2 l 2
M
P/4 P/4
XA
XB
YA
解:
YB
M 2 Pl / 4(右侧受拉) M1 Pl / 4(上侧受拉) M1 M 2 (外侧受拉)
x A A
A B B y A B A B
例2: 求图示刚架的支座反力 q ql 2 解: ql
l
F
A
x
0, X A ql 0, X A ql()
A A
XA
MA
YA
l 2 l 2ຫໍສະໝຸດ F 0,Y ql 0,Y ql() M 0, M ql l ql 0,
B
l
B
YA
l
YB
2)取DBE部分
A
YB
解: 1)取整体
F 0, X P() 1 M 0, Y 2 P()
x
A B
1 Fy 0, YA 2 P()
1 Fy 0, N DC 2 P() 1 M D 0, N BC 2 P() P Fx 0, N DA 2 ()
C
XA
A
B
XB
YA
l
2 ql
YB
A
l
B
C
XC
YC
XA
A YA
x
2 ql l
2)取AC为隔离体 Fx 0, X B X A ql / 2() Fy 0, YC YA ql 0 l M C 0, X A l ql 2 YB l 0, X A ql / 2()
P
l l
l
练习: 作图示结构弯矩图
P
l l l l
P
l
l
P
l
l
例题2: 作图示结构弯矩图
Pl / 2
P
Pl / 4 3Pl / 4 Pl / 4
Pl / 2
l
3Pl / 4
l
l
0
练习: 作图示结构弯矩图
P
l
Pl
Pl
Pl / 2
2l
2l
P
l
Pl / 2
例题3: 作图示结构弯矩图
ql2 / 2
q
练习: 作图示结构弯矩图
YC
B
XB
YB
例2: 求图示刚架的支座反力和约束力
C
P
l 2 l 2
解:1)取整体为隔离体
F 0,
x
X B P()
A
B
l 2 l 2
XB
MA
YB
YA
C
2)取右部分为隔离体 l M C 0, X B l YB 2 0, YB 2P() Fy 0,YC YB 0,YC YB 2P()
六.由做出的剪力图作轴力图
Pa / 2
Pa / 2 A
B
Pa
P
P/2
P
Pa / 2
P/4
2a
M
P/4
P/4
Q
P/4
a
a
a
A
P/2 P/2 P/4
B
P/4
P/2
N
P/2
P/4 P/4 3P / 2
练习:作轴力图
P
A
B
l
Pl Pl
l
P/2 P/2
M
Pl
Q
P
2l
P
2l
P/2
P
A
P
P/2
P P/2
B P
五.由做出的弯矩图作剪力图
Pa / 2
Pa / 2 Pa
P
P/2
P
Pa / 2
P/4
2a
M
P/4
P/4
Q
P/4
a
a
Pl Pl
a
P/2
l l
练习:作剪力图
P
P/2
M
Pl
Q
P
2l
2l
例:作剪力图
3ql / 2
2
3ql2 / 2
q
ql 2
B
ql
2
ql 2
B
A
A
QAB
l
QBA
M
ql
l ql2 / 2
QBA 0, QAB ql
2.三铰刚架(三铰结构)的支座反力(约束力)计算
方法:取两次隔离体,每个隔离体包含一或两个刚片,建立 六个平衡方程求解--双截面法. 解:1)取整体为隔离体 例1: 求图示刚架的支座反力
C
P
l 2 l 2
A
B
l 2 l 2
XA
XB
l P M A 0, P 2 YB l 0, YB 2 () P Fy 0, YA YB 0, YA YB 2 () Fx 0, X A P X B 0
y
2 A A
M A 2ql 2 (逆时针转)
C
l 2 l 2
B
XB MB
例3: 求图示刚架的支座反力
解:
M
Fy 0,YA 0
B
Fx 0, X B P()
P
A
0, M B pl / 2(顺时针转 )
YA
l
例4: 求图示刚架的约束力
q
C
l
C
XC
YC
A
A
B
N AB
l/2
l/4 l/4
P
A
l
XA
B
l
C
解:1)取附属部分 X D P()
YA
YD
YB
XD
YC
D
YC P / 4()
YD P / 4()
2)取基本部分
P
XD
A
X A P()
XA
B
YD
C
YA P()
YB P / 4() YC
YA
YB
思考题: 图示体系支反力和约束力的计算途径是怎样的?
C N CB 6.85kN 7.5kN A
N
6.85kN
§2-2 静定刚架受力分析
一. 刚架的受力特点
二. 刚架的支座反力计算
三. 刚架指定截面内力计算 四.刚架弯矩图的绘制
五.由做出的弯矩图作剪力图 六.由做出的剪力图作轴力图
七.计算结果的校核
作业
2-10
2-12
ql
P/2
QAB ql
QBA 0
ql ql
Q
ql
§2-2 静定刚架受力分析
一. 刚架的受力特点
二. 刚架的支座反力计算
三. 刚架指定截面内力计算 四.刚架弯矩图的绘制 五.由做出的弯矩图作剪力图 六.由做出的剪力图作轴力图 做法:逐个杆作轴力图,利用结点的平衡条件,由已 知的杆端剪力和求杆端轴力,再由杆端轴力画轴力 图.注意:轴力图画在杆件那一侧均可,必须注明符 号和控制点竖标.
2)取右部分为隔离体 l P M C 0, X B l YB 2 0, X B 4 () P Fy 0, YC YB 0, YC YB 2 () P Fx 0, X B X C 0, X C 4 ()
YA
C
YB
XC
例:作图示结构的M,Q,N图
3kN m B
4kN/m
B
QBC
2kN
C
A
7kN M
1 .5 m 1 .5 m
C
QCB QCB 5.8kN,QBC 7kN
4m
B
2kN
B
NCB
C
2kN
A
Q
5.8kN
C
2.75kN
B
N BC
N BA
YC
N BA 7.25kN N BC 2.75kN
解:1)取AB为隔离体 l M A 0,2ql 2 YB l 0, YB ql () Fy 0,YA YB 2ql 0,YA ql()
F 0,
X C X B ql / 2()
3)取AB为隔离体
例4: 求图示刚架的反力和约束力 P
YA P / 2() X B P / 4() X A P / 4()