大学物理(2.2.2)--常见力非惯性系惯性力
- 格式:pdf
- 大小:240.86 KB
- 文档页数:5






惯性力与非惯性参考系描述非惯性参考系下物体运动的力学原理惯性力是描述非惯性参考系下物体运动的力学原理。
在非惯性参考系中观察物体的运动时,会出现额外的力,即惯性力。
惯性力的出现是由于非惯性参考系的运动导致的,它并非真实存在的力。
惯性力的概念是为了使物体在非惯性参考系中的运动符合牛顿第二定律而引入的。
非惯性参考系是指相对于一个惯性参考系有加速度的参考系。
在非惯性参考系中观察物体的运动时,物体看似受到了额外的力,这些力就是惯性力。
惯性力的大小与物体的质量和非惯性参考系的加速度有关。
惯性力的方向则与非惯性参考系的加速度相反。
根据牛顿第二定律,物体在非惯性参考系中的运动需要考虑惯性力的作用。
以一个例子来说明惯性力的概念。
假设有一个物体在一辆加速的车厢中静止,如果我们在车厢外观察物体,它看起来就好像受到了一个向后的力。
这个力就是惯性力,它是为了使物体在非惯性参考系中的运动与惯性参考系中的运动一致而引入的。
在这个例子中,我们可以看到惯性力的方向与非惯性参考系的加速度相反。
在描述非惯性参考系下物体运动的力学原理时,需要考虑惯性力的作用。
在非惯性参考系中,物体的运动是由受力情况决定的。
根据牛顿第二定律,物体受到的合力等于质量乘以加速度。
而在非惯性参考系中,要使得物体的运动符合牛顿第二定律的描述,需要考虑惯性力的作用。
惯性力的引入使得我们可以在非惯性参考系中应用力学定律,从而简化对物体运动的描述。
通过考虑惯性力,我们可以用与在惯性参考系中相同的方式来分析非惯性参考系下的物体运动。
这使得力学定律的应用更加普适和统一。
总结起来,惯性力是为了描述非惯性参考系下物体运动的力学原理而引入的。
惯性力并非真实存在的力,而是由于非惯性参考系的运动导致的。
惯性力的引入使得我们可以应用力学定律来描述非惯性参考系下物体的运动,使得力学定律的应用更加普适和统一。

大学物理(2.2.2)--常见力非惯性系惯性力一、几种常见的力1.万有引力(Law of Gravitation )1)文字叙述:在两个相距为r ,质量分别为m 1,m 2的质点间有万有引力,其方向沿着它们的连线,其大小与它们的质量的乘积成正比,与它们之间的距离的平方成反比,即2)数学表示 0221r r m m G F = ——引力质量Gravitational Mass其中 211..1067.6--?=kg m N G ——引力常量。
2.重力(Gravity )——本质上归结于万有引力。
1)文字叙述:物体重力就是指忽略地球的自转效应时,地球表明附近物体所受的地球的引力,即物体与地球之间的万有引力。
其方向指向地心。
2)数学表示 G=mg g=9.8m.s -2——重力加速度。
3)思考题:赤道的重力加速度大还是两极的重力加速度大?为什么?3.弹性力(Elastic Force )大家知道,两个物体相互接触,彼此将产生形变,使其内部产生反抗力——形变恢复力(弹性力)。
形变是产生弹性力的条件之一。
例如:板擦和桌子相互接触,彼此有了一定的形变,在各自的接触部分产生弹性力。
所以,弹性力是一种与物体的形变有关的接触力。
即发生形变的物体,由于要恢复原状,对与它接触的物体会产生力的作用,这种物体因形变而产生欲使其恢复原来形状的力叫做弹性力。
常见的弹性力有:1)弹簧中的弹性力:弹簧被拉伸或压缩时产生的弹性力。
胡克定律(Hooke Law ):在弹性限度内,弹性力的大小与弹簧的伸长量成正比,方向指向平衡位置。
数学表示 f=-kx—— k 为弹簧的劲度系数(Stiffness )。
k 的值决定于弹簧本身的性质。
而弹簧弹性力的方向总是指向平衡位置。
2)绳子被拉紧时所产生的张力绳的张力:即绳内部各段之间的弹性作用力。
下面以AB 段为研究对象,设其质量为m A 点和B 点的张力:'A A T T -=、'B B T T -=由牛顿第二定律:a m T T B A =+(1)当a =0或者m →0时,F T T B A =-=',绳子上各点张力相同而且拉力相等。



一、几种常见的力1.万有引力(Law of Gravitation )1)文字叙述:在两个相距为r ,质量分别为m 1,m 2的质点间有万有引力,其方向沿着它们的连线,其大小与它们的质量的乘积成正比,与它们之间的距离的平方成反比,即2)数学表示 0221r r m m G F = ——引力质量Gravitational Mass其中 211..1067.6--⨯=kg m N G ——引力常量。
2.重力(Gravity )——本质上归结于万有引力。
1)文字叙述:物体重力就是指忽略地球的自转效应时,地球表明附近物体所受的地球的引力,即物体与地球之间的万有引力。
其方向指向地心。
2)数学表示 G=mg g=9.8m.s -2——重力加速度。
3)思考题:赤道的重力加速度大还是两极的重力加速度大?为什么?3.弹性力(Elastic Force )大家知道,两个物体相互接触,彼此将产生形变,使其内部产生反抗力——形变恢复力(弹性力)。
形变是产生弹性力的条件之一。
例如:板擦和桌子相互接触,彼此有了一定的形变,在各自的接触部分产生弹性力。
所以,弹性力是一种与物体的形变有关的接触力。
即发生形变的物体,由于要恢复原状,对与它接触的物体会产生力的作用,这种物体因形变而产生欲使其恢复原来形状的力叫做弹性力。
常见的弹性力有:1)弹簧中的弹性力:弹簧被拉伸或压缩时产生的弹性力。
胡克定律(Hooke Law ):在弹性限度内,弹性力的大小与弹簧的伸长量成正比,方向指向平衡位置。
数学表示 f=-kx—— k 为弹簧的劲度系数(Stiffness )。
k 的值决定于弹簧本身的性质。
而弹簧弹性力的方向总是指向平衡位置。
2)绳子被拉紧时所产生的张力绳的张力:即绳内部各段之间的弹性作用力。
下面以AB 段为研究对象,设其质量为m A 点和B 点的张力:'A A T T -=、'B B T T -=由牛顿第二定律:a m T T B A =+(1)当a =0或者m →0时,F T T B A =-=',绳子上各点张力相同而且拉力相等。
(2)当a ≠0,而且m ≠0(绳子质量不能忽略时),绳子上各点的张力不F 图2-2 弹簧的弹力m同。
(3)张力的大小取决于绳被拉紧的程度,它的方向总是沿着绳而指向绳要收缩的方向。
3)正压力(作用在支承面上)和支持力(作用在物体上)正压力(作用在支承面上)和支持力(作用在物体上),是两个物体相互接触且相互挤压时产生的,大小取决于相互挤压的程度,方向垂直与接触面指向对方。
小结:1.产生弹性力的条件:接触;形变。
2.弹性力的方向:恒垂直于接触点的切面。
4.摩擦力(Friction Force )1)文字叙述:两个物体相互接触,并且有相对运动(或者相对运动的趋势)时,在接触面之间产生一对阻碍相对运动(或阻碍相对运动趋势)的力,叫做摩擦力。
2)静摩擦力(Static Friction Force ):物体没有相对运动,但有相对运动的趋势时产生的阻碍相对运动趋势的力叫静摩擦力。
物体在外力F 的作用下,没有移动,存在一个静摩擦力f ,且外力F 增大时,静摩擦力f 也增大,存在最大静摩擦力max f 。
实验表明,最大静摩擦力max f 与正压力成正比,即数学表示 N f 0max μ= (max 0f f ≤≤)其中μ0为静摩擦因数(Coefficient Of Static Friction )。
它与两接触物体的材料性质以及接触面的情况有关,而与接触面的大小无关。
3)滑动摩擦力(Sliding Friction Force ):物体有相对运动,产生阻碍相对运动的力,叫做滑动摩擦力。
数学表示 Nf μ=其中μ为滑动摩擦系数(Coefficient of Kinetic Force )。
它与两接触物体的材料性质、接触表面的情况、温度、干湿度等有关,还与两接触物体的相对速度有关。
一般来说,滑动摩擦系数μ比静摩擦系数μ0小。
5、思考题下列几种说法是否正确?为什么?图2-3正压力图2-4 摩擦力图2-3 摩擦力与外力F f1)物体受到的摩擦力的方向总是与物体的运动方向相反。
2)摩擦力,总是阻碍物体运动的。
3)静摩擦的大小等于N F 0μ, 0μ为静摩擦因数,N F 为物体的正压力。
二、非惯性参考系(Inertial System )在运动学中,参考系可以任意选择。
但是在动力学中,应用牛顿运动定律时参考系就不能随便选择。
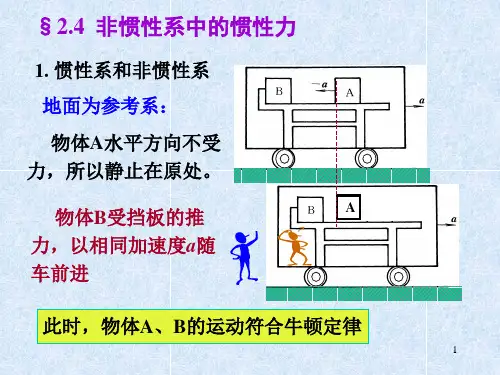
例如:在火车车厢内的一个光滑桌面上,放一个小球。
当车厢相对地面以匀速前进时,车厢内的乘客观察到此小球相对桌面处于静止状态,而路基旁的人则看到小球随车厢一起作匀速直线运动。
这时,无论是以车厢还是以地面作为参考系,牛顿运动定律都是适用的,因为小球在水平方向不受外力作用,它将保持静止或匀速直线运动状态。
但当车厢突然相对于地面以加速度a 向前的运动时,车厢内的乘客观察到此小球相对于车厢内的桌面以加速度-a 向后作加速运动。
这个现象,对处于不同参考系的观察者,可以得出不同的结论。
站在路基旁的人,觉得这件事是很自然的。
因为小球和桌面之间非常光滑,它们之间的摩擦力可以忽略不计,因此,当桌面随车厢一起以加速度a 向前运动时,小球在水平方向并没有受到外力作用,所以它仍欲保持原来的运动状态,牛顿运动定律此时仍然是适用的。
然而对于坐在车厢内的乘客来说,这就很不好理解了,既然小球在水平方向没有受到外力作用,小球怎么会在水平方向具有a -的加速度呢?由此可见,牛顿运动定律不是对任意的参考系都适用的。
我们把适用牛顿运动定律的参考系叫做惯性参考系,简称惯性系;反之,就叫非惯性系。
例如前面所述的地面以及相对地面作匀速直线运动的车厢,都是惯性系,相对地面作加速运动的车厢则是非惯性系。
在惯性系中,一个不受力的物体将保持静止或匀速直线运动状态。
由运动的相对性可知,相对于已知惯性系静止或匀速直线运动的参考系都是惯性系。
说明:要确定一个参考系是否惯性系,只能依靠观察和实验。
1. 地球可近似认为是一个惯性系。
附:地球公转向心加速度为: 5.9×10-3m ·s -2地球公转赤道向心加速度为:3.4×10-2m ·s -2太阳旋转的向心加速度为: 3×10-10m ·s -2目前最好的惯性系是以选定的1535颗恒星平均静止位形作为基准的参考系——FK4系。
2.相对于惯性系作匀速运动的参考系是惯性系;三、平动参照系的惯性力1.惯性力图2-6 惯性系与非惯性系前面讲过在非惯性系中牛顿运动定律不成立。
但在实际问题中,往往需要在非惯性系中观察和处理物体的运动,这时,我们要引入惯性力的概念,以便在形式上利用牛顿定律去分析问题。
惯性力是个虚拟的力。
它是在非惯性系中来自参照系本身加速效应的力,和真实力不同。
惯性力找不到相应的施力物体。
它的大小等于物体的质量m 与非惯性系加速度a 的乘积,方向和a 相反。
则表示式 am F i -=2.非惯性系中牛顿运动定律引入惯性力以后,如果作用在物体上的合外力为F ,则在非惯性系中,可以应用牛顿第二定律a m F F i =+其中a 为物体相对于非惯性系的加速度。
惯性力是由于非惯性系相对于惯性系的加速运动引起的。
它不是物体之间的一种相互作用力,所以它没有施力者,也没有反作用力;故惯性力是虚拟的力。
例题: 如图(a )所示的三棱柱以加速度a 沿水平面向左运动,它的斜面是光滑的,若质量为m 解:方法一、以地面为参考系,物体受到重力和支持力的作用,如图(b )所示。
根据牛顿第二定律,可得Ncosθ-mg=0 Nsinθ=ma由上面两式可得 22a g m N +=方法二:以三棱柱为参考系,它是一个非惯性系,物体除了受到重力和支持力的作用外,还受到惯性力的作用,在这三种力的作用下,物体相对于三棱柱处于静止状态。
如图(c )所示。
根据牛顿第二定律,可得Ncosθ-mg=0 Nsinθ-ma=0同样可得 22a g m N +=两种方法所得的结果是相同的。
四、转动参考系的惯性力——惯性离心力(Inertial Centrifugal Force )在水平放置的转台上,有一轻质弹簧一端系在转台的中心,另一端系一质量为m 的小球。
设转台平面非常光滑,它与小球和弹簧的摩擦力均可忽略不计。
弹簧的长度为l ,转台可绕竖直轴以角速度ω转动。
图2-5 (b )θθ θ(c )(a )图2-7 惯性离心力站在地面的观测者:小球受到向心力mlω2的作用作圆周运动;站在转台的观测者:小球除了受到向心力mlω2的作用,还将受到一个惯性力的作用,这个惯性力称为惯性离心力,大小也是mlω2,方向与向心力的方向相反。
小球在这两个力的作用下处于静止状态。
说明:1.向心力与惯性离心力大小相等,方向相反,时刻“平衡”,但二者不是平衡力,不能互相抵消,也不是作用力与反作用力,不服从牛顿第三定律;2.向心力是真实的力,可出现在惯性系和非惯性系中,而惯性离心力是虚拟力,只能出现在非惯性系中。