当前位置：文档之家 › 非惯性系中的力学

非惯性系中的力学

  • 格式：doc
  • 大小：32.00 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

第二章 非惯性系中的质点动力学

第二章 非惯性系中的质点动力学

M1-28
积分可得
mgR(cos jmax 1 1) m 2 R 2 sin 2 jmax 0 2
因 sin 2 jmax 1 cos2 jmax 上式变为
mgR(cos jmax 1) 1 m 2 R 2 (1 cos 2 jmax ) 0 2
z
或
2 R cos2 jmax 2 g cos jmax 2 g 2 R 0
2. 当加速度 ae 2 g tan 时，牵连惯性力 FIe 2mg tan ，应用 相对运动动能定理，有
m v 2 0 ( F cos )l (mg sin )l Ie 2 r
整理后得
y' m
FN FIe
mg θ ae x'
m 2 vr (mg sin )l 2
力大小为 FIe m 2 R sin j ，方向如图。 经过微小角度dj 时，此惯性力作功为
z
W FIe R cos jdj m 2 R sin j cos jRdj
相对运动的动能定理，得
R
0 0 mgR(1 cos j max )
jmax
0
Байду номын сангаас
j
mg
FIe
m 2 R 2 sin j cos j dj
vr 质点相对动参考系速度
M1-20
上式两端点乘相对位移
dr
dvr m dr F dr FIe dr FIC dr dt
dr 注意到vr , 且科氏惯性力垂直于vr , 有FIC dr 0, 则 dt mvr dvr F dr FIe dr

非惯性系中的力学(物理竞赛)

非惯性系中的力学(物理竞赛)
例 2.如图所示，定滑轮 A 的一侧持有 m1=5kg 的物体，另一侧挂有轻滑轮 B，滑轮 B 两侧挂着民 m2=3kg，m3=2kg 的物体，求每个物体的加速度。
例 3.一辆质量为 m 的汽车以速度 v 在半径为 R 的水平弯道上做匀速圆周运动。汽车左右轮相距为 d，重心离地高度为 h，车轮与路面之间的摩擦因数为 μ ，求： （1） 汽车内外轮各承受多大的支持力？ （2） 汽车能安全行驶的最大速度？
F 合+F 惯=0
例 1.在火车车厢内有一长 l，倾角为的斜面，当车厢以恒定加速度 a0 从静止开始运动时，物体自 倾角为 θ 的斜面顶部 A 点由静止开始下滑，已知斜面的静摩因数为 μ ，求物体滑至斜面底部 B 点时， 物体相对于车厢的速度，并讨论当 a0 与 μ 一定时，倾角 θ 为多大时，物体可静止于 A 点？
F 合+F 惯=ma 相 式中, F 合为物体实际受到的合力.
二,匀速转动系中的惯性力 圆盘以角速度 ω 绕铅直轴转动,在圆盘上用长为 r 的轻线将质量为 m 的小球系于盘心且小不球 相对于圆盘静止,即随盘一起作匀速圆周运动.从惯性系观察,小球在线拉力 T 的作用一下作圆周运动, 符合牛顿第二定律.以圆盘为参考系,小球受到拉力 T 的作用,却保持静止,没有加速度,不符合牛顿第 二定律.所以,相对于惯性系作匀速转动的参考系也是非惯性系,要在这种参考系中保持牛顿第二定律 形式不变,在质点静止于此参考系的情况下,应引入惯性力: F 惯=mω 2r.这个力叫做惯性离心力.若质点 静止于匀速转动的参考系中,则作用于此物体所有相互作用力与惯性离心力的合力等于只适用于惯性系,在非惯性系中,为了能得到形式上与牛顿第二定律一致的动力学方 程,就需要引入惯性力的概念.
一.直线加速系中的惯性力 设非惯性参考系的加速度为 a 参,物体相对于参考系的加速度为 a 相,物体实际的加速度为 a 绝, 则有: a 绝= a 参+a 相.那么,物体”受到”的惯性力 F 惯=－m a 参,其方向与 a 参的方向相反. 惯性力是虚构的力,不是真实力,因此,惯性力不是自然界中物体间的相互作用,因此不属于牛顿第 三定律涉及的范围之内,它没有施力物体,不存在与之对应的反作用力. 在非惯性系中,考虑到惯性力后的动力学方程为:

第四章非惯性系中的质点力学

第四章非惯性系中的质点力学


小结：选用不同的 s 系，其 加速度变换公式的具体分 析结果不同。
§4.3 非惯性系内质点动力学
当计入惯性力，就可在非惯性系中得到形式上和惯性 系一样的动力学规律（如三个定理，三个守恒定律）.
(x 0为势能零点 s系中 2. 当非惯性系以匀角速度 绕固定轴转动时, 2 1 2 2 F m ( r ) m e ( m ) Ic 2
牵连惯性 力 非惯性系中的 质点的动力学 方程
m a F
§4.2 非惯性系内质点的动力学方程
科氏 力
对惯性力作几点说明:
1.惯性力不是相互作用力,不遵从牛顿第三定律，它不 存在反作用力。 2.惯性力仅存在于非惯性系之中。 3.在非惯性系中惯性力真实存在，不是假想的力。 4.惯性离心力
m ( r )
三.落体偏东
以自由落体运动为例，研究科氏力对质点竖直运动的影响
在地面参照系oxyz中，其单位 矢量为i、j 、k.，且 i 水平向 南, j 水平向东, k 竖直向上. 质 点在z轴上 z h 处自由下落， 不计空气阻力，且不受其它物 体的作用， F 0


这里惯性离心力是保守力, 1 对应的势能为 V m 2r2 2
1 2 1 22 1 22 m m v r 0 m r 0 2 2 2
§4.4 地球自转的动力学效应
本节应用非惯性系内动力学理论解决实际问题的范例.
一. 质点相对地球的运动微分方程
1.有关地球运动的几个量. 2.地球为非惯性系时质点在地球表面附近运动微分方程. 地球既有自转又有公转,是非惯性参照系,以日心系为S系.
3. 通过前面分析,我们可利用运动系把质点的复杂运动 分解成为几个比较简单的运动的合成.

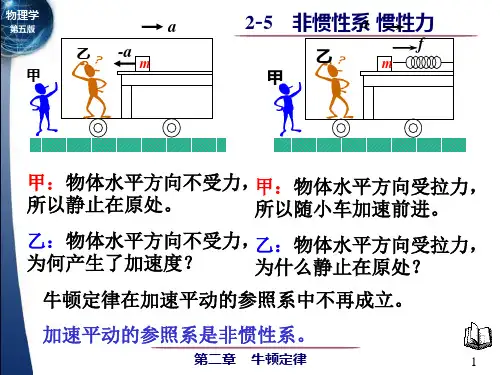
2-5 非惯性系惯性力

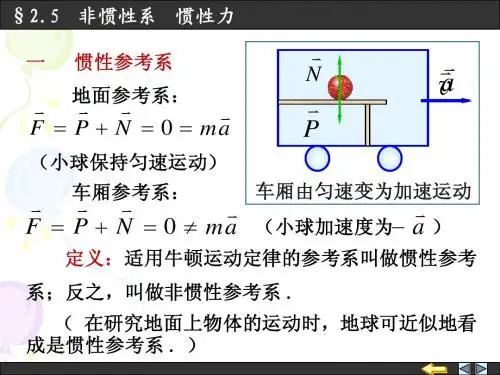
2-5 非惯性系惯性力
设想， 一个带有径向光滑沟槽的圆盘， 设想 ， 一个带有径向光滑沟槽的圆盘 ， 以匀角速度 ω绕通过盘心并垂直于盘面的 固定竖直轴O转动， 处于沟槽中的质量为 固定竖直轴 转动， 转动 m的小球以速度 沿沟槽相对于圆盘作匀 的小球以速度u沿沟槽相对于圆盘作匀 的小球以速度 速运动，如图 速运动 如图
在非惯性系中应用牛顿定律时， 在非惯性系中应用牛顿定律时，计算力要计入真 实力和假想的惯性力，加速度要用相对加速度。 实力和假想的惯性力，加速度要用相对加速度。 这时牛顿定律的形式为： 这时牛顿定律的形式为：
F' = F + Fi＝ma'
第二章 牛顿定律
3
物理学
第五版
2-5 非惯性系 惯性力 a0
m T A B T m
A:质点受绳子的拉力提供的向 质点受绳子的拉力提供的向 心力，所以作匀速圆周运动。 心力，所以作匀速圆周运动。
B：质点受绳子的拉力， ：质点受绳子的拉力， 为什么静止？ 为什么静止？
在匀速转动的非惯性系中， 在匀速转动的非惯性系中，设想小球受到一个 的作用，大小与绳子的拉力相等， 惯性离心力Fi 的作用，大小与绳子的拉力相等， 方向与之相反，所以小球处于静止的平衡状态。 方向与之相反，所以小球处于静止的平衡状态。
第二章 牛顿定律
2
物理学
第五版
2-5 非惯性系 惯性力 -
惯性力： 惯性力：大小等于运动质点的质量与非惯性系加 速度的乘积；方向与非惯性系加速度的方向相反。 速度的乘积；方向与非惯性系加速度的方向相反。 惯性力没有施力物体，所以不存在反作用力。 惯性力没有施力物体，所以不存在反作用力。
Fi＝ - ma0
Fi＝- mω r en
2
T + F＝ i 0

2-5 非惯性系 惯性力

2-5 非惯性系 惯性力

m T T
m
地面观察者： 地面观察者：质点受绳子 的拉力提供的向心力， 的拉力提供的向心力，所 以作匀速圆周运动。 以作匀速圆周运动。
圆盘上观察者： 圆盘上观察者：质点受绳 子的拉力，为什么静止？ 子的拉力，为什么静止？
§2.5 非惯性系 惯性力
Байду номын сангаас
在匀速转动的非惯性系中，小球受到一个惯性离心力的作用， 在匀速转动的非惯性系中，小球受到一个惯性离心力的作用， 大小与绳子的拉力相等，方向与之相反， 大小与绳子的拉力相等，方向与之相反，所以小球处于静止 的平衡状态。
−1
a0 g
l g
l → T = 2π a
§2.5 非惯性系 惯性力
例 如图 m与M保持接触 各接触面处处光滑求： 与 保持接触
m下滑过程中，相对M的加速度 amM 下滑过程中，相对 的加速度 下滑过程中
m
θ
M
解：画隔离体受力图 以M为参考系画 为参考系画m 为参考系画 的受力图 y′ N Mm x′ m ma
在惯性系中有： 在惯性系中有：
f = ma
= m a＝ m ( a' + a 0 )
在非惯性系中有： 在非惯性系中有： f
f－ma0＝ma'
惯性力： 惯性力：大小等于运动质点的质量与非惯性系加速度 的乘积；方向与非惯性系加速度的方向相反。 的乘积；方向与非惯性系加速度的方向相反。
f 惯＝− ma0
f + f 惯＝ma'
§2.5 非惯性系 惯性力 加速平动的非惯性系、 三 加速平动的非惯性系、惯性力
a -a
m
a f惯 f
m
地面观察者： 地面观察者：物体水平方

力学2动力学II-非惯性系讲解

力学2动力学II-非惯性系讲解

设有一质量为m的质点，在真实的外力F 的作 用下相对于某一惯性系S产生加速度 a ，
则根据牛顿第二定律，有:
F ma
假 沿设直线另运有动一。参在考S系参S考相系对中于,惯质性点系的S加以速加度速是度aa。0
则： a a a0
aAB aAC aCB
将此式代入上一式可得：
e
er
方向描述：er ：径向方向
e ：极角增加方向
O
位矢 r rer
速度
v

dr dt

d( rer dt
)

dr dt
er
r der dt

dr dt
er

r
d
dt
e

vr er

v e
r
P

X
e

r
der
d er
der der e der er d d
vr : v :
dt
参阅专业《力学》书
本地加速度
牵连横向 加速度
牵连向心 加速度
科里奥利 加速度
a a d r ( r ) 2 v
dt
a绝 a相 a牵
牵连加速度
f惯性力 ma牵
m
d
dt

r

[m

(

r
)]
2m(v )
欧拉力
对匀速转动的S'系：
非惯性系中的牛顿第二定律：
虚拟力
F ma F真实力 R
惯性力不是物体间的真实的相互作用,是一种假想的 力。它既无施力者, 也无反作用力, 不满足牛顿第三定律。

非惯性系惯性力

非惯性系惯性力

*地球自转对重力的影响
以地球为参照系，考虑地球的自转,于是地面上任何 一个物体都是在三个力：
N
支持力N、引力F引、惯性离性力ƒ*c作用下处于平 衡态，
F引
ƒ*c
W
而地面上的观察者通常总是把地面上 的物体作二力平衡来处理，即认为物 体在重力W和支持力N作用下达到平 衡态，
因此重力W实际上应是F引和ƒ*c的合力，即：
加速度。
YT
as
f﹡ X
解：以小车为参照系（非惯性系），
mg
因为a/=0,这时动力学可简化为静力学
重物受3个力:
张力T， 重力mg，
惯性力f﹡，
而处平衡态，故有
T cos mg 0 (1)
T sin f 0 (2) ( f * mas )
联立，得
tg as
g
as g tg
7
匀角速转动的非惯性系中的——惯性离心力 *惯性离心力的引入：
a 另外 f﹡ 与 s 有关，非惯性系相对于惯性系的加速度的形式不同，则 f﹡ 也不同。
后面将从三个方面加以说明。
4
3、 非惯性系中的运动定律的形式
a 设有惯性系O和非惯性系O，O系以加速度 s相对于O系运动，现在O系中有一 a 质点，其质量为m，且相对于O系以相对加速度 / 运动，于是质点m相对惯性系
19
江岸的冲刷（北半球）；
v fk* fk* v
v fk*
0
17
信风；
据历史记载，第一次世界大战期间，英、 德在阿根廷附近马尔维纳斯岛的洋面上进行 了一次大战。当德国军舰位于英国军舰北方 大约6-7km时，英舰炮手瞄准德舰开炮，奇怪 的是炮弹全都落在德舰的左侧大约100多米以 外的地方。怪就怪在英舰炮手都是经过严格 训练的富有作战经验的好炮手，不应发生如 此大的偏差。

牛顿第二定律的推广非惯性系中的力学定律

牛顿第二定律的推广非惯性系中的力学定律

牛顿第二定律的推广非惯性系中的力学定律在牛顿力学中，牛顿第二定律是描述质点在惯性系中运动的力学定律。

然而，在现实世界中，很多情况下质点并不总是在惯性系中运动，而是处于非惯性系中。

那么，在非惯性系中，牛顿第二定律是否仍然成立呢？本文将探讨牛顿第二定律在非惯性系中的推广及其力学定律。

一、牛顿第二定律的基本原理牛顿第二定律是经典力学中最重要的定律之一，它表明物体的加速度与作用在物体上的合力成正比，与物体的质量成反比。

具体公式为：F = m * a其中，F表示作用在物体上的合力，m表示物体的质量，a表示物体的加速度。

该公式说明了物体的加速度与作用在物体上的力的关系。

二、非惯性系中的力学定律在非惯性系中，质点的运动状态会受到惯性力的影响。

惯性力是由于参照系的加速度引起的，它会对质点产生额外的力，从而影响质点的实际运动状态。

为了在非惯性系中推广牛顿第二定律，我们需要引入“亚惯性力”的概念。

亚惯性力是指作用在非惯性系中质点上的力，它包括了惯性力和外力两部分。

牛顿第二定律在非惯性系中的表达式可以改写为：F' = m * (a - a')其中，F'表示亚惯性力，a表示实际加速度，a'表示非惯性系的加速度。

通过这个公式可以看出，在非惯性系中，实际的加速度是由物体受到的合力和亚惯性力共同决定的。

而亚惯性力的大小与非惯性系的加速度以及物体的质量有关。

三、非惯性系中的例子为了更好地理解非惯性系中的力学定律，我们可以举一个具体的例子来说明。

假设有一个质量为m的小球，它被放置在一个半径为R、线性加速度为a'的转盘上。

在这个转盘上旋转的过程中，小球会受到两个力的作用：重力和离心力。

重力是指向下的，大小为mg，其中g表示重力加速度。

而离心力是指向外的，大小为m * (a' * R)。

根据牛顿第二定律的推广公式，小球所受合力可以表示为：F' = mg + m * (a' * R)。

2.4 非惯性系中的惯性力

2.4 非惯性系中的惯性力

r0
E
ES
E
将地心看做非惯性系, 将地心看做非惯性系, 任何质量为m的质点受的平移惯性力为 任何质量为 的质点受的平移惯性力为
GMS a0 = 2 (r0 ) rES
r f sE
MS
S
v v GM S m Fi = ma0 = 2 r0 rES
6 第2章牛顿运动定律
v Fi
v v GMS m Fi = ma0 = 2 r0 rES
N mM sin θ = Ma0
(1)
(2)
为参考系( 以M为参考系(非惯性系)对m 列方程 为参考系 非惯性系)
ma0 cosθ + mg sin θ = mamM
NmM + ma0 sin θ mg cosθ = 0 (3)
联立求解得
5
amM
( M + m) sin θ = g 2 M + m sin θ
附:科里奥利力简单推导
下面以特例推导,然后给出一般表达式. 下面以特例推导,然后给出一般表达式. 如图,质点 在转动参考系 设为S 在转动参考系( 如图,质点m在转动参考系(设为 '系)中沿一光滑凹槽运 v 动,速度为 υ ′ 光滑凹槽 在惯性系(地面) : 在惯性系(地面)S:
v υ′
(v ′ + rω ) F =m
地
13 第2章牛顿运动定律
,
固体潮(形变): ▲固体潮(形变):
地 球
月
愝
:
月球自转 地球自转变 体 SL— 9 转
变形滞后,造成地 变形滞后 造成地 球对月球引力矩, 球对月球引力矩 阻止月球自转
:3惩
400
体 引潮力 引潮力
第2章牛顿运动定律

非惯性系力学

非惯性系力学

第三章 非惯性系力学引言：到目前为止，我们对质点的力学现象只是限制在惯性参考系中进行讨论的。

但是在某些实际问题中往往要求我们在非惯性系中研究力学问题。

而牛顿定律a m F =只适用于惯性系，在非惯性系中，它是不能适用的，那么相对于非惯性系中的运动定律要解决的是，质点在怎样的力作用下作怎样的运动，换句话来说，运动定律要解决的问题是，质点的受力情况与运动情况之间的联系。

1、对惯性系来说这种联系已经有了，就是牛顿第二定律a m F =。

提到了质点的受力情况，必须要明确力是物体之间的相互作用，既然力是物体间的互相作用，它与参照系的选择有没有关系？没有关系。

2、对非惯性系质点所受的力仍然为F 。

至于运动情况与参照系的选取却是有关的，对不同的参照系会给出不同的描述。

因此，质点相对惯性系和非惯性系的加速度当然是不同的，为了加以区分，就用a ' 表示质点相对非惯性系的加速度。

此时F 就不等于a m F '= ，F 虽然不等于a m F '= ，那么能不能找出F 与a ' 的关系呢？如果找到了它们之间的关系，也就等于找到了非惯性系中的运动定律，那么我们也就可以在非惯性系中讨论力学问题了。

F 与a '之间的关系总能够找到的。

3、只要能找到a 与a ' 的关系：)(a f a '=，根据运动描述的相对性，这个关系总是可以找到的。

那么根据)(a mf a m F '== 也就可以找到F 与a ' 的关系。

因此根据这条解决问题的途径，在这一章里我们准备要讲的4、内容：是①相对运动；②非惯性系动力学；③然后再做一个大题目——解决地球自转所产生的影响。

下面先讲质点相对运动的描述。

也就是讨论质点相对于两个不同参照系运动之间的关系。

§1． 作平动的参照系一、伽利略变换如右图所示，为叙述方便起见简称OX 坐标系为O 系，假定O 系为惯性系，并认为它是一个固定不动的参照系，就称它为固定坐标系。

非惯性系中的动力学

非惯性系中的动力学

在非惯性系中由于牛顿运动定律不成立, 不能直接用 牛顿运动定律处理力学问题。若仍希望能用牛顿运动定律 处理这些问题, 则必须在非惯性系中引入一种作用于物体 上的惯性力。惯性力不同于前面所说的力，因为惯性力既 没有施力物体，也不存在它的反作用力。
小车作加速运动a≠0时，单摆偏 转了一个角度，拉小球的弹簧被 拉伸，其状态不符合牛顿定律， 引入了惯性力后，就能把牛顿运 动定律应用于非惯性系。
a cos
g
sin
(m2 m1)sin m2 m1 sin2
g
m2g
二、转动参照系中的离心惯性力
m
FT
m
F*
观 察 者2
一光滑的圆盘以匀角速ω绕其铅直轴转动，将一质
量为m的小球用长为r的细线栓在轴上，并使小球在圆
盘上与圆盘一起以匀角速ω绕铅直轴转动。
如果在O则系对内于的观观察测者者1：1测F量T 到 m细a线对m小球2r的拉力为FT
§3.5 非惯性中的动力学
一、 直线加速参考系中的惯性力 二、 离心惯性力 *三、 科里奥利力
§3.5 非惯性中的动力学
一、 直线加速参考系中的惯性力
问题：如图，一单摆悬挂在小车的天花板上，另一个小
球用弹簧拉着，现均以小车为参考系来研究小球的运动
a =0
a 0
小车作匀速直线运动，即a = 0 时，单摆、小球均处于 静止状态符合牛顿定律。
小车作加速直线运动，即a≠0时，单摆偏转了一个角度，拉 小球的弹簧被拉伸，其状态不符合牛顿定律，为什么？
inertia force 1.avi
如图：O系为基本参考系，O 系为动参考系
设 O系相对O系以加速度 a 作直线加速运动,
z
质点在空间运动, 某时刻位于P点

牛顿第二定律的推广非惯性系中的力学定律与应用

牛顿第二定律的推广非惯性系中的力学定律与应用

牛顿第二定律的推广非惯性系中的力学定律与应用牛顿第二定律的推广：非惯性系中的力学定律与应用牛顿第二定律是经典力学的核心定律之一，描述了质点在惯性系中运动的力学规律。

然而，在现实生活中，不仅存在着许多非惯性系的情况，而且许多实际问题也需要考虑非惯性系下的力学定律。

本文将讨论牛顿第二定律在非惯性系中的推广以及其在实际应用中的意义。

一、牛顿第二定律的基本原理牛顿第二定律是指当一个质点受到外力作用时，其运动状态的变化率与外力成正比，与质点的质量成反比。

数学表达式为F=ma，其中F 表示作用力，m表示质点的质量，a表示质点的加速度。

在惯性系中，加速度与质点所受合外力成正比，符合牛顿第二定律的基本原理。

二、非惯性系下的力学定律非惯性系是指存在加速度的参考系，例如旋转参考系、加速度参考系等。

在非惯性系中，由于存在惯性力的作用，牛顿第二定律需要进行推广。

1. 载体非惯性系中的力学定律在旋转参考系中，我们需要考虑到离心力和科里奥利力的作用。

离心力是由于旋转参考系的加速度而产生的，其大小与质点与旋转轴的距离成正比。

科里奥利力是由于质点在旋转参考系中产生的运动而产生的，其方向垂直于质点的速度和旋转轴。

同时，仍要考虑质点所受的外力，其合力与加速度之间的关系可以用推广后的牛顿第二定律描述。

2. 加速度非惯性系中的力学定律在加速度参考系中，除了要考虑到质点所受外力之外，还需考虑到惯性力的作用。

在加速度参考系中，质点所受的惯性力的大小与加速度的大小成正比，方向与加速度相反。

同样地，牛顿第二定律需要进行推广以描述在加速度参考系中质点的运动规律。

三、非惯性系下的力学定律应用案例非惯性系下的力学定律在实际应用中具有重要意义。

以下将介绍两个应用案例：1. 磁悬浮列车磁悬浮列车是一种利用磁力悬浮并驱动的高速列车。

在列车内部，乘客感受不到列车的加速度，这是因为列车内的空气和人体与车体一起在同样的惯性参考系中运动。

然而，对于弯道等转弯情况，列车会产生向心力，需要进行修正。

第2章 -牛顿定律 1 非惯性系2 2

第2章 -牛顿定律 1 非惯性系2 2

l
dm
dx

F
T
l mF dT x dx (m＇ m)l
T dm T dT
dx
13
x F T (m＇ m ) l m＇ m
§2 牛顿运动定律的应用
解题的基本思路
（1）确定研究对象，并且进行受力分析； 对于连带运动，进行隔离物体受力分析，画受力图。
（2）选取适当的坐标系；
越大，
利用此原理，可制成蒸汽机的调速器（如图所示）。
例3
于定点 o ， t 0 时小球位于最低位置，并具有水平速度 v 0 ，
求小球在任意位置的速率及绳的张力。
如图长为 l 的轻绳，一端系质量为 m 的小球,另一端系
解
T mg cos man
mg sin ma
1 dv dv dv ( ) gdt gdt 2 k 2 k k 1 v 1 v y 1 v mg mg mg mg k mg k ln(1 v) ln(1 v) 2 gt c k mg k mg
2
d
o
fd


mg
t=0 时 选讲
v0
c0
F (t ) ma (t )
动量为 p 的物体，在合外力 F 的作用下，其动量随时
间的变化率应当等于作用于物体的合外力 。
dp(t ) F (t ) , p(t ) mv(t ) dt
当
v c
时，m为常量。
4
——是架起了质点运动学和动力学的桥梁。
dv F (t ) m ma dt dv y dv x dvz F m i m j m k dt dt dt 即 F ma x i ma y j maz k

非惯性系中的力学

非惯性系中的力学

非惯性系中的力学在经典力学中，我们通常将研究对象限定在惯性系中。

惯性系是指一个不受任何外力或惯性力作用的参考系。

然而，在许多实际情况下，我们无法避免研究非惯性系中的力学。

非惯性系中的力学研究相对复杂，但它在解释许多日常生活中的现象、工程设计以及航天飞行等方面具有重要的意义。

一、引言在力学研究中，我们常常使用牛顿定律来描述物体的运动，即F=ma，其中F为物体所受合力，m为物体的质量，a为物体的加速度。

然而，牛顿定律仅在惯性系中成立，当系统处于非惯性系中时，就需要考虑惯性力的作用。

二、非惯性力的概念和作用非惯性力是指在非惯性系中对物体产生的看似存在的力，实际上是由于非惯性系的运动而产生的惯性效应。

常见的非惯性力有离心力、科里奥利力以及向心力等。

离心力是一个物体在非惯性系中沿着旋转轴的方向产生的力，它的大小与物体的质量、距离旋转轴的距离以及角速度有关。

离心力在许多日常生活场景中起着重要作用，比如旋转游乐设施中的体验、地球自转引起的地球形状畸变等。

科里奥利力是一个物体在非惯性系中由于角速度的改变所产生的力。

科里奥利力的方向垂直于运动方向和旋转轴，在天文学、航天飞行等领域有重要的应用。

例如，地球上飞行的飞机或火箭就需要考虑科里奥利力的影响。

向心力是一个物体在非惯性系中沿着旋转轴的方向产生的力，它与物体的质量、旋转角速度以及距离旋转轴的距离有关。

向心力在转弯的机动车辆、垂直旋转的过山车等情况下起着重要作用。

三、非惯性系中的运动方程在非惯性系中，我们需要修正牛顿定律，使其适用于非惯性系的情况。

修正后的运动方程为F=m(a-a')，其中a'为非惯性系的加速度。

非惯性系中的运动方程相对复杂，因为我们需要考虑添加的惯性力对物体运动所产生的影响。

四、实例分析接下来，我们通过几个实例来说明非惯性系中的力学问题。

1. 旋转地球上的自由落体在地球自转的惯性系中，物体的自由落体可以简单地由重力加速度描述。

然而，在地球自转的非惯性系中，我们需要考虑离心力和科里奥利力的影响。

1-5 非惯性系 惯性力

1-5 非惯性系 惯性力
m相对于斜面向下的加速度为 a2
1

y a2 x a1
m相对于地的加速度为
a a1 a2
NHale Waihona Puke (3) 分析受力 m受力如图
mg
(4)列出方程 对m应用牛顿定律列方程： x方向: mgsin ＝m(a2－a1sin) y方向: N－mgcos ＝ma1cos 解方程，得: a2＝(g＋a1)sin N ＝m(g＋a1)cos
y a2 x a1
N
mg
物体对斜面的压力大小 N′=N=m(g＋a1)cos 垂直指向斜面. m沿斜面向下作匀变速直线运动，所以
1 2 1 l a2 t ( g a1 ) sin t 2 2 2
t 2l ( g a1 ) sin
(5)讨论结果 当＝0时, N′=N=m(g＋a1). 当＝0时， 无水平滑动，l=0 , t=0
a 0是非惯性系相对惯性系(如地面)的加速度。
在非惯性系中，动力学方程表示为
FI ma0
F FI ma
注意：惯性力不是真正作用在物体上的力！ 惯性力无施力者，也无反作用力。 惯性力的实质是物体的惯性在非惯性系中的表现。
例 一质量为m1、顶角为的三角形光滑物体上。放有 一质量为m2的物块。设各面间的摩擦力均可忽略不 计。试用非惯性系中力学定律求解三角形物块的加速 度。 解： 将坐标系建立在三角形物块上，方向如
例: 升降机内有一光滑斜面，固定在底板上，斜面倾 角为.当升降机以匀加速度a1竖直上升时，质量为m的 物体从斜面顶端沿斜面开始下滑，如图所示.已知斜面 长为l，求物体对斜面的压力，物体从斜面顶点滑到底 部所需的时间.
例: 升降机内有一光滑斜面，固定在底板上，斜面倾 角为.当升降机以匀加速度a1竖直上升时，质量为m的 物体从斜面顶端沿斜面开始下滑，如图所示.已知斜面 长为l，求物体对斜面的压力，物体从斜面顶点滑到底 部所需的时间. a 解: (1)选取对象 以物体m为研究对象. (2) 分析运动

第二章 - 非惯性系2

第二章 - 非惯性系2
r
2
v 2 m 2mv mr 2 r
v 2 ， 在非惯性系（圆盘）S′： 向心加速度 a r
非惯性系中牛二定律不适用
16
将惯性系（地面S）中的牛二定律式
2 v F m 2mv mr 2 r
转换到非惯性系（圆盘）S′中使用：
v F 2mv mr m r
m2 m1 m2 a m2 g m1 g m1a
a
m1 g m2 g m1a m2a m1ar m2ar m1 m2 ar ( g a) m1 m2
在非惯性系中，只要在受 2m1m2 FT ( g a ) 力分析时加上惯性力后， m1 m2 就可形式上使用牛顿定律。
注意：加速度是矢量，要有方向！ a = ax j + a yk
解法 二
物体受力：重力 W , 斜面对它的正压力 N N 惯性力 F惯 ma1 W 动力学方程为： W N F惯 ma F惯
以作加速平动的升降机为参考系，是非惯性系。
沿斜面向下方向和垂直斜面向上方向的受力分量式为：
速度 a0 相对地面向上运动时，求两物体相对
a
a
a0
为 a1、a2 ，且相对电梯的加速度为 a
m1 g T m1a1
m1 m 2
a1 a0 a
m2 g T m2a2
m1 m2 a ( g a0 ) m1 m2
0 y T aT 2
a2 a0 a
2m1m2 T ( g a0 ) m1 m2
a1
m1g
y
m2 g
9
0
若电梯以相同的加速度下降，结果又如何？

非惯性系下力学问题.

非惯性系下力学问题.

渤海大学本科毕业论文题目非惯性系下力学问题的研究完成人姓名张亚楠主修专业物理学教育所在院（系）数理学院物理系入学年度2008年完成日期2011年6月1日指导教师丁文波非惯性系下力学问题的探讨张亚楠渤海大学物理系摘要：非惯性参照系就是能够对同一个被观测的单元施加作用力的观测参照框架和附加非线性的坐标系的统称。

在经典机械力学中，任何一个使得“伽利略相对性原理”失效的参照系都是所谓的“非惯性参照系”。

了解非惯性系下的力学问题很重要。

对于非惯性系的研究已经从传统的理论已经从传统的理论教学扩展到实际生活应用领域，从宏观研究深入到微观领域。

随着生活领域的不断扩大，对非惯性系下的元器件动力学行为，特别是非线性动力学行为的研究还有很大的空间。

在直升机转子等航空发动机转子的动力学研究中，应用的也主要是非惯性系动力学的理论知识。

近年来通过研究发现，在非惯性系中两体问题、摩擦力、压强以及浮力问题等都得以解决。

本文阐述了惯性系和非惯性系的区别，由惯性力着手，把牛顿第二地定律引入到非惯性系中，分析了牛顿第二定律的适用条件，并对非惯性系下的力学问题进行研究。

第一部分对非惯性系和惯性系进行概述。

第二部分对非惯性系下摩擦力的研究进行了讲述，摩擦力从动于包括惯性力在内的其它力作用。

第三部分通过分析在非惯性系中液体内部浮力和压强的变化，阐述了在不同参考系下液体浮力和压强的变化规律。

关键词：非惯性系；摩擦力；压强；浮力Mechanics Problems in the non-inertial frameZhang Ya-nan Department of Physics，Bohai University Abstract:Collectively referred to as the coordinate system of the observation frame of reference and additional non-linear non-inertial frame of reference is the ability to exert force on the same observation unit. In classical mechanics, no one makes the "failure of the principle of Galilean relativity" frame of reference is the so-called "non-inertial frame of reference. Mechanical problem is very important to understand the non-inertial frame. For non-inertial frames from the traditional theory has been expanded from the traditional teaching of the theory to real-life applications, from a macro research into micro areas. With the continuous expansion of areas of life, the dynamic behavior of non-inertial frame components, especially the study of nonlinear dynamic behavior there is a lot of space. The study of helicopter rotor aero-engine rotor dynamics, the application of theoretical knowledge of non-inertial frame dynamics. In recent years, the study found that two-body problem in the non-inertial, friction, pressure and buoyancy problems are all resolved. This paper describes the difference between inertial frames and non-inertial frames, to proceed by the inertia force, the introduction of Newton's second law of land to the non-inertial reference frame, Newton's Second Law applies to conditions, mechanical problems and non-inertial frame study. The first part an overview of the non-inertial frames and inertial frames. Thesecond part of the non-inertial friction about the friction follower force, including the inertia force. The third part through the analysis of liquid internal buoyancy and pressure change in the non-inertial reference frame on a different reference liquid buoyancy and pressure variation.Key words: Non-inertial；Friction；Pressure；Buoyancy目录引言 (1)一、非惯性系概述 (3)（一）非惯性系和惯性系 (3)（二）平动非惯性参考系 (5)1.平动的非惯性系 (5)2. 非惯性系中牛顿运动定律的应用 (7)（三）转动非惯性参考系 (11)1. 转动坐标系中的运动学问题 (11)2. 转动非惯性系中的动力学问题 (13)3. 落体偏东——地球自转的动力学效应 (13)二、非惯性系中摩擦力的研究 (14)（一）摩擦力的从动性 (14)（二）非惯性系中的摩擦力 (15)1.惯性力的具体形式 (15)2.静摩擦力 (16)3.滑动摩擦力 (16)三、非惯性系中液体内部的浮力和压强的讨论 (17)（一）惯性系中液体内部浮力和压强的表达式 (17)（二）非惯性系中液体内部浮力和压强的表达式 (18)结论 (25)参考文献 (26)非惯性系下的力学问题的研究引言经典理论认为凡是牛顿运动定律适用的参照系为惯性系，牛顿运动定律不成立的参照系为非惯性系[1]。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

非惯性系中的力学
牛顿运动定律只适用于惯性系,在非惯性系中,为了能得到形式上与牛顿第二定律一致的动力学方程,就需要引入惯性力的概念.
一.直线加速系中的惯性力
设非惯性参考系的加速度为a
参,物体相对于参考系的加速度为a
相
,物体实际的加速度为a
绝,
则有:
a绝= a参+a相.那么,物体”受到”的惯性力F惯=－m a参,其方向与a参的方向相反.
惯性力是虚构的力,不是真实力,因此,惯性力不是自然界中物体间的相互作用,因此不属于牛顿第
三定律涉及的范围之内,它没有施力物体,不存在与之对应的反作用力.
在非惯性系中,考虑到惯性力后的动力学方程为:
式中, F
合
为物体实际受到的合力.
二,匀速转动系中的惯性力
圆盘以角速度ω绕铅直轴转动,在圆盘上用长为r的轻线将质量为m的小球系于盘心且小不球相对于圆盘静止,即随盘一起作匀速圆周运动.从惯性系观察,小球在线拉力T的作用一下作圆周运动,符合牛顿第二定律.以圆盘为参考系,小球受到拉力T的作用,却保持静止,没有加速度,不符合牛顿第二定律.所以,相对于惯性系作匀速转动的参考系也是非惯性系,要在这种参考系中保持牛顿第二定律
形式不变,在质点静止于此参考系的情况下,应引入惯性力:F
惯
=mω2r.这个力叫做惯性离心力.若质点静止于匀速转动的参考系中,则作用于此物体所有相互作用力与惯性离心力的合力等于零,即:
例1.在火车车厢内有一长l，倾角为的斜面，当车厢以恒定加速度a0从静止开始运动时，物体自倾角为θ的斜面顶部A点由静止开始下滑，已知斜面的静摩因数为μ，求物体滑至斜面底部B点时，物体相对于车厢的速度，并讨论当a0与μ一定时，倾角θ为多大时，物体可静止于A点？
例2.如图所示，定滑轮A的一侧持有m1=5kg的物体，另一侧挂有轻滑轮B，滑轮B两侧挂着民m2=3kg，m3=2kg的物体，求每个物体的加速度。

例3.一辆质量为m的汽车以速度v在半径为R的水平弯道上做匀速圆周运动。

汽车左右轮相距为d，重心离地高度为h，车轮与路面之间的摩擦因数为μ，求：
（1）汽车内外轮各承受多大的支持力？
（2）汽车能安全行驶的最大速度？
例4.长为L1和L2的不可伸长的轻绳悬挂质量都是m的两个小球。

如图所示，它们处于平衡状态，突然连接两绳中间的小球受水平向右的冲击（如另一球碰撞），瞬间内获得水平身体右的速度v0.求这瞬间连接m2的绳子的拉力为多大？。