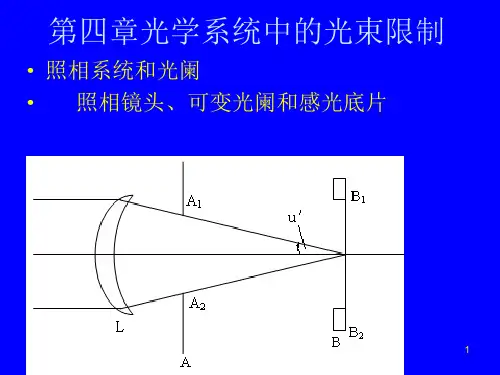
工程光学基础教程第四章

格式：ppt
大小：2.16 MB
文档页数：72

下载文档原格式

工程光学基础教程第四章

•Q1 对物点A的张角
•U'
称为物方孔径
•P'
•Q2 角2U．
•P2
•孔径光阑
•当孔径光阑前
方无光学系统，
•P'2
则孔径光阑就
PPT文档演模板
是入瞳。工程光学基础教程第四章
孔径光阑
•2、入射光瞳和出射光瞳
•P1P2 孔径光阑经后方光学系
统所成的像
•P''1
•P'1
P‘1P’2 称为出射
•测量显微镜物方远心光路。
工程光学基础教程第四章
像方远心光路
•另一类光学仪器是把标尺放在不同的位置，通过改变光学系统的放大率而使标尺像等于一个已知值，以求得仪器到标尺之间的距离。
PPT文档演模板
经纬仪
工程光学基础教程第四章
像方远心光路
•这种情况如果孔径光阑仍为物镜框，由于调焦不准，标尺的像不与分划板刻线平面重合，使读数产生误差而影响测量精度。
➢通常设置在系统
PPT文档演模板
•P''2
•出射光瞳
•孔径光阑
•P'2
的实像平面或物平面
•入射光瞳
工程光学基础教程第四章
•确定视场光阑的方法： •(1)把孔径光阑以外的所有光孔经前面的光学系统成像到物空间，确定入瞳中心位置 (实际上在确定孔径光阑时这一步骤已完成)。
•(2)计算这些像的边缘对入瞳中心的张角大小。张角最小者即为入射窗，入射窗对应的光学零件视场光阑.
渐晕光阑
PPT文档演模板
工程光学基础教程第四章
渐晕光阑
PPT文档演模板
工程光学基础教程第四章

工程光学第四章_光学系统中的光阑与光束限制

A 2 1
2′
B'
30 26.565o 2 (30) D2 2( l1 l2 )
) U1 ) U 2
U 2 (
U 2 arctg arctg
B
A'
44 23.749o 2 (30 20)
D2′的张角最小，最能限制轴上物点 A的成像光束，为入瞳，即光孔2为孔径光阑，U2为物方孔径角。光孔2后面无透镜，孔径光阑与出瞳重合，U2′为像方孔径角。
★景像平面（照片）上弥散斑直径的允许值 y D pp z2 D p z z1 y ★对准平面上对应弥散斑的允许值：z z1 z2 ★远景、近景到入瞳的距离：
z1 2a p1 p p1
z2 2a p p2 p2
z

p
2ap 2ap p1 p2 2a z1 2a z 2

，
以照相机为例，分析人眼看照片认为是清晰图像的情况：
★ 正确透视距离：观察距离满足照片上各点对人眼睛的张角，与直接观察空间时各对应点对眼睛的张角相等。
y y' ' tan tan p D
y' D p p y
以下推导不考虑正负号
眼睛
u
：人眼的
极限分辨角
p
p
清晰像：弥散斑直径对人眼的张角< 人眼的极限分辨角 1 ~ 2
2、透视失真
—— 投影中心前后移动，所得投影像与景物不成比例。
3、景像畸变
二、光学系统的景深
★ 成像空间的景深：在景象平面上所获得的成清晰像的物空间深度。
近景平面远景平面
1 2
入瞳中心：物空间参数的起算原点

工程光学第四章知识点总结

3：场镜的应用
（1）一般显微镜系统中，孔径光阑置于显微物镜上；一次实像面处安放系统的视场光阑；
（2）显微系统用于测焦面处，称为“物方远心光路”
五光学系统的景深
1物方空间点成像相当于以入射光瞳中心为投影中心，以主光线为投影线，使空间点投影在对准平面上，再成像在景象平面上。
（3）照相光学系统中，感光底片的边框就是视场光阑。
三：望远镜系统中成像光束的选择
（1）两个光学系统联用时，一般应满足光瞳衔接原则；
（2）目视光学系统的出瞳一般在外，且出瞳距不能短于6mm；
（3）望远系统的孔径光阑大致在物镜左右；
（4）可放分化板的望远系统中，分化板框是望远系统的视场光阑。
2按理想光学系统的特性，物空间一个平面，在像空间只有一个平面与之共轭。上述景象平面上的空间像，严格来讲除对准平面上的点能成点像外，其他空间点在景象平面上只能为一个弥散斑。
在景象平面上所获得的成清晰的像的空间深度称为成像空间的景深，简称景深。
2 ：视场光阑
（1）在实际的光学系统中，不仅物面上的没一点发出进入系统参与成像的光束宽度是有限的，而且能够清晰成像的这个物面范围成为光学系统的物方视场，相应的像面范围称为像方视场。光阑孔的大小就限定了物面或像面的大小，即限定了光学系统的成像范围。这个限定成像范围的光阑称为视场光阑。
（2）入射窗和出射窗。视场光阑经其前面的光学系统所成的像称为入射窗，视场光阑经过后面的光学系统所成的像称为出射窗。入射窗视场光阑和出射窗三者是互为物像关系的。
第四章
一光阑
1（1）孔径光阑的定义与作用
进入光学系统参与成像的光束宽度与系统分辨物体细微结构能力的高低、与进入系统的光能多少密切相关。因此在具体的光学系统的设计之前，光学系统的孔径要首先确定。

工程光学(光阑)ppt课件

入射窗
出瞳
入瞳
L1
L2
像
物
主光线
视场光阑出射窗
孔径光阑
以上只讨论了入射光瞳口径为无限小的情况。实际上，光学系统的入射
光瞳总是有一定大小。有时还可能很大。此时系统小光束被限制的情况就变
得复杂一些。下面我们就一般情况作精简品课要件分析。
15
当入射光瞳有一定大小时，由轴外物点发出的充满入瞳的光束，有时会被某些透镜框所遮拦。如图所示，透镜L1、L2分别位于孔径光阑D的两侧。由轴外物点B发出的充满入瞳的光束，其中只有一部分（画有阴影线部分）通过系统成像，而其上下各有一部分分别被透镜L2与L1的镜框所遮拦。因此，轴外物点成像光束的孔径显然要比轴上物点小。致使像面上从中央到边缘，光照度逐渐下降，这种现象称为“惭晕”。
B
C A
精品课件
4
（二）入射光瞳、出射光瞳入射光瞳：孔径光阑经其前面的光组在物空间的像。也就是从透镜左向右方观察所看到的孔径光阑的像。出射光瞳：孔径光阑经其后面的光组在像空间成的像。入射光瞳、出射光瞳和孔径光阑三者是共轭关系。入射光瞳是光束进入系统的公共入口，出射光瞳是光束射出系统的公共出口。
“光阑”。
在光学系统中，不单用装夹光学零件的金属框的内孔来限制光束，有
时还要专门设置一些带孔的金属薄片来限制光束，这些就是专用光阑。专
用光阑的通光孔一般为圆形，其中心线和光轴重合。多数专用光阑的孔径
是固定的，但也有可变的。孔径可变的光阑称为可变光阑，常用于照相物
镜中。又如人眼的瞳孔也是一个可变光阑，其孔径能随外界光线的强弱
视场光阑——决定物平面或物空间成像范围的光阑。在多数光学系统如照相机、显微系统中，视场光阑的位置常被设置在系统物镜的像平面上，这样，视场才能具有清晰的边界。

工程光学基础4演示模板.ppt

（1）在照像光学系统中，根据轴外光束的像质来选择孔径光阑的位置，其大致位置在照
像物镜的某个空气间隔中，如图4-6所示。（2）在照像光学系统中，感光底片的框子就
是视场光阑。
（3）孔径光阑的形状一般为圆形，而视场光阑的形状为圆形或矩形等。
0.0
11
对转向棱镜、一个分划板和一组目镜构成的，如图4-7所示。有关光学数据如下：
片框 B1B2 的大小确定的。超出底片框的范
围，光线被遮拦，底片就不能感光。
0.0
5
或者是限制成像范围的光孔或框，都统称为 “光阑”。
限制进入光学系统的成像光束口径的光阑称为“孔径光阑” ，例如照像系统中的可变光阑 A 就是孔径光阑。
限制成像范围的光阑称为“视场光阑” ，
例如照像系统中的底片框B1B2 就是视场光
16
（2）
30
31.5> D棱>16
16
（3） 31.6
31.5> D棱>16
16
0.0
D目 23.5 23.7 24.0
22
由表可见，物镜的通光口径无论在何种
光阑位置情况下都是最大的；出瞳距lz '相
差不大，且能满足预定要求。
所以选择使物镜口径最小的光阑位置是适宜的，故取第二种情况将物境框作为系统孔径光阑。
（4）可放分划板的望远系统中，分划板框是望远系统的视场光阑。
0.0
26
与分析
由前面两节的分析知道，光学系统中的光束选择一定要具体对象具体分析。这里再以显微镜系统为例，介绍一些光束选择的考虑与分析。
0.0
27
一、简单显微镜系统中的光束限制：
中成像光束的口径往往由物镜框限制，物镜框是孔径光阑。位于目镜物方焦面上的圆孔光阑或分划板框限制了系统的成像范围，成为系统的视场光阑，如下图所示。

工程光学基础教程习题答案(完整)

第一章几何光学基本定律1. 已知真空中的光速c ＝3810⨯m/s ，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s, 当光在冕牌玻璃中，n=1.51时，v=1.99 m/s, 当光在火石玻璃中，n ＝1.65时，v=1.82 m/s ，当光在加拿大树胶中，n=1.526时，v=1.97 m/s ，当光在金刚石中，n=2.417时，v=1.24 m/s 。

2. 一物体经针孔相机在屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm 。

3. 一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

工程光学第4章

y f tg 2 2 f
式中 y 可由分划板标尺读出，物镜焦距 f 已知，可求出平面镜转动的微小角度。
图3-4 测定微小角度和位移
若平面镜的转动是由一顶杆移动引起的，设顶杆到支点距离为a ，顶杆微小移动量为 x ,则 tg x a ,代入上式，得
y (2 f a)x Kx
图3-6 连续一次像
如图3-6所示，一右手坐标系的物体 xyz，经双面镜 QPR 的两个反射镜 PQ 、PR 依次成像为 xyz和 xyz。经 PQ 第一次反射的像 xyz为左手坐标系，经PR 第二次反射后成的像（称为连续一次像）xyz 还原为右手坐标系。由于
yPy yPy yPy 2RPy 2QPy 2
因此，连续一次像可认为是由物体绕棱边旋转 2角形成的，旋转方向由第一反射镜转向第二反射镜。只要双面镜夹角不变，双面镜转动时，连续一次像不动。
总之，双平面镜的成像特性可归结为：（1）二次反射像的坐标系与原物坐标系相同，成一致像。（2）连续一次像可认为是由物体绕棱边旋转 2 角形成的，其转向与光线在反射面的反射次序所形成的转向一致。
P1
当直角棱镜在水平面内以角2 速度
旋转时，道威棱镜绕其光轴以的角速
度同向转动，可使在目镜中观察到的像的
坐标方向不变。这样，观察者可以不改变
位置，就能周视全景。由于道威棱镜的入
射面和出射面与光轴不垂直，所以道威棱
镜只能用于平行光路中。
从上面的讨论可知，对于简单棱镜，在主
截面内的坐标改变方向，垂直于主截面的
图3-1 平面镜成像
1.1 平面镜成像特点有：
(1)像与物相对平面镜对称，物像虚物相反
由球面镜的物像位置公式 1 1 2 ，令 r = ∞可得 l l ，所以，

第四章工程光学基础

2 2
折射棱镜与光楔
由
1 sin I1 ' sin I1 n 1 sin I 2 sin I 2 ' n
1 sin 2 I1 1 sin 2 I 2 ' 1 1 2 1 2 sin I1 1 2 sin 2 I 2 ' n n
若上式成立，只有I1=I2’，再次利用折射定律有I1’=I2，也就是说，只有当光线的光路对称于棱镜时，为极值。
平面反射镜
图4-5 双平面镜对光线的变换
平面反射镜
结论：出射光线与入射光线的夹角与入射角无关，只取决于双面镜的夹角。假如物体是左手坐标，一次反射象是右手坐标，成镜像，二次反射象是左手坐标，和原物坐标相同，成一致象。物点A一次反射象A’和二次反射象A”均在以P为圆心，PA为半径的圆周上，可以把的位置看成是物点A以PA为半径绕P点转动2 α角处。按照反射面次序依次转向。 ∠Y”PY=∠Y”PY’-∠YPY’=2∠RPY’-2∠QPY’=2α
平行平面板
平行平面板
平行平板的性质:
（1）由于所以
U 2 ' U1
光线方向不变
sin I1 n sin I1 ' n sin I 2 sin I 2 '
I 1 I 2 ' ,U 2 ' U1
n1u1 n1 tg U1 1 n2 ' u2 ' n2 tg U 2 '
折射棱镜与光楔
由图得
BCD 180o ( I1 ' I 2 ) BCD 180o
I 1 ' I 2 FBD FDB I 1 I 1 ' I 2 I 2 ' I 1 I 2 '

工程光学第四章知识点

第四章平面系统第一节平面镜1,单平面镜的成像特性IPP为平面镜，物点A发出的光束中，取一条光线垂直于PP入射，反射光线在入射点P处原路返回;另一条AQ经反射后沿QB出射，反向延长交于A'点。

A就是A的反射像。

显然，△ AP啃\A PQir等，：AP=A P,即A'与A关于镜面对称。

A点发出的同心光束，经反射镜反射后为以 A '点为顶点的同心光束平面镜能对物体成完善像平面反射镜是唯一一种能对任意大物体以任意宽光束成完善像的实际光学元件实物成虚反射像，虚物成实反射像反射像是正立的，放大率0 = 1 ,像距l ' = -l反射像是“镜像”在平面镜的物空间取一左手坐标系xyz,根据平面镜成像的对称性质，可以确定反射像为右手坐标系x' v' z'一次反射或奇数次反射得镜像，偶数次反射得“一致像”摆动效应：光线以一定方向入射到平面镜，若平面镜摆动a角，则反射光将产生2 a角的摆角这一性质在精密计量中有广泛应用，通过扩大倍率来进行小角度或小位移的测量路、转像、倒像和扫描等光线从棱镜的一个面进入棱镜，在其内表面一次或多次反射，最后从出射面射出棱镜光轴：系统光轴在棱镜中的部分光轴截面：包含光轴的棱镜截面，又称主截面只有在光轴截面内才能正确反映棱镜每2个面之间的角度、光轴方向及反射次数1,反射棱镜类型1.简单棱镜只有一个光轴截面的单个棱镜。

其反射次数可以有成一致像1次、2次、3次反射，奇数次反射成镜像，偶数次反射2.棱镜系统成像的物像坐标变化2.屋脊棱镜带有屋脊面的棱镜为屋脊棱镜屋脊面：2个互相垂直的反射面，交线位于光轴截面内，用以取代棱镜的一个反射面屋脊面相当于2个反射面，因此奇数次反射棱镜将得到一致像屋脊棱镜的表达:在对应的简单棱镜上加一条表示屋脊面的线3.复合棱镜判断规则(1) o' z'与光轴一致(2) o' x'由屋脊面数确定，偶数个与 ox 同向，奇数个反向(3) o' y'由反射次数确定，偶数次为左手系，奇数次为右手系例判断屋脊斯密特棱镜的成像坐标方向数确定，共4次，故仍为左手系。

《工程光学第四章》PPT课件

3孔径光阑的形状一般为圆形光圈而视场光阑的形状为圆形或矩建筑精选课件22建筑精选课件23典型的双目望远镜系统是由一个物镜一对转像棱镜一个分划板和一组目镜构成的如图47所示
建筑精选课件
1
• 实际光学系统与理想光学系统不同，其参与成像的光束宽度和成像范围需要限制:
• (1) 自然限制：光学元件的有限尺寸； • (2) 人为限制：金属圈(框)或成像底片。
成像规则; 2.光瞳对成像的作用: 透视失真 3.视场对成像的影响: 景像畸变
4.二. 光学系统的景深
5.基本概念: 景深,远(近)景深度;
6.景深的计算: 正确透视位置条件下;
7.特殊情况讨论;
建筑精选课件
30
一.光学系统的空间像
理想光学系统: 点物成点像;平面物成平面像;空间物成空间像.
平面成像问题:
对准平面AB
景像平面A’B’
P P’
➢忽略入瞳的有限尺度清晰像点B1’
➢当入瞳具有一定尺建度筑精选课件弥散斑a’b’
34
成像规则: (1)先投影后成像:
在物空间内，以入射光瞳中心为投影中心,以主光线为投影线,将空间点在对准平面上投影,再将投影点成像于景像平面;
建筑精选课件
35
• (2)先成像后投影：
建筑精选课件
8
二、光阑的作用
1. 限制成像光束孔径角大小 2. 限制和选择轴外点成象光束 3. 控制光通量 4. 挡掉杂散光
建筑精选课件
9
孔径光阑：限制和选择成像光束，调节入射光能和像质；视场光阑：确定成像范围。
孔径光阑对入射光束有很直接的选择作用，对于轴上物点和轴外物点，其限制或选择作用不同。
建筑精选课件
5

工程光学4

2
• 孔径光阑对轴上点光束的限制：位置不同，没有差别。
3
• 孔径光阑对轴外点光束的限制：孔径光阑位置不同，参与成像的轴外光束不一样，轴外光束通过L镜的部位也不一样，需要透过全部成像光束的透镜口径大小也不一样。
MN光束较M′N′光束通过L镜的部位高一些；若要透过全部成像光束，光阑位于 A′所需的透镜口径要大，即N′光线投射高度的2倍，而光阑处于A所需的透镜口径要小，即2倍的N光线投射高度。
7
• 入射光瞳：孔径光阑经其前面的透镜或透镜组在光学系统物空间所成的像，它是入射光束的入口。 • 出射光瞳：孔径光阑景气后面的透镜或透镜组在光学系统像空间所成的像，它是出射光束的出口。 • 若孔径光阑位于系统的最前面，则其为系统入瞳；若孔径光阑位于系统最后面，则其为系统出瞳。 • 主光线：通过入瞳中心的光线。对理想光学系统，主光线（或主光线的延长线）必通过入瞳、孔径光阑和出瞳中心。
19
第三节显微镜系统中的光束限制与分析
• 孔径光阑：物镜框 • 视场光阑：目镜物方焦平面上的圆孔光阑或分划板框限制了系统的成像范围。
20
• 显微镜用于测长：在物镜的实像面上置一刻有标尺的透明分划板，要求像与分划板平面重合。 • 测量误差解决方法：孔径光阑移至像方焦平面上， AB和A1B1的主光线重合，分划板上弥散圆中心距不变。 • 光路特点：入瞳位于无穷远，轴外点主光线平行于轴，称“物方远心光路”。
为了减小光学零件的外形尺寸，实际光学系统的视场边缘都有一定的渐晕。有时渐晕系数达到0.5也是允许的，即视场边缘成像光束的宽度只有轴上点光束宽度的一半。
6
• 前面看到经过透镜L的全部出射光束从孔径光阑这个最小出口中通过。将孔径光阑A对其前面的光学系统在物空间成像为A〞，由于孔径光阑A与其像A〞为共轭关系，则入射光束全部从A〞这个入口中“通过”。

工程光学第4章

的入射面和出射面都与光轴垂直。工作面之间的交线称为棱镜的棱，垂直于棱的平面叫主截面，一般取主截面与光学系统的光轴重合，因此又叫光
轴截面。
反射棱镜种类繁多，形状各异，大体上可分为简单棱镜、屋脊棱镜、
立方角锥棱镜。下面分别予以介绍。
图4-8 反射棱镜的主截面
（1）简单棱镜
简单棱镜只有一个主截面，它所有的工作面都与主截面垂直。根据
1 1 1 1
A A1 ’ A2 ’
tgI1 d sin I1 (1 ) tgI1
tgI1 DG L d (1 ) sin I1 tgI1
4.2.2 近轴区平行平板的成像
当入射光线在近轴区以细光束通过平行平板成像，因为 I 1 很小，余弦可近似等于1，式 L
tgI1 cos I1 DG d (1 ) d (1 ) sin I1 tgI1 n cos I1
内容回顾
Q'
F1 F1 ' F2 F2 '
F
H'
F
H'
F'
H
F1
F
H'
内容回顾
Q'
F1 F1 ' F2 F2 '
xF
F
f'
H'

lF
f1 f 1
f f1 f 2
d ) f2
应用牛顿公式有
F f 2 f 2 x
xF
f 1 f 2
d ) f1
F1 F y
,物镜焦距为 f ,则
y f 2 2 f tg
式中 y 可由分划板标尺读出，物镜焦距 f 已知，可求出平面镜转动的微小角度。若平面镜的转动是由一顶杆移动引起的，设顶杆到支点距离为 a，顶杆微小移动量为 x ,则 tg x a , 代入上式，得 y (2 f a) x Kx 式中 K 2 f a 为光学杠杆的放大倍数。利用此式可测量顶杆的微小位移。

工程光学-第4章-PPT精选文档103页

23.11.2019
13
P
AP
I1 I’1 O1
O 2 I2 I2’
qN
q
M
P

两平面镜角度有q变化时，出射方向改变2q
23.11.2019
14
P
AP
I1 I’1 O1
O 2 I2 I2’
qN
q
M
P

当双平面镜绕棱线P旋转时，只要保持θ角不变，则出射光线的方向不变。出射光线发生平移。
23.11.2019
23.11.2019
25
（三）三次反射棱镜：三个反射面，成镜像斯密特棱镜，折叠光路，使仪器紧凑
23.11.2019
26
§4-3 屋脊面和屋脊棱镜
如果在不改变光轴方向和主截面内成像方向的条件下需要得到物体的一致像而又不想增加反射棱镜时，怎么办？
可用交线位于光轴面内的两个相互垂直的反射面来取代其中的一个反射面，使垂直于主截面内的坐标被这两个相互垂直的反射面依次反射而改变方向，从而得到物体的一致像。
称为平行平面板。
用棱镜来代替平面镜，就相当于在光学系统中多加了一块平行平面板。
如标尺、刻有标志的分划板、补偿板、滤光镜、保护玻璃等等
下面讨论光线经过平行平面板的折射情况假定平行平面板位于空气中
23.11.2019
52
应用折射定律
siIn1nsiIn1'
nsiIn 2siIn 2'
又： AB d
co s I1'
23.11.2019
54
Z d sinI1 I1'
c os I1 '
d 1

工程光学第4章

相关知识平行平板成非完善像物体经平行平板的光学系统后所成像的求法反射棱镜的作用；屋脊棱镜与一般反射棱镜的区别折射棱镜的折射面和折射棱；双光楔测量微小角度和微小位移透射材料的种类及特点；反射材料的特点
反射棱镜的分类及特点
折射棱镜与光楔
光学材料
第一节
1.单平面镜
平面镜成像
轴截面。
反射棱镜种类繁多，形状各异，大体上可分为简单棱镜、屋脊棱镜、
立方角锥棱镜。下面分别予以介绍。
图3-8 反射棱镜的主截面
1.1 简单棱镜
简单棱镜只有一个主截面，它所有的工作面都与主截面垂直。根据
反射面数的不同，又分为一次反射棱镜、二次反射棱镜和三次反射棱镜。
图3-9 简单棱镜
1.1.1 一次反射棱镜一次反射棱镜使物体成镜像，最常用的一次反射棱镜有等腰直角棱镜，如图3-9a所示，它使光轴折转90°；等腰棱镜，如图3-9b所示，它使光轴折转任意角度。这两种棱镜的入射面和出射面都与光轴垂直，在反射面上发生全反射。道威棱镜，如图3-9c所示，它是由直角棱镜去掉多余的直角形成的，其入射面和出射面与光轴不垂直，出射光轴与入
1
I 1 )用三角公式展开，并利用 sin I1 n sin I 1
，得
T d sin I1 (1
所以，轴向位移
L
cos I1 ) n cos I 1
cos I1 DG d (1 ) sin I1 n cos I1
应用折射定律 sin I
1
sin I 1 n，代入得
y 轴在左边；而当正对着像即沿 z O方向
l l
观察像时， y 在右边。
图3-2 平面镜成镜像图

《工程光学》课件第4章

第4章平面与平面系统
4.1 平面反射镜 4.2 平行平板 4.3 反射棱镜 4.4 折射棱镜 4.5 光楔
4.1 平面反射镜
4.1.1 单平面镜成像
如图4－1所示，PP′为平面反射镜，由物点A发出的光束被平面反射镜反射，其中任意一条光线AO经平面镜PP′ 反射后，沿OB方向射出；另一条光线AP垂直于镜面入射，并沿原路反射，这两条反射光线的反向延长线交于A′， A′点即为物点A被平面镜反射后所成的像。
折射后，射向第二面，经折射后沿EB 方向射出。出射光线的延长线与光轴交于点A2 ，此即为物点A 经平行平板后的虚像点。光线在第一、第二两面上的入射角和折射角分别为I1 I、1 和 I 2 、 I 2 ，按折射定律有
sin I1 nsin I1 n sin I 2 sin I 2
因两折射面平行，所以 I 2 I1 ，I 2 I1 ，故 U1 U 2 ，可见出射光线EB 和入射光线AD 相互平
垂直。根据反射面数目的不同，简单棱镜又分为一次反射棱镜、二次反射棱镜和三次反射棱镜。
1）一次反射棱镜一次反射棱镜具有一个反射面，相当于单块平面镜，对物成镜像，即垂直于主截面的坐标方向不变，位于主截面内的坐标方向改变。最常用的一次反射棱镜是等腰直角棱镜，如图4－10（a）所示为等腰直角棱镜，光线从一直角面入射，从另一直角面出射，使光轴折转90°。图4－10(b)所示的等腰棱镜可以使光轴折转任意角度。确定反射面角度时，只需使反射面的法线方向处于入射光轴与出射光轴夹角的平分线上即可。这两种棱镜的入射面与出射面都与光轴垂直，在反射面上的入射角大于临界角，能够发生全反射，反射面上无需镀反射膜。
l2 l1 d l
（4－6）
而无需对平行玻璃平板逐面进行计算。因此，在进行光

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

光阑位置对成像光束的影响
光阑位置对成像光束的影响
光阑位置对成像光束的影响
孔径光阑位置移动，对轴外成像光束有明显影响。
常见照相系统的光阑位置
渐晕光阑
渐晕光阑
渐晕光阑
渐晕光阑
渐晕光阑
渐晕光阑
渐晕光阑
轴外物点充满孔径光阑的光束被部分地拦截，称为 “渐晕”。该光阑称为“渐晕光阑”，渐晕光阑多为透镜框。渐晕光阑的作用是参与限制轴外点成像光束。
照相系统中的光阑
照相系统组成
f/1 f/1.4 f/2 f/2.8 f/4 f/5.6 f/8 f/11 f/16 f/22 f/32 f/45 f/64
光阑位置对成像光束的影响
光阑位置对成像光束的影响
光阑位置对成像光束的影响
孔径光阑位置移动，对轴上成像光束并无影响。
光阑位置对成像光束的影响
作业 B
F1 F2
O'4
A F1
O1
O3
O2
A' F'2 O4
B'
如图所示，有一光学透镜组 O1,O2 的口径 D1=D2=50mm,焦距f’1=f’2=150,两透镜间距为300mm, 并在中间置以光孔 O3, 口径 D3=20mm, 透镜 O2 右侧 150mm出置一光孔O4,孔径D4=40mm,平面物体处于透镜O1左侧150mm处。1）求孔径光阑和入瞳出瞳的大小和位置？2）求视场光阑和入窗出窗的大小和位置？
➢ 若物体位于无限远，此时仅比较各个像本身的大小，其口径最小者即为入射光瞳。
➢确定孔径光阑的方法，也可以先确定出射光瞳。
➢对称于光阑的对称式系统：入射光瞳和出射光瞳的大小和倒正都一样，入瞳和出瞳之间的倍率为+1，入射光瞳面和出射光瞳面分别与光学系统的物方主平面和像方主平面重合。
孔径光阑
3、关于孔径光阑需要注意的几个问题
•
D3
45 180
10
2.5mm
A
D1=4mm D3=10mm D3 D2=12mm
O1
F2
O2
45
180
195
透镜O2经O1成像
l'2
l2 f l2
'1 f '1
195 195
36 36
44.15mm
D'2
l'2 l2
•
D2
44.15 195
12
2.72mm
A
D1=4mm D3=10mm D3 D2=12mm
p2 p
P1
光圈值发生变化
Z'
焦深
Z'
焦深
对于固定焦距和拍摄距离，使用光圈越小，景深越大
B1
Z1
2a
Z2
B2
1
2
p2 p
p1
p'1 p' p'2
Z1
2a
p1 p1
p
Z2
2a
p
p2 p2
由相似三角形关系可得
Z1
2a
p1 p1
p
Z2
2a
p
p2 p2
远近点远景深近景深
p1
2ap 2a Z1
入瞳的大小是由光学系统对成像光能的要求或者对物体细节的分辨能力(分辨率)的要求来确定的。常以入瞳直径和焦距之比值来表示，D / f ' 称为相对孔径，它是光学系统的一个重要的性能指标。
孔径光阑
3、关于孔径光阑需要注意的几个问题孔径光阑的安放要遵循一定原则。
➢对于目视光学系统，出瞳必须在目镜外，便于与其衔接。 ➢在投影计量光学中，要求入瞳或出瞳位于无穷远。
U'
P'
Q2
➢Q'1Q'2为入射窗; ➢Q1Q2 本身也为出射窗。
➢通常设置在系统
的实像平面或物
P'2
平面
入射光瞳
确定视场光阑的方法： (1)把孔径光阑以外的所有光孔经前面的光学系统成像到物空间，确定入瞳中心位置 (实际上在确定孔径光阑时这一步骤已完成)。
(2)计算这些像的边缘对入瞳中心的张角大小。张角最小者即为入射窗，入射窗对应的光学零件视场光阑.
实际系统中，物镜框前后10mm左右放置孔径光阑；分划板为视场光阑；孔径光阑对目镜成的像距即为出瞳距离lz>6mm
照相系统中的光阑
简单显微系统中的光束限制
远心光路
➢物方远心光路 ➢像方远心光路
物方远心光路
光学仪器中的很大部分仪器用来测量长度。有一类光学仪器要求以“恒定放大率” 使被测物之像与一刻尺相比，以求得一被测物之长度。
第4章光学系统中的光束限制
➢ 光阑 ➢ 照相系统中的光阑 ➢ 望远系统中成像光束的选择 ➢ 显微镜系统中的光束限制与分析 ➢ 光学系统的景深
本章重点
孔径光阑、视场光阑的确定方法远心光路景深
孔径光阑
1、孔径光阑的定义与作用限制轴上物点光束大小的光孔，也称为“有效光阑” P1P2是孔径光阑,主要用于控制成像面的光能！
入射窗边缘对入瞳中心的张角为物方视场角 2 ，同
时也决定了视场边缘点。视场光阑经后面光学零件所成的像即为出射窗，出射窗对出瞳中心的张角即为像方视场角 2' 。视场光阑是对一定位置的孔径光阑而言的。
孔径光阑为无限小时，物面范围由入窗边缘与入瞳中心连线决定。
入射窗
A
O'2
ω
出孔射径光光瞳阑
孔径光阑
2、入射光瞳和出射光瞳
P''1
P'1
B
-U
A
P''
P1
Q1
U'
O1
P O2
P'
P2
Q2
P''2
出射光瞳
孔径光阑
P'2
入射光瞳
P1P2孔径光阑经后方光学系统所成的像 P‘1P’2 称为出射光瞳，简称出瞳，出瞳边缘对物点A 的张角称为像方孔径角2U’．
当孔径光阑后方无光学系统，则孔径光阑就是出瞳。
解决的方法：在物镜的成像面位置放置一个薄透镜。
场镜的应用
场镜的应用
加入薄透镜不会改变原成像系统的特性。加入薄透镜也不会改变轴上点光束的行进走向。
这种与像面重合或紧靠像面的薄透镜称为场镜。
场镜具有可以辅助延长光学系统长度且不增大后续透镜的孔径的功能！
光学系统的景深
前面讨论的只是在垂直于光轴的平面上点的成像问题，属于这种情况的光学系统有照相制版物镜，电影放映物镜等。实际上，有很多仪器需要把空间中的物点成像在一个像面上，如望远镜和照相机等。这就存在着空间物在平面上成像的清晰度问题。
物方远心光路
光学仪器中的很大部分仪器用来测量长度。有一类光学仪器要求以“恒定放大率” 使被测物之像与一刻尺相比，以求得一被测物之长度。
按工具显微镜的工作台的大小和可移动的距离、测量精度的高低以及测量范围的宽窄，一般分为小型，大型和万能型及重型。它们的测量精度和测量范围不同，但基本结构、测量方法大致相同
光学系统的空间像
光学系统的空间像
光学系统的空间像
光学系统的空间像
将物空间中的物点在同一个像平面上所成的像称为空间像。
光学系统的景深
当弥散斑直径小于人眼的鉴别能力，实际像产生的模糊是无法辨认的，可视为清晰像。此时，这个弥散斑称为容许弥散圆。
在对焦点前后各有一个容许弥散圆，这两个弥散圆在物空间对应的物平面之间的距离就叫景深。
孔径光阑
3、关于孔径光阑需要注意的几个问题
O'2 A
孔径光阑的确定方法
P'1
P1
O1
O2 P'
F'1
P2
P'2
➢首先，将系统中所有零件的光孔成像到物空间，用计算方法确定其位置和大小。
➢第二步，由物面中心A点对各个像的边缘引直线，入射光瞳是其中张角最小者，对应的物为孔径光阑。
孔径光阑
3、关于孔径光阑需要注意的几个问题
B
-U
A
P1
O1
P O2
P2
U' A’
B’
孔径光阑
孔径光阑
2、入射光瞳和出射光瞳
主光线
B
-U
A
P1
O2
O1
P
P2
孔径光阑
P'1
Q1
U'
P' Q2
P'2
P1P2孔径光阑经前方光学系统所成的像 P'1P'2 称为入射光瞳，简称入瞳，入瞳边缘对物点A 的张角称为物方孔径角2U．
当孔径光阑前方无光学系统，则孔径光阑就是入瞳。
大小和位置？
AD1=Βιβλιοθήκη mm D3=10mm D3 D2=12mm
O1
F2
O2
45
180
195
A
D1=4mm D3=10mm D3 D2=12mm
O1
F2
O2
45
180
195
解：光孔D3经O1成像
l'3
l3 f l3
'1 f '1
180 180
36 36
45mm
在O1左方与物点重合
D'3
l'3 l3
场镜的应用
在一些应用中，需要加长光学系统，以满足出瞳的匹配要求。
一种方法是在系统中加入一个放大倍率为-1倍的成像透镜。
场镜的应用
场镜的应用

工程光学基础教程第四章

合集下载