应用光学 郁道银版的课件 工程光学 第四章)
- 格式:ppt
- 大小:887.00 KB
- 文档页数:3


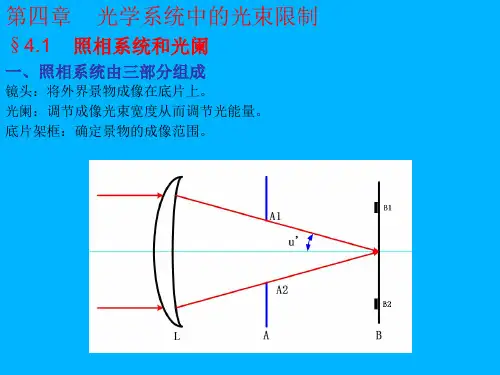



第一章1、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
2、一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=3、.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .4、一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,设凸面为第一面,凹面为第二面。
(1)首先考虑光束射入玻璃球第一面时的状态,使用高斯公式:会聚点位于第二面后15mm处。
(2)将第一面镀膜,就相当于凸面镜像位于第一面的右侧,只是延长线的交点,因此是虚像。

郁道银主编⼯程光学(知识点)第⼀章⼩结(⼏何光学基本定律与成像概念)1 、光线、波⾯、光束概念。
光线:在⼏何光学中,我们通常将发光点发出的光抽象为许许多多携带能量并带有⽅向的⼏何线。
波⾯:发光点发出的光波向四周传播时,某⼀时刻其振动位相相同的点所构成的等相位⾯称为波阵⾯,简称波⾯。
光束:与波⾯对应所有光线的集合称为光束。
2 、⼏何光学的基本定律(内容、表达式、现象解释)1 )光的直线传播定律:在各向同性的均匀介质中,光是沿着直线传播的。
2 )光的独⽴传播定律:不同光源发出的光在空间某点相遇时,彼此互不影响,各光束独⽴传播。
3 )反射定律和折射定律(全反射及其应⽤):反射定律:1、位于由⼊射光线和法线所决定的平⾯内;2、反射光线和⼊射光线位于法线的两侧,且反射⾓和⼊射⾓绝对值相等,符号相反,即I’’=-I。
全反射:当满⾜1、光线从光密介质向光疏介质⼊射,2、⼊射⾓⼤于临界⾓时,⼊射到介质上的光会被全部反射回原来的介质中,⽽没有折射光产⽣。
sinI m=n’/n,其中I m为临界⾓。
应⽤:1、⽤全反射棱镜代替平⾯反射镜以减少光能损失。
(镀膜平⾯反射镜只能反射90%左右的⼊射光能)2、光纤折射定律:1、折射光线位于由⼊射光线和法线所决定的平⾯内;2、折射⾓的正弦和⼊射⾓的正弦之⽐与⼊射⾓⼤⼩⽆关,仅由两种介质的性质决定。
n’sinI’=nsinI。
应⽤:光纤4 )光路的可逆性光从A点以AB⽅向沿⼀路径S传递,最后在D点以CD⽅向出射,若光从D点以CD ⽅向⼊射,必原路径S传递,在A点以AB⽅向出射,即光线传播是可逆的。
5 )费马原理光从⼀点传播到另⼀点,其间⽆论经历多少次折射和反射,其光程为极值。
(光是沿着光程为极值(极⼤、极⼩或常量)的路径传播的),也叫“光程极端定律”。
6 )马吕斯定律光线束在各向同性的均匀介质中传播时,始终保持着与波⾯的正交性,并且⼊射波⾯与出射波⾯对应点之间的光程均为定值。
折/反射定律、费马原理和马吕斯定律三者中的任意⼀个均可以视为⼏何光学的⼀个基本定律,⽽把另外两个作为该基本定律的推论。



HOHO....第一次发帖!请大家顶起哦!!谢谢啦!我这还要很多资料,稍后回传上来,大家一起分享哦!![ 本帖最后由ruanbingdu 于2009-5-4 10:39 编辑]
我虽然没有学习这一部分,但是物理的都有些兴趣以后说不定会下来看看应该是考研以后吧`
//viewth ... 26amp%3Btypeid%3D24
十分感谢楼主的无私分享!
很好的资料。
谢谢分享
正好需要,谢谢您的无私奉献。
thanks!
zhegeluntanhenhao
zhegeluntanhenhao
楼主,下点东西太难了
还没看,不知好不好,不过先谢谢LZ了!
thanks for sharing1
真是太好了,谢谢吼。
真是太感谢你了我找了好多天才找到功德无量啊
楼主你的无私,可以感到中国!太感谢了,我和你需要这些资料!
谢谢楼主很好的
太好了非常感谢!!!!!
我好喜欢,谢谢了!
好资料,感谢楼主分享。
非常感激。
考研屋:提供各大机构考研、公务员、四六级辅导视频课程。