工程光学习题参考答案第四章光学系统中的光束限制

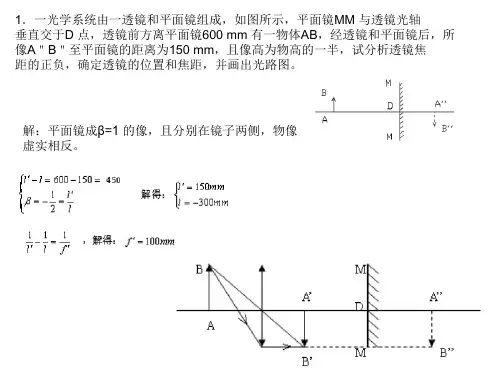
第一章 几何光学基本定律1. 已知真空中的光速c ＝3810⨯m/s ，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s, 当光在冕牌玻璃中，n=1.51时，v=1.99 m/s, 当光在火石玻璃中，n ＝1.65时，v=1.82 m/s ， 当光在加拿大树胶中，n=1.526时，v=1.97 m/s ，当光在金刚石中，n=2.417时，v=1.24 m/s 。

2. 一物体经针孔相机在 屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm 。

3. 一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

第四章光学系统中的光束限制1.设照相物镜的焦距等于75mm，底片尺寸为55×55㎜2，求该照相物镜的最大视场角等于多少？解：2.略。

3. 在本章第二节中的双目望远镜系统中，假定物镜的口径为30mm，目镜的通光口径为20mm，如果系统中没有视场光阑，问该望远镜最大的极限视场角等于多少？渐晕系数k =0.5的视场角等于多少？解：（1）151018108=++x xmm x 252=1081825218252108181815+++=+++=x x y714286.10=y︒=33.112目ω（2） 0793651.0181081021=+=+=’目‘物目f f D tg ω ︒︒==∴08.932492‘’‘ω答：极限视场角等于11.33︒渐晕系数为0.5的视场角为9.08︒。

总黄酮生物总黄酮是指黄酮类化合物，是一大类天然产物，广泛存在于植物界，是许多中草药的有效成分。

在自然界中最常见的是黄酮和黄酮醇，其它包括双氢黄（醇）、异黄酮、双黄酮、黄烷醇、查尔酮、橙酮、花色苷及新黄酮类等。

简介近年来，由于自由基生命科学的进展，使具有很强的抗氧化和消除自由基作用的类黄酮受到空前的重视。

类黄酮参与了磷酸与花生四烯酸的代谢、蛋白质的磷酸化、钙离子的转移、自由基的清除、抗氧化活力的增强、氧化还原作用、螯合作用和基因的表达。

它们对健康的好处有：（ 1 ）抗炎症（ 2 ）抗过敏（ 3 ）抑制细菌（ 4 ）抑制寄生虫（ 5 ）抑制病毒（ 6 ）防治肝病（7 ）防治血管疾病（8 ）防治血管栓塞（9 ）防治心与脑血管疾病（10 ）抗肿瘤（11 ）抗化学毒物等。

天然来源的生物黄酮分子量小，能被人体迅速吸收，能通过血脑屏障，能时入脂肪组织，进而体现出如下功能：消除疲劳、保护血管、防动脉硬化、扩张毛细血管、疏通微循环、活化大脑及其他脏器细胞的功能、抗脂肪氧化、抗衰老。

近年来国内外对茶多酚、银杏类黄酮等的药理和营养性的广泛深入的研究和临床试验，证实类黄酮既是药理因子，又是重要的营养因子为一种新发现的营养素，对人体具有重要的生理保健功效。

物理学：工程光学试题（题库版）1、单选原子发射光谱定性工作中，对粉末样品经常采用（）作为支持电极。

A、石墨电极B、铜电极C、锌电极D、银电极正确答案：A2、名词解释光程正确答案：光经过的实际路径长度与所在介质（江南博哥）折射率的乘积3、问答题什么叫“畸变”？它与什么因素有关？正确答案：轴外点的宽光束和细光束都有像差存在，即使只有主光线通过光学系统，由于球差影响，它不能和第二近轴光一致，主光线和高斯像面焦点的高度不等于理想像高，其差别就是系统的畸变。

4、名词解释电光效应正确答案：在电场作用下，可以使某些各向同性的透明介质变为各向异性，从而使光产生双折射，这种现象称为电光效应。

5、名词解释弧矢平面正确答案：包含主光线，且与子午平面正交的平面。

6、填空题我们通常把分界面两边折射率高的介质称为光密介质，折射率低的介质称为（）。

正确答案：光疏介质7、单选采用调制的空心阴极灯主要是为了（）。

A.延长灯寿命B.克服火焰中的干扰谱线C.防止光源谱线变宽D.扣除背景吸收正确答案：B8、问答题正弦光栅在自身所在平面内分别平移和转动时，对夫琅禾费衍射场的衍射斑有什么影响。

正确答案：正弦光栅在自身所在平面内移动时衍射斑光强分布不变，相位分布发生变化。

在自身平面内转动时，衍射光强和相位分布都发生变化。

9、名词解释物方远心光路正确答案：光学系统的物方光线平行于光轴，主光线的汇聚中心位于物方无限远处.10、填空题发光点发出的光波向四周传播时，某一时刻其振动位相相同的点所构成的等相位面称为波阵面，简称（）正确答案：波面11、填空题棱镜摄谱仪的结构主要由（），（），（），（）四部分（系统）组成。

正确答案：照明系统；准光系统；色散系统；投影系统12、名词解释物方空间正确答案：所有实物点和虚物点的集合构成的空间。

13、填空题交流电弧的激发能力强，分析的重现性好，适用于（），不足的是蒸发能力也稍弱，灵敏度稍低。

正确答案：定量分析14、问答题什么是景深，照相物镜的景深与什么有关？正确答案：能在像面上获得清晰像的物空间的深度是系统的景深。

工程光学第二章理想光学系统1、一个折射率为1.52的双凸薄透镜，其中一个折射面的曲率半径是另一个折射面的2倍，且其焦距为5cm，则这两个折射面的曲率半径分别是〔7.8〕cm和〔-3.9〕cm。

2、一个薄透镜折射率为1.5，光焦度500D。

将它浸入某液体，光焦度变成-1.00D，则此液体的折射率为〔1.502〕。

3、反远距型光组由〔一个负透镜和一个正透镜〕组成，其特点是〔工作距大于组合焦距〕。

4、远摄型光组由一个〔正透镜〕和一个〔负透镜〕组成，其主要特点是〔焦距大于筒长〕，因此该组合系统常用在〔长焦距镜头〕的设计中。

第三章平面与平面系统1、反射棱镜在光学系统中的主要作用有〔折叠光路〕、〔转折光路〕和转像、倒像等，在光路中可等效为平行平板加〔平面反射镜〕。

2、某种波长的光入射到顶角为60°的折射棱镜，测得最小偏向角为42°15′，则该种玻璃对于入射波长的折射率为〔1.557〕。

3、唯一能完善成像的光学元器件是〔平面反射镜〕，利用其旋转特性可制作光学杠杆进行放大测量；利用双光楔也可以实现〔微小角度和微小位移〕的测量，主要有〔双光楔旋转测微〕和〔双光楔移动测微〕两种形式。

4、用于制作光学元件的光学材料包括光学玻璃，〔光学晶体〕和〔光学塑料〕三类。

选用光学玻璃时的两个重要参数是〔折射率〕和〔阿贝常数〕。

5、一个右手坐标的虚物，经一个直角屋脊棱镜反射后，成〔右手〕坐标的〔虚〕像。

第四章光学系统中的光束限制1、限制轴上物点成像光束宽度的光阑是〔孔径光阑〕，而〔渐晕光阑〕在其基础上进一步限制轴外物点的成像光束宽度。

2、为减少测量误差，测量仪器一般采用〔物方远心〕光路。

3、测量显微镜的孔径光阑放置在〔物镜后焦平面上〕，视场光阑放置在〔一次实像面处〕，如果用1/2″的CCD接收图像并用14″的监视器观察图像，要求系统放大倍率为140倍，则显微镜的放大倍率是〔5倍〕。

第五章光线的光路计算及像差理论1、实际像与〔理想像〕之间的差异称为像差，包括单色像差和色差两大类。

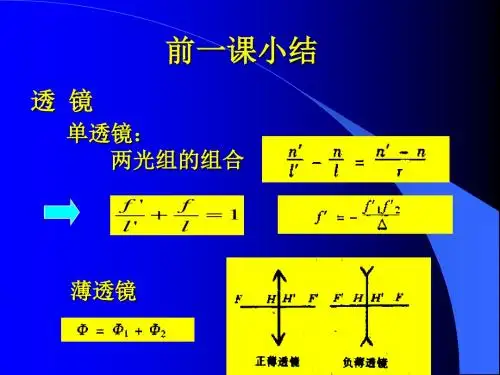
第一章习题1、已知真空中的光速c＝3×108 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1.5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

如果在凸面镀反射膜，其会聚点应在何处？如果在凹面镀反射膜，则反射光束在玻璃中的会聚点又在何处？反射光束经前表面折射后，会聚点又在何处？说明各会聚点的虚实。

解：该题可以应用单个折射面的高斯公式来解决，设凸面为第一面，凹面为第二面。

（1）首先考虑光束射入玻璃球第一面时的状态，使用高斯公式：会聚点位于第二面后15mm处。

（2）将第一面镀膜，就相当于凸面镜像位于第一面的右侧，只是延长线的交点，因此是虚像。

第四章光学系统的光阑与光束限制一、填空题I级I级1空1、在光学系统中，对光束起限制作用的光学元件通称为[1]。

光阑2、限制轴上物点成像光束大小的光阑称为[1]。

孔径光阑3、孔径光阑经过前面的光学系统在物空间所成的像称为[1]。

入射光瞳4、孔径光阑经过后面的光学系统在像空间所成的像称为[1]。

出射光瞳5、一般安置在物平面或像平面上，以限制成像范围的光阑称为[1]。

视场光阑6、视场光阑经其前面的光学系统所成的像称为[1]。

入射窗7、视场光阑经过后面的光学系统所成的像称为[1]。

出射窗8、轴外点发出的充满入瞳的光束受到透镜通光口径的限制，而部分被遮拦的现象称为[1]。

渐晕9、孔径光阑位于光学系统像方焦面处，光学系统的物方主光线平行于光轴，主光线汇聚中心位于物方无限远处，这样的光路称为[1]。

物方远心光路10、孔径光阑位于光学系统物方焦面处，光学系统的像方主光线平行于光轴，主光线汇聚中心位于像方无限远处，这样的光路称为[1]。

像方远心光路11、在长光路系统中，往往利用[1]达到前后系统的光瞳衔接，以减小光学零件的口径。

场镜12、在像平面上所获得的成清晰像的物空间深度称为成像空间的[1]。

景深13、像面边缘比中心暗的现象称为[1]。

渐晕14、为了减少测量误差，测量仪器一般采用[1]光路。

远心15、渐晕大小用渐晕系数衡量，线渐晕系数定义为轴外点成像光束与轴上点成像光束在[1]上线度之比。

入瞳16、与入射窗共轭的物是[1]。

视场光阑17、与入瞳共轭的物是[1]。

孔径光阑I 级2空1、在放大镜和人眼组成的光学系统中，放大镜的镜框是（ ），人眼是（ ）。

视场光阑，孔径光阑2、一个10倍的放大镜，通光直径为20mm ，人眼离透镜15mm ，眼瞳直径为3mm ，当渐晕系数为0.5时，人眼观察到的线视场为（ ）mm ；无渐晕时，线视场为（ ）mm 。

33.33，28.333、开普勒望远系统加场镜后，视放大率不变，目镜通光口径（ ），出瞳离目镜距离（ ）。

第四章 光学系统中的光束限制1.设照相物镜的焦距等于75mm ，底片尺寸为55×55㎜2，求该照相物镜的最大视场角等于多少？解：3.假定显微镜目镜的视角放大率Γ目=15⨯，物镜的倍率β=2.5⨯,求物镜的焦距和要求的通光口径。

如该显微镜用于测量，问物镜的通光口径需要多大（u =-︒3.42y =8mm 显微镜物镜的物平面到像平面的距离为180mm ）？ 解： （1）5.2'-==ll β mm l 428.51-=180'=-l l mm l 57.128'=‘物f l l 111'=- mm f 73.36=‘物 在此情况下，物镜即为显微镜的孔径光阑︒-=3.4u mm tg ltgu D 734.73.4428.5122=⨯⨯==︒物（2）用于测量时，系统中加入了孔径光阑，目镜是视场光阑 由于u 已知，根据u 可确定孔径光阑的大小 mm tg tgu L OM A 8668.33.4428.51=︒⨯=⋅=OA PA OM D A ’‘孔=2L 目-目fL ‘Zmm OM L f L D A 52.58668.357.12873.3657.12822'=⨯-⨯=⨯-⨯=∴’‘物孔在中M M B B '∆ OA P AB A O M B A D B ‘‘’‘’‘孔=++21 mm y 1045.2'=⨯= mm O M B 863.7=∴ mm D 726.15=物答：物镜的焦距为36.73mm ，物镜的孔径为7.734mm ，用于测量时物镜孔径为15.726mm 。

4. 在本章第二节中的双目望远镜系统中，假定物镜的口径为30mm ，目镜的通光口径为20mm ，如果系统中没有视场光阑，问该望远镜最大的极限视场角等于多少？渐晕系数k =0.5的视场角等于多少？ 解：（1）151018108=++x xmm x 252=1081825218252108181815+++=+++=x x y714286.10=y︒=33.112目ω （2）0793651.0181081021=+=+=’目‘物目f f D tg ω ︒︒==∴08.932492‘’‘ω答：极限视场角等于11.33︒渐晕系数为0.5的视场角为9.08︒。

第一章 几何光学基本定律1. 已知真空中的光速c ＝3810⨯m/s ，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s, 当光在冕牌玻璃中，n=1.51时，v=1.99 m/s, 当光在火石玻璃中，n ＝1.65时，v=1.82 m/s ， 当光在加拿大树胶中，n=1.526时，v=1.97 m/s ，当光在金刚石中，n=2.417时，v=1.24 m/s 。

2. 一物体经针孔相机在 屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm 。

3. 一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学？光学在人类生活中有哪些应用？答：光学是研究光的行为和性质的物理学科。

它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。

光学在人类生活中有着广泛的应用，如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。

1.2 光的波动性是如何描述的？答：光的波动性是指光是一种电磁波，具有振幅、频率、波长等特征。

它可以在空间中传播，并且可以表现出干涉、衍射等波动性质。

光的波动性可以通过波长、频率、振幅等参数进行描述。

1.3 什么是光的干涉？举例说明其应用。

答：光的干涉是指两列或两列以上的光波在空间中叠加时，由于光波的叠加产生明暗相间的干涉条纹的现象。

光的干涉在很多领域都有应用，例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。

1.4 什么是光的衍射？举例说明其应用。

答：光的衍射是指光在遇到障碍物或孔径时，会绕过障碍物或孔径边缘，产生明暗相间的衍射图案的现象。

光的衍射在很多领域也有应用，例如光学透镜、衍射光学器件、全息照相、光学存储等。

1.5 什么是光的偏振？举例说明其应用。

答：光的偏振是指光波的电矢量在振动时，只在某个方向上振动，而在其他方向上振动为零的现象。

光的偏振在很多领域也有应用，例如偏振眼镜、偏振片、偏振光学器件等。

第二章光学透镜与成像2.1 什么是透镜？列举几种常见的透镜及其特点。

答：透镜是一种光学器件，它由一块透明材料制成，可以聚焦或发散光线。

常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。

2.2 凸透镜的成像原理是什么？如何计算凸透镜的焦距？答：凸透镜的成像原理是光线经过凸透镜后，平行于主轴的光线会聚于一点，这个点称为焦点。

焦距是指从透镜中心到焦点的距离。

凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算，其中f为焦距，u为物距，v为像距。

2.3 凹透镜的成像原理是什么？如何计算凹透镜的焦距？答：凹透镜的成像原理是光线经过凹透镜后，平行于主轴的光线会朝透镜中心方向会聚于一点，这个点称为虚焦点。