第5讲 网络计划的基本概念

建设工程技术与计量(安装)-流水施工、网络计划、施工组织设计讲义一.内容提要主要介绍第二章第十节工程流水施工、第十一节工程网络计划技术和第十二节施工组织设计。

二.重点.难点1、熟悉流水作业和网络进度计划，掌握安装工程施工组织设计编制原理和方法。

2、重点是施工组织设计的编制,难点是流水作业和网络进度计划。

三.内容讲解大纲要求1、了解流水施工原理；2、熟悉工程网络计划技术的基本知识及应用；3、掌握施工组织设计编制原理及方法。

第十节工程流水施工一、流水施工概述（一）流水施工的技术经济效果流水施工在工艺划分、时间排列和空间布置上都是一种科学、先进和合理的施工组织方式，具有显著的技术经济效果。

主要表现在以下几点：（1）流水施工的节奏性、均衡性和连续性，减少了时间间歇，使工程项目尽早地竣工，能够更好地发挥其投资效益。

（2）工人实现了专业化生产，有利于提高技术水平，工程质量有了保障，也减少了工程项目使用过程的维修费用。

（3）工人实现了连续作业，便于改善劳动组织、提高操作技术和更加合理使用施工机具，有利于提高劳动生产率。

劳动生产率提高可以降低工程成本，增加承建单位利润。

（4）以合理劳动组织和平均先进劳动定额指导施工，能够充分发挥施工机械和操作工人的生产效率。

（5）流水施工高效率，可以减少施工管理费。

资源消耗均衡，可以减少物资损失，有利于提高承建单位经济效益。

例：组织流水施工的效果有（）。

A、可以实现均衡有节奏的施工B、可以节省时间C、可以提高劳动生产率D、可以把施工过程组成一个整体E、可以减少施工管理费答案：ABCE（二）流水施工分级1、分项工程流水施工分项工程流水施工也称为细部流水施工，即在一个专业工程内部组织的流水施工。

2、分部工程流水施工分部工程流水施工也称为专业流水施工，是在一个分部工程内部、各分项工程之间组织的流水施工。

3、单位工程流水施工单位工程流水施工也称为综合流水施工，是一个单位工程内部、各分部工程之间组织的流水施工。

什么是网络计划
网络计划是指利用计算机网络技术进行信息传输、数据处理和
资源共享的计划。

网络计划可以帮助我们更高效地进行工作和学习，也可以带来更多的便利和乐趣。

首先，网络计划可以帮助我们更高效地进行信息传输。

在过去，人们需要通过信件或传真来传递信息，而现在，借助网络计划，我
们可以通过电子邮件、即时通讯等方式实现快速的信息传输。

这样
不仅可以节省时间，也可以降低成本，提高工作效率。

其次，网络计划可以帮助我们更便捷地进行数据处理。

在传统
的数据处理过程中，人们需要手工录入数据、进行计算和分析，而
网络计划可以通过网络连接各种计算机和设备，实现数据的自动采集、处理和分析。

这样不仅可以减少人力成本，还可以提高数据处
理的准确性和效率。

另外，网络计划还可以带来资源共享的便利。

通过网络计划，
我们可以轻松地访问全球范围内的各种资源，如图书、资料、软件等。

这样不仅可以节省成本，还可以拓宽我们的视野，提升我们的
学习和工作效果。

总的来说，网络计划是一种利用计算机网络技术进行信息传输、数据处理和资源共享的计划，它可以帮助我们更高效地进行工作和
学习，带来更多的便利和乐趣。

希望大家可以充分利用网络计划，
发挥其最大的作用，为我们的生活和工作带来更多的便利和乐趣。

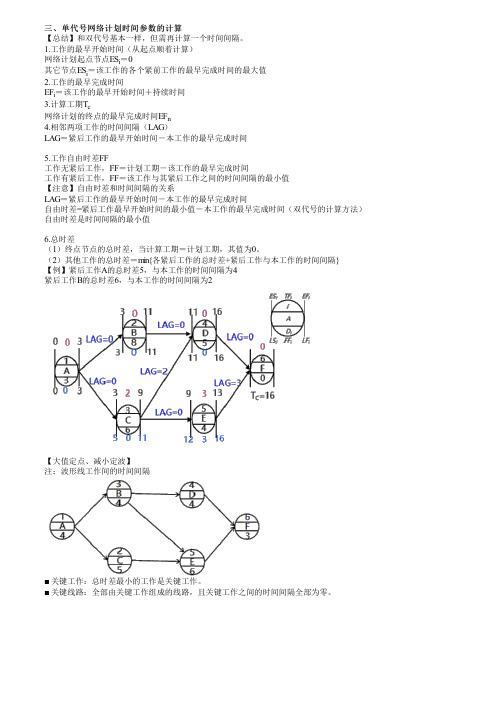
三、单代号网络计划时间参数的计算
三、单代号网络计划时间参数的计算
【总结】和双代号基本一样，但需再计算一个时间间隔。

1.工作的最早开始时间（从起点顺着计算）
网络计划起点节点ES i＝0
其它节点ES i＝该工作的各个紧前工作的最早完成时间的最大值
2.工作的最早完成时间
EF i＝该工作的最早开始时间＋持续时间
3.计算工期T c
网络计划的终点的最早完成时间EF n
4.相邻两项工作的时间间隔（LAG）
LAG＝紧后工作的最早开始时间－本工作的最早完成时间
5.工作自由时差FF
工作无紧后工作，FF＝计划工期－该工作的最早完成时间
工作有紧后工作，FF＝该工作与其紧后工作之间的时间间隔的最小值
【注意】自由时差和时间间隔的关系
LAG＝紧后工作的最早开始时间－本工作的最早完成时间
自由时差=紧后工作最早开始时间的最小值－本工作的最早完成时间（双代号的计算方法） 自由时差是时间间隔的最小值
6.总时差
（1）终点节点的总时差，当计算工期＝计划工期，其值为0。

（2）其他工作的总时差＝min{各紧后工作的总时差+紧后工作与本工作的时间间隔}
【例】紧后工作A的总时差5，与本工作的时间间隔为4
紧后工作B的总时差6，与本工作的时间间隔为2
【大值定点、减小定波】
注：波形线工作间的时间间隔
■ 关键工作：总时差最小的工作是关键工作。

■ 关键线路：全部由关键工作组成的线路，且关键工作之间的时间间隔全部为零。

网络分析与网络计划的概念网络剖析是图论的一个运用分支．它主要是运用图论的实际与方法来处置具有网络性质的管理决策效果．在理想生活和消费实际中，网络剖析方法有很普遍的运用．如在企业管理中，如何制定管理方案或设备置办方案，使收益最大或费用最小；在组织消费中，如何使各工序衔接好，使消费义务完成得既快又好；在交通网络中，如何使调运的物资数量多且费用最小等．由于网络剖析具有图形直观，方法简便，容易掌握的特点，因此失掉迅速的开展，且普遍地运用在各个范围，成为经济活动中许多管理决策的优化效果的重要手腕．网络方案方法是上世纪50年代开展起来的方案控制技术，主要包括方案评审技术(programme evaluation and review technique，简称PERT)和关键途径方法(critical path method或critical path analysis，简称CPM、CPA)．网络方案方法特别适用于现代管理中的多要素多环节的复杂方案的优化控制，成为管理运筹学的重要运用分支．本章在引入有关图的一些基本概念的基础上，引见最小生成树、网络最短路、最大流、最小费用最大流等网络剖析模型及其解法；并对网络方案图〔统筹图〕的制造、作业时间参数计算、关键线路方法和方案评审技术等网络方案基本技术和方法停止初步引见．第一节图的基本概念一、图理想世界中有许多详细事物及关系可以用图形来笼统表示．例如，路途关系、工序布置、区位规划等都可以用图来表达．我们先经过几个直观的例子，来看法什么是图．例6-1 歌尼斯堡七桥效果哥尼斯堡(Konigsbergs)城域有一个普雷格尔河系，由新河、旧河及其交汇而成的大河组成，它把该城分红了一岛三岸共四块陆地，陆地之间有七座桥连通，如图6-1(a)所示．事先城内居民在散步时热衷于这样一个效果：从某陆地动身，能否走遍七桥且每桥只过一次而最终回到原动身地．图6-1〔a〕图6-1〔b〕欧拉在1736年处置了这一效果．他用四个点表示四块陆地，用相应两点间的边表示桥，从而树立了该效果的图的模型，见图6-1(b)．于是效果归结为：在这个连通多重图中，能否找出一条回路，过每边一次且仅仅一次．欧拉在求解该效果时，把图6-1〔a〕所示的实践效果笼统为图6-1〔b〕所示图形．例6-2 竞赛布置效果5个球队之间布置赛事．其中a球队区分与b，c，d球队有赛事；b球队还与c球队，d球队还与e球队有赛事．综上，这5个球队之间的竞赛关系可用图6-2(a)来表示，也可用图6-2(b)来反映．图6-2〔a〕图6-2〔b〕以上两例都疏忽了效果的详细细节，而把效果的关键性质或关系笼统为图的方式．例6-1中两岸和岛的外形及桥的曲直都被疏忽，但陆地间的关联状况却失掉坚持．例6-2中把竞赛关系笼统为衔接关系．复杂些说，一个图代表了某些对象集合之间的关系，而图论是主要研讨这些对象在上述表示法中的许多能够的性质中的某些性质．详细些说，一个图指的是一些点以及衔接这些点的一些线的总体．这种衔接方式可以具有许多特征，而图论实质上就是研讨这种特征的．留意，这里所讲的图并不是解析几何与微积分书中罕见的图，在那里，点的位置，线的长度和斜率是它的重要局部．而在图论中，这些都是不重要的，而重要的只是哪些点之间有线相连．有时，衔接的先后次第也是重要的．二、几个基本概念一个图G 定义为一个有序二元组〔V ，E 〕，记为：G ＝〔V ，E 〕其中，V 是一个有限非空的集合，其元素称为G 的结点或顶点，简称点，而V 称为G 的结点集或顶点集，简称点集，普通表示为：V ＝{1v ，2v ，…，n v }而E 称为G 的边集，表示为：E ＝{1e ，2e ，…，n e }其中e 由V 中元素对(i v ，j v )所构成．假设(i v ，j v )是无序对，那么G 称为无向图．E 中元素e 称为G 的无向边，普通表示为e ＝(i v ，j v )关于给定的图可以作出其几何图．例6-3 无向图G ＝〔V ，E 〕，其中点集V ＝{1v ，2v ，3v ，4v ，5v }，E ＝{1e ，2e ，3e ，4e ，5e ，6e ，7e ,8e }，边与顶点的关联状况由表6-1给出．表6-1 边与顶点的关联状况依据表6-1，可作其几何图，如图6-3所示．在作几何图时，仅要求表示出顶点、边以及它们间的关联关系，而对顶点的位置以及边的曲直、长短都没有任何规则．图6-3基于无向图G 的结构特点，我们给出以下一些术语：平行边——假定两条不同的边e 与'e 具有相反的端点，那么称e 与'e 为G 的平行边．图6-3中2e 与7e 是平行边，由于它们的端点均为1v 、3v ．复杂图——假定G 无平行边，那么称图G 为复杂图．完备图——图G 中任两个顶点间恰有一条边相关联，G 为完备图．设顶点的非空集合V ＝〔1v ，2v ，…，n v 〕，边的集合A ＝〔1a ，2a ，…，n a 〕．假设A 中任一条边ij a 是V 的一个有序元素对(i v ，j v )(这里，i v ≠j v )，那么称A 为有向边集，A 中元素ij a 称为有向边或弧，记为ij a ＝(i v ，j v )其中i v 为ij a 的终点，j v 为ij a 的终点．V 和A 组成了一个有向图，记作D ＝〔V ，A 〕例6-4 给有向图D ＝〔V ，A 〕，其中V ＝〔1v ，2v ，3v ，4v 〕，A ＝〔1a ，2a ，…，7a 〕，边与顶点的关联状况如表6-2所给．表6-2 边与顶点的关联状况依据表6-2也可作出有向图，如图6-4〔a 〕图6-4(a)图6-4(b)图6-4〔c 〕有向图区别于无向图的关键，在于它的边〔或弧〕是有方向的，图6-4〔a 〕中边上的箭头所指即边的方向．在有向图中(i v ，j v )≠(j v ，i v )．相似于无向图，有向图G 也有以下术语：平行边——不同的弧a 与'a (i v ，j v )的终点与终点都相反．图6-4〔a 〕中3a 、4a 是平行边，而1a 、2a 却不是，1a ＝(2v ,1v )；而2a ＝(1v ,2v )．复杂图——无平行边的有向图称为复杂图．完备图——图中任两个顶点i v 与j v 间，恰有两条有向边(i v ，j v )及(j v ，i v )，那么称该有向图D 为完备图．基本图——把有向图D 的每条边除去方向就失掉一个相应的无向图G ，称G 为D 的基本图．例如图6-4〔b 〕是图6-4〔a 〕的基本图．3．同构关于无向图和有向图，假设图G ＝〔V ，E 〕和G '＝(V '，E ')的顶点集合V 和V '，以及边集E 和E '之间在坚持关联性质的条件下一 一对应，那么图G 和G '同构．例如图6-2(a)、(b)所示的两个图看似不同，其实是同构图．由于同构的图被以为是相反的，这就给我们在网络规划中树立网络模型带来许多方便，当我们用几何图来反映和剖析实践效果的内在关系而构建网络模型时，点的位置可以恣意布置，边的长短曲直也可恣意，故而我们尽量设计那种反映效果明晰、精练的几何图．4．链、路和连通性给定一个无向图G ＝〔V ，E 〕，其中的一个点与边的交织序列1i v ，1i e ，2i v ，2i e ，…，1-ik v ，1-ik e ，ik v ，假设序列中一切it e 都满足it e ＝〔it v ，1+it v 〕，〔t ＝1，2，…，k －1〕，那么称交织序列为结合1i v 和ik v 的链，记为μ＝〔1i v ，1i e ，2i v ，2i e ，…，1-ik v ，1-ik e ，ik v 〕或简记为〔1i v ，2i v ，…，1-ik v ，ik v 〕和〔1i e ，2i e ，…，2-ik e ，1-ik e 〕当k ＞0，且1i v ＝ik v ，那么链的终点等于终点，称为闭链．闭链中除终点和终点外没有相反的结点和边，那么该闭链称为圈．当1i v ≠ik v ，时称为开链．假定开链中一切结点均不相反，称为初等链． 例如图6-5中：图6-5μ1＝〔1v ，2v ，4v ，3v ，2v ，1v 〕是闭链，但不是圈；μ2＝〔1v ，2v ，3v ，1v 〕是闭链，同时也是圈；μ3＝〔1v ，2v ，4v ，3v ，2v 〕是开链；μ4＝〔1v ，2v ，4v ，3v 〕是初等链．关于有向图D ＝〔V ，A 〕，可以经过其相应的基本图来定义它的链．但由于有向图中弧是有方向的，能够出现链中的弧的方向与链的方向不分歧的状况．假设链中一切弧的方向与链的方向分歧，那么称该链为单向路，简称路．显然，在有向图中链和路的概念并不分歧，而在无向图中两者没有区别．假设路的终点和终点相反，那么称为回路．关于无向图而言闭链和回路概念分歧．在图6-4〔a 〕中：μ1＝〔1a ，3a ，8a 〕是链，但不是路；μ2＝〔8a ，3a ，1a 〕是链，同时也是路和回路．在D 中恣意两个结点v i1和v ik ，从v i1到v ik 存在路，那么称v i1可达v ik ．假定D 中恣意两结点间存在链，那么称D 为连通图．假定D 中恣意两结点间相互可达，那么称D 为强连通图．关于无向图而言连通图等价于强连通图．例如图6-4〔a 〕所示的是强连通图，由于1v 、2v 、3v 、4v 都是相互可达的．假设我们将图中弧8a 删去，如图6-4〔c 〕所示，那么成为普通的连通图．由于这时1v 、3v 不能相互可达．5．网络一个图连同定义在其边集上的实函数一同称为一个网络．网络普通是连通图．定义在边集上的实函数称为边的权数记为ij w ＝w (i v ，j v )它与边(i v ，j v )具有逐一对应关系，可以用以表达网络上的各种有关性质，如路长、流量、费用等等．网络的图解即在每条边旁标上相应的权数．假定一网络的每条边都是无向边，那么称为无向网络，记为N ＝〔G ，w 〕或N ＝(V ，E )假定一网络的每条边都是有向边，那么称为有向网络，记为N＝〔D，w〕或N＝(V，A)假定一网络中既有无向边，也有有向边，那么称为混合网络．所谓网络剖析，复杂地说，即对网络停止定性和定量剖析，以便为完成某种优化目的而寻求最优方案．这方面的典型效果有：最小树效果，最短路效果，中心效果，重心效果，最大流效果，最小费用最大流效果，最短回路效果，网络方案效果，等等．第二节最小树效果一、树的基本概念1．子图、真子图、生成子图设有图G＝(V，E)和图G'＝(V'，E')，假设V'⊆V，E'⊆E，那么称G'为G的子图，并记为G'⊆G，而G那么为G'的原图．当子图的边集或点集不同于原图时，即G'≠G时，称子图G'为G的真子图，记为G'⊂G．当子图的点集等于原图的点集时，那么称子图G'为原图G的生成子图或支撑子图．在图6-6中，〔a〕，〔b〕，〔c〕，〔d〕均是〔a〕的子图；〔a〕，〔b〕，〔c〕是〔a〕的真子图；〔a〕，〔b〕，〔c〕均是〔a〕的生成子图．由于〔d〕比〔a〕少一个点，所以〔d〕不是〔a〕的生成子图．2．树无圈且连通的无向图称为树．树普通记为T．作为树定义还可以有以下几种表述：(1)T连通且无圈或回路；(2)T无圈且有n－1条边〔假设有n个结点〕；(3)T连通有n－1条边；(4)T无回路，但不相邻的两个结点之间联以一边，恰得一个圈；(5)T连通，但去掉T的恣意一条边，T就不连通了；(6)T 的恣意两个结点之间恰有一条初等链．二、最小生成树及其算法1．最小生成树假设T 是无向图G 的生成子图，同时T 又是树，那么称T 是G 的生成树或支撑树．例如图6-7〔b 〕，〔c 〕是〔a 〕的生成树．一个网络图可以有多个生成树．记N 的一切生成树的集合为：T ＝{k T | k ＝1，2，…，L }设i T ＝〔V ，k E 〕是网络图N ＝〔G ，w 〕的一棵生成树，那么边集k E 中一切边的权数之和称为树k T 的权数，记为w 〔k T 〕＝∑∈Eke e w )(假定*T ∈T ，使w 〔*T 〕＝TT k ∈min {w 〔k T 〕} 那么称*T 为网络N 的一棵最小生成树，简称最小树．2．最小树的求法定理8-1 假设把网络N 的点集V 联系成两个不相交的非空集合S 和_S ，那么结合S 和_S 的最小边必包括于N 的最小树内．依据定理8-1，可以给出求最小树的两种方法，这就是避圈法与破圈法，分述如下：(1)避圈法其计算步骤如下：①从网络N 中任选一点i v ，令S ＝{i v }，_S ＝V \{i v }；②从结合S 与_S 的边中选取最小边，无妨设为(i v ，j v )，那么它必包括于最小树内；③令S ∪{j v }⇒S ，_S \{j v }⇒_S ；④假定_S ＝∅，那么中止，已选出的诸边即给出最小树；否那么返②． 例6-5 试求图6-8所示网络的最小树，各边旁边的数字为各边的权．解 由题意可知这是一个最小树效果．先按原图画出7个点，令S ＝{1}，_S ＝{2，3，4，5，6，7}．由于结合S 与_S 的边共有三条，其中最短边为(1，2)故用线把点1和2连结起来，令S ＝{1，2}，_S ＝{3，4，5，6，7}，如图6-8(a)所示，重复上述步骤，直到7个点全都连通为止．详细求解进程如图6-8〔a 〕到图6-8〔f 〕所示，其中图6-8〔f 〕)即给出本例的最小树*T ，w (*T )＝13．图6-8〔a 〕〔b 〕(2)破圈法用破圈法求最小树时，先从图中任取一圈，去掉该圈的一条最大边，然后重复这一步骤，直到无圈为止．例6-6 图6-9所示的一赋权连通图是某一具有9个居民点的交通网络图，其中边权表示该段路途的长，现欲沿小区路途架设一联络各个居民点的闭路电视系统，求可使闭路电视系统所架线路总长最短的方案．图6-9解 这是一个求网络最小树的效果．可应用破圈法求解．进程如图6-9〔a —i 〕所示．图6-9〔a ——i 〕图6-9〔i 〕所示的是网络最小树*T ．按图布置闭路电视系统可使所架线路总长最短，w (*T )＝19．第三节 最长途径效果在消费实际，运输管理和工程树立的很多活动中，诸如各种工艺路途的布置、厂区及货场的规划、管道线网的铺设及设备的更新等等效果，都与寻觅一个〝图的最长途径〞效果(shortest-path problem )亲密相关，它是网络规划中的一个最基本的效果．一、基本概念给定一个赋权有向图D ＝(V ，A )，对每一条弧ij a ＝(i v ，j v )，相应地有权w 〔ij a 〕＝ij w ，又有两点s v 、t v ∈V ，设p 是D 中从s v 到t v 的一条路，路p 的权是p 中一切弧的权之和，记为w (p )．最短路效果就是求从s v 到t v 的路中一条权最小的路*p ：w (*p )＝pmin w (p ) 二、最短路效果的算法1．Dijkstra 算法(Dijkstra algorithm )该算法是由Dijkstra 于1959年提出来，用于求解指定两点之间的最短路，或从指定点到其他各点的最短路，目前被以为是求解最短路效果的最好方法．算法的基本思绪基于以下原理.定理6-2 假定p 是从s v 到t v 的最短路，i v 是p 中的一个点，那么从s v 沿p 到i v 的路肯定是从s v 到i v 的最短路．引理 假定p 是从s v 到t v 的最短路，i v 是p 中的一个点，那么从s v 到i v 的最短路肯定包括于p 之内．依据定理6-2及引理，我们可以从v s 动身试探一切能够抵达v t 的下一个结点v i ，取距离最短的一个弧〔s v ，i v 〕，那么肯定包括于从s v 到t v 的最短路中；从i v 末尾对没有试探过的结点停止进一步的试探、推进，直至t v ，最终可以找出从s v 到t v 的最短路．Dijstra 算法采用〔双标号法〕T 标号与P 标号，来完成这一试探、推进进程．T 标号为试探性标号；P 为永世性标号．给i v 点一个P 标号时，表示从s v 到i v 点的最短路权，一旦i v 点失掉P 标号那么意味着从s v 到i v 点的最短距离曾经确定，标号不再改动．给i v 点一个T 标号时，表示从s v 到i v 点的估量最短路权的上界，这是一种暂时标号．凡没有失掉P 标号的点都有T 标号．算法每一步都把某一点的T 标号改为P 标号，当终点t v 失掉P 标号时，全部计算完毕．Dijstra 算法基本步骤：(1)给s v 以P 标号，P(s v )＝0，其他各点均给T 号，T(i v )＝＋∞． (2)假定i v 点为刚失掉P 标号的点，思索j v ，(i v ，j v )∈A 且j v 为T 标号．对j v 的T 标号停止如下的更改：T(j v )＝min[T(j v )，P(i v )＋ij w ] (6-1)(3)比拟一切具有T 标号的点，把最小者'i v 改为P 标号，即：P('i v )＝min[ T(i v ) ] (6-2)当存在两个以上最小者时，可同时改为P 标号．(4)假定全部点均为P 标号，那么中止计算．否那么用'i v 替代i v 并转至步骤〔2〕．例6-7 用Dijkstra 算法求图6-10中从1v 到7v 的最短距离，以及相应的路途．解 〔1〕首先给1v 以P 标号，P 〔1v 〕＝ 0，给其他一切点T 标号，T 〔v i 〕＝＋∞〔i = 2，3，… 7〕．〔2〕调查1v ，由于〔1v ，2v 〕，〔1v ，3v 〕，〔1v ，4v 〕∈A ，且2v 、3v 、4v 是T 标号，所以修正T 标号为：T 〔2v 〕＝min [ T 〔2v 〕，P 〔1v 〕＋12w ]＝min [∞，0＋2]＝233113T 〔4v 〕＝min [ T 〔4v 〕，P 〔1v 〕＋14w ]＝min [∞，0＋3]＝3在一切T 标号中，T(2v )＝2最小，于是令P(2v )＝2．将结果记在图6-10〔a 〕上：P 标号以〔〕方式标在结点旁边，T 标号以不带〔〕的数字标在结点旁边，图中没有标号的结点均代表T 〔i v 〕＝＋∞(3)调查2v ．由于〔2v ，3v 〕，〔2v ，6v 〕∈A ，且3v 、6v 是T 标号，故3v 、6v 新的T 标号为：T 〔3v 〕＝min [ T 〔3v 〕，P 〔2v 〕＋23w ]＝min [∞，2＋2]＝4 T 〔6v 〕＝min [ T 〔6v 〕，P 〔2v 〕＋26w ]＝min [∞，2＋7]＝9在一切T 标号中，T(4v )＝3最小，故令P(4v )＝3．图上标号如图6-10〔b 〕．(4)调查4v ，因〔4v ，5v 〕∈A ，T 〔5v 〕＝min [ T 〔5v 〕，P 〔4v 〕＋45w ]＝min [∞，3＋5]＝8在一切T 标号中，T(3v )＝4最小，令P(3v )＝4．图上标号如图6-10〔c 〕．(5)调查3v ，〔3v ，5v 〕，〔3v ，6v 〕∈A ，T 〔5v 〕＝min [ T 〔5v 〕，P 〔3v 〕＋35w ]＝min [∞，4＋3]＝7 T 〔6v 〕＝min [ T 〔6v 〕，P 〔3v 〕＋36w ]＝min [∞，4＋5]＝9在一切T 标号中，T(5v )＝7最小，令P(5v )＝7．图上标号如图6-10〔d 〕．(6)调查5v ，〔5v ，6v 〕，〔5v ，7v 〕∈A ，T 〔6v 〕＝min [ T 〔6v 〕，P 〔5v 〕＋56w ]＝min [∞，7＋1]＝8 T 〔7v 〕＝min [ T 〔7v 〕，P 〔6v 〕＋57w ]＝min [∞，7＋7]＝14 在一切T 标号中，T(6v )＝8最小，故令P(6v )＝8．图上标号如图6-10〔e 〕．(7)调查6v ，〔6v ，7v 〕∈A ，77667令P(7v )＝13，图上标号如图6-10〔f 〕．一切点都标上P 标号，计算完毕．从1v 到7v 的最长途径，可从7v 末尾依据永世性标号数值回溯失掉．最长途径是：1v →2v →3v →4v →5v →6v →7v ，路长13．同时失掉1v 到其他各点的最短路，即各点的永世性标号P 〔v i 〕．Dijkstra 算法只适用于一切ij w ≥0的情形，当赋权有向图中存在负权时，那么算法失效．图6-10〔a 〕〔b 〕〔c 〕〔d 〕〔e 〕〔f 〕2．逐次迫近算法为方便起见，无妨设从任一点i v 就任一点j v 都有一条弧，假设在D 中，不存在弧(i v ，j v )，那么添加虚设弧(i v ，j v )，令ij w ＝＋∞．从终点s v 到恣意点j v 的最短路可以视为一个两阶段进程，如图6-11所示：(1)从s v 动身，沿着一条路走k －1步到某点i v ，其最短距离表示为)1(-k d (s v ，i v )(2)再从i v 沿(i v ，j v )到j v ，其最短距离就是弧(i v ，j v )上的权ij w ． 所以，从s v 到j v 的最短距离必满足如下递推公式：）（1d (s v ，j v )＝sj w 〔j ＝1，2，…，n 〕 〔6-3〕)(k d (s v ，j v )＝imin {)1(-k d (s v ，i v )＋ij w } 〔6-4〕式〔6-3〕是恣意两点间的一步距离，由前面假定可知其存在，这可以作为初始条件．式〔6-4〕是恣意两点间的k 步距离，这是一个递推公式．应用初始条件和递推公式经过逐渐迭代就可以确定网络D 中恣意点之间经k 步抵达的最短距离并失掉与之相应的路途．下面以实例来说明迭代进程．例6-8 用逐次迫近算法求例6-6图6-10中从1v 到各点的最短距离． 解 依据初始条件可知）（1d (1v ，1v )＝0 ）（1d (1v ，2v )＝2 ）（1d (1v ，3v )＝5 ）（1d (1v ，4v )＝3 ）（1d (1v ，5v )＝＋∞ ）（1d (1v ，6v )＝＋∞）（1d (1v ，7v )＝＋∞；初始条件仅仅表达了1v 从动身到j v 的一步抵达的距离，在有向复杂网络中即为从1v 到各点的最短距离．1v 到各点的k 步距离由公式〔6-4〕递推得出．为方便、直观可列表计算如表6-3：表6-3 1v 到各点的k 步距离表的左半部是一个n ×n 的关于结点两两之间的一步距离矩阵，由式〔6-3〕可知，i v 到j v 的一步距离就是弧〔i v ，j v 〕上的权ij w ．一步距离矩阵中0元素表示原地踏一步，没有填写数字的空格是∞的省略．表右半部是公式〔6-4〕的计算结果．k =h 时，第h +n 列数据表示1v 到各点的h 步最短距离．譬如k =3为第 ⑽ 列，表示1v 经3步抵达各点的最短距离．计算进程如下：〔1〕当k =1时）（1d (1v ，j v )＝jw 1这是初始条件，表示从1v 动身到各点的一步距离，将其依次列于第 ⑻列．由此推算）（2d (1v ，j v )．〔2〕k =2时）（2d (1v ，j v )＝imin {）（1d (1v ，i v )＋ij w }即用表中第 ⑻ 列数字与表左边一步距离矩阵中第j 列相应数字相加取小，失掉从1v 动身到各点的二步距离：〔0 ＋ 0〕 〔∞ ＋ 2〕 〔∞ ＋ 5〕）（2d (1v ，1v )＝min 〔∞ ＋ 3〕 ＝0〔∞ ＋ ∞〕 〔∞ ＋ ∞〕 〔∞ ＋ ∞〕〔2 ＋ 0〕〔0 ＋ 2〕 〔∞ ＋ 5〕）（2d (1v ，2v )＝min 〔∞ ＋ 3〕 ＝2〔∞ ＋ ∞〕 〔∞ ＋ ∞〕 〔∞ ＋ ∞〕同理： ）（2d (1v ，3v )＝4 ）（2d (1v ，4v )＝3 ）（2d (1v ，5v )＝8）（2d (1v ，6v )＝∞ ）（2d (1v ，7v )＝∞得：2 4）（2d (1v ，j v )＝ 38 ∞ ∞将其填入表6-3第 ⑼ 列〔3〕重复上述步骤失掉）（3d (1v ，j v )、)4(d (1v ，j v )、)5(d (1v ，j v )、)6(d (1v ，j v )；区分填入表6-3第 ⑽、⑾、⑿、⒀ 列〔4〕当k=6时，发现)6(d (1v ，j v )＝)5(d (1v ，j v )，说明关于整个有向图D 而言，继续添加步数已不起作用，即已失掉从1v 到各点的最短距离，即表中 ⑿ 或 ⒀ 列数字：1v →1v ＝0；原地一步 1v →2v ＝2；一步抵达 1v →3v ＝4；二步抵达 1v →4v ＝3；一步抵达 1v →5v ＝7；三步抵达1v →6v ＝8；四步抵达 1v →7v ＝13；五步抵达从表6-3中还可以用回溯方法推知1v 到各点最短距离的相应最短路途，以1v 到7v 为例：由第⑿列7v 行可知，1v 到7v 经5步抵达，最短距离13．回溯13的来源：d 〔1v ，7v 〕=13因d 〔1v ，7v 〕＝[ ⑿ 列6v 行 ]＋[ ⑺ 列6v 行 ]＝d 〔1v ，6v 〕＋67w ＝8＋5＝13故记下〔6v ，7v 〕．因d 〔1v ，6v 〕＝ [ ⑽ 列5v 行 ]＋[ ⑹ 列5v 行 ]＝d 〔1v ，5v 〕＋56w ＝7＋1＝8故记下〔5v ，6v 〕.因d 〔1v ，5v 〕＝ [ ⑼ 列3v 行 ]＋[ ⑸ 列3v 行 ]＝d 〔1v ，3v 〕＋35w ＝4＋3＝7故记下〔3v ，5v 〕．因d 〔1v ，3v 〕＝ [ ⑻ 列2v 行 ]＋[ ⑶ 列2v 行 ]＝d 〔1v ，2v 〕＋23w ＝2＋2＝4故记下〔2v ，3v 〕．因d 〔1v ，2v 〕＝12w ＝0＋2＝2，记下〔1v ，2v 〕． 失掉最长途径：1v →2v →3v →5v →6v →7v ．当网络图存在负权时，Dijkstra 算法失效，必需采取逐次迫近算法来求解最短路．例6-9 试求网络图6-12中1v 到各点的距离．图6-12解 初始条件：）（1d (1v ，1v )＝0 ）（1d (1v ，2v )＝1）（1d (1v ，3v )＝＋∞ ）（1d (1v ，4v )＝2 ）（1d (1v ，5v )＝＋∞ ）（1d (1v ，6v )＝＋∞计算结果如表6-4所示：表6-4 1v 到各点的距离求失掉1v 各点的最短距离：）（1d (1v ，1v )＝0；原地一步)4(d (1v ，2v )＝-1；四步抵达1v →4v →5v →3v →2v ）（3d (1v ，3v )＝1；三步抵达1v →4v →5v →3v）（1d (1v ，4v )＝2；一步抵达）（2d (1v ，3v )＝-1；二步抵达1v →4v →5v）（k d (1v ，6v )＝∞；无法抵达逐次迫近算法，因其相似于矩阵乘法，在有些书籍表述为距离矩阵摹乘法，它们的实质分歧．这种算法在n 个结点的网络图中，至少经过n -1次迭代肯定收敛．但前提条件是图中不含有总权小于0的回路，否那么最短路权没有下界．第四节 最大流效果网络流(network flow )是一类普遍存在的现象．例如在交通运输网络中有人流、车流、货物流；供水网络中有水流；金融系统中有现金流；通讯系统中有信息流；等等．在20世纪50年代Ford 和Fulkerson 树立的〝网络流实际〞是网络运用的重要组成局部．网络最大流效果(max-flow problem )尤为重要．这是由于绝大局部网络流研讨，旨在寻求在一定条件下使网络流到达最大的方法．如图6-13是输油管道网，s v 为终点，t v 是终点，1v ，2v ，3v ，4v 为中转站，弧上的数表示该管道的最大输油才干，问应如何布置各管道输油量，才干使从s v 到t v 的总输油量最大?一、基本概念和基本定理1．网络流．所谓网络流，是指在一定的条件下流过一个网络的某种流在各边上的流量的集合．表达为F ＝{f (i v ，j v )| (i v ，j v )∈A }所谓一定条件，普通是指如下规则：(1)网络有一个始点s v 和一个终点t v ，始点是流的源，终点是流的汇； (2)流具有一定的方向，流经各弧的流，其方向就是相应弧的方向；(3)对每一弧(i v ，j v )∈A ，都赋予一个容量r (i v ，j v )≥0，简记为ij r ，表示允许经过该弧的最大流量．并称f (i v ，j v )为经过弧(i v ，j v )流，简记为ij f ．凡做出上述规则的网络都可称为容量网络，记为N ＝〔V ，A ，r 〕图6-13所示的就是一个容量网络．图中每条弧上的数对为(ij r ，ij f )，标明了弧的容量以及流经该弧的流量．2．可行流和最大流可行流是指满足容量限制条件战争衡条件的流．(1)容量限制条件：关于任一弧(i v ，j v )∈A ，都有0≤ij f ≤ij r ，即任何弧上的流量不能超越弧的容量．(2)平衡条件：关于任一中间点i v ，都有∑∈Avj vi ),(ij f ＝∑∈Avi vk ),(ki f即每个中间点的流出量必需等于流入量，其净流量为0．关于始点和终点，有∑∈Avi vs ),(si f ＝∑∈Avt vi ),(it f即始点流出量等于终点的流入量，这个流量即是可行流F 的流量，记为v 〔f 〕．所谓最大流效果，就是在可行流恒存在的前提下，满足max v (f )f i ＝ss .t .∑∈Avj vi ),(ij f －∑∈Avi vk ),(ki f ＝ 0 i ≠s 、t0≤ij f ≤ij r ； －f i ＝t这是一个特殊的线性规划效果，可用单纯形法求解．但用图形方法求解更为直观和复杂．3．增广链假设μ是网络中结合始点和终点的一条链，且链的方向从s v 到t v ，那么与链方向分歧的弧称为前向弧，用μ＋来表示前向弧集合；与链方向相反的弧称为后向弧，用μ－来表示后向弧集合．如图6-13中 μ＋＝{(s v ，2v )，(1v ，4v )，(3v ，t v )}μ－＝{(1v ，2v )，(3v ，4v )}设f 是一个可行流，μ是一条从s v 到t v 的链，假定μ满足以下条件，那么μ是可行流的一条增广链：〔1〕在弧(i v ，j v )∈μ＋上， 0≤ij f ＜ij r ；〔2〕在弧(i v ，j v )∈μ－上， 0＜ij f ≤ij r ．这就意味着在增广链上每一个前向弧的流量都没有到达最大容量〔即不饱和前向弧〕,而每一个后向弧的流量均不为0〔即非零后向弧〕．如图6-13中链μ＝s v 2v 1v 4v 3v t v 、'μ＝ s v 1v 4v 3v t v 、''μ＝ s v 1v 4v t v 都是增广链．可以指出，沿增广链调整各弧的流量可以使网络流量v 〔f 〕增大，而寻求网络最大流的方法正是以增广链为基础的．4．截集与截量在一个网络N ＝(V ，A )中，假定把点集V 剖分红不相交的两个非空集合S 和S ，使s v ∈S ，t v ∈S ，且S 中各点不须经由S 中的点而均连通，S 中各点也不须经由S 中的点而均连通，那么把始点在S 中而终点在S 中的一切弧所构成的集合，称为一个分别s v 和t v 的截集，记为(S ，S )．截集实质上是网络N 从s v 到t v 通路的横截面表达，它反映了网络从s v 到t v 的必经之路．一个网络可以有多个截集，表6-5反映了图6-13网络的截集集合．表6-5 图6-13网络的截集集合给定一截集(S，S)，其中一切弧的容量之和称为这个截集的截量，记为r(S，S)＝ [ij r|〔i v，j v〕∈(S，S)]一个网络可以有多个截集和截量，其中截量最小的截集称为最小截集，记为(*S，*S)，其截量称为最小截量(min-cut)，记为r(*S，*S)．图6-13的最小截量由表6-5看出为11，最小截集为(*S，*S)＝{(1,3), (4,t)}．二、基本原理为了引见一种寻求网络最大流的标号法，这里将论述其原理．定理6-3〔流量截量定理〕 在网络N =(V ，A ，r )中，设f 为一可行流，(S ，S )是任一截集，那么v 〔f 〕≤r (S ，S )定理6-3说明，网络的任一可行流的流量恒不超越任一截集的截量．因此，网络的最大流量也不会超越最小截量．定理6-4〔最大流量最小截量定理〕 网络中从v s 到v t 的最大流的流量等于分别v s 和v t 的最小截集的截量．即，v 〔*f 〕＝r (*S ，*S ) 定理6-4实践上是定理6-3的推论．定理6-5〔最大流的充要条件〕 设*f 是网络N ＝(V ，A ，r )的一个可行流，那么*f 为最大流的充要条件是：网络N 中不存在关于*f 的增广链μ(*f )．定理6-6〔增广链调整法〕 设f ＝{ij f }是N ＝(V ，A ，r )的一个可行流，μ是关于f 的一条增广链．令ij r －ij f 当μ＋≠∅ 1θ＝+μmin ∞ 当μ＋＝∅ij r －ij f 当θ＋≠∅ 〔6-5〕 2θ＝-μmin ∞ 当μ＋＝∅θ＝min 〔1θ，2θ〕结构一个新的可行流，令ij f ＋θ 当〔i v ，j v 〕∈μ＋'ij f ＝ ij f －θ 当〔i v ，j v 〕∈μ－ 〔6-6〕 ij f 当〔i v ，j v 〕∉μ那么'f ＝('ij f )也是N 的一个可行流，其流量为v 〔ij f 〕＝v 〔ij f 〕＋θ 〔6-7〕定理6-4说明：只需网络中还存在关于可行流f 的增广链μ，那么f 就非最大流，最少其流量还能增大θ．这样就给出了一种沿着增广链上的各弧去调整流量，从而失掉一个流量增大θ的新可行流f '的方法，故称之为增广链调整法．三、寻求网络最大流的标号法这种标号法由福特(Ford )和富尔克逊(Fulkerson )于1956年提出，故称为福特一富尔克逊标号法(Ford- Fulkerson algorithm )．1．基本算法思想：该法从某一可行流f 动身，按一定规那么找出一条增广链μ(f )，并按定理8-6的方法调整f ，失掉一个流量增大θ的新可行流'f ．对'f 重复上述做法直到找不出增广链为止，这时就失掉一个最大流，同时还失掉一个最小截集．2．算法步骤〔1〕给出一个初始可行流f ．初始可行流可以是零流或非零流；〔2〕标号、反省进程：给顶点标号，标号用[i v ，L (j v )]表示，其中第一个重量表示该标号是从。

网络计划项目培训内容一、培训介绍网络计划是指通过对一个工程项目中各项活动的工作内容、工期和资源进行逻辑分析和优化，确定各项活动的开始时间、完成时间和工作量，并反映在时间和资源轴上的一种计划表。

网络计划项目培训内容旨在培养学员对网络计划方法的理解与应用，使其掌握和应用网络计划技术，达到进度控制与管理的目的。

二、培训目标1. 了解网络计划的概念与原理2. 掌握网络计划的制作方法3. 掌握网络计划的应用与分析4. 能够独立制定和管理项目网络计划三、培训内容1. 网络计划的基本概念（1）网络计划的初步了解（2）网络计划的历史与发展（3）网络计划的概念与特点2. 网络计划的基本原理（1）网络计划的相关术语（2）网络计划的理论基础（3）网络计划的工作原理3. 网络计划的制作方法（1）确定工作内容与活动（2）确定活动的工期（3）绘制网络图（4）确定关键路径4. 网络计划的应用与分析（1）网络计划在项目管理中的应用（2）网络计划的分析方法（3）网络计划的应用案例分析5. 实际案例分析（1）实际项目中网络计划的应用（2）网络计划中的问题与解决方法（3）网络计划的优化与改进6. 网络计划软件的应用（1）常用的网络计划软件介绍（2）网络计划软件的操作方法（3）网络计划软件在实际项目中的应用7. 网络计划的制定与管理（1）网络计划的制定流程（2）网络计划的管理方法（3）网络计划的实施与控制四、培训方法1. 理论讲解：通过专家讲师的全面讲解，让学员深入理解网络计划的概念与原理。

2. 案例分析：通过实际案例的分析，让学员了解网络计划在实际项目中的应用与管理方法。

3. 软件操作：通过组织软件操作实践，让学员掌握网络计划软件的操作方法。

4. 互动讨论：通过学员的互动讨论，加深对网络计划的理解与应用。

五、培训时间安排本次网络计划项目培训内容共设置5天，每天培训时间为8小时。

具体安排如下：第一天：网络计划的基本概念与原理（理论讲解）第二天：网络计划的制作方法（理论讲解 + 案例分析）第三天：网络计划的应用与分析（理论讲解 + 案例分析）第四天：网络计划软件的应用（软件操作 + 案例分析）第五天：网络计划的制定与管理（理论讲解 + 互动讨论）六、培训考核与证书通过本次网络计划项目培训内容学员需参加“网络计划项目培训内容”考核，通过考核者可获得网络计划项目培训内容的结业证书。

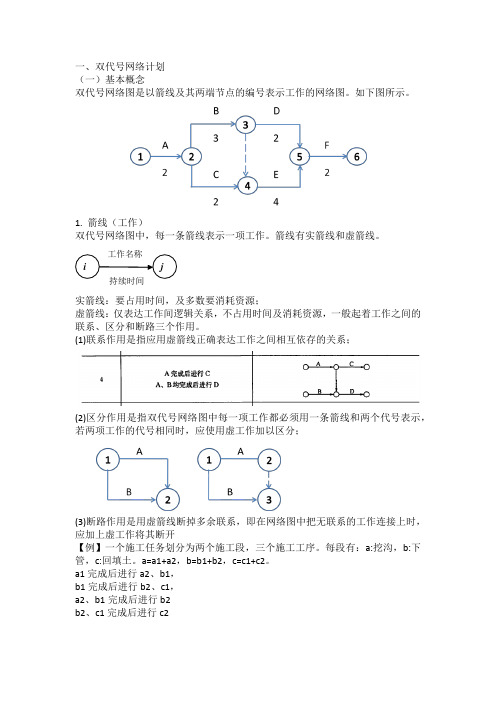
一、双代号网络计划（一）基本概念双代号网络图是以箭线及其两端节点的编号表示工作的网络图。

如下图所示。

1. 箭线（工作）双代号网络图中，每一条箭线表示一项工作。

箭线有实箭线和虚箭线。

实箭线：要占用时间，及多数要消耗资源；虚箭线：仅表达工作间逻辑关系，不占用时间及消耗资源，一般起着工作之间的联系、区分和断路三个作用。

(1)联系作用是指应用虚箭线正确表达工作之间相互依存的关系；(2)区分作用是指双代号网络图中每一项工作都必须用一条箭线和两个代号表示，若两项工作的代号相同时，应使用虚工作加以区分；(3)断路作用是用虚箭线断掉多余联系，即在网络图中把无联系的工作连接上时，应加上虚工作将其断开【例】一个施工任务划分为两个施工段，三个施工工序。

每段有：a:挖沟，b:下管，c:回填土。

a=a1+a2，b=b1+b2，c=c1+c2。

a1完成后进行a2、b1，b1完成后进行b2、c1，a2、b1完成后进行b2b2、c1完成后进行c2a2与c1本无联系，但上图把这两者也连接上了。

故需要加上虚工业使其断开，如下图所示。

或者：{上面两个图是一个意思。

}与教材内容对照学习，二者类同。

2. 节点（1）起始节点：即网络图的第一个节点，它只有外向箭线，一般表示一项任务或一个项目的开始。

（2）终点节点：即网络图的最后一个节点，它只有内向箭线，一般表示一项任务或一个项目的完成。

（3）中间节点：即网络图中既有内向箭线，又有外向箭线的节点。

节点编号原则：（1）一项工作应当只有唯一的一条箭线和相应的一对节点，且要求箭尾节点的编号小于其箭头节点的编号，即i<j。

（2）网络图节点的编号顺序应从小到大，可不连续，但不允许重复。

3. 线路：网络图中从起始节点开始，沿箭头方向顺序通过一系列箭线与节点，最后达到终点节点的通路称为线路。

关键线路：线路总时间最长，可能不止一条；非关键线路：线路持续时间小于关键线路的。

4. 逻辑关系：工艺关系（不可调整）、组织关系（可调整）（二）绘图规则1. 正确表达各项工作之间的逻辑关系。

《建筑施工组织》课程教学大纲一、课程代码：5081二、课程类型：必修课三、课程性质：专业课四、学分：3 课时：64五、考核方式：考试六、先修课程：《建筑施工技术》、《工程概预算》七、适用专业：施工技术八、课程教学目标：通过本课程的学习：培养学生的法律意识、合同管理意识、合同管理能力和参与工程招投标的竞争意识和能力，理论联系实际，独立完成项目招投标文件编写能力、合同执行与管理能力。

学完该课程后必须达到以下要求：1、通过本课程的学习,要求了解建筑施工组织的基本内容；了解与建筑施工组织有关的几个基本概念及基本建设程序。

2、掌握技术准备的主要内容，掌握施工现场准备的主要内容，掌握劳动力及物资准备的主要内容。

3、要求理解并掌握流水施工原理及实质，理解流水施工有关参数的概念及流水施工参数的确定方法，重点掌握流水施工的组织方式，通过实例的学习掌握流水施工原理及组织方式。

4、要求熟练掌握双代号网络计划的绘制方法，理解各种时间参数的概念及计算方法，了解单代号网络计划的绘制及时间参数的计算方法，掌握网络计划优化的基本原理及方法，能手工进行简单的网络计划的优化。

5、要求了解施工组织总设计的编制程序、依据；了解施工部署与施工方案的基本内容，了解施工总进度计划的编制方法及施工准备工作和各项资源需要量计划的编制方法，了解施工总平面图的基本内容及设计方法。

6、要求掌握施工方案与施工方法的编制方法，掌握施工进度计划和施工准备及各项资源需要量计划的编制方法，掌握施工平面图设计的基本方法。

九、说明本课程是高等院校施工技术专科专业的一门必修课。

使用教材及参考资料教材：毛小玲涂胜危道军主编，建筑施工组织，武汉理工大学出版社，2010，ISBN：978-7-5629-1197-5。

主要参考书：（1）蔡雪峰.建筑施工组织.武汉：武汉理工大学出版社，2002（2）建筑工程技术与计量.北京：中国计划出版社，2003（3）全国一级建造师执业资格考试用书编写委员会。