2023中考九年级数学分类讲解 - 第十二讲 圆(含答案)(全国通用版)

中考专题训练——圆的计算和证明1．如图，在ABC中，AB AC=，以AB为直径作O，交BC于点D，交AC于点E，过点B作O的切线交OD的延长线于点F．(1)求证：A BOF∠=∠；(2)若4AB=，1DF=，求AE的长．2．如图，AB是O的直径，点C在O上，ABC∠的平分线与AC相交于点D，与O过点A的切线相交于点E．(1)猜想EAD的形状，并证明你的猜想；(2)若8AB=，6AD=，求BD的长．3．如图所示，Rt△ABC中∠ACB＝90°，斜边AB与∠O相切于D，直线AC过点O并于∠O相交于E、F两点，BC与DF交于点G，DH∠AC于H．(1)求证：∠B＝2∠F；(2)若HE＝4，cos B＝35，求DF的长．4．如图，O 的直径AB =C 为O 上一点，CF 为O 的切线，OE AB ⊥于点O ，分别交AC ，CF 于D ，E 两点．(1)求证：ED EC =；(2)若30A ∠=︒，求图中两处（点C 左侧与点C 右侧）阴影部分的面积之和．5．已知PA ，PB 分别与O 相切于点A ，B ，C 为O 上一点，连接AC ，BC ．(1)如图∠，若70APB ∠=︒，求ACB ∠的大小；(2)如图∠，AE 为O 的直径交BC 于点D ，若四边形PACB 是平行四边形，求EAC ∠的大小． 6．如图，AB 是O 的直径，点C 在AB 的延长线上，BDC A ∠=∠，CE AD ⊥，交AD 的延长线于点E ．(1)求证：CD 与O 相切：(2)若4CE =，2DE =，求AD 的长，7．如图，四边形ABCD 为平行四边形，边AD 是O 的直径，O 交AB 于F 点，DE 为O 的切线交BC 于E ，且BE BF =，BD 和O 交于G 点．(1)求证：四边形ABCD 为菱形．(2)若O 半径52r =，BG =BF 长． 8．如图，O 为ABC 的外接圆，AB 为直径，ABC ∠的角平分线BD 交O 于点D ，过点D 作O 的切线DE ，交BC 的延长线于点E ．(1)求证：DE BC ⊥；(2)若1CE =，DE =O 的半径．9．如图，AB 是O 的直径，CA 与O 相切于点A ，且AB AC =．连接OC ，过点A 作AD OC ⊥于点E ，交O 于点D ，连接DB ．(1)求证：ACE BAD △△≌；(2)连接BC 交O 于点F ．若6AD =，求BF 的长．10．在Rt ABC 中，90C ∠=︒，以AC 为直径的O 与AB 相交点D 、E 是BC 的中点．(1)判断ED 与O 的位置关系，并说明理由；(2)若O 的半径为3，DEC A ∠=∠，求DC 的长．11．如图，在ABC 中，以ABC 的边AB 为直径作O ，交AC 于点D ，DE 是O 的切线，且DE BC ⊥，垂足为点E ．(1)求证AB BC =；(2)若3DE =，AC =O 的半径．12．如图，∠O 是∠ABC 的外接圆，O 在AC 上，过点C 作∠O 的切线，与AB 延长线交于点D ，过点O 作OE BC ，交∠O 于点E ，连接CE 交AB 于点F ．(1)求证：CE平分∠ACB；(2)连接OD，若CF=CD=6，求OD的长．13．如图，∠ABC中，AB=AC，以AB为直径∠O的交BC于点D，过点D作∠O的切线DE，交BA延长线于点E，延长CA交∠O于点F，交DE于点G，连接DF．(1)求证：点E为线段CF垂直平分线上一点；(2)若sin∠E=35，BE=8，求AF的长．14．如图，四边形ABCD内接于∠O，AB是∠O的直径，点D是AC的中点，连接OD，交AC于点E，作BF∥CD，交DO的延长线于点F．(1)求证：四边形BCDF是平行四边形．(2)若AC=8，连接BD，tan∠DBF=34，求直径AB的长及四边形ABCD的周长．15．如图，在∠ABC中，AB＝AC，以AB为直径作∠O，交AC于点F，交BC于点D，过点D作∠O的切线DE，交AC于点E．(1)求证：DE∠AC；(2)若∠O的直径为5，sin B EF的长．16．如图，AB是∠O的直径，点E为线段OB上一点（不与O，B重合），作CE∠OB，交∠O于点C，垂足为点E ，作直径CD ，过点C 的切线交DB 的延长线于点P ，作AF ∠PC 于点F ，连接CB ．(1)求证：∠CBE ∠∠CPB ；(2)当AB =34CF CP =时，求扇形COB 的面积． 17．如图，AB 为O 的直径，ACB ∠的角平分线交O 于点D ，交AB 于点E ，CAB ∠的角平分线交CD 于点F ．(1)求证：ADB 为等腰直角三角形；(2)求证：2DF DE DC =⋅．18．如图，AB 是圆O 的直径，C ，D 是圆上的点（在AB 同侧），过点D 的圆的切线交直线AB 于点E ．(1)若2AB =，1BC =，求AC 的长；(2)若四边形ACDE 是平行四边形，证明：BD 平分ABC ∠．19．如图，AB 与O 相切于点B ，BC 为O 的弦，OC OA ⊥，OA 与BC 相交于点P ．(1)求证：AP AB =；(2)若4OB =，3AB =，求线段BP 的长．20．如图，ABC ∆为O 的内接三角形，AD BC ⊥，垂足为D ，直径AE 平分BAD ∠，交BC 于点F ，连接BE ．(1)求证：AEB AFD ∠=∠；(2)若10AB =，5BF =，求DF 的长；(3)若点G 为AB 的中点，连接DG ，若点O 在DG 上，求:BF FC 的值．参考答案1．(1)见解析 (2)83AE =【分析】(1)首先根据等边对等角可证得C ODB ∠=∠，再根据平行线的判定与性质，即可证得结论；(2)首先根据圆周角定理及切线的性质，可证得AEB OBF ∠=∠，即可证得ABE OFB △∽△，再根据相似三角形的性质即可求得．（1）证明：AB AC =C ABC ∴∠=∠ OB OD =ODB OBD ∴∠=∠C ODB ∴∠=∠AC OD ∴∥A BOF ∴∠=∠（2）解：如图：连接BEAB 是O 的直径，AB =490AEB ∴∠=︒，122OB OD AB === BF 是O 的切线90OBF ∴∠=︒AEB OBF ∴∠=∠又A BOF ∠=∠ABE OFB ∴△∽△AE AB OB OF∴= 又213OF OD DF =+=+=423AE ∴=，解得83AE = 【点评】本题考查了等腰三角形的性质，平行线的判定与性质，圆周角定理，切线的性质，相似三角形的判定与性质，作出辅助线，证得ABE OFB △∽△是解决本题的关键．2．(1)等腰三角形，证明见解析； (2)145.【分析】（1）利用角平分线和∠C =∠BAE =90°，得出∠E =∠4，从而得到AD =AE 可得三角形的形状；（2）先证明△BCD ∠∠BAE ，利用相似比得到得出即34AE DC AB BC ==，若设CD =3x ，则BC =4x ，BD =5x ，再利用勾股定理得到（4x ）2+（6+3x ）2=82，然后解方程求出x 后计算5x 即可．(1)猜想：△EAD 是等腰三角形,证明：∠BE平分∠ABC，∠∠1=∠2，∠AB为直径，∠∠C=90°，∠∠2+∠3=90°，∠AE为切线,∠AE∠AB，∠∠E+∠1=90°，∠∠E=∠3，而∠4=∠3，∠∠E=∠4，∠AE=AD，∠∠EAD是等腰三角形；(2)∠∠2=∠1，∠Rt△BCD∠Rt△BAE，∠CD：AE=BC：AB，即34 AE DCAB BC==，设CD=3x，BC=4x，则BD=5x，在Rt△ABC中，AC=AD+CD=3x+6，∠（4x）2+（6+3x）2=82，解得x1=1425，x2=-1（舍去），∠BD=5x=145．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径；也考查了利用勾股定理和相似比进行几何计算．3．(1)见解析；(2)【分析】（1）连接OD ，由题意可得：90ODA =∠°，再根据∠ACB ＝90°，可得B AOD ∠=∠，由圆周角定理可得2AOD F ∠=∠，即可求解；（2）由（1）可得B AOD ∠=∠，则3cos 5OH AOD OD ∠==，设OD OE r ==，求得半径r ，由勾股定理求得DH ，再由勾股定理即可求得DF ．（1）解：连接OD ，如下图：∠AB 与∠O 相切于D ，∠OD AB ⊥，即90ODA =∠°，∠90A AOD ∠+∠=︒，又∠∠ACB ＝90°，∠A B ∠∠=︒+90，∠B AOD ∠=∠，由圆周角定理可得：2AOD F ∠=∠，∠2B F ∠=∠；（2）解：∠DH ∠AC∠90DHO ∠=︒，由（1）得B AOD ∠=∠， ∠3cos cos 5OH B AOD OD =∠==， 设OD OE OF r ===，则4OH r =-， 则435r r -=，解得10r =， 则6OH =，16HF OH OF =+=由勾股定理可得：8DH =，由勾股定理可得：DF =【点评】此题考查了圆的综合应用，涉及了切线的性质定理，圆周角定理，三角形内角和的性质，解直角三角形，勾股定理，解题的关键是灵活运用相关性质进行求解．4．(1)见解析【分析】（1）连接OC ，则OC CF ⊥，故90ACE ACO ∠+∠=︒，又90ADO A ∠+∠=︒，且A ACO ∠=∠，可得ACE ADO EDC ∠=∠=∠，故ED EC =；（2）过点C 作CG AB ⊥于G ，结合三角函数的知识求得CG 与CE 的长，从而利用COE BOC COB COH S S S S S =+--△△阴影扇形扇形求得阴影部分的面积之和． （1）证明：连接OC ，CF 是O 的切线，∴OC CF ⊥，∴90ACO ACE ∠+∠=︒，OE AB ⊥，∴90ADO A ∠+∠=︒，OA OC =，∴A ACO ∠=∠，∴ACE ADO ∠=∠， 又ADO CDE ∠=∠，∴ACE CDE ∠=∠，∴ED EC =．（2）解：过点C 作CG AB ⊥于G ，30A ACO ∠=∠=︒，∴260BOC A ∠=∠=︒，∴3sin 602CG OC =︒==， 9030COE BOC ∠=︒-∠=︒，90OCE ∠=︒，∴tan 301CE OC =︒==．11122COE S OC CE =⨯⨯==△，2603602COB S ππ=⨯⨯=扇形，2303604COH S ππ=⨯⨯=扇形，113222BOC S OB CG =⨯⨯==△∴24COE BOC COB COH S S S S S ππ=+--=-=△△阴影扇形扇形 【点评】本题属于圆的综合题，涉及到了圆的切线的性质，扇形面积的计算方法，以及三角函数相关知识，解题的关键是学会常用辅助线的作法．5．(1)55°(2)30°【分析】（1）连接OA 、OB ，根据切线的性质可得∠OAP =∠OBP =90°，再根据四边形内角和等于360度求出AOB ∠，再由圆周角定理即可求出结果；（2）连接AB ，EC ，由切线长定理以及平行四边形的性质可证明四边形PACB 是菱形，进而证明∠ABC 是等边三角形，进一步可得结论．（1）如图∠，连接OA 、OB ，∠P A ，PB 是∠O 的切线，∠∠OAP =∠OBP =90°，∠∠APB =70°，∠∠AOB =360°-90°-90°-70°=110°∠∠ACB =12∠AOB =11102⨯︒=55°； （2）如图∠，连接AB ，EC ，∠,BAE BCE ∠=∠∠PA ，PB 分别与O 相切于点A ，B ，∠,PA PB =∠四边形PACB 是平行四边形，∠四边形PACB 是菱形，∠,AC BC =∠PA 是O 的切线，且AE 是O 的直径，∠,AE PA ⊥∠四边形APBC 是平行四边形，∠PA //BC∠,AE BC ⊥即∠90,ADB ︒=∠∠90,BAD ABD ︒+∠=∠AE 是O 的直径，∠∠90,ACE ︒=即∠90,ACD BCE ︒+∠=∠∠,BAD BCE =∠∠∠,ABD ACB =∠∠,AB AC =∠,AB AC BC ==即∠ABC 是等边三角形，∠∠60,ABC BAC ACB ︒=∠=∠=∠,AE BC ⊥ ∠116030.22EAC BAC ︒︒∠=∠=⨯= 【点评】本题考查的是切线的性质、圆周角定理、等腰三角形的判定与性质，平行四边形的性质，菱形的判定与性质等知识，掌握圆的切线垂直于经过切点的半径是解题的关键．6．(1)见解析(2)6【分析】(1) 连接OD ，然后根据圆的性质和已知可以得到90ODC ∠=︒，即可证得CD 与O 相切； （2）由已知可以得到AEC CED ∽，再根据三角形相似的性质和已知条件即可求出AD 的值．（1）证明：连接OD ，∠AB 为O 的直径，∠90ADB ∠=︒，即90ODB ADO ∠+∠=︒，∠OA OD =，∠ADO A ∠=∠，又∠BDC A ∠=∠；∠90ODB BDC ∠+∠=︒，即90ODC ∠=︒∠CD 是O 切线.（2）∠CE AE ⊥，∠90∠=∠=︒E ADB ，∠DB //EC ，∠DCE BDC ∠=∠，∠BDC A ∠=∠，∠A DCE ∠=∠，∠E E ∠=∠，∠AEC CED ∽， ∠CE AE DE CE=， ∠2CE DE AE =⋅，∠162(2)AD =+，∠6AD =．【点评】本题考查圆的综合应用，熟练掌握圆切线的判定方法、三角形相似的判定和性质是解题关键．7．(1)证明过程见解析(2)2【分析】（1）连接DF ，通过证明Rt ∠DFB ∠Rt ∠DEB （HL ）得到DF =DE ，证明∠ADF ∠∠CDE （ASA ）得到AF =CE ，即可证明四边形ABCD 是菱形；（2）连接AG ，根据等腰三角形三线合一的性质得到DG =GB ，设BF =x ，则AF =5-x ，利用勾股定理可得2222AD AF DB BF -=-，列出方程求解即可得到BF 的长．（1）证明：连接DF ，如图所示∠DE 是切线，AD 是直径∠∠ADE =90°，∠DF A =90°∠四边形ABCD 是平行四边形∠∠DEB =90°，∠CDF =90°∠∠DFB =∠DEB =90°又∠BF =BE ，DB =DB∠Rt ∠DFB ∠Rt ∠DEB （HL ）∠DF =DE∠四边形ABCD 是平行四边形∠∠A =∠C又∠∠AFD=∠DEC∠∠ADF ∠∠CDE （AAS ）∠AF =CE∠AB =CB∠四边形ABCD 是菱形（2）解：连接AG ，如图所示∠AD 是直径∠∠AGD =90°，即AG ∠BD∠四边形ABCD 是菱形∠AB =AD∠DG =GB∠DB 设BF =x ，则AF=5-x∠2222AD AF DB BF -=-∠()(222255x x --=-，解得x =2∠BF 的长为2【点评】本题考查了菱形的判定、平行四边形的性质、直径所对圆周角是直角、全等三角形的判定与性质、勾股定理等知识，正确作出辅助线，掌握这些知识点是解答本题的关键．8．(1)见解析(2)2【分析】（1）根据切线性质得90ODE ∠=︒，再根据圆及角平分线的性质，证得//OD BC ，最后根据平行线的性质，证得结论．（2）连接OD 交AC 于点F ，证明四边形CEDF 是矩形，再设O 的半径r ，在Rt AOF 中运用勾股定理，建立关于r 的方程，求解即可．(1)证明：如图，连接OD ，DE与O相切于点D，∴⊥，DE OD∴∠=︒，ODE90=，OD OB∴∠=∠，ODB OBD∠，BD平分ABCOBD DBC，ODB DBC，OD BC∴，//∴∠=︒-∠=︒，E ODE18090∴⊥．DE BC(2)解：如图，连接OD交AC于点F，AB是O的直径，∴∠=︒，ACB90∴∠=︒-∠=︒，ECF ACB18090ECF E EDF∴∠=∠=∠=︒，90∴四边形CEDF是矩形．∴∠=∠=︒，1==，DF CE90AFO CFD∴⊥，FO AC∴===AF CF DE设O 的半径为r ，则OA OD r ==，222OA OF AF =+，1OF r =-，()2221r r ∴=-+， 解得2r =，O ∴的半径为2．【点评】本题考查了与圆有关的综合问题，灵活运用切线性质，勾股定理进行推理求值是解题的关键．9．(1)证明见解析【分析】（1）根据切线的性质可得90BAD CAE ∠+∠=︒，根据圆周角定理的推论可得90BAD ABD ∠+∠=︒，即得出CAE ABD ∠=∠．结合题意即可利用“AAS ”证明ACE BAD △△≌； （2）连接AF ．由垂径定理可得132AE ED AD ===．再根据全等三角形的性质可得6CE AD ==，3AE ED BD ===，利用勾股定理可求出AC AB ==．再根据圆周角定理的推论结合等腰三角形“三线合一”的性质即可求出12BF BC == (1) 证明：∠CA 与O 相切于点A ，∠90BAC ∠=︒，∠90BAD CAE ∠+∠=︒．∠AB 为直径，∠90BDA ∠=︒，∠90BAD ABD ∠+∠=︒，∠CAE ABD ∠=∠．∠AD OC ⊥，∠90AEC ADB ∠=∠=︒．又∠AB AC =，∠()ACE BAD AAS ≌△△；(2)如图，连接AF ．∠AD OC ⊥， ∠132AE ED AD ===． ∠ACE BAD △△≌，∠6CE AD ==，3AE ED BD ===∠在Rt AEC 中，AC AB ===，∠BC ==∠AB 为直径，∠90AFB ∠=︒．∠AB =AC ，∠12BF BC ==． 【点评】本题为圆的综合题．考查切线的性质，圆周角定理，三角形全等的判定和性质，等腰直角三角形的性质以及勾股定理．掌握与圆相关的知识点是解题关键．10．(1)相切；理由见解析(2)2π【分析】（1）连接OD ，CD ，再根据直径所对的圆周角是直角及直角三角形斜边上的中线性质证明OD ∠DE 即可；（2）根据DEC A ∠=∠证明三角形DEC 是等边三角形，即可得到DC 的圆心角是120°，再根据弧长公式计算即可．(1)ED 与∠O 相切．理由：连接OD ，CD ．∠AC 是直径，∠ ∠ADC =90°，在Rt △BDC 中，E 为BC 的中点，∠DE=EC ，∠∠3=∠2，又∠OD =OC ，∠∠1=∠4，∠∠1+∠2=90°，∠∠ODE=∠3+∠4=90°，∠ED 与∠O 相切；(2)∠∠A +∠1=90°，∠1+∠2=90°，∠∠A =∠2，∠∠DEC =∠A ，∠∠2=∠3=∠DEC =60°，∠∠A =60°，∠∠DOC =2∠A =120° ，∠弧DC 的长=12032180ππ⨯=． 【点评】本题考查圆的性质及弧长公式，熟记直径所对的圆周角是直角、切线的证明、弧长公式是解题的关键．11．(1)见解析；(2)5【分析】（1）连接OD 、BD ，根据切线的性质得到OD ∠DE ，推出OD ∥BC ，证得∠ODB =∠CBD ，由此推出∠OBD =∠CBD ，根据AB 为O 的直径，得到∠ADB =∠CDB =90°，证得∠ABD ∠∠CBD （ASA ），即可得到AB =BC ；（2）根据AB =BC ，BD ∠AC ，求出AD =CD =12AC =CE =9，证得∠CDE ∠∠CBD ，求出CB ，即可得到O 的半径．(1)证明：连接OD 、BD ，∠DE 是O 的切线，∠OD ∠DE ，∠DE BC ⊥，∠OD ∥BC ，∠∠ODB =∠CBD ，∠OD =OB ，∠∠ODB =∠OBD ，∠∠OBD =∠CBD ，∠AB 为O 的直径，∠∠ADB =∠CDB =90°，∠BD =BD ，∠∠ABD ∠∠CBD （ASA ）， ∠AB =BC ；(2)∠AB =BC ，BD ∠AC ，∠AD =CD =12AC = ∠DE =3，∠9CE ==， ∠∠C =∠C ，∠CED =∠CDB =90°， ∠∠CDE ∠∠CBD ，∠2CD CE CB =⋅，∠(22109CD CB CE ===， ∠AB =CB =10，∠O的半径为5．【点评】此题考查了切线的性质定理，圆周角定理，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，熟记各知识点并综合应用是解题的关键．12．(1)见解析(2)【分析】（1）根据OC=OE，可得∠OCE=∠E，再由OE BC，可得∠E=∠BCE，从而得到∠OCE=∠BCE，即可求证；（2）根据CD=CF，可得∠BCD=∠BCE=∠OCE，再由CD是∠O的切线，可得∠BCD=30°，再证得∠A=∠BCD=30°，根据直角三角形的性质，即可求解．【解析】（1）证明：∠OC=OE，∠∠OCE=∠E，∠OE BC，∠∠E=∠BCE，∠∠OCE=∠BCE，∠CE平分∠ACB；（2）解：如图，∠CD=CF，∠∠BCD=∠BCE，∠CE平分∠ACB，∠∠BCD=∠BCE=∠OCE，∠CD是∠O的切线，∠∠ACD=90°，即∠BCD+∠ACB=90°，∠∠BCD=30°，∠AC是∠O的直径，∠∠ABC=90°，∠∠A+∠ACB=90°，∠∠A=∠BCD=30°，∠CD=6，∠AD=2CD=12，∠AC∠OC=∠OD=【点评】本题主要考查了切线的性质，圆周角定理，直角三角形的性质，勾股定理，熟练掌握切线的性质，圆周角定理，直角三角形的性质，勾股定理是解题的关键．13．(1)见解析(2)AF=185．【分析】（1）根据圆周角定理可得AD∠BC，再由等腰三角形的性质可得BD=CD，进而得出OD是三角形的中位线，由切线的性质可得OD∠FC，证出三角形DFC是等腰三角形即可；（2）在Rt∠ODE中，根据锐角三角函数可求出半径OD，进而得出直径AB，在Rt∠ABF中，由锐角三角函数可求出AF．(1)证明：如图，连接OC，AD，∠AB=AC，∠∠ABC=∠ACB，又∠∠ABC=∠F，∠∠F=∠ACB，∠DF=DC，∠AB是∠O的直径，∠∠ADB=90°，即AD∠BC，∠AB=AC，∠BD=CD，又∠OA=OB，∠OD是∠ABC的中位线，∠OD∠AC，∠DE是∠O的切线，∠OD∠DE，∠FC∠DE，∠DF=DC，∠DE是FC的垂直平分线，即点E为线段CF垂直平分线上一点；(2)解：连接BF，在Rt△ODE中，设OD=x，则OE=BE-OB=8-x，∠sin∠E=35=ODOE，∠8xx=35，解得x=3，经检验x=3是原方程的根，∠AB=2OD=6，∠AB是∠O的直径，∠∠AFB=90°，∠DG∠BF，∠∠E=∠ABF，在Rt△ABF中，AB=6，sin∠ABF=sin∠E=35，∠AF=AB•sin∠ABF=6×35=185．【点评】本题考查切线的性质，圆周角定理，等腰三角形的判断和性质，直角三角形的边角关系，掌握切线的性质，圆周角定理，等腰三角形的判断和性质，直角三角形的边角关系是正确解答的前提．14．(1)见解析(2)AB=10，周长16+【分析】（1）根据AB是∠O的直径，得∠C=90°，根据点D是AC的中点，得CA∠DF，即有∠AEO=90°，则有BC DF∥，即可得证；（2）先利用平行及圆周角定理证得∠DBF=∠BAC，则根据正切值和勾股定理即可求出CB、AB，在Rt∠AEO中，利用勾股定理得OE=3，在Rt∠AED中，利用勾股定理，得AD（1）证明：∠AB是∠O的直径，∠∠C=90°，∠点D是AC的中点，∠DO垂直平分AC，且AD=DC，∠CA∠DF，AE=EC，∠∠AEO=90°，∠BC DF∥，∠BF CD∥，∠四边形BCDE是平行四边形；（2）∠BC DF∥，∠∠DBF=∠CDB，又∠根据圆周角定理有∠CDB=∠BAC，∠∠DBF=∠BAC，即tan∠BAC=34，∠AC=8，∠CB=6，则在Rt∠ACB中，利用勾股定理可得AB=10，即AO=5=OD，∠AE=EC=12AC，∠AE=EC=4，在Rt∠AEO中，利用勾股定理得OE=3，∠DE=OD-OE=5-3=2，在Rt∠AED中，利用勾股定理，得AD CD∠四边形ABCD的周长=AB+BC+CD+AD【点评】本题考查了平行四边的判定与性质、同弧所对的圆周角相等、同弧所对的弦相等、勾股定理以及解直角三角形的知识，利用正切值以及同弧所对的圆周角相等是解答本题的关键．15．(1)见解析(2)1【分析】（1）连接OD，由AB=AC，OB=OD，则∠B=∠ODB=∠C，则OD∠AC，由DE为切线，即可得到结论成立；（2）如图所示，连接BF，AD，先解直角三角形ACD求出AD的长，从而求出CD的长，然后分别解直角三角形BCF，直角三角形DCE，求出BF，DE，进而求出CF，CE，即可得到EF．（1）解：连接OD，如图：∠AB=AC，∠∠B=∠C，∠OB=OD，∠∠B=∠ODB，∠∠B=∠ODB=∠C，∠OD∠AC，∠DE是切线，∠OD∠DE，∠AC∠DE；（2）解：如图所示，连接BF，AD，∠AB是圆O的直径，∠∠AFB=∠ADB=90°，∠∠BFC=90°，∠DE∠AC，∠∠DEC=90°∠AB=AC，∠BC=2CD，∠ABD=∠C，∠sin sin ADABD C∠===AC∠AD AC==∠CD=∠BC=∠sin2BF BC C=⋅，DE CD C=⋅=，sin=4∠1CF=，CE=，2∠EF=CF-CE=1．【点评】本题主要考查的是切线的性质、等腰三角形的性质、平行线的性质与判定，解直角三角形、勾股定理，解题的关键是熟练掌握所学的性质定理，正确的求出边的长度．．16．(1)见解析(2)2π【分析】（1）先证明∠CEB=∠CBP＝90°，再由∠D+∠P=90°，∠CAB＋∠CBE＝90°，∠CAB=∠D，推出∠CBE=∠P，即可证明结论；（2）设CF=3k，CP=4k，先证明∠F AC=∠CAB，得到CE=CF=3k，再由相似三角形的性质得到BC2＝CE•CP；∠CBE=60°，即可证明∠OBC是等边三角形，得到∠COB=60°，据此求从而求出sin∠CBE解即可．（1）解：∠CE∠OB，CD为圆O的直径，∠∠CEB=∠DBC＝90°，∠∠CEB=∠CBP＝90°，∠PF是切线，∠∠DCP=90°，∠∠D+∠P=90°，∠AB是直径，∠∠ACB=90°∠∠CAB＋∠CBE＝90°，∠∠CAB=∠D，∠∠CBE=∠P，∠∠CBE∠∠CPB；（2）解：∠34CF CP =， ∠设CF =3k ，CP =4k ，∠PF 是切线，∠OC ∠PF ，∠AF ∠PF ，∠AF ∠OC ．∠∠F AC =∠ACO ，∠OA =OC ，∠∠OAC =∠ACO ，∠∠F AC =∠CAB ，∠CE =CF =3k ，∠∠CBE ∠∠CPB ， ∠CB CE CP CB=， ∠BC 2＝CE •CP ；∠BC =∠sin∠CBE= ∠∠CBE =60°，∠OB =OC ，∠∠OBC 是等边三角形，∠∠COB =60°，∠AB =∠扇形COB 的面积2602360ππ⨯=（ 【点评】本题主要考查了圆切线的性质，相似三角形的性质与判定，圆周角定理，角平分线的性质，解直角三角形，扇形面积，等边三角形的性质与判定等等，熟练掌握圆的相关知识是解题的关键．17．(1)证明见解析(2)证明见解析【分析】（1）根据AB 为O 的直径，可得90ADB ACB ∠=∠=︒，由ACB ∠的角平分线交O 于点D ，可得45ACD BCD ∠=∠=︒，AD BD =，AD BD =，进而结论得证；（2）由CAB ∠的角平分线交CD 于点F ，得到CAF BAF ∠=∠，结合（1）可得ACD BAD ∠=∠，再由∠=∠+∠DFA CAF ACD ，∠=∠+∠DAF BAF BAD ，得到DFA DAF ∠=∠，从而说明DA DF =，最后再证明ADE CDA △∽△，利用相似三角形的性质即可得证．(1)证明：∠AB 为O 的直径，∠90ADB ACB ∠=∠=︒，∠ACB ∠的角平分线交O 于点D ，∠45ACD BCD ∠=∠=︒，∠AD BD =，∠AD BD =，∠ADB 为等腰直角三角形；(2)证明：∠CAB ∠的角平分线交CD 于点F ，∠CAF BAF ∠=∠，由（1）可知：45ACD ∠=︒，AD BD =，90ADB ∠=︒∠45BAD ABD ∠=∠=︒，∠ACD BAD ∠=∠，∠∠=∠+∠DFA CAF ACD ，∠=∠+∠DAF BAF BAD ，∠DFA DAF ∠=∠，∠DA DF =，在ADE 和CDA 中DAE DCA ADE CDA ∠=∠⎧⎨∠=∠⎩， ∠ADE CDA △∽△， ∠AD DE CD AD=， ∠2AD DE DC =⋅，∠2DF DE DC =⋅．【点评】本题考查的是圆和三角形的综合题，考查了直径所对的圆周角为90°，角平分线，圆周角，等腰三角形的判定，相似三角形的判定与性质等知识．对知识的熟练掌握与灵活运用是解题的关键．18．(1)AC =(2)见解析【分析】（1）根据直径所对的圆周角是直角可得90ACB ∠=︒，再根据勾股定理进行计算即可； （2）连结BD ，连结OD 与AC 交于F 点．根据切线的性质及平行四边形的性质可证明四边形OBCD 是菱形，即可得到结论．(1)∠AB 是圆O 的直径，∠90ACB ∠=︒∠2223AC AB BC =-=，∠AC =．(2)连结BD ，连结OD 与AC 交于F 点．∠ED 与圆O 相切于D 点，∠OD ED ⊥，∠四边形ACDE 是平行四边形，∠ED AC ∥， CD EA ∥，∠OD AC ⊥，90OFA ACB ∠=︒=∠，∠OD BC ∥，∠CD EB ∥，OD OB =，∠四边形OBCD 是菱形，∠BD 平分ABC ∠．【点评】本题考查了圆周角定理、切线的性质、勾股定理、平行四边形的性质及菱形的判定和性质，熟练掌握知识点是解题的根据．19．(1)见解析【分析】（1）根据等角的余角相等，ABP CPO ∠=∠，进而证得APB ABP ∠=∠，最后结论得证； （2）作OH BC ⊥于H ，在Rt POC △中，求出OP ，PC ，OH ，CH 即可解决问题．（1）证明：∠OC OB =， ∠OCB OBC ∠=∠， ∠AB 是O 的切线， ∠OB AB ⊥， ∠90OBA ∠=︒， ∠90ABP OBC ∠+∠=︒， ∠OC AO ⊥， ∠=90AOC ∠︒， ∠90OCB CPO ∠+∠=︒， ∠ABP CPO ∠=∠， ∠APB CPO ∠=∠， ∠APB ABP ∠=∠， ∠AP AB =．（2）解：作OH BC ⊥于H ,在Rt OAB 中， ∠4OB =，3AB =，∠5OA =， ∠3AP AB ==， ∠2PO =．在Rt POC △中， ∠4OC OB ==∠PC = 1122POC S PC OH OC OP ==△， ∠455OC OP OH PC ==∠CH ==∠OH BC⊥，∠CH BH=，∠2BC CH==，∠PB BC PC=-=【点评】本题考查切线的性质、解直角三角形、勾股定理、等腰三角形的判定和性质、垂径定理等知识，学会添加适当的辅助线，构造直角三角形解决问题是解本题的关键．20．(1)见解析(2)3DF=2【分析】（1）由题意得BAE DAE∠=∠，且90ABE︒∠=，即90BAE AEB︒∠+∠=，根据AD BC⊥得90DAE AFD︒∠+∠=，即可得；（2）根据AEB AFD∠=∠，AFD BFE∠=∠得BEF BFE∠=∠，即BE BF=，根据BAE DAF∠=∠，90ABE ADF︒∠=∠=得ΔΔABE ADF∽，根据10AB=，5BF=得12BEAB=，设DF x=，则2AD x=，在Rt ABD∆中，根据勾股定理，即()()2221052x x=++，即可得；（3）根据点G为AB中点，点O在DG上得OG是ABE∆的中位线，即OG BE∥，12OG BE=，根据90ABE︒∠=得OD DF=，AEB∠和ACB∠是AB所对的圆周角得AEB ACB∠=∠，即ACB AFC∠=∠，即有AC AF=，设BF a=，DF b=，有1122BE OD a bDGBD BF DF a b++==++，即可得．(1)解：∠直径AE平分BAD∠，∠BAE DAE∠=∠，且90ABE︒∠=，∠90BAE AEB︒∠+∠=，∠AD BC⊥，∠90DAE AFD︒∠+∠=，∠AEB AFD∠=∠．(2)解：∠AEB AFD∠=∠，AFD BFE∠=∠，∠BEF BFE∠=∠，∠BE BF=，∠BAE DAF ∠=∠，90ABE ADF ︒∠=∠=，∠ΔΔABE ADF ∽，∠10AB =，5BF =， ∠51102BE BF DF AB AB AD ====， 设DF x =，则2AD x =，在Rt ABD ∆中，根据勾股定理，222AB BD AD =+，即()()2221052x x =++，解得：13x =，25x =-，舍去负值，得到3DF =．(3)解：如图所示，∠点G 为AB 中点，点O 在DG 上，∠OG 是ABE ∆的中位线，∠OG BE ∥，12OG BE =， ∠90ABE ︒∠=，∠DG AB ⊥，ABD ∆是等腰直角三角形，AOG AEB AFD ∠=∠=∠，∠OD DF =，∠AEB ∠和ACB ∠是AB 所对的圆周角，∠AEB ACB ∠=∠，∠ACB AFC ∠=∠，即有AC AF =，∠AD CF ⊥，∠DF CD =．设BF a =，DF b =，有11222BE OD a b DG BD BF DF a b ++===++，解得a =，∠::22==．BF FC a b【点评】本题考查了圆与三角形，解题的关键是掌握垂径定理，相似三角形的判断与性质，中位线，勾股定理．。

[选择题]必考重点02 圆的性质关于圆的性质的考查 ,在江苏省各地级市中都有考查 ,考点主要集中在切线的性质与判定、圆周角定理 ,其中切线的考查较多 ,难度由简单到较难不等 ,对于圆的考查在选择题中并不仅限于考查圆的性质 ,垂径定理、圆与多边形以及与圆有关的计算等也都有考查 ,大多比较简单 ,没有作为一个单独的专题进行讲解。

在解决圆周角有关题目时 ,首先要把握圆周角的概念 ,能够在图形中找到圆周角是解决此类题目的关键 ,然后运用圆周角定理及其推论找到相等的角、弧、弦等 ,通过转化即可求解。

在解决圆的切线的有关题目时 ,应熟练掌握圆的切线的概念和判定定理以及圆的切线的性质 ,能够运用切线的性质 ,证明角度、线段之间的关系 ,重点掌握利用切线性质证明三角形相似的方法。

[2022·江苏镇江·中考母题]如图 ,在等腰ABC 中 ,120BAC ∠=︒ ,BC = ,O 同时与边BA 的延长线、射线AC 相切 ,O 的半径为3．将ABC 绕点A 按顺时针方向旋转()0360αα︒<≤︒ ,B 、C 的对应点分别为B '、C ' ,在旋转的过程中边B C ''所在直线与O 相切的次数为（ ）A ．1B ．2C ．3D ．4[考点分析]本题主要考查了圆的切线 ,涉及到等腰三角形的性质、两圆的位置关系和特殊角的三角函数等知识 ,熟练掌握相关知识 ,精准识图并准确推断图形的运动轨迹 ,进行合理论证是本题的解题关键．[思路分析]首先以A 为圆心 ,以BC 边的中线为半径画圆 ,可得⊙A 的半径为3 ,计算出OA 的长度 ,可知⊙O 与⊙A 相切 ,根据两个相切圆的性质 ,即可得到答案．[2021·江苏镇江·中考母题]如图 ,∠BAC ＝36° ,点O 在边AB 上 ,⊙O 与边AC 相切于点D ,交边AB 于点E ,F ,连接FD ,则∠AFD等于（）A．27°B．29°C．35°D．37°[考点分析]本题考查了切线的性质,圆周角定理,正确的作出辅助线构造直角三角形是解题的关键．[思路分析]连接OD ,根据切线的性质得到∠ADO＝90° ,根据直角三角形的性质得到∠AOD＝90°﹣36°＝54° ,根据圆周角定理即可得到结论．∠的度数是（）[2020·江苏淮安·中考母题]如图,点A、B、C在圆O上,54∠=,则ABOACBA．54B．27C．36D．108[考点分析]本题考查了圆周角定理、等腰三角形的性质,熟练掌握圆周角定理,会用等边对等角求角的度数是解答的关键．[思路分析]先由圆周角定理得到∠AOB,再利用等腰三角形的性质求解即可．⊥,OC交AB于点P．若[2020·江苏徐州·中考母题]如图,AB是O的弦,点C在过点B的切线上,OC OA∠的度数等于（）∠=︒,则ABC70BPCA．75︒B．70︒C．65︒D．60︒[考点分析]本题考查的是圆切线的运用,熟练掌握运算方法是关键.[思路分析]根据题意可求出∠APO 、∠A 的度数 ,进一步可得∠ABO 度数 ,从而推出答案.1．（2022·江苏南通·一模）如图 ,AB 为⊙O 的弦 ,C ,D 为⊙O 上的两点 ,OC AB ⊥ ,垂足为E ,22.5ADC ∠=︒．若2OC = ,则AB 的长为（ ）．A ．2B ．C ．3D ．2．（2022·江苏徐州·模拟）如图 ,O 是正方形ABCD 的内切圆 ,切点分别为E ,F ,G ,H ,ED 与O 相交于点M ,则tan MFG ∠的值是（ ）A ．13B ．12CD 3．（2022·江苏南京·一模）如图 ,四边形ABCD 内接于⊙O ,D 是AC 的中点 ,若∠B ＝70°,则∠CAD 的度数为（ ）A ．70°B ．55°C ．35°D ．20°4．（2022·江苏连云港·二模）如图 ,弦CD 所对的圆心角为120︒ ,AB 为直径 ,CD 在半圆上滑动 ,F 是CD 的中点 ,过点D 作AB 的垂线 ,垂足为E ,则∠DEF 的值为（ ）A ．30B ．45︒C ．60︒D ．75︒5．（2022·江苏苏州·一模）阅读材料：一般地 ,当αβ、为任意角时 ,sin()αβ+与sin()αβ-的值可以用下面的公式求得：()sin sin cos cos sin αβαβαβ+=⋅+⋅：()sin sin cos cos sin αβαβαβ-=⋅-⋅根据以上材料 ,解决下列问题：如图 ,在O 中 ,AB 是直径 ,AB ,点C 、D 在圆上 ,点C 在半圆弧的中点处 ,AD 是半圆弧的13,则CD 的长为（ ）A B C ．2D ．16．（2022·江苏无锡·模拟）如图 ,P 为半⊙O 直径BA 延长线上一点 ,PC 切半⊙O 于C ,且P A ：PC ＝2：3 ,则sin ∠ACP 的值为（ ）A ．23 B C D ．无法确定7．（2022·江苏南通·二模）如图 ,O 的直径为10cm ,△ABC 内接于O ,3cos 5A =,则下列量中不能确定的是（ ）A．∠A的度数B．弦BC的长C．弦AC的长D．BAC的长8．（2022·江苏·景山中学三模）如图,AB是O的直径,CD是O的弦,连结AC、AD、BD ,若35CAB∠=,∠的度数为()则ADCA．35B．55C．65D．709．（2022·江苏·连云港市新海实验中学二模）如图,AB为O的直径,,C D为O上两点,若40＝,BCD∠︒则ABD∠的大小为（）．A．60°B．50°C．40°D．20°10．（2022·江苏扬州·模拟）如图,点A ,B ,C ,D在O上,,=∠CAD=30° ,∠ACD=50° ,则∠ACB=（）CB CDA．30B．50︒C．70︒D．80︒11．（2022·江苏·宜兴市实验中学二模）如图 ,AB 为半圆O 的直径 ,M ,C 是半圆上的三等分点 ,8AB = ,BD 与半圆O 相切于点B ．点P 为AM 上一动点（不与点A ,M 重合） ,直线PC 交BD 于点D ,BE OC ⊥于点E ,延长BE 交PC 于点F ,则下列结论正确的个数有（ ）①PB PD = ;②BC 的长为43π ;③45DBE ∠=︒ ;④BCF PCB ∽△△ ;⑤CF CP ⋅为定值 A ．2个 B ．3个 C ．4个 D ．5个12．（2022·江苏苏州·一模）如图 ,点P 在以AB 为直径的半圆内 ,连接AP 、BP ,并延长分别交半圆于点C 、D ,连接AD 、BC 并延长交于点F ,作直线PF ,下列说法：①AC 垂直平分BF ;②AC 平分∠BAF ;③FP ⊥AB ;④BD ⊥AF ．其中 ,一定正确的是（ ）A ．①③B ．①④C ．②④D ．③④13．（2022·江苏无锡·一模）如图 ,O 与正五边形ABCDE 的两边,AE CD 相切于,A C 两点 ,则AOC ∠的度数是（ ）A ．144︒B ．130︒C ．129︒D ．108︒14．（2022·江苏苏州·模拟）如图 ,点P 在以AB 为直径的半圆内 ,连接AP 、BP ,并延长分别交半圆于点C 、D ,连接AD 、BC 并延长交于点F ,作直线PF ,下列说法一定正确的是（ ）①AC 垂直平分BF ;②AC 平分BAF ∠ ;③FP AB ⊥ ;④BD AF ⊥．A ．①③B ．①④C ．②④D ．③④15．（2022·江苏·江阴市周庄中学一模）如图 ,ABC 是O 的内接三角形 ,65A ∠=︒ ,过点C 的圆的切线交BO 的延长线于点P ,则P ∠的度数为（ ）A ．55︒B ．50︒C ．45︒D ．40︒16．（2022·江苏徐州·模拟）如图 ,AB 是O 的直径 ,PA 切O 于点A ,PO 交O 于点C ,连接BC ．若20B ∠=︒ ,则P ∠等于（ ）A ．20︒B ．30C ．40︒D ．50︒17．（2022·江苏·苏州高新区实验初级中学三模）如图 ,AB 是O 的直径 ,点C 在O 上 ,过点C 的切线与AB 的延长线交于点E ,点D 在弧AC 上（不与点A ,C 重合） ,连接AD ,CD ．若110D ∠=︒ ,则AEC ∠的度数为（ ）A ．55°B ．50°C ．45°D ．40°18．（2022·江苏·南通市东方中学一模）如图 ,在△ABC 中 ,AB =10 ,AC =8 ,BC =6 ,以边 AB 的中点 O 为圆心 ,作半圆与 AC 相切 ,连接 OC 与半圆相交于点 D ,则 CD 的长为（ ）A ．2B ．3C ．1D ．2.519．（2022·江苏无锡·一模）如图 ,等腰Rt △ABC 中 ,AB ＝AC ＝6 ,∠BAC ＝90° ,D 是BC 边的中点 ,过点D 作DE ⊥DF 分别交AB 、AC 于E 、F （不与B 、C 重合）．取EF 的中点O ,连接AO 并延长交BC 于G ,连接EG 、FG ．随着点E 、F 的位置的变化 ,有以下四个结论：①DE ＝DF ;②四边形AEDF 的面积始终为9 ;③∠EGF ＝90° ;④四边形AEGF 的面积有最小值为9．其中正确的是（ ）A ．①②③B ．①②④C ．①③④D ．②③④20．（2022·江苏盐城·一模）如图 ,O 是△ABC 的外接圆 ,半径为,若6BC = ,则A ∠的度数为（ ）A ．120°B ．135°C ．150°D ．160°21．（2022·江苏无锡·一模）如图 ,矩形ABCD 中 ,E 是BC 上一点 ,连接AE ,将矩形沿AE 翻折 ,使点B 落在CD 边F 处 ,连接AF ,在AF 上取点O ,以O 为圆心 ,OF 长为半径作⊙O 与AD 相切于点P ．若AB ＝6 ,BC ＝,则下列结论：①F 是CD 的中点 ;②⊙O 的半径是2 ;③AE ＝92CE ;④S 阴影号是（ ）A ．①②B ．②③C ．①②④D ．②③④22．（2022·江苏南京·模拟）如图 ,在ABC 中 ,490,5cm,cos 5C AB B ∠=︒==．动点D 从点A 出发沿着射线AC 的方向以每秒1cm 的速度移动 ,动点E 从点B 出发沿着射线BA 的方向以每秒2cm 的速度移动．已知点D 和点E 同时出发 ,设它们运动的时间为t 秒．连接BD ．下列结论正确的有（ ）个①4BC = ;②当AD AB =时 ,tan 2ABD ∠= ;③以点B 为圆心、BE 为半径画B ,当2513t =时 ,DE 与B 相切 ; ④当CBD ADE ∠=∠时 ,2511t． A ．1 B ．2 C ．3 D ．423．（2022·江苏南京·模拟）如图 ,△ABC O ,AB 为直径 ,点M 是AC 的中点 ,AD 平分∠CAB 交BM 于点D ,且D 为BM 的中点 ,则BC 的长为（ ）A B C D 24．（2022·江苏·扬州中学教育集团树人学校一模）如图 ,直线l 与⊙O 相切于点A ,M 是⊙O 上的一个动点 ,MH ⊥l ,垂足为H ．若⊙O 的半径为4 ,则MA ―MH 的最大值为（ ）A ．12B ．34C ．1D ．225．（2022·江苏·苏州市第十六中学一模）如图 ,在ABC 中 ,90ACB ∠=︒ ,AC ＝BC ,AB ＝4cm ,CD 是中线 ,点E 、F 同时从点D 出发 ,以相同的速度分别沿DC 、DB 方向移动 ,当点E 到达点C 时 ,运动停止 ,直线AE 分别与CF 、BC 相交于G 、H ,则在点E 、F 移动过程中 ,点G 移动路线的长度为（ ）A ．2B ．πC D[选择题]必考重点02 圆的性质关于圆的性质的考查 ,在江苏省各地级市中都有考查 ,考点主要集中在切线的性质与判定、圆周角定理 ,其中切线的考查较多 ,难度由简单到较难不等 ,对于圆的考查在选择题中并不仅限于考查圆的性质 ,垂径定理、圆与多边形以及与圆有关的计算等也都有考查 ,大多比较简单 ,没有作为一个单独的专题进行讲解。

专题12 圆与正多边形一．选择题1．（2022·湖北鄂州）工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A 、B 、E 三个接触点，该球的大小就符合要求．图（2）是过球心及A 、B 、E 三点的截面示意图，已知⊙O 的直径就是铁球的直径，AB 是⊙O 的弦，CD 切⊙O 于点E ，AC ⊥CD 、BD ⊥CD ，若CD =16cm ，AC =BD =4cm ，则这种铁球的直径为（ ）A ．10cmB ．15cmC ．20cmD ．24cm【答案】C【分析】连接OA ，OE ，设OE 与AB 交于点P ，根据AC BD =，AC CD ⊥，BD CD ⊥得四边形ABDC 是矩形，根据CD 与O 切于点E ，OE 为O 的半径得OE CD ⊥，OE AB ⊥，即PA PB =，PE AC =，根据边之间的关系得8PA cm =，4AC BD PE cm ===，在Rt OAP △，由勾股定理得，222+=PA OP OA ，进行计算可得10OA =，即可得这种铁球的直径．【详解】解：如图所示，连接OA ，OE ，设OE 与AB 交于点P ，∵AC BD =，AC CD ⊥，BD CD ⊥，∴四边形ABDC 是矩形，∵CD 与O 切于点E ，OE 为O 的半径，∴OE CD ⊥，OE AB ⊥，∴PA PB =，PE AC =，∵AB =CD =16cm ，∴8PA cm =，∵4AC BD PE cm ===，在Rt OAP △，由勾股定理得，222+=PA OP OA 2228+(4)=OA OA -解得，10OA =，则这种铁球的直径＝221020OA cm =⨯=，故选C ．【点睛】本题考查了切线的性质，垂径定理，勾股定理，解题的关键是掌握这些知识点．2．（2022·湖南娄底）如图，等边ABC 内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边ABC 的内心成中心对称，则圆中的黑色部分的面积与ABC 的面积之比是（ ）A B C D 【答案】A【分析】由题意，得圆中黑色部分的面积是圆面积的一半，令BC =2a ，则BD =a ，根据勾股定理，得出AD =，同时在Rt △BOD 中，OD ，进而求出黑色部分的面积以及等边三角形的面积，最后求出答案．【详解】解：令内切圆与BC 交于点D ，内切圆的圆心为O ，连接AD ，OB ，由题可知，圆中黑色部分的面积是圆面积的一半，令BC =2a ，则BD =a ，在等边三角形ABC 中AD ⊥BC ，OB 平分∠ABC ，∴∠OBD =12∠ABC =30°，由勾股定理，得AD，在Rt △BOD 中，OD =tan30°×BD，∴圆中的黑色部分的面积与ABC=A ．【点睛】本题考查了等边三角形的性质，内切圆的性质和面积，等边三角形的面积以及勾股定理求边长，正确地计算能力是解决问题的关键．3．（2022·山东聊城）如图，AB ，CD 是O 的弦，延长AB ，CD 相交于点P ．已知30P ∠=︒，80AOC ∠=︒，则 BD的度数是（ ）A ．30°B ．25°C ．20°D ．10°【答案】C【分析】如图，连接OB ，OD ，AC ，先求解100OAC OCA ∠+∠=︒，再求解50PAO PCO ∠+∠=︒，从而可得260BOA COD ∠+∠=︒，再利用周角的含义可得3608026020BOD ∠=︒-︒-︒=︒，从而可得答案．【详解】解：如图，连接OB ，OD ，AC，∵80AOC ∠=︒，∴100OAC OCA ∠+∠=︒，∵30P ∠=︒，∴50PAO PCO ∠+∠=︒，∵OA OB =，OC OD =，∴OBA OAB ∠=∠，OCD ODC ∠=∠，∴50OBA ODC ∠+∠=︒，∴260BOA COD ∠+∠=︒，∴3608026020BOD ∠=︒-︒-︒=︒．∴ BD的度数20°．故选：C ．【点睛】本题考查的是圆心角与弧的度数的关系，等腰三角形的性质，三角形的内角和定理的应用，掌握“圆心角与弧的度数的关系”是解本题的关键．4．（2022·湖北黄冈）如图，在Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝8，以点C 为圆心，CA 的长为半径画弧，交AB 于点D ，则弧AD 的长为（ ）A ．πB ．43πC ．53πD ．2π【答案】B【分析】连接CD ，根据∠ACB =90°，∠B =30°可以得到∠A 的度数，再根据AC =CD 以及∠A 的度数即可得到∠ACD 的度数，最后根据弧长公式求解即可．【详解】解：连接CD ，如图所示：∵ACB =90°，∠B =30°，AB =8，∴∠A =90°-30°=60°，AC =12AB =4，由题意得：AC =CD ，∴△ACD 为等边三角形，∴∠ACD =60°，∴ AD 的长为：604180π⨯＝43π，故选：B ．【点睛】本题考查弧长公式，解题的关键是：求出弧所对应的圆心角的度数以及弧所在扇形的半径．5．（2022·四川达州）如图所示的曲边三角形可按下述方法作出：作等边ABC ，分别以点A ，B ，C 为圆心，以AB 长为半径作 BC ， AC ， AB ，三弧所围成的图形就是一个曲边三角形．如果一个曲边三角形的周长为2π，则此曲边三角形的面积为（ ）A ．2π-B ．2πC ．2πD ．π【答案】A【分析】根据此三角形是由三段弧组成，所以根据弧长公式可得半径，即正三角形的边长，根据曲边三角形的面积等于三角形的面积与三个弓形的面积和，边长为a 【详解】解：设等边三角形ABC 的边长为r ，6012,1803r ππ∴⋅⋅=⨯解得2r =，即正三角形的边长为2，∴2226022322360ππ⎛⎫⨯+⨯=- ⎪ ⎪⎝⎭故选A 【点睛】本题考查了扇形面积的计算．此题的关键是明确曲边三角形的面积等于三角形的面积与三个弓形的面积和，然后再根据所给的曲线三角形的周长求出三角形的边长．6．（2022·江苏无锡）在Rt △ABC 中，∠C =90°，AC =3，BC =4，以AC 所在直线为轴，把△ABC 旋转1周，得到圆锥，则该圆锥的侧面积为（ ）A ．12πB ．15πC ．20πD ．24π【答案】C【分析】先利用勾股定理计算出AB ，再利用扇形的面积公式即可计算出圆锥的侧面积．【详解】解：∵∠C =90°，AC =3，BC =4，∴AB ，以直线AC 为轴，把△ABC 旋转一周得到的圆锥的侧面积=12×2π×4×5=20π．故选：C ．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．7．（2022·湖北荆州）如图，以边长为2的等边△ABC 顶点A 为圆心、一定的长为半径画弧，恰好与BC 边相切，分别交AB ，AC 于D ，E ，则图中阴影部分的面积是（ ）A 4πB ．πC D 2π-【答案】D【分析】作AF ⊥BC ，再根据勾股定理求出AF ，然后根据阴影部分的面积=A B C A D E S S - 扇形得出答案．【详解】过点A 作AF ⊥BC ，交BC 于点F ．∵△ABC 是等边三角形，BC =2，∴CF=BF=1．在Rt △ACF 中，A F ==∴1==222ABCADE S S S π-⨯ 阴影扇形．故选：D ．【点睛】本题主要考查了求阴影部分的面积，涉及等边三角形的性质，勾股定理及扇形面积计算等知识，将阴影部分的面积转化为三角形的面积-扇形的面积是解题的关键．8．（2022·广西贺州）如图，在等腰直角OAB 中，点E 在OA 上，以点O 为圆心、OE 为半径作圆弧交OB 于点F ，连接EF ，已知阴影部分面积为π2-，则EF 的长度为（ ）AB ．2C ．D ．【答案】C【分析】根据题意可得：OE =OF ，∠O =90°，设OE =OF =x ，利用阴影部分面积列出等式，得出24x =，然后由勾股定理求解即可．【详解】解：根据题意可得：OE =OF ，∠O =90°，设OE =OF =x ，∴2OEF OEF S S S π=-=- 阴影扇形2290123602x x ππ-=-，解得：24x =，∴EF ===故选：C ．【点睛】题目主要考查不规则图形的面积，一元二次方程的应用，勾股定理解三角形等，理解题意，综合运用这些知识点是解题关键．9．（2022·江苏无锡）如图，AB 是圆O 的直径，弦AD 平分∠BAC ，过点D 的切线交AC 于点E ，∠EAD ＝25°，则下列结论错误的是（）A．AE⊥DE B．AE//OD C．DE=OD D．∠BOD=50°【答案】C【分析】过点D作DF⊥AB于点F，根据切线的性质得到OD⊥DE，证明OD∥AE，根据平行线的性质以及角平分线的性质逐一判断即可．【详解】解：∵DE是⊙O的切线，∴OD⊥DE，∵OA=OD，∴∠OAD=∠ODA，∵AD平分∠BAC，∴∠OAD=∠EAD，∴∠EAD=∠ODA，∴OD∥AE，∴AE⊥DE．故选项A、B都正确；∵∠OAD=∠EAD=∠ODA=25°，∠EAD=25°，∴∠BOD=∠OAD+∠ODA=50°，故选项D正确；∵AD平分∠BAC，AE⊥DE，DF⊥AB，∴DE=DF<OD，故选项C不正确；故选：C．【点睛】本题考查的是切线的性质，角平分线的性质定理，平行线的性质，掌握圆的切线垂直于经过切点的半径是解题的关键．10．（2022·黑龙江大庆）已知圆锥的底面半径为5，高为12，则它的侧面展开图的面积是( )A ．60πB ．65πC ．90πD ．120π【答案】B【分析】根据圆锥侧面展开图的面积πS rl =，计算求解即可．【详解】解：由题意知，圆锥侧面展开图的半径即圆锥的母线长l 13=，∴圆锥侧面展开图的面积为ππ51365S rl π==⨯⨯=，故选B ．【点睛】本题考查了圆锥侧面展开图的面积，勾股定理．解题的关键在于明确圆锥侧面展开图的面积πS rl =，其中r 为圆锥底面半径，l 为圆锥侧面展开图的半径即圆锥的母线长．11．（2022·内蒙古包头）如图，,AB CD 是O 的两条直径，E 是劣弧 BC的中点，连接BC ，DE ．若22ABC ∠=︒，则CDE ∠的度数为（ ）A ．22︒B ．32︒C ．34︒D ．44︒【答案】C【分析】连接OE ，由题意易得22OCB ABC ∠=∠=︒，则有136COB ∠=︒，然后可得68COE ∠=︒，进而根据圆周角定理可求解．【详解】解：连接OE ，如图所示：∵OB =OC ，22ABC ∠=︒，∴22OCB ABC ∠=∠=︒，∴136COB ∠=︒，∵E 是劣弧 BC 的中点，∴1682COE COB ∠=∠=︒，∴1342CDE COE ∠=∠=︒；故选C ．【点睛】本题主要考查圆周角定理及垂径定理，熟练掌握圆周角定理及垂径定理是解题的关键．12．（2022·辽宁锦州）如图，线段AB 是半圆O 的直径。

专题12 点、直线与圆的位置关系【思维导图】◎考点题型1 点和圆的位置关系PO=，则点P与⊙O的位例．（2022·河北邯郸·九年级期末）平面内有两点P，O，⊙O的半径为5，若6置关系是（）A．圆内B．圆上C．圆外D．圆上或圆外【答案】C【分析】根据点到圆心的距离小于半径即可判断点P在⊙O的内部．【详解】∵⊙O的半径为5，PO＝6，∴点P到圆心O的距离大于半径，∴点P 在⊙O 的外部，故选C ．【点睛】本题考查了点与圆的位置关系，理解点与圆的位置关系是解题的关键．变式1．（2021·江苏淮安·九年级期中）O e 的半径为5cm ，点A 到圆心O 的距离3cm OA ＝，则点A 与O e 的位置关系为（ ）A ．点A 在O e 上B ．点A 在O e 内C ．点A 在O e 外D ．无法确定【答案】B【分析】根据点与圆的位置关系的判定方法进行判断．【详解】解：O Q e 的半径为5cm ，点A 到圆心O 的距离为3cm ，即点A 到圆心O 的距离小于圆的半径，\点A 在O e 内．故选：B ．【点睛】本题考查了点与圆的位置关系：设⊙O 的半径为r ，点P 到圆心的距离OP ＝d ，则有点P 在圆外⇔d ＞r ；点P 在圆上⇔d ＝r ；点P 在圆内⇔d ＜r ．变式2．（2022·全国·九年级专题练习）在平面直角坐标系中，以原点O 为圆心，4为半径作圆，点P 的坐标是（5，5），则点P 与⊙O 的位置关系是（ ）A ．点P 在⊙O 上B ．点P 在⊙O 内C ．点P 在⊙O 外D ．点P 在⊙O 上或在⊙O 外变式3．（2021·江苏常州·九年级期中）数轴上有两个点A 和B ，点B 表示实数6，点A 表示实数a ，⊙B半径为4．若点A在⊙B内部，则a的取值范围是（ ）A．a＜2或a＞10B．2＜a＜10C．a＞2D．a＜10【答案】B【分析】先表示出AB=|6-a|，从而列出|6-a|＜4，进而即可求解．【详解】解：∵点B表示实数6，点A表示实数a，∴AB=|6-a|，∵⊙B半径为4．若点A在⊙B内部，∴|6-a|＜4，即：2＜a＜10，故选B．【点睛】本题主要考查点与圆的位置关系，熟练掌握点在圆的内部则点与圆心的距离小于圆的半径，是解题的关键．◎考点题型2 三角形的外接圆1）经过三角形三个顶点的圆叫做三角形的外接圆，外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心，这个三角形叫做这个圆的内接三角形．2）三角形外心的性质：①三角形的外心是指外接圆的圆心，它是三角形三边垂直平分线的交点，它到三角形各顶点的距离相等；②三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合.3）外接圆圆心和三角形位置关系：1.锐角三角形外接圆的圆心在它的内部（如图1）；2.直角三角形外接圆的圆心在斜边中点处（即直角三角形外接圆半径等于斜边的一半，如图2）；3.钝角三角形外接圆的圆心在它的外部（如图3）.例．（2022·江苏·九年级）如图，在平面直角坐标系中，()0,3A-，()2,1B-，()2,3C．则△ABC的外心坐标为（）图2C CA ．()0,0B ．()1,1-C ．()2,1--D ．()2,1-【答案】D 【分析】由BC 两点的坐标可以得到直线BC ∥y 轴，则直线BC 的垂直平分线为直线y =1，再由外心的定义可知△ABC 外心的纵坐标为1，则设△ABC 的外心为P （a ，-1），利用两点距离公式和外心的性质得到()()()22222222131621148PA a a PB a a a =++=+==-++=-+，由此求解即可．【详解】解：∵B 点坐标为（2，-1），C 点坐标为（2， 3），∴直线BC ∥y 轴，∴直线BC 的垂直平分线为直线y =1，∵外心是三角形三条边的垂直平分线的交点，∴△ABC 外心的纵坐标为1，设△ABC 的外心为P （a ，1），∴()()()22222222131621148PA a a PB a a a =++=+==-++=-+，∴221648a a a +=-+，解得2a =-，∴△ABC 外心的坐标为（-2， 1），故选D ．【点睛】本题主要考查了坐标与图形，外心的性质与定义，两点距离公式，解题的关键在于能够熟知外心是三角形三边垂直平分线的交点．变式1．（2022·湖南邵阳·中考真题）如图，⊙O 是等边△ABC 的外接圆，若AB =3，则⊙O 的半径是（ ）A ．32BCD ．52∵△ABC 为等边三角形，∴∠B =60°，变式2．（2022·全国·九年级）如图，小东在同一平面上按照如下步骤进行尺规作图：（1）作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧交于点C；（2）以C为圆心，以AB长为半径作弧交AC的延长线于点D；（3）连接BD，BC．则下列说法中不正确的是（ ）A．∠ABD＝90°B．sin2A+cos2D＝1C．DB D．点C是△ABD的外心变式3．（2022·河北·宽城满族自治县教研室模拟预测）如图，△ABC和△DBC中，点D在△ABC内，AB＝AC＝BC＝2，DB＝DC，且∠D＝90°，则△ABC的内心和△DBC的外心之间的距离为（）B．1C DA．12◎考点题型3 三点定圆的方法1）经过点A的圆：以点A以外的任意一点O为圆心，以OA的长为半径，即可作出过点A的圆，这样的圆有无数个．2）经过两点A、B的圆：以线段AB中垂线上任意一点O作为圆心，以OA的长为半径，即可作出过点A、B 的圆，这样的圆也有无数个．3）经过三点时：情况一：过三点的圆：若这三点A、B、C共线时，过三点的圆不存在；情况二：若A、B、C三点不共线时，圆心是线段AB与BC的中垂线的交点，而这个交点O是唯一存在的，这样的圆有唯一一个．三点定圆的画法：1）连接线段AB,BC。

专题23圆的有关性质（46题）1．（2023·四川自贡·统考中考真题）如图，ABC 内接于O ，CD 是O 的直径，连接BD ，41DCA ，则ABC 的度数是（）A ．41B ．45C ．49D ．59【答案】C 【分析】由CD 是O 的直径，得出90DBC ，进而根据同弧所对的圆周角相等，得出41ABD ACD ，进而即可求解．【详解】解：∵CD 是O 的直径，∴90DBC ，∵ AD AD ，∴41ABD ACD ，∴904149ABC DBC DBA ，故选：C ．【点睛】本题考查了圆周角定理的推论，熟练掌握圆周角定理是解题的关键．2．（2023·四川凉山·统考中考真题）如图，在O 中，3023OA BC ADB BC ，，，则OC （）A ．1B ．2C ．23D ．430ADB ∵，2230AOB ADB ∵OA BC ，60COE BOE ，在Rt OCE 中，COE 32sin 6032CE OC ，故选：B ．【点睛】本题主要考查了圆周角定理，垂径定理，解直角三角形，解题的关键是熟练掌握圆周角定理，垂径定理，添加适当的辅助线．3．（2023·四川宜宾·统考中考真题）术”．如图， AB 是以点O 长l 的近似值计算公式：得ON AB ，∴点M ，N ，O 三点共线，∵4OA ，60AOB ∴OAB 是等边三角形，∴4,OA AB OAN ∴4,OA AB OAN ∴ 244MN l AB OA 故选：B ．【点睛】本题考查了等边三角形的性质，垂径定理，勾股定理，特殊角的函数值，熟练掌握相关知识是解题的关键．4．（2023·四川宜宾·统考中考真题）如图，已知点AOB 等于（）A ．140 B∵点A B C 、、在O 上， BC AC ，12BOC AOC AOB∵35BAC ，根据圆周角定理可知BOC 2140AOB BOC 故选：A ．【点睛】本题考查圆中求角度问题，涉及圆周角定理，找准各个角之间的和差倍分关系是解决问题的关键．5．（2023·安徽·统考中考真题）A ．60B 【答案】D 【分析】先计算正五边形的内角，再计算正五边形的中心角，作差即可．【详解】∵180BAE ∴180BAE COD 故选：D ．A ．只有甲是扇形B ．只有乙是扇形C ．只有丙是扇形【答案】B 【分析】根据扇形的定义，即可求解．扇形，是圆的一部分，由两个半径和和一段弧围成．【详解】解：甲是由一条直径、一条弦及一段圆弧所围成的图形：乙是由两条半径与一段圆弧所围成的图A ．66B ．【答案】B 【分析】根据圆周角定理即可求解．【详解】解：∵ BCBC ，∴1332A BOC ，故选：B ．【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．A ．12【答案】B 【分析】根据圆周角定理求得【详解】解：∵∴60AOB ∴260π6360S 故选：B.【点睛】本题考查了圆周角定理，扇形面积公式，熟练掌握扇形面积公式以及圆周角定理是解题的关键．9．（2023·浙江温州3AD ，则 A ．10°，1B 【答案】C 【分析】过点O 作OE 30OAD ODA ，122,2CD OC CF 【详解】解：过点O 作OE∵BC AD ∥，∴CBD ADB ，∵CBD CAD ，∴CAD ADB ，∵AC BD ，∴90AFD ，∴45CAD ADB ∵120AOD ，OA ∴30OAD ODA ∴CAO CAD OAD ∴290COD CAD ∴22,CD OC CF ∴21BC CF ；故选：C ．【点睛】本题主要考查平行线的性质、圆周角定理及三角函数，熟练掌握平行线的性质、圆周角定理及三A ．2则EA 的长度为圆上任意一点到正方形边上任意一点距离的最小值，由题意可得：OE AB 由勾股定理可得：OA ∴422AE ，故选：D.【点睛】此题考查了圆与正多边形的性质，勾股定理，解题的关键是熟练掌握圆与正多边形的性质，确定出圆上任意一点到正方形边上任意一点距离的最小值的位置．11．（2023·山东枣庄则B 的度数为（A ．32B 【答案】A 【分析】根据圆周角定理，可以得到【详解】解：A D ∵48D ，A ．30【答案】C 【分析】先计算正六边形的中心角，再利用同圆或等圆中，等弧对的圆心角相等，圆周角定理计算即可．【详解】如图，连接∵正六边形ABCDEF ∴COD DOE ∴COQ COD ∴12CPQ COQ 故选：Ｃ．【点睛】本题考查了正多边形与圆，圆周角定理，熟练掌握正多边形中心角计算，圆周角定理是解题的关键．13．（2023·湖北十堰过点O 作OF ACA ．43【答案】B 【分析】作BM AC 60GEF EGF ，由勾股定理求出AB 的长．【详解】解：作BM 在AEB △和DEC 中，A D AE ED AEB DEC，∴ ASA AEB DEC ≌ ∴EB EC ，又∵BC CE ，∴BE CE BC ，∴EBC 为等边三角形，∴60GEF ，BC ∴30EGF ，∵2EG ，OF AC ∴112EF EG ，A ．40【答案】B 【分析】由同弧所对圆周角相等及直角三角形的性质即可求解．【详解】解：∵ BC∴40BDC BACA．5B．【答案】B【分析】根据等腰三角形的性质得出A ．a bB ．a bC ．a bD ．a ，b 大小无法比较【答案】A 【分析】连接1223,PP P P ，依题意得12233467PP P P P P P P ，4617P P PP ，137PP P 的周长为131737a PPPP P P ，四边形3467P P P P 的周长为34466737b P P P P P P P P ，故122313b a PP P P PP ，根据123PP P 的三边关系即可得解．【详解】连接1223,PP P P ，∵点18~P P 是O 的八等分点，即 1223345566778148PP P P P P P P P P P P P P P P ∴12233467PP P P P P P P ， 464556781178P P P P P P P P P P PP ∴4617P P PP 又∵137PP P 的周长为131737a PPPP P P ，四边形3467P P P P 的周长为34466737b P P P P P P P P ，∴ 34466737131737b a P P P P P P P P PP PP P P12172337131737PP PP P P P P PP PP P P 122313PP P P PP 在123PP P 中有122313PP P P PP ∴1223130b a PP P P PP 故选：A ．【点睛】本题考查等弧所对的弦相等，三角形的三边关系等知识，利用作差比较法比较周长大小是解题的关键．A ．23B ．【答案】D 【分析】根据,OA OB 互相垂直可得再根据三角形内角和定理即可求解．【详解】解：如图，∵半径,OA OB 互相垂直，90AOB ，ADB 所对的圆心角为270 ADB 所对的圆周角ACB 又∵19ABC ，180BAC ACB 故选：D ．【点睛】本题考查圆周角定理、三角形内角和定理，解题的关键是掌握：同圆或等圆中，同弧所对的圆周角等于圆心角的一半．18．（2023·湖北黄冈·统考中考真题）如图，在若20C ，70BPCA ．70【答案】D 【分析】先根据圆周角定理得出BDP BPC ADB ADC 【详解】解：∵ ∴20B ，∵70BPC ，∴BDP BPC 又∵AB 为直径，即∴ADC ADB 故选：D ．【点睛】此题主要考查了圆周角定理，三角形外角和定理等知识，解题关键是熟知圆周角定理的相关知识．19．（2023·广西·统考中考真题）赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥图，主桥拱呈圆弧形，跨度约为A ．20mB ．28mC ．35mD ．【答案】B 【分析】由题意可知，37m AB ，7m CD ，主桥拱半径R ，根据垂径定理，得到定理列方程求解，即可得到答案．【详解】解：如图，由题意可知，37m AB ，7m CD ，主桥拱半径R【点睛】本题考查了垂径定理，勾股定理，利用直角三角形求解是解题关键．20．（2023·四川·统考中考真题）如图，124BOD ，则ACD 的度数是（A ．56B ．【答案】C 【分析】根据圆周角定理计算即可．【详解】解：∵124BOD ∴18012456AOD Ð=°-°=°∴1282ACD AOD，故选：C ．【点睛】此题考查圆周角定理，熟知同弧所对的圆周角是圆心角的一半是解题的关键．A ．15B 【答案】C 【分析】根据三角形内心的定义可得定理以及等腰三角形的性质得出答案．【详解】解：连接OC ，∵点I 是ABC 的内心，∴270BAC CAI ∴2140BOC BAC ，∵OB OC ，∴180OBC OCB故选：C ．【点睛】本题主要考查了三角形内心的定义和圆周角定理，熟知三角形的内心是三角形三个内角平分线的交点是解题的关键．22．（2023·福建·统考中考真题）我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的利用圆的内接正多边形逼近圆的方法来近似估算，指出则与圆周合体，而无所失矣3.1416．如图，O 的半径为计值为332，若用圆内接正十二边形作近似估计，可得A．3【答案】CA ．20B ．40C ．50D ．80【答案】B 【分析】根据圆周角定理可进行求解．【详解】解：∵AB 是O 的直径，∴90ACB ，∵50BAC ，∴9040ABC BAC ，∵ AC AC ，∴40D ABC ；故选：B ．【点睛】本题主要考查圆周角的相关性质，熟练掌握直径所对圆周角为直角是解题的关键．24．（2023·河南·统考中考真题）如图，点A ，B ，C 在O 上，若55C ，则AOB 的度数为（）A ．95B ．100C ．105D ．110【答案】D 【分析】直接根据圆周角定理即可得．【详解】解：∵55C ，∴由圆周角定理得：2110AOB C ∠∠，故选：D ．【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题关键．25．（2023·全国·统考中考真题）如图，AB ，AC 是O 的弦，OB ，OC 是O 的半径，点P 为OB 上任意A ．70【答案】D 【分析】根据圆周角定理得出【详解】解：∵ BC∴2140BOC BAC ∵BPC BOC PCO ∴BPC 的度数可能是故选：D ．【点睛】本题考查了圆周角定理，三角形的外角的性质，熟练掌握圆周角定理是解题的关键．26．（2023·内蒙古赤峰BD ，2BOC COD A ．25B ．30 【答案】A 【分析】根据圆内接四边形对角互补得出根据已知条件得出13COD BOD 【详解】解：∵圆内接四边形ABCD ∴18010575AA ．35B ．30 【答案】A 【分析】证明35NMO MNO 35AOC BOC ．【详解】解：∵35MNO ，MO ∴35NMO MNO ，∴23570AOB ，∵OA OB ，C 为AB 的中点，∴35AOC BOC ，故选A ．【点睛】本题考查的是圆的基本性质，等腰三角形的性质，平行线的判定，三角形的外角的性质，熟记等腰三角形的性质是解本题的关键．【答案】4【分析】根据圆周角定理得出OM AC ，且AD CD 【详解】解：∵AB 是O ∴90ACB ，∵12,5AC BC ，∴13AB ，∴11322AO AB ，∵点D ，M 分别是弦AC ∴OM AC ，且AD CD ∴2252OD AO AD ∴MD OM OD AO 故答案为：4．【点睛】题目主要考查圆周角定理、垂径定理及勾股定理解三角形，理解题意，综合运用这些知识点是解题关键．29．（2023·浙江金华·统考中考真题）如图，在【答案】56【分析】连接AD ，即可．【详解】解：如图，连接∵AB 为直径，∴AD AB ，∵6cm,AB AC BAC ∴BD CD ，BAD ∴2DOE BAD ∴弧DE 的长为50180 故答案为：56cm ．【点睛】本题考查了等腰三角形三线合一性质，中位线定理，弧长公式，熟练掌握三线合一性质，弧长公式，圆周角定理是解题的关键．30．（2023·四川广安·度为___________．【答案】7360BAC ∵，2BOC BAC ,OB OC OD BC Q 12BOD BOC ∵圆的半径为7，7OB ，sin 60BD OB 273BC BD ，故答案为：73．【点睛】本题考查了圆周角定理、解直角三角形、等腰三角形的三线合一，熟练掌握圆周角定理和解直角三角形的方法是解题关键．31．（2023·甘肃武威【答案】35【分析】由同弧所对的圆周角相等，然后由直角三角形的性质即可得出结果．【详解】解：,A CDB Q 是 BC所对的圆周角，55,A CDB AB ∵是O 的直径，90ACB ∵，在Rt ACB △中，90905535ABC A ，故答案为：35．【点睛】本题考查了圆周角定理，以及直角三角形的性质，利用了转化的思想，熟练掌握圆周角定理是解本题的关键．32．（2023·浙江绍兴·统考中考真题）如图，四边形ABCD 内接于圆O ，若100D ，则B 的度数是________．【答案】80【分析】根据圆内接四边形的性质：对角互补，即可解答．【详解】解：∵四边形ABCD 内接于O ，∴180B D �邪＝，∵100D ，∴18080B D ＝﹣＝．故答案为：80 ．【点睛】本题主要考查了圆内接四边形的性质，掌握圆内接四边形的对角互补是解答本题的关键．33．（2023·山东烟台·统考中考真题）如图，将一个量角器与一把无刻度直尺水平摆放，直尺的长边与量角器的外弧分别交于点A ，B ，C ，D ，连接AB ，则BAD 的度数为_______．方法二∶解∶连接,OB OD ，由题意可得：15550105BAD ，根据圆周角定理，知1110522BAD BOD故答案为：52.5 ．【点睛】本题主要考查了角的度量、圆周角定理等知识点，掌握圆周角的度数等于它所对弧上的圆心角度数的一半是解答本题的关键．34．（2023·湖南·统考中考真题）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中边形的位置．要完成这一圆环排列，共需要正五边形的个数是【答案】10【分析】先求出正五边形的外角为【详解】解：根据题意可得：∵正五边形的一个外角3605∴1272 ，∴18072236AOB ∴共需要正五边形的个数36036故答案为：10．【点睛】本题主要考查了圆的基本性质，正多边形的外角，解题的关键是掌握正多边形的外角的求法．35．（2023·湖南永州·统考中考真题）如图，最深处到水面AB 的距离为4cm∵水的最深处到水面AB 的距离为∴1046OD cm ，在Rt AOD 中，AD AO ∴216AB AD cm故答案为：16．【点睛】本题考查了垂径定理的应用，勾股定理，熟练掌握垂径定理是解题的关键．36．（2023·湖北随州·统考中考真题）如图，在___________．【答案】30【分析】根据垂径定理得到【详解】解：∵OA ∴»»AB AC ，∴12ADC AOB故答案为：30 ．【点睛】本题考查的是垂径定理和圆周角定理，掌握同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．37．（2023·湖南·统考中考真题）如图所示，点A 、B 、C 是O 上不同的三点，点O 在ABC 的内部，连接BO 、CO ，并延长线段BO 交线段AC 于点D ．若6040A OCD ，，则ODC _______度．【答案】80【分析】先根据圆周角定理求出BOC 的度数，再根据三角形的外角定理即可得出结果．【详解】解：在O 中，2260120BOC A Q ，1204080ODC BOC OCD故答案为：80．【点睛】本题考查了圆周角定理，三角形的外角定理，熟练掌握圆周角定理是本题的关键．38．（2023·湖南郴州·统考中考真题）如图，某博览会上有一圆形展示区，在其圆形边缘的点P 处安装了一台监视器，它的监控角度是55 ，为了监控整个展区，最少．．需要在圆形边缘上共安装这样的监视器___________台．【答案】4【分析】圆周角定理求出P 对应的圆心角的度数，利用360 圆心角的度数即可得解．【详解】解：∵55P ，【答案】2【分析】连接,,OA OC OE 得到BAC AFE CDE S S S 【详解】如图所示，连接∵六边形ABCDEF 是 ∴AC AE CE ，∴ACE △是O 的内接正三角形，∵120B ，AB BC ∴ 11802BAC BCA∵60CAE ，【答案】35【分析】由题意易得【详解】解：∵AB ∴90ACB ，∵ AC AC ，ADC ∴ADC ABC ∴70BAC ，即226x ，26CD （寸）．故答案为：26．【点睛】本题考查了垂径定理和勾股定理，解题的关键是正确作出辅助线构造直角三角形．(1)求证：四边形ABOH 为矩形．(2)已知A 的半径为4，【答案】(1)见解析(2)6【分析】（1）根据切线的性质及有三个角是直角的四边形是矩形判定即可．（2）根据矩形的性质、垂径定理及圆的性质计算即可．【详解】（1）证明：∵ ∴AB x 轴．∵,AH CD HO OB ，∴AHO HOB OBA ∴四边形AHOB 是矩形．（2）如图，连接AC ．∵四边形AHOB 是矩形，7AH OB ．在Rt AHC 中，2CH AC 224(7)3CH ．∵点A 为圆心，AH CD 2CD CH 6 ．【点睛】本题考查了矩形的判定，垂径定理，圆的性质，熟练掌握矩形的判定和垂径定理是解题的关键．43．（2023·甘肃武威·统考中考真题）圆规可以完成一切尺规作图．规的几何学》中．请你利用数学家们发现的结论，完成下面的作图题：如图，已知O ，A 是 ①以点A 为圆心，OA 长为半径，自点②分别以点A ，点D 为圆心，③以点A 为圆心，OE 长为半径作弧交【答案】见解析【分析】根据作图提示逐步完成作图即可．再根据图形基本性质进行证明即可．【详解】解：如图，即点A ，G ，D ，H 把理由如下：如图，连接,,,OB OC AG 由作图可得： AB BC ∴AOB 为等边三角形，同理可得：BOC COD ∴AOB BOC COD ∴A ，O ，D 三点共线，∴=90ACD ，设CD x ，而30DAC ∴2AD x ，3AC x ，由作图可得：DE AE52 (1)求O的半径；(2)求BAC的正切值．【答案】(1)5(2)9 4【分析】（1）延长BC得10BD ，由此即可得；（2）过点C作CE AB然后根据正切的定义即可得．【详解】（1）解：如图，延长由圆周角定理得：BAD∵弦AB的长为8，且cosO ∵ 的半径为5，5OB ，12OC OB∵，31522BC OB ，4cos 5ABC∵，45BE BC ，即152BE 解得6BE ，2AE AB BE ，则BAC 的正切值为【点睛】本题考查了圆周角定理、解直角三角形、勾股定理等知识点，熟练掌握解直角三角形的方法是解题关键．45．（2023·湖北武汉·(1)求证：2AOB【点睛】本题主要考查了勾股定理，垂径定理，圆周角定理，解题的关键是作出辅助线，熟练掌握圆周角定理．46．（2023·贵州·统考中考真题）交O 于点E ，连接EA (1)写出图中一个度数为(2)求证：AED CEB ∽△△(3)连接OA ，OB ，判断四边形【答案】(1)1 、2 、(2)见详解(3)四边形OAEB 是菱形【分析】（1）根据外接圆得到90ADC BDC （2）根据（1）得到 （3）连接OA ，OB ，结合即可得到证明；【详解】（1）解：∵ ∴CO 是ACB 的角平分线，∴1230 ，∵CE 是O 的直径，∴90CAE CBE ，∴3430 ，∴30 的角有：1 、2 、3 、4 ，∵CO 是ACB 的角平分线，∴90ADC BDC ，56903060 ，在ACD 与BCD △中，∵1290CD CD ADC BDC，∴ACD BCD ≌，故答案为：1 、2 、3 、4 ，BCD △；（2）证明：∵56 ，3=230 ，∴AED CEB ∽△△；（3）解：连接OA ，OB ，∵OA OE OB r ，5660 ，∴OAE △，OBE △是等边三角形，∴OA OB AE EB r ，∴四边形OAEB 是菱形；【点睛】本题考查垂径定理，菱形判定，等边三角形的判定和性质，相似三角形的判定等知识，解题的关键是熟练掌握垂径定理，从而得到相应角的等量关系．。

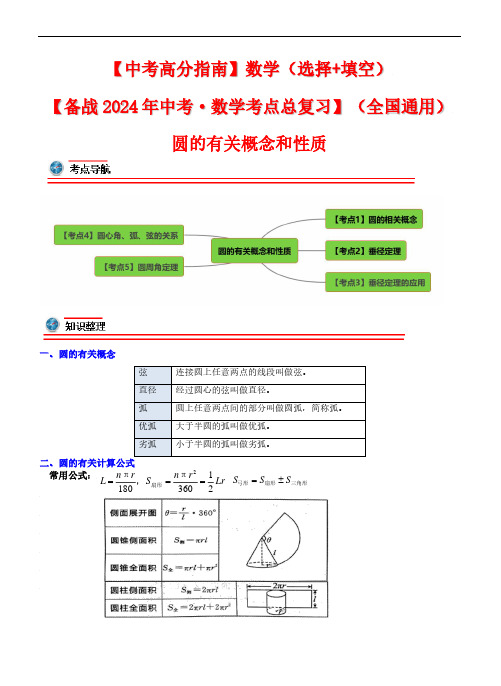
【中考高分指南】数学（选择+填空）【备战2024年中考·数学考点总复习】（全国通用）圆的有关概念和性质一、圆的有关概念弦 连接圆上任意两点的线段叫做弦。

直径经过圆心的弦叫做直径。

弧 圆上任意两点间的部分叫做圆弧，简称弧。

优弧 大于半圆的弧叫做优弧。

劣弧小于半圆的弧叫做劣弧。

常用公式：Lr r n S r n L 213601802===π，π扇形三角形扇形弓形S S S ±=三、垂径定理1．定理:垂直于弦的直径平分弦，并且平分弦所对的两条弧.2．推论1:①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.②弦的垂直平分线经过圆心，并且平分弦所对的两条弧.③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧.3．推论2:圆的两条平行弦所夹的弧相等.注意：轴对称性是圆的基本性质，垂径定理及其推论就是根据圆的轴对称性总结出来的，它们是证明线段相等、角相等、垂直关系、弧相等和一条弦是直径的重要依据.遇弦作弦心距是圆中常用的辅助线.二、弧、弦、圆心角、圆周角的关系定理1．弧、弦、圆心角的关系定理:在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等.推论:在同圆或等圆中，两个圆心角、两条弧、两条弦中如果有一组量相等，则它们所对应的其余各组量也分别相等.2．圆心角:顶点在圆心，角的两边和圆相交的角叫做圆心角.圆周角:顶点在圆上且角的两边和圆相交的角叫做圆周角.3．圆周角定理定理:一条弧所对的圆周角等于它所对的圆心角的一半.推论:①同弧或等弧所对的圆周角相等.②半圆(或直径)所对的圆周角是直径，90°的圆周角所对的弦是圆的直径.③圆内接四边形的对角互补.【考点1】圆的相关概念⏜上的点，连接AD并延长与OB的延长线交于点C，若CD=OA，【例1】（2023·江苏）如图，在扇形AOB中，D为AB∠O=75°，则∠A的度数为( )A. 35°B. 52.5°C. 70°D. 72°【答案】C【分析】本题考查了圆的认识：熟练掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了三角形内角和定理、等腰三角形的性质．连接OD ，如图，设∠C 的度数为n ，由于CD =OA =OD ，根据等腰三角形的性质得到∠C =∠DOC =n ，则利用三角形外角性质得到∠ADO =2n ，所以∠A =2n ，然后利用三角形内角和定理得到75°+n +2n =180°，然后解方程求出n ，从而得到∠A 的度数． 【解析】解：连接OD ，如图，设∠C 的度数为n ， ∵CD =OA =OD ， ∴∠C =∠DOC =n ，∴∠ADO =∠DOC +∠C =2n ， ∵OA =OD ， ∴∠A =∠ADO =2n ，∵∠AOC +∠C +∠A =180°，∠AOC =75°， ∴75°+n +2n =180°， 解得n =35°， ∴∠A =2n =70°． 故选：C ．【例2】（2024·全国模拟）如图，在△ABC 中，∠C =90°，AB =10.若以点C 为圆心，CA 长为半径的圆恰好经过AB 的中点D ，则⊙C 的半径为( ) A. 5√ 3 B. 8 C. 6 D. 5 【答案】D【解析】解：如图，连结CD ， ∵CD 是直角三角形斜边上的中线， ∴CD =12AB =12×10=5． 故选：D ．连结CD ，根据直角三角形斜边中线定理求解即可．本题考查了直角三角形斜边上的中线，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键． 【例3】（2024·江西模拟）一张直径为10cm 的半圆形卡纸，过直径的两端点剪掉一个三角形，以下四种裁剪图中，所标数据(单位：cm)长度不合理的是( )A.B.C.D.【答案】D【解析】解：A 、B 、C 图形中的三角形，满足三角形三边关系定理，且三角形三边长度合理，故A 、B 、C 不符合题意；D 、如图，过A 作AH ⊥BC 于H ，∵AB =AC ，∴BH =12BC =12×10=5(cm)， ∴AH =√ AB 2−BH 2=√ 39， ∴AH >5， ∴A 在圆外，∴三角形三边长度不合理， 故D 不符合题意． 故选：D ．由三角形三边关系定理，点和圆的位置关系即可判断．本题考查三角形三边关系，等腰三角形的性质，勾股定理，点和圆的位置关系，关键是由等腰三角形的性质，勾股定理求出AH 的长．1.（2024·湖北模拟）以下命题：(1)等弧所对的弦相等；(2)相等的圆心角所对的弧相等；(3)三点确定一个圆；(4)圆的对称轴是直径；(5)在同圆或等圆中，同一条弦所对的圆周角相等；(6)三角形三边的垂直平分线的交点到三角形三个顶点的距离相等.其中正确的命题的个数是( )A. 2个B. 3个C. 4个D. 5个【答案】A【分析】本题主要考查圆的相关概念和性质，深刻理解圆的相关性质是解题的关键．根据圆的相关概念和性质，对各个选项逐一分析判断即可得出答案．【解析】解：(1)等弧所对的弦相等；正确；(2)在同圆或等圆中，相等的圆心角所对的弧相等；故(2)错误；(3)不在同一直线上的三点确定一个圆；故(3)错误；(4)圆的对称轴是直径所在直线；故(4)错误；(5)在同圆或等圆中，同一条弦所对的弧有两条，每一条弧所对的圆心角不一定相等，则所对的圆周角也不一定相等；故(5)错误；(6)三角形三边的垂直平分线的交点即为其外接圆的圆心，外心到三角形三个顶点的距离相等.故(6)正确；综上所述，正确的有(1)(6)，故选A．2.（2024·江苏模拟）下列说法中，正确的是①对角线垂直且互相平分的四边形是菱形；②对角线相等的四边形是矩形；③同弧或等弧所对的圆周角相等；④半圆是弧，但弧不一定是半圆．( )A. ①④B. ②③C. ①③④D. ②③④【答案】A【解析】解：①、对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形为菱形，故该项正确；②、对角线相等的平行四边形为矩形，故该选项错误；③、在同圆或等圆中，同弧或等弧所对的圆周角相等，故该选项错误；④、弧分为优弧、劣弧、半圆弧，则半圆是弧，但弧不一定是半圆，故该项正确；故选：A．根据对角线互相垂直的平行四边形为菱形，对角线相等的平行四边形为矩形，在同圆或等圆中，同弧或等弧所对的圆周角相等，弧分为优弧、劣弧、半圆弧分别判断即可．本题考查基本概念，熟记知识点是解题关键．3.（2023·全国模拟）下列说法中，不正确的是( )A. 直径是最长的弦B. 同圆中，所有的半径都相等C. 圆既是轴对称图形又是中心对称图形D. 长度相等的弧是等弧【答案】D【分析】本题主要考查了圆的基本概念，解答此题的关键是正确理解弦，弧的定义，解答此题根据圆的基本概念判断即可．【解析】解：A.直径是最长的弦，正确；B.同一个圆的半径相等，正确；C.圆既是轴对称图形，也是中心对称图形，正确；D.长度相等的弧不一定是等弧，同圆或等圆中长度相等的弧才是等弧，故该选项的说法错误．故选D．4.（2024·广东模拟）如图所示，MN为⊙O的弦，∠N=52°，则∠MON的度数为( )A. 38°B. 52°C. 76°D. 104°【答案】C【分析】本题考查了圆的认识：掌握与圆有关的概念．根据半径相等得到OM=ON，则∠M=∠N=52°，然后根据三角形内角和定理计算∠MON的度数．【解析】解：∵OM=ON，∴∠M=∠N=52°，∴∠MON=180°−2×52°=76°．故选：C．【考点2】垂径定理【例1】（2023·四川）如图，在⊙O中，OA⊥BC，∠ADB=30°，BC=2√ 3，则OC=( )A. 1B. 2C. 2√ 3D. 4【答案】B【解析】解：连接OB，设OA交BC于E，如图：∵∠ADB=30°，∴∠AOB=60°，∵OA⊥BC，BC=2√ 3，BC=√ 3，∴BE=12，在Rt△BOE中，sin∠AOB=BEOB，∴sin60°=√ 3OB∴OB=2，∴OC=2；故选：B．连接OB，设OA交BC于E，由∠ADB=30°，得∠AOB=60°，根据OA⊥BC，BC=2√ 3，得BE=1BC=√ 3，2故sin60°=√ 3，从而OC=OB=2．OB本题考查垂径定理，圆周角定理及勾股定理的应用，解题的关键是掌握含30°角的直角三角形三边关系．【例2】（2024·湖南模拟）如图，AB是⊙O的直径，弦CD⊥OA于点E，连接OC，OD.若⊙O的半径为m，∠AOD=α，则下列结论一定成立的是A. OE=m·tanαB. CD=2m·sinαC. AE=m·cosαD. S△OCD=m2·sinα【答案】B【分析】本题考查了垂径定理，解直角三角形，解决本题的关键是掌握垂径定理，解直角三角形等知识.根据垂径定理和锐角三角函数计算则可进行判断．【解析】解：A．∵AB是⊙O的直径，弦CD⊥OA于点E，CD，∴DE=12在Rt△EDO中，OD=m，∠AOD=∠α，∴tanα=DEOE，∴OE=DEtanα=CD2tanα，故选项A错误不符合题意；B.∵AB是⊙O的直径，CD⊥OA，∴CD=2DE，∵⊙O的半径为m，∠AOD=∠α，∴DE=OD⋅sinα=m⋅sinα，∴CD=2DE=2m⋅sinα，故选项B正确符合题意；C.∵cosα=OEOD，∴OE=OD⋅cosα=m⋅cosα，∵AO=DO=m，∴AE=AO−OE=m−m⋅cosα，故选项C错误不符合题意；D.∵CD=2m⋅sinα，OE=m⋅cosα，∴S△COD=12CD×OE=12×2m⋅sinα×m⋅cosα=m2sinα⋅cosα，故选项D错误不符合题意；故选B．【例3】（2024·全国模拟）如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF的边心距OG为．( )A. 3√ 3B. 32C. 3√ 32D. 3【答案】C【解析】连接OC、OD，如图所示，∵正六边形ABCDEF是圆的内接多边形，∴∠COD=60°．∵OC=OD，OG⊥CD，∴∠COG =30°． ∵⊙O 的周长等于6π，∴OC =3，∴CG =32，∴OG =3√ 32． 故选C ．1．垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．2．根据垂径定理构造直角三角形，一般为过圆心作已知弦的弦心距，常用于求线段的长度.1.（2024·广东模拟）已知：如图，在⊙O 中，OA ⊥BC ，∠AOB =70°，则∠ADC 的度数为( )A. 30°B. 35°C. 45°D. 70°【答案】B【分析】本题考查的是垂径定理、圆周角定理、圆心角与弧的关系定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．先根据垂径定理得出AB ⏜=AC ⏜，再由圆周角定理即可得出结论． 【解析】解：如图，连接OC ．∵OA ⊥BC ， ∴AB⏜=AC ⏜， ∴∠AOC =∠AOB =70°，∴∠ADC =12∠AOC =35°． 故选B ．2.（2024·江苏模拟）如图，AB 是⊙O 的直径，弦CD ⊥AB 于E 点，若AD =CD =2√3.则BC ⌒的长为( ) A. π3B.2π3C. √3π3D.2√3π3【答案】B【解析】解：连接AC 、OC ， ∵AB 是⊙O 的直径，CD ⊥AB ， ∴CE =ED =12CD =√3，BC ⌒=BD ⌒，∴AB 是线段CD 的垂直平分线， ∴AC =AD ， ∵AD =CD ， ∴AC =AD =CD ， ∴△ACD 为等边三角形， ∴∠CAD =60∘， ∴∠COB =60∘，在Rt △COE 中，OC =CEsin∠COE =2， ∴BC ⌒的长=60π×2180=2π3， 故选：B.连接AC 、OC ，根据垂径定理得到CE =ED =12CD =√3，BC ⌒=BD ⌒，根据线段垂直平分线的性质得到AC =AD ，根据等边三角形的性质求出∠CAD =60∘，根据正弦的定义求出OC ，根据弧长公式计算，得到答案． 本题考查的是弧长的计算、垂径定理，掌握弧长公式：l =nπr180是解题的关键． 3.（2024·陕西模拟）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，且∠ACD =22.5°，CD =4，则⊙O 的半径长为( ) A. 2 B. 2√ 2 C. 4 D. 10【答案】B【解析】解：连接OD ，如图所示：∵AB 是⊙O 的直径，弦CD ⊥AB ，CD =4，∴CE =DE =12CD =2，∵∠ACD =22.5°，∴∠AOD =2∠ACD =45°，∴△DOE 为等腰直角三角形，∴OD =√ 2DE =2√ 2，即⊙O 的半径为2√ 2，故选：B ．连接OD ，由圆周角定理得出∠AOD =45°，根据垂径定理可得CE =DE =2，证出△DOE 为等腰直角三角形，利用特殊角的三角函数可得答案．此题主要考查了圆周角定理、垂径定理、以及三角函数的应用；关键是掌握圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．4.（2023·江苏）如图，矩形内接于⊙O ，分别以AB 、BC 、CD 、AD 为直径向外作半圆.若AB =4，BC =5，则阴影部分的面积是( )A. 414π−20B. 412π−20C. 20πD. 20【答案】D【解析】解：如图，连接BD ，则BD 过点O ，在Rt △ABD 中，AB =4，BC =5，∴BD 2=AB 2+AD 2=41，S 阴影部分=S 以AB 为直径的圆+S 以AD 为直径的圆+S 矩形ABCD −S 以BD 为直径的圆=π×(42)2+π×(52)2+4×5−π×(BD 2)2 =41π4+20−41π4=20，故选：D ．根据矩形的性质可求出BD ，再根据图形中各个部分面积之间的关系，即S 阴影部分=S 以AB 为直径的圆+S 以AD 为直径的圆+S 矩形ABCD −S 以BD 为直径的圆进行计算即可．本题考查勾股定理，矩形的性质以及圆形面积的计算，掌握矩形的性质、勾股定理以及圆形面积的计算方法是正确解答的前提．5.（2023·内蒙古）如图，⊙O 是锐角三角形ABC 的外接圆，OD ⊥AB ，OE ⊥BC ，OF ⊥AC.垂足分别为D ，E ，F ，连接DE ，EF ，FD.若DE +DF =6.5，△ABC 的周长为21，则EF 的长为( )A. 8B. 4C. 3.5D. 3【答案】B【解析】解：∵OD ⊥AB ，OE ⊥BC ，OF ⊥AC ，∴AD =BD ，AF =CF ，BE =CE ，∴DE ，DF ，EF 是△ABC 的中位线，∴DE =12AC,DF =12BC,EF =12AB ，∴DE +DF +EF =12(AB +BC +AC)=12×21=10.5，∵DE +DF =6.5，∴EF =10.5−6.5=4，故选：B ．根据垂径定理得到AD =BD ，AF =CF ，BE =CE ，根据三角形的中位线定理得到DE +DF +EF =12(AB +BC +AC)=12×21=10.5，于是得到结论．本题考查了三角形外接圆与外心，三角形中位线定理，垂径定理，熟练掌握三角形中位线定理是解题的关键．【考点3】垂径定理的应用【例1】（2023·湖北）如图，一条公路的转弯处是一段圆弧(AC⏜)，点O 是这段弧所在圆的圆心，B 为AC ⏜上一点，OB ⊥AC 于D.若AC =300√ 3m ，BD =150m ，则AC⏜的长为( )A. 300πmB. 200πmC. 150πmD. 100√ 3πm【答案】B【解析】解：如图所示：∵OB ⊥AC ，∴AD =12AC =150√ 3m ，∠AOC =2∠AOB ，在Rt △AOD 中，∵AD 2+OD 2=OA 2，OA =OB ，∴AD 2+(OA −BD)2=OA 2，∴(150√ 3)2+(OA −150)2=OA 2解得：OA =300m ，∴sin∠AOB =AD OA =√ 32， ∴∠AOB =60°，∴∠AOC =120°，∴AC ⏜的长=120×300π180=200πm ．故选：B ．先根据垂径定理求出AD 的长，由题意得OD =OA −BD ，在Rt △AOD 中利用勾股定理即可求出OA 的值，然后再利用三角函数计算出AC⏜所对的圆心角的度数，由弧长公式求出AC ⏜的长即可． 本题考查的是垂径定理，勾股定理及弧长的计算公式，根据垂径定理得出AD 的长，再由勾股定理求出半径是解答此题的关键，同时要熟记圆弧长度的计算公式．【例2】（2024·山东模拟）唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导.如图，某桨轮船的轮子被水面截得的弦AB 长8m ，轮子的吃水深度CD 为2m ，则该桨轮船的轮子直径为( )A. 10mB. 8mC. 6mD. 5m【答案】A【解析】解：设半径为r m ，则OA =OC =r m ，∴OD =(r −2)m ，∵AB =8m ，∴AD =4m ，在Rt △ODA 中，有：OA 2=OD 2+AD 2，即：r 2=(r −2)2+42，解得r =5m ，则该桨轮船的轮子直径为10m ．故选：A ．设半径为r ，再根据圆的性质及勾股定理，可求出答案．本题考查垂径定理，勾股定理，关键在于知道OC 垂直平分AB 这个隐藏的条件．垂径定理及其推论方法技巧：1.圆中模型“知2得3”由图可得以下5点：①AB ⊥CD ；②AE=EB ；③AD 过圆心O ；④⋂⋂=BC AC ；⑤⋂⋂=BD AD ；以上5个结论，知道其中任意2个，剩余的3个都可以作为结论使用。

2023年中考数学高频考点--圆的综合1．如图，AB 是O 的直径，弦CD AB ⊥于点E ，点P 在O 上，PBC C ∠=∠.（1）求证：CB PD ；（2）若82CD BE ==，，求O 的半径.2．如图，AB 是⊙O 的直径，F 为⊙O 上一点，AC 平分⊙FAB 交⊙O 于点C.过点C 作CD⊙AF 交AF的延长线于点D.（1）求证：CD 是⊙O 的切线. （2）若DC ＝3，AD ＝9，求⊙O 半径.3．如图，在Rt ABC 中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，O 为AB 上一点，经过点A ，D 的O 分别交AB ，AC 于点E ，F ．（1）求证：BC 是O 的切线；（2）若8AF =，=1CF ，求O 的半径．4．已知O 的直径为10，四边形ABDC 内接于O ，AD 平分CAB ∠．（1）如图1，若BC 为O 的直径，求BD 的长； （2）如图2，若120BDC ∠=︒，求BD 的长．5．如图，以ABC 的边AB 为直径作O ，交BC 于D 点，交AC 于E 点，BD DE =．（1）求证：ABC 是等腰三角形；（2）若E 是AC 的中点，O 的半径为2，连接BE ，求阴影部分的面积（结果保留π）．6．如图，在ΔABC 中，90C ∠=︒，BAC ∠的角平分线交BC 于点D ，点O 在AB 上，以点O 为圆心，OA 为半径的圆恰好经过点D ，分别交AC 、AB 于点E ，F ．（1）试判断直线BC 与⊙O 的位置关系，并说明理由； （2）若25BD =2BF =，求⊙O 的半径．7．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，连接BC ，AC ，点E 是BC 的中点，连结并延长OE 交圆于点D ．（1）求证：OD //AC ．（2）若DE ＝2，BE ＝38．如图，以ABC 的边AB 为直径作⊙O ，交边AC 于点D ，BC 为⊙O 的切线，弦DE AB ⊥于点F ，连接BE ．（1）求证：ABE C ∠=∠．（2）若点F 为OB 中点，且1OF =，求线段ED 的长．9．如图，AB 是O 的直径，BD 是弦，C 是BD 的中点，弦CE AB ⊥，H 是垂足，BD 交CE ，CA 于点F ，G ．（1）求证：CF BF GF ==；（2）若6CD =，8AC =，求圆O 的半径和BD 长．10．如图，AB 是O 直径，弦CD AB ⊥于点E ，过点C 作DB 的垂线，交AB 的延长线于点G ，垂足为点F ，连结AC ，其中A D ∠=∠．（1）求证：AC CG =；（2）若8CD EG ==，求O 的半径．11．如图，AB 为O 的直径，BC 是圆的切线，切点为B ，OC 平行于弦AD .（1）求证：DC 是O 的切线；（2）直线AB 与CD 交于点F ，且4DF =，2AF =，求O 的半径.12．如图，在Rt ABC 中，90ACB ∠=︒，以BC 为直径作O ，交AB 边于点D ，在CD 上取一点E ，使BE CD =，连接DE ，作射线CE 交AB 边于点F ．（1）求证：A ACF ∠=∠；（2）若8AC =，6BC =，求BF 的长．13．如图，A 、P 、B 、C 是O 上的四个点，60APC CPB ∠=∠=︒.（1）判断ABC 的形状，并证明你的结论；（2）探究PA 、PB 、PC 之间的数量关系，并证明你的结论.14．如图，点 A B ，在圆O 上，BAO ∠的平分线交圆O 于点D ，点C 在OA 的延长线上，且CBA D ∠=∠.（1）求证：CB 是圆O 的切线；（2）若//DB OA ，3BD =，求圆O 的半径．15．如图，AB 是半圆O 的直径，C 、D 是半圆O 上的两点，且//OD BC ，OD 与AC 交于点E .（1）若72B ∠=︒，求CAD ∠的度数； （2）若13AB =，12AC =，求DE 的长.16．如图，在平面直角坐标系中，O 为原点，A （3，0），B （-3，0），D 是y 轴上的一个动点，⊙ADC ＝90°（A 、D 、C 按顺时针方向排列），BC 与经过A 、B 、D 三点的OM 交于点E ，DE 平分⊙ADC ，连结AE ，BD 。

九年级数学圆知识点及习题(含答案)1.圆上各点到圆心的距离都等于半径。

2.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴；圆又是中心对称图形, 圆心是它的对称中心。

3.垂直于弦的直径平分这条弦 ,并且平分弦所对的弧；平分弦（不是直径）的直径垂直于弦,并且平分弦所对的弧。

4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量相等 ,那么它们所对应的其余各组量都分别相等。

5.同弧或等弧所对的圆周角相等 ,都等于它所对的圆心角的一半。

6.直径所对的圆周角是 90° ,90°所对的弦是直径。

7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫外心,是三角形三边垂直平分线的交点。

8.与三角形各边都相切的圆叫做三角形的内切圆 ,内切圆的圆心是三角形三条角平分线的交点的交点,叫做三角形的内心。

9.圆内接四边形：顶点都在圆上的四边形,叫圆内接四边形．10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角2、与圆有关的位置关系1.点与圆的位置关系共有三种：①点在圆外 ,②点在圆上 ,③点在圆内；对应的点到圆心的距离d和半径r之间的数量关系分别为：①d > r,②d = r,③d < r.2.直线与圆的位置关系共有三种：①相交 ,②相切 ,③相离；对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为：①d < r,②d = r,③d > r.3.圆与圆的位置关系共有五种：①内含 ,②相内切 ,③相交 ,④相外切 ,⑤外离；两圆的圆心距d和两圆的半径R、r（R≥r）之间的数量关系分别为：①d < R-r,②d = R-r,③ R-r < d < R+ r,④d = R+r,⑤d > R+r.4.圆的切线垂直于过切点的半径；经过直径的一端,并且垂直于这条直径的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长相等,这点与圆心之间的连线平分这两条切线的夹角。

中考圆的问题【考纲解读】在中考数学中，圆的试题不再是考查学生综合能力的压轴题，更多的是出现在选择、填空等客观性试题中，或者位置靠前的解答题中．【命题形式】“圆”的中考命题将立足于圆的基本性质、切线的判定及性质等知识的理解，圆的有关计算和常见推理方法的掌握，更加趋于基础性、开放性和大众化的特点．【满分技巧】一、四点共圆：模块一：辅助圆思想平面几何中有很多题目的背景中并没有出现圆，但是如果能够适当添加辅助圆，能让题目解起来变得十分简单，因此，辅助圆思想是学习四点共圆的基础．几何条件：OA OB OC ==．辅助圆：以O 为圆心、OA 为半径作圆O ⊙．∵OA OB OC ==，∴点B 、C 在O ⊙上．几何条件：OC OD =,2COD CAD ∠=∠．辅助圆：以O 为圆心、OC 为半径作圆O ⊙．∵OC OD =，2COD CAD ∠=∠，∴点A 、D 在O ⊙上．模块二：四点共圆的判定（一）判定定理①（常用）：如图，若D A ∠=∠，则A 、B 、C 、D 四点共圆.特别地，若︒=∠=∠90D A ，则BC 为直径.判定定理②（常用）：如图，若︒=∠+∠180D A ，则A 、B 、C 、D 四点共圆.特别地，若︒=∠=∠90D A ，则BC 为直径.判定定理③：（相交弦定理的逆定理）如图，若ED EB EC EA ⋅=⋅，则A 、B 、C 、D 四点共圆.判定定理④：（割线定理的逆定理）如图，若EC ED EB EA ⋅=⋅，则A 、B 、C 、D 四点共圆.一、单选题例1．如图，在矩形ABCD 中，AB ＝4，BC ＝3，将 BCD 沿射线BD 平移a 个单位长度（a >0）得到B C D ''' ，连接AB '，AD '，则当AB D '' 是直角三角形时，a 的值为（）A ．75B ．165C ．75或165D ．75或3【答案】C【解析】【分析】分两种情况：①当∠D ′AB ′=90°时，分别过点B ′、D ′作B ′M ⊥AB ，D ′N ⊥AB ，先证明△B ′MB ∽△DAB ，于是可设B ′M =3k ，MB =4k ，则BB ′=a =5k ，再判定四边形C ′D ′NM 为矩形，然后再利用Rt △D ′AN ∽Rt △AB ′M ，得到关于k 的方程，求解即可；②当∠D ′B ′A =90°时，根据勾股定理求出BD 的长，再证明△ABB ′∽△DBA 得到AB BB DB BA '=，即454BB '=，由此可求出BB ′的长，从而可得答案．【详解】：①当∠D ′AB ′=90°时，如图所示：分别过点B ′、D ′作B ′M ⊥AB ，D ′N ⊥AB ，∵AB =4，BC =3，且B M AD ' ，∴△B ′MB ∽△DAB ，∴'34B M DA MB AB ==，∴设B ′M =3k ，MB =4k ，则BB ′=a =5k ，∴AM =AB −BM =4−4k ，∵∠N =∠B ′MA =∠C ′=90°，∴四边形C ′D ′NM 为矩形，∴D ′N =C ′M =C ′B ′+B ′M =3+3k ，MN =C ′D ′=4，∴NA =NM −AM =4−(4−4k )=4k ，∵∠D ′AB ′=90°，∴∠B ′AM +∠D ′AN =∠D ′AN +∠AD ′N =90°，∴∠B ′AM =∠AD ′N ，∴Rt △D ′AN ∽Rt △AB ′M ，∴AN B M D N AM '='，∴43(0)3344k k k k k =≠+-，解得725k =∴755BB a k '===；②当∠D ′B ′A =90°时，如图所示：∵AB =4，AD =3，∴在Rt △ABD 中，5BD ===，∵AB ′⊥BD ，∴△ABB ′∽△DBA ，∴AB BB DB BA '=，∴454BB '=，∴165BB a '==，∵在平移过程中，∠AD ′B ′≠90°，∴综上所述，当△AB ′D ′为直角三角形时，a 的长为：75或155，故选：C ．【点睛】本题主要考查了相似三角形的判定与性质，矩形的性质，平移的性质，勾股定理，掌握分类讨论方法和构造合适的相似三角形是解题的关键．例2．己知两个等腰直角三角形的斜边放置在同一直线l 上，且点C 与点B 重合，如图①所示．△ABC 固定不动，将△A ′B ′C ′在直线l 上自左向右平移．直到点B ′移动到与点C 重合时停止．设△A ′B ′C ′移动的距离为x ，两个三角形重叠部分的面积为y ，y 与x 之间的函数关系如图②所示，则△ABC 的直角边长是（）A ．B ．4C ．D ．3【答案】C【解析】【分析】由当A B ''与AB 重合时，即x m =，此时B '走过的距离为m ，重叠部分面积达到最大值，为A B C '''V 的面积，结合题意即可求出m 的值．再根据，当A C ''与AC 重合时，此时4x m =+．此时B '走过的距离为m +4，由此可求出BB '的长，从而可求出BC 的长，进而即可求出结果．【详解】如图，当A B ''与AB 重合时，即点B '到达B 点，此时x m =．此时B '走过的距离为m ，即为B C ''的长．且此时重叠部分面积达到最大值，为A B C '''V 的面积，大小为1．∵A B C '''V 为等腰直角三角形∴112A B C S A B A C '''''''=⋅= ，∴A B A C ''''=∴2B C B m ''''===．如图，当A C ''与AC 重合时，即点C '到达C 点，此时4x m =+．此时重叠部分面积即将变小，且B '走过的距离为m +4．∴此时44BB m m '=+-=．∴4426BC BB B C m ''''=+=+=+=，即6BC =．∵ABC 为等腰直角三角形，∴6AB BC =⨯=故选C ．【点睛】本题考查图形的平移，等腰直角三角形的性质，勾股定理，函数的图象．解题的关键是通过函数图象得到A B C '''V 平移过程中重合部分的形状．二、填空题例3．如图，在平面直角坐标系xOy 中，已知菱形ABCD 的顶点A （0，C （2，0），顶点B 在x 轴上，顶点D 在反比例函数k y x=的图象上，向右平移菱形ABCD ，对应得到菱形''''A B C D ，当这个反比例函数图象经过''C D 的中点E 时，点E 的坐标是________．【答案】(8【解析】【分析】连接AC ，由题意易得出OA 和OC 的长，再根据tan OA ACO OC∠=及特殊角的三角函数值，可确定60ACO ∠=︒，即可证明ABC 和ACD △都是等边三角形，还可求出AC 的长，即得出4AD AC ==，从而得出D 点坐标为(4，．将D 点坐标代入反比例函数解析式，即可求出k 的值．设菱形ABCD 向右平移a 的单位后，反比例函数图象经过C D ''的中点E ．由此即可用a 表示出C '和D ¢的坐标，再由中点坐标公式即可表示出E 点坐标，将E 点坐标代入反比例函数解析式，即可求出a ，即得出E 点坐标．【详解】如图，连接AC ，∵A (2，、C （2，0），∴=OA 2OC =，∵tan 2OA ACO OC ∠==∴60ACO ∠=︒．∴4sin 60OA AC ==︒．∵四边形ABCD 是菱形，∴AB =BC ，ABC 和ACD △全等，∴ABC 和ACD △都是等边三角形，∴4AD AC ==，∴D 点坐标为(4，．∵D 点在反比例函数k y x=的图象上，∴4k =，解得：k =，∴反比例函数的解析式为y x=．设菱形ABCD 向右平移a 的单位后，反比例函数图象经过C D ''的中点E ，∴此时C '的坐标为C （2+a ，0），D ¢的坐标为(4+a ，，∴此时E 点的坐标为240()22a a ++++，，即E (3a +，3a=+，解得：5a =，∴E 点的坐标为(35+，即E (8．故答案为：(8．【点睛】本题考查菱形的性质，解直角三角形，等边三角形的判定和性质，反比例函数图象上点的坐标特征，平移的性质以及中点坐标公式，综合性强，较难．作出辅助线并利用数形结合的思想是解答本题的关键．例4．在综合实践课上，小明把边长为2cm 的正方形纸片沿着对角线AC 剪开，如图l 所示．然后固定纸片△ABC ，把纸片△ADC 沿AC 的方向平移得到△A ′D ′C ′，连A ′B ，D ′B ，D ′C ，在平移过程中：（1）四边形A ′BCD ′的形状始终是__；（2）A ′B +D ′B 的最小值为__．【答案】平行四边形【分析】（1）利用平移的性质证明即可．（2）如图2中，作直线DD ′，作点C 关于直线DD ′的对称点C ″，连接D ′C ″，BC ″，过点B 作BH ⊥CC ″于H ．求出BC ″，证明A ′B +BD ′=BD ′+CD ′=BD ′+D ′C ″≥BC ″，可得结论．【详解】解：（1）如图2中，∵A ′D ′=BC ，A ′D ′∥BC ，∴四边形A ′BCD ′是平行四边形，故答案为：平行四边形．（2）如图2中，作直线DD ′，作点C 关于直线DD ′的对称点C ″，连接D ′C ″，BC ″，过点B 作BH ⊥CC ″于H ．∵四边形ABCD 是正方形，∴AB =BC =2，∠ABC =90°，∴AC ∵BJ ⊥AC ，∴AJ =JC ，∴BJ =12AC ，∵∠BJC =∠JCH =∠H =90°，∴四边形BHCJ 是矩形，∵BJ =CJ ，∴四边形BHCJ 是正方形，∴BH =CH ，在Rt △BHC ″中，BH HC∴BC ''=∵四边形A ′BCD ′是平行四边形，∴A ′B +BD ′=BD ′+CD ′=BD ′+D ′C ″≥BC ″，∴A ′B +BD∴A ′B +D ′B 的最小值为故答案为：【点睛】本题考查作图-平移变换，轴对称最短问题，勾股定理等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．三、解答题例5．如图1，在平面直角坐标系中，大正方形OABC 的边长为m 厘米，小正方形ODEF 的边长为n 厘米，且40m -=．(1)求点B 、点D 的坐标．(2)起始状态如图1所示，将大正方形固定不动，小正方形以1厘米/秒的速度沿x 轴向右平移，如图2．设平移的时间为t 秒，在平移过程中两个正方形重叠部分的面积为S 平方厘米．①当t=1.5时，S=________平方厘米；②在24t ≤≤这段时间内，小正方形的一条对角线扫过的图形的面积为________平方厘米；③在小正方形平移过程中，若S=2，则小正方形平移的时间t 为________秒．(3)将大正方形固定不动，小正方形从图1中起始状态沿x 轴向右平移，在平移过程中，连接AD ，过D 点作DM ⊥AD 交直线BC 于M ，∠DAx 的角平分线所在直线和∠CMD 的角平分线所在直线交于N （不考虑N 点与A 点重合的情形），求∠ANM 的大小并说明理由．【答案】(1)(4,4)B ，(0,2)D ；(2)①3；②4；③1秒或5秒；(3)135︒或45︒，理由见解析．【解析】【分析】（1）由非负数的性质以及算术平方根的性质可得出m ，n 的值，则答案可求出；（2）①1.5秒时，小正方形向右移动1.5cm ，即可计算出重叠部分的面积；②画出图形，计算所得图形面积即可；③小正方形的高不变，根据就即可求出小正方形平移的距离和时间；（3）分当点N 在射线MG 的反向延长线上或当点N 在射线MG 上时，过D 作DQ x ∥轴，过N 作NP x ∥轴，设CMG DMG y ∠=∠=，则PNM NMB y ∠=∠=，2MDQ CMD y ∠=∠=，则902ADQ OAD y ∠=∠=︒-，180180(902)902DAx AOD y y ∠=︒-∠=︒-︒-=︒+，得出1452NAx DAx y PNA ∠=∠=︒+=∠，从而得出4545ANM PNA PNM y y ∠=∠-∠=︒+-=︒．(1)解：∵40m -=．2n ∴=，4m =，(4,4)B ∴，(0,2)D ，(2)解：①当t=1.5时，小正方形向右移动1.5cm ，S =2×1.5=3cm 2；②如图1所示，小正方形的一条对角线扫过的面积为红色平行四边形，面积为2×2=4cm 2；③如图2，小正方形平移距离为4+1=5cm ，∴小正方形平移的距离为1cm 或5cm ，∴t=1或5．综上所述，小正方形平移的时间为1或5秒，(3)解：如图3，当点N 在射线MG 的反向延长线上时，过D 作DQ ∥x 轴，过N 作NP ∥x 轴，∵MN平分∠CMD，∴设∠CMG=∠DMG=y，则∠PNM=∠NMB=y，∠MDQ=∠CMD=2y，∵DM⊥AD，∴∠ADQ=∠OAD=90°−2y，∴∠DAx=180°−∠OAD=180°−（90°−2y）=90°+2y，∵AN平分∠DAx，∴∠NAx=12∠DAx=45°+y=∠PNA，∴∠ANM=∠PNA−∠PNM=45°+y−y=45°，当点N在射线MG上时，同理∠ANG=45°，∴∠ANM=135°，综上：∠ANM=135°或45°．【点睛】本题考查了非负数的性质，坐标与图形的性质，平移的性质，平行线的性质，角平分线的定义等知识，熟练掌握平行线的性质及平移的性质是解题的关键．例6．如图①，在平面直角坐标系中，△OAB的顶点A，B的坐标分别为（﹣2，4），（﹣5，0）．将△OAB沿OA翻折，点B的对应点C恰好落在反比例函数ykx（k≠0）的图象上．(1)求反比例函数的表达式；(2)如图②，将△OAB沿y轴向下平移得到△O'A'B'，设平移的距离为m（0＜m＜4），平移过程中ΔO'A'B'与△OAB重叠部分的面积为S．若点B的对应点B'恰好落在反比例函数ykx=（k≠0）的图象上，求m的值及此时S的值；(3)如图③，连接BC交AO于点D，已知P是反比例函数ykx=（k≠0）的图象上一点，在x轴上是否存在点Q，使得以O，D，P，Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点P，Q的坐标；若不存在，请说明理由．【答案】(1)y12 x =(2)m125=，S＝85；(3)当点P（6，2），点Q为（7，0）或（﹣7，0）时，以点O，D，P，Q为顶点的四边形是平行四边形，当点P（﹣6，﹣2），点Q（﹣7，0）时，以点O，D，P，Q为顶点的四边形是平行四边形．【解析】【分析】（1）根据菱形的性质求得点C的坐标，进而求得反比例函数解析式；（2）根据平移求得点B'的横坐标为﹣5，即可求得m的值，连接AA'，并延长AA'交BO于点E，求得A E'的值，进而求得S△A'B'O'＝10，证明△ANP∽△A'B'O'，根据相似三角形的性质可得S的值，（3）根据菱形的性质求得点D的坐标，进而分点P（6，2）或（﹣6，﹣2），结合图形求解即可．(1)解：∵四边形ABOC是菱形，∴AC∥BO，且A点坐标（﹣2，4），AC＝AB＝5，∴点C（3，4）．∵点C恰好落在反比例函数ykx=（k≠0）的图象上，∴k ＝3×4＝12，∴反比例函数表达式为y 12x =；(2)∵将△OAB 沿y 轴向下平移得到△O ′A ′B ′，∴点B '的横坐标为﹣5，∴y 125=-，∴m 125=，连接AA '，并延长AA '交BO 于点E，∴AE ＝4，AA '125=，∴A 'E 85=，∵S △ABO 12=⨯5×4＝10，且将△OAB 沿y 轴向下平移得到△O ′A ′B ′，∴S △A 'B 'O '＝10，∵BO ∥B 'O '，∴△ANP ∽△A 'B 'O '，∴'''ANP A B O S S = （854）2，∴S ＝1048255⨯=；(3)∵四边形ABOC 是菱形，∴AD ＝OD ，∵A（﹣2，4），点O（0，0），∴点D（﹣1，2），若OD为边，则点P在纵坐标为2或﹣2，∴y122==6或y122==--6，∴点P（6，2）或（﹣6，﹣2），如图3，当P（6，2）时，∵四边形ODPQ是平行四边形，∴DP＝OQ＝7，∴点Q（7，0），如图4，当P（﹣6，﹣2）时，∵四边形ODQP是平行四边形，∴OQ与PD互相平分，∴点H（72-，0）∴点Q（﹣7，0），若DO为对角线，∵四边形QOPD 是平行四边形，∴PQ 与OD 互相平分，∵OD 中点坐标（12-，1），∴点P 纵坐标为2，∴点P 坐标为（6，2）．∴点Q 坐标为（﹣7，0）．综上所述：当点P （6，2），点Q 为（7，0）或（﹣7，0）时，以点O ，D ，P ，Q 为顶点的四边形是平行四边形，当点P （﹣6，﹣2），点Q （﹣7，0）时，以点O ，D ，P ，Q 为顶点的四边形是平行四边形．【点睛】本题考查了平移的性质，相似三角形的性质与判定，反比例函数与几何图形几何，平行四边形的性质与判定，掌握以上知识是解题的关键．二、证明切线的7种方法：证明一条直线是圆的切线的方法及辅助线的作法1、连半径、证垂直：当直线和圆有一个公共点时，把圆心和这个公共点连接起来，然后证明直线垂直于这条半径,简称“连半径，证垂直”2、作垂直,证半径：当直线和圆的公共点没有明确时，可以过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直，证半径”类型一、有公共点：连半径，证垂直方法1、勾股定理逆定理法证垂直方法2、特殊角计算法证垂直方法3、等角代换法证垂直方法4、平行线性质法证垂直方法5全等三角形法证垂直类型二、无公共点:做垂直，证半径方法6角平分线的性质法证半径方法7全等三角形法证半径例1．如图，直线AB 经过⊙O 上的点C ，并且OA=OB ，CA=CB ，直线OB 交⊙O 于点E 、D ，连接EC 、CD ．（1）试判断直线AB 与⊙O 的位置关系，并加以证明；（2）求证：2BC BD BE =⋅；（3）若1tan 2E =，⊙O 的半径为3，求OA 的长．【答案】（1）相切，见解析；（2）见解析；（3）5．【解析】【分析】（1）连接OC，由等腰三角形“三线合一”性质证明OC⊥AB，据此解题；（2）连接OC，90°圆周角所对的弦是直径，证明DE为⊙O的直径，再证明△BCD∽△BEC，最后根据相似三角形的对应边成比例解题；（3）根据正切定义得到12CDEC ，解得OC=OE=3，再由△BCD∽△BEC，设BC=x，根据相似三角形对应边成比例，及勾股定理得到9+x2=（2x-3）2，解此一元二次方程，验根即可解题．【详解】解：（1）AB与⊙O相切，连接OC，∵OA=OB，CA=CB，∴OC⊥AB，∵点C在⊙O上，∴AB与⊙O相切；（2）连接OC，∵OC⊥AB，∴∠OCB=90°即∠1+∠3=90°，又∵DE为⊙O的直径，∴∠ECD=90°即∠2+∠3=90°，∴∠1=∠2，∵OE=OC，∴∠E=∠2，∴∠1=∠E，∵∠B =∠B ，∴△BCD ∽△BEC ，∴BC BD BE BC=，∴BC 2=BD •BE ；（3）∵1tan 2E ∠=，∠ECD =90°，∴12CD EC =，∵⊙O 的半径为3，∴OC =OE =3，∵△BCD ∽△BEC ，∴BC CD BE EC =，设BC =x ，∴132x OB =+，∴OB =2x -3，∵∠OCB =90°，∴OC 2+BC 2=OB 2，∴9+x 2=（2x -3）2，∴x 1=0（舍去），x 2=4，∴OA =OB =5．【点睛】本题考查直线与圆的位置关系，相似三角形的判定与性质等知识，切线的证明方法有两种：1、有点连接此点与圆心，证明夹角为直角；2、无点作垂线，证明垂线段等于圆的半径，利用方程思想解题是关键．例2．如图，在Rt ABC 中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，O 为AB 上一点，经过点A ，D 的⊙O 分别交AB ，AC 于点E ，F 连接OF 交AD 于点G ．（1）求证：BC 是⊙O 的切线；（2）求证：2AD AB AF=⋅（3）若12BE =，5tan 12B =，求AD 的长．【答案】（1）见解析；（2）见解析；（3）4513【解析】【分析】（1）如图所示，连接OD ，则OA OD =，根据等边对等角可知ODA OAD ∠=∠，由AD 是BAC ∠的平分线，可得OAD CAD ∠=∠，等量代换得ODA CAD ∠=∠，从而可得//OD AC ，进而得90ODB C ∠=∠=︒即可得证；（2）连接OD ，DF ，EF ，由（1）及已知条件证明ABD ADF ∽△△，根据相似三角形的性质即可得证；（3）连接OD ，设O 的半径为R ，由（1）知，OD BC ^，根据已知条件12BE =，5tan 12B =，求得半径R ,连接EF ，由（2）知，AEF B ∠=∠，根据sin sin AEF B ∠=∠，7513AF =，进而根据（2）的结论求得AD ．【详解】解：（1）如图所示，连接OD ，则OA OD =，∴ODA OAD ∠=∠，∵AD 是BAC ∠的平分线，∴OAD CAD ∠=∠，∴ODA CAD ∠=∠，∴//OD AC ，∴90ODB C ∠=∠=︒，∵点D 在O 上，∴BC 是O 的切线；（2）如图所示，连接OD ，DF ，EF ，∵AE 是O 的直径，∴90AFE C ∠=︒=∠，∴//EF BC ，∴B AEF ∠=∠，∵AEF ADF ∠=∠，∴B ADF ∠=∠，由（1）知，BAD DAF ∠=∠，∴ABD ADF ∽△△，∴AB AD AD AF=，∴2AD AB AF =⋅；（3）如图所示，连接OD ，由（1）知，OD BC ^，∴90BOD ∠=︒，设O 的半径为R ，则OA OD OE R ===，∵12BE =，∴12OB BE OE R =+=+，在Rt BDO △中，∵5tan 12B =，设5,12AC k BC k ==则13AB k=∴5sin 13B =，∴5sin 1213OD R B OB R ===+，∴152R =，∴215AE OE ==，227AB BE OE =+=，连接EF ，由（2）知，AEF B ∠=∠，90∠=∠=︒AFE C ，∴5sin sin 13AEF B ∠==，在Rt AFE 中，5sin 1513AF AF AEF AE ∠===，∴7513AF =由（2）知，2752025 271313AD AB AF=⋅=⨯=，∴4513 AD=.【点睛】本题考查了圆的切线的判定，三角形相似的判定与性质，勾股定理，锐角三角函数实际应用，添加辅助线，综合运用以上知识是解题的关键．例3．已知：如图1，AB是⊙O的直径，DB是⊙O的切线，C是⊙O上的点，连接OD，AC∥OD．（1）求证：DC是⊙O的切线；（2）求证：AB2＝2AC•OD；（3）如图2，AB，tan∠ABC＝13，连接AD交⊙O于点E，连接BC交OD于点F，求EF的长．【答案】（1）见解析；（2）见解析；（3）26【解析】【分析】（1）先判断出∠COD＝∠BOD，再判断出∠OBD＝90°，进而得出△COD≌△BOD（SAS），即可得出结论；（2）先判断出△ABC∽△ODB，得出AC•OD＝AB•OB，即可得出结论；（3）先判断出BD2＝DE•DA，再判断出△BDF∽△OBF∽△ODB，得出BF2＝OF•DF，BD2＝DF•DO，进而求出AC＝1，BC＝3，进而判断出DF•DO＝DE•DA，即可判断出△DEF∽△DOA，即可得出结论．【详解】（1）证明：如图1，连接OC，∵OA＝OC，∴∠A＝∠OCA，∵AC∥OD，∴∠A＝∠BOD，∠ACO＝∠COD，∴∠COD＝∠BOD，∵DB是⊙O的切线，AB是⊙O的直径，∴∠OBD＝90°，∴△COD≌△BOD（SAS），∴∠OCD＝∠OBD＝90°，∴DC是⊙O的切线；（2）连接BC，如图1，∵AB是⊙O的直径，∴∠ACB＝90°，∵∠A＝∠BOD，∠ACB＝∠OBD，∴△ABC∽△ODB，∴AB AC OD OB，∴AC•OD＝AB•OB，∴AC•OD＝AB•12 AB，∴AB2＝2AC•DO；（3）如图2，连接BE，∵AB是⊙O的直径，∴∠AEB＝∠ACB＝90°，∵∠ABD＝90°，∴△BDE∽△ADB，∴BD DE DA BD=，∴BD 2＝DE •DA ，∵AC ∥OD ，∴OD ⊥BC ，∴△BDF ∽△OBF ∽△ODB ，∴BF 2＝OF •DF ，BD 2＝DF •DO ，∵AB ，tan ∠ABC ＝AC BC ＝13，∴BC ＝3AC ，∴BC 2+AC 2＝AB 2，∴9AC 2+AC 2＝10，∴AC ＝1，∴BC ＝3，∴OB ＝12AB ＝2，BF ＝12BC ＝32，OF ＝12AC ＝12，∴DB ＝2，DA ＝2，OD ＝5，DF ＝92，∴DF •DO ＝DE •DA ，∴DF DA DE DO=，∵∠EDF ＝∠ODA ，∴△DEF ∽△DOA ，∴DF EF DA OA=，∴EF ＝DF OA DA ⋅=【点睛】此题是圆的综合题，主要考查了切线的判定和性质，相似三角形的判定和性质，锐角三角函数，作出辅助线，构造出相似三角形是解本题的关键．例4．如图，以线段AB 为直径的O 交ABC 边BC 于点D ，连接AD ，作ADB ∠平分线DE 交AB 于点F ，交O 于点E ，连接AE ，作AG DE ⊥于点G ，连接OG ，CAD E ∠=∠．（1）求证：AC 为O 切线；（2）求证：OG AD ⊥；（3）若tan 2C =，OFG △的面积为S ，求DAE △的面积（用S 的代数式表示）．【答案】（1）见解析；（2）见解析；（3）18S ．【解析】【分析】（1）根据根据同弧所对的圆周角相等得到∠E =∠B ，再根据直径所对的圆周角的直角、利用等角的余角相等推出∠CAB =90°，即可得到结论（2）连接OD ，根据角平分线的性质，利用等角对等边得GD =GA ，结合全等得到∠AOG =∠DOG ，推出OG 是∠AOD 的平分线，根据等腰三角形三线合一的性质即可得到结论；（3）由题意根据相等的角的正切值相等推出边之间的关系，不妨设AD =2a ，由直角三角形中的勾股定理推出线段OG =a ，DE =，再根据圆周角定理和角之间的互余关系得到△FGO ∽△ADE ，最后根据相似三角形的性质求解即可．【详解】（1）证明：由题意可知在⊙O 中，∠E =∠B ，∵∠CAD =∠E ，∴∠CAD =∠B ，∵∠B +∠DAB =90°，∴∠CAD +∠DAB =90°，即∠CAB =90°，∴CA ⊥AB ，∴AC 为⊙O 切线．（2）如图，连接OD ，∵∠ADB =90°，DE 平分∠ADB ，∴∠ADF =∠BDF =45°，又∵AG ⊥DE ，∴△AGD 是等腰直角三角形，在△OGA 和△OGD 中，AG DG OG OG OA OD =⎧⎪=⎨⎪=⎩，∴△OGA ∽△OGD （SSS ），∴∠AOG =∠DOG ，∴OG 是∠AOD 的平分线，∴OG ⊥AD ．（3）如图，连接OD，由（2）可知OG ⊥AD ，令其垂足为M ，∵∠BAD =∠C ，∴tanC =tan ∠BAD =2，不妨设AD =2a ，则BD =4a ，AB=，∴OA =OB =OD，∵△AGD是等腰直角三角形，且OM⊥AD，∴AM=DM=MG=12AD=a，∴AG=DG=2AD，∴MO2a =，∴OG=MO-MG=a，由（1）可知在Rt△AGE和Rt△CAD中，∠E=∠CAD，∴∠GAE=∠C，∴tan∠GAE=tanC=2，∴EG=2AG=，∴DE=DG+EG=，由（2）可知OM⊥AD，BD⊥AD，∴OM∥BD，∴∠FOG=∠B，∠OGF=∠BDF又由（1）可知∠E=∠B，∠ADF=∠BDF=45°∴∠FOG=∠E，∠OGF=∠EAD，∴△FGO∽△ADE，∵OGDE=∴221(()618FGOADES OGS DE∆∆===，∵S△OFG=S，∴S△DAE=18S．【点睛】本题考查切线的判定与性质、等腰直角三角形的判定与性质、相似三角形的判定与性质、垂径定理、圆周角定理及解直角三角形，需要善于观察结合图形找到相等的角，根据角的关系推导出边的关系、三角形的形状及相似三角形等，进而求解．例5．如图，AB是⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B 作//BD OP，交⊙O于点D，连接PD．（1）求证：PD 是⊙O 的切线（2）当四边形POBD 是平行四边形时，求APO ∠的度数．【答案】（1）见解析；（2）45︒【解析】【分析】（1）连接OD ，证明PAO PDO △≌△即可；（2）证明四边形PAOD 是正方形，即可求解．【详解】（1）如图，连接OD ，则OD OA OB== AC 是⊙O 的切线90A ∴∠=︒//BD OP13,2B ∴∠=∠∠=∠又OD OB= 1B ∴∠=∠23∴∠=∠在PAO 和PDO △中23PO PO OA OD =⎧⎪∠=∠⎨⎪=⎩()PAO PDO SAS ∴△≌△=90PDO A ∴∠=∠︒∴PD 是⊙O 的切线．（2）如图，连接OD 四边形POBD是平行四边形PD OBPD OB∴=,//OB OA=∴=PD OA∴四边形PAOD是平行四边形又OD OAQ=∴四边形PAOD是菱形∠=︒90A∴四边形PAOD是正方形∴∠︒．APO=45【点睛】本题考查了圆的切线的性质，三角形全等的证明，平行四边形的性质与判定，正方形的性质与判定，圆的切线的性质，熟练掌握以上知识点是解题的关键．例6．如图，在ABC 中，AB AC =，以AB 为直径的O 与BC 相交于点,D DE AC ⊥，垂足为E ．（1）求证：DE 是O 的切线；（2）若弦MN 垂直于AB ，垂足为1,,4AG G MN AB ==O 的半径；（3）在（2）的条件下，当36BAC ∠=︒时，求线段CE 的长．【答案】（1）见解析；（2）O 的半径为1；（3）34CE =．【解析】【分析】（1）连接OD ，由题意可得∠B =∠C ，由半径OB 和OD 可得∠B =∠ODB ，从而∠C =∠ODB ，在Rt △DEC 中可知∠C +∠CDE =90°，则∠OBD +∠CDE =90°，从而得出∠ODE =90°，即可得证DE 是O 的切线；（2）连接OD ，过点D 作DG ⊥AB ，垂足为G ，设AC 与O 交于点H ，连接OH ，分别求解S △OAH ，S 扇形OAH ，S △OBD ，S 扇形O OD ，然后根据S 阴影=S 扇形OAH +S 扇形OBD –S △OAH –S △OBD 求解即可得到阴影部分的面积．【详解】（1）证明：方法一：连接,AD ODAB Q 为直径90ADB ∴∠=︒AD BC∴⊥AB AC = ，D ∴为BC 中点O 为AB 中点OD AC∴∥DE AC⊥ DE OD∴⊥OD是O的半径的切线∴是ODE方法二：连接ODOB OD=∴∠=∠OBD ODB⊥DE AC∴∠+∠=︒EDC C90AB AC=∴∠=∠ABC C∴∠=∠ODB C∴∠+∠=︒EDC ODB90 ODE∴∠=︒．90∴⊥OD DE的半径OD是O的切线∴是ODE方法三：连接ODOB OD=∴∠=∠OBD ODB=AB AC∴∠=∠ABC ACB∴∠=∠ODB ACB∴∥OD ACDE AC⊥ DE OD∴⊥OD 是O 的半径DE ∴是O 的切线（2）解：方法一：连接OM ，MN AB⊥ 90OGM ∴∠=︒AB Q 是直径MN =MG NG =∴=14AG AB =13AG GB ∴=12AG OG OM ∴==在Rt MGO 中222222()2OM OG MG OM OM ∴+=+=1OM ∴=即O 的半径为1方法二：连接AM MB、AB Q 是O 的直径90AMB ∴∠=︒MN AB⊥ 90AMG MAG AMG BMG ∴∠+∠=∠+∠=︒MAG BMG∴∠=∠AMG MBG∴ ∽MG AG BG MG=∴2MG AG BG=∴⨯:1:4AG AB = :1:3AG BG ∴=12AO BO AB == G ∴为OA 中点MN AB MN ⊥=2MG ∴=2MG AG BG=⨯ 12AG ∴=1AO ∴=即O 的半径为1（3）作ABC ∠的平分线BF 交AC 于F 连接AD36BAC AB AC∠=︒= 72ABC ACB ∴∠=∠=︒BF 平分ABC∠36ABF CBP ∴∠=∠=︒72BFC ∴∠=︒即,BAF ABF BFC ACB∠=∠∠=∠BC BF AF∴==CBF BAC C C∠=∠∠=∠CBF CAB∴ ∽2BC CF AC∴=⋅设BC x =则AF x=2CF x∴=-()222x x ∴=-解得：51x =±-51BC ∴=-AB ∴是O 的直径90ADB ∴∠=︒AB AC= 12CD BD BC ∴==512CD -∴=DE AC AD BC⊥⊥ 90ADC DEC C C∴∠=∠=︒∠=∠CDE CAD∴∽△△2CD CE AC∴=⋅2251(35224CD CE AC -∴===【点睛】本题主要考查了圆的切线的判定，以及与扇形面积相关的不规则阴影部分面积求解问题，灵活添加辅助线将不规则图形转换为规则图形的面积表示是解题关键．。

第十二讲关于圆的基本知识趣题引路】20世纪40年代美国数学家冯•诺伊曼等人编写了一本研究取胜对策的书.在这本书中有一个有趣的问题: 一只鼠在圆形的湖边碰上了猫，鼠连忙纵身跳到水里，猫不会游水，于是紧紧地盯住鼠，在湖边跟着鼠跑动，打算在鼠爬上岸时抓住它•已知猫奔跑的速度是鼠游水速度的2. 5倍.聪明的读者，你知道鼠怎样才能逃脱猫的追捕？解析如图12-1,鼠在点A碰上了猫，若鼠跳到湖里后径宜游到对岸点C；则猫从A到C要跑半个圆周，由于半圆长是直径的-^1.58（倍）＜2.5（倍），因此猫还是能抓住鼠，所以，鼠若要逃脱猫的追捕，就必须（原文是经字，好像不通）利用猫环湖跑动这一特点，跳下水以后先游到圆心O,看准猫当时所在的位垃如立刻转身朝着B对岸的点£＞游去，这时鼠要游的距离是半径OD,猫要跑的距离是半圆BCD,也就是OD的兀倍，兀〜3. 14＞2.5,所以当猫到点D时，鼠已经逃之夭夭了.图12-1知识延伸】圆是初中数学中重要的内容，圆的基本性质虽然比较简单但具有较强的适用性•确定圆的条件就是通过三个点找到圆心和半径，然后画图.弧、弦和直径的关系（垂径左理）是研究有关圆的知识的基础，垂径左理指的是：垂直于弦的直径平分这条弦，并且平分弦所对的弧，立理的题设和结论共涉及5条：（1）过圆心；（2）垂直弦：（3）平分弦：（4）平分劣弧：（5）平分优弧.在这5条中只要2条成立，那么剩下3条也是成立的.这样理解和记忆垂径左理即揭示了定理中的条件和结论的内在联系.圆既是轴对称图形，又是中心对称图形，它具有旋转对称性，这是圆的最基本最重要的性质，是证明其他定理的工具.例两人轮流在一个圆桌上放同样大小的硬币.每人每次只能放一枚，且任何两枚硬币不能有重叠部分，谁先放完最后一枚使得对方再也找不到空地可以放下一枚硬币时，谁就获胜•问谁一左能获胜？他要想获胜，必须采取怎样的策略？解析先放的那个人一左能获胜，他首先在圆心放一枚硬币，然后不论对方怎样放一枚硬币，他都在对方放硬币的位宜关于圆心对称的位巻上再放一枚硬币，由于圆是关于圆心对称的图形，故只要对方有放硬币的地方，他就有放硬币的地方，可见最后胜利一左属于先放硬币的人.（下页提上来的，保持语段的完整性）点评几何中，（X，刃一（一X，—刃是以原点为对称中心的映射，这种映射叫做对称变换•圆是中心对称图形，先耙硬币放在圆桌的正中央，以后不管对方放在哪里，他下一步都把硬币放在对方硬币关于中心对称的地方，先放硬币的肯左获胜.例2 如图12-2, AABC中，周长AB+BC+AC=2・求证：ZEC —定能被一个直径为1的圆盖住.证明设A、D两点将zMBC周长分成相等的两部分，即AB+BD=AC+CD=\.似钢笔改动的录入）以AD的中点0为圆心，丄为半径画圆，它一立能盖住△ABC.这是因为在三角形中.一边上的中线小于2另两边和的一半，即OB<1（AB+BD）=1, OC<1（AC+CD）=1 ,2 2 2 2・・・B、C两点均在圆O内.而A2XAB+BD=1・：.OA<L，点 A 在<90 内，2即OO盖住了/XABC.点评这一问题典型地反映了覆盖问题的证明思路，第一部分是设计，第二部分是运用了一个熟知的结论证明（即三角形一边上的中线小于另两边和的一半）.从表面上看，是先设汁后证明，苴实，只有证明在胸, 才能得出设计.例3在美国的亚利桑那州，有一个巨大的右坑，它的直径1280m,深180m,据说它是在数千年以前, 一个巨大的陨石落到地上砸出来的•请你估算一下，这个巨大的陨石直径有多大？因此，(OC-DC)2+DB2=OB2.即（片180）2+（竺）2=妙2X2-360X+18024-6402=JI2,解得x= 1228m.这个巨大的陨石直径为2456m.点评有关弦、弦心距、半径、弓高的计算或涉及到弦、弦的中点的问题，通常是构造直角三角形或运用垂径立理.好题妙解】佳题新题品味例1已知如图12-4, AB为00的弦，OC丄于C,问O C+AC何时取最大值?S12-4解析连04、0B,过A作AD丄OB于D,设0A = OB=R, ZAOB=a,则AD=0A• sin a=R• sin a.S DAOB=—AD • OB2= -R• Rsin a= 1 /?2sin a,2 2（OC+ACgOG+AU+LAO OC=OA2^2S AAOH=/?2+/?2sin a.当“=90°时，sin 有最大值1,即（OC+AC）有最大值2疋，因而，当ZAOB=90° , OC+AC取得最大值R.点评一般地，最大、最小值常在某个特殊点取得，经试验后猜测，点A运动到和圆心的连线垂直于OB 时，OC+AC取得最大值.例2 一条60m宽的河上架有一座半径为55m的圆弧形拱桥，请问一顶部宽12m且高出水而8m的船能否通过此桥，请说明理由.E@12-5解析假左该船恰能通过桥时，桥的半径为/?，如图12-5, 表示水而宽，EF为船宽，MP为船顶到水面AB的距离，设O P=x(O为圆心)，依题意得，在RtZkOBP中，R2=302+F,①在RtAOEM中，用=(8+X)2+62,②①、②求得 /?= 10^34 >55,即船恰能通过时，桥的半径为10炉m,但现在桥的半径为55m,所以该船不能通过此桥.点评可先假定该船恰能通过桥，则12m宽的船顶为圆弧形拱桥的一弦，作出垂径和一条过该弦端点的半径，运用垂径左理及勾股立理求出这条半径/?，就能解决此问题.中考真题欣赏例1 (重庆市中考题)如图12-6, AM是00的直径，过00上一点B作BN丄AM,垂足为N,其延长线交OO于点C,弦CD交AM于点E(1)如果CD丄/W,求证：EN=NW(2)如果弦CD交AB于点F,且CD=AB,求证：C&=EF・ED；(3)如果弦CD、AB的延长线(根据网上2002年重庆中考数学试题添加，后而的解答也是这个意思)交于点F,且CD=AB.那么(2)的结论是否仍成立？若成立，请证明：若不成立，请说明理由.图12』证明(1)连结BW 9：AM是直径，•••ZABM=90°・•: CD丄AB, :.BM〃CD A ZECN=ZMBN.9：AM丄BC,:・CN=BN.ARtACE/V^RtABM/V,:・EN=NM・(2)连结BD, BE、AC.•••点E是BC垂直平分线AM上一点,:.BE=EC.I CD=AB9 :. CD =AB , :. AD =BC , ••• ZACD=ZBDC.9：AB=AC, AE=AE. :.AABE^AACE,:・ZABE=ZACD=ZBDC, ZBED是公共角，•••△BEDs△FEB,—EF BE:.BE2=EF • ED. :.CE2=EF • ED.(3)结论成立证明如图12-7仿⑵可证ZBEQ'ACE、:・BE=CE, ZABE= ZACE.•••AB=CD, :. ZACB=ZDBC:.BD//AC. ZBDE+ZACE=180°=ZFBE+ZABE,:・ZBDE=ZFBE, ZBED是公共角，•••△BEDs&EB, A—=—EF EB:.BE^EF • ED、:.CE2=EF • ED.点评本题利用直径AM垂直BC和弦CD=AB这两个条件，得到弧相等，角相等，再利用三角形全等, 相似来解决问题.例2 (黄冈市中考题)已知，如图12-8, C为半圆上一点，AC =CE ,过点C作直径AB的垂线QP, P为垂足，弦AE分别交PC, CB于点D, F.(1)求证：AD=CD；气2(2)若DF=二，tanZ£C5=- > 求的长.4 4cE@12-7证明（1）连结人（7, V AC =CE , :.ZCEA = ZCAE.9：ZCEA=ZCBA, •••ZCBA=ZCAE・VAB是直径，A ZACB=90°・•:CP丄AB, :.ZCBA=ZACP・:.ZCAE= ZACP,:・AD=CD・⑵解析：ZACB=90° , ZCAE=ZACP.:.ZDCF=ZCFD. ：・AD=CD=DF=-・4••• ZECB= ZDAP. tanZEC5=-,4DP 3A tan ZDAP=一 =-PA 49：OP2+PA2=DA2, :.DP= - , PA=1, CP=2・4A ZAC5=90° , CP丄AB.:.'APCs'CPB, , APB=4.PC PB点评（1）利用AC =CE ,把圆周角，互余的角联系起来，从而解决问题.⑵利用RtAACF和ZACP=ZCAD这两个条件得到CD=DF,再转化ZECB为ZDAP,问题便迎刃而解.竞赛样题展示例(2000年“鲁中杯”绍兴四市、县初中数学联赛试题)已知如图12-9,在以O为圆心的圆中，弦CD 垂直于直径AB,垂足为H,弦BE与半径OC相交于点F,且OF=FC,弦DE与弦AC相交于点G.(1)求证：AG=GCx⑵若AG=* , AH:AB=\:3,求△CDG的面积与△BOF的而积.证明(1)连结AD. 9：AB是直径，AB丄CD••• BC =BD , ••• ZCAB=ZDAB. :. ZDAG=2ZCAB.V ZBOF= ZCAB+ZOCA,又9： ZCAB=ZOCA,:.ZB0F=2ZCAB, :. ZBOF= ZDAG.•••ZOBF=ZADG,:仏OBFs厶DAG,故竺=21r)A |•：0B=0C=20F, 9：AC=2AG,即AG=GC.(2)解析连结BC, A ZBCA=90° ,又••'CH丄AB, :.A^AH - AB・• •AH—— X AB= — X 6=2・3 3CH=J AC—AH丄=J(2®-22 = 2迈.:.S^ACD =丄CD • AH= - X4x/2 X2= 4迈.・・・AG=CG,：皿心沁=尹心= 由•: HBOF S HDAG点评由垂径左理处BC =BD ,从而得到孤所对的圆周角相等，将已始与未知之间的关系联系起来，再通过三角形相似、射影定理等解决问题.OF AGAG 2團12-9过关检测】4级1 •如图12-10, 00的直径AB 和弦CD 相交于点& 已知AE=\ cm. EB=5 cm, ZDEB=60c,,求仞 的长. 2•如图12-11,公园里大观览车半径为25m,已知观览车绕圆心O 顺时针匀速转动，旋转一周用12mim 某人从观览车的最低处（地面A 处）乘车，问经过4min 后，此人距地而CD 的髙度是多少米？（观览车最低 处距地而的髙度忽略不讣）4•已知AB 是00的直径，M 是OA 上的点，弦P0经过点M,且PM=M0•求证：3AP =B （）.3•如图12-12, AB 是OO 的直径，P 是OA 上一点,C 是00上一点，求证:D@12-115.如图12-13, 一根木棒(AB )长为么“斜靠在与地而(0M)垂直的墙壁(ON)上，与地而的倾角为60° , 若木棒A端沿NO下滑，B端沿OM向右滑行，于是木棒的中点P也随之运动.已知A端下滑到A'时，Af =(筋-血)心则中点P随之运动的路线有多长？6.当湖泊结冰时，有一只球浮在湖而上，将球取岀后在冰上留下一个球形凹洞，深8cm,洞口直径为24cm, 球的半径是多少厘米？B级1・已知点P到00的最小距藹为4cm,最大距离为8cm,求00的半径.2 •如图12-14,已知00的直径为4cm, M是劣弧AB的中点，从M作弦且MN=2苗cm, MN、AB交于点P,求ZAPM的度数.3•已知OO的半径为乩C、D是直径AB同侧圆周上的两点，AC的度数为96° , BD的度数为36。

2023年中考数学高频考点突破——圆的综合1．如图，在中，，是的角平分线，平分交于点，点在边上，以点为圆心的经过、两点，交于点．（1）求证：是的切线；（2）若，，求阴影部分的面积．2．如图，在△ABC中，AB=AC，以AB为直径⊙O分别交AC，BC于点D，E，过点B作⊙O 的切线，交AC的延长线于点F．（1）求证：∠CBF=∠BAC；（2）若⊙O的半径为5，tan∠CBF=，求BC和BF的长．3．如图，AB是⊙O的直径，点D是⊙O上一点，∠BAD的平分线交⊙O于点C，过点C 的直线与AD互相垂直，垂足为点E，直线EC与AB的延长线交于点P，连接BC，已知PB∶PC=1∶．（1）求证：CP是⊙O的切线；（2）若⊙O的半径为r，试探究线段PB与r的数量关系并证明．4．如图，为的直径，弦，垂足为是延长线上一点，，垂足为，．（1）求证：为的切线；（2）已知，求的半径和的长．5．如图，已知AB是⊙O的直径，C是⊙O上一点，连接AC，BC．OE∥BC交AC于E，过点A作⊙O的切线交OE的延长线于点D，连接DC并延长交AB的延长线于点F．（1）求证：DC是⊙O的切线；（2）若∠BAC＝30°，AB＝4，直接写出线段CF的长．6．如图．是的直径，为上一点，，的延长线交于点，连接，且．（1）求证：是的切线；（2）若，求的长．7．如图，△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O经过点E，交BC于点F．（1）求证：AC是⊙O的切线；（2）已知∠A＝30°，⊙O的半径为4，求图中阴影部分的面积．8．如图，四边形内接于，，对角线经过点O，过点D作的切线，交的延长线于点E．（1）求证：；（2）若，求的长．9．如图，AC是⊙O的直径，AD是⊙O的切线．点E在直径AC上，连接ED交⊙O 于点B，连接AB，且AB＝BD．(1)求证：AB＝BE；(2)若⊙O的半径长为5，AB＝6，求线段AE的长．10．如图，已知是半圆的直径，圆心为为半圆上的两个动点，且，过点C作的切线，交的延长线于点于点F．（1）四边形的形状是______________________．（2）连接，若，则当时四边形为平行四边形；若四边形为菱形，四边形的面积是，求直径的长．11．如图，已知AB为半圆O的直径，过点B作PB⊥OB，连接AP交半圆O于点C，D为BP上一点，CD是半圆O的切线．（1）求证：CD＝DP．（2）已知半圆O的直径为，PC＝1，求CD的长．12．如图所示，已知A，B两点的坐标分别为（2，0），（0，10），P是△AOB外接圆⊙C 上的一点，OP交AB于点D．（1）当OP⊥AB时，求OP；（2）当∠AOP＝30°时，求AP．13．已知如图：在⊙O中，直径AB⊥弦CD于G，E为DC延长线上一点，BE交⊙O于点F．（1）求证：∠EFC＝∠BFD；（2）若F为半圆弧AB的中点，且2BF＝3EF，求tan∠EFC的值．14．如图，在△ABC中，，是的平分线，的平分线交于点，点在上，以点为圆心，的长为半径的圆经过点，交于点，交于点．（1）求证：为⊙O的切线；（2）当，时，求⊙O的半径．15．如图，E是的斜边AB上一点，以AE为直径的与边BC相切于点D，交边AC于点F，连结AD．（1）求证：AD平分．（2）若，，求的长．16．如图，在△中，∠＝90°，＝，＝10，以为直径作⊙交于点，作⊥交⊙于点，交于点，连结交于点．（1）求证：＝．（2）求的长．17．如图，CD为⊙O的直径，AB，AC为弦，且∠ADC=∠DAB+∠ACD，AB交CD于E 点．（1）求证：AB=AC．（2）DF为切线，若DE=2，CE=10，求cos∠ADF的值．18．如图，在中，，点为上一点，以点为圆心，为半径的与相切于点，交的延长线于点．（1）求证：；（2）若，，求的半径和的长．参考答案：1．（1）详见解析；（2）【分析】(1)连接OE,由半径相等得出角度相等,再由角平分线得出角度相等从而得出OE∥BC,由等腰三角形的三线合一性质得出∠ADB＝90°,由平行得出∠AEO＝90°,即可证明．(2)根据条件先算出AOE的面积,再算出扇形EOF的面积,相减即可得出阴影部分的面积．【解析】（1）连接∵，∴．∵平分，∴，∴，∴∵，是的角平分线，∴，∴∴即∵是的半径，∴是的切线．（2）∵是的角平分线，∵∴由（1）知，∴，∴，，∴，∵，，∴∵，，∴，∴，在中，由勾股定理得，∵∴【点评】本题考查切线的证明和扇形的面积公式,关键在于熟练掌握基础知识,结合题意灵活运用定理．2．（1）证明见解析；（2）BC=4，．【分析】（1）连接AE，根据圆周角定理得到∠AEB=90°，根据切线的性质即可得到结论；（2）解直角三角形得到，过C作CG⊥AB于G，根据三角形的面积公式得到，求得AG=AB-BG=6，根据相似三角形的性质即可得到结论．【解析】解：（1）连接AE，∵AB为⊙O直径，∴∠AEB=90°，∵AB=AC，∴∠BAE=∠BAC，∵BF是⊙O的切线，∴∠BAE+∠ABE=∠CBF+∠ABE=90°，∴∠CBF=∠BAE=∠BAC；（2）在Rt△BAE中，∵tan∠BCE=tan∠CBF=，∴，∴，∴，过C作CG⊥AB于G，AE=2BE=4，BC=4，AB=10，∴，∴BG=4，∴AG=AB-BG=6，∵CG∥BF，∴△AGC∽△ABF，∴，即，∴．【点评】本题考查了切线的性质，相似三角形的判定和性质，解直角三角形，正确的作出辅助线是解题的关键．3．（1）证明见解析；（2）PB=r，证明见解析【分析】（1）先判断出∠CAE=∠CAB，进而得出∠CAE=∠OCA，即可得出OC∥AE，即可得出结论；（2）设出PB=x，则PC=x，先判断出△PBC∽△PCA，即可得出比例式即可得出PA=3x，即可得出结论．【解析】（1）连接OC，∴OA=OC，∴∠OAC=∠OCA，∵AC是∠BAD的平分线，∴∠CAE=∠CAB，∴∠CAE=∠OCA，∴OC∥AE，∵PC⊥AE，∴PC⊥OC，∵点C在⊙O上，∴PC是⊙O的切线；（2）PB=r，理由：由（1）知，∠PCB＋∠OCB=90°，∠OCB＋∠OCA=90°，∠OAC=∠OCA，∴∠PCB=∠PAC，∵∠A=∠A，∴△PBC∽△PCA，∴，∵PB∶PC=1∶．∴设PB=x，则PC=x，∴，∴PA=3x，∴PA=PB＋AB=x＋2r=3x，∴r=x，∴PB=r．【点评】本题主要考查了角平分线定理，圆周角定理，切线的判定和性质，相似三角形的判定和性质，勾股定理，解（1）的关键是判断出OC∥AE，解（2）的关键是证出△PBC∽△PCA．4．（1）详见解析；（2）半径，DE=【分析】（1）连接OA，根据垂线的定义结合角的运算，即可得出，即可证AE为的切线；（2）设的半径为，在中，根据勾股定理可求出的值，再由得出，进而得出，根据相似三角形的性质即可求出的长度．【解析】（1）证明：证明：连接OA，如图所示，又又点A在圆上，AE为的切线．（2）设的半径为，在中，，即解得：的半径为．，即解得：．【点评】本题考查切线的判定与性质、相似三角形的判定与性质、垂径定理，借助于辅助线OA，利用平行得出相似是解题的关键，属于中考常考题型．5．（1）见解析；（2）2【分析】（1）连接OC，根据平行线的性质得到∠OEA＝∠ACB，由圆周角定理得到∠OEA＝∠ACB＝90°，根据线段垂直平分线的性质得到DA＝DC，证明△ADO≌△CDO（SSS），得出∠DAO＝∠OCD，根据切线的性质得到∠DAO＝90°，求得OC⊥DC，于是得到结论；（2）证明△BOC是等边三角形，得出∠BOC＝60°，解直角三角形即可得到结论．【解析】（1）证明：连接OC，∵OE∥BC，∴∠OEA＝∠ACB，∵AB是⊙O的直径，∴∠OEA＝∠ACB＝90°，∴OD⊥AC，由垂径定理得OD垂直平分AC，∴DA＝DC，∵DO＝DO，OC＝OA，∴△ADO≌△CDO（SSS），∴∠DAO＝∠OCD，∵DA为⊙O的切线，OA是半径，∴∠DAO＝90°，∴∠OCD＝∠DAO＝90°，即OC⊥DC，∵OC是⊙O的半径，∴DC是⊙O的切线；（2）解：在Rt△ABC中，∠BAC＝30°，∴∠ABC＝60°，又∵OB＝OC，∴△BOC是等边三角形，∴∠FOC＝60°，又∵AB＝4，∴OB＝OC＝OA＝2，在Rt△COF中，tan∠FOC＝，∴CF＝2．【点评】本题主要考查了切线的判定、等边三角形、特殊角的锐角三角函数值，掌握切线的判定及特殊角的锐角三角函数值是解题的关键．6．（1）证明见解析；（2）．【分析】（1）如图（见解析），先根据圆周角定理可得，，再根据等腰三角形的性质可得，然后根据等量代换可得，最后根据圆的切线的判定即可得证；（2）先根据线段的和差可得，再根据相似三角形的判定与性质即可得．【解析】（1）如图，连接∵是的直径∴，即∵∴由圆周角定理得：又∵∴∴，即∴是的切线；（2）∵∵∴∴，即解得或（不符题意，舍去）故CH的长为．【点评】本题考查了圆周角定理、圆的切线的判定、相似三角形的判定与性质等知识点，较难的是题（1），通过作辅助线，利用到圆周角定理是解题关键．7．（1）见解析；（2）【分析】（1）连接OE．根据OB＝OE得到∠OBE＝∠OEB，然后再根据BE是△ABC的角平分线得到∠OEB＝∠EBC，从而判定OE∥BC，最后根据∠C＝90°得到∠AEO＝∠C＝90°证得结论AC是⊙O的切线．（2）连接OF，利用S阴影部分＝S梯形OECF﹣S扇形EOF求解即可．【解析】解：（1）连接OE．∵OB＝OE∴∠OBE＝∠OEB∵BE是∠ABC的角平分线∴∠OBE＝∠EBC∴∠OEB＝∠EBC∴OE∥BC∵∠C＝90°∴∠AEO＝∠C＝90°∴AC是⊙O的切线；（2）连接OF．∵∠A＝30°，⊙O的半径为4，∴AO＝2OE＝8，∴AE＝4，∠AOE＝60°，∴AB＝12，∴BC＝AB＝6，AC＝6，∴CE＝AC﹣AE＝2．∵OB＝OF，∠ABC＝60°，∴△OBF是正三角形．∴∠FOB＝60°，CF＝6﹣4＝2，∴∠EOF＝60°．∴S梯形OECF＝＝6．S扇形EOF＝＝，∴S阴影部分＝S梯形OECF﹣S扇形EOF＝【点评】本题考查了切线的判定与性质及扇形面积的计算，解题的关键是连接圆心和切点，利用过切点且垂直于过切点的半径来判定切线．8．（1）见解析（2）．【分析】（1）连接，根据为直径，，再根据，得，根据是的切线，，根据同旁内角互补可证；（2）根据，为直径，可得，，根据，，可得，再根据等腰直角三角形得性质可得．【解析】（1）证明：如图，连接，为直径，．，．是的切线，，．（2）解：，．为直径，．在中，，，，．【点评】本题考查平行的证明，切线的性质定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．9．(1)证明见解析；(2)．【分析】（1）过B作BF⊥AD于点F，由等腰三角形的性质得F是AD的中点，再由切线的性质得AC⊥AD，进而得BF是△ADE的中位线便可得结论；（2）过O作OM⊥AB于点M，过B作BN⊥AC于点N，根据垂径定理求得AM，再解直角三角形求得cos∠OAM，进而在Rt△ABN中求得AN，便可求得结果．【解析】解：（1）过B作BF⊥AD于点F，如图1，∵AB＝BD，∴AF＝DF，∵AD是⊙O的切线，∴AC⊥AD，∴AC∥BF，∵AF＝DF，∴BD＝DE，∴AB＝BE；（2）过O作OM⊥AB于点M，过B作BN⊥AC于点N，如图2，∵AB＝6，AB＝BE，∴AM＝BM＝＝3，AE＝2AN，∵OA＝5，∴cos∠OAM＝，∴cos∠BAN＝，∴AN＝，∴AE＝2AN＝．【点评】本题主要考查了圆的基本性质，切线的性质，等腰三角形的性质，三角形的中位线定理，解直角三角形，第（2）关键是构造直角三角形，利用解直角三角形的知识解决问题．10．（1）矩形；（2）k＝1，【分析】（1）依据“有三个角是直角的四边形是矩形”进行证明即可得到结论；（2）先假设四边形AOCE为平行四边形，可证明四边形AOCE是菱形得AO=EC，再证明Rt△AOF≌Rt△ECD得DE=AF，从而可证DE=EF，进而可得结论；解Rt△EDC得，根据矩形OCDF的面积是可求得，从而可得结论.【解析】（1）∵CD是的切线，∴OC⊥CD，∠OCD=90°，∵∴F为AE的中点，∠OFE=90°,∵∴∠OFE+∠COF=90°，∠COF=90°∴四边形是矩形.故答案为：矩形（2）假设四边形AOCE为平行四边形，连接EC、EO，如图，∵OA=OC，四边形AOCE是菱形，∵OE=OA，OF⊥AE，∴AF=EF，在Rt△AOF和Rt△ECD中，∴Rt△AOF≌Rt△ECD，∴DE=AF，∴DE=EF，∴，即k=1时，四边形AOCE为平行四边形；故答案为：1；若四边形AOCE是菱形，则由于四边形OCDF是矩形，所以在Rt△EDC中，∴由于矩形OCDF的面积是所以所以【点评】本题考查了圆综合题，全等三角形的判定与性质、平行四边形的判定与性质、矩形的判定与性质、菱形的判定与性质等知识，解题的关键是灵活运用所学知识解决问题．11．（1）证明见解析，（2）CD＝．【分析】（1）如图1（见解析），连接OC，先根据圆的切线的性质得出，从而可得，再根据直角三角形的性质可得，然后根据等腰三角形的性质可得，从而可得，最后根据等腰三角形的性质即可得证；（2）如图2（见解析），连接OC、BC，先根据圆周角定理得出，再根据相似三角形的判定与性质可得，从而可求出，然后在中利用勾股定理可求出，最后根据角的和差、等腰三角形的性质可得，结合题（1）的结论可得，由此即可得．【解析】（1）如图1，连接OC∵CD是半圆O的切线∴OC⊥CD，即∴∵PB⊥AB∴∴又∴∴；（2）如图2，连接OC、BC∵AB是半圆O的直径∴，∴又∵∴∴，即∵∴解得或（不符题意，舍去）∴在中，由（1）得即∵∴∴∴由（1）知∴．【点评】本题考查圆的切线的性质、圆周角定理、等腰三角形的性质、相似三角形的判定与性质等知识点，较难的是题（2），通过作辅助线，构造相似三角形是解题关键．12．（1）OP＝；（2）AP＝2．【分析】（1）当OP⊥AB时，由垂径定理可知OD=DP，根据等面积可求出斜边上的高OD 的长，进而可求出PO的长；（2）连接CP，由圆周角定理可知∠ACP=60°，进而可证明△ACP为等边三角形，则AP=AC，即求出圆的半径即可．【解析】（1）∵A，B两点的坐标分别为（2，0），（0，10），∴AO＝2，OB＝10，∵AO⊥BO，∴AB＝＝4，∵OP⊥AB，∴＝，CD＝DP，∴CD＝，∴OP＝2CD＝；（2）连接CP，如图所示：∵∠AOP＝30°，∴∠ACP＝60°，∵CP＝CA，∴△ACP为等边三角形，∴AP＝AC＝AB＝2．【点评】考查了三角形的外接圆与外心的性质、圆周角定理的运用、勾股定理的运用以及等边三角形的判定和性质，解题关键是熟记和圆有关的各种性质定理．13．（1）见解析；（2）【分析】（1）连接BD，圆心角、弧、弦间的关系得到∠BFD＝∠CDB；根据邻补角的定义和园内接四边形对角互补的性质推知∠EFC＝∠CDB，则∠EFC＝∠BFD；（2）如图，连OF，OC，BC，由于∠EFC所在的三角形不是直角三角形，欲求求正切值，需要将其转化为求∠BCG的正切值，据此推知相关线段的长度即可．【解析】（1）证明：如图，连接BD，∵AB⊥CD且AB为直径，∴弧CB=弧BD．∴∠BFD＝∠CDB．又∵∠EFC+∠CFB＝180°，而∠CFB+∠CDB＝180°，∴∠EFC＝∠CDB，∴∠EFC＝∠BFD；（2）解：如图，连OF，OC，BC，∵弧CB=弧BD，∴∠DCB＝∠CDB，∵∠EFC＝∠CDB，∴∠EFC＝∠BFD＝∠BCG，又F为半圆AB的中点，∴∠FOB＝∠FOA＝90°，∴OF//CD，∴OG：OB＝EF：FB＝2：3．设OG＝2x，则OB＝OC＝3x，则CG＝x，∴tan∠EFC＝tan∠BCG＝＝．【点评】本题考查了圆周角定理，垂径定理，平行线分线段成比例定理，解直角三角形以及圆心角、弧、弦的关系等知识点，解题的关键是正确作出辅助线，运用好圆的有关基础知识．14．（1）见解析；（2）⊙O的半径为3【分析】（1）连接OM，利用角平分线的性质和平行线的性质得到AE⊥OM，后即可证得AE 是⊙O的切线；（2）设⊙O的半径为r，根据OM∥BE，得到△OMA∽△BEA，利用平行线的性质得到，即可解得, ⊙O的半径为3．【解析】解：（1）证明：连接.∵，平分，∴，∵，∴，∵平分，∴，∴，∴，又∵，∴，∴是⊙O的切线；（2）设⊙O的半径为，∵，∴，∵，∴，∴，即，解得，∴⊙O的半径为3．【点评】本题属于圆的综合题，考查了切线的证明，相似三角形的判定与性质等，属于中考热点题型，证明切线的思路：连接圆心和准切点，证明半径垂直准切线，准切点在圆上即可．15．（1）证明见解析；（2）．【分析】（1）连结OD，由切线的性质及∠C=90°可得OD∥AC，进而得∠CAD=∠ODA，再由OA=OD得∠OAD=∠ODA，等量代换即可得证；（2）先由∠CAD=25°求得∠EOF=100°，再利用弧长公式计算即可．【解析】（1）如图，连结OD．∵⊙O与边BC相切于点D，∴OD⊥BC，∴∠ODB=90°．∵∠C=90°，∴∠C=∠ODB=90°，∴OD∥AC，∴∠CAD=∠ODA．∵OA=OD，∴∠OAD=∠ODA，∴∠OAD=∠CAD．∴AD平分∠BAC．（2）如图，连结OF．∵AD平分∠BAC，且∠CAD=25°，∴，∴∠EOF=100°，∴的长为．【点评】本题考查了切线的性质，等腰三角形的性质，弧长公式等知识，熟练掌握切线的性质是解题的关键．16．（1）证明见解析；（2）CG=6【分析】（1）首先解直角三角形ABC，求出BC=6，AB=8，再证明∠CGB=∠CBG，从而可得GC=BC；（2）由BC=6根据（1）的结论可得到CG=6．【解析】在中，，，，，由勾股定理得，，（2），∴【点评】此题主要考查了解直角三角形以及垂径定理的应用，证明是解此题的关键．17．（1）见解析；（2）【分析】（1）根据圆周角定理即以及等腰三角形的判定即可求出答案．（2）连接AO并延长交BC于点G，连接BD，根据切线的性质以及锐角三角函数的定义即可求出答案．【解析】（1）由圆周角定理可知：∠ADC=∠B，∠DAB=∠DCB，∵∠ADC=∠DAB+∠ACD，∴∠ADC=∠DCB+∠ACD，∴∠B=∠ACB，∴AB=AC．（2）连接AO并延长交BC于点G，连接BD，∵DF为切线，∴∠CDF=90°，∴∠ADF=∠ACD，∵DE=2，CE=10，∴CD=12，∴OD=OA=6，∴OE=OD﹣DE=4，∵CD是⊙O的直径，∴∠DAC=∠DBC=90°，∴BD∥AG，∴△BDE∽△AOE，∴，∴BD=3，∵OG是△BCD的中位线，∴OG=，在Rt△OCG中，由勾股定理可知：CG=，在Rt△AGC中，由勾股定理可知：AC=3，∴cos∠ADF=cos∠ACD=．【点评】本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定．18．（1）见解析；（2）的半径是6，的长是．【分析】(1)利用切线的性质证得OD=OC，证得BO为的平分线，利用等角的余角相等结合对顶角相等即可证得结论；(2)利用正切函数求得AB=20，设的半径为R，在中，利用切线长定理求得AD=8，AO=16-R，根据勾股定理求得R的值，在中，求得，利用正弦函数即可求解．【解析】(1)如图，连接，∵与相切于点，∴，∵，∴，∴BC是的切线，又，∴为的平分线，∴，∵于点，∴，∴，，∴，∵，∴；(2)∵，，∴AC=16，∵，即，∴AB=20，由(1)得，BD、BC都是切线，∴BD=BC=12，∴AD=AB-BD=20-12=8，设的半径为R，在中，OD=R，AO=16-R，AD=8，∵，即，∴R=6，在中，BC=12，OC=6，∵，即，∴，∵，∴，即，∴．【点评】本题主要考查切线的判定与性质，勾股定理的应用，锐角三角函数的知识，解题的关键是掌握切线的判定、切线长定理以及解直角三角形的应用．。

圆的有关性质（30道）一、单选题 为O 的两条弦，的中点，O 的 【答案】D 【分析】连接,,OA OB AB ，圆周角定理得到290AOB C ∠=∠=︒，勾股定理求出AB ，三角形的中位线定理，即可求出DG 的长．【详解】解：连接,,OA OB AB ，∵O 的半径为2．45C ∠=︒，∴2,290OA OB AOB C ==∠=∠=︒，∴AB ∵D ，G 分别为,AC BC 的中点，∴DG 为ABC 的中位线，∴12DG AB ==故选D ．【点睛】本题考查圆周角定理和三角形的中位线定理．熟练掌握相关定理，并灵活运用，是解题的关键．2．（2023·辽宁阜新·统考中考真题）如图，A ，B ，C 是O 上的三点，若9025AOC ACB ∠=︒∠=︒，，则BOC ∠的度数是（ ）A ．20︒B ．25︒C ．40︒D ．50︒【答案】C 【分析】先利用圆周角定理求出50AOB ∠=︒，然后利用角的和差关系进行计算，即可解答．【详解】解：∵25ACB ∠=︒，∴250AOB ACB ∠=∠=︒，∵=90AOC ∠︒，∴40BOC AOC AOB ∠=∠−∠=︒，故选：C ．【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．3．（2023·黑龙江哈尔滨·统考中考真题）如图，AB 是O 的切线，A 为切点，连接OA ﹐点C 在O 上，OC OA ⊥，连接BC 并延长，交O 于点D ，连接OD ．若65B ∠=︒，则DOC ∠的度数为（ ）A ．45︒B ．50︒C ．65︒D ．75︒【答案】B 【分析】利用垂线的性质及切线的性质得到90OAB ∠=︒和=90AOC ∠︒，再利用四边形的内角和为360︒进而可求得65OCD ∠=︒，再利用等边对等角及三角形的内角和即可求解．【详解】解：OC OA ⊥Q ，90AOC ∴∠=︒，又AB 是O 的切线，OA AB ∴⊥，90OAB ︒∴∠=，又65B ∠=︒，360115OCB OAB AOC B ∴∠=︒−∠−∠−∠=︒，18065OCD OCB ∴∠=︒−∠=︒，又OC OD =，65ODC OCD ∴∠=∠=︒，180250DOC ODC ∴∠=︒−∠=︒，故选B ．【点睛】本题考查了圆的切线的性质，四边形内角和是360︒，等腰三角形的性质及三角形的内角和，熟练掌握其基本知识是解题的关键． 是O 的一部分，，则O 的半径 A ．13cmB ．16cmC ．17cmD ．26cm【答案】A 【分析】首先利用垂径定理的推论得出OD AB ⊥，1122AC BC AB cm ===，再设O 的半径OA 为cm R ，则()8cmOC R =−．在Rt OAC 中根据勾股定理列出方程22212(8)R R =+−，求出R 即可． 【详解】解：AB 是O 的一部分，D 是AB 的中点，24cm AB =，OD AB ∴⊥，112cm 2AC BC AB ===． 设O 的半径OA 为cm R ，则(8)cm OC OD CD R =−=−．在Rt OAC 中，90OCA ∠=︒，222OA AC OC ∴=+，22212(8)R R ∴=+−，13R ∴=，即O 的半径OA 为13cm ．故选：A ．【点睛】本题考查了垂径定理、勾股定理的应用，设O 的半径OA 为cm R ，列出关于R 的方程是解题的关键． 在O 上，∠．若O 的 【答案】D 【分析】先利用圆周角定理求出AOC ∠的度数，然后利用扇形面积公式求解即可．【详解】解：∵40ABC ∠=︒，∴280AOC ABC ∠=∠=︒，又O 的半径为3，∴扇形AOC （阴影部分）的面积为28032360ππ⨯=．故选：D ．【点睛】本题考查的是圆周角定理，扇形面积公式等，掌握“同弧所对的圆周角是它所对的圆心角的一半”是解题的关键．6．（2023·湖南娄底·统考中考真题）如图，正六边形ABCDEF 的外接圆O 的半径为2，过圆心O 的两条直线1l 、2l 的夹角为60︒，则图中的阴影部分的面积为（ ）A ．433π−B ．【答案】C【分析】如图，连接AO ，标注直线与圆的交点，由正六边形的性质可得：A ，O ，D 三点共线，COD △为等边三角形，证明扇形AOQ 与扇形COG 重合，可得COD COD S S S =−阴影扇形，从而可得答案．【详解】解：如图，连接AO ，标注直线与圆的交点，由正六边形的性质可得：A ，O ，D 三点共线，COD △为等边三角形，∴AOQ DOH ∠=∠，60COD GOH ∠=∠=︒，∴COG DOH AOQ ∠=∠=∠，∴扇形AOQ 与扇形COG 重合，∴COD COD S S S =−阴影扇形，∵COD △为等边三角形，2OC OD ==，过O 作OK CD ⊥于K ，∴60COD ∠=︒，1CK DK ==，OK∴260212236023COD COD S S S ππ⨯=−==⨯=阴影扇形故选C【点睛】本题考查的是正多边形与圆，扇形面积的计算，勾股定理的应用，熟记正六边形的性质是解本题的关键．内接于O ，O 的半径为 A ．π【答案】C 【分析】根据圆内接四边形的性质得到=60B ∠︒，由圆周角定理得到120AOC ∠=︒，根据弧长的公式即可得到结论．【详解】解：四边形ABCD 内接于O ，120D ∠=︒，60B ∴∠=︒，2120AOC B ∴∠=∠=︒，AC ∴的长12032180ππ⨯==． 故选：C ．【点睛】本题考查的是弧长的计算，圆内接四边形的性质和圆周角定理，掌握圆内接四边形的对角互补是解题的关键．A ．225πm 3B ．2125πm 3【答案】B【分析】种草区域的面积等于大扇形面积减去小扇形面积，利用利用扇形的面积公式计算即可．【详解】解∶∵120AOB ∠=︒，15m OA =，10m OC =，∴种草区域的面积为2221201512010125(m )3603603πππ⋅⋅−=，故选：B ． 【点睛】本题考查扇形的面积，解题的关键是记住扇形的面积公式：扇形面积2360n r π=． 如图，O 是ABC 的外接圆， 【答案】C【分析】先根据等腰三角形的性质以及三角形内角和定理求得180302120BOC ∠=︒−︒⨯=︒，再根据扇形的面积公式即可求解．【详解】解：∵OC OB =，OA =，40CAO ∠=︒，∴40OCA OAC ∠=∠=︒，OCB OBC ∠=∠，∵70ACB ∠=︒，∴704030OBC OCB ACB ACO ∠=∠=∠−∠=︒−︒=︒，∴180302120BOC ∠=︒−︒⨯=︒，∴22120116ππ4π36033S r ︒=⨯=⨯⨯=︒阴影，故选：C ．【点睛】本题考查等腰三角形的性质、三角形内角和定理以及扇形的面积公式等知识，求出120BOC ∠=︒是解答的关键．10．（2023·山东泰安·统考中考真题）如图，AB 是O 的直径，D ，C 是O 上的点，115ADC ∠=︒，则BAC ∠的度数是（ ）A ．25︒B ．30︒C ．35︒D ．40︒【答案】A 【分析】根据圆内接四边形对角互补和直径所对圆周角等于90度求解即可．【详解】解：∵115ADC ∠=︒，∴65B ∠=︒，∵AB 是O 的直径，∴90ACB ∠=︒，∴180906525BAC ∠=︒−︒−︒︒=，故选：A ．【点睛】本题考查圆的性质，涉及到圆内接四边形对角互补和直径所对圆周角等于90度，熟记知识点是关键．11．（2023·黑龙江牡丹江·统考中考真题）如图，A ，B ，C 为O 上的三个点，4AOB BOC ∠=∠，若60ACB ∠=︒，则BAC ∠的度数是（ ）A ．20︒B ．18︒C ．15︒D ．12︒【答案】C 【分析】由60ACB ∠=︒，可得2120AOB ACB ∠=∠=︒，结合4AOB BOC ∠=∠，可得1120304BOC ∠=⨯︒=︒，再利用圆周角定理可得答案．【详解】解：∵60ACB ∠=︒，∴2120AOB ACB ∠=∠=︒，∵4AOB BOC ∠=∠， ∴1120304BOC ∠=⨯︒=︒， ∴1152BAC BOC ∠=∠=︒，故选C ．【点睛】本题考查的是圆周角定理的应用，熟记圆周角定理的含义是解本题的关键． 统考中考真题）如图，等圆1O 和2O 相交于两点，1O 经过2O 的圆心 A ．2πB ．43π 【答案】D【分析】先证明12ACO BCO ≌，再把阴影部分面积转换为扇形面积，最后代入扇形面积公式即可．【详解】如图，连接2O B ，1O B ，∵等圆1O 和2O 相交于A ，B 两点 ∴12O O AB ⊥,AC BC = ∵1O 和2O 是等圆 ∴11212O A O O O B O B === ∴12O O B 是等边三角形∴1260O O B ∠=︒∵1290ACO BCO ∠=∠=︒,AC BC =,21O A B O =∴12ACO BCO ≌ ∴121211*********ACO BCO BCO BCO BO O S S S S S S ππ=+=+===图形图形扇形．故选：D ．【点睛】本题考查了相交弦定理，全等的判定及性质，扇形的面积公式，转化思想是解题的关键． 13．（2023·辽宁营口·统考中考真题）如图所示，AD 是O 的直径，弦BC 交AD 于点E ，连接AB AC ，，若30BAD ∠=︒，则ACB ∠的度数是（ ）A ．50︒B ．40︒C ．70︒D ．60︒【答案】D 【分析】如图所示，连接CD ，先由同弧所对的圆周角相等得到30BCD BAD ∠=∠=︒，再由直径所对的圆周角是直角得到=90ACD ∠︒，则60ACB ACD BCD =−=︒∠∠∠．【详解】解：如图所示，连接CD ，∵30BAD ∠=︒，∴30BCD BAD ∠=∠=︒，∵AD 是O 的直径，∴=90ACD ∠︒，∴60ACB ACD BCD =−=︒∠∠∠，故选D ．【点睛】本题主要考查了同弧所对的圆周角相等，直径所对的圆周角是直角，正确求出ACD BCD ∠，∠的度数是解题的关键． 统考中考真题）如图，在ABC 中，ACA ．3533π−B ．【答案】C 【分析】连接OD ，BD ，作OH CD ⊥交CD 于点H ，首先根据勾股定理求出BC 的长度，然后利用解直角三角形求出BD 、CD 的长度，进而得到OBD 是等边三角形，60BOD ∠=︒，然后根据30︒角直角三角形的性质求出OH 的长度，最后根据ACB COD ODB S S S S =−−形阴影扇进行计算即可．【详解】解：如图所示，连接OD ，BD ，作OH CD ⊥交CD 于点H∵在ABC 中，90ABC ∠=︒，30ACB ∠=︒，4AB =，∴tan tan 30AB AB BC ACB ===∠︒， ∵点O 为BC 的中点，以O 为圆心，OB 长为半径作半圆，∴BC 是半圆的直径，∴90CDB ∠=︒，∵30ACB ∠=︒，∴12BD BC ==cos 6CD BC BCD =⋅∠==，又∵12OB OC OD BC ==== ∴OB OD BD ==，∴OBD 是等边三角形，∴60BOD ∠=︒，∵OH CD ⊥，30OCH ∠=︒，∴12OH OC ==∴(2601146222360ACB COD ODB S S S S ππ∆∆⨯=−−=⨯⨯−=形阴影扇．故选：C ． 【点睛】本题考查了30︒角直角三角形的性质，解直角三角形，等边三角形的性质和判定，扇形面积，勾股定理等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键． 15．（2023·甘肃兰州·统考中考真题）我国古代天文学确定方向的方法中蕴藏了平行线的作图法．如《淮南子天文训》中记载：“正朝夕：先树一表东方；操一表却去前表十步，以参望日始出北廉．日直入，又树一表于东方，因西方之表，以参望日方入北康．则定东方两表之中与西方之表，则东西也．”如图，用几何语言叙述作图方法：已知直线a 和直线外一定点O ，过点O 作直线与a 平行．（1）以O 为圆心，单位长为半径作圆，交直线a 于点M ，N ；（2）分别在MO 的延长线及ON 上取点A ，B ，使OA OB =；（3）连接AB ，取其中点C ，过O ，C 两点确定直线b ，则直线a b ∥．按以上作图顺序，若35MNO ∠=︒，则AOC ∠=（ ）A ．35︒B ．30︒C ．25︒D ．20︒【答案】A 【分析】证明35NMO MNO ∠=∠=︒，可得23570AOB ∠=⨯︒=︒，结合OA OB =，C 为AB 的中点，可得35AOC BOC ∠=∠=︒．【详解】解：∵35MNO ∠=︒，MO NO =，∴35NMO MNO ∠=∠=︒，∴23570AOB ∠=⨯︒=︒，∵OA OB =，C 为AB 的中点，∴35AOC BOC ∠=∠=︒，故选A ．【点睛】本题考查的是圆的基本性质，等腰三角形的性质，平行线的判定，三角形的外角的性质，熟记等腰三角形的性质是解本题的关键． 16．（2023·内蒙古赤峰·统考中考真题）如图，圆内接四边形ABCD 中，105BCD ∠=︒，连接OB ，OC ，OD ，BD ，2BOC COD ∠=∠．则CBD ∠的度数是（ ）A ．25︒B ．30︒C ．35︒D ．40︒【答案】A 【分析】根据圆内接四边形对角互补得出18010575A ∠=︒−︒=︒，根据圆周角定理得出2150BOD A ∠=∠=︒，根据已知条件得出1503COD BOD ∠=∠=︒，进而根据圆周角定理即可求解．【详解】解：∵圆内接四边形ABCD 中，105BCD ∠=︒，∴18010575A ∠=︒−︒=︒∴2150BOD A ∠=∠=︒∵2BOC COD ∠=∠∴1503COD BOD ∠=∠=︒，∵CD CD =∴11502522CBD COD ∠=∠=⨯︒=︒,故选：A ．【点睛】本题考查了圆内接四边形对角互补，圆周角定理，熟练掌握以上知识是解题的关键．17．（2023·内蒙古·统考中考真题）如图，O 是锐角三角形ABC 的外接圆，,,OD AB OE BC OF AC ⊥⊥⊥，垂足分别为,,D E F ，连接,,DE EF FD ．若 6.5,DE DF ABC +=△的周长为21，则EF 的长为（ ）A ．8B ．4C ．3.5D ．3【答案】B 【分析】根据三角形外接圆的性质得出点D 、E 、F 分别是AB BC AC 、、的中点，再由中位线的性质及三角形的周长求解即可．【详解】解：∵O 是锐角三角形ABC 的外接圆，,,OD AB OE BC OF AC ⊥⊥⊥，∴点D 、E 、F 分别是AB BC AC 、、的中点， ∴111,,222DF BC DE AC EF AB ===，∵ 6.5,DE DF ABC +=△的周长为21，∴21CB CA AB ++=即22221DF DE EF ++=，∴4EF =，故选：B ．【点睛】题目主要考查三角形外接圆的性质及中位线的性质，理解题意，熟练掌握三角形外接圆的性质是解题关键． 18．（2023·湖南·统考中考真题）如图，圆锥底面圆的半径为4，则这个圆锥的侧面展开图中AA '的长为（ ）A ．4πB ．6πC ．8πD ．16π【答案】C 【分析】根据底面周长等于AA '的长，即可求解．【详解】解：依题意，AA '的长2π48π=⨯=，故选：C ．【点睛】本题考查了圆锥的侧面展开图的弧长，熟练掌握圆锥底面周长等于AA '的长是解题的关键． 19．（2023·吉林·统考中考真题）如图，AB ，AC 是O 的弦，OB ，OC 是O 的半径，点P 为OB 上任意一点（点P 不与点B 重合），连接CP ．若70BAC ∠=︒，则BPC ∠的度数可能是（ ）A ．70︒B ．105︒C ．125︒D ．155︒【答案】D 【分析】根据圆周角定理得出2140BOC BAC ∠=∠=︒，进而根据三角形的外角的性质即可求解．【详解】解：∵BC BC =，70BAC ∠=︒，∴2140BOC BAC ∠=∠=︒，∵140BPC BOC PCO ∠=∠+∠≥︒，∴BPC ∠的度数可能是155︒故选：D ．【点睛】本题考查了圆周角定理，三角形的外角的性质，熟练掌握圆周角定理是解题的关键．A ．26π+B ．【答案】A 【分析】由于AD l 是定值，只需求解AC CD +的最小值即可，作点D 关于OB 对称点D ¢，连接AD '、CD '、OD '，则AC CD +最小值为AD '的长度，即阴影部分周长的最小最小值为AD AD l '+．利用角平分线的定义可求得90AOD '∠=︒，进而利用勾股定理和弧长公式求得AD '和AD l 即可．【详解】解：如图，作点D 关于OB 对称点D ¢，连接AD '、CD '、OD '，则CD CD '=，OD OD '=，DOB BOD '∠=∠，∴AC CD AC CD AD ''+=+≥，当A 、C 、D ¢共线时取等号，此时，AC CD +最小，即阴影部分周长的最小，最小值为AD AD l '+．∵OD 平分AOB ∠，60AOB ∠=︒， ∴1302AOD DOB AOB ∠=∠=∠=︒， ∴90AOD '∠=︒，在Rt OAD '中，1OA OD '==，∴AD '== 又30π1π1806AD l ⨯==，∴阴影部分周长的最小值为π6AD AD l '+=，故选：A ． 【点睛】本题考查弧长公式、勾股定理、角平分线的定义、轴对称性质，能利用轴对称性质求解最短路径问题是解答的关键．二、填空题 21．（2023·江苏·统考中考真题）如图，AD 是O 的直径，ABC 是O 的内接三角形．若DAC ABC ∠=∠，4AC =，则O 的直径AD = ．【答案】【分析】连接CD ，OC ，根据在同圆中直径所对的圆周角是90︒可得=90ACD ∠︒，根据圆周角定理可得COD COA ∠=∠，根据圆心角，弦，弧之间的关系可得AC CD =，根据勾股定理即可求解．【详解】解：连接CD ，OC ，如图：∵AD 是O 的直径，∴=90ACD ∠︒，∵DAC ABC ∠=∠，∴COD COA ∠=∠，∴AC CD =，又∵4AC =，∴4CD =，在Rt ACD △中，AD ，故答案为：【点睛】本题考查了在同圆中直径所对的圆周角是90︒，圆周角定理，圆心角，弦，弧之间的关系，勾股定理，熟练掌握以上知识是解题的关键． 22．（2023·江苏南通·统考中考真题）如图，AB 是O 的直径，点C ，D 在O 上．若66DAB ∠=︒， 则ACD ∠= 度．【答案】24【分析】连接BC ，根据直径所对的圆周角是直角，同弧所对的圆周角相等，可得90ACB ∠=︒，66DCB DAB ∠=∠=︒，进而即可求解．【详解】解：如图所示，连接BC ，∵AB 是直径，∴90ACB ∠=︒，∵BD BD =，66DAB ∠=︒，∴66DCB DAB ∠=∠=︒，∴906624ACD ACB DCB ∠=∠−∠=︒−︒=︒，故答案为：24．【点睛】本题考查了直径所对的圆周角是直角，同弧所对的圆周角相等，熟练掌握圆周角定理的推论是解题的关键． 23．（2023·山东济南·统考中考真题）如图，正五边形ABCDE 的边长为2，以A 为圆心，以AB 为半径作弧BE ，则阴影部分的面积为 （结果保留π）．【答案】65π【分析】根据正多边形内角和公式求出正五边形的内角和，再求出A ∠的度数，利用扇形面积公式计算即可．【详解】解：正五边形的内角和()52180540=−⨯︒=︒，5401085A ︒∴∠==︒， 2108263605ABE S ππ∴==扇形，故答案为：65π．【点睛】本题考查了扇形面积和正多边形内角和的计算，熟练掌握扇形面积公式和正多边形内角和公式是解答本题的关键． 24．（2023·宁夏·统考中考真题）如图，四边形ABCD 内接于O ，延长AD 至点E ，已知140AOC ∠=︒，那么CDE ∠= ︒．【答案】70【分析】根据圆周角定理得到70B ∠=︒，再根据圆内接四边形性质和平角的定义即可得解．【详解】解：∵140AOC ∠=︒，∴7201B AOC ∠∠=︒=，∵四边形ABCD 内接于O ，∴180B ADC ∠+∠=︒，∵180CDE ADC ∠+∠=︒，∴70CDE B ∠=∠=︒，故答案为：70．【点睛】此题考查了圆内接四边形的性质、圆周角定理，熟记圆内接四边形的性质、圆周角定理是解题的关键．25．（2023·湖南·统考中考真题）如图，点A ，B ，C 在半径为2的O 上，60ACB ∠=︒，OD AB ⊥，垂足为E ，交O 于点D ，连接OA ，则OE 的长度为 ．【答案】1【分析】连接OB ，利用圆周角定理及垂径定理易得60AOD ∠=︒，则30OAE ∠=︒，结合已知条件，利用直角三角形中30︒角对的直角边等于斜边的一半即可求得答案．【详解】解：如图，连接OB ，∵60ACB ∠=︒，∴2120AOB ACB ∠=∠=︒，∵OD AB ⊥，∴AD BD =，90OEA ∠=︒， ∴1602AOD BOD AOB ∠=∠=∠=︒，∴906030OAE ∠=︒−︒=︒， ∴112122OE OA ==⨯=，故答案为：1．【点睛】本题考查圆与直角三角形性质的综合应用，结合已知条件求得60AOD ∠=︒是解题的关键． 26．（2023·江苏徐州·统考中考真题）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥母线l =6，扇形的圆心角120θ=°，则该圆锥的底面圆的半径r 长为 ．【答案】2【分析】结合题意，根据弧长公式，可求得圆锥的底面圆周长．再根据圆的周长的公式即可求得底面圆的半径长．【详解】∵母线l 长为6，扇形的圆心角120θ=°，∴圆锥的底面圆周长12064180ππ⨯==，∴圆锥的底面圆半径422r ππ==．故答案为：2． 【点睛】本题考查圆锥的侧面展开图的相关计算，弧长公式等知识．掌握圆锥侧面展开图的弧长等于圆锥底面圆的周长是求解本题的关键． 27．（2023·山东东营·统考中考真题）“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”．用现在的几何语言表达即：如图，CD 为O 的直径，弦AB CD ⊥，垂足为点E ，1CE =寸，10AB =寸，则直径CD 的长度是 寸．【答案】26【分析】连接OA 构成直角三角形，先根据垂径定理，由DE 垂直AB 得到点E 为AB 的中点，由6AB =可求出AE 的长，再设出圆的半径OA 为x ，表示出OE ，根据勾股定理建立关于x 的方程，求解方程可得2x 的值，即为圆的直径．【详解】解：连接OA ，AB CD ⊥，且10AB =寸，5AE BE ∴==寸，设圆O 的半径OA 的长为x ，则OC OD x ==，1CE =Q ，1OE x ∴=−，在直角三角形AOE 中，根据勾股定理得：222(1)5x x −−=，化简得：222125x x x −+−=，即226x =，26CD ∴=（寸）．故答案为：26．【点睛】本题考查了垂径定理和勾股定理，解题的关键是正确作出辅助线构造直角三角形． 28．（2023·内蒙古·统考中考真题）如图，正方形ABCD 的边长为2，对角线,AC BD相交于点O ，以点B 为圆心，对角线BD 的长为半径画弧，交BC 的延长线于点E ，则图中阴影部分的面积为 ．【答案】π【分析】根据正方形的性质得出阴影部分的面积为扇形BED 的面积，然后由勾股定理得出BD =再由扇形的面积公式求解即可．【详解】解：正方形ABCD ，∴,,AO CO BO DO AD CD ===，45DBE ∠=︒，∴(SSS)AOD COB ≌，∵正方形ABCD 的边长为2，∴BD ==∴阴影部分的面积为扇形BED 的面积，即(245360ππ⨯⨯=，故答案为：π． 【点睛】题目主要考查正方形的性质及扇形的面积公式，理解题意，将阴影部分面积进行转化是解题关键． 29．（2023·吉林·统考中考真题）如图①，A ，B 表示某游乐场摩天轮上的两个轿厢．图②是其示意图，点O 是圆心，半径r 为15m ，点A ，B 是圆上的两点，圆心角120AOB ∠=︒，则AB 的长为 m ．（结果保留π）【答案】10π 【分析】利用弧长公式π180n r l =直接计算即可．【详解】∵半径15m OA =，圆心角120AOB ∠=︒，∴AB l 120π1510π180⨯⨯==，故答案为：10π． 【点睛】本题考查了弧长计算，熟练掌握弧长公式π180n r l =，并规范计算是解题的关键． 30．（2023·广东深圳·统考中考真题）如图，在O 中，AB 为直径，C 为圆上一点，BAC ∠的角平分线与O 交于点D ，若20ADC ∠=︒，则BAD ∠= °．【答案】35【分析】由题意易得90ACB ∠=︒，20ADC ABC ∠=∠=︒，则有70BAC ∠=︒，然后问题可求解．【详解】解：∵AB 是O 的直径，∴90ACB ∠=︒，∵AC AC =，20ADC ∠=︒，∴20ADC ABC ∠=∠=︒，∴70BAC ∠=︒，∵AD 平分BAC ∠，∴1352BAD BAC ∠∠==︒；故答案为35．【点睛】本题主要考查圆周角的性质，熟练掌握直径所对圆周角为直角是解题的关键．。

专题23圆的基本性质的核心知识点精讲1.理解圆心角及其所对的弧、弦之间的关系；2.理解并运用圆周角定理及其推论；3.探索并证明垂径定理会应用垂径定理解决与圆有关的问题；4.理解并运用圆内接四边形的性质.考点1：圆的定义及性质圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫圆。

这个固定的端点O叫做圆心，线段OA叫做半径。

圆的表示方法：以O点为圆心的圆记作⊙O，读作圆O。

圆的特点：在一个平面内，所有到一个定点的距离等于定长的点组成的图形。

圆的对称性：1）圆是轴对称图形，经过圆心的每一条直线都是它的对称轴；2）圆是以圆心为对称中心的中心对称图形。

考点2：圆的有关概念弦的概念：连结圆上任意两点的线段叫做弦(例如：右图中的AB)。

直径的概念：经过圆心的弦叫做直径（例如：右图中的CD）。

备注：1）直径是同一圆中最长的弦。

2）直径长度等于半径长度的2倍。

弧的概念：圆上任意两点间的部分叫做圆弧，简称弧。

以A、B为端点的弧记作AB ，读作圆弧AB或弧AB。

等弧的概念：在同圆或等圆中，能够互相重合的弧叫做等弧。

半圆的概念：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

优弧的概念：在一个圆中大于半圆的弧叫做优弧。

劣弧的概念：小于半圆的弧叫做劣弧。

考点3：垂径定理垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推论1：1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

常见辅助线做法（考点）：1）过圆心，作垂线，连半径，造Rt △，用勾股，求长度；2）有弧中点，连中点和圆心，得垂直平分考点4：垂径定理的应用考点5：圆心角的概念圆心角概念：顶点在圆心的角叫做圆心角。

弧、弦、弦心距、圆心角之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。

初三数学圆(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（初三数学圆(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为初三数学圆(word版可编辑修改)的全部内容。

初三数学 圆一、知识点1、与圆有关的角——圆心角、圆周角（1）图中的圆心角 ；圆周角 ；（2)如图，已知∠AOB=50度,则∠ACB= 度；（3)在上图中，若AB 是圆O 的直径，则∠AOB= 度； 2、圆的对称性：（1）圆是轴对称图形，其对称轴是任意一条 的直线；圆是中心对称图形，对称中心为 ．(2 如图，∵CD 是圆O 的直径，CD ⊥AB 于E∴ = ， =3、点和圆的位置关系有三种:点在圆 ，点在圆 ，点在圆 ； 例1:已知圆的半径r 等于5厘米，点到圆心的距离为d ， （1）当d =2厘米时，有d r ,点在圆 （2）当d =7厘米时，有d r ，点在圆 (3）当d =5厘米时,有d r ,点在圆4、直线和圆的位置关系有三种：相 、相 、相 ．例2：已知圆的半径r 等于12厘米，圆心到直线l 的距离为d , （1）当d =10厘米时,有d r ，直线l 与圆 （2）当d =12厘米时，有d r ，直线l 与圆 （3）当d =15厘米时，有d r ，直线l 与圆5、圆与圆的位置关系：例3:已知⊙O 1的半径为6厘米，⊙O 2的半径为8厘米，圆心距为 d ， 则：R+r= ， R －r= ；（1)当d =14厘米时，因为d R+r ，则⊙O 1和⊙O 2位置关系是： (2）当d =2厘米时， 因为d R －r ，则⊙O 1和⊙O 2位置关系是： （3)当d =15厘米时，因为 ，则⊙O 1和⊙O 2位置关系是： （4）当d =7厘米时, 因为 ，则⊙O 1和⊙O 2位置关系是： （5）当d =1厘米时， 因为 ，则⊙O 1和⊙O 2位置关系是: 6、切线性质:例4：(1）如图，PA 是⊙O 的切线，点A 是切点，则∠PAO= 度（2）如图，PA 、PB 是⊙O 的切线，点A 、B 是切点， 则 = ，∠ =∠ ；7、圆中的有关计算 (1）弧长的计算公式:例5：若扇形的圆心角为60°，半径为3,则这个扇形的弧长是多少？ 解：因为扇形的弧长=()180所以l =()180= （答案保留π)OBPA（2）扇形的面积：例6：①若扇形的圆心角为60°，半径为3，则这个扇形的面积为多少？解：因为扇形的面积S= ()360= （答案保留π)所以S=()360②若扇形的弧长为12πcm，半径为6㎝,则这个扇形的面积是多少？解：因为扇形的面积S= 所以S= =（3)圆锥：例7：圆锥的母线长为5cm，半径为4cm，则圆锥的侧面积是多少？解：∵圆锥的侧面展开图是形,展开图的弧长等于∴圆锥的侧面积=8、三角形的外接圆的圆心——三角形的外心——三角形的交点；三角形的内切圆的圆心-—三角形的内心——三角形的交点;例8:画出下列三角形的外心或内心(1）画三角形ABC的内切圆, (2）画出三角形DEF的外接圆，二、练习：(一）填空题初三数学圆(word 版可编辑修改)OBAC 1、如图，弦AB 分圆为1:3两段，则AB 的度数= 度，ACB 的度数等于 度；∠AOB ＝ 度，∠ACB ＝ 度，2、如图，已知A 、B 、C 为⊙O 上三点，若AB 、CA 、BC 的 度数之比为1∶2∶3，则∠AOB ＝ ,∠AOC ＝ ， ∠ACB ＝ ，3、如图1－3－2，在⊙O 中，弦AB=1.8cm ，圆周角∠ACB=30○， 则 ⊙O 的半径等于=_________cm ．4、⊙O 的半径为5，圆心O 到弦AB 的距离OD=3，则AD= ，AB 的长为 ；5、如图，已知⊙O 的半径OA=13㎝，弦AB ＝24㎝，则OD= ㎝。

中考数学《圆》知识详解知识点一、圆的定义及有关概念1、圆的定义：平面内到定点的距离等于定长的所有点组成的图形叫做圆。

集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

2、有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。

圆上任意两点间的部分叫做圆弧，简称弧。

连接圆上任意两点间的线段叫做弦，经过圆心的弦叫做直径，直径是最长的弦。

在同圆或等圆中，能够重合的两条弧叫做等弧。

例 P为⊙O内一点，OP=3cm，⊙O半径为5cm，则经过P点的最短弦长为________；?最长弦长为_______．解题思路：圆内最长的弦是直径，最短的弦是和OP垂直的弦，答案：10 cm，8 cm.知识点二、平面内点和圆的位置关系平面内点和圆的位置关系有三种：点在圆外、点在圆上、点在圆内当点在圆外时，d＞r；反过来，当d＞r时，点A在圆外。

当点在圆上时，d＝r；反过来，当d＝r时，点B在圆上。

当点在圆内时，d＜r；反过来，当d＜r时，点C在圆内。

例如图，在Rt△ABC中，直角边AB?3，BC?4，点E，F分别是BC，AC的中点，以点A为圆心，AB的长为半径画圆，则点E在圆A的_________，点F在圆A的_________．解题思路：利用点与圆的位置关系，答案：外部，内部 A，?4)．试判断点P(3，?1)与圆O 的位置练习：在直角坐标平面内，圆O的半径为5，圆心O的坐标为(?1关系．答案：点P在圆O上．- 1 -。

圆知识点一、圆旳概念集合形式旳概念： 1、圆可以看作是到定点旳距离等于定长旳点旳集合；2、圆旳外部：可以看作是到定点旳距离不小于定长旳点旳集合；3、圆旳内部：可以看作是到定点旳距离不不小于定长旳点旳集合轨迹形式旳概念：1、圆：到定点旳距离等于定长旳点旳轨迹就是以定点为圆心，定长为半径旳圆；（补充）2、垂直平分线：到线段两端距离相等旳点旳轨迹是这条线段旳垂直平分线（也叫中垂线）；3、角旳平分线：到角两边距离相等旳点旳轨迹是这个角旳平分线；4、到直线旳距离相等旳点旳轨迹是：平行于这条直线且到这条直线旳距离等于定长旳两条直线；5、到两条平行线距离相等旳点旳轨迹是：平行于这两条平行线且到两条直线距离都相等旳一条直线。

二、点与圆旳位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆旳位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一种交点；3、直线与圆相交⇒d r<⇒有两个交点；四、垂径定理垂径定理：垂直于弦旳直径平分弦且平分弦所对旳弧。

推论1：（1）平分弦（不是直径）旳直径垂直于弦，并且平分弦所对旳两条弧；（2）弦旳垂直平分线通过圆心，并且平分弦所对旳两条弧；（3）平分弦所对旳一条弧旳直径，垂直平分弦，并且平分弦所对旳另一条弧A以上共4个定理，简称2推3定理：此定理中共5个结论中，只要懂得其中2个即可推出其他3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。

推论2：圆旳两条平行弦所夹旳弧相等。

即：在⊙O 中，∵AB ∥CD ∴弧AC =弧BD五、圆心角定理圆心角定理：同圆或等圆中，相等旳圆心角所对旳弦相等，所对旳弧相等，弦心距相等。

此定理也称1推3定理，即上述四个结论中， 只要懂得其中旳1个相等，则可以推出其他旳3个结论， 即：①AOB DOE ∠=∠；②AB DE =；③OC OF =；④ 弧BA =弧BD 六、圆周角定理1、圆周角定理：同弧所对旳圆周角等于它所对旳圆心旳角旳二分之一。