下载文档原格式
最大流问题的求解方法及应用
最大流问题，是指在一个有向图中，从源点 s 到汇点 t 的最大
流量。
在实际应用中，最大流问题往往用于描述网络传输、油管输送等流量分配问题。
求解最大流问题的方法包括以下几种：
1. 网络流算法：这是一种基于图论和线性规划的算法。
通过构建网络流图，将最大流问题转化为最小割问题，再利用线性规划求解最小割问题的对偶问题来求解最大流问题。
2. 增广路算法：这是一种经典的最大流算法，其基本思想是不断找到增广路径，即从源点 s 到汇点 t 的一条路径，沿途边权
均有剩余容量，使得该路径上的边的剩余容量中的最小值最大化，最终得到最大流。
3. 矩阵树定理：这是一种基于图论和矩阵运算的算法，适用于有向图和无向图。
通过计算图的拉普拉斯矩阵的行列式等方法，求得图的生成树个数，从而计算最大流。
4. Dinic算法：是对增广路算法的改进。
在增广路算法中，每
次查找增广路径的过程需要遍历整个图，为了提高效率，
Dinic算法引入了分层图的概念，将图分层之后只在图的一层
中查找增广路径，最终求得最大流。
这些方法在实际应用中常常被用来解决路由选择、网络流量优化、模拟电路分析等问题。
例如，最大流可以被用来优化数据传输、流水线设计、流量管道的运营和管理，提高资源利用率和数据传输速度。
最大流问题解题步骤一、什么是最大流问题？最大流问题是指在一个有向图中，给定源点和汇点，每条边都有一个容量限制，求从源点到汇点的最大流量。
该问题可以用于网络传输、电力调度等实际应用中。
二、最大流问题的解法1. 增广路算法增广路算法是最基本的解决最大流问题的方法。
其基本思想是不断地寻找增广路，并将其上的流量加入到原来的流中，直到不存在增广路为止。
具体步骤如下：（1）初始化网络中各边上的流量均为0；（2）在残留网络中寻找增广路；（3）如果存在增广路，则将其上的最小剩余容量作为增量加入到原来的流中；（4）重复步骤2和步骤3，直到不存在增广路。
2. Dinic算法Dinic算法是一种改进型的增广路算法，其核心思想是通过层次分析和分层图来减少搜索次数，进而提高效率。
具体步骤如下：（1）构建分层图；（2）在分层图上进行BFS搜索寻找增广路径；（3）计算路径上可行流量并更新残留网络；（4）重复步骤2和步骤3，直到不存在增广路。
3. Ford-Fulkerson算法Ford-Fulkerson算法是一种基于增广路的算法，其核心思想是不断地寻找增广路，并将其上的流量加入到原来的流中，直到不存在增广路为止。
具体步骤如下：（1）初始化网络中各边上的流量均为0；（2）在残留网络中寻找增广路；（3）如果存在增广路，则将其上的最小剩余容量作为增量加入到原来的流中；（4）重复步骤2和步骤3，直到不存在增广路。
三、最大流问题解题步骤1. 确定源点和汇点首先需要确定问题中的源点和汇点，这是解决最大流问题的前提条件。
2. 构建残留网络在有向图中，每条边都有一个容量限制。
我们可以将这些边看作管道，容量看作管道的宽度。
在实际传输过程中，某些管道可能已经被占用了一部分宽度。
因此，在求解最大流问题时，需要构建一个残留网络来表示哪些管道还能够继续传输数据。
具体方法是：对于每条边(u,v)，分别构造两条边(u,v)和(v,u)，容量分别为c(u,v)-f(u,v)和f(u,v)，其中c(u,v)表示边的容量，f(u,v)表示当前流量。
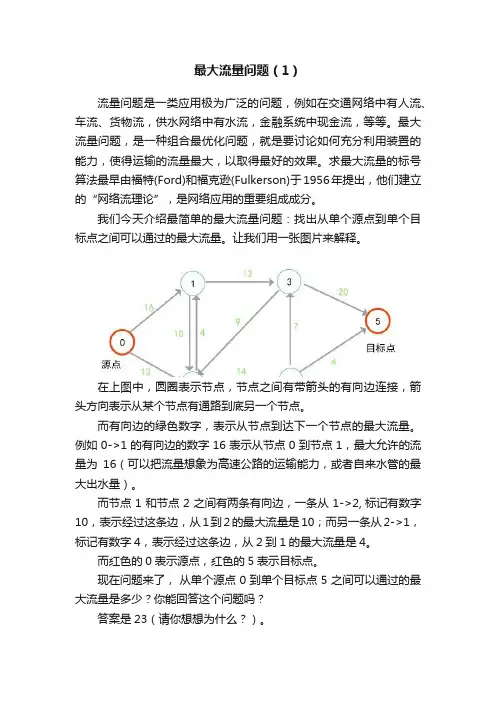
最大流量问题（1）流量问题是一类应用极为广泛的问题，例如在交通网络中有人流、车流、货物流，供水网络中有水流，金融系统中现金流，等等。
最大流量问题，是一种组合最优化问题，就是要讨论如何充分利用装置的能力，使得运输的流量最大，以取得最好的效果。
求最大流量的标号算法最早由福特(Ford)和福克逊(Fulkerson)于1956年提出，他们建立的“网络流理论”，是网络应用的重要组成成分。
我们今天介绍最简单的最大流量问题：找出从单个源点到单个目标点之间可以通过的最大流量。
让我们用一张图片来解释。
在上图中，圆圈表示节点，节点之间有带箭头的有向边连接，箭头方向表示从某个节点有通路到底另一个节点。
而有向边的绿色数字，表示从节点到达下一个节点的最大流量。
例如0->1的有向边的数字16表示从节点0到节点1，最大允许的流量为16（可以把流量想象为高速公路的运输能力，或者自来水管的最大出水量）。
而节点1和节点2之间有两条有向边，一条从1->2, 标记有数字10，表示经过这条边，从1到2的最大流量是10；而另一条从2->1，标记有数字4，表示经过这条边，从2到1的最大流量是4。
而红色的0表示源点，红色的5表示目标点。
现在问题来了，从单个源点0到单个目标点5之间可以通过的最大流量是多少？你能回答这个问题吗？答案是23（请你想想为什么？）。
具体的分流的情况如下图所示，其中的粉色数字表示两点之间的实际流量，它必须不大于原来规定的最大流量。
朴素贪婪算法我们先尝试采用朴素的贪婪算法来解决最大流量问题。
从假设每条边的流量都是0开始，采用贪婪算法，逐步增加对应的流量。
也就是从源点s到目标点t的某个路径上逐步增加更多流量（当然必须满足每条边的流量不超过运行的最大流量）。
假设在例子中：E是边的集合f(e)是边对应的流量C(e)是边对应的最大流量s-t路径表示从源点到目标点存在的路径算法的描述如下：1) max_flow = 02) 当存在s-t路径时，对每一条路径重复下面的步骤：a) 采用DFS（深度优先）或BFS（宽度优先）找到从s-t的路径P，并且路径上的每一条边e 都满足 f(e) < C(e)b) 如果找不到路径, 返回 max_flow。
最大流问题标号法例题详解最大流问题标号法例题详解本文以一道标号法求解最大流问题的例题胶加以详细讲解，帮助读者了解其原理及运算步骤。
题目如下：给定一个网络结构如下：s (源点) 0----1----2----3----4---- t (汇点)a 25 10 12 15 20其中 s 是源点，t是汇点，aij（i,j=0,1,2,3,4)是每条弧的容量，求整个网络的最大流量。
解：1、设置标号：在最大流问题中，为了求解最大流，最常用的方法是标号法。
首先，要设置各结点标号，因为本题中有5个结点，s源点的标号为0，t汇点标号为4，其他结点即1，2，3依次标号，标号的设定不仅便于求解，而且可以在初始化的时候使用。
2、初始化标号：初始化标号即将各结点初始化为两个空集合{}，即各结点的访问和未访问标号都是空集合，即无访问的结点标号为{}，访问过的结点标号也为{}。
3、依据标号法，从源点(s=0)计算，得出每条弧的剩余容量Cij，具体推导如下：源点0 1 2 3 41 0 25 10 12 152 0 0 10 7 103 0 0 0 8 104 0 0 0 0 20其中：Cij=aij-fij (i,j=0,1,2,3,4)其中，aij 为每条弧的容量，fij 为每条弧的流量，在初始情况下，fij=0，故Cij=aij。
4、找增广路径：从源点s开始，用深度优先搜索法查找从s到t的增广路径，具体步骤如下：设置一个数组P[i]用以记录路径，P[i]表示从s到i节点所经过的上一个结点，先从源点s开始，P[0]=-1，然后查找s出发可以到达的结点，若Cij>0，则有路可达，将P[j]=i（j为s出发可达的结点），接着查找j出发可以到达的结点（该结点未被访问过）若Cjk>0，则有路可达，把P[k]=j，以此类推，直到找到P[t]=-1，即从s到t 的一条增广路径找到，这条增广路径的路径上的容量称为Cmin，它是该增广路径上各结点之间的容量最小值。
运筹学最大流问题例题（原创版）目录一、运筹学最大流问题的基本概念二、最大流问题的求解方法三、最大流问题例题详解四、总结与展望正文一、运筹学最大流问题的基本概念运筹学最大流问题是一种在网络中寻找最大流量的问题。
给定一个有向图 G(V,E)，其中仅有一个点的入次为零称为发点（源），记为 vs；仅有一个点的出次为零称为收点（汇），记为 vt；其余点称为中间点。
对于G 中的每一条边 (vi,vj)，相应地给一个数 cji（cji 0），称为边 (vi,vj) 的容量。
最大流问题的目标是找到从源点到汇点的最大流量。
二、最大流问题的求解方法求解最大流问题的方法主要有两种：增广链路算法（如Ford-Fulkerson 算法）和最短路算法（如 Dijkstra 算法和Bellman-Ford 算法）。
增广链路算法主要思想是不断寻找增广链路，即在网络中寻找一条从源点到汇点的路径，使得路径上的每条边都有剩余容量。
最短路算法则是通过寻找源点到汇点的最短路径来解决最大流问题。
三、最大流问题例题详解假设有如下网络图：```vs --> v1 --> v2 --> vt| | |3 2 1```其中，vs 为源点，vt 为汇点，边 (vs,v1) 的容量为 3，边 (v1,v2) 的容量为 2，边 (v2,vt) 的容量为 1。
现在需要求解从 vs 到 vt 的最大流量。
利用增广链路算法，我们可以得到如下流程：1.初始化流量为 0，即所有边的流量均为 0。
2.从源点 vs 开始，遍历所有邻接点，找到有剩余容量的边，将其流量加 1，直到所有邻接点都遍历完毕。
3.更新流量，将当前点的流量分配给下一个邻接点，直到到达汇点 vt。
4.重复步骤 2-3，直到网络中不存在增广链路。
按照以上步骤，我们可以得到最大流量为 2。
四、总结与展望运筹学最大流问题是网络科学中的一个基本问题，有着广泛的应用。
通过增广链路算法和最短路算法，我们可以有效地解决最大流问题。
给定一个有向图D=(V,A),在V中指定一点称为发点(记为 )，该点只有出发去的弧，指定另一点称为收点(记为，)，该点只有指向它的弧，其余的点叫做中间点。
对于A中的每一条弧W f,对应一个数*亠20(简记片)，称之为弧的容量。
通常我们把这样的D叫做网络，记为D=(V,A,C)。
(2)网络流：在弧集A上定义一个非负函数y_ (Z(Pl JV P)是通过弧的实际流量，简记匚，称扌是网络上的流函数，简称网络流或流，称计Q为网络流的流量。
■ ⅛~ "»丄 / √ 第七章F⅛wearch ι§ 4网络最大流问题网络最大流冋题是网络的另一个基本冋题。
许多系统包含了流量问题。
例如交通系统有车流量，金融系统有现金流，控制系统有信息流等。
许多流问题主要是确定这类系统网络所能承受的最大流量以及如何达到这个最大流量。
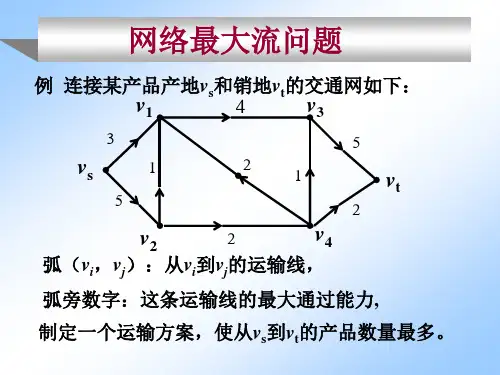
4.1基本概念与定理1. 1.网络与流定义14 (1)网络：例1如图7-20是连结某产品产地二和销地一的交通图。
弧∣∕Λ√<.;表示从二到的运输线，弧旁的数字表示这条运输线的最大通过能力IL ,括号内的数字表示该弧上的实际流一］。
现要求制定一个运输方案，使从-r运到甘t的产品数量最多。
可行流与最大流4⑴5(3)IO （I ）输网络的实际问题中，我们可以看出，对于流有两个基本要求：一是每条弧上的流量必须是非负的且不能超过该弧的最大通过能力（即该弧的容量）二是起点发出的流的总和（称为流量），必须等于终点接收的流的总和，且各中间点流 入的流量之和必须等于从该点流出的流量之和， 即流入的流量之和与流出的流量之和的差为 零，也就是说各中间点只起转运作用，它既不产出新的物资，也不得截留过境的物资。
因此有下面所谓的可行流的定义。
定义14对于给定的网络 D= （ V,A,C ）和给定的流 ."H ■...， 若一.满足下列条件：（1） 容量限制条件：对每一条弧工宀L ,有(7.9)（2）平衡条件： 对于中间点：流出量=流入量，即对于每一个i （i ≠ s,t ）,有(7.10)对于出发带点二，有∑Λ ■J l ）对于收点■■-，有⑺12)则称」_'；丨为一个可行流，’.丄 称为这个可行流的 流量。
注意，我们这里所说的出发点 I 是指只有从二发出去的弧，而没有指向「的弧；收点二是指只有弧指向V.，而没有从它的发出去的弧。
在运(7.11)可行流总是存在的。
例如令所有弧上的流J1. ,就得到一个可行流，（称为零流）, 其流量.I : 一。
如图7-20中，每条弧上括号内的数字给出的就是一个可行流/ = UJ ,它显然满足定义中的条件（1）和（2）。
其流量v（7）= 5+3 = 8 O所谓网络最大流问题就是求一个流」；_•： .,使得总流量达到最大，并且满足定义15中的条件（1）和（2）,即⑺13)网络最大流问题是一个特殊的线性规划问题。
我们将会看到利用图的特点，解决这个问题的方法较直线性规划的一般方法要简便和直观的多。
例2写出图7-20所表示的网络最大流问题的线性规划模型。
解设< I,则其线性规划模型为max1 l.Z3-Λ⅛-/M-Λ⅞ 二0 仏+fy -儿-九-几=0Λ⅛ + Λ6-∕⅛ = 0Λ+‰ ÷∕⅛ = V(Z)j ≠ ff,t f(7 14)牙人~~ 丁JE二* ⅛在网络D=(V,A,C)中，若给定一个可行流J ；...,我们把网络中使的弧称为饱和弧，使θ≤Λ<⅛ 的弧称为非饱和弧。
把九•二O的弧称为零流弧，把O <√⅛∙≤c if.的称为非零流弧。
如图7-20中的弧都是非饱和弧，而弧A八J为零流弧。
若"是网络中联结发点和收点匕的一条链，我定义链的方向是从I r到一则链上S的弧被分为两：一类是：弧的方向与链的方向一致，我们称此类和为前向弧，所有前向弧的集合记为.J。
另一类是：弧的方向与链的方向一致，我们称此类弧为后向弧，所有后向弧的集合记为,。
如图7-20中，设/■'. "√,.. J ''j∖ - \ - : Il L 1.〕是一条从儿到V 的链，则J 'j> 3 1：■ ：' ：1 . , ■- ^r-∙v√-'定义15设匚A-是网络D=(V ,A,C)上的一个可行流，门是从二到匕的一条链，若门满足下列条件：(1)在弧\ - J - . J (V i,V j) ∈μ+上，即.」J中的每一条弧都是非饱和弧；⑵在弧■丄上，即」中的每一条弧都是非零流弧。
则称尸是关于J的一条增广链。
如前面所说的链就是一条增广链。
因为其中μ+上的弧均非饱和，如(V s,V2) ∈μ+ ,f s2=5<C s2=13 ；而μ上的弧为非零流弧，如(V3,V2) ∈μ,f32 = 1>0 ,。
显然这样的增广链不止一条。
4.截集与截量定义16给定网络D=(V ,A,C)，若点集V被分割成两个非空集合V1和V2,使得V=V 1+V2,V1 ∩ V2=φ(空集)，且V s ∈V1,v t∈V2，则把始点在V1,终点在V 2的弧的集合称为分离V S和V t的一个截集，记为(V 1,V2)o如图9.26 中，设V1= {V s,v2,v5}, V 2= {v3,v4,V6,vJ 则截集为"?- V 1 '. —I ,而弧(v3,V2)和(V4,V5)不是该集中的弧。
因为这两条弧的起点在V2中，与定义17不符。
显然，一个网络的截集是很多的(但只有有限个) ，例如在图7-20中，还可以取叫-—∙I，二：「，则截集为另外，若把网络D=(VAC)中某截集的弧从网络D中去掉，则从V S到V t便不存在路，所以直观上说，截集是从V S到V t的必经之路。
定义17在网络D=(V ,A,C)中，给定一个截集(V1,V2)，则把该截集中所有弧的容量之和，称为这个截集的容量，简称为截量，记为c(V1,V2),即C(Vι,V2)=二二(7.16)叫•他例如在上面我们所举的两个截集中，有Λ)=⅛+⅛ +⅛ =9+6+9 = 24而= r j3÷c24+ c15= 9 + 6÷5 = 20显然，截集不同，其截量也不同。
由于截集的个数是有限的，故其中必有一个截集的容量是最小的，称为最小截集，也就是通常所说的“瓶颈”不难证明，网络D=(V ,A,C)中，任何一个可行流f= {f j}的流量V(f),都不会超过任—截集的容量，即v( f ) ≤C (V1,V2) (7.17) 如果存在一个可行流f*= {f*j},网络D=(V,A,C)中有一个截集(％：町)，使得' (7.18)则八: 必是最大流，而(W) 必是D中的最小截集。
为了求网络最大流f*,我们也说明下面的重要定理。
*定理4在网络D=(V ,A,C)中，可行流f 二忧}是最大流的充要条件是D中不存在关于f*的增广链。
证先证必要性。
用反证法。
若f*是最大流，假设D中存在着关于f*的增广链μ,令(7.19)由增广链的定义可知θ>0 ,令(7.20)不难验证」"是一个可行流，且有这与f*是最大流的假定矛盾。
、、 * * *再证充分性：即证明设D中不存在关于f的增广链，f是最大流。
用下面的方法定义：令-八"若WL ,且有7-.. ■< <■ ■，则令「一：；若L f ,且有、D ,则令YL ［。
因为不存在着关于」J的增广链，故「「记-J i - I1P,于是得到一个截集(V*,/)。
显然有所以V(f )=c I ∣'.，于是f必是最大流。
定理得证。
由上述证明中可见，若「'是最大流，则网络必定存在一个截集使得(7.18)式成立。
7定理5 (最大流一一最小截集定理)对于任意给定的网络D=(V ,A,C),从出发点VS到收点Vt的最大流的流量必等于分割I和二的最小截集V的容量，即VG re)= (Pix)由定理4可知，若给定一个可行流「' . ■/ ',只要判断网络D有无关于/'：'的增广链。
如果有增广链，则可以按定理4前半部分证明中的办法，由公式(7.19)求出调整量Q, 再按式(7.20)的方法求出新的可行流。
如果流有增广链，则得到最大流。
而根据定理4后半部分证明中定义的办法，可以根据Vt是否属于来判断D中有无关于f的增广链。
在实际计算时，我们是用给顶点标号的方法来定义的，在标号过程中，有标号的顶点表示是• 1中的点，没有标号的点表示不是「中的点。
一旦有了标号，就表明找到一条从V S到V t的增广链；如果标号过程无法进行下去，而V t尚未标号，则说明不存在从V S到V t的增广链，于是得到最大流。
这时将已标号的点（至少有一个点V S）放在集合！中，将未标号点（至少有一个点V t）放在集合中，就得到一个最小截集。
4.2 寻求最大流的标号法（FOrd , FUIkerSOn）从一个可行流出发「Γ（若网络中没有给定Li ,则可以设’是零流），经过标号过程与调整过程。
1）1）标号过程在这个过程中，网络中的点或者是标号点（又分为已检查和未检查两种），或者是未标号点，每个标号点的标号包含两部分：第一个标号表明它的标号是从哪一点得到的，以便找出增广链；第二个标号是为确定增广链的调整量θ用的。
标号过程开始，总先给V S标上（0,+ ∞）,这时V S是标号而未检查的点，其余都是未标号点，一般地，取一个标号而未检查的点V i，对一切未标号点V j:（1）在弧上S .打，孕，则给V j标号一「】.。
这里＞：■'.■ I：.-：. 一，。
这时点V j成为标号而未检查的点。
（2）若在弧［上，［「，给V j标号丄小。
这里-:'：'°这时点V j成为标号而未检查的点。
于是一成为标号而已检查过的点，重复上述步骤，一旦一被标上号，表明得到一条从到-的增广链-,转入调整过程。
若所有标号都是已检查过，而标号过程进行不下去时，则算法结束，这时的可行流就是最大流。
2）2调整过程首先按★及其它点的第一个标号，利用“反向追踪”的办法，找出增广链μ。
例如设V t的第一个标号为咗（或呢），则弧（V il V J）（或相应地（VJ）是μ上的弧。
接下来检查U的第一个标号，若为（或），则找出何J ifc）（或相应地（V tr V J））°再检查勺的第一个标号，依此下去，直到I为止。
这时被找出的弧就构成了增广链H。
令调整量θ是,即二的第二个标号。
几•+&⅛√令A' j甘-R(V in V J.) (=j LT^去掉所有的标号，对新的可行流,重新进入标号过程。
下面，以例题说明此算法求解过程。
