图与网络模型_最大流问题
- 格式:pdf
- 大小:138.71 KB
- 文档页数:6

网络最大流问题一产生背景流量问题在实际中是一种常见的问题,在许多实际的网络系统中都存在着流量和最大流问题。
例如铁路运输系统中的车辆流,城市给排水系统的水流问题,控制系统中的信息流问题,常见的人流,物流,水流,气流,电流,现金流等。
在一定条件下,求解给定系统的最大流量,就是网络最大流问题.网络系统最大流问题是图与网络理论中十分重要的最优化问题,它对于解决生产实际问题起着十分重要的作用。
二基本概念与定理设cij为弧(i,j)的容量,fij为弧(i,j)的流量。
容量是弧(i,j)单位时间内的最大通过能力,流量是弧(i,j)单位时间内的实际通过量,流量的集合f={fij}称为网络的流。
发点到收点的总流量记为v=v(f)。
设D=(V,A)是一有向图且对任意E均有容量cij =(vi,vj),记C={cij︱(vi,vj)∈A},此外D中只有一个源vs和汇vt( 即D中与vs相关联的弧只能以vs为起点,与vt相关联的弧只能以vt为终点),则称D=(V,A,C, vs,vt)为一网络。
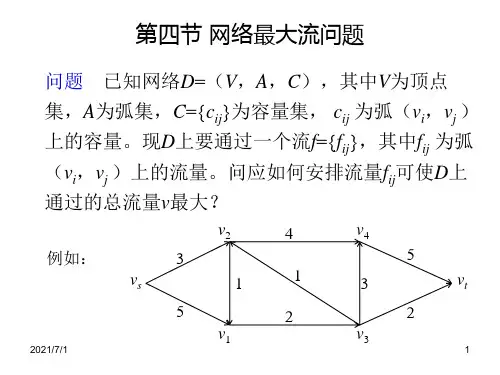
引例1:图1给出了一张网络,其中:vs为源,vt为汇,弧旁的数字为该段弧的容量cij与流量fij,则显然有0≤fij ≤ cij 。
v2 (3,3) v4(3,3)(5,5)vt (2,2) (2,2) (2,2) vt(6,4) (6,2)v1 (6,6) v3图1最大流问题可以建立如下形式的线性规划数学模型。
图1最大流问题的线性规划数学模型为12max 0(,)0s s ij ij j i ij ij v f f f f i s t f c =+⎧-=≠⎪⎨⎪≤≤⎩∑∑所有弧(i,j)由线性规划理论知,满足式上式的约束条件的解{fij}称为可行解,在最大流问题中称为可行流。
可行流满足下列三个条件:(1)0(2)(3)i j i j m j i m j i sj it vs vt f cf fv f f ≤≤===∑∑∑∑条件(2)和条件(3)也称为流量守恒条件。









最大流问题实际应用场景引言最大流问题是图论中的常见问题之一,也是一种典型的网络流问题。
其应用场景广泛,涉及到物流配送、通信网络、水资源管理等领域。
通过对最大流问题的深入研究和解决,可以优化资源利用,提升系统性能,实现资源的合理分配与调度。
铁路货运优化铁路货运优化是最大流问题在实际应用中的一个典型场景。
铁路系统通常由一系列的节点(火车站)和边(铁路线路)组成,货物需要在不同的火车站之间进行运输。
通过求解最大流问题,可以确定铁路货运系统的最大吞吐量,从而在不同的火车站之间合理调度货物的运输量,提高铁路货运的效率。
问题建模1.将所有火车站表示为图的节点,铁路线路表示为图的边。
2.将每个火车站看作一个节点,引入超级源点S和超级汇点T。
3.设置超级源点S和超级汇点T,并将超级源点与火车站相连,容量设置为该站发出货物的总量;将超级汇点与火车站相连,容量设置为该站需要接收货物的总量。
4.将铁路线路表示为图的边,设置其容量为该线路的运输能力。
求解方法1.构建图模型后,可以利用网络流算法(如Ford-Fulkerson算法)求解最大流问题,得到最大的货物运输量。
2.根据最大流的结果,可以对不同的火车站之间的货物进行分配和调度,优化运输效率。
电力网络优化电力网络是一个复杂而庞大的系统,其中电力的产生、输送和分配需要进行合理的管理和优化。
最大流问题可以用于解决电力网络中的优化问题,如电力输送、线路负载平衡等。
问题建模1.将电力网络中的输电线路表示为图的边,变电站、发电站、负荷站等设备表示为图的节点。
2.引入超级源点S和超级汇点T,将变电站与超级源点S相连,容量设置为变电站的最大供电能力;将负荷站与超级汇点T相连,容量设置为负荷站的需求。
3.通过将发电站、变电站和负荷站之间的连接路径建模为图的边,设置其容量为线路的输送能力。
求解方法1.构建图模型后,可以使用最大流算法求解最大流问题,得到电力网络的最大输送能力,即最大负荷容量。
图论与网络流问题的LINGO 求解技巧我们介绍使用LINGO 求解图论与网络问题中的一些典型问题。
如最短路问题、最大流问题、关键路径问题、最优树问题,以及TSP 问题。
这里主要介绍使用LINGO 求解的方法,重在应用和解决问题。
1 最短路问题的Lingo 求解设图共有个节点,其赋权图的邻接矩阵为n n n w ×.ij w p =表示节点i 到j 的权值为.当为有向图时,p ji w w ij =;当为无向图时,和ij w ji w 分别由图得到,通常不一样。
当,表示节点i 与节点0ij w =j 不连通。
令0ii w =。
假设图的所有权值 0ij w ≥现求节点a 到节点b 的最短路,其线性规划模型为:模型一、决策变量:设1ij i j x i j ⎧=⎨⎩节点与节点连通节点与节点不连通目标函数为寻找一条节点到节点的通路,使其上权值和最小,故目标函数为:a b 11min .nnij ij i j Z w x ===∑∑1. 对节点恰有一条路出去,却不能有路回来,故有:a 11najj j ax=≠=∑ 且10nkak k a x=≠=∑2. 对节点恰有一条路到达,却不能有路出去,故有:b 11nkbk k bx=≠=∑ 且10nbjj j bx=≠=∑3. 对除起始点a 和目标点之外,其它点进入和出去的路是一样多(可都为0),则:b 11,nnkiijk j xx i a ===≠∑∑b4. 对不通的路不取,约束为:,1,2,ij ijx w i j ≤=L n总的线性规划模型为:11111111min .,10..10,1,2,,01n nij iji j nnki ijk j naj j j a n ka k k a n kb k k a nbj j j a ij ijijZ w x x x i a b x x s t x x x w i j x =====≠=≠=≠=≠=⎧=≠⎪⎪⎪=⎪⎪⎪⎪=⎪⎪⎪⎪=⎨⎪⎪⎪=⎪⎪⎪≤=⎪⎪=⎪⎪⎪⎩∑∑∑∑∑∑∑∑L 或n示例演示。
最大流问题在许多实际的网络系统中都存在着流量和最大流问题。
例如铁路运输系统中的车辆流,城市给排水系统的水流问题等等。
网络系统流最大流问题是图与网络流理论中十分重要的最优化问题,它对于解决生产实际问题起着十分重要的作用。
基本概念设一个赋权有向图D=(V , A),在V 中指定一个发点(源)vs 和一个收点(汇)vt ,且只能有一个发点vs 和一个收点vt 。
(即D 中与vs 相关联的弧只能以 vs 为起点,与vt 相关联的弧只能以 vt 为终点),其他的点叫做中间点。
对于D 中的每一个弧(vi, vj)A ∈,都有一个权cij 叫做弧的容量。
我们把这样的图 D 叫做一个网络系统,简称网络,记做D =(V , A, C)。
VsVt 图1图1是一个网络。
每一个弧旁边的权就是对应的容量。
网络D 上的流,是指定义在弧集合A 上的一个函数f={f(vi, vj)}={fij},f(vi,vj)=fij 叫做弧在(vi,vj)上的流量。
VsVt 图2图2中,每条弧上都有流量fij ,例如fs1=5,fs2=3,f13=2等。
容量是最大通过能力,流量是单位时间的实际通过量。
显然,0≤fij≤cij 。
网络系统上流的特点:(1)发点的总流出量和收点的总流入量必相等;(2)每一个中间点的流入量与流出量的代数和等于零;(3)每一个弧上的流量不能超过它的最大通过能力(即容量)。
网络上的一个流f={fij}叫做可行流,如果f 满足以下条件: (1)容量条件:对于每一个弧(vi,vj)A ∈,有0≤fij≤cij 。
(2)平衡条件:对于发点vs ,有∑f sj −∑f js =v (f ) 对于收点vt ,有∑f tj −∑f jt =−v (f )对于中间点,有∑f ij −∑f ji =0其中发点的总流量(或收点的总流量)v(f)叫做这个可行流的流量。
网络系统中最大流问题就是,在给定的网络上寻求一个可行流f={fij},其流量v(f)达到最大值,即从vs 到vt 的通过量最大。
最大流问题可以通过线性规划数学模型来求解。
图1的最大流问题的线性规划数学模型为max v =f s 1+f s 2s.t.{∑jf ij −∑if ij =0i ≠s,t 0≤f ij ≤c ij所有弧(v i ,v j )fs1和fs2是与起点相连的两条弧上的流量。
满足上式的约束条件的解{fij}称为可行解,在最大流问题中称为可行流。
对有多个发点和多个收点的网络,可以另外虚设一个总发点和一个总收点,并将其分别与各发点、收点连起来,就可以转换为只含一个发点和一个收点的网络。
ST所以一般只研究具有一个发点和一个收点的网络。
我们把fij=cij 的弧叫做饱和弧,fij<cij 的弧叫做非饱和弧,fij>0的弧为非零流弧,fij=0的弧叫做零流弧。
在图3(图1与2合并图)中,(v4,v3)是饱和弧,其他的弧是非饱和弧,并且都是非零流弧。
VsVt,fij )图3网络D 中,从发点νs 和收点vt 的一条路线称为链(记为μ)。
从发点νs 到收点vt 的方向规定为链的方向。
链μ上的弧被分为两类:一,弧的方向与链的方向相同,叫做前向弧,前向弧的集合记做μ+。
二,弧的方向与链的方向相反,叫做后向弧,后向弧的集合记做μ-。
在图3中,假设链μ=(vs,v1,v2,v3,v4,vt)中,则μ+={(vs,v1),(v1,v2),(v2,v3),(v4,vt)},μ-={(v4,v3)}。
设f={fij}是一个可行流,如果存在一条从发点vs到收点vt到的链μ满足:1.前向弧集μ+中的每一条弧是非饱和弧,即 fij<cij。
2.后向弧集μ-中的每一条弧是非零流弧,即0<fij。
则称链μ为增广链。
例如在图3中,链μ=(vs,v1,v2,v3,v4,vt)就是一条增广链。
定理 网络中的一个可行流f是最大流的充分必要条件是,不存在关于f的增广链。
定理实际上提供了一个寻求最大流的方法:如果网络D中有一个可行流f,只要判断网络是否存在关于可行流f的增广链。
如果没有增广链,那么f一定是最大流。
如有增广链,那么通过不断改进和增大可行流f的流量,最终可以得到网络中的一个最大流。
标号法(Ford-Fulkerson 算法)标号法是一种图上迭代计算方法,该算法首先从发点开始,通过标号找出一条增广链,然后增加增广链上的流量,得到更大的流量。
再通过标号找出一条新的增广链,再增加流量,…,重复这个过程,直到收点不能标号为止,这时就得到网络中的一个最大流。
在标号过程中,一个点仅有下列三种状态之一:●标号已检查(有标号且所有相邻点都标号了)●标号未检查(有标号,但某些相邻点未标号)●未标号每个标号点的标号包含两部分:第一个标号表示这个标号是从那一点得到的。
以便找出增广链。
第二个标号是为了用来确定增广链上的调整量I(vi)。
1,标号过程标号过程开始,先给发点vs标号(0,+∞)。
这时,vs是标号未检查的点,其他都是未标号点。
一般地,选一端已标号未检查且另一端未标号的弧,然后向收点方向依次标号。
选择一个已标号未检查的点vi,1)对每一个弧(vi, vj),如果vj未标号,且fij<cij,即流出未饱和弧,那么给vj标号(vi,l(vj))。
其中I(v)=min[I(v i),c ij−f ij]j这时,vj成为标号未检查点。
2)对每一个弧(vj, vi),如果vj未标号,且fij>0,即即流入非零流弧,那么给vj标号(-vi, l(vj))。
其中I(v)=min[I(v i),f ij]j这时,vj成为标号未检查点。
然后vi就成为标号已检查的点。
重复以上步骤,如果所有的标号都已经检查过,而标号过程无法进行下去,则标号法结束。
这时的可行流就是最大流。
但是,如果vt 被标上号,表示得到一条增广链μ,转入下一步调整过程。
2,调整过程首先按照vt 和其他的点的第一个标号,反向追踪,找出增广链μ。
例如,令vt 的第一个标号是vk ,则弧(vk,vt)在μ上。
再看vk 的第一个标号,若是vi ,则弧(vi,vk)都在μ上。
依次类推,直到vs 为止。
这时,所找出的弧就成为网络D 的一条增广链μ。
取收点调整量θ=l(vt),即vt 的第二个标号,对增广链上的弧流量进行调整,令f ij ′={f ij +θ当(v i ,v j )∈μ+f ij −θ当(v i ,v j )∈μ-其他不变去掉所有的标号,得到新的可行流f '={fij'},再从发点开始,重新进行标号过程,直到收点不能标号为止。
例1,求图4的网络最大流,弧旁的权数表示(cij, fij)。
VsVt,fij )图4解:用标号法。
1,标号过程。
(1)首先给vs 标号(0, +∞)(2)看vs :在弧(vs,v2)上,fs2=cs2=3,不具备标号条件。
在弧(vs,v1)上,fs1=1<cs1=5,故给v1标号(vs,l(v1)),其中l(v1)=min[l(vs), (cs1-fs1)]=min[+∞,5-1]=4。
(3)看v1:在弧(v1,v3)上,f13=c13=2,不具备标号条件。
在弧(v2,v1)上,f21=1>0,故给v2标号(-v1,l(v2)),其中l(v2)=min[l(v1), f21]=min[4,1]=1。
(4)看v2:在弧(v2,v4)上,f24=3<c24=4,故给v4标号(v2,l(v4)),其中l(v4)=min[l(v2), (c24-f24)]=min[1,1]=1。
在弧(v3,v2)上,f32=1>0,故给v3标号(-v2, l(v3)),其中l(v3)=min[l(v2),f32]=min[1,1]=1。
(5)在v3,v4中任意选一个,比如v3。
在弧(v3,vt)上,f3t=1<c3t=2,故给vt 标号(v3,l(vt)),其中l(vt)=min[l(v3),(c3t-f3t)]=min[1,1]=1。
因为vt 被标上号,根据标号法,转入调整过程。
标号过程,v1v2vsv3v4vtVs Vt,fij )(0,+∞(vs,4)(-v1,1)(-v2,1)(v2,1)图52,调整过程从vt 开始,按照标号点的第一个标号,用反向追踪的方法,找出一条从vs 到vt 的增广链μ,如图5中粉红线所示。
不难看出,μ+={(vs,v1),(v3,vt)},μ-={(v2,v1),(v3,v2)}。
取θ=1,在μ上调整f ,得到f ′={f s 1+θ=1+1=2在μ+上f 3t +θ=1+1=2在μ+上f 21−θ=1−1=0在μ-上f 32−θ=1−1=0在μ-上其他的不变调整后的可行流f ',如图6所示,去掉原有标号,再对这个可行流从新进行标号过程,寻找增广链。
首先给vs 标号(0, +∞),看vs ,给v1标号(vs,3)。
看v1,在弧(v1,v3)上,f13=c13,弧(v2,v1)上,f21=0,均不符合条件。
因此标号过程无法进行下去,不存在从vs 到vt 的增广链,算法结束。
Vt ,fij')图6设一个网络D=(V , A, C)。
如果点集V 被剖分为两个非空集合V 1和¯V1,发点vs V ∈1,收点vt ∈¯V1,那么将弧集(V 1,¯V 1)叫做是分离vs 和vt 的截集。
(V 1,¯V1)={(v i ,v j )∣v i ∈V 1,v j ∈¯V 1}将截集(V 1,¯V1)中所有的弧的容量的和叫做截集的截量,记做c(V 1,¯V 1),c (V 1,¯V 1)=∑(v i ,v j )∈(V 1,¯V1)c ij下面的事实是显然的:一个网络D 中,任何一个可行流f 的流量v(f)都小于或等于这个网络中任何一个截集(V 1,¯V1)的截量。
并且,如果网络上的一个可行流f '和网络中的一个截集(V 1*,¯V 1*),满足条件v(f ')=c(V 1*,¯V 1*),那么f '一定是D 上的最大流,而(V 1*,¯V 1*)一定是D 的所有的截集中截量最小的一个(即最小截集)。
定理2 在一个网络D 中,最大流的流量等于分离vs 和vt 的最小截集的截量。
例如在图6中,V 1*={vs, v1},¯V1*={v2, v3, v4, vt}。
虚线框中的点集即为V 1*。
(V 1*,¯V 1*)={(vs, v2),(v2, v1),(v1, v3)}c(V 1*,¯V 1*)=fs2+f21+f13=5采用Ford-Fulkerson 标号算法求解最大流问题,同时得到一个最小割集。