当前位置：文档之家 › 图与网络分析 最大流问题

图与网络分析 最大流问题

  • 格式：ppt
  • 大小：4.34 MB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

运筹学05_图与网络分析3-最大流

运筹学05_图与网络分析3-最大流
去掉所有点的标号，对新的可行流f ' {fij '}进行标号
min 1 ,2
例6：用标号法求如下图所示的网络最大流
v1
(5,2)
v3
vs
(6,5)
(6,0)
vt
v2
(10,4)
v4
(s,+) v1 *
(5,2)
(1,+) v3 *
vs* (0,+)
(6,5)
(6,0)
vt (4,+)(3,+)
1
(2 )
(3) V3 V5
定理4：在网络D中，对可行流f，若存在增广链， 那么f一定可以改进，以使流值增大。
定理5：可行流f*是最大流，当且仅当不存在关于 f*的增广链

根据定理，对于给定的可行流f，要判断它是不 是最大流只需要判断D中有没有关于f的增广链。

如果有则需要对f进行改进；如果没有增广链， 则已经得到最大流。
f =10
(4,5)
v1 (6,6) (0,3) (2,2) v5 (0,3) (0,4) v2
(4,10)
v0
(0,3)
(4,4)
(6,6) vn (4,10) v4 (0,5)
(2,5)
(0,3) v3
(4,5)
v1 (6,6) (0,3) (2,2) v5 (0,3) (0,4) v4 (0,5) v2
选择标号但是未检查的点，如vi，对于一切未标号的点v j
若在弧(vi , v j )上，f ij cij , 则给v j标号(i, ), 从vi出发的弧 则v j变为标号但是未检查的点, 否则不标号
若在弧(v j , vi )上，f ji 0, 则给v j标号(i, -), 则v j变为标号但是未检查的点, 否则不标号

《运筹学》第8章_图与网络分析

《运筹学》第8章_图与网络分析
V = {v1 ,v 2 , v 3 , v 4 , v 5 , v 6 }
v1 e1 e2 e5 e8 v5 e6 e7 v3 v2 e3 e v4 4
e 5 = { v1 , v 3 }
e9 = {v 6 , v 6 }
E = {e1 ，2 , e3 , e4 , e5 , e6 , e7 , e8 , e9 , e10 } e e1 = {v1 , v 2 } e 2 = { v1 , v 2 } e10 e 3 = {v 2 , v 3 } e = {v , v }
引
C
言
B A
D
图的基本概念与基本定理
在实际的生产和生活中，人们为了 反映事物之间的关系，常常在纸上用点 点 和线来画出各式各样的示意图。 和线 是我国北京、上海、重庆等十四个城 市之间的铁路交通图，这里用点表示城 市，用点与点之间的线表示城市之间的 铁路线。诸如此类还有城市中的市政管 道图，民用航空线图等等。
例
v6
v1 3 6
4 7 3
v2 2 v3 5
3
4 2
权矩阵
v1 0 v 2 4 v 3 0 A= v4 6 v5 4 v6 3 v1
v5
v4
邻接矩阵
v1 0 v 2 1 v 3 0 B= v 4 1 v 5 1 v 6 1 v1 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 0 v 2 v 3 v4 v5 v6
4 3 4
e6 = {v 3 , v 5 }
e8 = {v 5 , v 6 } e10 = {v1 , v6 }
v6
e 7 = {v 3 , v 5 }

网络最大流问题-xfj

网络最大流问题-xfj

b.终点得到标号，反向追踪即可找到从起点到终点由标号 点及相应的弧连接而成的一条增广链。
(0, +∞)
s (5, 2)
(S+,3)
v1
(7, 5)
(v1-,5)
t
h
18
3．调整过程：
修改流量，其中流量调整量
， mjinj
指增广链上所有点的流量修正量； j
调整方法：
在增广链的正向弧上增加 ；
反向弧上减少 ；
是，则不加标记； 不是，则加标记为(vs+,j)，其中 j =csj-fsj；
✓对反向弧，检查其是否是零流弧？
是，则不加标记； 不是，则加标记为(vs-, j)，其中 j =fsj；
h
17
重复步骤二，但要注意把vs换成已得到标号的点；可能
出现两种结局：
a.标号过程中断，终点得不到标号。说明该网络中不存在 增广链，现行的可行流就是最大流；
h
13
定理8：
可行流f *是最大流，当且仅当 存不 在
关于f *的增广链。
➢思路：可行流f*是最大流<=>不存在关于f*的增广链.
[证] 必要性→ 用反证法。若 f* 是D中的最大流，假定存在关于f* 的增
广链u，令
。那么，由增广链的定义可
知 m ，现令m iu n (c i{ ijn fi* j)m ,u fii* j} n
令 vsV1*（ ; 起点属V 于 1*）点集 若 vi V1*,且 fi*j cij,则令 vj V1*(正向非饱和弧 都 的 属 起 V1于 *)终 若 vi V1*,且 fj*i 0,则令 vj V（ 1* 反向非零弧 都 的 属 起 V1于 *） 终
因D中不存在关于f*的增广链，故必有

运筹学(第6章 图与网络分析)

运筹学(第6章 图与网络分析)
a1 (v1) 赵
(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈

定义: 图中的点用v表示，边用e表示。对每条边可用它
所连接的点表示，记作：e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后，可用图来表示相遇情况，如 下图所示。
运动员 A
B C
D
E
F G
H

例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系，那么只用两点之间的联线就很难刻画他们之间的关 系了，这是我们引入一个带箭头的联线，称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj]，称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点，反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联，称点vi和vj相邻；若边ei和
e5
e7

图与网络分析 - 最大流问题

图与网络分析 - 最大流问题



其中f(vi ,vj) =fij 叫做弧(vi，
vj)上的流量。
（2）可行流：称满足下列条件的流为可行流： 1）容量约束：对于每一个弧（vi ,vj）∈A有 0 fij cij 。 2）守恒条件：对于所用的中间点 v V {v s , v t )
有
( vi , v j )E

v4
5 (0)
vt
10 (1)
v3
v6
图中 (v 3 , v 6 ) 为零流弧，其余为非饱和弧、非零流弧。
流量v(f ) =8
最大流
• 网络上的流量最大的可行流称作的最大流 •所谓最大流问题就是求给定网络的最大流
（二）最大流的算法
1、由图编写程序
2、由lingo8.0软件求最大流
例8 现需要将城市s 的石油通过管道运送到城市 t,中间有4个中转站v1,v2,v3 和v4，城市与中转站的 连接以及管道的容量如下图所示，求从城市s 到城 市t 的最大流
Global optimal solution found at iteration: 6 Objective value: 14.00000 Variable Value Reduced Cost FLOW 14.00000 0.000000 F( S, 1) 7.000000 0.000000 F( S, 2) 7.000000 0.000000 F( 1, 2) 2.000000 0.000000 F( 1, 3) 5.000000 0.000000 F( 2, 4) 9.000000 -1.000000 F( 3, 2) 0.000000 0.000000 F( 3, T) 5.000000 -1.000000 F( 4, 3) 0.000000 1.000000 F( 4, T) 9.000000 0.000000 v1 (9,5) (2,0) (5,2) (7,7) v2 (9,9) v3 (5,5) (6,0) v4 t (10,9)

图与网络模型_最大流问题

图与网络模型_最大流问题

最大流问题在许多实际的网络系统中都存在着流量和最大流问题。

例如铁路运输系统中的车辆流，城市给排水系统的水流问题等等。

网络系统流最大流问题是图与网络流理论中十分重要的最优化问题，它对于解决生产实际问题起着十分重要的作用。

基本概念设一个赋权有向图D=(V , A)，在V 中指定一个发点（源）vs 和一个收点（汇）vt ，且只能有一个发点vs 和一个收点vt 。

（即D 中与vs 相关联的弧只能以 vs 为起点，与vt 相关联的弧只能以 vt 为终点），其他的点叫做中间点。

对于D 中的每一个弧(vi, vj)A ∈，都有一个权cij 叫做弧的容量。

我们把这样的图 D 叫做一个网络系统，简称网络，记做D =(V , A, C)。

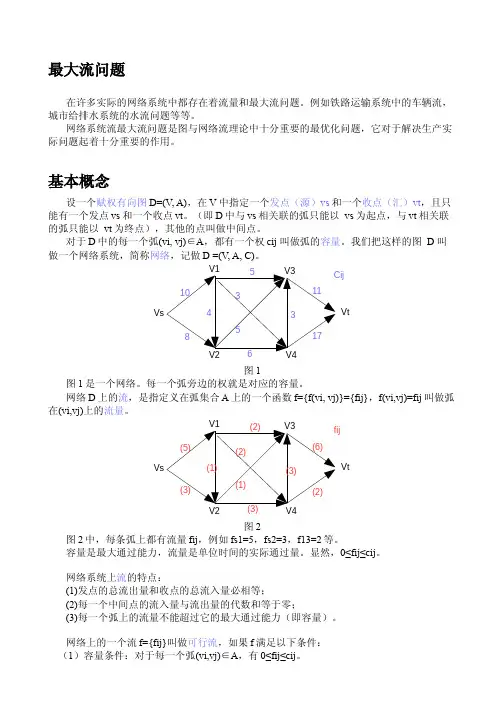
VsVt 图1图1是一个网络。

每一个弧旁边的权就是对应的容量。

网络D 上的流，是指定义在弧集合A 上的一个函数f={f(vi, vj)}={fij}，f(vi,vj)=fij 叫做弧在(vi,vj)上的流量。

VsVt 图2图2中，每条弧上都有流量fij ，例如fs1=5，fs2=3，f13=2等。

容量是最大通过能力，流量是单位时间的实际通过量。

显然，0≤fij≤cij 。

网络系统上流的特点：(1)发点的总流出量和收点的总流入量必相等；(2)每一个中间点的流入量与流出量的代数和等于零；(3)每一个弧上的流量不能超过它的最大通过能力（即容量）。

网络上的一个流f={fij}叫做可行流，如果f 满足以下条件： （1）容量条件：对于每一个弧(vi,vj)A ∈，有0≤fij≤cij 。

（2）平衡条件：对于发点vs ，有∑f sj −∑f js =v (f ) 对于收点vt ，有∑f tj −∑f jt =−v (f )对于中间点，有∑f ij −∑f ji =0其中发点的总流量（或收点的总流量）v(f)叫做这个可行流的流量。

网络系统中最大流问题就是，在给定的网络上寻求一个可行流f={fij}，其流量v(f)达到最大值，即从vs 到vt 的通过量最大。

运筹学第六章图与网络分析

运筹学第六章图与网络分析

S
2
4
7
2 A
0 5
S
5 45 B
98
14
5
13
D
T
C
E
4
4
4
7
最短路线：S AB E D T
最短距离：Lmin=13
2．求任意两点间最短距离的矩阵算法
⑴ 构造任意两点间直接到达的最短距离矩阵D（0）= dij（0）
S A B D（0）= C D E T
SABCDET 0 25 4 2 02 7 5 20 1 5 3 4 1 0 4 75 0 15 3 41 0 7 5 7 0
e1 v1
e5
v0 e2
e3
v2
e4
e6 e7
v3
v4
（4）简单图：无环、无多重边的图称为简单图。
（5）链：点和边的交替序列，其中点可重复，但边不能 重复。
（6）路：点和边的交替序列，但点和边均不能重复。
（7）圈：始点和终点重合的链。
（8）回路：始点和终点重合的路。
（9）连通图：若一个图中，任意两点之间至少存在一条 链，称这样的图为连通图。 （10）子图，部分图：设图G1=｛V1,E1｝, G2={V2,E2}, 如果有V1V2，E1E2，则称G1是G2的一个子图；若 V1=V2，E1E2，则称G1是G2的一个部分图。 （11）次：某点的关联边的个数称为该点的次，以d(vi)表示。
步骤：
1. 两两连接所有的奇点，使之均成为偶点；
2. 检查重复走的路线长度，是否不超过其所在 回路总长的一半，若超过，则调整连线，改 走另一半。
v1
4
v4
4
1
4
v2
v5
5

第四节 网络系统最大流问题

第四节 网络系统最大流问题
2 2
5 6
6 0
7
V6
V 8 V 10
V3
6 10
V5
前向弧： 1 min{Cij fij } 2
后向弧：
2
min{ 1 , 2 } 2
V2
8 8
5 5 3 2 5
1
V4
10 19
4
V1
2 2
5 6
6 0
7
V6
V 8 V 10
而对于实际问题来说，通常需要求最大流．
那么，如何求最大流呢？ 最大流可以从任何一个可行流出发来求．
这需要下面的可扩充路的概念．
定义 6.17 设 { fij }是一组可行流，如果存在一 条从起点V1 到终点V 的路P，满足 ①在P的所有前向弧上 0 fij Cij ( fij Cij ) ( fij 0) ②在P的所有后向弧上 0 fij Cij 则称P是一条关于流 { fij }的可扩充路．
对于P的所有后向弧 (0 fij Cij ) (若P无后向弧，则令 2 ) 令 2 min{ fij }
再令 min{ 1 , 2 }
最后，构造新的可行流 { f ij }, 使得
f ij fij fij
f ij
若弧 (Vi ,Vj )不在路P上 若弧 (Vi ,Vj )是路P的前向弧 若弧 (Vi ,Vj ) 是路P的后向弧
V3 V2
8
8
6 10
V5 V4
5
1
2 5
最大流不唯一
7
3 0 6 6
19
4
V1
2 2
6 3
7
V6

8 图与网络4--最大流问题

8 图与网络4--最大流问题

v2
9(9)
v4
网络的最大流
Page 18
(2) 检查与v1点相邻的未标号的点，因f13<c13，故对v3标号 (3) =min{1, c13-f13}= min{1, 6}= 1
(1)
v1
9(3)
(1)
v3
5(4)
8(7)
(∞)
s
7(6)
5(4)
2(0)
6(1)
●
t
10(8) v2 9(9) v4
i j j i j j
si j
(i s, t )
f
i
f jt W ，W为网络流的总流量。
(即从vs点发出的物资总量等于vt点输入的量。)
网络的最大流
Page 6
结论：任何网络上一定存在可行流。（零流即是 可行流） 网络最大流问题：
指满足容量限制条件和中间点平衡的条件下，使v(f)值 达到最大。
o v6 o
Page 8
2 4 v 5 2
o
v2
o
v3 7 3
o
2 1
6
2
o v4
分离vs和vt的截 o vt 集往往不只一个， 称截量最小的为 1 最小截集。
上图中，若令Vs={vs,v1,v6},Vt={v2,v3,v4,v5, vt},则：截集为{(vs,v5), (v1,v2),(v1,v5), (v6,v5) ,(v6,v4)},截量为3+2+4+2+3=14； 截集是 vs 到 vt 的必经之路，无论去掉哪个截集，从 vs 到 vt就不存在 路了,因此,任何一个可行流的流量不会超过任何一个截集的容量。
(2) (2)
v1 8(8)

10.4 网络最大流问题

10.4 网络最大流问题

V1
v2
v4
C( V1 , V1 ) w s1 w 24 w 23 7 6 5 18
5 (3)
v2
13 (5) 6(3) 4 (1) 5 (2) 5 (2)
v5
4 (2) 4 (1) 5 (0)
9 (5)
v1
9 (3)
v4
v7
10 (1)
v3
v6
设 V1 v1 , v2 , v5 V2 v3 , v4 , v6 , v7 则截集为：
③对于中间点: 流入量=流出量。 即对每个i(i≠s,t)有 f(vi,vj) - f(vj,vi)=0(is，t) (简记为 fij- fji= 0(is，t) )
即总流量=发点的净输出量=收点的净输入量

容量网络的可行流总是存在的， 如当所有弧的流均取零，即对所有的i,j,有 f(vi,vj)=0就是一个可行流
图10-24表示的就是这个网络上的一个流（运输方案），
每一个弧上的流量fij就是运输量。 例如：f12=1 , f13=2 , f24=3 等等。
v1
（2）
v3
（5） vs
（2）
（1） （1） （3） （3） v2
图10-24
fij （6） （3） vt （2）
v4
对于实际的网络系统上的流，有几个显著的特点：
截集为黄色弧集：
(V1 , V1 ) ( v 2 , v5 ) , ( v 2 , v4 ) , ( v 3 , v4 ), ( v 3 , v5 )
截集 ( V1 , V 1 ) 中所有弧的容量之和，称为这个截集 的容量，记为 C( V1 , V 1 ) ，也称截量，则有：

第5章图与网络分析163页PPT

第5章图与网络分析163页PPT

bi j 0wi j
(vi ,vj)E (vi ,vj)E
例6.4 下图所表示的图可以构造权矩阵B如下:
v1 4
v2
36
72
v6 4
3
3
v3
5
2
v5
v4
v1 0 4 0 6 4 3
v
2

4
0
2
7
0
0

B

v3
0
2
0
5
0
3
v4 6 7 5 0 2 0
v
5
4
17
v4
树与图的最小树
v1 23 v6
20
v2
1
4
v7
9
15 v3
28 25
16 3
v5
17
v4
v1
v2
23 v6
1
4
v7
9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23 v6
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
16 3
v5
17
v4
v1
②
15
9
7 ④ 14
⑤
①
10
19
20
6 ⑥
③
25
图的矩阵描述： 邻接矩阵、关联矩阵、权矩阵等。
1. 邻接矩阵 对于图G=（V，E），| V |=n， | E |=m，有nn阶方矩阵

第7章图与网络分析练习题及答案

第7章图与网络分析练习题及答案

第七章图与网络分析一、单项选择题1．关于可行流，以下叙述不正确的是（）A.可行流的流量大于零而小于容量限制条件B．在网络的任一中间点，可行流满足流人量=流出量C．各条有向边上的流量均为零的流是一个可行流D．可行流的流量小于或等于容量限制条件而大于或等于零2．关于最小树，以下叙述（）正确。

A.最小树是一个网络中连通所有点而边数最少的图B．最小树是一个网络中连通所有的点，而权数最少的图C．一个网络中的最大权边必不包含在其最小树内D．一个网络的最小树一般是唯一的。

3．最小树的算法关键是把最近的某些结点连接到那些已接结点上去，前者所指结点是（）A. 边缘结点B.未接结点C.已接结点D.最重要结点4.最小树问题就是在网络图中，找出若干条边，连接所有结点，而且（）A.连接的总长度最大B.连接的总长度最小C.连接的总长度为0D.计算总长度5．最小树问题就是在网络图中，找出若干条边，连接（）A.相邻结点B.头尾结点C.部分结点D.所有结点6．任一树中的边数和它的点数之间的关系是（）A.边数等于点数减1B.边数等于点数加1C.点数等于边数减1D.点数等于边数加17．最大流问题中，对于一个可行流，Vi Vj有向边上的流量fij必须满足的条件之一是（）A.0≤fij ≥cijB.0≥fij≤cijC. 0≤fij≤cijD.0≥fij ≥cij8.一个连通图中的最小树可能不唯一，其权（）A.是唯一确定的B.可能不唯一C.可能不存在D.一定有多个二、多项选择题1.关于图论中图的概念，以下叙述正确的的（）A.图中的边可以是有向边，也可以是无向边B.图中的各条边上可以标注权C.结点数等于边数的连通图必含圈D.结点数等于边数的图必连通E.图中的边只能是有向边2.关于最短路，以下叙述不正确的有（）A. 从起点出发到终点的最短路不一定是唯一的，但其最短路线的长度是确定的B．从起点出发到终点的最短路是唯一的C．从起点出发的有向边中的最小权边，一定包含在起点到终点的最短路上D．从起点出发的有向边中的最大权边，一定不包含在起点到终点的最短路上E．整个网络的最大权边的一定不包含在从起点到终点的最短路线上3.关于增广链，以下叙述正确的有（）A．增广链是一条从发点到收点的有向路，这条路上各条边的方向必一致 B．增广链是一条从发点到收点的有向路，这条路上各条边的方向可不一致 C．增广链上与发收点方向一致的边必是非饱和边，方向相反的边必是流量大于零的边D．增广链上与发收点方向一致的边必是流量小于容量的边，方向相反的边必是流量等于零的边E．增广链上与发收点方向一致的边必是流量为零的边，方向相反边必是流量大于零的边4.在下图中，根据（a）生成的支撑树有（）三、应用题1.下图是6个城市的交通图，为将部分道路改造成高速公路，使各个城市均能通达，又要使高速公路的总长度最小，应如何做?最小的总长度是多少?2．对下面的连通图，试求出最小树。

图与网络分析试题及答案

图与网络分析试题及答案

图与网络分析试题及答案一、填空题1．图的最基本要素是点、点与点之间构成的边2．在图论中，通常用点表示，用边或有向边表示研究对象，以及研究对象之间具有特定关系。

3．在图论中，通常用点表示研究对象，用边或有向边表示研究对象之间具有某种特定的关系。

4．在图论中，图是反映研究对象_之间_特定关系的一种工具。

5．任一树中的边数必定是它的点数减1。

6．最小树问题就是在网络图中，找出若干条边，连接所有结点，而且连接的总长度最小。

7．最小树的算法关键是把最近的未接_结点连接到那些已接结点上去。

8．求最短路问题的计算方法是从0≤f ij≤c ij开始逐步推算的，在推算过程中需要不断标记平衡和最短路线。

二、单选题1、关于图论中图的概念，以下叙述(B)正确。

A图中的有向边表示研究对象，结点表示衔接关系。

B图中的点表示研究对象，边表示点与点之间的关系。

C图中任意两点之间必有边。

D图的边数必定等于点数减1。

2．关于树的概念，以下叙述(B)正确。

A树中的点数等于边数减1 B连通无圈的图必定是树C含n个点的树是唯一的D任一树中，去掉一条边仍为树。

3．一个连通图中的最小树(B)，其权(A)。

A是唯一确定的 B可能不唯一 C可能不存在 D一定有多个。

4．关于最大流量问题，以下叙述(D)正确。

A一个容量网络的最大流是唯一确定的B达到最大流的方案是唯一的C当用标号法求最大流时，可能得到不同的最大流方案D当最大流方案不唯一时，得到的最大流量亦可能不相同。

5．图论中的图，以下叙述(C)不正确。

A．图论中点表示研究对象，边或有向边表示研究对象之间的特定关系。

B．图论中的图，用点与点的相互位置，边的长短曲直来表示研究对象的相互关系。

C．图论中的边表示研究对象，点表示研究对象之间的特定关系。

D．图论中的图，可以改变点与点的相互位置。

只要不改变点与点的连接关系。

6．关于最小树，以下叙述(B)正确。

A．最小树是一个网络中连通所有点而边数最少的图B．最小树是一个网络中连通所有的点，而权数最少的图C．一个网络中的最大权边必不包含在其最小树内D．一个网络的最小树一般是不唯一的。

最大流问题算法

最大流问题算法

最大流问题算法一、最大流问题简介最大流问题是图论中的一个经典问题，是指在给定一个有向图中，找到一个流量最大的流，从源节点流向汇节点的过程。

最大流问题在物流、通信网络、电力系统等领域有广泛的应用。

二、最大流问题算法分类2.1 Ford-Fulkerson算法Ford-Fulkerson算法是最大流问题的经典解法之一，基于增广路径的思想，通过多次寻找增广路径，不断增加网络中的流量，直到无法找到增广路径为止。

2.2 Edmonds-Karp算法Edmonds-Karp算法是对Ford-Fulkerson算法的一种改进。

它利用BFS（广度优先搜索）找出最短增广路径，从而加快了算法的收敛速度。

2.3 Dinic算法Dinic算法是一种高效的最大流算法，它基于分层图的思想，通过构建分层图和阻塞流的概念，有效地降低了算法的时间复杂度。

2.4 Push-relabel算法Push-relabel算法是一种基于预流推进和重贴标签操作的最大流算法。

它通过动态调整节点的剩余容量和高度来寻找最大流。

三、Ford-Fulkerson算法详解3.1 算法思想Ford-Fulkerson算法的思想很简单，即通过不断寻找增广路径，将增加的流量加到原有的流上，直到无法找到增广路径为止。

3.2 算法步骤1.初始化网络的流为0；2.利用DFS或BFS寻找一条增广路径；3.如果找到增广路径，则确定这条路径上的最小容量；4.增加流量，并更新网络中相关的容量；5.重复步骤2~4，直到无法找到增广路径。

3.3 算法复杂度Ford-Fulkerson算法的时间复杂度依赖于增广路径的选择策略。

最坏情况下，算法的时间复杂度为O(E * |f|)，其中E为边的数量，|f|为最大流的流量。

四、Dinic算法详解4.1 算法思想Dinic算法基于分层图的思想，通过构建分层图和阻塞流的概念，有效地降低了算法的时间复杂度。

4.2 算法步骤1.构建分层图，确定每个节点的层次，并初始化节点的过剩容量；2.通过DFS在分层图上寻找阻塞流，直到找不到增广路径为止；3.更新每个节点的过剩容量和残余网络的容量；4.重复步骤2~3，直到无法找到阻塞流。

网络最大流问题

网络最大流问题

中弧皆未饱 ，则称为D中关于可行流
中弧皆非零
f的
一条可增值链。
v2 （4，3） v4
（3，3）
（5，3）
vs
（1，1） （1，1）
（3，0）
vt
（5，1）
v1 （2，2）
（2，1）
v3
v2 （4，3）
v4
（3，3）
（5，3）
vs
（1，1） （3，0）
vt
（1，1）
（5，1）
v1
（2，2）
（2，1）
1、对增广链中的前向弧，令 f=f+q(t)，q(t) 为节点 t 的
标记值
2、对增广链中的后向弧，令 f=fq(t)
3、非增广链上的所有支路流量保持不变
第三步：抹除图上所有标号，回到第一步
例1 用标号法求下面网络的最大流。
[1,v ]
[1,v ]
1
2
（3，3） v2• （4，3） v•4 （5，3）
8(8)
2(0)
s
5(4)
(0, )
7(5)
9(9)
v2 (s,2)
v3 (v1,2)
5(5)
6(1)
10(8)
v4 (v3 ,1)
t (v4,1)
v1(v2 ,1) 9(5)
v3 (v1,1)
8(8)
s
5(3)
(0, )
7(6)
v2 (s,1)
5(5)
2(0)
6(0)
9(9)
k
10(9)
v4 (v3 ,1)
中国邮递员问题用图论的观点来看就是： 在 一个赋权连通图中，找一个过每边至少一次的闭链 （圈），并且使闭链的权最小。它的算法与一笔画 问题有关。

运筹学图与网络分析(高级课堂)

运筹学图与网络分析(高级课堂)

E
I
A
2 C
2
4
G
5
1S
2
3
3K
B2
2 F 2 26 J
D
H
高等课堂
26
[例]今有煤气站A，将给一居民区供应煤气，居民区各 用户所在位置如图所示，铺设各用户点的煤气管道所需 的费用（单位：万元）如图边上的数字所示。要求设计 一个最经济的煤气管道路线，并求所需的总费用。
E
I
A
2 C
2
4
G
5
1S
2
3
3K
例 ： G1为不连通图， G2为连通图
G1
高等课堂
G2
8
5、支撑子图
图G=(V，E)和G'=(V ' ，E ')，若V =V ' 且E ' E ，
则称G' 为G的支撑子图。
例 ：G2为G1的支撑子图
v5
v5
v1
v4 v1
v4
v2
v3
v2
v3
G1
G2
高等课堂
9
例 ： G2 是G1 的子图；
v2
e1 v1
H
高等课堂
24
[例]今有煤气站A，将给一居民区供应煤气，居民区各 用户所在位置如图所示，铺设各用户点的煤气管道所需 的费用（单位：万元）如图边上的数字所示。要求设计 一个最经济的煤气管道路线，并求所需的总费用。
E
I
A 3.5
2
C
2
4
G
5
1S
2
3
3K
B2
2 F 2 26 J
D
H
高等课堂
25
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D=（V，A，C，Vs，Vt）。
2、流量、可行流、流出量、流入量 ： （1）流量：是指定义在网络 D上的每一条弧上的一个
? ? 函数 f (a ) ? f (vi , v j ) ? { f i j } 其中f(vi ,vj) =fij 叫做弧(vi，
vj)上的流量。
（2 ）可行流 ：称满足下列条件的流为可行流：
14.00000
Variable
Value Reduced Cost
FLOW 14.00000
0.000000
C( S, 1) 8.000000
0.000000
C( S, 2) 7.000000
0.000000
C( 1, 2) 5.000000
0.000000
C( 1, 3) 9.000000
0.000000
v4
9 (3)
v3
5 (0)
4 (2) 4 (1)
v6
9 (5)
vt
10 (1)
图中 (v3 , v6 ) 为零流弧，其余为非饱和弧、非零流弧。
流量v(f ) =8
最大流
? 网络上的流量最大的可行流称作的最大流 ?所谓最大流问题就是求给定网络的最大流
（二）最大流的算法
1、由图编写程序
2、由lingo8.0 软件求最大流
C( 2, 4) 9.000000
0.000000
C( 3, 2) 2.000000
0.000000
C( 3, T) 5.000000
0.000000
C( 4, 3) 6.000000
0.000000
C( 4, T) 10.00000
0.000000
F( S, 1) 7.000000
0.000000
图与网络分析
(Graph Theory and Network Analysis)
赵芳玲
图论是运筹学的一个重要分支，它是建立 和处理离散类数学模型的一个重要工具。用图 论的方法往往能帮助人们解决一些用其它方法 难于解决的问题。图论的发展可以追溯到 1736 年欧拉所发表的一篇关于解决著名的“哥尼斯 堡七桥问题”的论文。由于这种数学模型和方 法直观形象，富有启发性和趣味性， 深受人们 的青睐。到目前为止，已被广泛地应用于系统 工程、通讯工程、计算机科学及经济领域。传 统的物理、化学、生命科学也越来越广泛地使 用了图论模型方法。
1）容量约束：对于每一个弧（ vi ,vj）∈A有 0 ? fij ? cij 。
2）守恒条件：对于所用的中间点 v ? V ? {vs , vt )
有
?
? f i j ?
f ji
(vi , v j )? E
(v j , vi )? E
顶点vi 的流
顶点vi的流
入量
出量
则称f 为D上的可行流。其流量 v(f )为
图与网络分析
(Graph Theory and Network Analysis)
图的基本知识 树及最小生成树 最短路问题 最大流问题 最小费用最大流问题
四、 最大流问题
（一）、 基本概念
1、网络：设一个 赋权有向图 D=（V, A）,在V中指定一
个发点 vs和一个收点 vt ,其它的点叫做中间点。对于 D中的 每一个弧（ vi , vj）∈A ,都有一个非负数 cij,叫做弧的容量 。我们把这样的图 D叫做一个容量网络，简称网络，记做
s,1 s,2 1,2 1,3 2,4 3,2 3,t 4,3 4,t/:c,f; endsets
s.t
? f ij ?
?
f ji
?
?? ?
v ?
f, vf
,
i? s i?t
j? V (i,j)? A
j? V ( j,i )? A
??0,
i ? s,t
data: c= 8 7 5 9 9 2 5 6 10;
F( 4, 3) 0.000000
1.000000
F( S, 2) 7.000000
0.000000
F( 1, 2) 2.000000
0.000000
F( 1, 3) 5.000000
0.000000
F( 2, 4) 9.000000
-1.000000
F( 3, 2) 0.000000
0.000000
F( 3, T) 5.000000
-1.000000
例8 现需要将城市 s 的石油通过管道运送到城市 t, 中间有4个中转站v1,v2,v3 和v4，城市与中转站的连 接以及管道的容量如下图所示，求从城市 s 到城市t
的最大流
v1
9
v3
8
5
2
s
5
6
t
7
v2
9
10 v4
v1
9
v3
8
5
s
5
2
6
t
7
v2
9
10 v4
附程序
max v f
MODEL: sets: nodes/s,1,2,3,4,t/; arcs(nodes,nodes)/
v( f ) ? ?
? f s j ?
f js
(vs , v j )? E
(v j , vs )? E
v( f ) ? ? f j t ? ? f t j(v j , v Nhomakorabea )? E
(vt , v j )? E
(发点vs )
(收点vt )
（3）饱和弧：可行流中 fij＝cij 的弧叫做饱和弧。
（4）非饱和弧： 可行流中fij＜cij的弧叫做非饱和弧。 （5）零流弧： fij＝0 的弧叫做零流弧。 （6）非零流弧 ： fij＞0 的弧为非零流弧。
0 ? f ij ? cij , (i,j) ? A
enddata
max = flow; @for(nodes(i)|i #ne# 1 #and# i #ne# @size(nodes):
程序结构
@sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=0); @sum(arcs(i,j)|i #eq# 1:f(i,j)) = flow;
1、集合定义部分（sets 到endsets)
@for(arcs:@bnd(0,f,c)); END
2、数据输入部分（data 到enddata) 3、其他部分（优化目标和约束）
Global optimal solution found at iteration: 6
Objective value:
例6 下图给出一个可行流 （容量约束、守恒条件）
5 (3)
v2
v5
13 (5)
6(3) 5 (2)
vs
4 (1) 5 (2)
v4
9 (3)
v3
5 (0)
4 (2) 4 (1)
v6
9 (5)
vt
10 (1)
例7 下图给出一个可行流
5 (3)
v2
v5
13 (5)
6(3)
5 (2)
vs
4 (1) 5 (2)