当前位置：文档之家 › 第四节 网络系统最大流问题

第四节 网络系统最大流问题

  • 格式：ppt
  • 大小：1.40 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

最大流问题

最大流问题

网络最大流问题一产生背景流量问题在实际中是一种常见的问题，在许多实际的网络系统中都存在着流量和最大流问题。

例如铁路运输系统中的车辆流，城市给排水系统的水流问题,控制系统中的信息流问题，常见的人流，物流，水流，气流，电流，现金流等。

在一定条件下,求解给定系统的最大流量,就是网络最大流问题.网络系统最大流问题是图与网络理论中十分重要的最优化问题，它对于解决生产实际问题起着十分重要的作用。

二基本概念与定理设cij为弧（i，j）的容量，fij为弧（i，j）的流量。

容量是弧（i，j）单位时间内的最大通过能力，流量是弧（i，j）单位时间内的实际通过量，流量的集合f={fij}称为网络的流。

发点到收点的总流量记为v=v(f)。

设D=(V,A)是一有向图且对任意E均有容量cij =（vi，vj），记C={cij︱（vi，vj）∈A},此外D中只有一个源vs和汇vt( 即D中与vs相关联的弧只能以vs为起点，与vt相关联的弧只能以vt为终点)，则称D=(V,A,C, vs,vt)为一网络。

引例1：图1给出了一张网络，其中：vs为源，vt为汇，弧旁的数字为该段弧的容量cij与流量fij，则显然有0≤fij ≤ cij 。

v2 （3,3) v4（3,3）（5,5）vt (2,2) (2,2) (2,2) vt(6,4) (6,2)v1 (6,6) v3图1最大流问题可以建立如下形式的线性规划数学模型。

图1最大流问题的线性规划数学模型为12max 0(,)0s s ij ij j i ij ij v f f f f i s t f c =+⎧-=≠⎪⎨⎪≤≤⎩∑∑所有弧(i,j)由线性规划理论知，满足式上式的约束条件的解{fij}称为可行解，在最大流问题中称为可行流。

可行流满足下列三个条件：(1)0(2)(3)i j i j m j i m j i sj it vs vt f cf fv f f ≤≤===∑∑∑∑条件（2）和条件（3）也称为流量守恒条件。

网络最大流问题

网络最大流问题

V2 (4,3) Vs (4,2) (8,2) V1
(4,0) (1,1)
V4 (7,2) (6,0) Vt
(2,2) (2,2) V3
(9,3)
现在的问题是： 1) 从Vs到Vt的运输量是否可以增多？ 2) 从Vs到Vt的最大运输量是多少？
1 基本概念
(一)容量网络和网络流
1) 容量网络：D=(V,A,C) 设D是一个简单有向图( D=(V,A) )。在V中指定了一个 顶点，称为源点(记为Vs)和另一个顶点，称为汇点(记为 Vt)，对于每一条弧(Vi,Vj)∈A，对应有一个Cij＞0，称 为弧的容量。通常我们就把这样的D叫做一个容量网络， 记作D＝(V,A,C)。 2) 网络流 – 流量：通过D中弧(Vi,Vj)的物流量fij，称为弧(Vi,Vj)上 的流量。 – 网络流：所有弧上流量的集合f={fij}称为该网络D的 一个网络流。
V2
(4,0) (1,1)
V4
(4,3)
Vs (4,2) (8,2) V1
(7,2)
(6,0) Vt (b) (9,3) V3
(2,2) (2,2)
在图(b)中，弧旁边括号中的两个数字(Cij,fij)，第1个数字 表示弧容量，第二个数字表示通过该弧的流量。弧(Vs,V1)上 的(8,2)，前者是弧容量，表示可通过该弧最大流量的能力 为8，后者是目前通过该弧的实际流量为2。 从图(b)中可见：1)通过每弧的流量均不超过弧容量；2) 源点vs流出的总量为3+2=5，等于流入汇点vt的总量2+3=5； 3)各中间点的流出量等于其流入量。中间点v2的流出量减去 其流入量等于0,即3-(2+1)=0
(4,3)
Vs (4,2)
(8,2)

第4节 网络最大流问题

第4节 网络最大流问题

(v i , v j ) u
[-v1, 1] v
Vs
（4,3）
2
[-v v4 2, 1]
Vt
[v4, 1]
[0, +∞]
[vs, 4]v1 Nhomakorabea（2,2）
[-v2, 1]
调 整 （4,4）
v3
v2 Vs v1
v4 Vt
（2,2）
v3
v2
（4,4）
v4
Vs
Vt
[0 ,+∞]
v1
（2,2）
v3
[vs, 3]
[-v1 , 1]
v2
（4,3）
v4
Vs [0 , +∞] （2,2）
Vt v1 v3
[vs , 4]
(3)考虑所有弧(vi , vj)或(vj , vi) ,其中vi∈ VA, vj∈ VB，若该弧为
流出未饱弧,则给vj标号[vi , θj],其中θj=min{θi, cij- fij}
流入非零弧,则给vj标号[-vi , θj] ,其中θj= min{θi, fij}
Vi 所有点
未标号 未检查
Vi
标号 未检查
标号 考查 （Vi, Vj) 检查 Vj 标号 未检查
所有
标号点 检查
注: 给发点Vs标上（0，＋∞），则Vs成为标号未检查
网络最大流问题—标号法
1.标号过程 给vs标上(0，+∞)，这时vs是标号而未检查点，其余为 未标号点。 若在弧(vi，vj)上，fij<cij，则给vj标(vi，l(vj))， 其中 l v j min l vi , cij fij 若在弧(vj，vi)上，fji>0，则给vj标(-vi，l(vj))， 其中l v j min l vi , f ji vi成为标号而已检查过的点，重复上述步骤，

运筹学-图论4

运筹学-图论4

3、增广链
对可行流f={fij}：
非饱和弧：fij<Cij 非零流弧：fij>0
饱和弧：fij=Cij 零流弧：fij=0
链的方向：若µ是联结vs和vt的一条链，定义链的
方向是从vs到vt。 v2
5.2
v4
10.5
3.2
11.6
v1
4.1 5.1
8.3
v3
6.3
3.3
v6
17.2
v5
前向弧：弧的方向与链的方向一致，前向弧全体记为µ+。
V5
4、截集与截量
设S，TV，ST= ，始点在S，终点在T中 的所有弧的集合，记为（S，T）。
S
T
定义4 网络D=（V，A，C），若点集V被剖分为两个 非空集合V1和V1，使vs∈V1，vt ∈ V1，则把弧集
（V1，V1）称为是分离vs和vt的截集。
v2
10.5
v1
4.1
8.3
v3
5.2
3.2 5.1
(1，1)
（0，∞）vs
(1，1)
(5，1)
（s，v14） (2，2)
v4
(5，3)
(3,0) vt
(2，1)
v3
（4）检查v2，在弧（v3，v2）上，f32=1>0， 给v3标号
(-2, l(v3)), 这里 l(v3) min l(v2 ), f32 min 1,1 1,
（-1，1）
v2
(4，3)
6.3
v4
11.6
3.3
v6
17.2
v5
V1 =(v1,v2,v3)
V1=(v4,v5,v6)
v2
10.5

10.4 网络最大流问题

10.4 网络最大流问题

9 (5)
v1
9 (3)
v4
v7
10 (1)
v3
v6
V 设 V1 v1 ,v2 ， 2 v3 , v4 , v5 , v6 , v7 则截集为 (V1,V2) (v1v3 ), (v2 , v4 ), (v2 , v5 )
截量为20
v1 8(8) s 7(5) 5(4)
图10-24表示的就是这个网络上的一个流（运输方案），
每一个弧上的流量fij就是运输量。 例如：f12=1 , f13=2 , f24=3 等等。
v1
（2）
v3
（5） vs
（2）
（1） （1） （3） （3） v2
图10-24
fij （6） （3） vt （2）
v4
对于实际的网络系统上的流，有几个显著的特点：
f2>0 s f4<c4 t
f1<c1
f3>0
f5<c5
v2
10-5 3-2 4-1 5-1
5-2
3-3
v4
11- 6
v1
8-3
v6
17-2
v3
µ 1,v2,v3,v4,v5,v6) =(v
6-3
v5
后向弧
+ µ ={(v1,v2) ,(v2,v3), (v3 , v4),(v5,v6)} µ ={(v5,v4)}
v(f ) C( V1 , V1 )
即任何一个可行流的流量都不会超过任一截集的容量
若对割 ( V , V ) 和割 V , V ) (
用
f(V，V) 表示割中所有 V V 方向的弧的流量的总和， f (V，V) 表示割中所有 V V方向的弧的流量的总和，

最大流问题

最大流问题
vs
33
v2
43 1
v4
5 1 1 v1
1 22
3 0
1
3
vt
2
51
v3
2 标号法(Ford-Fulkerson算法）
算法思想:
首先得到一条可行流。
然后在可行流的基础上,寻找增广链.如果 找到,得到新的流量更大的可行流; 如果找不 到，说明当前的可行流就是最大流。 由于可行流的流量不能无限增大，因而总 可以得到最大流。
33 (0, M) vs 5 2
v2 1 0
4 4
v4 5 3 0 1 v3 4
11
22
vt
2
v1 (vs, 3) 33 (0, M) vs
v2
1 0
4 3
10 22 3 0
v4 5 3
5
vt
2 2
2 v1 (vs, 3) v3
最大流问题应用举例
下图中，A,B,C,D,E,F分别表示陆地和岛屿，①，②，…，14 表示桥梁及其 编号。若河两岸分别为互为敌对的双方部队占领，问至少应切断几座桥梁 （具体指出编号）才能达到阻止对方部队过河的目的。试用图论方法进行分 析。 3 1 2 12 A
v4
(0, M) vs
33
5 1 0 1
v1
1 22
3 0
1 v3 (-v2, 1)
4 (v , 1) 3 4
vt
51 2
2
(vs, 4)
第二步：再标号过程
33 (0, M) vs 5 v2 1 0 4 4 11 22 v4 5 3 0 1 v1 (vs, 3) v3 4
vt
2
2
最大流可能有多条
最大流问题

网络最大流问题

网络最大流问题

专题六图与网络分析Graph & Network Analysis 6.1 图与网络的基本知识6.2 树6.3 最短路问题6.4 网络最大流问题6.4 网络最大流问题如何充分利用和有效提升现有网络资源的能力，使系统的流量达到最大并有效运行？➢引例如图是连结某物资产地至销地的铁路运输网，弧上的数字表示该路段的最大通过能力，现在要求制定一个运输方案，使从运到的该物资数量最多。

v 5v 3v sv 2v 4v 6v t43103854317493283532140581313s v t v s v t v➢基本概念与基本定理：◆网络与流网络：，其中; ;，称为弧的容量，为中间点集流：定义在网络弧上的一个函数或(),,D V A C ={},,=s t Vv I v (){},i j A v v ={}|0ij ij C c c =≥ij c I(),i j f v v ijfGP/ORv 5v 3v sv 2v 4v 6v t43103854317493283532140581313◆可行流与最大流可行流：满足以下条件的流为可行流。

(1)容量限制条件:(2)中间点的平衡条件：流入量＝流出量(3)发点的总发量最大流：网络D 上流量最大的可行流称为最大流。

f 0ij ijf c ≤≤s v ()()()()t v f =v 收点的总收量-v fGP/OR()()()(),()0(,)()0(,1,2,,1;2,3,,)ij i j ij ij ji j j ijM ax v f A v f i s st i s t v f i t i s t j t f c v v f f f ⎧≤∈⎪⎪=⎧⎪⎪⎪−=≠⎨⎨⎪⎪−=⎩⎪⎪≥=−=⎪⎩∑∑◆可行流与最大流的关系：最大流问题实际上是一个特殊的线性规划问题，即求一组,在满足可行流的条件下使得达到最大，其数学模型：{}ij f ()v fGP/ORv 5v 3v sv 2v 4v 6v t4310385431749328353214058◆增广链（增流链）【术语】若给一个可行流,则有饱和弧﹠非饱和弧零流弧﹠非零流弧{}ij f f =()ij ij f c =()ij ij f c <()0ij f =()0ij f >v 5v 3v sv 2v 4v 6v t4310385431749328353214058若 是网络D 中从起点到终点的一条链，链上的弧分为两类：前向弧：弧的方向与链的方向一致后向弧：弧的方向与链的方向相反s v t v◆增流链：设是一个可行流，μ是一条从到的链，若μ上所有的前向弧均为不饱和弧，所有的后向弧均非零流弧，则μ称为关于可行流的增流链（增广链）。

第四节最大流问题

第四节最大流问题

1． 标号过程
在标号过程中，网络中的点或者是标号点（分为已 检查和未检查两种）。或者是未标号点。每个标号点 的标号包含两部分：第一个标号表示这个标号是从那 一点得到的。以便找出增广链。第二个标号是为了用 来确定增广链上的调整量θ。 标号过程开始，先给 vs 标号（ 0 ， +∞ ）。这时 vs 是 标号未检查的点，其他都是未标号点。一般地，取一 个标号未检查点vi，对一切未标号点vj：
fij ,当（vi v j ) ， 令fij fij , 当（vi v j ) 其他不变
再去掉所有的标号，对新的可行流f’={f’ij},重新 进行标号过程，直到找到网络D的最大流为止。
V2 （4,3）
（3,3） （1,1）
V4

三．标号法


从网络中的一个可行流 f 出发（如果 D 中没 有f，可以令f是零流），运用标号法，经过标号 过程和调整过程，可以得到网络中的一个最大流。 用给顶点标号的方法来定义 V1*. 在标号过程 中，有标号的顶点是 V1* 中的点，没有标号的点 不是 V1* 中的点。如果 vt 有了标号，表示存在一 条关于f 的增广链。如果标号过程无法进行下去， 并且vt 未被标号，则表示不存在关于f的增广链。 这样，就得到了网络中的一个最大流和最小截集。
(Cij,fij)
（5,3）
Vs
（5,1）
（3,0）
（1,1）
Vt
（2,1）
V1
（2,2）
V3
图8.21





例8.8: 求图8.21的网络最大流，弧旁的权数 表示（cij,fij）。 解.用标号法。 1.标号过程。 （1）首先给vs 标号（0，+∞） （2）看vs:在弧(vs,v2)上,fs2=cs3=3,不具备标号 条件。在弧 (vs,v1) 上 ,fs1=1<cs1=5, 故给 v1 标号 (vs, l(v1)), 其中 l(v1)=min[l(vs),(cs1-fs1)]=min[+∞,51]=4. （3）看v1:在弧（v1,v3）上,f13=c13=2,不具备标 号条件 . 在弧 (v2,v1) 上 ,f21=1>0, 故给 v2 标号（ -v1, l(v2)）,其中l(v2)=min[l(v1),f21]=min[4,1]=1.

网络最大流问题

网络最大流问题
vs
v1
vt
v3
2
1
3
1
4
5
3
2
5
7.4.1 网络的最大流的概念 网络流一般在有向图上讨论 定义网络上弧的容量为其最大通过能力，记为 cij ，弧上的实际流量记为 fij 图中规定一个发点s，一个收点t 节点没有容量限制，流在节点不会存储 容量限制条件：0 fij cij 平衡条件：
v4
v2
vs
v1
vt
v3
（2，2）
（1，1）
（3，3）
（1，1）
（4，3）
（5，1）
（3，0）
（2，1）
（5，3）
（3） 截集与截量
截量：截集上所有弧的容量和，记 。
例4 对于下图，若V1={vs，v1}，请指出相应的截集与截量。
v4
v2
vs
v1
vt
v3
（2，2）
（假如邮递员从V1点出发，求他的最优投递路线。
4
4
4
4
4
5
9
6
5
5
V1
3
2
V9
V4
V3
V2
V8
V7
V6
V5
解：
考虑加边的圈：V1, V2, V9, V8 中，加边的长度是4+6=10，而不加边的长度是4+5=9 ，故需改进如下。
4
4
4
4
第一步：标号过程，找一条增广链 1、给源点 s 标号[s+,q(s)=]，表示从 s 点有无限流出潜力 2、找出与已标号节点 i 相邻的所有未标号节点 j，若 (1) (i, j)是前向弧且饱和，则节点 j 不标号； (2) (i, j)是前向弧且未饱和，则节点 j 标号为[i+,q(j)]， 表示从节点 i 正向流出，可增广 q(j)=min[q(i),cijfij] ； (3) (j, i)是后向弧，若 fji=0，则节点 j 不标号； (4) (j, i)是后向弧，若 fji>0，则节点 j 标号为[i,q(j)]， 表示从节点j 流向i，可增广 q(j)=min[q(i),fji] ；

《网络最大流问题》PPT课件

《网络最大流问题》PPT课件
《网络最大流问题》PPT课件
本课件仅供大家学习学习 学习完毕请自觉删除
谢谢 本课件仅供大家学习学习
学习完毕请自觉删除 谢谢
第六章 图与网络分析
第一节 图的基本知识 第二节 树 第三节 最短路问题 第四节 网络最大流问题 第五节 最小费用最大流问题
第四节 网络最大流问题
图10-23是联结某产品产地v1和销地v6的交通网，每一
给vt标号为(v4, l(vt))，这里 l(vt)＝min[l(v4), (c4t- f4t)]=min[1, 2]=1
因vt有了标号，故转入调整过程。
(3,3) (0,+∞) vs
(5,1)
v2 (-v1,1) (4,3) v4 (v2,1) (5,3)
(1,1) (1,1) (3,0)
vt (v4,1)
(3,3)
(5,3)
(0,+∞) vs (5,1)
(1,1) (1,1)
(3,0) vt (2,1)
v1 (vs,4) (2,2) v3
(4) 检查v2。
在弧(v2，v4)上，f21=3， c24=4，f24< c24，则给
v4标号(v2, l(v4)) 。
l(v4) = min[l(v2), (c24- f24)]=min[1, 1]=1 在 弧 (v3 ， v2) 上 ， f32=1>0 ， 给 v3 标 号 ： (-v2,
便不存在路。所以，截集是从vs到的vt必经之路。
定义5 给一截集(V1, V)__，1 把截集(V1, )中V__1 所有弧的 容量之和称为这个截集的容量(简称为截量)，记为
c(V1, )，即V__1
cV1,V1
cij
(vi,vj)(V 1,V1)

最大流问题算法

最大流问题算法

最大流问题算法最大流问题算法介绍最大流问题是在网络流中的一个重要问题，它是指在一个有向图中，给定一个源点和汇点，每条边都有一个容量上限，求从源点到汇点的最大流量。

最大流问题有很多应用，如交通网络、电力系统、通信网络等。

本文将介绍最大流问题的算法。

Ford-Fulkerson算法Ford-Fulkerson算法是最早提出的解决最大流问题的方法之一。

该算法通过不断地增广路径来寻找增广路，并更新残留网络中的边权值。

具体步骤如下：1. 初始化残留网络：对于原图G(V, E)，构造残留网络Gf(V, Ef)，其中Ef包含所有满足c(u, v)>0或f(u, v)>0的(u, v)。

2. 寻找增广路：在残留网络中寻找从源点s到汇点t的增广路。

3. 更新残留网络：根据增广路更新残留网络中的边权值。

4. 重复步骤2和3直到不存在增广路为止。

该算法存在多种实现方式，如DFS、BFS等。

Edmonds-Karp算法Edmonds-Karp算法是Ford-Fulkerson算法的一种特殊实现方式，使用BFS来寻找增广路。

该算法的时间复杂度为O(VE^2)，其中V和E分别为原图G(V, E)的顶点数和边数。

Dinic算法Dinic算法是一种基于分层图的最大流算法，它通过构造分层图来寻找增广路。

该算法的时间复杂度为O(V^2E)，其中V和E分别为原图G(V, E)的顶点数和边数。

Push-Relabel算法Push-Relabel算法是一种基于预流推进的最大流算法，它通过不断地调整节点之间的流量来求解最大流。

该算法存在多种实现方式，如FIFO、HL等。

其中HL算法是一种比较优秀的实现方式，它将节点按照高度进行划分，并使用桶来管理节点。

总结以上介绍了最大流问题的四种常见算法：Ford-Fulkerson、Edmonds-Karp、Dinic和Push-Relabel。

这些算法各有优缺点，在实际应用中需要根据具体情况选择合适的算法。

运筹学课件第四节最大流问题

运筹学课件第四节最大流问题

fij
fi j t , (vi , v j ) fi j t , (vi , v j )
一f．○i j令调, (整v过i ,程v j )不在可增广链
○ 但是，如果vt 被标上号，表示得到一条增广链μ，转入下一
步调整过程。
例 求图的网络最大流，弧旁的权
数表示（cij , fij）。
S
量，记为C(S, ) 。
v1
2
4 3
1 v3 2
2
vs
2
3
4 3
v4
v2 4 vt
边集{(vs,v1),(vs,v3),(vs,v4)} 边集{(vs,v1),(v1,v3),(v2,v3),(v3,vt)} 为图的割集，割集容量分别为11，9
最大流-最小割定理
定理10：设f为网络G=（V，E，C）
v1
(5,5) vs
(4,2)
v2
(3,2)
v3
(5,2)
v4
(3,3) v5
(3,3)
(2,2)
(2,2)
v6
(4,2) vt
(5,4)
v1
(5,2)
v4
(5,5)
(+ vs,2) (3,3)
(4,2)
vs
(∆ ，+∞)
(4,2)
v2
(3,2)
v5
(3,3)
(2,2)
vt
(5,4)
v3
(2,2)
(- v5,2)
(+ v1,2)
v1
(5,2)
v4
(5,5)
(+ vs,2) (3,3) (+ v2,2) (4,2)
vs
(∆ ，+∞)

第四节---最大流问题

第四节---最大流问题
第四节 最大流问题
• 最大流问题是一类应用极为广泛旳问题，例如在交通运送网 络中有人流、车流、货品流，供水网络中有水流，金融系统 中有现金流，通讯系统中有信息流，等等。50年代福特 （Ford）、富克逊（Fulkerson）建立旳“网络流理论”， 是网络应用旳主要构成部分。
一、最大流有关概念
• 假点如，u我1,u们2 ,把u3,图u45-4为1中年转做站输，油边管上道旳网数，表us达为该起管点道，旳ut 最为大终
属于 S, S ，满足：① G V , E E不连通；②E为E
旳真子集，而G V , E E 仍连通，则称 E为G旳割
集，记 E S, S 。
• 割集 S, S 中全部始点在S，终点在 S 旳边旳容量 之和，称为 S, S 旳割集容量，记为 C S, S 。如图 5-41中，边集 vs ,v1 ,v1,v3 ,v2,v3 ,v3,vt ,v4,vt 和边集 vs ,v1 ,vs ,v3 ,vs ,v4 都是G旳割集，它们
输油能力，问应该怎样安排各管道输油量，才干使从 us
到 ut 旳总输油量最大？
• 管道网络中每边旳最大经过能力即容量是有限旳，实际 流量也不一定等于容量，上述问题就是要讨论怎样充分 利用装置旳能力，以取得最佳效果（流量最大），此类 问题一般称为最大流问题。
•（定非称汇义负为）2发数，0点称其设（c他有i源j为点向）边为连，容中通一量间图种，点G出仅，次有这V为一么, E0种旳旳,Gr网点入旳络次每vG为t条称称0边为为旳上容收点有量点vs
44，调整后旳可行流见图5-45。
• 重新开始标号过程，寻找可增广链，当标 到 v3 点为 vs ,1后来，与 vs , v3 点邻接旳 v1, v2, v6 点都不满足标号条件，所以标号无法再继续， 而 点并vt 为得到标号，如图5-45。

网络最大流问题

网络最大流问题

给定一个有向图D=(V,A)，在V中指定一点称为发点（记为），该点只有出发去的弧，指定另一点称为收点（记为），该点只有指向它的弧，其余的点叫做中间点。

对于A中的每一条弧，对应一个数（简记），称之为弧的容量。

通常我们把这样的D叫做网络，记为D=(V,A,C)。

（2）网络流：在弧集A上定义一个非负函数。

是通过弧的实际流量，简记，称是网络上的流函数，简称网络流或流，称为网络流的流量。

§4 网络最大流问题网络最大流问题是网络的另一个基本问题。

许多系统包含了流量问题。

例如交通系统有车流量，金融系统有现金流，控制系统有信息流等。

许多流问题主要是确定这类系统网络所能承受的最大流量以及如何达到这个最大流量。

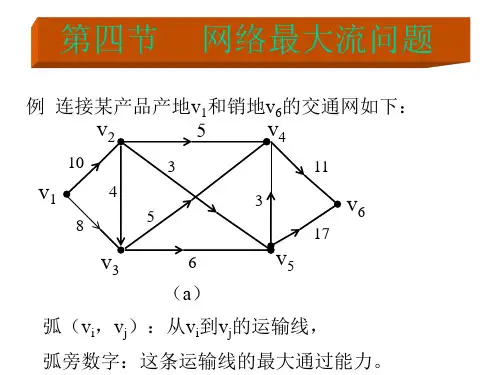
4.1 基本概念与定理1．1．网络与流定义14 （1）网络：例1如图7-20是连结某产品产地和销地的交通图。

弧表示从到的运输线，弧旁的数字表示这条运输线的最大通过能力，括号内的数字表示该弧上的实际流。

现要求制定一个运输方案，使从运到的产品数量最多。

可行流与最大流在运输网络的实际问题中，我们可以看出，对于流有两个基本要求：一是每条弧上的流量必须是非负的且不能超过该弧的最大通过能力（即该弧的容量）；二是起点发出的流的总和（称为流量），必须等于终点接收的流的总和，且各中间点流入的流量之和必须等于从该点流出的流量之和，即流入的流量之和与流出的流量之和的差为零，也就是说各中间点只起转运作用，它既不产出新的物资，也不得截留过境的物资。

因此有下面所谓的可行流的定义。

定义14对于给定的网络D=（V,A,C）和给定的流，若满足下列条件：（1）容量限制条件：对每一条弧，有(7.9)（2）平衡条件：对于中间点：流出量=流入量，即对于每一个i (i≠s,t)，有(7.10)对于出发带点，有(7.11)对于收点，有(7.12)则称为一个可行流，称为这个可行流的流量。

注意，我们这里所说的出发点是指只有从发出去的弧，而没有指向的弧；收点是指只有弧指向，而没有从它的发出去的弧。

8.4_最大流问题

8.4_最大流问题

v3 ( v s ,1)
则称弧
集 (V1 , V1 ) 为分离发点 v s 和收点 v t 的割集(截集).
• 给定一割集 (V1 , V1 ) ,割集(V1 , V1 ) 中所有弧的容量之和称为
此割集的容量,简称割量,记作 C (V1 , V1 ),即
C (V1 , V1 )

( v i , v j ) ( V1 ,V1 )

的方向为 v s v t ,则链上的弧被相应地分为两类：
前向弧：弧的方向与链 的方向一致.

{前 向 弧 }
的方向相反. {后 向 弧 } 后向弧：弧的方向与链
• 设f 是一可行流, 是从 v s 到 v t 的一条链, 若 满足：
1） 上前向弧均为非饱和弧 ( v i , v j ) , 0 fij cij .
15
( v1 , v 2 ), ( v 3 , v 5 ) ( v 2 , v 4 ), ( v 2 , v 5 ), ( v 3 , v 5 )
( v1 , v 3 ), ( v 2 , v 3 ), ( v 2 , v 5 ), ( v 4 , v 5 ), ( v 4 , v 6 )
A
且 且
f ij c ij
,则令 j ,则令 j
m in { c ij f ij , i } ,
给 v j 标号( v i , j ) ,否则不标号.
A
f ij 0
m in { f ij , i } ,
给 v j 标号( v i , j ) ,否则不标号.
f
*
是最大流的充要条件是不存在关于流
的增广链.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 2
5 6
6 0
7
V6
V 8 V 10
V3
6 10
V5
前向弧： 1 min{Cij fij } 2
后向弧：
2
min{ 1 , 2 } 2
V2
8 8
5 5 3 2 5
1
V4
10 19
4
V1
2 2
5 6
6 0
7
V6
V 8 V 10
而对于实际问题来说，通常需要求最大流．
那么，如何求最大流呢？ 最大流可以从任何一个可行流出发来求．
这需要下面的可扩充路的概念．
定义 6.17 设 { fij }是一组可行流，如果存在一 条从起点V1 到终点V 的路P，满足 ①在P的所有前向弧上 0 fij Cij ( fij Cij ) ( fij 0) ②在P的所有后向弧上 0 fij Cij 则称P是一条关于流 { fij }的可扩充路．
对于P的所有后向弧 (0 fij Cij ) (若P无后向弧，则令 2 ) 令 2 min{ fij }
再令 min{ 1 , 2 }
最后，构造新的可行流 { f ij }, 使得
f ij fij fij
f ij
若弧 (Vi ,Vj )不在路P上 若弧 (Vi ,Vj )是路P的前向弧 若弧 (Vi ,Vj ) 是路P的后向弧
V3 V2
8
8
6 10
V5 V4
5
1
2 5
最大流不唯一
7
3 0 6 6
19
4
V1
2 2
6 3
7
V6
V 10
V3
7 10
V5
求最大流的方法：
从零流开始或者从某一取值的已知可行流 开始，选取不同的可扩充路，确定调整量ε， 不断提高可行流的值，最后得到最大流．
求可扩充路的方法：（标号法）
首先，标号法把顶点分为两种类型：已标 号的和未标号的；已标号的又分为两种类 型：已检查的和未检查的． 标号：
n
V2
7
5 5 3 0 5
1
V4
8
19
2
8
V1
2 2
6
6
1
V6
7

V3
3 10
V5
定义 6.17 设 { fij }是一组可行流，如果存在一 条从起点V1 到终点V 的路P，满足 ①在P的所有前向弧上 0 fij Cij ( fij Cij ) ( fij 0) ②在P的所有后向弧上 0 fij Cij 则称P是一条关于流 { fij }的可扩充路．
§6.4
最大流问题
例1：某公司要从起始点 vs 发送货物到目的 地 v t ，其网络如下图所示．图中每条弧旁边 的权表示这段运输路线的最大通过能力。要 求指定一个运输方案，使得从 vs 到 v t 的运货 量达到最大．
v1
60 50 30 40 50 50
v4 v5
vs
70 70 30 40
50 30 80
n
V2
7
5 5 3 0 5
1
V4
8
19
2
8
V1
2 2
6
6
1
V6
7

V3
3 10
V5
定理 6.4 对于一组可行流 { fij }来说，如果能 找到一条可扩充路P，那么 { fij }就可以改进 成一个值更大的可行流． 证明过程就是改进可行流的过程： 对于P的所有前向弧 (0 fij Cij ) ) 令 1 min{Cij fij } (若P无前向弧，则令 1
v2
40 50
vt
30 30 70 30 40
v3
vs 为起点，v t 为终 例2：下图是输油管道网， 点，其余点为中转站，弧上的数字表示该管 道的最大输油能力，问应如何安排各管道的 输油量，才能使从 vs 到 v t 的总输油量最大？
11
5 5
4 4
v1
5 4
2 3 2
v4
4 4
vs
3
v2
3 1
7
19
4
V1
2
1
6 0
7
V6
V3
6 10
V5
1. v1 , v6 称为起点和终点，其余的点称为中间点； 2. 每条弧对应一个数字 Cij ，称为弧容量； 3. 在实际问题中，每条弧都会有一个实际 流量 fij 构成网络 G 上的一个流．
网络 G
6 8
V2
2 5
V4
5
1
3 2 6 6
7
19
4
V1
2
1
V1 V2 V5 V6 逆向追踪得可扩充路：
求可扩充路的步骤： 1、给起点 V1 标号 V1 (0, )； 2、如果终点 Vn 已标号，则转向第5步； 3、对于已标号而未检查的点，转入第4步； 此时如果标号过程进行不下去，则算法结束， 所得可行流即为最大流；
4、对第3步已标号未检查的点进行检查；
3 3
2 2
v5 v6
vt
5 2 2
2
v3
2
以上两例都属于最大流问题． 最大流问题的应用非常广泛． 例如，在交通运输网络中有车流、 货物流；供水系统中有水流；金融系统 中有现金流； 通信系统中有信息流等 等． 下面首先介绍一下最大流问题的有 关概念．
网络 G
6 8
V2
2 5
V4
5
1
3 2 6 6
V2
6 8
2 5
V4
5
1
3 2 6 6
7
19
4
V1
2
1
6 0
7
V6
V 7
V3 V2
7
6 10
V5 V4
5
1
5 5 3 0
8
19
2
8
V1
2 2
2 6
6
1
V6
7
Байду номын сангаас
V 9
V3
3 10
V5
V2
8
8
2 5
V4
5
1
7
3 0 6 6
19
4
V1
2 2
6 3
7
V6
V 10
V3
7 10
V5
最大流
一个网络可能有多种可行流，值最小的可 行流显然是零流：fij 0 ．
min{ 1 , 2 } 1
fij
f ij f ij f ij
若弧 (Vi ,Vj )不在路P上 若弧 (Vi ,Vj )是路P的前向弧 若弧 (Vi ,Vj ) 是路P的后向弧
V2
8 6 8
5 3 5 3 2 5
1
V4
10 8 19
4
V1
6 0
7
V6
V3
6 10
V5
可行流
定义 6.16 称满足下述条件的流为网络G的一 个可行流：
①容量限制条件：0 fij Cij ②平衡条件：
可行流的值
起点和终点：起点的净流出量=终点的净流入量；
中间点：流入总量=流出总量．
值最大的可行流称为最大流． 最大流问题就是找出某网络值最大的可行流．
5、逆向追踪得可扩充路．
请练习
171页
习题六
第5题
n
V2
6 8
4 5
V4
5
1
3 0
2
7
19
2
V1
2 2
6
6
1
V6
7
√
V3
3 10
V5
定义 6.17 设 { fij }是一组可行流，如果存在一 条从起点V1 到终点V 的路P，满足 ①在P的所有前向弧上 0 fij Cij ( fij Cij ) ( fij 0) ②在P的所有后向弧上 0 fij Cij 则称P是一条关于流 { fij }的可扩充路．
如果原可行流 { fij }的值是 V , 则新可行流 { f ij } 的值是 V .
V2
6 8
3 5 2 3 2 5
1
V4
7 8
19
4
V1
2
1 2
5 6 6
6 0
7
V6
V 7 V 8
V3
6 10
V5
前向弧： 1 min{Cij fij } 1
后向弧： 2 min{ fij } 6
V3 (2、 )
(V2 ,V3)是
V3来自V2
前向弧
检查：如果和Vi相连接的所有顶点都已 经获得标号，就称Vi已检查．
V2
6 8 3 2 6 6
1
5 2 5
1
V4
7
19
4
V1
2
6 0
7
V6
V3
6 10
V5
V4 (2, ) V2 (1, ) V1 (0, ) V5 (2, - ) V6 (5, ) V3 (1, )